What is a moment? Transient synchrony as a collective mechanism for spatiotemporal integration

Abstract

A previous paper described a network of simple integrate-and-fire neurons that contained output neurons selective for specific spatiotemporal patterns of inputs; only experimental results were described. We now present the principles behind the operation of this network and discuss how these principles point to a general class of computational operations that can be carried out easily and naturally by networks of spiking neurons. Transient synchrony of the action potentials of a group of neurons is used to signal “recognition” of a space–time pattern across the inputs of those neurons. Appropriate synaptic coupling produces synchrony when the inputs to these neurons are nearly equal, leaving the neurons unsynchronized or only weakly synchronized for other input circumstances. When the input to this system comes from timed past events represented by decaying delay activity, the pattern of synaptic connections can be set such that synchronization occurs only for selected spatiotemporal patterns. We show how the recognition is invariant to uniform time warp and uniform intensity change of the input events. The fundamental recognition event is a transient collective synchronization, representing “many neurons now agree,” an event that is then detected easily by a cell with a small time constant. If such synchronization is used in neurobiological computation, its hallmark will be a brief burst of gamma-band electroencephalogram noise when and where such a recognition event or decision occurs.

How is information about spatiotemporal patterns integrated over time to produce responses selective to specific patterns and their natural variants? Such integration over time is a fundamental component of sensory perception. Information must of course also be integrated over space, but this problem is understood much better: for example, visuospatial information is encoded initially in the retina through a “labeled line” code (1) whereby individual retinal ganglion cells respond only to stimuli in a restricted part of visual space (their receptive field). Integration over space is then a straightforward matter of converging inputs from cells with different receptive fields. In contrast, the fundamentals of how temporal information is represented and how it can be integrated remain mysteries. This problem exists particularly for timescales longer than a few tens of milliseconds, at which point transmission delay times can no longer be used as biologically plausible building blocks for bringing information from different times together (2, 3). Integration over times on the order of 0.5 sec or longer in biologically plausible networks is a principal focus of our report. The principles underlying such integration over time, in fact, belong to a broader and more general class of computations.

The ideas will be illustrated by studying a particular case of recognizing spatiotemporal patterns of events. Short spoken words can be encoded into such a representation by detecting features in different frequency bands of a spectrogram (4, 5). The specific example used in the previous companion paper (paper 1; ref. 6), and used here again, will be that of recognizing the spoken word “one” after it has been encoded into a spatiotemporal pattern of events.

The Natural Coding of Time in Decaying Delay Activity.

Neuronal responses to transient stimuli decay with a wide variety of different timescales, ranging from tens of milliseconds to tens of seconds. At the longest timescales, the activity is often referred to as “delay activity” (7–10). When such activity decays with time, the ratio of the present activity to the activity at initiation implicitly encodes the time that has elapsed since the initiating event occurred. Thus, time, on many different scales, is encoded naturally, if implicitly, at many levels of processing in the nervous system.

Consider a set of decaying activities where the initial firing rate for each neuron is the same for all events that are able to trigger that neuron. Then the neuron's firing rate is, by itself, an implicit measure of time since the triggering event. We will describe how a network of spiking neurons can carry out computations on such a representation of time. In the discussion section, we will describe briefly how to generalize to the situation in which the initial firing rates are not stereotyped.

Recognizing a Spatiotemporal Pattern.

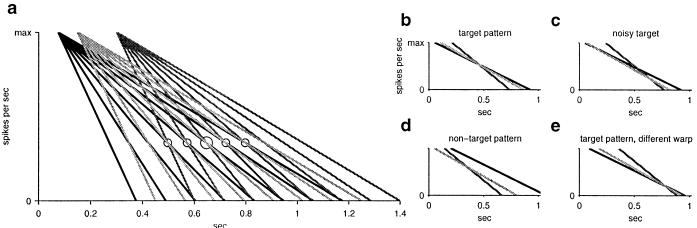
We wish to recognize whether a pattern of space–time events described by a set of times t_i lying within an interval of ≈0.5 sec approximately match with a model of events t_i^m. Only relative time differences within each pattern are important—the overall time at which the test pattern of events occurs is arbitrary. We will refer to each index i as an “input channel.” Consider a pattern composed of three events, one in each of three channels. One event occurs at 0.075 sec, one at 0.150 sec, and one at 0.300 sec. Let each of these events trigger a set of currents with a variety of fixed decay rates, illustrated in Fig. 1a. Now suppose that this pattern (0.075, 0.150, 0.300) is the target pattern to be used as a model. It is possible to select three decay rates, one per channel, that generate currents that reach almost the same level at some time t_r (rings in Fig. 1a). There are many possibilities for t_r, but once t_r (larger ring in Fig. 1a) has been picked, the set of decay rates is unique (selected currents shown in Fig. 1b). When the pattern of input event times is close but not identical to the target pattern, the selected currents will be triggered at times such that the convergence neck is not a point but is still small (Fig. 1c). When the input pattern has no relationship to the target pattern, there is no such convergence (see Fig. 1d). Thus, the degree of convergence of these currents is an indicator of the degree of similarity to the original pattern.

Figure 1.

Time-warp invariant convergence of decaying currents. (a) Decaying currents triggered by events in three different channels: one current at 0.075 sec, one at 0.15 sec, and one at 0.3 sec. Responses for different channels are shown in different shades of gray. The rings identify points at which three currents, one for each channel, converge. (b) The converging currents for the three currents selected by the larger ring in a. (c) An input pattern that is a noisy version of the target pattern. (d) A temporal pattern very different from the target pattern. (e) A time-warped version of the original pattern.

How can the convergence of current levels be detected? Suppose each of the selected currents drives an integrate-and-fire neuron. Synaptic connections between neurons that have similar firing rates often produce synchrony between the action potentials of these neurons (11, 12). When the input pattern matches the model, the currents driving the neurons will converge at some point in time, the firing rates of the driven neurons will then be similar, and synaptic coupling between neurons should lead to strong transient synchronization of their action potentials near this time. When the input pattern is very different from the model, there will be no convergence of input currents and firing rates, and therefore, there will be little synchronization. Thus, transient synchronization of neurons with convergent firing rates is the fundamental recognition event. The precise degree of synchronization depends on how close together the firing frequencies are, the strength of coupling between the neurons, and the number of neurons involved.

Invariance with respect to some parameters is often a desirable feature of recognition systems (e.g., recognizing the identity of a face independent of its spatial scale or recognizing an odor independent of its overall concentration). The convergence of current levels contains a natural invariance. When the target pattern is rescaled in time (time-warped) and presented to the system, the selected currents converge (Fig. 1e), albeit at a different common level. We have illustrated this point in Fig. 1 by using linear decays, but as we will now show, the result holds more generally, including exponential decays. A uniform time-warp by a scale factor s changes the intervals {t_i − t₂, t₂ − t₃, … } to the pattern {s(t₁ − t₂), s(t₂ − t₃)}. Suppose that after an event at time t_i, the currents that respond to this event with a variety of decay times τ_j are a function only of the variable (t − t_i)/τ_j. That is, there is a universal form function f ((t − t_i)/τ_j) for the decaying currents, and the different decay rates are obtained by having different values of τ_j. For each input channel i, we choose a decay time τ_i such that the currents from the different channels are all of the same at time t_r: (t_r − t_i)/τ_i = (t_r − t₁)/τ₁ for all i. But for an input pattern scaled by s, it is also true that (st_r − st_i)/τ_i = (st_r − st₁)/τ₁ for all i, so the same set of currents with the same decay rates will reach a point again at which they are all equal (although the time and level at which they meet will be different from the case of s = 1). This result, which does not depend on the form of the decay function f(), is what makes the time-warped example of Fig. 1e still have a convergence, even though the warp-factor s is quite different from unity. The degree of convergence of current levels is a time-warp invariant indicator of degree of similarity to the original pattern.

The recognition can be described in terms of a pattern match of times of occurrence t_i with a model for these events t_i^m. The match is carried out including an arbitrary scaling factor s and an arbitrary shift t_shift. Events present in the model but missing in the presented pattern merely decrease the size of the signal at recognition, and thus require a better match of other times to generate recognition. When most of the events agree on t_shift and s, events that greatly disagree essentially are ignored, viewed as not even occurring. The essence of the algorithm implemented can be described mathematically by finding the maximum over s and t_shift of the function

Recognition score = Σ_i W((st_i − t_i^m − t_shift)² + W²)⁻¹.

The sum is carried out over all channels i that contain events both in the model and in the incoming pattern. W is a width parameter determined by the strength of the synaptic coupling in the synchronizing system. The particular functional shape of the terms in the sum is arbitrary. This form of recognition score is extended readily to more elaborate systems with multiple events within a single channel, to weighting events differentially, and to having events that are inhibitory in character.

Experiments on Speech

Paper 1 was a demonstration of these ideas applied to speech. There, sound waveforms were transformed into spatiotemporal patterns of events by detecting onsets, offsets, and peaks of power within various frequency bands. There were 40 different input channels, each of which corresponded to a particular detector type (i.e., onset, peak, or offset) and frequency-band combination. An event on any one of these channels was analogous to one of the events shown in Fig. 1a and triggered the start of a set of slowly decaying currents, of which there were 20 for each channel. With 40 channels, this made a total of 800 different input lines. The full set of 800 such inputs was labeled in paper 1 as “inputs from area A.” Most speech files had events on all 40 channels; thus, typically all 800 input lines were activated in response to any single speech file. Each one of these 800 input currents was used to drive a single excitatory and a single inhibitory cell in a pool of otherwise-identical integrate-and-fire neurons that were labeled in paper 1 as “α (excitatory) and β (inhibitory) neurons of area W.” Each of the smooth input currents from area A can be thought of as the sum of the inputs from a large set of closely similar unsynchronized neurons. Responses of single area A neurons were illustrated in figure 4 of paper 1.

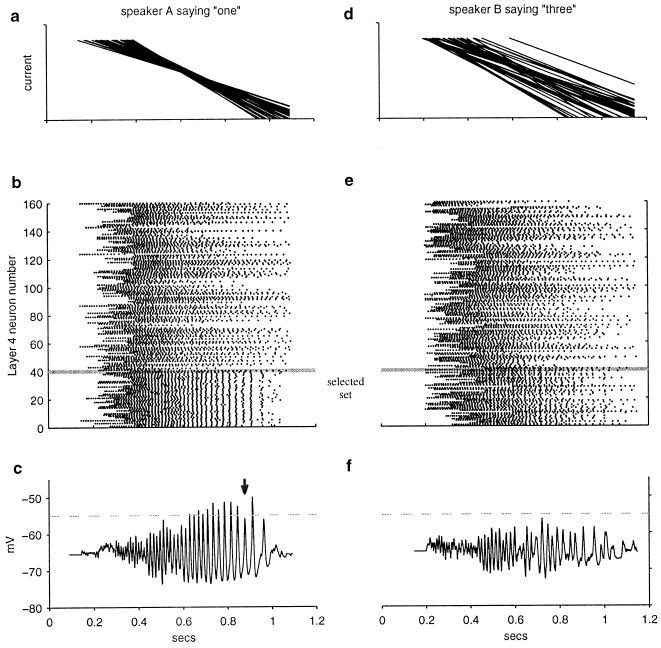
“Training” the network to recognize a particular template of spatiotemporal events consisted simply of selecting a set of α and β neurons that would have converging firing rates in response to the target template (analogous to selecting the large ring in Fig. 1a) and creating mutual all-to-all connections within this set. Importantly, the strength of excitation and inhibition in the all-to-all coupling within this set was balanced, such that even when many neurons were driven by speech, the net input current to a cell came chiefly from its input from area A. All of the excitatory connections were made equally strong, and all of the inhibitory connections were made equally strong. The fast excitatory synapses and longer-duration inhibitory synapses then led the neurons to synchronize in response to the target template. These neurons also synchronized in response to input patterns that were similar, although not identical, to the template and in response to time-warped versions of the template (Fig. 2 a and b). Time-warp invariance was a key component of the ability to generalize from a single example. In contrast, stimuli that were significantly different from the target template did not lead to convergence of the neurons' firing rates (Fig. 2d), and in this case, the neurons did not synchronize strongly (Fig. 2e). The selected set of excitatory and inhibitory neurons was also connected directly to an output neuron (labeled as a γ cell in paper 1). When the neurons synchronized, the γ cell received a high-amplitude oscillating input current that drove it to fire in a characteristic burst of 30–60 Hz (Fig. 2c). When the neurons synchronized weakly or not at all, the γ cell was not driven to fire (Fig. 2f).

Figure 2.

Synchronization indicates recognition of an input pattern that is a similar (within time warp) version of the target pattern. (a) The 40 currents from area A that converge in response to the target template. Here, they almost converge near t = 0.6 sec in response to a pattern similar but not identical to the target. (b) Spike rasters of responses of 160 α or β neurons. Each dot represents an action potential, and each row corresponds to a single neuron. Shown below the gray line, 40 of the neurons belong to the selected set, driven by the currents shown in a, that corresponds to the target pattern. Note the neurons' synchronization. The other 120 neurons (above the gray line) are drawn randomly from the rest of the population of α and β neurons. (c) Intracellular potential of the γ neuron that receives input from the selected set of α and β neurons. The γ neuron spiking threshold has been set to infinity here to allow full observation of the synaptically driven membrane potential; γ neuron-firing threshold is normally −55 mV (horizontal dashed line). Synchronized input leads to strong oscillations and many threshold crossings. Random fluctuations in the oscillation amplitude can lead to occasional “missing” γ spikes (arrow). (d, e, and f) Same format as in a, b, and c in response to a nontarget pattern. (d) Input currents do not converge. (e) Neurons synchronize only weakly. (f) γ cell does not fire.

Very strong oscillatory drive can generate close doublets of action potentials on each cycle, with separations little more than the absolute refractory period. We have seen such doublets in all cell types.

Possible Enhancements.

Two enhancements to the system, one having to do with multiple events and one with the role of negative evidence, improve the performance of the system on speech and probably in other pattern recognition problems. For simplicity, we refrained from implementing these enhancements in paper 1. In the system described, once a cell in area A was launched on its stereotyped response, it continued that response until the end of its decay. A second event of the same type occurring within the response time of this cell was simply ignored. The system functions better when the information carried by second or further events is not lost, even if the events occur within the response time. This goal can be achieved by having a pool of cells of each type in area A, with each having a small probability (for example, 0.3) of being activated when its appropriate feature arises. In this case, two different sets of neurons (statistically) will be turned on at two different times by two features of the same type, even though they occur close together in time. When two features of the same type occur within a given word, both features can then contribute to the recognition.

A second enhancement is in regard to the fact that events at particular times may sometimes be evidence against recognition of a target pattern. For example, a particular event occurring at a particular time might be characteristic of a pattern that is similar to, but different from, the target. By using slightly modified inhibitory synaptic biophysics, such negative contributions to the recognition computation can be included easily in the framework we have described. Let the new inhibitory synapses have a fast, almost instantaneous rise time similar to the excitatory rise time, but let them still have a slower decay constant of 6 msec. Keeping total excitation and inhibition currents balanced means that the initial peak current caused by simultaneously activated excitatory and inhibitory synapses will still be excitatory. This early excitation was the key feature that enabled rapid synchronization, so the network of cells will still synchronize. Now let the α and β cells that correspond to a negative-evidence event receive the usual input from the other positive-evidence cells. These negative-evidence cells will synchronize then with the positive-evidence cells if their input from area A drives them at the right time. Finally, connect the negative-evidence β cells to the γ cell and the positive-evidence cells with the fast-rise-time inhibitory synapses described above, but connect the negative-evidence α cells to the γ cell and positive-evidence cells with slow excitatory synapses (e.g., N-methyl-D-aspartate synapses). Then the fast part of the synaptic current received from the synchronized negative-evidence α–β cells will be inhibitory. This method will make the γ cell less likely to fire and inhibit the synchronization of the positive-evidence cells. This enhancement is possible because in a system of synchronizing neurons, details of synapse time response and membrane time constants can strongly affect the computation that will be performed.

We have carried out explorations that suggest that, with these two enhancements, interesting discrimination is achievable even with connected speech and speech-like noise in the background.

Properties and Extensions of the Recognition System.

Multiple patterns.

Embedding multiple patterns within the same network of α and β neurons is straightforward. In paper 1, we trained for the template that corresponded to an example of the spoken word “one.” In addition, we then trained for 9 other randomly chosen templates [lists of 40 times drawn independently from a uniform distribution in the range (0, 0.5)]. This training was done by simply adding the synaptic connections between α and β cells that corresponded to each successive template if the connections did not already exist. At the end of this process, each α or β neuron was a member of the selected set of, on average, 1.45 target patterns. (The final number of α and β neurons in the network was less than 800, because neurons that did not participate in any patterns were deleted.) Nevertheless, when testing with one pattern, the overlap between the different sets did not cause a disabling spread of synchronization to neurons participating in patterns other than the one presented (see rasters of neurons above the gray line in Fig. 2b). In a small set of exploratory experiments, we have successfully embedded 25 random patterns in the network so each α or β cell participated, on average, in the memory of more than 2 patterns. In this regime, excitatory and inhibitory currents caused by the numerous recurrent synaptic connections between α or β neurons are larger than the input currents from area A, but the cells still synchronize selectively for their input patterns. The capacity, however, is limited. In the limit of an infinite number of embedded patterns, all α and β cells are connected to each other, and the neurons synchronize under all circumstances. The transition between the two regimes (selective synchronization in response to specific patterns, “epileptic” synchronization in response to all patterns) seems to have the nature of a phase transition. We also tried selectively deleting the few α or β neurons that, in any particular instantiation of the network, randomly happened to participate in the largest number of patterns. When this deletion was done, the number of embeddable patterns per cell that could be stored before reaching the epileptic regime was made substantially larger. Thus, the topology of the patterns and connections between them seems highly relevant to the capacity of the network.

Extensions.

The properties of the system we have described do not critically depend on the details of its construction. In this sense, there is a large “space” of neural circuits with properties similar to the ones demonstrated. For example, the system described had a balance between excitation and inhibition, achieved by having both excitatory and inhibitory cells driven from area A. However, an equivalent balance can be achieved in a neural circuit in which area A drives only α cells, and the inhibitory β cells receive input only from α cells. We have shown in simulations that such a system works as well as the one described, even when using cell properties such that the inhibitory cells show little synchronization.

Balance prevents the corruption of the basic input information arriving at the α and β cells (i.e., the input currents from area A) by the recurrent synaptic inputs that are essential to generate the collective synchronization. Balance between excitation and inhibition is important in the present network when multiple patterns and multiple γ cells are to be supported by the same set of α and β cells. (An unbalanced system may also be useful in some contexts.) Balanced excitation and inhibition has been proposed as the mechanism behind the irregular firing of cortical cells (13–15). Brief explorations with large networks have shown that even at large noise levels that lead to characteristically irregular firing of single α−β cells, network-level collective synchronization, practically undetectable at the single or paired neuron level, still can occur.

In paper 1 and our multiple pattern experiments described above, all excitatory synapses from α cells onto α and β cells were equally strong, and all inhibitory synapses from β cells were equally strong. Similar simplifications were made in connections to γ cells. This arrangement was arbitrary. That large random variations in synaptic strengths (see paper 1) did not affect the recognition is a strong indicator that the pattern of connections, not the detailed synaptic strengths, is the key to pattern-selective synchrony. Fine-tuning for optimality would involve synapses having a range of strengths.

Discussion.

To learn to recognize a pattern, the synaptic strengths must change as a result of pre- and postsynaptic cell activity. The kind of relationship between synapse change and the neuronal activity that is desirable for recognizing a new pattern is closely related to known neurobiological temporal-learning protocols. If α and β cells are connected to γ cells with initial excitatory and inhibitory synapses, the γ cells will not be driven until the α and β cells develop collective synchrony. When this happens, γ cells will fire just after the α cells do, and plasticity protocols that have been described experimentally (16, 17) will lead to strengthening and pruning appropriate for α to γ cell synapses. For developing appropriate α-to-α connections, slightly more complex learning rules are necessary: for example, a synaptic enhancement requiring the occurrence of two to four near coincidences (but not on average, by a single near coincidence) between consecutive action potentials of the pair of cells, with both cells firing each time, over a time period of ≈0.1 sec, would be very powerful. This event will be common when two cells are firing at almost the same rate and would be generated by the temporal crossing of the firing rates of a pair of cells; it is unlikely otherwise. Synaptic modifications caused by crossing firing rates seem not to have been studied experimentally.

The stereotyped response strengths used in paper 1, in which area A neurons responded with the same initial firing rate regardless of the intensity of the event that triggered them, are not common in biology, but are also not necessary in the present system. If the initial amplitudes of the signals from area A are a function of the salience of the events, all scaling together when the events are more salient, the convergence properties that led to synchronization and pattern selectivity are preserved. Such a system has two scalar invariants to its recognition process: invariance with respect to time-warp and invariance with respect to pattern salience. More clever encodings of signals into responses of area A cells could lead to the ability to generate convergence and transient synchronization with more complex invariants.

The mammalian olfactory bulb shows strong gamma-band local electroencephalogram behavior (18), and there is evidence in lower systems for the role of synchrony and of oscillation in olfactory pattern discrimination and learning (19). In mammals, each of ≈2,000 glomeruli has an input that is proportional to the time-dependent odor strength during a sniff, with a proportionality coefficient that depends on the type of receptor cells that impinge on that glomerulus. To form a collective synchronizing system of the type described here in response to a time-varying input (20), it is essential to link together mitral cells which transiently receive the same strength of synaptic input. A given odor will drive different glomeruli with different strengths. These two facts need not contradict if the different mitral cells driven by a single glomerulus have systematically different responses to the drive of that glomerulus, either in the current that they receive from that glomerulus or in their threshold characteristics. The 1:25 ratio of glomeruli to mitral cells then would have the computational function for olfaction that the 20 different time decays in area A have for the speech problem.

There is potential for analytical treatment of the transient synchronization in special cases. An “effective field” treatment, exact only in the limit of infinite N, will be quantitatively useful for large but finite N, the biological case, and has some prospect for treating the real dynamical problem in which the distribution of input currents is broad, then narrows, and returns to being broad. For studying such effects, the system can be simplified through amalgamating α and β cells into a single cell type with a synaptic current that sums the excitatory postsynaptic current and inhibitory postsynaptic current. Indeed, the simplest biological network of this sort may be a set of mutually connected inhibitory neurons coupled by synapses and gap junctions (21).

Conclusion.

Many possible roles have been suggested for synchrony (19, 22–25). Here we have focused on the description of a mechanism by which transient synchrony may arise and a computational algorithm that exploits this mechanism. The fundamental observation made in this paper was that because weakly coupled neurons with similar firing rates can easily synchronize (11, 12), neurons with transiently similar firing rates can transiently synchronize, and this transient synchronization can serve as a powerful computational tool. Detecting transiently similar firing rates is an operation that is carried out very naturally and easily by networks of spiking neurons: simple mutual connections between neurons suffice to carry it out. The resulting collective synchronization event, which might be described as a “MANY VARIABLES ARE CURRENTLY APPROXIMATELY EQUAL” operation, is a basic computational building block. An understanding of transient synchrony as a computational building block allowed the design of a network that displayed time-warp-invariant spatiotemporal pattern recognition of real-world speech data. The recognition event in this network was a collective transient synchronization effective in repeatedly driving an otherwise silent γ neuron. Stimulus-dependent synchrony in computational networks of neurons or neuron-like elements has been previously described (e.g., ref. 26), but generally with respect to static patterns that do not involve temporal integration or transient synchrony.

Just as integrate-and-fire neurons can be thought of as naturally implementing a fuzzy “AND” or fuzzy “OR” operation (depending on the settings of the cell's parameters), networks of appropriately configured spiking neurons naturally implement a fuzzy “MANY ARE NOW EQUAL” operation. This operation can serve many computational roles in addition to the one demonstrated here. For example, it could be used to segment two odors that fluctuate independently in time (20), or the output of the γ cells themselves could be turned again into a smooth current, on which further computational operations could be carried out. The MANY ARE NOW EQUAL synchronization operation may be as fundamental and general a computational building block at the level of spiking neuron networks as the firing threshold is in single spiking cells.

Networks of neurons in which excitation and inhibition are roughly balanced, often described in the computational neuroscience literature (13–15), can carry out computation easily by transient synchronization on top of and separately from the encoding of information in the neurons' firing rates.

When neurons are arranged in an orderly fashion, synchronized activity in a cell type is expected to produce a burst of gamma-band electroencephalogram. One could be led easily to wonder to what extent the frequently observed local burst of γ activity (27) can be associated with decisions of the type described here.

Connectionist modeling of higher nervous function is based often on nonspiking units, the characteristics of which are inspired by approximate rate-model properties of single neurons. Such units are used typically to represent many individual neurons, averaged into a single effective processing unit. In contrast, the collective effects and decisions we have presented here cannot be described in a similar fashion. That is, the higher-level mathematical description of a decision by a group of synchronizing neurons bears no resemblance whatsoever to the mathematical description of a single neuron. Hydrodynamics serves as a useful analogy: we know that the mathematics of aerodynamics relevant to airplane design cannot be described in terms of huge “effective molecules” colliding with an airplane wing. Similarly, we wonder how much of higher nervous function will be usefully describable with the mathematics of sigmoid units as its basis.

Appendix

How did the single unit results of paper 1 Point the way? We have claimed that the experimental information presented in paper 1 was sufficient to deduce the principles of operation behind the system. Now we describe one deductive chain that leads ineluctably from the experiments to the principles. Examining the implications of the raw basic data, and not merely relying on a conventional and incomplete summary of that data (in this case, the peristimulus time histogram), is key to finding the computing principle of this system.

What could be responsible for the spike rasters of a γ cell in a recognition event consisting of a slow burst of 3–8 action potentials at 30–60 Hz? (i) Bursting could be an intrinsic cellular property caused by complex biophysics, (ii) the input current could rise briefly from below threshold to a nearly fixed plateau, or (iii) the input current could itself contain the rhythm and have a strong 30- to 60-Hz oscillation.

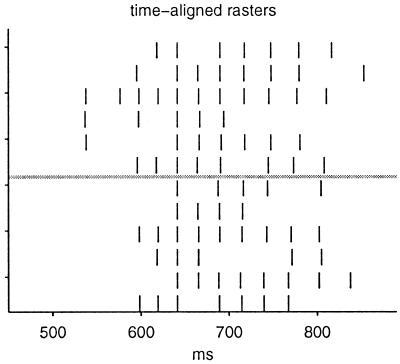
Because the γ neurons are simple leaky integrate-and-fire neurons, they do not have an intrinsic ability to generate bursts making i impossible. The slow bursts must be caused by synaptic currents. A comparison of the different rasters of a single file shows compellingly that ii cannot be the case. Most of the spikes of one raster correspond well to spikes in another if small shifts are made in the time axis, except that some of the spikes seem to be missing. Fig. 3 shows six spike rasters from paper 1's figure 1a (Upper) and six rasters from figure 1c (Lower) time-shifted by small arbitrary amounts into alignment. All of these spike trains are virtually identical except for occasional missing spikes. Noise fluctuations in a fairly steady current would produce fluctuating intervals and a loss of registry between different rasters after a short time because of accumulated differences rather than an appearance of missing spikes and doubled or even quadrupled interspike intervals. These γ cell spike rasters cannot be due to a nearly constant input current plateau plus noise.

Figure 3.

Aligned spike rasters from figure 1 a and c of paper 1.

We are left with only the third possibility, which then must be true, as Sherlock Holmes said (28). Given the size of excitatory postsynaptic potentials, the firing rates of the α cells at the time of recognition, and the number of excitatory synapses impinging on a γ cell, above-chance overlaps of excitatory postsynaptic potentials are necessary to drive a γ cell. The burst must be due to almost periodic pulses of total synaptic input currents caused by roughly synchronous, almost periodic spiking of the α and β cells that drive this γ cell. When an utterance is not recognized, the synchronization of α and β activity must be at a lower level. Missing spikes are now logical in the presence of noise fluctuations, because the rhythm of the transient coherent oscillation in the α and β system will continue even though its amplitude fluctuates (see arrow in Fig. 2c). Given this observation, the entire question of how the system “computes” must involve the collective synchronization of the subset of α and β neurons that drive a γ cell.

In order for α and β neurons to fire synchronously for more than one spike, their interspike intervals must be similar; therefore, the net input current to the two neurons must also be similar. This analysis immediately suggests looking for crossings of the inputs from area A, as in Fig. 1, and this in turn leads to reasoning that completes an understanding of the principles of operation of the system, including time-warp invariance.