Special phase transformation and crystal growth pathways observed in nanoparticles†

Abstract

Phase transformation and crystal growth in nanoparticles may happen via mechanisms distinct from those in bulk materials. We combine experimental studies of as-synthesized and hydrothermally coarsened titania (TiO₂) and zinc sulfide (ZnS) with thermodynamic analysis, kinetic modeling and molecular dynamics (MD) simulations. The samples were characterized by transmission electron microscopy, X-ray diffraction, synchrotron X-ray absorption and scattering, and UV-vis spectroscopy. At low temperatures, phase transformation in titania nanoparticles occurs predominantly via interface nucleation at particle–particle contacts. Coarsening and crystal growth of titania nanoparticles can be described using the Smoluchowski equation. Oriented attachment-based crystal growth was common in both hydrothermal solutions and under dry conditions. MD simulations predict large structural perturbations within very fine particles, and are consistent with experimental results showing that ligand binding and change in aggregation state can cause phase transformation without particle coarsening. Such phenomena affect surface reactivity, thus may have important roles in geochemical cycling.

Introduction

The transformation of structure between stable or metastable phases reveals basic thermodynamical information about the state of matter. Consequently, investigations into the phase stability of nanoparticles have given some of the clearest demonstrations of the differences between nanoscale and bulk material of the same stoichiometry. For example, a reversal in phase stability at small particle size is observed in some systems; [1-4] melting temperatures are generally lower in nanoparticles;[5] transition temperatures to high temperature phases are often lower,[6] while transition pressures to high pressure phases can be higher [7-9] or lower.[10]

By now, it is clear that the phase diagrams for materials can be size dependent.[11] Using the concepts of classical thermodynamics, observed size dependencies can be associated with the large surface area present in nanoscale materials. In particular, the excess energy of a nanoparticles relative to that of the bulk material (normalized by the surface area) is defined as the surface energy (usually in J m^-2). Many of the observed data can be explained once surface energy contributions are considered. Yet, this quantity is difficult to measure accurately, and depends on the details of both surface and interior structure. The excess energy need not be confined to the surface: the effect of finite size on interior structure is currently a topic of interest.[12,13]

In the field of nanoscience, it is generally difficult to translate specific experimental observations and thermodynamic principles into a precise quantitative theory of energy and structure. Structural and thermodynamic experiments are complicated by the fact that nanoparticles are metastable with respect to macroscopic crystals: ultimately, extremes of temperature or pressure, and aggregation, will lead to coarsening. An additional consideration is that conditions on both sides of the nanoparticle/environment interface are significant.

In this review, we show how classical thermodynamics can be combined with microscopic predictions from molecular dynamics (MD) simulations to consider the energetics and phase stability of two nanoparticle systems. In addition, non-equilibrium kinetic theory allows growth and phase transformation processes to be understood, revealing novel transformation mechanisms. We principally review work performed by this group on titanium dioxide (TiO₂) and zinc sulfide (ZnS), environmentally significant model systems that are also relevant due to the utility of these materials as fine metal oxide catalysts and semiconducting electrooptic materials, respectively.

We first consider nanoparticle growth, followed by examples of phase transitions accompanying growth. The final topic is structural transition without growth, stimulated by changes in surface environment. Overall, this review illustrates the significance of the surface in considerations of thermodynamic phase stability, and highlights the significance of particle–particle contacts for interpretation of the kinetics of transformation and growth.

Methods

Theory and modelling

1. Phase stability

We seek to understand the stability of a particular nanoparticle structure of a certain size. For a given temperature and pressure, this requires minimization of the Gibbs free energy (G(p, T) for bulk materials). The original calculation of the surface contribution to the free energy of a small particle is due to Gibbs.[14,15] In a similar treatment we can write an expression for G(p, T, γ), where γ is an interfacial free energy. If the nanoparticles are kinetically stable against coarsening or dissolution, we can write:

G(p, T, γ) = E - TS + (p + p')V + γA + other terms     (1)

where T and p are ambient temperature and pressure, p' is an excess internal pressure associated with strain at the surface;[2] A is the surface area. The other terms include additional contributions at the surface, such as edge or defect free energies. An expansion γ = c₁ + c₂/r, where c₁ and c₂ are constants and r is the particle radius, is sometimes adopted to empirically include the additional terms.[8] From eqn. (1), it is clear that an evaluation of γ is required for consideration of phase stability at small particle sizes. Furthermore, changes in the nanoparticle environment can be directly included in this description by modification of γ.

Experimental determination of interfacial free energy of solids is difficult,[17] and theoretical approaches are an attractive alternative. In MD calculations, the interactions between atoms are usually parametrized as pair potentials.[16] Static (low temperature) or dynamic (300 K or higher) energetic relaxation of the common termination surfaces of bulk crystals allows calculation of surface energy. [18-20] The errors in equating surface energy with surface free energy are expected to be small.[17] Combining these values with known, or assumed crystal habits provides average surface free energy values for different phases that can be used to predict the variation in phase stability with particle size.

Empirical and theoretical studies (below) have shown that the size dependence of the relative phase stability of polymorphs often follows the trend given in Fig. 1. Below a critical size, D_c, one of the bulk metastable phases becomes thermodynamically favored. For ZnS, bulk sphalerite is stable relative to wurtzite by ΔG_bulk ≈ 13 kJ mol^-1, and a stability inversion is predicted to occur for particle sizes below D_c ≈ 7 nm (in vacuum).[18] For TiO₂, bulk rutile is stable relative to anatase by ΔG_bulk ≈ 67 kJ mol^-1, and the predicted D_c ≈ 14 nm,[22] in good agreement with experimental observation.[23] An additional important result of MD simulations is that the free energy curves may be modified in the presence of alternative solvents or vacuum. The simulations show that, in the presence of surface water, the calculated phase stability inversion for ZnS is shifted to smaller particle sizes, or absent all together.

Figure 1.

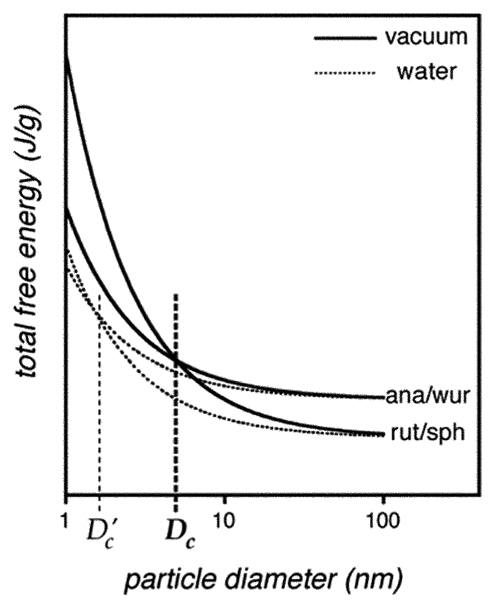
Illustration of the particle size dependence of the total free energy of two phases. The diagram is appropriate for the materials studied in this paper. At room temperature and pressure, for TiO₂, rutile is the bulk stable phase, anatase the metastable phase. For ZnS, sphalerite is the bulk stable phase and wurtzite the metastable phase. Solid lines: vacuum environment, dotted lines: aqueous environment. Below particle diameter D_c in vacuum, a phase stability crossover occurs. In the presence of water, the phase stability crossover is shifted to diameter D_c' <D_c.

2. Mechanisms of growth and phase transformation

Due to the extremely low solubility of TiO₂ and ZnS, suspensions of capped (organic ligand coated) or uncapped nanoparticles are kinetically stabilized against dissolution-based coarsening at room temperature. For example, the size of aqueous ZnS nanoparticles in pure water at room temperature is unchanged in XRD determination for at least six months. (However, increasing the ionic strength of the solution leads to much more rapid coarsening.) Uncapped particles carrying surface charge (and, generally, capped nanoparticles) are kinetically or thermodynamically stable against aggregation.[24] If the ionic strength of the room temperature solution containing ZnS nanoparticles is increased, aggregation occurs and is accompanied by coarsening. At elevated temperatures, or if aggregation can occur, nanoparticle growth may be observed, with coarsening kinetics characteristic of the pathway.

For nanoparticles in solution, the mechanism of crystal growth may be surface precipitation of solvated atoms or few-atom clusters (diffusion-based), or crystallographically-specific aggregation-based growth (oriented aggregation) involving whole nanoparticles.[12] For ZnS, hydrated species may be Zn₁S₁,[25] or Zn₃S₃ and Zn₄S₆.[26] Diffusion-based growth is called Ostwald ripening, and the kinetics are described further below. Aggregation-based growth has been described mathematically by Smoluchowksi.[27] It includes consideration of whether successful coalescence accompanies every contact, or whether the probability of coalescence is less than unity per collision, in which case additional constraints (activation barriers; orientation dependence) may apply. This is a current topic for large-scale molecular modeling.[28,29] However, the crystallographic requirements and interfacial reactions implicit in growth via oriented aggregation have not been fully explored and the kinetic consequences have only been formulated in a few examples.

If structure transformation accompanies growth, the rate of transformation may be limited by the growth rate, or it may be affected by the aggregation state. The universal phenomenological Johnson–Mehl–Avrami–Kolmogorov (JMAK) equation is widely used in the former situation.[30] Aggregation-based transformation pathways are introduced with specific examples below.

Experimental methods

1. Synthesis and characterization of nanocrystalline TiO₂ and ZnS

TiO₂ is prepared by controlled hydrolysis, in which a titanium precursor (titanium alkoxide, titanium chloride or titanium isopropoxide) is hydrolyzed in an aqueous solution. The results are dependent on temperature, solution composition, stirring conditions, etc. Using these methods, we have prepared (1) 5–7 nm nanocrystalline anatase based on a sol–gel method[31] (dried as pieces of membranes, rather than as a powder);[33] (2) 8–21 nm nanocrystalline anatase samples, tuning the particle size by heat treatment of nanometer-sized amorphous TiO₂;[34,35] (3) ~3 nm nanocrystalline anatase by dripping a mixture of the titanium isopropoxide and ethanol into a 1.1 pH solution at 5°C.[36] The samples have been further processed under hydrothermal conditions (T = 100–250°C, pH = 2–12) to obtain TiO₂ nanoparticle products that differ widely in morphology, phase and size distribution.

ZnS is prepared by controlled precipitation. We have prepared ~3 nm ZnS nanoparticles by reaction of zinc chloride and sodium sulfide in an aqueous solution with and without capping surfactant (e.g. mercaptoethanol),[37] or in a non-aqueous solvent such as methanol, without surfactant.[49] The ZnS nanoparticles may subsequently be treated in hydrothermal conditions.

The phase composition of the prepared samples is characterized by X-ray diffraction (XRD) and high resolution transmission electron microscopy (TEM). Particle size and size distribution is studied by TEM, UV absorption spectroscopy, small angle X-ray scattering (SAXS) and dynamic light scattering (DLS). Note that particle sizes given in this paper refer to the mean particle diameter. TEM imaging additionally shows particle morphology. Additional structural studies include synchrotron-based wide angle X-ray scattering (WAXS), X-ray adsorption near-edge structure (XANES) and extended X-ray adsorption fine structure (EXAFS). BET (Brunauer–Emmett–Teller) and BJH (Barrett–Johner–Halenda) measurements provide surface area and micro-pore size distribution by nitrogen adsorption.

Results and discussion

Growth pathways

1. Growth in solution

Ostwald-ripening (O-R) refers to a dissolution–precipitation based mechanism for particle growth (coarsening) in solution. The chemical potential of surface atoms of small solid nanoparticles is elevated with respect to larger particles due to the presence of the excess energy associated with the surface. This increases the relative solubility of small particles, and larger particles grow preferentially. The kinetics of O-R crystal growth can usually be described by the following power law,[30]

D(t) = D₀ + k·t^1/n

where D₀ is the initial particle size, D(t) is the size at time t, k is a rate constant for the limiting step, and the exponent, n, is determined by the nature of the rate limiting step. The rate of the growth may be controlled by diffusion in solution (n ≈ 1), diffusion at the particle surface (n ≈ 2), or the interface dissolution/precipitation step (n ≈ 3). Diffusion-based growth can occur without a solvent matrix (sintering), given particle contact, by atomic diffusion from smaller particles to bigger ones.

For systems of nanoparticles, in addition to O-R, the nanoparticles can themselves act as the building blocks for crystal growth. An oriented pair of nanoparticles can attach to each other, eliminating the attaching free surfaces and releasing the surface energies associated with the free surfaces. This new mechanism for nanoparticle growth through oriented-attachment (OA) was first discovered in samples of hydrothermally treated nanocrystalline TiO₂. [38-40] Natural nanoparticles of iron oxy-/hydroxyl oxides were also found to grow by OA under certain geochemical conditions.[41] Imperfect OA can produce defects (e.g. edge dislocations, stacking faults, twins) in the OA-grown crystal, that often mark the original boundaries between component nanocrystals growing via the OA pathway.[42]

Evidence for OA-based growth comes both from interpretation of microstructure, and the deviation of the growth kinetics from the O-R model. OA growth does not follow Ostwald ripening kinetics. During hydrothermal coarsening of ~3 nm uncapped ZnS nanoparticles,[43] TEM and growth kinetics indicate that O-R occurs throughout (Fig. 2a), but that OA dominates in the early stages. If the nanoparticles are capped by mercaptoethanol, a distinct initial growth stage is observed (Fig. 2b), during which O-R is suppressed and pure OA-based growth occurs. The capping layer provides a barrier to dissolution before it is thermally desorbed. In the second growth stage, both OA and O-R contribute to the growth of ZnS nanoparticles. In the analysis of the first growth stage, assuming particle volume doubles after OA events, the evolution of particle size is well described by the following expression:

Figure 2.

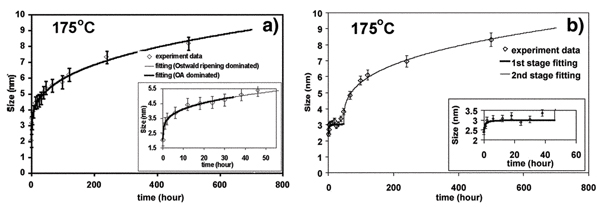
The kinetics of hydrothermal coarsening of (a) uncoated and (b) mercaptoethanol-coated nanocrystalline ZnS. In (a), the kinetics are described by combined oriented attachment (OA) and Ostwald ripening (O-R). In (b) there are clearly two coarsening regimes. TEM and kinetic analysis indicates the first stage is dominated by oriented attachment. The second stage kinetics are described by combined (OA) and (O-R). (Fig. 2a from ref. 50. Fig. 2b from ref. 43, reproduced by permission of the Editor.)

D(t) = D₀(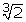kt + 1)/(kt + 1)

where D, k and t are as defined above.

The occurrence of OA-based growth in hydrothermally coarsened TiO₂ depends on pH, as expected. Away from the zero point of charge (pH_zpc ≈ 6 for nanocrystalline anatase[31]), the presence of surface charge prevents aggregation and promotes dissolution/precipitation based growth.[32]

2. Growth in air or vacuum

OA-based growth has been observed during the thermal coarsening of dry samples. For nanoparticles suspended in solution, thermal motion coupled with interparticle electrostatic interactions may promote particle contact, oriented alignment and hence growth. In some cases, if the nanoparticles are dry, or tightly aggregated in solution, thermal energy will not be sufficient to explore many configurations. Nevertheless, a subset of the vast number of contact points may be sufficiently well aligned to allow joining and interface elimination.

During the heating in air of nanoscale amorphous TiO₂, the formation of nanocrystalline anatase was accompanied by OA-based growth. The time-evolution of the phase composition, the average particle size and the particle size distribution (Fig. 3) of anatase nanoparticles were described quantitatively using the Smoluchowski equation.[34]

Figure 3.

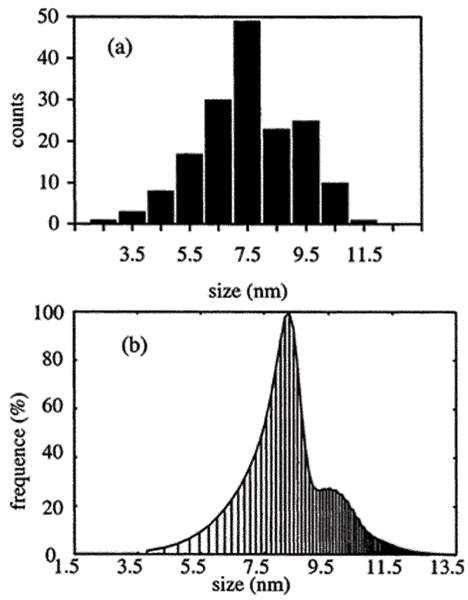
Particle size distribution of nanocrystalline anatase particles in a sample of initially nanometer-sized amorphous TiO₂, heated at 325°C for 4 h. (a) Experimental particle size distribution measured from TEM images, (b) Particle size distribution calculated from the kinetic model adopting the Smoluchowski equation with specially derived model kernels. (From ref. 34, reproduced by permission of the Editor.)

Phase stability and transformation in nanocrystalline TiO₂

At room temperature, rutile is the stable macroscopic phase of TiO₂, yet rutile is rarely observed in the synthesis of nanoscale titania. The majority of the products is nanocrystalline anatase (plus a small brookite fraction) or amorphous TiO₂. Static MD calculations predict average surface energies of anatase and rutile to be ~1.3 and 1.9 J m^-2, respectively.[22,44] Consequently, the surface contribution to the total free energy is a more rapid function of surface area (i.e. particle size) for rutile relative to anatase, and anatase becomes the stable phase in nanocrystalline TiO₂ when the size is below a certain value (Fig. 1). Calorimetric determination found the surface enthalpies of anatase and rutile to be 0.4 and 2.2 J m^-2, respectively, and confirmed the crossover instability of the nanophase polymorphs.[3] Experimental evidence that the crossover in phase stability occurs around D_c ≈ 14 nm (see below) is in better agreement with the surface energies derived from MD.

1. Heating in air

During the heating of nanocrystalline anatase in air, the formation of rutile accompanies the coarsening of anatase, but only after the anatase particle size exceeds 10–15 nm. The transformation temperature is 465°C, a few hundred degrees below that for bulk materials.[33] Partially transformed anatase nanoparticles are seldom seen in TEM, suggesting rapid nuclei growth rate following nucleation. The kinetics of the transformation was observed by quantitative XRD phase analysis. None of the available kinetic models derived for phase transformation in bulk materials, including the JMAK equation, were suitable for the experimental data.

Thermodynamic analysis (illustrated by the scheme in Fig. 1) showed that at the particle size of D_c ≈ 14 nm, the free energies of anatase and rutile are equal.[2] This may explain why nanocrystalline anatase is the majority phase of the nanocrystalline TiO₂ products in most syntheses, and rutile forms only after anatase coarsens above 10–15 nm.[2,22,33] The relative phase stability of nanophases is the driving force for phase transformation.

The unusual kinetic behavior of the transformation was explained with a microscopic model. High resolution TEM analysis showed that rutile-like structural elements can be produced in nanocrystalline anatase twin {121} interfaces.[45] Such structural elements may serve as nuclei for transformation from nanocrystalline anatase to rutile. Nucleation at preexisting structural sites would require much lower activation energy (transformation temperature) than for nucleation on surface or in the bulk.

Analysis of the kinetic data lead to a rate law for a phase transformation that explictly includes particle size. This novel approach showed that the kinetics of the transformation is second order with respect to the number of anatase nanoparticles (Fig. 4). This result is consistent with a model in which the number of anatase particles transformed to rutile in a unit time is proportional to the chances of contact between anatase nanoparticles. In a dry powder, this model requires the making and breaking of interparticle contacts. Successful (oriented) contacts lead to rutile nucleation and rapid transformation of the joined nanoparticle pair. Thus, structural and kinetic analysis lead to the development of a new kinetic model, termed interface nucleation (IN) model.[46] The activation energy for IN in nanocrystalline anatase was derived to be ~166 kJ mol^-1. Interface nucleation is dominant at lower temperatures (< ~600°C) for phase transformation of nanocrystalline anatase, At higher temperatures (> 600°C), both surface nucleation and interface nucleation govern the phase transformation.[47]

Figure 4.

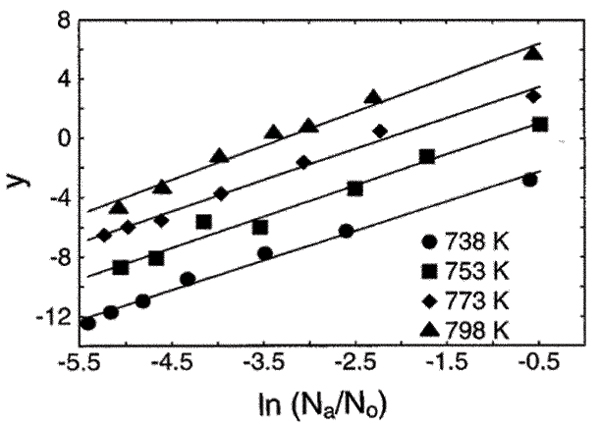
Kinetic plot for the anatase to rutile phase transformation in nanocrystalline TiO₂ heated in air. Here, y = In [-Δ(N_a/N₀)/Δt]; N_a is the anatase particle number, N₀ the initial particle number, and t is time. The slope of the lines (2) indicates a second order dependence on the number of particles. (From ref. 46, reproduced by permission of the Editor.)

Subsequent experiments are consistent with the IN model. Dilution of anatase nanoparticles by mixing them with inert nanoparticles (e.g. A1₂O₃) reduced the the transformation rate.[47] Conversely, in denser nanocrystalline anatase samples, the transformation rate was enhanced.[48] Due to the lack of large interfaces in bulk materials, phase transformation from bulk anatase to rutile mainly happens via surface nucleation and/or bulk nucleation at high temperatures,[47] both of which have higher activation energies.

Phase stability and transformation in nanocrystalline ZnS

Dynamic MD simulations of free (vacuum) faces predict the average surface energies of sphalerite and wurtzite are 0.86 and 0.57 J m^-2, respectively.[18] Hence, ZnS nanoparticles are more destabilized by the surface when they possess the sphalerite rather than the wurtzite structure. Consequently, nanocrystalline wurtzite is predicted to become more thermodynamically stable than sphalerite when the particle size is below D_c ≈ 7 nm at 300 K.

Water is ubiquitous in our environment, and MD simulations predict that the presence of water on the surface on ZnS nanoparticles can significantly affect phase stability. MD simulations explored the effect of water adsorption on the phase stability of 2–5 nm nanocrystalline ZnS particles at 300 K, with increasing water coverage (1–5 H₂O molecules nm^-2 ZnS surface).[18,49] In these simulations, when enough water was adsorbed, the energy of sphalerite nanoparticles becomes lower than that of wurtzite once again as in the bulk. Thus, in model nanoparticles, the phase stability is inverted in the presence of water (dotted lines, Fig. 1).

1. Heating in vacuum

Experimental measurements of the transformation temperature from nano-sphalerite to nano- wurtzite agree very well with the phase boundary predicted by thermodynamic analysis.[18] In TEM observations of reacted sphalerite samples (larger than 10 nm), wurtzite domains are always observed to be sandwiched between sphalerite structures. Such observations suggest that the wurtzite nucleation occurs at interfaces of two sphalerite particles, i.e. interface nucleation. Stacking faults, twining and polytype structures are readily formed, as illustrated in the TEM image shown in Fig. 5b.

Figure 5.

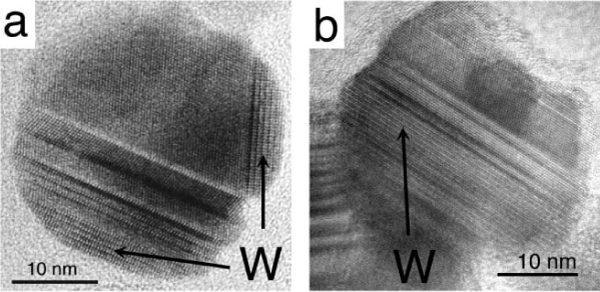
TEM images of thermally coarsened nanocrystalline ZnS in different environments. (a) Hydrothermal coarsening for 32 h at 225°C. (b) Vacuum coarsening for 2 h at 350°C. "W" indicates the location of wurtzite domains in the predominantly sphalerite particles. For further information on the data of Figs. 5a and 5b, see refs. 50 and 18, respectively.

2. Heating in wet environments

Experimentally we observe that wurtzite is formed during the heating of initially ~3 nm sphalerite at 350°C for 2 h in vacuum. In contrast, no wurtzite formation is observed when the same initial material was heated at 350°C for 2 h in air. This is consistent with the MD results, because nanoparticles exposed to the ambient air readily adsorb water moisture. Water may be able to chemically bind with ZnS nanoparticles even at this temperature.

Transformation from sphalerite nanoparticles to wurtzite was also investigated under hydrothermal conditions (140–225°C in water).[50] As shown in Fig. 5a, TEM examinations of the nanoparticles reacted for different lengths of time found wurtzite domains always at the nanoparticle surface, and never sandwiched between sphalerite domains, in striking contrast to the results of vacuum coarsening experiments (Fig. 5b). During hydrothermal treatment, the interfacial area between the outer wurtzite phase and the inner sphalerite phase (≈ 20 nm²) is invariant with time. This distinctive phenomenon suggests that the activation energy of the sphalerite → wurtzite transformation has a dependence on the reaction area (i.e. the wurtzite/ sphalerite interface area).

3. Transformation without growth: water binding

As experiment and simulation indicate that the presence of water can invert the sphalerite–wurtzite stability relations in nanosize materials, we investigated the possibility that water binding may induce a structural transition. From eqn. (1), at a fixed particle size, modifications to the free energy via the surface term, γ A, may be achieved if γ_vacuum ≠ γ_water.

Experimentally we synthesized ~3 nm nanocrystalline ZnS in anhydrous methanol, and performed in situ structural analyses, such as WAXS, Fig. 6, before and after the addition of water (50 μl H₂O/ml methanol). The ZnS nanoparticles in methanol retain a structure based on ZnS₄ tetrahedra, but diffraction peak broadening renders definite phase analysis (i.e. sphalerite vs. wurtzite) very difficult. Diffraction peak broadening is due to small particle size and the presence of substantial lattice strain. It was not possible to model the data by the inclusion of stacking faults to otherwise undistorted nanoparticles. As shown in Fig. 6, the addition of water had a profound effect on nanoparticle structure. Water addition causes a significant removal of lattice strain, and a sphalerite structure is observed, with no trace of wurtzite. UV absorption and TEM analysis showed no associated growth.

Figure 6.

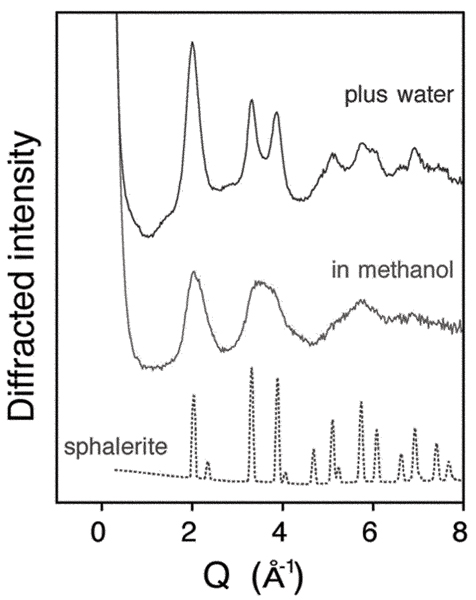
Wide angle X-ray scattering (WAXS) patterns showing a water-driven room temperature structural transformation in 3 nm ZnS nanoparticles. The WAXS pattern of nanoparticles synthesized in methanol is distinct from the pattern for bulk sphalerite due to size-related peak diffraction peak broadening, and to internal distortion, as described in the text. Water addition transforms nanoparticle structure, causing a considerable decrease in internal distortion without coarsening. Diffraction vector, Q = 4πsin(θ)/λ, where 2θ is the scattering angle, λ the X-ray wavelength. Data acquired at beamline 11-ID-C, APS.

MD simulations yielded nanoparticle structures in good agreement with the WAXS data,[49] providing an interpretation of the effect of water on nanoparticle structure. In the absence of any strong surface interactions, nanocrystalline ZnS in methanol is highly distorted. Atomic positions and tetrahedral bond angles are significantly distributed around equilibrium bulk values. The distortion is greatest at the surface, but all interior atoms are affected. Water binding relieves distortion, resulting in a more crystalline sphalerite-like structure. MD simulations indicate a strong enthalpy of adsorption (including structural stabilisation energy), which is consistent with the fact that the water induced transition cannot presently be reversed. Nevertheless, other work on surface interactions, such as methanol desorption,[49] and aggregation in methanol,[51] observed reversible structural transitions.

Challenges and future work

We have demonstrated that particle size, surface environment, and particle–particle contacts can affect phase stability and transition pathways. Much remains to be learned about these fundamental scientific phenomena. The results may have relevance to processes occurring in a wide diversity of environments, ranging from star dust to colloids in drinking water. The behavior of nanoscale systems shows an interdependence of size, structure, aggregation state and surface chemistry that is relevant to complex interlinked environmental phenomena. Nanoparticle aggregation is difficult to characterize, yet can affect growth,[34,46] particle structure,[51] electronic structure,[52] and transport, both of aggregated clusters[53,54]and of potential adsorbates within nanoporous aggregates.[55] Fig. 7a, shows preliminary work to study the kinetics of the water-driven transformation by observing the appearance and growth of sphalerite diffraction peaks following water addition. As shown in Fig. 7b, however, the extent of transformation approximately 20 h after water addition is considerable less for these data with respect to the data shown in Fig. 6. The ZnS nanoparticle batches differed only in their age since synthesis, suggesting that the kinetics of transformation can be slowed by aggregation. Hence, any kinetics experiments that involve the interaction between reagents and nanoparticle surfaces must consider the extent and nature of nanoparticle aggregation. In situ small angle X-ray scattering,[56,57] which can be combined with XRD structural characterization,[58] is a promising approach.

Figure 7.

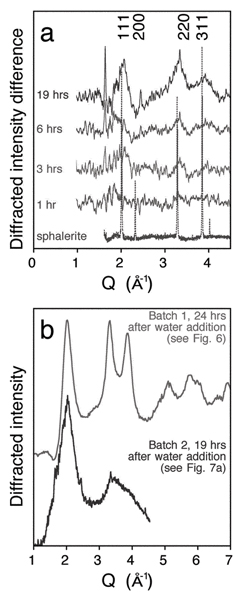
(a) Preliminary study of the kinetics of the water-driven structural transformation shown in Fig. 6. Displayed are difference XRD patterns at various times following addition of water (the initial pattern has been subtracted). The appearance and growth of sphalerite-like (111), (220) and (311) diffraction peaks show the time evolution of the structural transformation. Data acquired at beamline 2.1, SSRL. (b) The X-ray diffraction pattern of ZnS nanoparticles, 19 h following water addition (data from Fig. 7a), is compared with the pattern acquired 24 h after water addition to a prior synthesis batch (data from Fig. 6). The extent of transformation is considerably different in the two cases. This is attributed to differences in the nanoparticle aggregation state in the two batches.

A further area of research will be the combination of MD structural simulations and experimental determination of structure and structural dynamics.[60] Surface ligand interactions clearly are highly significant, but require considerable theoretical work.[61]

Conclusion

In this article, we summarized special pathways for crystal growth and phase transformations in nanocrystalline materials using TiO₂ and ZnS as examples. Inversion in phase stability can be induced by small particle size. This occurs as the result of differences in surface energies between polymorphs. Surface ligand binding and nanoparticle aggregation can exert significant influences on the structures and the properties of small nanoparticles because these factor change the surface energy, thus phase stability. In addition, particle–particle contacts allow mechanisms for growth and transformation not observed in macroscopic materials. Nanoparticle contact can result in oriented attachment-based crystal growth under favorable conditions. Oriented attachment is quite common in synthetic nanomaterials (e.g., TiO₂, ZnS, FeOOH) and in natural nanomaterials (e.g. FeOOH, ZnS etc). In addition, structural elements of a new phase may be generated at nanoparticle interfaces and the structural elements can serve as the nuclei for phase transformations. Thus, aggregation and phase transformation can be strongly coupled. In these cases, the activation barrier for interface nucleation is significantly lower than for surface or bulk nucleation, thus the reaction can proceed at lower temperatures.

Note

† Presented at the ACS Division of Geochemistry Symposium 'The Impact of Nanoparticle Growth and Transformation Processes on Contaminant Geochemical Cycling', New Orleans, March 2003.