Energetics of nanoparticle oxides: interplay between surface energy and polymorphism†

Abstract

Many oxides tend to form different structures (polymorphs) for small particles. High temperature oxide melt solution calorimetry has been used to measure the enthalpy as a function of polymorphism and surface area for oxides of Al, Ti, and Zr. The results confirm crossovers in polymorph stability at the nanoscale. The energies of internal and external surfaces of zeolitic silicas with open framework structures are an order of magnitude smaller than those of oxides of normal density.

Introduction

Nanoscale phenomena are ubiquitous and important to geoscience. The realization is growing that many outcomes and rates of geochemical processes are governed by phenomena at the nanometer scale, often in or at the surface of small particles. Surface interactions probably exert a disproportionate influence on the structure, chemistry, and movement of natural and anthropogenic nanomaterials in the Earth. In many cases, traditional distinctions between solutes, colloids and solids become vague. Nanoparticles, with sizes in the 1–100 nm range, lie in the realm between dissolved molecular clusters and crystalline macroscopic solids. Their properties are different from those of either.

Fine grained oxides precipitated from aqueous solution often crystallize in structures different from those of coarsely crystalline materials: γ-alumina instead of corundum, anatase and brookite instead of rutile, maghemite instead of hematite, and a host of complex hydrous iron oxyhydroxides. It has been suspected that differences in surface energy stabilize, as nanoparticles, polymorphs that are metastable in the bulk.[1,2] Oxide melt solution calorimetry has recently been used to measure enthalpies of phase transformation and surface enthalpies of different oxide polymorphs.[3] Calorimetric measurements are generally confirming this hypothesis of energy crossover between polymorphs at the nanoscale. This review summarizes recent work in the UC Davis Thermochemistry Facility on the energetics of nanophase oxides. For a broader overview of nanoparticles and Earth processes, the recent review volume on nanoparticles in the environment[4] should be consulted.

Energetics of various oxides

Aluminum oxides and oxyhydroxides

Corundum, α-Al₂O₃, is the thermodynamically stable phase of coarsely crystalline aluminum oxide at standard temperature and pressure conditions, but syntheses of nanocrystalline A1₂O₃ usually result in γ-Al₂O₃. Based on earlier molecular dynamics simulations and their own thermochemical data, McHale et al.[5] predicted that γ-Al₂O₃ should become the energetically stable polymorph for specific surface areas exceeding ~125 m² g^-1. The thermodynamic stability of γ-Al₂O₃ should be even greater than implied by this energy. Due to the presence of tetrahedral and octahedral sites in its spinel-type structure, and the fairly random distribution of A1³⁺ and vacancies over these sites, γ-Al₂O₃ has a greater entropy than α-Al₂O₃. The entropy change of the α-Al₂O₃ to γ-Al₂O₃ transition, ΔS_α→γ, is about +5.7 J K^-1 mol^-1.[6] Therefore, at room temperature, γ-Al₂O₃ could be thermodynamically stable with respect to α-Al₂O₃ at specific surface areas > 100 m² g^-1, and at 800 K (a temperature typical of oxyhydroxide decomposition) γ-Al₂O₃ might become thermodynamically stable at specific surface areas greater than only 75 m² g^-1.

McHale et al.[5] measured the enthalpies of drop solution in molten lead borate of several nanosized α- and γ-alumina samples. However, the surfaces of the A1₂O₃ were modified by adsorbed H₂O which could not be completely removed without severe coarsening. The surface energies of the hydrated polymorphs appeared nearly equal, indicating that the heat of chemisorption of H₂O is directly proportional to the surface energy of the anhydrous phase. Consequently, McHale et al.[5] could not determine the anhydrous surface energies without accurate knowledge of the heats of chemisorption of H₂O. These measurements were made on two samples each of α- and γ-Al₂O₃ with a Calvert type microcalorimeter operating near room temperature.[6] The differential heat of H₂O adsorption on γ-Al₂O₃ decreases logarithmically with increasing coverage (Freundlich behavior). In contrast, the differential heat of H₂O adsorption on α-Al₂O₃ does not show regular logarithmic decay, and decreases far less rapidly with increasing coverage. This indicates a greater number of high energy sites on α-Al₂O₃ per unit surface area, which are relaxed by the most strongly chemisorbed hydroxyls. This observation is strong evidence that the surface energy of α-Al₂O₃ is higher than that of γ-Al₂O₃.

A quantitative analysis of the heat of adsorption data enables the separation of hydration enthalpies and surface enthalpies for the two alumina polymorphs.[6] The resulting variation of enthalpy of the anhydrous material with surface area is shown in Fig. 1. The enthalpy (and free energy) crossover postulated above is clearly demonstrated. Table 1 lists the surface and transformation energies. Calorimetric studies of water adsorption on alumina[5,6] suggest that the higher energy surfaces have the strongest affinity for water, and that α-alumina has more strongly bonded H₂O than γ-alumina.

Figure 1.

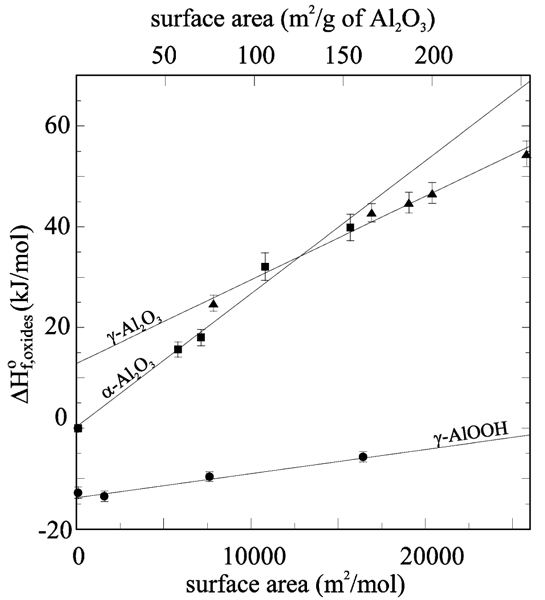
Enthalpy as a function of surface area for aluminum oxides and oxyhydroxides.[7]

Table 1.

Surface energies and transformation energies relative to bulk stable polymorph for several oxides

Oxide	Surface energy/J m-2	Transformation energya/kJ mol-1
α-Al2O3	2.6 ± 0.2	0
γ-A1203	1.7 ± 0.1	13.4 ± 2.0
A1OOH (boehmite)	0.5 ± 0.1	-17 ± 1
TiO2 (rutile)	2.2 ± 0.2	0
TiO2 (brookite)	1.0 ± 0.2	0.7 ± 0.4
TiO2 (anatase)	0.4 ± 0.1	2.6 ± 0.4
ZrO2 (monoclinic)	6.5 ± 0.2	0
ZrO2 (tetragonal)	2.1 ± 0.05	9.5 ± 0.4
ZrO2 (amorphous)	0.5 ± 0.05	34 ± 4
Zeolitic silicas	0.09 ± 0.01	7–15

^a Enthalpy relative to stable bulk anhydrous polymorph plus H₂O (liquid) if applicable.

Polymorphs of aluminum oxyhydroxide (boehmite, diaspore) and aluminum hydroxide (gibbsite, bayerite, nordstrandite) are common fine-grained constituents of soils, unconsolidated sediments, and sedimentary rocks. Their occurrence in nature is controlled by their thermodynamic properties and the kinetics involved in transformations. A recent study of the surface enthalpy of boehmite[7] was prompted by an apparent contradiction between common occurrence of boehmite and gibbsite and the thermodynamic stability of diaspore. Furthermore, fine-grained boehmite is also an important industrial product used because of its relative ease of synthesis and its ability to retain high surface area.

The results of calorimetric studies are shown in Table 1 and Fig. 1. The data clearly show that surface enthalpy is lowest for boehmite, intermediate for γ-alumina, and highest for corundum. In a first approximation, the surface energy of an ionic solid will be proportional to the charges of the ions within the structure. Thus, replacing the oxygen anions with hydroxyls will lower the surface energy, in agreement with experiment. Furthermore, the hydroxyls offer a termination at the crystal surface that is compatible with an aqueous environment.

Titania

Energy crossovers have also been confirmed for the rutile, anatase, and brookite forms of titanium dioxide.[8] Relative to bulk rutile, bulk brookite is 0.71 ± 0.38 kJ mol^-1 and bulk anatase is 2.61 ± 0.41 kJ mol^-1 higher in enthalpy. The surface enthalpies of rutile, brookite, and anatase are 2.2 ± 0.2 J m^-2, 1.0 ± 0.2 J m^-2 and 0.4 ± 0.1 J m^-2, respectively. The closely balanced energetics (see Table 1) directly confirm the crossover in stability of nanophase TiO₂ polymorphs inferred by Zhang and Banfield.[2] The heavy lines in Fig. 2 show the energetically stable phases as a function of surface area. Depending on the competition between coarsening and phase transformation kinetics; the transition anatase-to-brookite or the transition brookite-to-anatase can lower the enthalpy and free energy of the system. Thus the observation of both transitions in heated samples is not a violation of thermodynamic principles. The final stable phase upon grain growth is always rutile.

Figure 2.

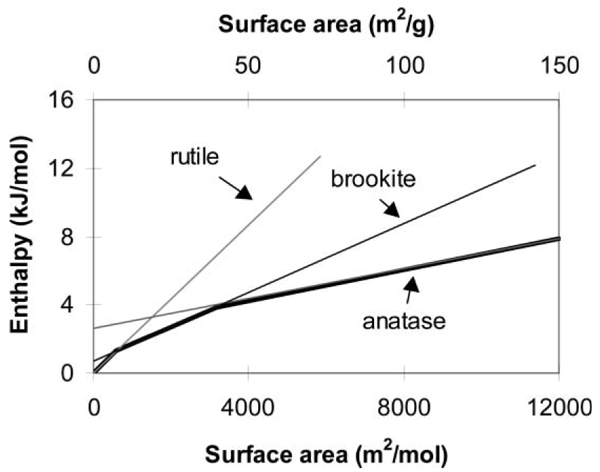
Enthalpy relative to bulk rutile for rutile, anatase, and brookite of various surface area. Figure modified from Ranade et al.[8] The slope of each line gives the surface energy, see Table 1.

Zirconia

Fig. 3 shows the energetics, as measured by oxide melt solution calorimetry, of monoclinic, tetragonal, and amorphous zirconia.[9] Once more, clear enthalpy crossovers are seen, with surface energy decreasing in the order monoclinic, tetragonal, amorphous. These crossovers correspond well to observation that monoclinic zirconia, the stable bulk polymorph, is readily synthesized with particle size greater than 50 nm, tetragonal zirconia is synthesized with intermediate particle size, and the amorphous material exists for particles smaller than about 4–8 nm. Calorimetric data, Rietveld refinements of crystal structures, and Raman spectra all indicate that nanophase crystalline zirconia is tetragonal rather than cubic.

Figure 3.

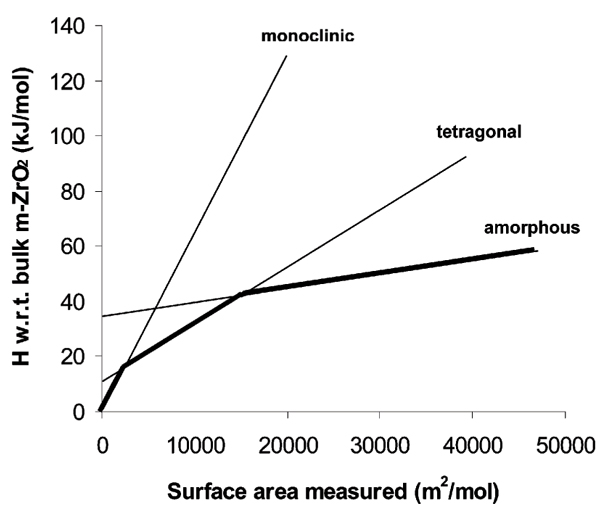
Enthalpy relative to bulk monoclinic zirconia (baddeleyite) for monoclinic, tetragonal, and amorphous ZrO₂ of various surface areas (in preparation). The slope of each line gives the surface energy, see Table 1.

Iron and manganese oxides and oxyhydroxides

These are characterized by extensive polymorphism. Measurements of the enthalpies of several iron oxides and oxyhydroxides[10,11] complement earlier work on MnO₂ phases.[11,12] Our focus thus far has been on polymorphism rather than on control of surface area; the latter studies are just beginning. What is noteworthy is that many polymorphs are only 5–10 kJ mol^-1 higher in enthalpy than the stable well-crystallized forms, opening the door to crossovers in stability.

Silica

Silica shows extensive polymorphism. Phases having a reasonable degree of P–T stability are quartz, tridymite, cristobalite, coesite, stishovite, and melt. Phases which are probably always metastable, but can be synthesized from aqueous solutions, with or without inorganic or organic structure directing agents, include amorphous silica, moganite, clathrasils, and zeolitic and mesoporous materials. These very low density metastable materials have been studied extensively by oxide melt solution calorimetry. [13-16] They all lie in a narrow band or energies about 7–15 kJ mol^-1 above quartz and overlapping amorphous silica.

In general, the less dense silicas have higher energies. Moloy et al.[17] have shown that the metastability of the silica polymorph (ΔH_tr for the hypothetical transition quartz → less dense silica phase) correlates linearly with the internal surface area calculated by molecular modeling (see Fig. 4). The internal surface energy calculated from the slope of the line relating enthalpy to internal surface area[16] is 0.09 ± 0.01 J m^-2, which is more similar to the external surface energy of amorphous silica than to that of quartz, the latter being significantly higher (see ref. 17 for discussion). Melanophlogite, a clathrasil with large but not interconnected pores falls on the same trend as the zeolitic silicas.[16]

Figure 4.

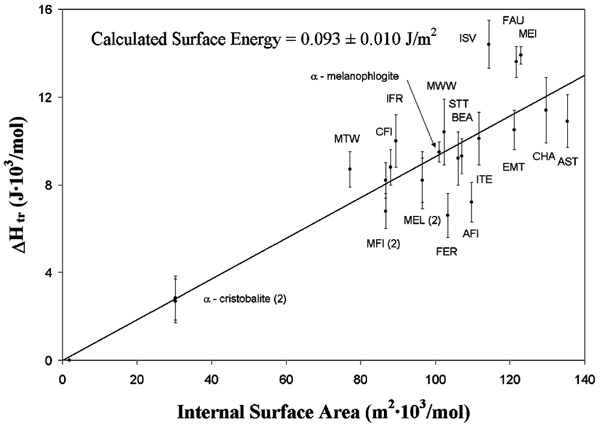
Correlation between enthalpy of less dense silica phases relative to quartz and calculated internal surface area.[15,16] Symbols are International Zeolite Association (IZA) codes for various zeolite frameworks.

One of these zeolitic silicas, silicalite-1, has been synthesized as nanocrystals with different sizes (40, 95 and 180 nm) and the organic structure directing agent removed by calcination. X-ray diffraction, SEM, nitrogen adsorption, FT IR and thermogravimetric analysis were used for characterization. Nitrogen adsorption of the zeolite containing the organic template gave the external surface area, while that of the calcined sample gave the total surface area. The internal surface area is then the total surface area minus the external surface area. High-temperature solution calorimetry was used to determine the enthalpies (ΔH_tran) relative to quartz at 298 K. The ΔH_tran values are 8.2 ± 0.4 kJ mol^-1 (40 nm), 8.3 ± 0.3 kJ mol^-1 (95 nm) and 8.0 ± 0.5 kJ mol^-1 (180 nm).[18] These values are essentially the same as ΔH_tran for microsized MFI crystals, 8.0 ± 0.8 kJ mol ^-1.[15] Thus, the enthalpy does not depend on the particle size, that is, the external surface area, at least for particles ≥ 40 nm. The ratio of internal surface area to external surface area is 4.1 (40 nm); 10.6 (95 nm), and 18.1 (180 nm), indicating the internal surface area dominates the external and total surface area even for nanosized zeolites. From the viewpoint of energetics, the large internal surface area of zeolite requires a small surface energy to make the system energetically accessible. If the surface enthalpy calculated by Moloy et al.[17] reflects the energetics of both internal and external surfaces, the external surface energy of silica zeolites can be also estimated to be 0.09 ± 0.01 J m^-2.

Discussion

Table 1 presents surface energies for various oxides. Compared to that for zeolites and amorphous silica, and even quartz (see ref. 17 for discussion), the surface energy is considerably larger for oxides which do not form framework structures with low density. For 40 nm α-Al₂O₃ (which is unstable relative to 40 nm γ-Al₂O₃) the excess enthalpy relative to bulk is as large as 10 kJ mol^-1. Even for 40 nm brookite (the stable polymorph at the nanometer scale, the excess enthalpy is 1.2 kJ mol^-1. For 40 nm silicalite-1, the surface area of 95 m² g^-1 yields an excess enthalpy relative to bulk of only 0.53 kJ mol^-1, which is within the experimental error of ΔH_tran. This indicates that the effect of particle size on energetics is too small to measure accurately by oxide melt solution calorimetry for silica zeolites, at least for ≥ 40 nm particles.

These observations lead to several general inferences. (1) The existence of a large number of polymorphs with microporous structures requires them to be similar in energy and not too much higher than dense frameworks. If the energy of internal and external surfaces is similar, this implies little dependence of energy on particle size for microporous materials in general. Because of the small surface energy, crossovers in stability of microporous materials as a function of particle size are unlikely, in contrast to the behavior of dense polymorphs. The thermodynamic driving force for particle coarsening of microporous materials is very small. This may explain why it is often difficult to grow large crystals of porous materials. If similar trends hold for other types of microporous materials, for example manganese oxides, it can be predicted that the enthalpy of formation of a nanosized microporous MnO₂ polymorph will be similar to that of micrometer sized MnO₂ having the same structure. Many natural manganese oxide minerals are nanosized and do not coarsen readily, consistent with the arguments above.

The data presented above have several geochemical implications. If hydrous phases like oxyhydroxides generally have smaller surface energies than their anhydrous counterparts, then small particle size will favor the hydrated forms. This has been discussed[7] for the dehydration of boehmite to corundum plus water. It is concluded that the P–T stability field of the hydrous assemblage can be extended significantly in nanophase materials, and that dehydration and coarsening often occur simultaneously. Thus, the seemingly "metastable" retention of boehmite and other oxyhydroxides may in fact be "stable" under the additional constraint of retaining small particle size.

The extensive polymorphism of open framework micro-porous structures like zeolites and manganese oxides may be linked to their small internal and external surface energies as discussed above. Their tendency to remain fine-grained, and to produce intergrowths of different structures at the unit cell scale (as seen by TEM) may reflect not just the small energy differences between polymorphs, but small surface and interfacial energies as well.

The regime explored here shows a linear dependence between enthalpy and surface area, i.e., a constant surface energy (or enthalpy). As particles get even smaller, one may expect this linearity to break down. The transition from crystalline nanoparticle to amorphous nanoparticle to cluster needs further exploration of both structure and energetics. The current calorimetric data suggest that the amorphous phase generally has a smaller surface energy than the crystalline polymorphs. Is this a general feature?

Nanoparticles in the aqueous environment have hydrated surfaces. The enthalpy of hydration has been explored for alumina[5,6] but not for other oxides. Further work by adsorption and immersion calorimetry is planned. The enthalpy of adsorption of other inorganic ions and organic molecules on nanoparticles can also be studied by calorimetry. Such adsorption is expected to be sensitive to polymorphism and, for particles below 10 nm or so in size, new phenomena, reflecting the breakdown of the assumption of constant surface energies, may come into play.[19]

Note

† Presented at the ACS Division of Geochemistry Symposium 'The Impact of Nanoparticle Growth and Transformation Processes on Contaminant Geochemical Cycling', New Orleans, March 2003.