Reversible and Irreversible Unfolding of Mitotic Newt Chromosomes by Applied Force

Abstract

The force–extension behavior of individual mitotic newt chromosomes was studied, using micropipette surgery and manipulation, for elongations up to 80 times native length. After elongations up to five times, chromosomes return to their native length. In this regime chromosomes have linear elasticity, requiring ∼1 nN of force to be stretched to two times native length. After more than five times stretching, chromosomes are permanently elongated, with force hysteresis during relaxation. If a chromosome is repeatedly stretched to ∼10 times native length and relaxed, a series of hysteresis loops are obtained that converge to a single reversible elastic response. For further elongations, the linear dependence of force on extension terminates at a force “plateau” of ∼15–20 nN, near 30 times extension. After >30 times extensions, the elastic moduli of chromosomes can be reduced by more than 20-fold, and they appear as “ghosts”: swollen, elongated, and with reduced optical contrast under both phase and differential interference contrast imaging. Antibody labeling indicates that histone proteins are not being lost during even extreme extensions. Results are interpreted in terms of extension and failure of chromatin-tethering elements; the force data allow estimates of the number and size of such connectors in a chromosome.

INTRODUCTION

During cell division, eukaryote chromosomes are transformed from a transcriptionally active, dispersed interphase state into neatly compacted mitotic chromatids. They are then bent and stretched by motors associated with the mitotic spindle. The forces directly applied to chromosomes by the mitotic spindle are in the nanonewton range (Nicklas, 1983). During mitosis, chromosomes are also deformed by collisions with polymerizing microtubules (Koshland, 1994). Understanding mitotic and other cell machinery from a mechanistic biophysical perspective thus requires understanding physical properties of chromosomes. A fundamental property of mitotic chromosomes that has not been studied in detail is how they elongate under tension (Nicklas, 1983; Claussen et al., 1994; Fritzsche and Henderson, 1997; Houchmandzadeh et al., 1997; Houshmandzadeh and Dimitrov, 1999). Small, reversible deformations, as occur during mitosis (Nicklas, 1983), are of interest because they indicate how tightly the chromatin is tethered together. However, the way chromosomes gradually irreversibly elongate as they are stretched to their maximum limits is also potentially interesting because it may provide information about the as yet unknown way in which mitotic chromosomes are folded.

The folding of mitotic eukaryote chromosomes is increasingly suspected to be based on the folding of chromatin by protein fasteners (Paulson and Laemmli, 1977). Recently, members of the SMC (structural maintenance of chromosomes) family of proteins have been shown to mediate chromatin condensation (Hirano, 1998). For example, antibody depletion of certain SMCs from in vitro-assembled artificial chromatids results in their gradual dissolution into a cloud of chromatin fibers (Hirano and Mitchison, 1994), indicating that those SMCs are chromatin-tethering elements. Microelasticity measurements could be used in such experiments to quantify exactly the time course and the structural changes resulting from biochemical modifications of SMCs and other chromosome-folding factors; however, measurements of elasticity of native chromosomes are required as a baseline for such studies.

This paper reports force–extension measurements for single mitotic chromosomes. Glass micropipettes were used to extract and manipulate chromosomes from live cells. The micropipettes were used as force transducers via calibration and observation of their bending, allowing forces in the nanonewton range to be measured. This technique was developed previously and used to carry out rough measurements of chromosome elasticity (Houchmandzadeh et al., 1997); however, dynamics of extension and relaxation were not studied, and no systematic measurements of the elastic response during chromosome unfolding were performed.

An important feature of this paper is quantification of the rate at which chromosomes come to mechanical equilibrium while being stretched or after stress is released. If one carries out experiments at elongation rates faster than roughly 0.1 μm/s, one does not observe the intrinsic elastic response of a chromosome, but instead some complicated combination of elasticity and relaxation dynamics. By performing experiments at slow rates of elongation, we have been able to fully characterize reversible chromosome elasticity for small amounts of stretching. For extreme stretching at slow elongation rates, we observe a new unfolding behavior: after slow elongations to >30 times native length and retraction, mitotic chromosomes become not only permanently stretched, but also swollen. Antibody labeling indicates that even after such dramatic extensions, native quantities of histones remain on chromosomes. This supports the hypothesis that mitotic chromatids are held together by chromatin-tethering elements and that the chromatin tends to disperse as those elements are broken.

MATERIALS AND METHODS

Cell Culture and Medium Preparation

Standard protocols for newt lung cell cultures (Rieder and Hard, 1990) adapted for micromanipulation (Houchmandzadeh et al., 1997) were followed. Male newts (Notophthalmus viridescens, Connecticut Valley, Southampton, MA) were killed by immersion for 20 min in 1 mg/ml tricaine (Acros, Pittsburgh, PA) and immediately dissected. Lungs were cut into 1-mm³ pieces and soaked in culture medium for 24 h. Culture medium was 50% L-15 (Cellgro, Henderson, VA), 46% water (BioWhittaker, Walkersville, MD), 4% FBS (BioWhittaker), 50 U/ml penicillin, 50 μg/ml streptomycin (BioWhittaker), and 5 μg/ml fungizone (BioWhittaker). Culture dishes (60 × 15 mm, Falcon, Franklin Lakes, NJ) had a 3-cm-diameter hole cut out of the bottom covered with a 4-cm-diam no. 1 cover glass (Fisher Scientific, Pittsburgh, PA) and sealed with paraffin. Before assembly, the culture dishes were cleaned with a detergent, and the cover glass was cleaned with Sparkle (A.J. Frank, Elgin, IL); culture dishes, cover glass, and Teflon rings were soaked in 70% ethanol for 2 h. After drying and assembly, the dishes and Teflon rings were UV-irradiated for 40 min. Lung fragments were divided into six dishes, lightly squashed onto the glass, covered by a dialysis filter, and held down by a Teflon ring. Epithelial cells began to migrate onto the glass in 3–4 d. The culture medium was replaced and the filters removed after 7 d. Ten days after culture preparation, mitotic activity reached its peak. Experiments were performed between the seventh and fourteenth day.

Experimental Setup

Extension–relaxation experiments were imaged using a differential interference contrast (DIC) inverted light microscope with 60×, 1.25 N.A. and 10×, 0.3 N.A. objectives (IX-70, Olympus Optical, Tokyo, Japan). A three-axis stage-focus control with XY resolution 1 μm and Z resolution 0.1 μm (Prior, Cambridge, United Kingdom) were used to position the dish. Surgery was performed with a pipette mounted to a motorized XYZ micromanipulator with a resolution of 0.04 μm (MP-285, Sutter, Novato, CA). A second pipette was attached to a manual XYZ micromanipulator (Taurus, WPI, Sarasota, FL) mounted on the microscope. This was all mounted on a vibration isolation workbench (Newport, Irvine, CA). A 233-MHz Pentium-I PC with Labview (National Instruments, Austin, TX) was used to control the stage and motorized manipulator. Images were recorded by a charge-coupled device video camera (Panasonic, Yokohama, Japan) and captured with an NI-IMAQ PCI-1408 card and NI-IMAQ (National Instruments) software onto a PC.

Pipette Fabrication

Borosilicate pipettes with 1-mm outer diameter and 0.7-mm inner diameter (WPI) were pulled by a micropipette puller (P-97, Sutter) to have a taper of ∼1 cm. A micropipette forge was used to cut the tip to have an inner diameter of ∼2 μm. The forge is a standard microscope with a 10× objective and with a 0.5-mm-long, 0.1-mm-diam platinum wire mounted below the lens and connected to a power supply. A small bead of borosilicate glass is melted onto the platinum wire. The current is set to ∼2.2 A, which causes the wire to expand out and heat up. The micropipette is brought into contact with the glass bead, and the current is then turned off. The wire retracts and cools quickly, resulting in a clean break at the point where the pipette was in contact with the glass bead (Brown and Flaming, 1986). The pipettes are then filled with 60% PBS.

Pipette Calibration

Pipettes are used as force transducers; force deflection constants of ∼0.5 nN/μm were determined by pushing them against a calibration pipette of known force constant. An absolute calibration of a very stiff pipette was directly measured to have a force constant of 3.0 × 10⁴ nN/μm by bending it against a scale. A series of successively weaker pipettes were made and calibrated to have force constants of 2.9 × 10³, 7.3 × 10², 71, 7.6, 2.2, and 0.1 nN/μm. Thus we obtained a calibration pipette with known force constant. All experimental pipettes were calibrated against the same calibration pipette. Because of the successive calibration steps, the absolute uncertainty of experimental pipettes is 30%; however, the relative uncertainty between experimental pipettes is 10% because they all had their force constant measured with the same calibration pipette.

Extension–Retraction Experiment

A pipette was used to penetrate the cell membrane of a mitotic cell ∼20–30 min after nuclear envelope breakdown. Cytoplasm flows out of the cell and typically causes some chromosomes to be partially pushed out of the cell. The pipette is then used to aspirate on the tip of a chromosome with ∼500 Pa of suction; the chromosome permanently adheres to the inside of the pipette after 2 min of contact. If the chromosome can easily be freed from the cell, a second pipette is then moved nearby and used to aspirate on its other end. In the event that the chromosome cannot be freed from the cell, the second pipette is used to anchor the chromosome of interest by aspirating near the apparent attachment of it to the other chromosomes. The pipettes are then lined up so they are antiparallel and the chromosome is perpendicular to the pipettes. A Labview program moves the pipette perpendicular to its axis at a constant strain rate and periodically saves images of the pipette and the position of the manipulator to disk.

We describe the rate at which extension–retraction experiments are performed in terms of strain rate, which is the ratio of the linear velocity of the pipette that is being moved in micrometers per second, to the native length of the chromosome in micrometers. Thus strain rate is measured in sec⁻¹, and its reciprocal is the time over which a chromosome is stretched from native length to double its native length.

Step–Strain Experiment

This type of experiment was used to quantify the relaxation rate of chromosomes. Chromosomes were pulled out of a mitotic cell with a pipette as described above; chromosomes that had one end strongly anchored in the cell were used for step–strain experiments. A Labview program was used to rapidly step the pipette perpendicular to the chromosome at a rate of 250 μm/s and to capture images of the pipette and chromosome at two frames per second. Images were taken for 30–60 s to allow the time course of pipette bending to be measured.

Force–Extension Analysis

The position of the pipettes and length of the chromosome were measured directly from the images using a Labview program. The resolution of distance measurements is 0.1 μm, limited by the resolution of DIC and the pixel size of our images. Pipette deflection was deduced from the difference between the recorded position of the manipulator and the image of the pipette tip. Deflection during relaxation contains an offset of 1–2 μm caused by mechanical backlash of the MP-285. The known force constant of the pipette allowed conversion of the deflection into a force.

Preparation of Fluorescein-labeled Antihistone

Antihistone, pan (1492 519, Boehringer Mannheim, Indianapolis, IN) was prepared at a concentration of 0.04 mg/ml with 1 mg/ml BSA in PBS (BioWhittaker). Fluorescein (Boehringer Mannheim) was prepared at a concentration of 0.2 mg/ml in PBS; 1 μl was added to 50 μl of antihistone solution and the mixture was gently stirred for 2 h at room temperature. Labeled protein was separated from free fluorescein on a column (Microspin G-25, Amersham, Arlington Heights, IL) by 600 × g centrifugation for 2 min.

Antihistone Labeling Experiments

A pipette was pulled and cut, and then the tip was filled with 1 μl of labeled antihistone solution using a microinjection pump (PV830, WPI). The pipette was moved to ∼20 μm from the chromosome with the manual micromanipulator and then was sprayed with antihistone for ∼1 min at a pressure of 1 psi. The chromosome was then incubated for 15 min to allow unbound protein to diffuse away. Fluorescence images were recorded with a CCD camera (Pictor 416XT, Meade, Irvine, CA) and PC.

RESULTS

Dynamical Relaxation Behavior

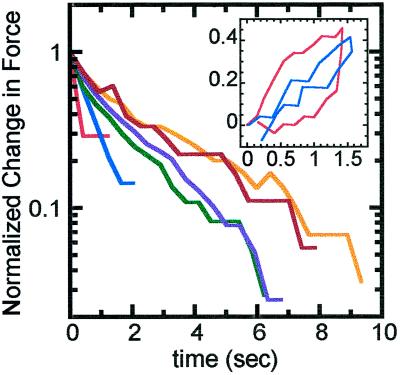
Before doing force–extension measurements to study chromosome elasticity, we had to roughly determine dynamical relaxation properties of chromosomes. This was done by studying the dynamics of force relaxation in chromosomes after essentially instantaneous elongations. Step–strain experiments were performed to various extensions to determine the relaxation time of chromosomes. Jumps of 2–100 times the native length gave rise to an initial force jump followed by a force decay (Figure 1). Extensions of up to five times displayed decay times of <2 s; after these relatively short step strains, chromosomes returned to essentially native length after the stress was released. Longer step strains of 5–100 times display longer force relaxation times on the order of 10 s. After these longer step strains, chromosomes were noticeably elongated when the stress was released.

Figure 1.

Log–linear plot of force relaxation in a chromosome in a step–strain experiment. The time courses start immediately after successive chromosome elongations to 2 times (red), 4 times (blue), 8 times (green), 16 times (purple), 60 times (brown), and 100 times (orange) native length. The elongations were done at a fast strain rate of 50 s⁻¹. Time courses of force are shown relative to the final force reached after relaxation and normalized to the initial force measured just after the rapid elongation. Thus we plot (measured force − final force)/initial force, making all the time courses run from 1 to 0 and allowing easier comparison of time scales. All of the relaxation data shown were done on the same chromosome, initially of native length 5 μm. For extensions to less than five times, force relaxation occurs over roughly 2 s; for longer extensions the force relaxation took up to 10 s. Inset, force versus extension curves of a second chromosome extended at two different strain rates. The first extension–relaxation was done at 0.08 s⁻¹ (red); the second extension–retraction was done at 0.02 s⁻¹ (blue). The y-axis is in units of nanonewtons, and the x-axis is in units of normalized extension. The native length was 4.8 μm. The faster experiment shows a force “loop” because the chromosome is not being given time to relax as the extension–retraction is being done. During the slower experiment the chromosome stays in mechanical equilibrium, and coincident force–distance curves are obtained during extension and retraction.

The relaxation times indicate what strain rates should be used in force–extension experiments. Strain rates below ∼0.1 times the inverse of the relaxation time allow stress inside the chromosome to fully equilibrate as it is stretched. Thus a strain rate <0.05 s⁻¹ should be used to study chromosome elasticity during extension up to five times native length. To illustrate the misleading results that can originate from exceeding this strain rate, we show force–extension obtained from extending and then relaxing a chromosome at different strain rates (Figure 1, inset). The blue curve is the force versus extension of a chromosome elongated and then relaxed at 0.02 s⁻¹, whereas the red curve is a plot of the same chromosome elongated and then relaxed at 0.08 s⁻¹. The slower (blue) extension and return curves lie close to each other, indicating elastic response; however, the faster run (red) on the same chromosome shows what looks to be a “hysteresis loop.” In fact, in the faster run the chromosome is just not given enough time to come to mechanical equilibrium during the extension–retraction cycle, and consequently one is not observing elastic behavior.

The red loop in the inset of Figure 1 is not what we consider proper hysteresis. We define hysteresis as failure to obtain the same force curve during extension and retraction, at a strain rate for which the chromosome equilibrates during extension and retraction. To avoid misleading dynamical hysteresis-like effects like those shown in Figure 1, we performed all of our further studies of chromosome elasticity at slow strain rates. Extensions to less than 5 or 100 times the native length were elongated at strain rates <0.05 or 0.01 s⁻¹, respectively, to allow measurement of equilibrated forces and extensions.

Short Extensions

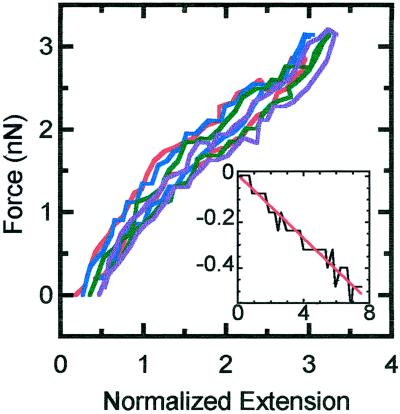
Extension–retraction cycles were performed using chromosomes manipulated with two pipettes, out to three times the native length at slow strain rates, to quantify the elasticity of chromosomes. Extensions up to three times the original length are fully reversible and linear for strain rates <0.04 s⁻¹ (Figure 2). This experiment was repeated seven times, giving elastic constants 1.5 ± 0.2, 1.1 ± 0.2, 1.0 ± 0.2, 0.9 ± 0.2, 0.6 ± 0.1, 0.4 ± 0.1, and 0.4 ± 0.1 nN. Eight additional extension–retraction experiments were performed with one pipette, where one end of the chromosome was anchored inside the cell. Again, extensions up to three times the native length are fully reversible and linear. The elastic constants were measured to be 1.4 ± 0.3, 1.0 ± 0.2, 0.8 ± 0.2, 0.6 ± 0.2, 0.3 ± 0.1, 0.2 ± 0.1, and 0.2 ± 0.1 nN. There was an appreciable variation in elastic constant from chromosome to chromosome, possibly attributable to our sampling different moments between the end of prophase and the end of metaphase. Sometimes the pipette aspirates and attaches only one of the two chromatids; it is conceivable (but not obvious from the microscope images) that this has led to some of the run-to-run scatter. Finally, it is possible that different chromosomes have different elasticity. In general, however, the stretching constant of metaphase chromosomes is ∼1 nN, in accord with measurements of Houchmandzadeh et al. (1997).

Figure 2.

Force versus extension of a chromosome for small extensions and retractions. The native length of the chromosome is 7.5 μm. The strain rates are 0.007 s⁻¹ (red), 0.01 s⁻¹ (blue), 0.02 s⁻¹ (green), and 0.03 s⁻¹ (purple). The inset plot is the normalized change in width versus normalized change in length of the same chromosome. The black line is the data, and the red line is the linear fit (y = −0.005 + 0.067x).

A linear decrease in chromosome width was observed to occur with increasing extension (Figure 2, inset), as is usual for an elastic object (Landau and Lifshitz, 1970). The ratio of this width decrease to extension (the “Poisson ratio”) was 0.069 ± 0.005 during the run of Figure 2.

Intermediate Extensions

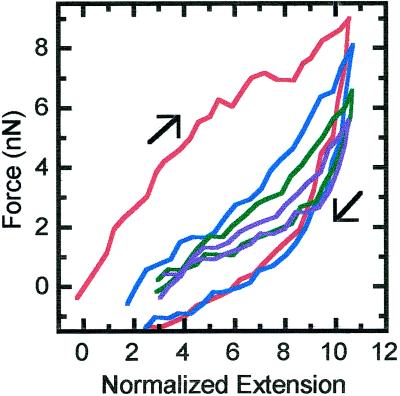
Once a chromosome is extended beyond five times its original length, irreversibility and hysteresis occur. Figure 3 shows repeated extensions out to 10 times the original length. Initially, hysteresis occurs, but by the fourth cycle extension and retraction, plots converge to a single curve. The final relaxed length is three times the original length, and most of this lengthening occurs during the first three extensions. Also, the force–extension curves change from nearly linear and slightly concave to a very nonlinear convex shape.

Figure 3.

Repeated extension–relaxation curves to an extension of 10 times the native length (3.8 μm). Each extension and relaxation was done at a strain rate of 0.008 s⁻¹; shown are the first (red), second (blue), fourth (green), and sixth (purple) extensions.

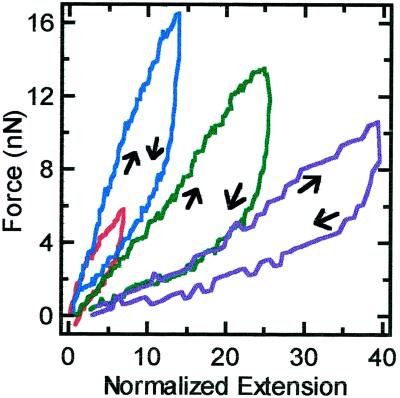
Figure 4 shows repeated extensions out to gradually increasing lengths. Hysteresis occurs in each extension–retraction cycle, and the initial slope decreases for each extension. Also, the final length after each cycle increases. The final state of the chromosome is also optically distinct from the initial native state (Figure 5); when imaged by DIC, the contrast between the final chromosome and the surrounding medium is much less then the native chromosome. Phase contrast shows the final chromosome to be inhomogeneous on the micrometer scale, unlike the native chromosome. Also, the chromosome with a native width of 2.3 μm is swollen to a width of 3.3 μm. The elastic constant is reduced from 1.9 to <0.1 nN, as can be seen from Figure 4.

Figure 4.

Force versus extension of a chromosome to increasing maximum extensions. The strain rate for all loops was 0.008 s⁻¹. The order of maximum extension are 7 times (red), 14 times (blue), 26 times (green), and 40 times (purple) the native length (7.5 μm).

Figure 5.

Images of the chromosome following the experiment plotted in Figure 4. A is a DIC image of the chromosome before the experiment; B is a DIC image, and C is a phase-contrast image of the chromosome after the experiment. Bar, 10 μm.

Long Extensions

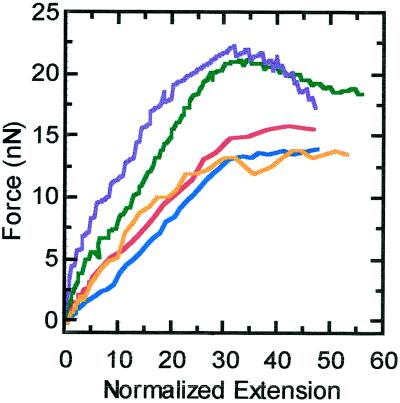
Chromosomes break when extended roughly 100 times their original length (Houchmandzadeh et al., 1997). In the experiments of this paper, chromosomes were stretched to up to 80 times without breakage. The force–extension response during stretching, at a strain rate of 0.008 s⁻¹, continues to be linear to an extension of 30, after which the slope gradually reduces to a plateau (Figure 6). This plateau begins at a force varying from 15 to 20 nN. Chromosomes with lower plateaus display smaller elastic constants. After a single long extension and retraction, the ghost state of a chromosome is produced with the same characteristics as described in the previous section.

Figure 6.

Force versus extension of chromosomes for large extensions. These extensions were all done with a strain rate of 0.008 s⁻¹. The native lengths of each chromosome were 2.5 μm (red), 6 μm (blue), 4 μm (green), 5.9 μm (purple), and 5.5 μm (orange).

Force–Extension Experiments on Antihistone-labeled Chromosomes

Force–extension experiments were performed on a newt chromosome before and after labeling the chromosome with fluorescein-labeled antihistone. The elastic constant before labeling was measured to be 0.6 ± 0.2 nN. The chromosome was then sprayed with antihistone and incubated for 15 min. Fluorescent images were then taken to show the localization of antihistone on the chromosome. The force–extension experiments were performed again, and the elastic constant was 0.8 ± 0.2 nN; chromosome elasticity was thus not qualitatively altered by addition of antihistone.

Measurement of the Relative Number of Histones on a Native Chromosome and a Ghost Chromosome

Two chromosomes were stretched at rates of 0.003 and 0.007 s⁻¹ to 23 and 50 times the original length, respectively, in separate experiments. Following relaxation, the chromosomes were sprayed with fluorescein-labeled antihistone. In the 23 times run we were able to simultaneously spray a native, unstretched chromosome. Fluorescence images (Figure 7) were collected, and after subtracting out background, the fluorescence intensity (counts per pixel) of the native chromosome was 4600 ± 700, whereas the 23 times stretched chromosome gave 1600 ± 300 counts. The 50 times stretched chromosome had a fluorescence intensity of 1400 ± 300.

Figure 7.

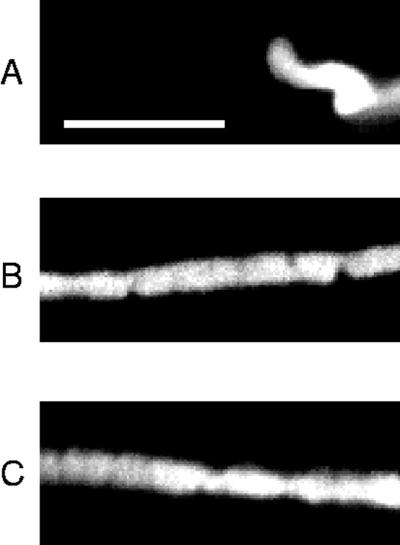
Immunolocalization of antihistone on newt chromosomes. A is a native chromosome; B is a chromosome labeled after a 23 times extension, and C is a chromosome labeled after a 50 times extension. Bar, 10 μm.

The increased volume of the stretched chromosomes accounts for their lower fluorescence intensity. The initial volume of the portion of the chromosome extended to 23 times was 70 ± 10 μm³, and the final volume was 290 ± 40 μm³. The initial volume of the portion of the chromosome extended to 50 times was 20 ± 5 μm³, and the final volume was 220 ± 30 μm³. These results indicate that native numbers of undamaged histones remain bound to the chromosomes after being stretched as much as 50 times.

DISCUSSION

Mitotic Chromosomes Display Reversible Elasticity at Extensions Over Fivefold

Metaphase mitotic chromosomes display reversible and nearly linear elasticity for extensions up to approximately five times their length (Figure 2). By comparison, most solid materials fracture if extended by more than a small fraction of their initial length; polymer gels can sometimes show this kind of extensibility (Houchmandzadeh et al., 1997). Chromosome linear elasticity is described by a force constant of roughly 1 nN. The variability from chromosome to chromosome was roughly 0.5 nN; this is larger than our experimental error and must be intrinsic to the chromosomes themselves or to precise position in the cell cycle. Houchmandzadeh et al. (1997) reported a fivefold decrease in force constant from prometaphase to metaphase.

The chromosome force constant of 1 nN may be expressed as a Young modulus Y by dividing it by the cross-sectional area of the unstretched chromosome, 4 × 10⁻¹² m², giving Y = 250 Pa. This is a very low modulus; covalently bonded solids usually have a modulus near 10¹⁰ Pa; molecular crystals and hydrogen-bonded solids such as single molecules of DNA have a modulus near 10⁸ Pa; polymer gels usually have moduli of 10³-10⁴ Pa. This again suggests a comparison of a mitotic chromosome to a polymer gel; however, as discussed previously (Houchmandzadeh et al., 1997), this scale of Young modulus is in fact too large to be associated with the elasticity of a gel of chromatin fiber: to obtain the observed fivefold extensibility, a very loose chromatin gel would be required, which would have a very low modulus.

Another possible origin of the reversible elasticity is stretching and reversible modification of chromatin fiber structure. This explanation requires chromatin fibers themselves to have a force constant of <1 pN to explain the 1 nN force constant, because there will be at least 1000 chromatin fibers piercing any given chromosome cross-section of area 4 μm². First, this is a rather low value for a chromatin force constant because a doubling of length would require disruption of linker histones; preliminary data on single chromatin fibers suggest that forces in the 25–100 pN range are required for this (Cui et al., 1998). The alternative is that only a small subset of chromatin fibers in a given cross section support most of the tension, but this implies that the stress is also supported by connections between them. Our result that antihistone has no effect on chromosome elasticity also suggests that we are not observing principally chromatin elasticity. Instead, we propose that chromosome linear elasticity is mainly due to reversible modification of chromosome-folding proteins, which connect chromatin fibers.

Chromosomes Are Irreversibly Lengthened When Slowly Extended More Than Five Times

The elasticity of chromosomes becomes irreversible, i.e., the force observed during retraction is below that found during extension, after extensions more than five times at strain rates small enough to allow stress relaxation to occur: <0.01 s⁻¹ (Figure 3). After such irreversible extension–retraction cycles, chromosomes are permanently lengthened; for example, an eight times extension–retraction cycle results in the chromosome being permanently lengthened by two times when relaxed; after a 25 times extension–retraction, a four times permanently extended chromosome is obtained. The force at which this hysteresis begins is 5 nN, indicating that a structural element that holds the chromosome together is failing when the chromosome as a whole is under ∼5 nN of stress.

There is no obvious signature of this 5 nN transition, such as a force plateau, that can be seen during initial extension beyond five times. Instead, a smooth, first linear and then slightly concave force–distance response is observed during initial extensions of up to 30 times (Figure 6). The first sign of the 5-nN transition is irreversibility during retraction and then a modified elastic response if extension–retraction cycles are then repeated (Figures 3 and 4). This suggests that the failure occurring near 5 nN is probably not due to breaking of chromosome-folding proteins or protein–chromatin connections; breaking should result in a plateau or drop in force as the chromosome is extended. Instead, this irreversibility is possibly due to overextension of proteins or protein–chromatin connections to the point where they are unable to recover their native conformation. Repeated extension–relaxation cycles to, e.g., 10 times extension (Figure 3) result in a gradual transformation of the force versus distance from a slightly concave shape to a highly convex shape typical of the polymer elasticity of stiff biopolymers (Smith et al., 1992; Kellermayer et al., 1997; Reif et al., 1997; Tskhovrebova et al., 1997). Modifications of nucleosome structure are most likely not contributing to this irreversibility, because antihistone binding does not significantly change for a chromosome extended to 23 times its native length.

A Force Plateau Occurs Near 30-Fold Extension to a Soft Ghost Chromosome

A force plateau at 15–20 nN (Figure 6) begins at 30 times extension and can go out to 100 times extension; extensions beyond this break the chromosome. Dramatic changes in the chromosome coincide with this force plateau: the chromosome is transformed to a dilute ghost state with a low elastic modulus. This state was produced by both slow repeated extension–retraction cycles out to increasing extensions (Figure 5) and by a single, slow extension (Figure 6). There are two requirements for transforming a native chromosome into this distinct state. First, the chromosome must be elongated past 30 times. Second, the chromosome must be extended at strain rates of <0.01 s⁻¹. If the chromosome is extended too quickly, a stiff “thin fiber” is produced instead (Houchmandzadeh et al., 1997). Repeated extension–relaxation cycles as in Figure 4 are not required to produce a ghost state: a single elongation and retraction produce the same state, whereas repeated cycles to extensions of <30 times do not (Figure 3).

A ghost chromosome is up to 10 times longer than native and swollen to a width 1.5 times the native width, and there is a severe reduction in the optical contrast of the chromosome viewed in DIC and phase contrast (Figure 5). The force constant of a ghost chromosome is 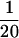of its native value. The fluorescence intensity of a chromosome extended to 50 times, relaxed to zero force, and then labeled with antihistone shows a 300 ± 40% increase in total fluorescence intensity. This suggests that the swelling is not due to a loss of histones. The increase in fluorescence is possibly due to increased accessibility to histones as a result of the chromosome swelling. The chromosome width cannot be measured accurately during the long force–extension experiments because to measure chromosome length a 10× lens with 1 μm resolution is used; however, to the best of our ability to determine it, the swelling occurs as a chromosome is relaxed after being stretched. All of the above changes are consistent with breakage of the connector proteins discussed above starting at a force of 15 nN.

A Rough Model Explaining the Reversible and Irreversible Behavior of a Mitotic Chromosome

Our results suggest that there are chromosome-folding elements, most likely proteins, that first deform and then break in response to applied force. Three regions are observed for the elastic response of these elements. Extensions to five times reversibly extend chromosome-folding elements, so they recover their initial conformation when slowly relaxed. Extensions between 5 and 30 times irreversibly change the chromosome-folding proteins so that when the chromosome is relaxed the elements' conformation is permanently altered. Extensions beyond 30 times irreversibly break or unfold chromosome-folding elements such that their ability to maintain chromosome structure is eliminated.

This model allows for a rough estimate of the number of folding elements supporting the 5-nN failure threshold force, assuming our folding elements to be proteins. The typical force required to start irreversibly changing protein secondary structure is ∼10 pN (Kellermayer et al., 1997); dividing the 5-nN threshold by this value indicates that there are ∼500 connector proteins per chromosome cross section.

Assuming these connectors to be evenly distributed in a chromosome cross section indicates that there are 125/μm², giving an average spacing of 0.1 μm between connectors. This average number per area is converted to a density of approximately 1500 connectors/μm³ by assuming that the connector proteins are uniformly distributed in the chromosome volume. Multiplying the density of proteins by 100 μm³, the volume of the chromosome, results in a total of 1.5 × 10⁵ connector proteins per newt chromosome or 7.5 × 10⁴ per newt chromatid. The ∼10⁶ kb per newt chromatid (Bennett, 1977) indicates that there is approximately one connector protein per 6 kb.

An estimate of the average length of the connector proteins can be roughly calculated from the total work that must be done to reach the end of the initial irreversibility regime, which ends at the 15-nN plateau. This is approximately the area under a curve in Figure 6 from 5 to 30 times extension and is 1 × 10⁹ k_BT. Each of the proposed connector proteins therefore has 6 × 10³ k_BT of work done on it as the chromosome is extended to 30-fold. Because the work that is done unfolding a protein by force is roughly 2 k_BT per residue (Kellermayer et al., 1997), we can estimate the average size of the connector proteins to be roughly 3 × 10³ aa.

A similar argument can be used to estimate the number of proteins supporting the 15-nN plateau force. That the force needed to break a protein chain is roughly 100 pN indicates that there should be roughly 150 connectors per chromosome cross section, consistent with our separate estimate of 500 connectors per cross section made above. Because the plateau begins at 30 times and continues to at least 100 times, the work done in this breakage regime creating a ghost chromosome is roughly 5 × 10⁹ k_BT, indicating that the work done per each of the 1.5 × 10⁵ connectors should be ∼3 × 10⁴ k_BT. To bring a denatured protein to its breaking point requires roughly 10 k_BT of work to be done per residue (Kellermayer et al., 1997; Reif et al., 1997; Tskhovrebova et al., 1997), again consistent with the connectors being ∼3 × 10³ aa.

These force and energy threshold arguments are highly approximate but suggest that the mitotic chromosome is a mass of flexible chromatin fibers that do not have an intrinsic tendency to self-aggregate and are cross-linked together by extensible connector proteins. This protein model gives a rough estimate of the connector protein concentration to be approximately one per 6 kb and on average ∼3000 aa long. Additional evidence for identifying the observed chromosome elasticity with the elasticity of such connector proteins is the general similarity between our results and the results for the elasticity and failure of titin proteins. Finally, SMC-type protein complexes, “condensins,” which are known to have a chromosome-folding function (Hirano and Mitchison, 1994; Hirano et al., 1997), occur in mitotic chromosomes at a level of one per every 5 kb and contain long, hinged coiled-coil domains containing ∼2000 residues (Melby et al., 1998). Thus, the chromosome force–extension behavior described here may be due to the elasticity, unfolding, and breakage of the condensin–SMCs themselves. An alternative protein that could give similar elastic response is titin, which has recently been reported to be present in mitotic chromosomes (Machado et al., 1998).

A Comparison of the Elasticity of In Vivo and In Vitro Assembled Mitotic Chromosomes

Houchmandzadeh and Dimitrov (1999) recently studied the elasticity of “artificial” chromosomes assembled using Xenopus egg extracts by a method similar to this study. Much of the force–extension behavior of the two systems agree: extensions of less then five times are reversible, repeated extensions to increasing maximum lengths result in hysteresis and a gradual reduction in the Young modulus, and single long extensions result in a force plateau; however, there are some differences between the two systems. The average Young modulus of an in vitro assembled chromosome is approximately four times higher then the average Young modulus of an in vivo assembled chromosome. This difference may be due to the in vivo and in vitro chromosomes being derived from different animals. It could also be explained by cell-cycle differences, because a fivefold decrease in the Young modulus from prometaphase to metaphase has been observed for newt chromosomes (Houshmandzadeh et al., 1997). Also, Houchmandzadeh and Dimitrov (1999) do not observe swelling or a ghost morphology when a chromosome is extended into the force plateau region. Instead, thinned regions of the chromosome are produced. This could be a result of extending the chromosome quickly; strain rates of ∼0.1 s⁻¹ were used. Indeed, if we stretch newt chromosomes at a rate of 0.1 s⁻¹, we then observe permanent thinning and no ghost.