Ab Initio Study of ¹³C_α Chemical Shift Anisotropy Tensors in Peptides

Abstract

This study reports magnitudes and the orientation of the ¹³C_α chemical shift anisotropy (CSA) tensors of peptides obtained using quantum chemical calculations. The dependency of the CSA tensor parameters on the energy optimization of hydrogen atom positions and hydrogen bonding effects and the use of zwitterionic peptides in the calculations are examined. Our results indicate that the energy optimization of the hydrogen atom positions in crystal structures is necessary to obtain accurate CSA tensors. The inclusion of intermolecular effects such as hydrogen bonding in the calculations provided better agreement between the calculated and experimental values; however, the use of zwitterionic peptides in calculations, with or without the inclusion of hydrogen bonding, did not improve the results. In addition, our calculated values are in good agreement with tensor values obtained from solid-state NMR experiments on glycine-containing tripeptides. In the case of peptides containing an aromatic residue, calculations on an isolated peptide yielded more accurate isotropic shift values than the calculations on extended structures of the peptide. The calculations also suggested that the presence of an aromatic ring in the extended crystal peptide structure influences the magnitude of the δ₂₂ which the present level of ab initio calculations are unable to reproduce.

Introduction

Determination of high-resolution three-dimensional structure and dynamics of peptides and proteins is one of the major goals of structural proteomics. The knowledge of protein structure is essential in order to effectively manipulate and regulate its function, making the determination of protein structure indispensable to virtually every field of structural biology and proteomics. High-resolution NMR spectroscopy has been extensively used to solve the structures of globular proteins. Similarly, solid-state NMR techniques have been used to study membrane-associated proteins, fibrils, and microcrystalline proteins. These applications of NMR spectroscopy utilize CSA tensors and also indicate that it is essential to understand the variation of the CSA tensor.^1-7 Particularly, interpretations of results from applications of TROSY⁸ and PISEMA⁹ and experiments that measure relaxation parameters require well-characterized CSA tensors.¹⁰ In addition, CSA tensors are essential for NMR experimental studies on fully or partially aligned samples.¹¹ Therefore, accurately determined CSA tensors are absolutely essential, and understanding the variation of CSA tensors would be of considerable importance in determining the structure, dynamics, and topology of proteins using NMR spectroscopy.

However, using NMR spectroscopy alone, it is often difficult to completely characterize and understand the variation of the CSA tensor. On the other hand, quantum chemical calculations can be utilized in the determination of the CSA tensor of an NMR active nucleus. Quantum chemical calculations can be used to efficiently observe the behavior of CSA tensors when spectroscopic methods are difficult to carry out. In addition, this method can be used as a predictive tool for protein structure, or as an aid to both solution and solid-state NMR studies. In this paper, we report ¹³C_α CSA tensors determined from quantum chemical calculations and the calculated results are compared with experimentally determined values.

Recently, NMR studies have reported the CSA tensors of ¹³C_α on a few short peptides.^2,12-17 It has been shown that the isotropic chemical shift value of ¹³C_α depends on the backbone conformation of a peptide. This is due to changes in individual CSA tensor elements, as has been shown that the variation in the span of ¹³C_α CSA correlates with the protein secondary structure.¹ Theoretical studies reported in the literature have shown that the ¹³C_α CSA tensor is influenced by a number of structural factors.^18-20 In addition to the identity of the side chain, the backbone and side chain conformation (where applicable) have been shown to have the largest influence on the magnitudes of the principal components of the tensor,^18,20 while bond lengths and bond angles between ¹³C_α and its neighbors have a lesser effect.¹⁸

All these previous theoretical studies on ¹³C_α tensors were based on single amino acids or N-formyl amino acid amide fragments.^18,20 The effects of neighboring residues and intermolecular interactions, such as hydrogen bonding, have been largely ignored. Hydrogen bonding has been shown to have a significant effect on the amide-¹⁵N nucleus.^21,22 It is likely that the ¹³C_α also experiences a similar effect as a result of hydrogen bonding. It is our intention to systematically investigate the ¹³C_α CSA tensor in peptides using quantum chemical calculations. We will specifically focus on the effects of intermolecular and intramolecular interactions on the ¹³C_α CSA tensor. In addition, we show that our calculated values are in good agreement with the experimentally determined CSA tensor data and are more accurate than the previously reported ab initio values.

Method

Calculation of ¹³C_α chemical shift tensors was carried out using the gauge-including atomic orbitals (GIAO) method²³ and DFT level of theory in the Gaussian98 program.²⁴ B3PW91 hybrid functionals were used for density functional calculations. Several different basis sets were used, ranging from 4-31G to 6-311++G(2d,p), to understand the effect of the basis set size on the accuracy of CSA tensors. These calculations were performed on several different peptides. Except for α-glycyl-glycine (*GG), which was obtained from a neutron diffraction study,²⁵ structures for all other peptides were obtained from reported X-ray data: l-alanyl-l-serine (*AS),²⁶ l-alanyl-glycine (*AG and A*G),²⁷ l-alanyl-l-aspartic acid (A*D and *AD),²⁸ glycyl-l,d-phenylalanine (*GF),²⁹ d,l-alanyl-l,d-methionine (*AM),³⁰ glycyl-l-asparagine (*GN),³¹ l-alanyl-l-alanyl-l-alanine (*AAA and A*AA),³² α-l-glutamyl-glycine (E*G),³³ glycyl-l-alanyl-l-leucine trihydrate (G*AL•3H₂O),³⁴ glycyl-glycyl-glycine (G*GG),³⁵ glycyl-glycyl-l-valine dihydrate (G*GV•2H₂O and GG*V•2H₂O),³⁶ l-alanyl-glycyl-glycine monohydrate (A*GG•H₂O),³⁷ l-valyl-glycyl-glycine (V*GG),³⁸ l-phenylalanyl-glycyl-glycine (F*GG),³⁹ l-prolyl-glycyl-glycine (P*GG),⁴⁰ tryptophanyl-glycyl-glycine dihydrate (W*GG•2H₂O),⁴¹ l-tyrosyl-glycyl-glycine monohydrate (Y*GG•H₂O),⁴² and N-acetyl valine (Ac-V)⁴³ (where * indicates the amino acid residue of interest). Since the position of hydrogen atoms in X-ray crystal structures are inherently inaccurate, energy minimization was performed on the hydrogen atoms of the crystal structures using the PM3⁴⁴ semiempirical level of theory in the program CAChe.⁴⁵ This step leaves the positions of the heavy atoms unaltered. Gaussian98 calculations provide absolute shielding values, which were arbitrarily assigned such that σ₃₃ ≥ σ₂₂ ≥ σ₁₁. The absolute shielding values obtained from all calculations were converted to chemical shifts (δ₁₁ ≥ δ₂₂ ≥ δ₃₃) relative to the absolute shielding of liquid TMS at room temperature of 184.1 ppm⁴⁶ such that

$${\delta }_{\text{calcd}}=-{\sigma }_{\text{absolute}}+184.1$$

The CSA tensor orientation is described relative to the peptide backbone. The tensor orientation can be described either as a set of Cartesian axes with respect to the C_α—H bond vector or as another set of axes with respect to the C_α—N bond vector; hence, data for two different sets of axes are reported.

To efficiently calculate CSA values on the peptides of interest, four parameters were considered in our calculations: (1) basis set size, (2) energy optimization of hydrogen atom position, (3) the effect of hydrogen bonding on peptides, and (4) the use of zwitterionic structures in calculations. Our results on the basis set size dependence of the CSA tensor is given in the Supporting Information. These results are in good agreement with previous studies.^47-49 The locally dense basis set method,⁵⁰ which involved using a larger basis set, 6-311++G(2d,2p), on the neighboring atoms of C_α and 4-31G on all other atoms, was used in all other calculations presented in this paper.

Results and Discussion

Effect of Energy Optimization of H Atom Positions in Crystal Structures. Previous ab initio studies on small N-formyl amino acid amide fragments of the peptide backbone suggested that the use of ab initio geometry optimized structures has a very small effect on the observed ¹³C shieldings.^6,18,20,51 However, a recent study on melanostatin that compared the results of quantum chemical calculations with accurately determined ¹³C_α and ¹⁵N CSA tensors from solid-state NMR experiments suggested that energy optimization significantly improved the calculated values.⁵² In this study, peptide structures were derived from X-ray diffraction data. Since X-ray crystal structures do not accurately define the location of hydrogen atoms, energy minimization using PM3⁴⁴ parameters was used to optimize hydrogen atom positions without altering the coordinates of other atoms in the peptide. Calculations were performed on nonoptimized structures (hydrogen positions were obtained directly from X-ray crystal data) and compared to the data obtained from the optimized structures of the same peptides (see Supporting Information). Calculated chemical shift values for nonoptimized structures tend to be significantly lower than those for optimized structures. The difference is as large as 35 ppm. Comparison of calculated and experimental data for A*AA, A*G, E*G, and Ac-*V (see the last table in the Supporting Information) suggests that calculations on optimized structures considerably improved the accuracy of CSA values. Our calculations also suggested that, like the magnitudes of the principal components of the tensor, the angles defining the orientation of the ¹³C_α CSA tensor in the molecular frame are also affected by the optimization of hydrogen atom positions in the crystal structures (see Supporting Information). The tensor orientation relative to the C_α—H bond, in particular, differs greatly between optimized and nonoptimized structures because the positions of the hydrogen atom differ between optimized and nonoptimized structures. These results suggest that energy optimization of hydrogen atom positions is necessary in the calculation of CSA tensors when using structures derived from X-ray crystal data.

Effects of Intermolecular Interactions. Protein structure is greatly influenced by intermolecular effects such as hydrogen bonding, van der Waals forces, and hydrophobic interactions. Previous studies on the quantum chemical calculations of amide-¹⁵N CSA tensors of peptides suggested that hydrogen bonding interactions significantly influence the magnitudes but not the orientation of the principal elements of the tensor.^21,53,54 In this study, calculations were performed on extended and isolated crystal structures of the peptides in order to understand the effect of intermolecular forces on the ¹³C_α CSA tensor. To keep the calculation time within reasonable limits, only the functional groups of nearby molecules having atoms within 3 Å of the ¹³C_α center of interest were considered. The resulting simplified version of the crystal structure for GAL•3H₂O along with the isolated peptide structure is shown in Figure 1.

Figure 1.

X-ray crystal structure³⁴ of single-unit (A) and extended (B) forms of GAL•3H₂O.

¹³C_α CSA tensor values calculated from isolated peptides and extended structures are compared in Tables 1 and 2. Both the magnitude and orientation of the principal elements of the tensor significantly differ between the two structures. There is, however, no uniformity in the change between CSA tensors of single peptide structures or extended crystal structures for the peptides studied, indicating that the effects of intermolecular interactions vary from peptide to peptide. These results suggest that inclusion of intermolecular interactions is important in determining accurate ¹³C_α CSA tensors of peptides. This prediction is in good agreement with a recent study that compared ¹³C and ¹⁵N CSA data from quantum chemical calculations and solid-state NMR experiments on melanostatin.⁵²

Table 1.

¹³C_α Chemical Shift Tensors Obtained from ab Initio Calculations of Glycine-Containing Tripeptides^a

peptide	δ11	δ22	δ33	Ω	δiso	C-H δ11b	C-H δ22	C-H δ33	C-N δ11c	C-N δ22	C-N δ33
GGG I	61.7	49.5	20.3	41.4	43.8	141(77)	52(113)	99(153)	39	58	71
II	60.9	50.5	21.5	39.4	44.3	16(121)	105(141)	94(110)	103	82	16
III	62.2	50.2	19.5	42.7	44.0	143(125)	54(119)	98(131)	40	56	72
IV	60.5	50.9	21.3	39.2	44.2	12(106)	95(150)	101(65)	98	42	49
experimentale	58.1	48.9	22.9	35.2	43.3
GGV·2H2O I	71.5	43.1	18.8	52.7	44.5	126(54)	88(36)	36(88)	55	145	87
II	70.8	45.5	18.8	52.0	45.0	125(42)	109(56)	42(65)	65	141	118
III	75.0	41.5	20.8	54.2	45.8	126(47)	83(43)	37(88)	62	152	86
IV	73.4	43.2	21.0	52.4	45.9	123(48)	111(52)	41(66)	61	138	117
experimentale	70.6	42.0	21.7	48.9	44.8
AGG·H2O I	71.2	43.1	9.9	61.3	41.4	102(74)	94(19)	167(81)	40	127	79
II	69.7	45.4	16.1	53.6	43.7	110(65)	126(127)	137(48)	46	53	113
III	74.1	40.4	11.6	62.5	42.0	103(78)	105(12)	160(91)	35	120	74
IV	73.7	40.7	16.3	57.4	43.6	108(66)	143(111)	121(32)	45	63	122
experimentale	69.9	41.8	16.9	53.0	42.9
PGGd I	71.5	40.2	10.3	61.2	40.7	123(63)	75(34)	37(109)	45	131	73
II	70.2	42.7	13.0	57.2	42.0	115(119)	26(121)	92(45)	18	83	74
experimentald	69.4	40.8	18.8	50.6	43.0
VGG I	58.5	48.5	17.5	41.0	41.5	103(84)	13(102)	94(14)	31	99	119
II	59.3	46.2	19.1	40.2	41.5	89(85)	135(28)	45(63)	39	98	128
III	60.3	51.4	18.7	41.6	43.5	100(80)	20(89)	106(9.7)	36	109	119
IV	60.9	48.3	19.6	41.3	42.9	83(86)	140(33)	51(57)	43	92	133
experimentald	57.8	48.1	23.1	34.7	43.0
FGG I	71.9	43.4	19.6	52.3	45.0	107(99)	28(87)	112(9.8)	14	100	100
II	71.4	50.0	26.7	44.7	49.4	125(76)	38(85)	103(15)	33	90	123
III	75.7	42.1	19.5	56.2	45.8	102(97)	23(87)	110(7.7)	20	105	102
IV	74.8	47.8	26.5	48.3	49.7	131(75)	44(83)	102(16)	35	85	125
experimentald	69.6	43.3	20.5	49.1	44.5
YGG·H2O I	69.0	44.7	21.2	47.8	45.0	58(48)	98(73)	33(133)	134	45	81
II	67.5	46.2	25.8	41.7	46.5	111(24)	76(112)	26(80)	87	34	124
III	73.1	43.8	21.8	51.3	46.2	57(53)	92(66)	33(133)	143	55	81
IV	71.2	43.8	27.0	44.2	47.3	113(19)	78(105)	27(80)	92	35	125
experimentald	66.3	41.3	25.0	41.3	44.2
WGG·2H2O I	76.2	46.1	16.9	59.3	46.4	113(125)	97(47)	156(64)	22	69	94
II	68.8	48.3	18.4	50.4	45.2	123(115)	57(83)	130(26)	21	69	88
III	81.4	43.8	19.2	62.2	48.1	124(122)	86(62)	146(45)	31	60	97
IV	72.6	45.8	19.6	53.0	46.0	116(127)	92(120)	26(128)	28	118	87
experimentald	69.5	44.2	19.2	50.3	44.3

^aResults obtained from calculations on the central glycine residue from neutral isolated (I), neutral extended crystal structure (II), isolated zwitterionic (III), and zwitterionic extended crystal structure (IV) peptides. The magnitudes of the principal components are given with respect to TMS (at 184.1 ppm).46

^bC-H δ₁₁, C-H δ₂₂, and C-H δ₃₃ are determined relative to the C-H bond vector and given in degrees. Angles with respect to the other hydrogen C-H bond for C-H δ₁₁, C-H δ₂₂, and C-H δ₃₃ are given in parentheses.

^cC-N δ₁₁, C-N δ₂₂, and C-N δ₃₃ are determined relative to the C-N bond vector and given in degrees.

^dDue to the unique nature of the proline residue, a zwitterionic structure is not possible.

^eExperimental data obtained from ref 17.

Table 2.

¹³Cα Chemical Shift Tensors Obtained from ab Initio Calculations on Peptides^a

peptide	δ11	δ22	δ33	Ω	δiso	C-H δ11b	C-H δ22	C-H δ33	C-N δ11c	C-N δ22	C-N δ33
*AAA I	78.6	59.4	39.0	39.6	59.0	148	87	58	77	18	102
II	66.2	59.2	35.8	30.4	53.7	130	47	70	68	117	36
A*AA I	68.6	56.6	30.1	38.5	51.8	19	104	102	108	126	42
II	67.4	55.7	28.1	39.3	50.4	39	118	116	111	49	132
experimental16	70.2	54.9	23.6	46.6	49.6
*AG I	67.8	60	30.6	37.2	52.8	102	151	65	144	54	90
II	65.8	61.8	26.6	39.2	51.4	167	88	103	59	112	141
Zw	70.9	61.4	23.1	47.8	51.8	166	103	84	56	139	70
experimental16	58.7	56.7	34.0	24.7	49.8
A*G I	69.5	47.7	15.5	54.0	44.2	117(88)	69(41)	35(130)	124	137	113
II	71.1	47.9	16.4	54.7	45.1	106(21)	78(111)	20(87)	127	135	112
Zw	78.0	40.3	18.4	59.7	45.5	104(30)	77(120)	20(87)	135	126	113
experimental16	66.6	43.7	24.7	41.9	45.0
*AD I	67.7	62.2	27.7	40.0	52.5	124	41	110	85	87	6
II	65.2	63.2	25.6	39.6	51.3	113	50	131	84	64	26
experimental16	57.4	55.9	34.5	22.9	49.3
A*D I	70.4	56.2	28.0	42.4	51.5	75	133	133	35	62	72
II	70.8	58.7	26.8	44.0	52.1	66	80	154	56	64	46
experimental16	71.8	57.9	28.4	43.4	52.7
*AM I	65.3	61.4	34.9	30.4	53.9	95	107	163	141	52	81
II	77.4	54.7	35.5	41.9	55.9	104	136	131	147	76	61
*AS I	60.7	58.8	46.7	14.0	55.4	74	151	114	78	45	133
II	61.4	55.2	39.0	22.3	51.9	109	66	148	99	47	44
*GG I	51.3	27.1	-19.8	71.1	19.5	122(34)	100(61)	146(106)	74	151	67
II	56.7	40.9	22.4	34.3	40.0	104(88)	16(104)	83(166)	137	121	64
experimentald	55.8	39.5	23.5	32.3	39.6
*GN I	67.2	54.5	15.1	52.1	45.6	81(30)	11(120)	95(87)	122	100	34
II	65.2	53.7	13.4	51.7	44.1	100(33)	13(103)	99(120)	82	98	11
*GF I	58.2	40.8	-6.8	64.9	30.7	21(102)	108(54)	81(39)	129	141	94
II	73.8	52.6	25.6	48.2	50.7	105(103)	146(65)	60(152)	123	88	147
E*G I	68.0	38.1	18.6	49.4	41.6	138(94)	132(56)	92(146)	30	120	91
II	79.1	36.0	10.7	68.4	41.9	36(90)	80(53)	56(37)	49	125	120
experimentald	78.0	37.5	10.5	67.5	42.0
Ac-V I	85.4	50.6	36.3	49.1	57.4	105	59	144	16	101	102
II	86.6	52.5	35.8	50.9	58.3	29	80	117	123	33	92
experimental4	82.6	53.2	36.1	46.5	57.3	22				36
G*AL·2H2O I	74.2	47.8	36.2	38.0	52.7	82.1	157	112	101	94	12
II	74.1	48.3	38.0	36.1	53.5	68.1	135	127	147	69	114
Zw	79.1	48.2	41.6	37.5	56.3	64	130	129	154	77	112
experimental15	70.0	51.0	35.0	35.0	52.0	116	46	70	108	40	56
GG*V·2H2O I	79.7	61.3	48.1	31.6	63.0	59.8	144	73	60	89	150
II	82.2	61.3	50.7	31.5	64.7	42.8	70	126	65	110	32
Zw	81.1	69.1	54.3	26.8	68.2	54	117	48	58	42	114
experimental15	75.0	70.0	51.0	24.0	65.3	155	89	115	63	28	98

^aResults obtained from isolated peptide with geometry optimization (I), extended crystal structure of the peptide (II), and extended crystal structures of zwitterionic peptides (Zw) are compared. The magnitudes of the principal tensor components are given with respect to TMS (at 184.1 ppm).⁴⁶

^bAngles C-H δ₁₁, C-H δ₂₂, and C-H δ₃₃ are determined relative to the C-H bond vector and given in degrees. Angles with respect to the other hydrogen C-H bond for C-H δ₁₁, C-H δ₂₂ and C-H δ₃₃ are given in parentheses.

^cC-N δ₁₁, C-N δ₂₂, and C-N δ₃₃ are determined relative to the C-N bond vector and given in degrees.

^dUnpublished data measured from 2D PASS solid-state NMR experiments on powder samples of peptides as explained in our previous publication.¹⁴

Comparison to Experimental Results. Experimentally obtained accurate magnitudes of the principal elements of the ¹³C_α CSA tensor of central glycine residues of several tripeptides enabled the examination of the accuracy of our calculated values.¹⁷ Single peptide structures and extended crystal structures of several glycine-containing tripeptides derived from X-ray crystal structures^35-42 were used to calculate CSA tensors; the data are given in Table 1 and are compared in Figure 2. Calculated values agree well with experimental CSA tensor data of the peptides; calculated isotropic chemical shifts are within ±2.7 ppm for calculations on single peptide structures, and within ±1.5 ppm for calculations on extended crystal structures with the exception of F*GG. In addition, the magnitude of δ₁₁ is overestimated for most of the centers examined, and the magnitude of δ₃₃ is generally underestimated in these peptides, with the exception of calculations on extended crystal structures of the aromatic-residue-containing peptides. For F*GG, the single peptide structure yields a less accurate isotropic shift value. The reasoning can be traced back to the principal elements of the tensor, where the extended crystal structure overestimates δ₂₂ and δ₃₃ by over 6 ppm each. In fact, extended crystal structures of all aromatic-residue-containing peptides overestimate δ₂₂ by 4-6.6 ppm, though the overestimation of δ₃₃ in the F*GG extended crystal structure makes the isotropic shift less accurate than the other aromatic-residue-containing peptides. Single-peptide structures of the aromatic-residue-containing peptides yield more accurate isotropic shifts, within ±2.1 ppm. This implies that the presence of an aromatic ring in the extended crystal peptide structure influences the magnitude of the δ₂₂ which the present level of ab initio calculations are unable to reproduce.

Figure 2.

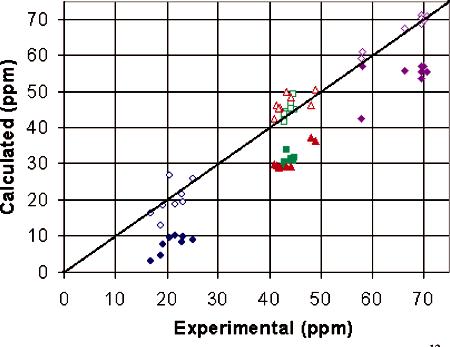
Comparison of the magnitudes of the principal components of the ¹³C_α CSA tensor obtained from previous²⁰,⁵⁵ (filled symbols) and present (open symbols) ab initio calculations (locally dense basis set) and solidstate NMR experiments.¹⁷ Values of δ₁₁, δ₂₂, δ₃₃, and δ_iso are represented by diamonds, triangles, circles, and squares, respectively.

Since these are short peptides, charges on the terminal residues could affect the CSA tensor values. The peptide crystals from which structures were derived contained zwitterionic peptides.^35-42 To determine if the zwitterionic nature of these peptides affects the ¹³C_α CSA tensor, calculations were carried out on zwitterionic structures of these tripeptides (both isolated peptide and extended crystal structures), and the results are compared with the values obtained from neutral peptides (Table 1). With the exception of G*GG, the calculations on zwitterionic peptides (both single and extended crystal peptides) yielded slightly more accurate results for the most shielded tensor element, δ₃₃· However, the least shielded element, δ₁₁, is overestimated to a greater extent in zwitterionic peptides than in neutral peptides. For peptides (F*GG, Y*GG•H₂O, and W*GG•2H₂O) containing an aromatic residue, calculations of extended crystal structures of zwitterionic structures do not grossly overestimate the δ₂₂ component as neutral peptide extended crystal structure calculations did (although the δ₂₂ component of F*GG is still 4.5 ppm greater than the experimentally observed value), indicating that the use of zwitterionic structures in calculations containing aromatic residues near the center of interest may yield more accurate results.

When taken together, these data indicate that extended peptide structures of neutral peptides give the most accurate CSA tensor results as compared to experimental data with the exception of aromatic-residue-containing peptides. Single-peptide structures give slightly less accurate results than extended crystal structures, though they appear to be more accurate in the calculation ¹³C_α CSA tensors when the neighboring amino acid contains an aromatic ring. Calculated isotropic shifts are in excellent agreement with the experimental data, indicating that the summation of the errors in the calculated magnitudes of the principal elements cancel out.

Comparison with Previous ab Initio Data. The availability of solid-state NMR experimental¹⁷ and structural data on a large number of glycine-containing tripeptides^35-42 allows for the comparison of theoretical data obtained in this study with the data obtained in previous ab initio studies of ¹³C_α CSA tensors on the N-formyl glycyl amide fragment.²⁰ Data obtained from calculations on extended crystal structures as well as from the glycine shielding surfaces from the previous study²⁰ are correlated with the experimental data¹⁷ in Figure 2. A recent solid-state NMR experimental study¹⁷ showed that the ab initio calculations of ¹³C_α CSA span from the previous report correlate well with the experimental data. However, as seen in Figure 2, the ab initio calculations of Sun et al. consistently underestimated the magnitudes of the principal components of the CSA tensor and the isotropic shift⁵⁵ (absolute shielding values were converted to chemical shifts). Our calculations on the same peptides showed much better correlation between theoretical and experimental values of both the principal tensor elements and (especially) the isotropic shift. This implies that the energy optimization of the H atom positions in crystal structures and the inclusion of hydrogen bonding interactions are important in determining the CSA tensors accurately. Also, the identities of the neighboring residues of the ¹³C_α of interest are important to consider in the calculation of the magnitude of the CSA tensor: the presence of a neighboring residue cannot be substituted by an N-formyl or amide-protecting group on either side of the residue of interest.

Comparison to Additional Experimental Data. The availability of solid-state NMR experimental data on A*AA, *AG, A*G, *AD, A*D, *GG, E*G, GG*V•2H₂O, G*AL•3H₂O, and Ac-V allows for additional comparison of our calculation methods.^12-14 For the ¹³C_α centers examined in this section, isotropic shift values show a high degree of accuracy with respect to experimentally determined values (Table 2). However, the magnitudes of the principal elements of the tensor differ greatly for some of the peptides examined. Most notable are the tensor elements of *AG, *AD, and GG*V extended crystal structures. The magnitude of δ₁₁ is overestimated for most of the centers examined, and the magnitude of δ₃₃ is generally underestimated in the glycine-containing peptides examined earlier; however, this trend is less clear among these peptides, especially in the results obtained for δ₁₁ from calculations on single-peptide structures. Similarly, δ₃₃ is not uniformly underestimated in these calculations. However, with some peptides, the individual tensor components are all close to experimental values, including the tensor span, Ω. A*D, *GG, E*G, and G*AL•3H₂O all have tensor spans within 2.0 ppm (for extended crystal structures).

We were also interested in observing the effects that charge on terminal residues would have on CSA tensors in these peptides. Zwitterionic forms of the peptides were used in the calculations on the extended crystal structures of GG*V•2H₂O, *AG, A*G, and G*AL. The results obtained show that there was no significant improvement in the isotropic shift as compared to calculations on neutral extended peptide structures. In addition, there is no improvement in the tensor span, and individual tensor elements are less accurate than calculations on neutral peptides, except for δ₂₂ of GG*V. These results indicate that the calculation of zwitterionic peptides does not improve the calculated values of the principal tensor elements relative to experimentally obtained results, which is consistent with the results obtained from the glycine-containing tripeptides examined earlier.

The accuracy of the angles defining the tensor obtained by our calculation methods can be estimated by comparing calculated results to experimental results available for Ac-V, GG*V•2H₂O, and G*AL•3H₂O^12,13 (Table 2). For Ac-V, tensor orientation angles between C—H and δ₁₁ and C—N and δ₂₂ measured using solid-state NMR experiments on a powder sample were reported to be 22°(158°) and 36°(144°), respectively.¹² Angles calculated using an isolated Ac-V peptide are 75°(105°) and 80°(100°), respectively, differing greatly from the experimental values. However, calculations on the extended crystal structure provided tensor orientation angles that are much closer to the experimental values: 29°(151°) and 33°(147°). This indicates that it is likely that intermolecular effects, such as hydrogen bonding, influence tensor orientation angles. However, the tensor orientation angles calculated for GG*Vδ2H₂O and G*ALδ3H₂O extended crystal structures do not match experimentally obtained values. It should be noted that the values obtained from previous ab initio studies²⁰ also do not match well with the experimental results as shown in ref 13. Since values obtained for all other peptides match well with the experimental data, the inability to reproduce the experimental results for GG*Vδ2H₂O and G*ALδ3H₂O may be because of the difference in the X-ray crystal structures used to calculate the CSA tensors and that of the powder samples used in the experimental studies. On the other hand, inclusion of long-range electrostatic interactions⁵² in the calculations may provide results that will better agree with the experimentally determined results. Also, the availability of more experimentally determined CSA tensor orientations would be useful to confirm the role of longrange electrostatic interactions. Nevertheless, results in this study suggest that the basis set size and selection have minimal influence on the angles that define the orientation of the tensor.

Conclusions

The goal of this study was to investigate the variation of ¹³C_α CSA tensors in small peptides and establish an accurate method to calculate them. A number of small peptides were studied with respect to several different variables using the quantum calculation method. The use of X-ray crystal structures as a basis for constructing the peptides for calculation, as well as the use of locally dense basis sets and geometry optimization of hydrogen atoms, proved to be a reliable technique. Calculations on extended crystal structures showed that the magnitudes of the principal tensor elements are sensitive to intermolecular effects, while the orientation of the tensor is very sensitive to such effects. The values obtained from different peptides suggest that the CSA dependency on intermolecular interactions is not uniform and is likely related to the location of hydrogen bonding partners. Calculated values from the extended crystal structures are in good agreement with experimental results. Use of zwitterionic structures, both single-peptide and extended crystal structures, in calculations do not improve the accuracy of the least and most shielded components, while they do improve the accuracy of the δ₂₂ component of the CSA tensor. Based on the accuracy of our calculations of ¹³C_α CSA tensors, the method outlined in this paper establishes a reliable means to predict the magnitude of the principal elements of ¹³C_α CSA tensors. While the calculated angles defining the orientation of the tensor for N-acetyl-valine matches well with the experimental data, more experimental data are needed to evaluate the accuracy of the calculated values. We believe that the results reported in this paper will be useful in the structural studies of peptides and proteins using both solution and solid-state NMR techniques.