Abstract
The molecular machinery of cell cycle control is known in more detail for budding yeast, Saccharomyces cerevisiae, than for any other eukaryotic organism. In recent years, many elegant experiments on budding yeast have dissected the roles of cyclin molecules (Cln1–3 and Clb1–6) in coordinating the events of DNA synthesis, bud emergence, spindle formation, nuclear division, and cell separation. These experimental clues suggest a mechanism for the principal molecular interactions controlling cyclin synthesis and degradation. Using standard techniques of biochemical kinetics, we convert the mechanism into a set of differential equations, which describe the time courses of three major classes of cyclin-dependent kinase activities. Model in hand, we examine the molecular events controlling “Start” (the commitment step to a new round of chromosome replication, bud formation, and mitosis) and “Finish” (the transition from metaphase to anaphase, when sister chromatids are pulled apart and the bud separates from the mother cell) in wild-type cells and 50 mutants. The model accounts for many details of the physiology, biochemistry, and genetics of cell cycle control in budding yeast.
INTRODUCTION
To reproduce itself, a cell must duplicate all its components and separate them, more or less evenly, to two daughter cells, so that each daughter has the information and machinery necessary to repeat the process (Murray and Hunt, 1993; Alberts et al., 1994, chap. 17). In general, eukaryotic cells replicate and partition their genetic material in two distinct, coordinated processes. During S phase, the DNA molecule in each chromosome is precisely replicated to form two identical sister chromatids that are held together by cohesins (tethering proteins). During M phase, the cell builds a mitotic spindle, condenses its replicated chromosomes, aligns them on the midplane of the spindle, and then, at anaphase, removes the cohesins and separates sister chromatids to opposite poles of the spindle (Biggins and Murray, 1998; Zachariae and Nasmyth, 1999). Shortly after anaphase, the cell divides into two daughter cells, each one containing a complete set of chromosomes. S and M phases are usually separated temporally by gaps (G1 and G2 phases).
It is crucial that each DNA molecule be replicated once and only once per cycle in eukaryotes. Were this not the case, then each chromosome would contain multiple sister chromatids, and segregation of the correct balance of DNA molecules to the spindle poles would be a difficult affair. This requirement is imposed by a set of proteins called licensing factors (Mcm2–7 and Cdc6). In the gap between the end of mitosis and the beginning of S phase, licensing factors bind to and prime the origins of replication. At the G1/S boundary, several cyclin-dependent protein kinases (CDKs) become active and initiate replication at licensed origins. In the process, the CDKs apparently incapacitate the license at each origin that fires. As long as CDKs remain active, throughout S, G2, and M, licensing factors remain incapacitated, and rereplication is impossible (Botchan, 1996; Wuarin and Nurse, 1996; Leatherwood, 1998).
It is also crucial that the cell does not commence anaphase (sister chromatid separation) until DNA replication is complete and each pair of sister chromatids is properly aligned on the metaphase plate. Completion of DNA synthesis is usually a requirement for entry into M phase, whereas chromosome alignment is required for activation of the anaphase-promoting complex (APC) that initiates degradation of an inhibitor of sister chromatid separation (Amon, 1999; Nasmyth, 1999). At anaphase, the APC also mediates proteolysis of mitotic cyclins, thereby destroying CDK activities and allowing licensing factors to accumulate and origins to be primed for replication.
Third, the cell must coordinate its DNA replication–segregation cycle to cell growth, to maintain cell size within certain bounds, generation after generation. To achieve balanced growth and division, it is likely that some essential step in the cell cycle depends on the cell growing to a critical mass (Carter, 1981; Polymenis and Schmidt, 1999).
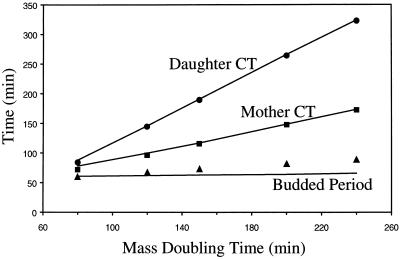
Although most eukaryotic cells satisfy these three requirements of DNA replication and division, there are notable exceptions, such as the cell cycles that produce oocytes, embryonic blastulas, and megakaryocytes. Furthermore, there are many variations in specific details from one cell type to another. For instance, budding yeast cells are peculiar in that they divide asymmetrically (Hartwell and Unger, 1977; Lord and Wheals, 1980). At Start, a bud emerges from the mother cell, and subsequent cytoplasmic growth is directed primarily to the bud. S and M phases are completed before the bud grows as large as its progenitor; thus cell separation produces a large mother cell and a small daughter cell. Shortly after division, the mother cell produces a new bud, but the daughter cell enters an extended G1 phase, during which it apparently must grow to a critical size before it can make a bud of its own. The whole process is quite sensitive to growth rate. At the fastest growth rates, division is almost symmetrical, and daughter cells have a short G1 phase as well. As growth rate is decreased, cell division becomes increasingly asymmetrical, and the G1 period of the daughter cell lengthens dramatically, whereas that of the mother cell remains relatively constant (Figure 1).
Figure 1.
Mother and daughter cycle times (CT) as functions of the mass-doubling time of a culture. Lines, model simulations, calculated from the differential equations and parameter values in Tables 1 and 2. Symbols, experimental results from Lord and Wheals (1980): interdivision times of mothers (▪) and daughters (●) and intervals from bud emergence to division (▴).
Another peculiarity of budding yeast is that cells progress simultaneously through S and M phases (DNA synthesis, spindle formation, and chromosome alignment), without any noticeable condensation of chromosomes. In this case, completion of DNA synthesis is not required for the early events of M phase but is required for the metaphase–anaphase transition (Nasmyth, 1995).
Nasmyth (1996) has proposed that the heart of the budding yeast cell cycle is an alternation between two self-maintaining states: the G1 state, in which APC is active, CDK activity is low, and origins are licensed; and the S/M state, in which APC is shut off, CDK activity is high, and origins are fired and incapable of firing again. The G1 state is self-reinforcing because APC destroys S-phase and M-phase cyclins. The S/M state is self-reinforcing, suggested Nasmyth (1996), because CDKs inactivate the APC by phosphorylating some of its components. Although Nasmyth's proposal contradicted conventional wisdom that B-type cyclins activate the APC, recent experiments in budding yeast confirmed his hypothesis (Amon, 1997; Zachariae et al., 1998; Jaspersen et al., 1999). In Nasmyth's view, the budding yeast division cycle is an alternating sequence of “Start” transitions from G1 to S/M and “Finish” transitions from S/M back to G1. Our goals are to show how these two stable cell cycle states (G1 and S/M) arise from the underlying molecular machinery and to reveal the dynamical nature of the transitions (Start and Finish) between them.
To this end, we summarize experimental results from many sources to construct a consensus picture of the molecular signals controlling cell cycle events in budding yeast. The present picture is built on a simpler model of cell cycle controls in budding yeast (Tyson et al., 1995) and on a mathematical description of Nasmyth's alternating-states hypothesis (Novak et al., 1998). (Those models, along with earlier studies and reviews [Novak and Tyson, 1993, 1995, 1997; Tyson et al., 1996, 1997], should be consulted for an introduction to our theoretical methods, strategies, and tools.)
After casting the mechanism into a set of kinetic equations, we study the dynamical properties of the control system by numerical simulations. Experimental data are used to estimate the crucial kinetic parameters in the model. Then the model is compared with the phenotypes of mutant cells in which various components of the control system are knocked out or overexpressed.
The model, which accounts for most of the distinctive characteristics of the budding yeast cell cycle, is valuable in bringing together a huge amount of hard-won experimental data in a convenient mathematical repository. As experimentalists think about yet unknown details around the “edges” of the consensus picture, the model can be used to explore the properties of hypothetical mechanisms. As new advances are made, the model can be extended to give an ever more comprehensive picture of cell cycle controls in budding yeast.
A CONSENSUS PICTURE OF CELL CYCLE CONTROLS IN BUDDING YEAST
Cyclin-dependent Kinase Activities
Major cell cycle events in budding yeast are controlled by a single CDK (Cdc28) in conjunction with two families of cyclins: Cln1–3 and Clb1–6 (Nasmyth, 1993; Mendenhall and Hodge, 1998). Cln1/Cdc28 and Cln2/Cdc28 play major roles in budding and spindle pole body duplication. Cln3/Cdc28 seems to govern the size at which newborn cells execute Start. Clb5/Cdc28 and Clb6/Cdc28 are essential for timely DNA replication. Clb3/Cdc28 and Clb4/Cdc28 seem to assist in DNA replication and spindle formation. Clb1/Cdc28 and Clb2/Cdc28 are necessary for proper completion of mitosis.
The roles of these cyclins overlap. All the single mutants are viable and nearly normal, except cln3 mutants, which execute Start at about twice the size of wild-type cells (Dirick et al., 1995). (Notation, for example, wild-type allele = CLN3, recessive mutant allele = cln3, dominant mutant allele = CLN3D, and gene product = Cln3.) Although the triple-cln mutant, cln1 cln2 cln3, is lethal (Richardson et al., 1989), the cln1 cln2 double mutant is large and viable and able to bud. Apparently any one of the Clns can do the essential jobs of the other two, if the cell is large enough. The double mutant clb3 clb4 is normal (Richardson et al., 1992; Schwob and Nasmyth, 1993), so their roles can be played by other Clbs. Because a clb5 clb6 mutant cell carries out DNA synthesis (although with some delay), whereas a cell with all six CLB genes deleted (clb1–6) does not, Clb1–4 can trigger DNA synthesis in the absence of Clb5–6 (Schwob et al., 1994). Only the Clb1–2 pair is special in the sense that at least one of them is necessary for completing mitosis (Surana et al., 1991). Because of these redundancies, it will be sufficient to consider the interaction of Cdc28 with only four classes of cyclins: “Cln2” (representing the combined activities of Cln1 and Cln2), Cln3, “Clb2” (Clb1 and Clb2 combined), and “Clb5” (Clb5 and Clb6 combined). We do not keep track of Clb3–4 in this model.
Regulation of Cyclin-dependent Kinase Activities
Cyclin/Cdc28 activities come and go in a characteristic sequence during the budding yeast cell cycle. Regulation is achieved mainly through the synthesis and degradation of cyclin components and of the Clb-dependent kinase inhibitor Sic1. Cln3 is present at low and nearly constant levels throughout the cell cycle; Cln2 and its associated kinase activity are maximal at Start (Wittenberg et al., 1990; Tyers et al., 1993). The pattern of Clb5 is similar to that of Cln2 (Schwob and Nasmyth, 1993), whereas Clb2 and its associated kinase activity peak ∼10 min before anaphase (Surana et al., 1991). Furthermore, Sic1 is present in high concentration in G1 and decreases to low levels after Start (Donovan et al., 1994; Schwob et al., 1994).
In many eukaryotic organisms, Cdk activity is also controlled by inhibitory phosphorylation at a conserved tyrosine in the N terminus of its kinase subunit. Although budding yeast has this tyrosine residue (Tyr-19 in Cdc28) and the kinase and phosphatase (Swe1 and Mih1) that regulate phosphorylation of this site, tyrosine phosphorylation does not play an important role in regulating Cdk activities during normal vegetative growth (Amon et al., 1992; Sorger and Murray, 1992).
Transcription Factors
Expression of the CLN2 gene (Koch et al., 1996) is controlled by the transcription factor SBF (Swi4/Swi6) (Nasmyth and Dirick, 1991), which can be activated by all three Cln-associated as well as Clb5-associated kinases (Cross and Tinkelenberg, 1991; Schwob and Nasmyth, 1993) and inactivated by Clb2-associated kinase (Amon et al., 1993). The transcription factor MBF (Mbp1/Swi6) for the CLB5 gene is activated, like SBF, by the Cln- and Clb5-associated kinases (Koch et al., 1993; Schwob and Nasmyth, 1993) but inactivated in G2 by some yet unknown mechanism other than Clb2/Cdc28 kinase (Amon et al., 1993). Transcription of CLB2 is autocatalytic, because Clb2/Cdc28 activates its own transcription factor (Mcm1/SFF) (Amon et al., 1993; Maher et al., 1995). Finally, SIC1 transcription, regulated by Swi5, peaks at anaphase (Knapp et al., 1996). Swi5 is inactivated by Clb2-dependent phosphorylation, which prevents it from entering the nucleus (Nasmyth et al., 1990). It is activated, on the other hand, by a phosphatase, Cdc14, which is in turn activated indirectly by Cdc20 (Visintin et al., 1998; Jaspersen et al., 1999), an ancillary protein for the APC-dependent degradation machinery to be described in the next section.
Proteolysis
All cyclins are degraded by proteasomes, which destroy proteins that have been tagged by ubiquitin. Ubiquitin tagging is carried out by complex enzymatic machinery that activates ubiquitin molecules, recognizes appropriate proteins to be destroyed, and transfers activated ubiquitin to these doomed proteins (King et al., 1996; Peters, 1998; Zachariae and Nasmyth, 1999). For cyclins, two ubiquitin-conjugating protein complexes are known: the APC and the SCF. The APC is composed of a dozen proteins, including Cdc16, -23, and -27, (Zachariae et al., 1996). The SCF is a complex of Skp1, Cdc34, Cdc53, and an F box-containing protein, like Cdc4 or Grr1 (Jackson, 1996; Krek, 1998). The APC is responsible for destruction of Clb2 (Irniger et al., 1995), Clb5 (partly) (Irniger and Nasmyth, 1997), Cdc20 (Shirayama et al., 1998), and Pds1 (Yamamoto et al., 1996), a protein that promotes sister chromatid cohesion until anaphase. The SCF is responsible for destruction of Cln2 (Deshaies et al., 1995; Willems et al., 1996), Cln3 (Yaglom et al., 1995), and Sic1 (Feldman et al., 1997). Because Clb5 is more stable in skp1 mutants than in wild-type cells (Bai et al., 1996), Clb5 may be partly degraded by SCF.
Both APC and SCF require ancillary proteins, whose job is to recognize appropriate protein substrates and present them to the ubiquitin-conjugating machinery. For example, Cdc4 presents Sic1, and Grr1 presents Cln2 and Cln3 to the SCF (Barral et al., 1995; Feldman et al., 1997; Li and Johnston, 1997; Skowyra et al., 1997). In like manner, Hct1 (also called Cdh1) presents Clb2, and Cdc20 presents Pds1 and Clb5 to the APC (Schwab et al., 1997; Visintin et al., 1997).
The SCF seems to be active at all times in the cell cycle. Degradation of its target proteins is controlled by the phosphorylation state of the target (Willems et al., 1996). For example, in G1 phase, Sic1 is unphosphorylated and stable, even though the SCF is active. When Cln2-associated kinase activity rises at Start, Sic1 is phosphorylated, and Sic1P is rapidly presented by Cdc4 to the SCF for ubiquitination and subsequent proteolysis (Verma et al., 1997). Likewise, Cln2 must be phosphorylated before it is recognized by Grr1 (Barral et al., 1995; Li and Johnston, 1997).
APC-dependent proteolysis, on the other hand, is controlled by phosphorylation of the ubiquitination machinery itself, rather than the target proteins. There is evidence in clam oocyte extract (Lahav-Baratz et al., 1995; Sudakin et al., 1995), Xenopus egg extract (Felix et al., 1990; Peters et al., 1996), and mammalian cells (Kotani et al., 1998) that the APC core is activated by phosphorylation and that CDKs may be involved in this activation indirectly via a polo-like kinase (whose homologue in budding yeast is Cdc5) (Descombes and Nigg, 1998; Kotani et al., 1998). But such effects are not yet well established in budding yeast, so we do not try to model them in the present paper.
Rather, we focus on the ancillary proteins, which seem to exist in active and inactive forms. For the Hct1-dependent degradation machinery, Amon (1997) showed that, in vivo, cyclin proteolysis can be turned off by ectopic expression of Clb2 (and back on again by expression of Sic1). Recent experiments (Zachariae et al., 1998; Jaspersen et al., 1999) show that, in vitro, CDKs can phosphorylate Hct1, rendering it incapable of interaction with the APC core. Together, these findings confirm Nasmyth's (1996) hypothesis that CDK activity and Clb proteolysis are antagonistic events: CDK inactivates APC by phosphorylation, whereas APC destroys CDK activity by degradation of cyclin components. The phosphatase that opposes CDK (and thereby activates Hct1) is Cdc14. Notice that the kinase-phosphatase pair, CDK-Cdc14, regulates not only the activity of Hct1 but also the synthesis (Swi5) and degradation (phosphorylation state) of Sic1 (Visintin et al., 1998; Jaspersen et al., 1999).
The Cdc20-dependent degradation machinery is more complicated still. As cells exit from mitosis, it is responsible for degradation of Pds1, which restrains the dissociation of cohesins by binding to and inhibiting Esp1, a protein essential for sister chromatid separation (Ciosk et al., 1998). Cdc20 is also responsible for loss of an inhibitor of Cdc14 (Novak et al., 1999), leading to activation of Hct1 and Swi5 (Visintin et al., 1997; Lim et al., 1998; Shirayama et al., 1998). The RENT complex, recently identified by Shou et al. (1999) and Visintin et al. (1999), may inhibit Cdc14 by reversible sequestration.
Mitotic Checkpoint
It has been shown (Hwang et al., 1998) that Cdc20 is a likely target for signals from unaligned chromosomes, unreplicated DNA, and damaged DNA, all of which keep Cdc20 in its inactive form. Unreplicated DNA, in addition to keeping Cdc20 inactive, seems to impinge on the APC-activating pathway as well (Hwang et al., 1998; Kotani et al., 1998). The end result is that, when DNA replication is complete and all chromosomes are in tension on the metaphase plate, APC is phosphorylated, and Cdc20 is activated, leading to degradation of Pds1 (hence, dissolution of cohesions) and to activation of Hct1 (hence, destruction of Clb2).
KINETIC MODEL
From these facts we construct a consensus picture (Figure 2) of cell cycle controls in budding yeast. Using standard principles of biochemical kinetics, we cast the molecular mechanism into a set of nine, nonlinear, ordinary differential equations governing the temporal changes of cyclins and their regulatory proteins, plus four auxiliary differential equations describing cell growth and CDK-induced events (activation of DNA replication origins, bud emergence, and spindle assembly), plus three algebraic equations determining the activities of SBF, Mcm1, and Swi5 transcription factors (Table 1). About 50 parameters enter into the definitions of these equations, and their values (for wild-type cells) are specified in Table 2. Appendix A, describes how these parameter values were estimated.
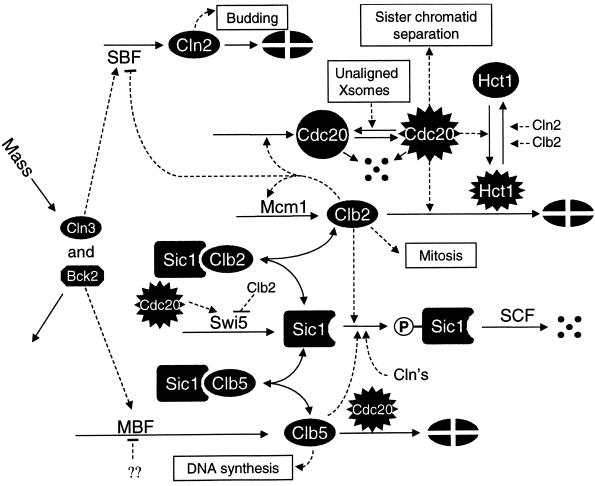
Figure 2.
Molecular model of the control of CDK activities during the budding yeast cell cycle. We lump together redundant cyclins (Cln1 + Cln2 = “Cln2,” Clb1 + Clb2 = “Clb2,” and Clb5 + Clb6 = “Clb5”) and ignore Clb3 and Clb4. (Notice that we do not draw the kinase subunit, Cdc28, that is associated with each cyclin, because we assume it is in excess.) At the beginning of the cycle, the cell has few cyclin molecules, because the transcription factors (SBF, MBF, and Mcm1) that regulate cyclin synthesis are inactive. Clb-dependent kinases, in addition, are suppressed by a stoichiometric inhibitor (Sic1) and by efficient proteolysis of cyclin subunits. Cln3/Cdc28, which is present at low and nearly constant activity throughout the cycle, triggers a sequence of events leading ultimately to cell division. The sequence can be read from left to right. When the cell grows to a sufficiently large size, Cln3/Cdc28 and Bck2 activate SBF and MBF (by phosphorylation, so we assume), causing Cln2 and Clb5 to begin to accumulate. At first, Clb5 accumulates in inactive trimers, Clb5/Cdc28/Sic1, but Cln2/Cdc28 is not so inhibited. Rising Cln2/Cdc28 activity plays three important roles. First, it initiates bud formation. Second, it phosphorylates Sic1, priming the inhibitor for ubiquitination by SCF and ultimate degradation by the proteasome. Third, it inactivates Hct1, which, in conjunction with APC, was responsible for Clb2 degradation in G1 phase. When Sic1 is destroyed, Clb5/Cdc28 activity rises abruptly and drives the cell into S phase. These are the major physiological events associated with the Start transition. With Sic1 gone and Hct1 inactivated, Clb2-dependent kinase can begin to rise, with some lag, because Clb2/Cdc28 activates its own transcription factor, Mcm1. In addition, Clb2/Cdc28 inactivates SBF, so Cln2-dependent kinase activity begins to fall as Cln2 synthesis shuts off. At about the same time, MBF is inactivated, and the Clb5 level starts to fall. Rising Clb2/Cdc28 activity induces progress through mitosis. The metaphase–anaphase transition is regulated by a pair of proteins, Cdc20 and Hct1, that target substrates to the APC for ubiquitination. At metaphase, they are inactive, but when DNA is fully replicated and all chromosomes are aligned on the metaphase plate, Cdc20 is activated. Indirectly Cdc20 promotes 1) dissociation of sister chromatids (anaphase A), 2) activation of Hct1, which conducts Clb2 to the APC, thereby initiating anaphase B and cell separation, and 3) activation of Swi5, the transcription factor for Sic1. With all CDK activity gone (except for a little associated with Cln3), Sic1 can make a comeback, and the cell returns to G1.
Table 1.
Mathematical model of the budding yeast cell cycle
| Equations governing cyclin-dependent kinases | Notes |
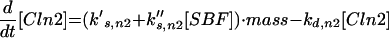
| |
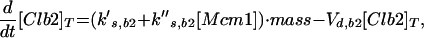 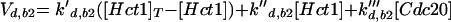
| |
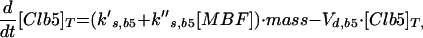 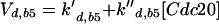
|
a |
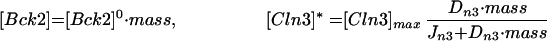
| |
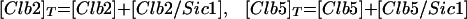
| |
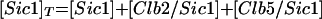
| |
| Equations governing the inhibitor of Clb-dependent kinases | |
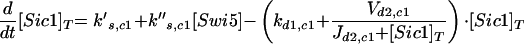
|
b |
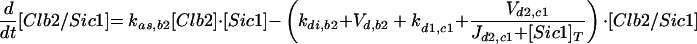
| |
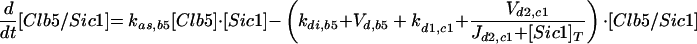
| |
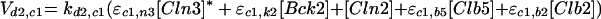
| |
| Equations governing the Clb degradation machinery | |
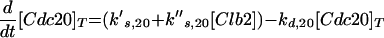
| |
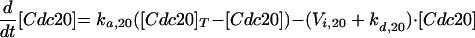
| |
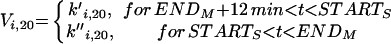
|
c |
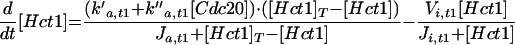
| |
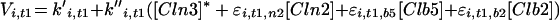
| |
| Equations for growth, DNA synthesis, budding and spindle formation | |
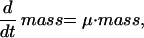 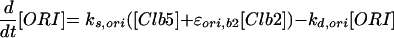
|
d |
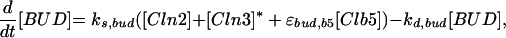 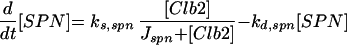
| |
| Equations governing transcription factors | e |
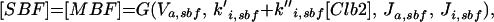 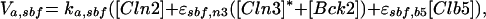
| |
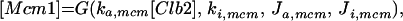 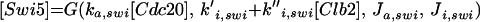
|
Symbols, V = rate functions, k = rate constant, J = Michaelis constant. Subscripts, s = synthesis, d = degradation, a = activation, i = inactivation, as = association, di = dissociation, T = total.
k′d,b5 refers to SCF-mediated degradation of Clb5, and k″d,b5 refers to its APC-mediated degradation.
d1,c1 refers to the degradation of unphosphorylated Sic1. d2,c1 refers to the rate of phosphorylation of Sic1 by cyclin-dependent kinases, assuming that phosphorylated Sic1 is rapidly proteolyzed, releasing active Cdc28/Clb dimers.
START_S is the time when [ORI] = 1, and END_M when [SPN] = 1. For START_S < t < END_M, there is a strong inhibitory signal on Cdc20 (Vi,20 = 10). Once the cell reaches metaphase (t = END_M), Vi,20 drops linearly from 10 to 0.1 over 12 min. Thereafter, Vi,20 = 0.1 until the start of the next S phase.
Cell division occurs, we assume, when [Clb2] drops below a threshold (0.3). At this time, we divide mass between mother and daughter cells as follows: (mass of daughter cell at birth) = f × (mass at cell separation), (mass of mother cell at birth) = (1 − f) × (mass at cell separation), with f = e−μD, where D = (1.026/μ) − 32 is the observed daughter cell cycle time (Lord and Wheals, 1980). (See text for a discussion of the rule for asymmetric division.) At division, we also reset BUD and SPN to zero; however, we reset ORI to zero (for licensing factor to reappear after mitosis) only when [Clb2] + [Clb5] drop below a different threshold (0.2).
G(Va, Vi, Ja, Ji) is the Goldbeter–Koshland function described in Appendix B.
Table 2.
Kinetic constants for the budding yeast model
| Rate constants (min−1) | |||
| k′s,n2 = 0 | k″s,n2 = 0.05 | kd,n2 = 0.1 | |
| k′s,b2 = 0.002 | k″s,b2 = 0.05 | ||
| k′d,b2 = 0.01 | k″d,b2 = 2 | k‴d,b2 = 0.05 | |
| k′s,b5 = 0.006 | k″s,b5 = 0.02 | k′d,b5 = 0.1 | k″d,b5 = 0.25 |
| k′s,c1 = 0.02 | k″s,c1 = 0.1 | kd1,c1 = 0.01 | kd2,c1 = 0.3 |
| kas,b2 = kas,b5 = 50 | kdi,b2 = kdi,b5 = 0.05 | ||
| k′s,20 = 0.005 | k″s,20 = 0.06 | kd,20 = 0.08 | |
| ka,20 = 1 | k′i,20 = 0.1 | k″i,20 = 10 | |
| k′a,t1 = 0.04 | k″a,t1 = 2 | k′i,t1 = 0 | k″i,t1 = 0.64 |
| ks,ori = 2 | ks,bud = 0.3 | ks,spn = 0.08 | |
| kd,ori = kd,bud = kd,spn = 0.06 | ka,sbf = ka,mcm = ka,swi = 1 | ||
| k′i,sbf = 0.5 | k″i,sbf = 6 | k′i,swi = 0.3 | k″i,swi = 0.2 |
| ki,mcm = 0.15 | μ = 0.005776 | ||
| Characteristic concentrations (dimensionless) | |||
| [Cln3]max = 0.02 | [Bck2]0 = 0.0027 | [Hct1]T = 1 | |
| Jspn = 0.2 | Jd2,c1 = 0.05 | ||
| Ja,sbf = Ji,sbf = 0.01 | Ja,mcm = Ji,mcm = 1 | Ja,swi = Ji,swi = 0.1 | Ja,t1 = Ji,t1 = 0.05 |
| Kinase efficiencies (dimensionless) | |||
| ɛc1,n3 = 20 | ɛc1,k2 = 2 | ɛc1,b2 = 0.067 | ɛc1,b5 = 1 |
| ɛi,t1,n2 = 1 | ɛi,t1,b2 = 1 | ɛi,t1,b5 = 0.5 | |
| ɛori,b2 = 0.4 | ɛbud,b5 = 1 | ɛsbf,n3 = 75 | ɛsbf,b5 = 0.5 |
| Other parameters (dimensionless) | |||
| f = 0.433 | Jn3 = 6 | Dn3 = 1 | |
The model involves a number of specific kinetic assumptions that are introduced either to simplify the model or to explain specific characteristics of wild-type and mutant cell cycles, as we shall describe. Here we list these assumptions for easy reference.
1) Cell size is coupled to the CDK engine by assuming that the synthesis of each cyclin is proportional to mass, a variable representing overall cell “size.” (For simplicity, we assume that mass increases exponentially.) We have in mind that cyclins are synthesized in the cytoplasm, where ribosome number increases throughout the cycle, and accumulate in the nucleus, whose volume does not change much. Thus, the concentrations of cyclins in the nucleus, [Cln2], [Clb2], etc., tend to increase as mass increases. Although many experiments demonstrate that budding yeast division cycles are controlled by cell size (Carter, 1981) through effects on CDK activities (Baroni et al., 1994; Tokiwa et al., 1994; Polymenis and Schmidt, 1997), the molecular mechanism whereby cells measure their nucleocytoplasmic ratio has not yet been elucidated. Our hypothesis, although speculative, is the simplest way to couple growth and division.
2) Transcription of CLB5 is controlled by MBF, but the signal that inactivates MBF is unknown at present, so our picture is incomplete. Because MBF and SBF turn on and off at similar times in the cell cycle, under most conditions (Koch and Nasmyth, 1994; Cho et al., 1998; Spellman et al., 1998), we assume for the time being that [MBF] = [SBF]. When MBF regulation is better understood, this part of the model can be easily improved.
3) The activation and inactivation of transcription factors (SBF, Mcm1, and Swi5) are modeled as Goldbeter–Koshland (1981) ultrasensitive switches, as described in Appendix B. We could have represented the sigmoidal behavior of these switches by simpler functions, but the Goldbeter–Koshland function is particularly suitable for the phosphorylation–dephosphorylation reactions typical of cell cycle controls.
4) Bck2 cooperates with Cln3 in activating SBF at Start.
5) At high dosage, the activity of Cln3-dependent kinase plateaus.
6) We assume first-order kinetics for degradation of Cln2 and Clb5 by SCF. We are aware that SCF-catalyzed ubiquitination depends on prior phosphorylation of its substrates, most likely by CDKs themselves. Nonetheless, we choose simple first-order kinetics for cyclin degradation in the present model. Later versions can be improved in this regard, if necessary.
7) To describe how CDK activities drive DNA synthesis, bud emergence, and mitotic events, we introduce three “target” variables: ORI, BUD, and SPN. These targets are phosphorylated by CDKs, and the associated physiological events occur when their cumulative level of phosphorylation reaches a threshold (1 in each case).
8) In the present model, Clb2-dependent kinase stimulates the synthesis of Cdc20 (Prinz et al., 1998) and indirectly activates it by driving [SPN] toward 1. The function of [SPN] is to provide a time delay between the appearance of Clb2 and the activation of Cdc20. To model the effect of nocodazole, we block the activation of Cdc20.
9) Metaphase checkpoint controls are the most primitive part of the model. We assume that Cdc20 is kept inactive until all chromosomes are properly aligned on the mitotic spindle ([SPN] = 1). After it is activated, Cdc20 helps activate Hct1 and Swi5, presumably by degrading some inhibitor of Cdc14 (Novak et al., 1999). In a later model, we will track the kinetics of Cdc14 and its sequestration in RENT complexes, but for now we simply allow Cdc20 to activate Hct1 and Swi5 directly.
10) Cdc20 degrades Clb2, to some extent.
Intuitively, the diagram in Figure 2 seems appealing, but the hand-waving arguments used to justify it are not entirely convincing. Exactly what experiments can this model account for and what does it leave unexplained? The only way to address this question is to study the mathematical model (Table 1) thoroughly and rigorously, comparing its solution with the physiology of real cells. Where there is a correspondence between the model and reality, we can have some confidence that our understanding of the budding yeast cell cycle is adequate. Where the model fails will point to aspects of the control system that need further study.
RESULTS
Wild-Type Cell Cycle
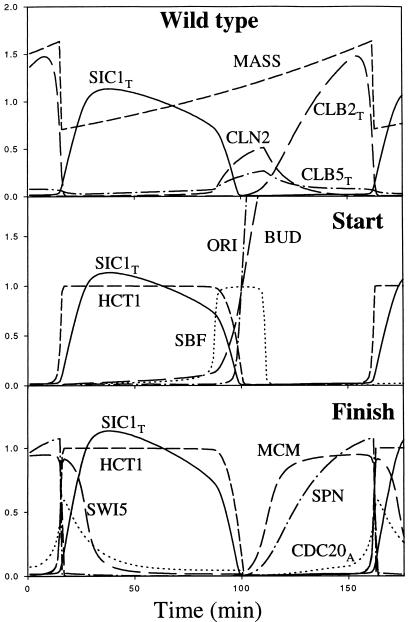
Figure 3 presents a numerical solution of the kinetic equations (Table 1), using a basal set of rate constants (Table 2), suitable for wild-type division cycles (see Appendix A for a justification of the parameter values). In this case, the mass-doubling time (Td) of the culture is 120 min (specific growth rate = μ = 0.693/Td = 0.005776 min−1). Because division is asymmetrical, we must distinguish between mother and daughter cells. The smaller daughter cells (Table 3, line 1) have a longer cycle time (146 min from birth to division), because they require more time to grow to the critical size when SBF turns on. (In our model, SBF is turned on abruptly by Cln3 when mass ≈ 1.1; see Appendix B.) Mother cells have a cycle time of 100 min, because they turn on SBF more quickly after division. On the other hand, the budded phases of mother and daughter cells are quite similar (∼60 min).
Figure 3.
Wild-type cell cycle in daughter cells. Computed from equations and parameter values in Tables 1 and 2.
Table 3.
Properties of wild-type cells and cln mutants
| Mass at birth | Mass at SBF 50% | Mass at DNA repl. | Mass at bud ini. | Mass at division | TG1 (min) | Changed parameter | Comments (Experimental results in boldface type) | ||
|---|---|---|---|---|---|---|---|---|---|
| 1 | wild type | 0.71 | 1.07 | 1.15 | 1.15 | 1.64 | 84 | CT 146 min | |
| (daughter) | (71′) | (84′) | (84′) | (146′) | (time of occurrence of event) | ||||
| 1st parent | 0.93 | 1.07 | 1.17 | 1.16 | 1.67 | 39 | CT 101 min | ||
| 2nd parent | 0.95 | 1.08 | 1.18 | 1.17 | 1.68 | 37 | CT 99 min | ||
| 3rd parent | 0.96 | 1.08 | 1.18 | 1.17 | 1.69 | 36 | CT 98 min | ||
| 2 | cln3 | 1.24 | 2.04 | 2.20 | 2.15 | 2.88 | 99 | Dn3 = 0 | Dirick, 1995, Fig. 3, size 1.7 × WT |
| 3 | cln3 sic1 | 1.09 | 1.85 | 1.28 | 1.90 | 2.54 | 28 | Dn3 = 0 | G1 short, size 1.5 × WT, smaller than cln3 |
| k′s,c1 = 0 | |||||||||
| k″s,c1 = 0 | |||||||||
| 4 | CLN3D | 0.44 | 0.45 | 0.49 | 0.52 | 1.02 | 17 | Dn3 = 8 | Yaglom, 1995, protein 8×, size 75% WT |
| Cross, 1988, Fig. 3, Nash, 1988, Fig. 1, size 60% WT | |||||||||
| cln3 GAL-CLN3 | 0.43 | 0.43 | 0.46 | 0.50 | 0.99 | 14 | Dn3 = 20 | Tyers, 1992, Table 1, protein 20 × WT, size 44% WT | |
| 5 | cln3 GAL-CLN3 sic1 | 0.42 | 0.42 | 0.45 | 0.49 | 0.98 | 12 | Dn3 = 20 | SBF activated early, G1 short, cells small |
| k′s,c1 = 0 | |||||||||
| k″s,c1 = 0 | |||||||||
| 6 | cln1 cln2 | 1.46 | 1.47 | 2.47 | 2.58 | 3.39 | 91 | k″s,n2 = 0 | Dirick, 1995, Fig. 3, size 3.2 × WT |
| 7 | cln1 cln2 sic1 | 0.81 | 1.12 | 0.97 | 1.29 | 1.89 | 31 | k″s,n2 = 0 | Dirick, 1995, Fig. 4, size between cln1 cln2 and WT |
| k′s,c1 = 0 | |||||||||
| k″s,c1 = 0 | |||||||||
| 8 | cln1 cln2 | 0.71 | 1.23 | [11.66] | No bud | [14.44] | k″s,n2 = 0 | Schwob, 1993, Fig. 5, G1 arrest | |
| clb5 clb6 | k′s,b5 = 0 | We consider cells arrested in G1 if mass at DNA replication exceeds 5 | |||||||
| k″s,b5 = 0 | |||||||||
| 9 | cln1 cln2 | 0.34 | 0.34 | 0.38 | 0.35 | 0.78 | 23 | k′s,n2 = 0.1 | Dirick, 1995, Fig. 6, size small, budding is |
| GAL-CLN2 | (1′) | (23′) | (6′) | (146′) | k″s,n2 = 0 | advanced more than DNA replication when compared with WT | |||
| 10 | cln1 cln2 | 0.33 | 0.33 | 0.36 | 0.34 | 0.76 | 19 | k′s,n2 = 0.1 | SBF activated early, G1 short, cells small. |
| GAL-CLN2 sic1 | k″s,n2 = 0 | ||||||||
| k′s,c1 = 0 | |||||||||
| k″s,c1 = 0 | |||||||||
| 11 | cln1 cln2 | 0.39 | 0.39 | 0.48 | 0.40 | 0.90 | 38 | k′s,n2 = 0.1 | Birth size between GAL-CLN2 and GAL-SIC1 |
| MET-CLN2 | k″s,n2 = 0 | (0.80) | |||||||
| GAL-SIC1 | k′s,c1 = 0.1 | ||||||||
| k″s,c1 = 0 | |||||||||
| 12 | cln1 cln2 | 0.20 | No SBF | 0.33 | 0.22 | 0.47 | 85 | k′s,n2 = 0.1 | Steady-state mass at birth = 0.20 (28% WT); |
| MET-CLN2 | k″s,n2 = 0 | cells may not be viable at this size. See Fig. 7 | |||||||
| clb1 clb2 | k′s,b2 = 0.1 | ||||||||
| GAL-CLB2 | k″s,b2 = 0 | ||||||||
Note: to simulate mutants that synthesize cyclins constitutively, e.g., cln1 cln2 GAL-CLN2, we set the rate constant for regulated synthesis to zero (k″s = 0) and the rate constant for unregulated synthesis to a uniform value (k′s = 0.1) to represent a constant rate of expression from the GAL promoter. This is a neutral assumption, in the absence of any quantitative data about levels of mRNA expression driven by the GAL promoter.
Start and Finish.
Two major transitions characterize wild-type cell cycles (Figure 3). At Start, a series of events is initiated in rapid succession: SBF turns on, Cln2 and Clb5 levels rise, Sic1 disappears, Hct1 turns off, and DNA synthesis and bud emergence commence. Shortly thereafter, Clb2 level rises and a spindle starts to form. At Finish, Cdc20 and Hct1 turn on, Clb2 is destroyed, and Sic1 makes a comeback. In simulations of various mutant strains, we will see how these chains of events can be dissociated.
The first event of Start is abrupt activation of SBF, when cells grow to a critical size, as demonstrated experimentally (Dirick et al., 1995; Stuart and Wittenberg, 1995). In our simulations, SBF turns on abruptly because it is modeled as an ultrasensitive switch (Goldbeter and Koshland, 1981), driven by the accumulation of Cln3 and Bck2 in the nucleus as the cell grows to the critical size. When the combined activities of Cln3 and Bck2, ka,sbf × ɛsbf,n3 × ([Cln3]* + [Bck2]), exceed the activity of the opposing phosphatase, ki,sbf, then SBF turns on (see Appendix B). With our parameter values, Cln3 and Bck2 contribute about equally to the activation of SBF.
Finish (exit from mitosis) is triggered by activation of Cdc20. After cells pass Start and begin to synthesize Clb2, Cdc20 accumulates at an increasing rate. But it remains inactive because of inhibitory signals from unreplicated DNA and unaligned chromosomes. When those events are completed and the inhibitory signals disappear, Cdc20 is activated. Active Cdc20 turns on Hct1 by overwhelming the inhibition exerted on Hct1 by Clb2 (presumably by degrading some inhibitor of Cdc14). When Hct1 turns on, Clb2 is degraded, and the control system switches to the G1 state, in which the enemies of Clbs (Hct1 and Sic1) are active.
Response to α-Factor.
When an asynchronous population of budding yeast cells is exposed to α-factor (mating pheromone), pre-Start cells are blocked in G1, but post-Start cells finish DNA replication, divide, and stop in the next G1 phase. α-factor initiates a signal transduction pathway that ultimately eliminates all Cln-dependent kinase activities (Chang and Herskowitz, 1990; Peter and Herskowitz, 1994; Wittenberg and Reed, 1996). To simulate α-factor treatment, we set the catalytic efficiencies of Cln2- and Cln3-dependent kinases to zero, 10 min after the time of α-factor addition (i.e., assuming a 10-min delay for signal transduction). We found a point of no return shortly before the onset of S phase.
Dependence of Cell Cycle Time on Growth Rate and Birth Size.
Figure 1 shows how certain characteristics of wild-type cell cycles depend on mass-doubling time, as reported by Lord and Wheals (1980) and Hartwell and Unger (1977). As Td increases (specific growth rate, μ, decreases), cell division becomes increasingly asymmetrical, daughter size at birth decreases, and the duration of its unbudded phase increases. The unbudded phase of mother cells also increases slightly with Td.
To fit the model to these data, we must adopt a rule for partitioning cell size to mother and daughter at cell separation. The simplest rule (“Rule 1”) would be to give to the daughter cell all growth from bud emergence to cell division and let mother retain the mass it had when the bud emerged. However, in this case, the mother would be able to bud soon after its birth; hence it should not have an appreciable unbudded period, which is in contradiction to the observations of Lord and Wheals (1980) and Hartwell and Unger (1977). For the mother cell to have an unbudded period, its birth size must be smaller than the critical size for bud emergence. Furthermore, the calculated daughter cycle times at various growth rates are longer than the observed values. Both results reflect that Rule 1 is inadequate, it gives too much mass to mothers and too little to daughters.
Therefore, we adopt a different rule (Rule 2). Let f = fraction of mass given to the daughter at cell division (0 < f ≤ ½), and choose f to give the observed daughter cycle time (D) at any particular growth rate (μ = 0.693/Td). From our assumption that cells grow exponentially, (mother size at division) = (daughter size at birth) × eμD, so f = (daughter size at birth)/(mother size at division) = e-μD. By using the empirical formula for daughter cycle time, D = 1.48 Td − 32 (Lord and Wheals, 1980, their Table 2) to calculate f, we ensure that the model fits the data for D as a function of Td (Figure 1, top line).
Furthermore, (mother size at division) = (mother size at birth) × eμP, where P = mother cycle time, and (mother size at division) = (mother size at birth) + (daughter size at birth). Therefore, 1 = e-μP + e-μD. This relation was originally derived by Hartwell and Unger (1977) in a more complicated manner and shown by them to be consistent with the data. Consequently, by choosing f to fit D as a function of Td, we also ensure a good fit to P as a function of Td (Figure 1, middle line).
The dependence of budded period on growth rate (Figure 1, bottom line) is unconstrained, so its fit to the data is a valid test of the model. Progression through the budded part of the cycle is slightly dependent on growth rate but not nearly so much in the model as in experiments.
Under Rule 2, simulations show that mother cells become slightly larger each cycle for the first few cycles (Table 3, line 1) but not as much as the observed 25% increase (Hartwell and Unger, 1977; Johnston et al., 1979); furthermore, mother cells soon reach a steady size. This discrepancy is tied inevitably (in our model) to the prominent unbudded phase of mother cells (Figure 1). Under Rule 2, mother cell birth size is less than the critical mass for SBF activation. Hence, mother cells have an extended unbudded phase, as they grow to this critical mass, and mother cell cycles, like daughter cell cycles, are size regulated. Consequently, mother size at division does not increase steadily with each generation. Under Rule 1, size control is absent from mother cells, and they do grow larger each generation, as observed, but Rule 1 does not fit the observations in Figure 1. We do not know how to resolve this problem.
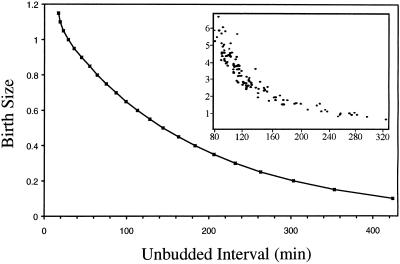
Similar to the observation of Lord and Wheals (1980), Johnston et al. (1977) reported that the smaller a cell is at birth the longer its unbudded interval is. These data support the proposal that smaller cells need more time to grow to a critical size for bud initiation. Our simulations (Figure 4) agree closely with these observations.
Figure 4.
Length of the unbudded interval of daughter cells depends inversely on birth size. Inset, experimental results from Figure 5 of Johnston et al. (1977), used by permission.
Analysis of Mutants
Dependence of Cell Size on CLN3 Gene Dosage.
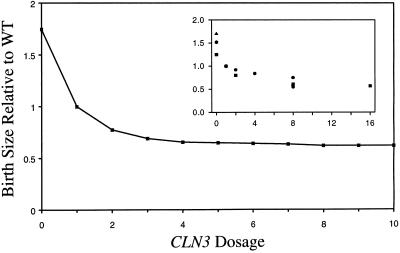
That Cln3 plays a major role in size control of budding yeast is suggested by the strong dependence of mean cell size on CLN3 gene dosage (Cross, 1988; Nash et al., 1988; Dirick et al., 1995; Yaglom et al., 1995). Figure 5 presents the model's simulation of this effect. The fact that cells approach a minimal size as CLN3 dosage increases suggests that the activity of Cln3-dependent kinase plateaus at high concentration (assumption 5). The parameter Jn3 determines how fast [Cln3]*, the kinase activity of Cln3, saturates with increasing CLN3 dosage, Dn3.
Figure 5.
Dependence of cell size on CLN3 dosage. Inset, experimental results compiled from Cross (1988), Dirick et al. (1995), Nash et al. (1988), and Yaglom et al. (1995).
Role of the Positive Feedback Loop.
Experimental evidence clearly shows that SBF can be activated by Cln1–2 and Clb5–6 as well as Cln3 (Cross and Tinkelenberg, 1991; Schwob and Nasmyth, 1993), hence the appearance of all three CDK activities in Va,sbf (Table 1). In wild-type cells Clb5 can play no role in SBF activation at Start, because any Clb5 present in G1 phase will be tied up in inactive trimers, Sic1/Clb5/Cdc28. However, some active Cln2-dependent kinase is likely present in G1, and it could cooperate with Cln3 and Bck2 in activating SBF. This positive feedback loop (SBF turns on Cln2 synthesis, and Cln2/Cdc28 activates SBF) could potentially play a major role in the activation of SBF at Start.
Dirick et al. (1995) and Stuart and Wittenberg (1995) addressed the role of positive feedback by comparing cell size at SBF activation in two mutant strains, cln1 cln2 and cln3. Each strain was made artificially small at birth by ectopic expression of a wild-type CLN gene carried on a plasmid. Dirick et al. (1995) used CLN2 under the control of a methionine-repressible promoter. In the presence of methionine (plasmid-borne CLN2 not expressed), both strains are larger than normal, and SBF is activated soon after cell division. Cell size in this case is not indicative of the minimum size necessary to activate SBF. To assay the minimum size, cells were grown in the absence of methionine (plasmid-borne CLN2 expressed), so that they grow and divide, like wild type, at a much smaller size. The smallest newborn cells (volume ∼10 fl) were selected by centrifugal elutriation and resuspended in medium containing methionine. In this case, the cells needed to grow awhile before SBF was activated. Cells of the cln1 cln2 MET-CLN2 strain activated SBF at 19 fl, exactly the same size as control cells (CLN1 CLN2 CLN3 MET-CLN2). On the other hand, cells lacking Cln3 (the cln3 MET-CLN2 strain) activated SBF at ∼45 fl (Dirick et al., 1995, their Figure 2A).
These remarkable results indicate that 1) positive feedback does not play a determinative role in the activation of SBF at Start (because cell size at SBF activation is unchanged when the positive feedback loop is broken); and 2) there must be some component (other than Cln1–3 and Clb5,6) that turns on SBF in the absence of Cln3, albeit at a larger size. (Clb5,6 are excluded because deletion mutants have size similar to that of wild-type cells, not twice as big.)
To capture these features with our model, we assume that Cln3 is much more efficient than Cln2 in activating SBF (ɛsbf,n3 ≫ 1), and that Cln3 is assisted by Bck2 (reasons to be described later). Because the cln3 mutant is about twice the size of wild type, we choose parameters so that Bck2 and Cln3 contribute about equally to SBF activation. Simulations of the experiments of Dirick et al. (1995) are presented in Figure 6, A–C.
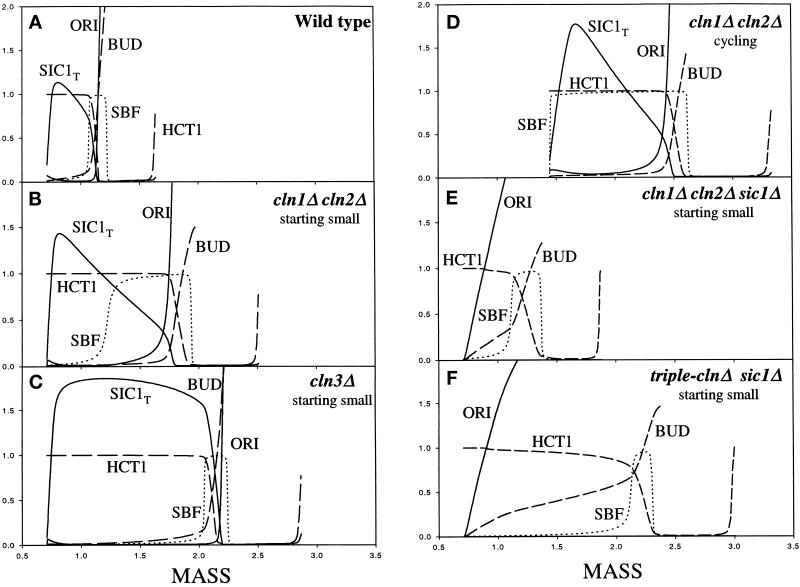
Figure 6.
Dissociation of Start events in cln mutants. (A–C) Compare with experiments of Dirick et al. (1995). (A) In wild-type cells, several molecular and physiological events occur together at Start: activation of SBF, inactivation of Hct1, proteolysis of Sic1, initiation of DNA synthesis, and emergence of a bud. (B) In cln1Δ cln2Δ cells, these events are dissociated: SBF is activated at wild-type size, but all other events are delayed until the cell gets much larger. (C) In cln3Δ cells, the events are again concurrent, but they occur at about twice the size of wild-type cells. (D) Under steady-state conditions, cln1Δ cln2Δ cells are much larger than wild type. SBF is activated immediately. However, DNA synthesis is much delayed (to mass = 2.47), beyond the size at which it would occur (at mass = 1.75) in B. This delay is due to the burst of Sic1 synthesis at anaphase. (E) Deletion of SIC1 from cln1Δ cln2Δ suppresses the delay of bud emergence, as observed by Dirick (1995), and pushes DNA synthesis to a size smaller than in wild-type (contrary to their observation). In the absence of inhibitor, the small level of Clb5 early in the cycle is effective in driving DNA synthesis and bud emergence. See text for further discussion. (F) Deletion of SIC1 rescues the inviable cln1Δ cln2Δ cln3Δ mutant. DNA synthesis begins at a small size (smaller than in wild type, as observed by Schneider et al., 1996), but all other events of Start are displaced to large size.
In the cln1 cln2 strain (Figure 6B), the events that normally occur together at Start are dissociated. First, SBF turns on at mass = 1.2 (volume = 24 fl), slightly larger than in wild-type cells (22 fl). (We use the conversion factor 1 mass unit = 20 fl.) Because Cln1 and Cln2 are missing, Sic1 degradation and Hct1 inactivation are delayed. Cells must grow larger (∼35 fl) before the combined effects of Cln3 and Clb5 can remove Sic1 (Cln3 phosphorylates and destabilizes Sic1, whereas Clb5 titrates away Sic1). With Sic1 gone, the rapidly rising Clb5-associated kinase activity initiates DNA synthesis, bud emergence, and Hct1 inactivation. Then, as Clb2 appears, cells enter mitosis.
Start events in the cln3 strain (Figure 6C) occur at even larger size, because these cells rely on Bck2 alone to activate SBF. Once SBF turns on (at ∼41 fl), subsequent events of the cell cycle occur normally.
Properties of cln Mutants.
When cycling, recessive cln3 mutant cells are 75% larger than wild-type cells, whereas dominant CLN3D mutant cells are 40% smaller, and double recessive cln1 cln2 mutant cells are twice as large, all in agreement with observations (Table 3, lines 2, 4, and 6; Cross, 1988; Nash et al., 1988; Dirick et al., 1995).
In the paper by Dirick et al. (1995), the authors reported an intriguing phenomenon. As previously described, cln1 cln2 mutants, when started very small (10 fl), initiate DNA synthesis and budding at ∼40 fl (their Figure 4). However, in cycling cln1 cln2 cells, DNA synthesis and budding is delayed further to 60 fl (their Figure 3). That is, although the birth size of the cycling cells is ∼32 fl, they are unable to initiate DNA synthesis and budding at 40 fl but have to grow larger still (60 fl) to do these jobs. Why?
Our simulation (Figure 6D) gives an explanation. In the cycling culture, when cells reach 40 fl (which occurs soon after birth), there is still abundant Sic1, because Swi5 is active in early G1, and Sic1 degradation is slow in the absence of Cln2. It takes ∼1 h to remove Sic1 by a combination of Cln3-dependent phosphorylation of Sic1 and Clb5 binding to Sic1. As soon as [Clb5]T ≈ [Sic1]T, Clb5-dependent kinase activity starts to rise and initiates DNA synthesis. In our simulation, cycling cln1 cln2 cells (born at mass = 1.46, 29 fl) begin DNA synthesis at mass = 2.47 (Table 3, line 6, equivalent to 49 fl); whereas for very small cells (born at mass = 0.71, 14 fl), DNA synthesis begins at mass = 1.75, equivalent to 35 fl. These results are in reasonable agreement with the observations of Dirick et al. (1995). Without the help of Clb5, as in the case of the cln1 cln2 clb5 clb6 mutant, Cln3-dependent kinase has a hard time fighting against Sic1 alone, and cells are inviable, blocked in G1 (Table 3, line 8).
When Cln2 is synthesized constitutively (cln1 cln2 GAL-CLN2; Table 3, line 9), cells are smaller than normal. Because Cln2-dependent kinase activity is always high, Start occurs shortly after division, and size control at the G1/S transition is lost. Nonetheless, this strain is perfectly viable, and its cell cycle is still size regulated. As pointed out by Futcher (1996), this observation implies a size control mechanism in M phase that is cryptic as long as size control at Start is operating. In our model, this stems largely from the mass dependence of the positive feedback loop that activates Clb2 transcription. In small cells, the rise of Clb2-dependent kinase activity is delayed, which lengthens the duration of M phase. Bypassing transcriptional control of Clb2 can test this explanation: cells constitutively expressing both Cln2 and Clb2 (cln1 cln2 MET-CLN2 clb1 clb2 GAL-CLB2) should be considerably smaller than cells constitutively expressing Cln2 alone (cln1 cln2 MET-CLN2) (Figure 7 and Table 3, lines 9 and 12). Such small cells may be inviable.
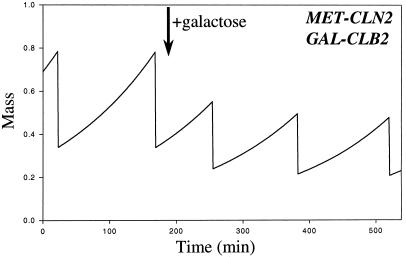
Figure 7.
Simulation of MET-CLN2 GAL-CLB2 (no transcriptional control of Cln2 or Clb2 synthesis). In the absence of both methionine and galactose, cells are smaller than wild type, because Cln2 is synthesized constitutively. When galactose is added (arrow), cells get smaller still, eventually dividing at ∼30% of wild-type size. Such small cells may be inviable.
Rescue of Triple-cln Mutant.
Especially noteworthy is the inviable triple-cln mutant cln1 cln2 cln3 (Table 4, line 2). SBF is activated by Bck2 (at a larger than normal size), but no other events of Start occur, because they all require CDK activity (the Clns are all missing, and the Clbs are all inhibited by Sic1). In our simulations, the cell eventually grows large enough for the low, G1 level of Clb5 to turn off Hct1 and Sic1 and then to initiate DNA synthesis and progress toward mitosis, but S/M commences at such a large size, 5 times larger than in wild-type, that the cell, we assume, has already died.
Table 4.
Mutations that rescue the cln1 cln2 cln3 strain
| Mass at birth | Mass at SBF 50% | Mass at DNA repl. | Mass at bud ini. | Mass at division | TG1 (min) | Changed parameter | Comments (Experimental results in boldface type) | ||
|---|---|---|---|---|---|---|---|---|---|
| 1 | wild type | 0.71 | 1.07 | 1.15 | 1.15 | 1.64 | 84 | CT 146 min | |
| (daughter) | (71′) | (84′) | (84′) | (146′) | (time of occurrence of event) | ||||
| 2 | cln1 cln2 cln3 | 0.71 | 2.47 | [6.20] | [6.48] | [8.11] | Dn3 = 0 | Richardson, 1989, inviable | |
| k″s,n2 = 0 | |||||||||
| 3 | cln1 cln2 cln3 | 0.65 | 0.65 | 0.75 | 0.95 | 1.50 | 25 | Dn3 = 20 | Schwob, 1993, Fig. 2, SBF activated soon |
| GAL-CLN3 | k″s,n2 = 0 | after galactose induction | |||||||
| 4 | cln1 cln2 cln3 | 0.34 | 0.34 | 0.39 | 0.35 | 0.79 | 25 | Dn3 = 0 | Cross, 1991, Fig. 4, GAL-CLN1 induces cln2 |
| GAL-CLN2 | k′s,n2 = 0.1 | ||||||||
| k″s,n2 = 0 | |||||||||
| 5 | cln1 cln2 cln3 | 2.81 | 2.83 | 4.96 | 5.15 | 6.52 | 98 | Dn3 = k″s,n2 = 0 | Epstein, 1992, viable |
| 2X CLB5 | k′s,b5 = 0.012 | ||||||||
| k″s,b5 = 0.04 | |||||||||
| 6 | cln1 cln2 cln3 | 1.23 | 2.07 | 2.05 | 2.14 | 2.86 | 88 | Dn3 = k″s,n2 = 0 | Schwob, 1993, Fig. 6, viable |
| GAL-CLB5 | k′s,b5 = 0.1 | ||||||||
| k″s,b5 = 0 | |||||||||
| 7 | cln1 cln2 cln3 | 0.71 | 2.57 | [5.49] | [6.64] | [7.38] | Dn3 = k″s,n2 = 0 | Amon, 1994, Fig. 8, G1 arrest | |
| GAL-CLB2 | k′s,b2 = 0.1 | We consider cells arrested in G1 if mass at | |||||||
| k″s,b2 = 0 | DNA replication exceeds 5 | ||||||||
| 8 | cln1 cln2 cln3 | 1.30 | 2.12 | 1.50 | 2.24 | 3.01 | 24 | Dn3 = k″s,n2 = 0 | Tyers, 1996, Fig. 2, viable but large |
| sic1 | (85′) | (24′) | (94′) | (146′) | k′s,c1 = 0 | ||||
| k″s,c1 = 0 | |||||||||
| 9 | cln1 cln2 cln3 | 0.71 | 2.48 | 4.62 | 5.03 | No mit | Dn3 = k″s,n2 = 0 | Schwab, 1997, Fig. 3, M phase arrest | |
| hct1 | k″d,b2 = 0.01 | ||||||||
| 10 | cln1 cln2 cln3 | 0.71 | 2.48 | 4.16 | 4.60 | No mit | Dn3 = k″s,n2 = 0 | Irniger, 1997, Fig. 2, M phase arrest | |
| apc-ts | k″d,b2 = 0.01 | ||||||||
| k‴d,b2 = 0 | |||||||||
| k″d,b5 = 0 | |||||||||
Clearly, the triple-cln mutant can be rescued by supplying CLN2 or CLN3 on a plasmid with a GAL promoter (Table 4, lines 3 and 4). It can also be rescued by GAL-CLB5 (Table 4, line 6) or simply by providing an extra genomic copy of CLB5 (Table 4, line 6), as observed (Epstein and Cross, 1992). In the latter case, Clb5 is made twice as fast, so cells are able to turn off Sic1 and Hct1 at a reasonable size. In addition, triple cln can be rescued by deleting the genomic copy of SIC1 (Schneider et al., 1996; Tyers, 1996) (see Figure 6F and Table 4, line 8; the mechanism for the rescue will be described later).
However, triple-cln mutants cannot be rescued by GAL-CLB2 (Table 4, line 7); cells remain arrested in G1 because active Hct1/APC keeps Clb2 level low (Amon et al., 1994). Nor can it be rescued by hct1 or apc mutations (Table 4, lines 9 and 10), as observed (Irniger and Nasmyth, 1997; Schwab et al., 1997); here DNA synthesis can be initiated, but cells cannot exit from mitosis (more on this later).
Role of Bck2.
Bck2 has not received much attention from molecular biologists, but what is known (Epstein and Cross, 1994; Di Como et al., 1995) is consistent with the role given to Bck2 in the model (assumption 4). As for the case of CLN3 mutants, cells overexpressing BCK2 are smaller than normal (66%), and bck2 loss-of-function mutants are larger than normal (180%) (Table 5, lines 1b and 1c). Although the triple mutant cln1 cln2 bck2 (line 2b) is viable and a little larger than cln1 cln2, the double mutant cln3 bck2 (line 3b) is inviable: SBF is never activated, and cells arrest in G1. The inviable cln3 bck2 cell can be rescued, just like the triple-cln mutant, by GAL-CLN2, GAL-CLB5, or sic1 (lines 4a–4c). However, because SBF is not activated in this case, it takes more copies of genomic CLB5 (10 copies vs. 2) for its rescue (line 4d). Modest overproduction of Bck2 rescues triple-cln mutants (line 5b), provided both Swi4 and Swi6 are present, suggesting that Bck2 works through SBF.
Table 5.
Properties of bck2 mutants
| Genotype | Cell size relative to wild type
|
||||
|---|---|---|---|---|---|
| Observed
|
Simulation | ||||
| Epsteina | Di Comob | Dirickc | |||
| 1a | CLN1 CLN2 CLN3 BCK2 | 1 | 1 | 1 | 1 |
| b | bck2 | 1.3 | 1.5 | 1.8 | |
| c | + low-copy BCK2 | 0.8 | 0.7 with 4 copies | ||
| 2a | cln1 cln2 CLN3 BCK2 | 1.5 | 3.2 | 2.1 | |
| b | bck2 | 1.7 | 2.6 | ||
| 3a | CLN1 CLN2 cln3 BCK2 | 1.7 | 1.5 | 1.7 | 1.7 |
| b | bck2 | Inviable | Inviable | Inviable | |
| 4a | CLN1 CLN2 cln3 bck2 | ||||
| + GAL-CLN2 | Rescued | 0.5 | |||
| b | + GAL-CLB5 | 1.9 | |||
| c | + sic1 | 2.8 | |||
| d | + low-copy CLB5 | 3.7 with 10 copies | |||
| 5a | cln1 cln2 cln3 BCK2 | Inviable | Inviable | Inviable | |
| b | + low-copy BCK2 | Rescued | 3.9 with 4 copies | ||
Regulation of Clb Proteins.
Because Start represents the commitment of a budding yeast cell to a new round of DNA synthesis and division, it is important that B-type cyclins (which drive S phase and mitosis in budding yeast) be inoperative before Start occurs. The Clbs are kept out of the picture in G1 by three mechanisms: 1) CLB mRNA transcription is repressed, 2) Clb proteolysis by the APC is active, and 3) a Clb-dependent kinase inhibitor, Sic1, is abundant. In this section we explore the interrelations of these three effects by simulating mutants that knock out the components singly and in combinations.
First of all, any one of these component processes is expendable. For instance, cells that synthesize Clb2 or Clb5 constitutively (clb1 clb2 GAL-CLB2 or clb5 clb6 GAL-CLB5) are viable (Table 6, lines 3 and 5, and Figure 8, top panel) (Schwob and Nasmyth, 1993; Surana et al., 1993). GAL-CLB2 cells are nearly identical to wild-type because active Hct1/APC keeps the Clb2 level low in G1. GAL-CLB5 cells have abnormally high levels of Clb5 in G1 phase, but abundant Sic1 inhibits the associated CDK activity. Start occurs on schedule when the cell grows large enough for Cln3 + Bck2 to activate SBF, which drives Cln2 accumulation and subsequent phosphorylation (and degradation) of Sic1.
Table 6.
Properties of clb, sic1, and hct1 mutants
| Mass at birth | Mass at SBF 50% | Mass at DNA repl. | Mass at bud ini. | Mass at division | TG1 (min) | Changed parameter | Comments | ||
|---|---|---|---|---|---|---|---|---|---|
| 1 | wild type | 0.71 | 1.07 | 1.15 | 1.15 | 1.64 | 84 | CT 146 min | |
| (daughter) | (71′) | (84′) | (84′) | (146′) | (time of occurrence of event) | ||||
| 2 | clb1 clb2 | 0.71 | 1.07 | 1.16 | 1.16 | No mit | k′s,b2 = 0 | Surana, 1991, Table 1, G2 arrest | |
| k″s,b2 = 0 | |||||||||
| 3 | clb1 clb2 1X GAL-CLB2 | 0.65 | 1.10 | 1.19 | 1.19 | 1.50 | 105 | k′s,b2 = 0.1 | Surana, 1993, Fig. 4, 1X GAL-CLB2 is OK, 4X GAL-CLB2 (or 1X GAL-CLB2db) causes telophase arrest |
| k″s,b2 = 0 | |||||||||
| clb1 clb2 4X GAL-CLB2 | 0.71 | No SBF | 1.50 | No bud | inviable | k′s,b2 = 0.4 | |||
| k″s,b2 = 0 | |||||||||
| clb1 clb2 GAL-CLB2db | 0.71 | No SBF | 0.73 | No bud | No mit | k′s,b2 = 0.1 | |||
| k″s,b2 = 0 | |||||||||
| k″d,b2 = 0.01 | |||||||||
| k‴d,b2 = 0 | |||||||||
| 4 | clb5 clb6 | 0.73 | 1.07 | 1.30 | 1.17 | 1.70 | 99 | k′s,b5 = 0 | Schwob, 1993, Fig. 4, DNA repl. begins 30 min after SBF activation |
| (65′) | (99′) | (80′) | (146′) | k″s,b5 = 0 | |||||
| 5 | clb5 clb6 GAL-CLB5 | 0.61 | 0.93 | 0.92 | 0.96 | 1.41 | 73 | k′s,b5 = 0.1 | Schwob, 1993, Fig. 6, DNA repl. concurrent with SBF activation in both GAL-CLB5 and GAL-CLB5db |
| k″s,b5 = 0 | |||||||||
| clb5 clb6 2X GAL-CLB5 | 0.71 (1st) | 0.87 | 0.87 | 0.89 | 1.33 | k′s,b5 = 0.2 | First cycle OK, but prerepl. complex | ||
| 0.57 (2nd) | 0.58 | No repl | 0.58 | k″s,b5 = 0 | cannot form after the first cycle and cell dies | ||||
| clb5 clb6 GAL-CLB5db | 0.71 | 1.01 | 1.02 | 1.04 | 1.51 | k′s,b5 = 0.1 | Schwob, 1994, Fig. 3, DNA repl. is | ||
| 0.65 | 0.65 | No repl | 0.66 | k″s,b5 = 0 | not advanced in the first cycle | ||||
| k″d,b5 = 0 | |||||||||
| 6 | sic1 | 0.66 | 1.00 | 0.82 | 1.06 | 1.52 | 38 | k′s,c1 = 0 | Schneider, 1996, Fig. 4, sic1Δ |
| (73′) | (37′) | (83′) | (146′) | k″s,c1 = 0 | uncouples S phase from budding | ||||
| 7 | sic1 GAL-SIC1 | 0.80 | 1.07 | 1.38 | 1.17 | 1.86 | 94 | k′s,c1 = 0.1 | Verma, 1997, Fig. 3B, Nugroho and Mendenhall, 1994, Fig. 2, most cells are viable |
| k″s,c1 = 0 | |||||||||
| sic1 GAL-SIC1db | 0.71 | 1.07 | No repl | 1.17 | No mit | k′s,c1 = 0.1 | Verma, 1997, Fig. 3, G1 arrest | ||
| k″s,c1 = 0 | |||||||||
| kd2,c1 = 0 | |||||||||
| 8 | hct1 | 0.73 | 1.08 | 1.17 | 1.18 | 1.69 | 82 | k″d,b2 = 0.01 | Schwab, 1997, Fig. 2, viable, size like WT, Clb2 level high throughout the cycle |
| 9 | sic1 hct1 | 0.71 | No SBF | 0.72 | No bud | No mit | k′s,c1 = 0 | Visintin, 1997, telophase arrest | |
| k″s,c1 = 0 | |||||||||
| k″d,b2 = 0.01 | |||||||||
| 10 | sic1 GAL-CLB5 | 0.71 (1st) | 0.74 | 0.73 | 0.76 | 1.20 | k′s,b5 = 0.1 | Schwob, 1994, Fig. 7C, inviable | |
| 0.52 (2nd) | No repl | k″s,b5 = k′s,c1 = k″s,c1 = 0 | First cycle OK, DNA repl. advanced; but prerepl. complexes cannot form and cell dies after the first cycle | ||||||
| 11 | hct1 GAL-CLB5 | 0.71 | No SBF | 0.72 | 0.77 | No mit | k′s,b5 = 0.1 | ||
| k″s,b5 = 0 | |||||||||
| k″d,b2 = 0.01 | |||||||||
| 12 | sic1 GAL-CLB2 | 0.71 | No SBF | 0.81 | No bud | No mit | k′s,b2 = 0.1 | Cells die in first cycle, no bud | |
| k″s,b2 = k′s,c1= | |||||||||
| k″s,c1 = 0 | |||||||||
| 13 | hct1 GAL-CLB2 | 0.71 | No SBF | 0.83 | No bud | No mit | k′s,b2 = 0.1 | ||
| k″s,b2 = 0 | |||||||||
| k″d,b2 = 0.01 | |||||||||
| 14 | sic1 clb5 clb6 | 0.74 | 1.08 | 1.32 | 1.18 | 1.72 | 99 | k′s,c1 = k″s,c1 = | Behaves very much like clb5 clb6 |
| k′s,b5 = k″s,b5 = 0 |
Figure 8.
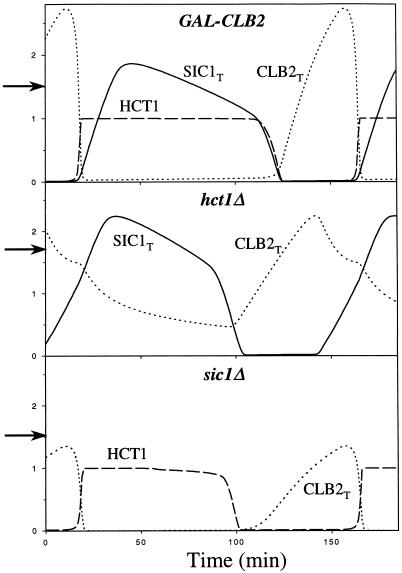
Cells are able to exit from mitosis when any single one of the three Clb2-inhibiting mechanisms is faulty. Top panel, constitutive transcription of CLB2 in G1 phase. Middle panel, no Hct1-mediated degradation of Clb2 at telophase. Bottom panel, no Sic1 to inhibit Clb2/Cdc28 in G1 phase. The arrow on the ordinate indicates mass at division; all three strains have size comparable with wild type.
Our model cell can tolerate overexpression of Clb2 better than Clb5. Up to three copies of GAL-CLB2 are tolerated; four copies or more lead to telophase arrest, as observed (Surana et al., 1993). Abnormally high levels of Clb2 can be tolerated because Clb2 induces its own degradation by stimulating Cdc20 synthesis (Prinz et al., 1998). Higher levels of Cdc20 effectively counteract higher levels of Clb2 at Finish. On the other hand, 2 × GAL-CLB5 is lethal because Clb5-associated kinase efficiently phosphorylates and destabilizes Sic1. As a consequence, Sic1 cannot make a comeback at Finish, Clb5/Cdc28 activity stays high, and DNA origins cannot be relicensed in G1.
The hct1 mutant is also viable (Table 6, line 8, and Figure 8, middle panel) (Schwab et al., 1997). Normally, Clb2 is degraded at the metaphase–anaphase transition, but hct1 mutants finish the cell cycle differently. At anaphase, Cdc20 activates Swi5 and degrades some Clb2, allowing Sic1 to make a comeback and inhibit any remaining Clb2-dependent kinase activity. Subsequently, Clb2 protein level drops because its transcription turns off.
To model hct1Δ mutants correctly, we must assume that Cdc20 accounts for some degradation of Clb2. Three lines of evidence support this assumption (10). Experiments of Irniger et al. (1995, their Figure 4) show that Clb2 is partially degraded in cdc15 telophase-arrested cells when (we presume) Cdc20 is active and Hct1 is not. Visintin et al. (1997, their Figure 2) showed that Clb2 is degraded by both Hct1 and Cdc20 in nocodazole-arrested cells. Finally, it is well known that sister chromatid separation and B-type cyclin degradation are mediated by a single Cdc20 homologue during early embryogenesis of Drosophila and Xenopus (Dawson et al., 1995; Sigrist et al., 1995; Lorca et al., 1998).
The ability of Sic1 to bring Hct1-deficient cells out of mitosis depends on cell size: in the presence of α-factor, hct1 cells grow very large, replicate their DNA, and block in mitosis (Schwab et al., 1997). Our simulation of cln1 cln2 cln3 hct1 behaves similarly (Table 6, line 9). By the time the mitotic checkpoint is satisfied and cells are ready to divide, they are so big and their accumulated Clb2 level is so high that Sic1 is unable to win over Clb2.
Although sic1 is sick (having many deficiencies in chromosome dynamics), it is still a viable mutant (Table 6, line 6, and Figure 8, bottom panel). The only major change in the timing of cell cycle events is the advancement of DNA synthesis (relative to bud emergence) by ∼35 min (Schneider et al., 1996, their Figure 4). These authors show that sic1 cells initiate DNA synthesis at a much smaller size than wild-type cells.
Because in wild-type cells DNA synthesis and SBF activation occur almost concurrently, and SBF activation depends mainly on the actions of Cln3 and Bck2 (not inhibited by Sic1), it follows that in sic1 mutants initiation of DNA synthesis is well ahead of SBF activation. That is, the small amount of Clb5, synthesized by an MBF-independent pathway, is able to initiate DNA synthesis at a small size (because there is no Sic1 present to inhibit it), well before the cell is large enough to activate SBF.
In contrast to the viability of single mutants (GAL-CLBs, hct1, and sic1), double mutants are all inviable (Table 6, lines 9–13). hct1 sic1 cells, being unable to eliminate Clb2-dependent kinase, cannot exit mitosis (Visintin et al., 1997). clb5 GAL-CLB5 sic1 cells complete one cycle after adding galactose but die in the second cycle because they cannot replicate their DNA (they cannot resynthesize licensing factor, because Clb-dependent kinase activity stays high after mitosis) (Schwob et al., 1994). clb2 GAL-CLB2 sic1 cells die after adding galactose, because they cannot bud (SBF is kept off by high Clb2-dependent kinase activity after mitosis). For the same reason, clb2 GAL-CLB2 hct1 and clb5 GAL-CLB5 hct1 cells are inviable.
Properties of SIC1op Mutants.
Twofold overexpression of Sic1 is tolerated (Verma et al., 1997), but (roughly) 10-fold overexpression is deleterious (Nugroho and Mendenhall, 1994): some 20% of the cells have elongated buds and fail to divide. Our simulations of sic1 GAL-SIC1 (Table 6, line 7, with k"s,c1 = 0 and increasing k′s,c1 up to fivefold from 0.1 to 0.5) give viable cells with increasing G1 period and larger sizes, but a sixfold increase is lethal (DNA synthesis commences at mass > 5). This behavior is consistent with the experimental observations, provided cells in a population have a distribution of levels of Sic1 production. Similarly, cells with the phosphorylation sites of Sic1 removed (protein stable) never enter S phase (Table 6, line 7), as observed (Verma et al., 1997).
The reason that cells tolerate high levels of Sic1 expression (i.e. 5 × GAL-SIC1) and still go through DNA synthesis and mitosis is because of the role played by CLN2. SBF activation is unaffected by Sic1; however, high levels of Sic1 inhibit Clb2 activity, so SBF inactivation is delayed. Cln2 will be synthesized at a high rate for longer time, and eventually they will be able to phosphorylate Sic1, causing it to degrade and Clb kinases to win.
Initiation of DNA Synthesis in the sic1 Mutant.
As described in the previous section, when compared with wild-type cells, sic1 mutants initiate S phase at a much smaller size, whereas cln1 cln2 mutants initiate it at a much larger size (Dirick et al., 1995). What will happen if the two mutations are combined?
Because, in sic1 mutants, initiation of DNA synthesis is driven mainly by the small amount of Clb5 present in early G1 cells, deletion of Clns should have little effect on its timing. Hence, the multiple mutants cln1 cln2 sic1 or cln1 cln2 cln3 sic1 all should initiate DNA synthesis at about the same size as the sic1 single mutant, at a size smaller than wild type.
Our simulation (Figure 6F) of cln1 cln2 cln3 sic1 agrees with observations of Schneider et al. (1996, their Figure 4B). Without Sic1 inhibition, Clb5 is able to initiate DNA synthesis early and to help Bck2 turn on SBF and MBF, causing more Clb5 accumulation, Hct1 inactivation, and eventually progression toward mitosis.
However, for cln1 cln2 sic1, the simulation (Figure 6E) does not agree with observations. Dirick et al. (1995, their Figure 4) reported that DNA synthesis occurs at about the same size for the mutant as for wild-type cells. If the observation of Schneider et al. (1996) is true, then how can the addition of a functional CLN3 gene (giving cln1 cln2 sic1) delay DNA synthesis to a larger mass, when Cln3 is a helper to Clb5? Thus, we are unable to fit all these observations with our present understanding of the control system, and we believe that the experimental observation of Dirick et al. (1995) requires closer investigation.
DISCUSSION
In Figure 2, we propose a realistic mechanism for regulating the cell division cycle in budding yeast. Its components are Cln1 and 2 (lumped together), Cln3 and Bck2, Clb1 and 2 (lumped), Clb5 and 6 (lumped), Sic1, Hct1 (=Cdh1), and Cdc20. (Cdc28, the kinase subunit that combines with the cyclins, is present in excess, so we need not keep track of its fluctuations.) In addition, the model tracks the relative activities of three transcription factors, Swi4/Swi6 (=SBF), Mcm1/SFF, and Swi5, which determine the rates of synthesis of Cln2, Clb2, and Sic1, respectively. At present, we assume that MBF, the transcription factor for Clb5, is regulated coordinately with SBF. In the model, overall cell growth is exponential, and the basic events of the yeast division cycle (DNA synthesis, budding, and spindle assembly) are driven by the integrated activities of cyclin-dependent kinases. These assumptions lead to a mathematical model (Table 1) consisting of 10 nonlinear, ordinary differential equations (for mass, the cyclins, and their consorting proteins), three algebraic functions for transcription factors, three “integrators” to trigger DNA synthesis, budding, and spindle assembly, and a simple rule for separating mother and daughter cells at division.
The kinetic model introduces ∼50 parameters (rate constants, binding constants, thresholds, relative efficiencies, etc.) that need to be determined by fitting specific experimental observations. For the present, we do this by trial and error (Appendix A), so we can only claim that our model equations and parameter set are sufficient to account for many properties of cell cycle control in budding yeast. Because we fit the model to the properties of dozens of different genotypes, we have enough data to fix the parameters and to provide meaningful confirmation of the mechanism in Figure 2.
Table 2 is in no sense an optimal parameter set, nor can we quantify how robust is the system, although our experience suggests that the model is quite hardy. Currently we are working on computational methods of parameter optimization and sensitivity analysis and hope to address these problems in a later publication.
Bistability and Hysteresis
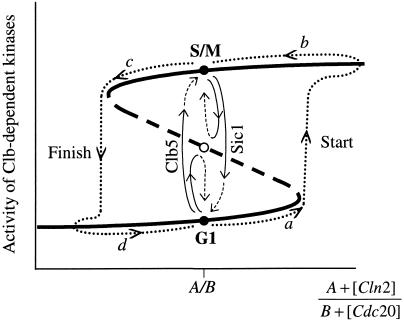
The crucial idea behind our model of the budding yeast cell cycle is Nasmyth's (1996) hypothesis that G1 and S/M are alternative, self-maintaining states, generated by mutual antagonism between Clb-dependent kinases and their opponents, Sic1 and Hct1. In theoretical terms, the molecular regulatory system exhibits bistability and hysteresis (Figure 9). In its “neutral” condition (no Cln2 or Cdc20), the control system can persist in either the stable G1 state or the stable S/M state. Transitions between these alternative steady states can be driven by changes in Cln2 and Cdc20 that push the control system past the “fold” points in Figure 9 (Novak et al., 1998).
Figure 9.
Bistability and hysteresis (schematic). Steady-state level of total Clb-dependent kinase activity depends on the expression of CLN2 and CDC20. When [Cln2] is large and [Cdc20] is small, the Clb1–6 regulatory system is in a state of high kinase activity (S/M), whereas in the other extreme, Clb-dependent kinase activity is low (G1). When [Cln2] and [Cdc20] are both small, the regulatory system is in neutral (background activity = A/B), and two stable states of Clb activity coexist (bistability). The system is driven around a hysteresis loop (dashed curve) by pulses of Cln2 (stages a and b) and Cdc20 (stages c and d).
At Start, Cln2-dependent kinase activity rises abruptly and pushes the cell from G1 to S/M by inactivating Hct1 and promoting Sic1 degradation (Figure 9, stage a). The Clns can drive this transition because they are neither degraded by Hct1 nor inhibited by Sic1. After Clb2 appears, Cln2 is removed, but the cell remains in S/M because the Clbs can now keep Hct1 and Sic1 in abeyance without further help from Clns (stage b). This effect, called hysteresis, makes the Start transition irreversible.
Cdc20, activated at metaphase, pushes the cell from S/M to G1 (Finish) by activating Hct1 and promoting Sic1 accumulation (Figure 9, stage c). Cdc20 can drive this transition, because it is not opposed by Clb-dependent kinase activities; indeed, Clb2 promotes Cdc20 accumulation and activation. As Cdc20 is destroyed in G1 (stage d), the control system does not flip back to the S/M state, because Hct1 and Sic1 can now keep the Clbs in abeyance without further help from Cdc20. The S-shaped curve in Figure 9 accounts for the characteristic irreversibility of entry into S phase and exit from mitosis.
In this picture, not merely may the “pushers” be removed and the control system will not revert, but they must be removed to make a repeated sequence of properly regulated Start and Finish transitions. For instance, once Start is accomplished, Cln2 must disappear; otherwise it will work against the Finish transition. Higher concentrations of Cdc20 will be required to trigger Finish. Furthermore, after the cell leaves mitosis, as Cdc20 disappears, Sic1 and Hct1 will not be able to hold the cell in G1. For these reasons, although GAL-CLN2 mutants are viable, they have short G1 and long S/M periods.
Similarly, removal of Cdc20 after Finish is crucial for the next Start transition. Because the phosphatase (Cdc14) activated by Cdc20 can overwhelm all CDK activity at metaphase and thereby induce Finish, then it will be difficult to induce the next Start if Cdc20 activity does not disappear in G1 phase so that this phosphatase can be inactivated. In this regard, notice that mild overproduction of Cdc20 (GAL-CDC20 in 0.2% galactose) induces prolongation of G1 (Prinz et al., 1998), and strong overproduction (3X GAL-CDC20 in 2% galactose) induces G1 arrest (Shirayama et al., 1998). GAL-CDC14 also induces G1 arrest (Visintin et al., 1998).
Direct experimental confirmation of bistability can be sought by holding the control system in neutral (Figure 9, position A/B) and then driving it between G1 and S/M by ectopic expression of Clb5 and Sic1 (Figure 9, vertical arrows). This experiment has been done in part by Dahmann et al. (1995). After arresting cells in mitosis with nocodazole, they induced transition to G1 (without nuclear or cell division) by ectopic expression of Sic1. When ectopic synthesis of Sic1 was repressed, their cells executed a second round of DNA synthesis, because endogenous production of Clns drove the cells through Start. To prevent autonomous reentry into S phase, we suggest that cells be blocked with α-factor as well as nocodazole.
We propose that a synchronous culture of MET-CLB5 TET-SIC1 cells (where MET = methionine-repressible promoter and TET = tetracyline-inducible promoter), about to execute Start and bud, be transferred from “growth” medium (containing methionine) to “arrest” medium (containing methionine, α-factor, and nocodazole). (Notice that the use of α-factor and nocodazole to arrest cells in neutral could be replaced by cln1–3Δ and clb1–4Δ, respectively.) Those cells that have not yet executed Start when the medium is changed will be kept in G1 phase by α factor (moving from a to G1 in Figure 9), whereas those cells that have already executed Start will be arrested in M phase by nocodazole (moving from b to S/M in Figure 9). The culture is now a mixed population of G1- and S/M-arrested cells, suggesting that, in this neutral position, there coexist two stable steady states of Clb activity. To prove the coexistence of these states, divide the culture into two batches. One batch is subjected to transient Clb5 synthesis by transferring the cells briefly to “Clb5” medium (α-factor + nocodazole) and then back to arrest medium. All cells in this batch are expected to arrest in the S/M state (in Figure 9, cells initially at G1 will be driven to S/M, whereas those initially at S/M will return there). Cells of the other batch, after brief exposure to “Sic1” medium (methionine + tetracycline + α-factor + nocodazole), are expected to arrest uniformly in G1 phase. Furthermore, the duration of the “brief” exposure is important: there should be threshold levels of exposure to Clb5 and Sic1 below which the transitions are not accomplished (see Figure 9).
Note that, at the end of treatment, all cells are of uniform size and are exposed to arrest medium. Nonetheless, if our model is correct, individual cells will be in different phases of the division cycle, depending on how they were perturbed. Those cells initially in G1 will be pushed into S/M by a Clb5 perturbation but not by a Sic1 perturbation (Schwob and Nasmyth, 1993) and vice versa for those cells initially in S/M (Dahmann et al., 1995). This behavior would indicate that two stable states of Clb activity coexist (bistability) when the regulatory system is in neutral. By alternating treatment with Clb5 and Sic1, one should be able to induce multiple rounds of endoreplication in cln1–3Δ clb1–4Δ cells.
Reversibility of the SBF Switch
In contrast to the irreversibility of the Start and Finish transitions, the activation of SBF in our model is a reversible, ultrasensitive switch. To test this feature of the model, one could modify slightly the experimental design of Dirick et al. (1995). The strain cln1Δ cln2Δ cln3ts MET-CLN2 is grown in the absence of methionine, so that newborn daughter cells are small. Small cells, transferred to methionine-containing medium at permissive temperature, will activate SBF (measured by expression of PCL1 mRNA, say) at wild-type size, but Sic1 degradation and Hct1 activation will be delayed to a much larger size. If, after SBF activation, the cells are transferred to restrictive temperature, then SBF should inactivate (i.e., this event is reversible), and the cells should remain in G1.
Autonomously Oscillating Versus Checkpoint-controlled Cell Cycles
Cell division cycles of budding yeast (and somatic cells in general) are blocked by drugs that inhibit DNA replication or spindle assembly (“checkpoint controls”), whereas early embryonic cell divisions are unrestrained by these same drugs (Murray and Hunt, 1993). If somatic and embryonic cells use the same cell cycle control machinery, why do they behave so differently?
In theoretical terms, checkpoints correspond to stable steady states (G1 and S/M in the current model), and drugs that inhibit growth, DNA synthesis, or spindle assembly abort the signals that normally push the cell from one checkpoint to the next. The existence of these checkpoints depends on the mutual antagonism between cyclin B-dependent kinases and their opponents (Sic1 and Hct1 homologues).
In early Xenopus embryos, there are no effective antagonists of cyclin B/Cdc2 kinase (also called MPF). 1) The only identified MPF inhibitors are p28Kix1 (Shou and Dunphy, 1996) and p27Xic1 (Su et al., 1995), but both are present at very low levels until the late gastrula stage. Furthermore, neither one inhibits MPF in vitro. 2) XFZR (the Xenopus homologue of HCT1) is not translated before the midblastula transition. Instead, X-FZY (the Xenopus homologue of Cdc20) is responsible for cyclin B degradation during early embryonic cell cycles (Lorca et al., 1998). X-FZY, like Cdc20, seems to be activated rather than inhibited by MPF (Felix et al., 1990). 3) Even the antagonistic relationship between MPF and Wee1 (a tyrosine kinase that inhibits Cdc2) seems to be ineffective, because Cdc2 shows very little tyrosine 15 phosphorylation during the early cycles of intact embryos (Ferrell et al., 1991).
Without effective antagonists in early embryonic cells, MPF cannot establish the alternative steady states characteristic of checkpoint controls. The only remaining control is a time-delayed negative feedback loop, whereby MPF activates X-FZY, which degrades cyclin B and thereby destroys MPF activity. The sufficiency of this mechanism to generate autonomous oscillations in MPF activity was shown first by Goldbeter (1991) and later by Novak and Tyson (1993). Because the early embryo lacks cyclin B antagonists, it supports rapid MPF oscillations that are insensitive to errors in DNA replication and spindle assembly; apparently the early embryo has sacrificed accuracy for speed. However, in frog egg extracts, checkpoint control can be elicited if a sufficient amount of unreplicated sperm DNA is added (Dasso and Newport, 1990; Smythe and Newport, 1992), which creates an effective antagonist by activating Wee1. If our hypothesis is right, one may be able to elicit checkpoint responses in Xenopus embryos before the midblastula transition by injecting XFZR mRNA (or protein) into the fertilized egg.
Models as Tools in Molecular Biology
Undoubtedly the genetic regulatory system of cell division in yeast and higher eukaryotes is even more complex than Figure 2. To understand regulatory systems of such complexity, we need analytical tools that can handle realistic biochemical control mechanisms. Our work confirms that modern methods of kinetic theory and computation are capable of connecting a realistic, multilayered, regulatory mechanism to the complex physiological behavior of cells.
In addition to its role in synthesizing molecular and physiological details about cell division, the model is a predictive tool. The rate constant estimates in Table 2 can be tested by more direct kinetic measurements. Tables 3–6 specify many quantitative properties of mutant cells that have never been reported, and they predict phenotypes of several mutants yet to be examined.
One can learn as much from the failures of the model as from its successes. Where there are inconsistencies between the model and experiment, we are prompted, first of all, to look for a better parameter set. If that fails, we consider slight changes in the mechanism, which might bring the model in accord with observations. If that fails, and if the experimental community is convinced that the observations are reliable and significant, then we have identified an area that deserves closer scrutiny to resolve the discrepancies. If the mechanism proves insufficient, that does not invalidate our approach. Mathematical modeling, as a tool, is no more “falsifiable” than gel electrophoresis. The tool tells us what a mechanism can and cannot explain. When the model fails, the fault lies with the mechanism, not the tool.
The molecular mechanism of cell cycle control in budding yeast is an evolving hypothesis that must be continually examined, revised, and improved as new observations tell us more about the control system. We intend to extend the model in several directions. First, we will provide a more detailed description of Finish (Novak et al., 1999), including roles for Cdc14 (Visintin et al., 1998; Jaspersen et al., 1999), RENT complexes (Shou et al., 1999), and Pds1/Esp1 interactions (Ciosk et al., 1998; Cohen-Fix and Koshland, 1999; Tinker-Kulberg and Morgan, 1999). The next step will be to connect mathematical representations of surveillance mechanisms to the underlying cell cycle engine. For instance, the mating factor pathway connects pheromone binding at the cell surface, through a protein kinase cascade, to the inhibition of Cln kinases, which arrests cells before Start (Wittenberg and Reed, 1996; Posas et al., 1998). Another important signal transduction pathway, through mad and bub gene products, arrests cells in mitosis, if the mitotic spindle is improperly assembled (Alexandru et al., 1999; Taylor, 1999).
APPENDIX A: ESTIMATION OF RATE CONSTANTS
First some definitions:
1) A Michaelis constant (J in our notation) carries units of concentration (nM). In the Michaelis–Menten rate law, J is the characteristic substrate concentration at which reaction rate is half-maximal.
2) A zero-order rate constant carries units of nM min−1. Examples include rates of synthesis (ks in our notation), and Vmax values in Michaelis–Menten rate laws (ka and ki in our notation).
3) A first-order rate constant carries units of min−1. Examples include degradation rate constants (kd) and dissociation rate constants (kdi).
4) A second-order rate constant, e.g., an association rate constant (kas), carries units of nM−1 min−1.
In writing the kinetic equations in Table 1, all concentration variables are scaled so that their maximal values are pure numbers of order 1. We are forced to do this because little is known about the actual concentrations (nM) of any of the molecular components in budding yeast cells. Because all concentration variables are dimensionless, the Michaelis constants are dimensionless, and all the zero-, first-, and second-order rate constants carry units of min−1 (Table 2).
Rates of Degradation
Because the stability of cyclins at various stages in the budding yeast cell cycle has been studied carefully by many experimental groups, we can estimate the cyclin degradation constants in our model with some confidence. For instance, the half-life Cln2 is 5–10 min (Salama et al., 1994; Barral et al., 1995; Lanker et al., 1996), implying that kd,n2 ≈ ln2/7 = 0.1 min−1, which is the value we use (Table 2). Because Hct1 is turned off at Start, Clb2 is more stable in S/M than in G1: half-life = 1 min in G1 and > 1 h in S/M (Amon et al., 1994; Irniger et al., 1995; Seufert et al., 1995). These observations imply that k′d,b2 ≈ ln2/70 = 0.01 min−1 and k"d,b2 ≈ ln2/1 = 0.7 min−1, which are close to the values in Table 2. Clb5, on the other hand, is only slightly more stable in S/M (half-life = 10 min) than in G1 (half-life = 2 min) (Irniger and Nasmyth, 1997). Hence, k′d,b5 ≈ ln2/10 = 0.07 min−1, and k′d,b5 + k"d,b5 ≈ ln2/2 = 0.35 min−1 (see Table 2).
From the observed half-life of Cdc20, 15 min (Shirayama et al., 1998), we estimate that kd,20 = 0.05 min−1.
Sic1 disappears at Start over the course of ∼20 min (Schwob et al., 1994). Because we use a Michaelis–Menten rate law for Sic1 phosphorylation (the rate-limiting step for Sic1 degradation at Start), it is not so obvious how to estimate our rate parameters, but the values Jd2,c1 ≪ 1 and kd2,c1 = 0.3 min−1 give reasonable agreement to Schwob's observation.
Rates of Synthesis
Rate constants for cyclin synthesis can be estimated from degradation rate constants and steady-state concentrations. However, because the concentrations are unknown, we cannot ascribe directly meaningful values to the synthesis rate constants. Instead, we choose ks ≈ kd, so that the maximum concentrations of all variables during a wild-type cycle are ∼1. The chosen values of ks reflect the relative concentrations of the cyclins, Sic1, and Cdc20, as best we can guess, but the arbitrary units (au) in which each concentration is expressed are unknown until we have better experimental data. For instance, suppose the peak concentrations of Sic1 and Cln2 were measured to be 100 and 30 nM, respectively. Then, from Figure 3, we would assign 1 au of Sic1 concentration = 90 nM and 1 au of Cln2 concentration = 60 nM, and we could predict that k′s,c1 = 1.8 nM min−1, k"s,c1 = 9 nM min−1 (when Swi5 is fully active), Jd2,c1 = 4.5 nM, and kd2,c1 = 0.3 min−1 (90/60 nM) = 0.45 min−1.
Rates of Association and Dissociation
The rate constant (kas) for association of Sic1 with Clb2/Cdc28 and Clb5/Cdc28 is an important parameter in the model. It must be large enough to account for strong binding, given reasonable lability of the complexes (kdi = 0.05 min−1, assumed). We choose kas = 50 min−1, which implies a binding constant of 103. The theory of diffusion-controlled reactions (Tinoco et al., 1978, p. 385) puts an upper limit on second-order rate constants: kmax = 8πrNoDavg, where r = encounter distance of a pair of reacting molecules, No = Avogadro's number, and Davg = average diffusion coefficient of the reacting molecules. Assuming r = 4 × 10−7 cm, and Davg = 2 × 10−6 cm2 s−1, we estimate that kmax = 1010 l mol−1 s−1 = 10 nM−1 s−1. If the concentration of protein partners is roughly 80 nM, then kmax (scaled) ≈ 5 × 104 min−1, which is 1000 times larger than the value assigned to kas.
Rates of Activation and Inactivation
The transcription factors SBF, Mcm1, and Swi5 are each described by Goldbeter–Koshland functions, G(Va, Vi, Ja, Ji). (Please refer to Appendix B for the definition of this function and a detailed description of its properties.) When Ja and Ji are much less than 1, a Goldbeter–Koshland function changes very abruptly in the neighborhood of G = ½. Because the SBF switch turns on abruptly as cells grow (Dirick et al., 1995), we choose Ja,sbf and Ji,sbf to be small (0.01). By contrast, we suppose that Mcm1 turns on and off more smoothly (Ja,mcm = Ji,mcm = 1).
Activation and inactivation of Hct1 is also governed by a Goldbeter–Koshland mechanism, but we do not make a pseudo–steady-state approximation (d[Hct1]/dt = 0). Rather,
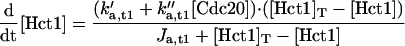 |
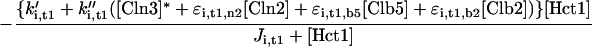 |
The rates at which Hct1 switches between more and less active forms depend on the rate constants, ka and ki. We expect they have values of order 1 min−1, so that changes occur in minutes rather than seconds or hours. More precise estimates cannot be made from presently available measurements.
To estimate the conditions for turning Hct1 on and off, we notice that [Hct1] ≈ ½[Hct1]T when
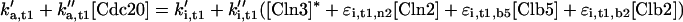 |
(provided Ja,t1 = Ji,t1). In metaphase, when Clb2 plays the major role in keeping Hct1 inactive, the condition for activating Hct1 is [Cdc20] = k"i,t1[Clb2]/k"a,t1 ≈ 0.5. That is, Hct1 turns on when Cdc20 activity exceeds 0.32 × Clb2 activity. The threshold can be adjusted by changing the ratio k"i,t1/k"a,t1. In late G1 phase, when [Cdc20] ≈ 0.05, [Clb2] ≈ 0, [Cln3]* ≪ [Cln2], and Clb5 is still inhibited by Sic1, the condition for inactivating Hct1 is [Cln2] = (k′a,t1 + k"a,t1[Cdc20])/k"i,t1 ≈ 0.2. With our choice of parameters, Cln2 plays the major role in turning off Hct1 at Start. It may be that Clb5 plays a more important role, in which case the relative efficiencies (ɛi,t1,b5 and ɛi,t1,n2) would have to be readjusted.
Other Parameters
[Cln3]max = 0.02 is chosen so that the amount of Cln3 at Start, [Cln3]* ≈ 0.003 when mass ≈ 1, is ∼100 times smaller than the maximum amounts of Cln1 and Cln2 during the cycle (Tyers et al., 1993). Although Cln3 is present in a very small amount, it plays an important role turning on SBF at Start (Dirick et al., 1995; Stuart and Wittenberg, 1995), because ɛsbf,n3 is very large. [Bck2]0 = 0.0027 is chosen to account for the observed size for SBF activation in the cln3 mutant.
Efficiencies
Our model contains many other dimensionless “efficiencies” of different CDKs for various phosphorylation reactions. These efficiencies simply represent the fact that budding yeast cyclins have overlapping specificities: they often catalyze the same reactions but with different relative turnover numbers. We adjusted the efficiencies to account for the relative timing of events in mutants where the primary cyclin is missing and the event is triggered by one of its backups.
For instance, in triple-clnΔ sic1Δ, Clb5 is the primary cyclin responsible for Hct1 inactivation. If ɛi,t1,b5 were too small, then Hct1 would never turn off, and the mutant would be inviable. If ɛi,t1,b5 were too large, then the small amount of uninhibited Clb5 early in the cycle (which drives premature DNA synthesis in this mutant) would inactivate Hct1 too soon. As a result, Clb2 would rise early, and SBF could never be activated, so the mutant would divide at a small size without ever making a bud. In our simulations, ɛi,t1,b5 ≈ 0.5 gives a correct phenotype to this mutant.
Integrators
Finally, we have introduced three “integrators” (ORI, BUD, and SPN), which determine when the events of 1) initiation of DNA synthesis, 2) bud emergence, and 3) chromosome alignment on the mitotic spindle will occur. Experiments show that 1) DNA synthesis can be initiated by Clbs but not by Clns (Schwob et al., 1994); 2) bud emergence can be driven by Clb5 as well as Clns (Schwob and Nasmyth, 1993), and 3) mitosis can be driven to completion only by Clb1 and Clb2 (Surana et al., 1991). These facts determine the forms taken by the integrators. The rate constants (ks,ori, ks,bud, and ks,spn) and efficiencies are chosen to give the right timing of these events in various mutants.
Note that some parameters are introduced only for notational consistency (e.g., ka,sbf, ka,mcm, ka,swi, and ki,t1) and are set equal to 1 or 0 in all computations. Other parameters are constrained to be identical (e.g., Ja, … = Ji, …), to limit the scope of the problem. Therefore, we had ∼50 parameters to estimate from the properties of ∼50 different genotypes. Wild-type cells provide us with enough information to estimate more than half of these parameters. The remaining parameters are constrained by the properties of all the mutants we have simulated. Because each viable mutant gives us at least two pieces of information (relative size and G1 duration), we have much more data to fit than parameters to vary. Therefore, because the model accounts for so many facts (in quantitative detail wherever possible), we conclude that the molecular mechanism in Figure 2 is essentially correct.
APPENDIX B: ZERO-ORDER ULTRASENSITIVITY
We model the kinetic behavior of the budding yeast transcription factors (SBF, Mcm1, and Swi5) as zero-order ultrasensitive switches (Goldbeter and Koshland, 1981; Ferrell, 1996). We assume that each transcription factor (TF) exists as either an active or inactive form (let F = fraction in active form), and that transitions between the two forms are enzyme-catalyzed reactions following Michaelis–Menten kinetics,
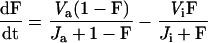 |
Va and Vi are Vmax values of the activating and inhibiting enzymes, and Ja and Ji are Michaelis constants (relative to the total concentrations of TF). If the transitions are fast enough (Va and Vi large enough) to keep each TF in its steady-state distribution, then
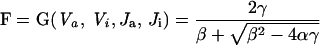 |
where α = Vi − Va, β = Vi − Va + VaJi + ViJa, and γ = VaJi. Notice that G = ½ when Va/Vi = (2Ja+1)/(2Ji+1). If Ja and Ji are both ≪ 1, then 50% of the TF is active when Va/Vi = 1. Moreover, Goldbeter and Koshland (1981) showed that G is a sharply sigmoidal function of Va/Vi if Ja and Ji are ≪ 1.
In our model, this behavior shows up as a sharp activation of SBF by Cln3-dependent kinase, as the cell grows through a critical size. To calculate the size at which [SBF] = ½, we set Va = Vi,
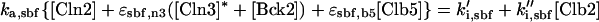 |
Noting that [Cln2] ≈ [Clb5] ≈ [Clb2] ≈ 0 in G1, we find that [SBF] = ½ when
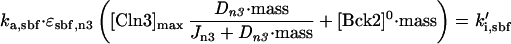 |
or, given the parameter values listed in Table 2,
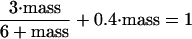 |
The solution of this quadratic equation is mass ≈ 1.2. This is the critical size for SBF activation; in wild-type cells, all other events of Start occur in rapid succession after the cell activates SBF. (In the full model, SBF activates at a slightly smaller size, presumably because of the residual activities of the other kinases in G1, which we neglected in this calculation.)
ACKNOWLEDGMENTS
We benefited greatly at various stages from conversations with Kim Nasmyth, Attila Toth, Jill Sible, Ray Deshaies, and Fred Cross and from the diligence of the anonymous referees. This work was supported by US National Science Foundation grants MCB-9600536 and DBI-9724085, National Science Foundation of Hungary grant T-022182, and Howard Hughes Medical Institute grant 75195-542501.
Abbreviations:
- APC
anaphase-promoting complex
- CDK
cyclin-dependent kinase
REFERENCES
- Alberts B, Bray D, Lewis J, Raff M, Roberts K, Watson JD. Molecular Biology of the Cell. 3rd ed. New York: Garland Publishing; 1994. [Google Scholar]
- Alexandru G, Zachariae W, Schleiffer A, Nasmyth K. Sister chromatid separation and chromosome reduplication are regulated by different mechanisms in response to spindle damage. EMBO J. 1999;18:2707–2721. doi: 10.1093/emboj/18.10.2707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amon A. Regulation of B-type cyclin proteolysis by Cdc28-associated kinases in budding yeast. EMBO J. 1997;16:2693–2702. doi: 10.1093/emboj/16.10.2693. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amon A. The spindle checkpoint. Curr Opin Genet Dev. 1999;9:69–75. doi: 10.1016/s0959-437x(99)80010-0. [DOI] [PubMed] [Google Scholar]
- Amon A, Irniger S, Nasmyth K. Closing the cell cycle circle in yeast: G2 cyclin proteolysis initiated at mitosis persists until the activation of G1 cyclins in the next cycle. Cell. 1994;77:1037–1050. doi: 10.1016/0092-8674(94)90443-x. [DOI] [PubMed] [Google Scholar]
- Amon A, Surana U, Muroff I, Nasmyth K. Regulation of p34CDC28 tyrosine phosphorylation is not required for entry into mitosis in S. cerevisiae. Nature. 1992;355:368–371. doi: 10.1038/355368a0. [DOI] [PubMed] [Google Scholar]
- Amon A, Tyers M, Futcher B, Nasmyth K. Mechanisms that help the yeast cell cycle clock tick: G2 cyclins transcriptionally activate G2 cyclins and repress G1 cyclins. Cell. 1993;74:993–1007. doi: 10.1016/0092-8674(93)90722-3. [DOI] [PubMed] [Google Scholar]
- Bai C, Sen P, Hofmann K, Ma L, Goebl M, Harper JW, Elledge SJ. Skp1 connects cell cycle regulators to the ubiquitin proteolysis machinery through a novel motif, the F-box. Cell. 1996;86:263–274. doi: 10.1016/s0092-8674(00)80098-7. [DOI] [PubMed] [Google Scholar]
- Baroni MD, Monti P, Alberghina L. Repression of growth-regulated G1 cyclin expression by cyclic AMP in budding yeast. Nature. 1994;371:339–342. doi: 10.1038/371339a0. [DOI] [PubMed] [Google Scholar]
- Barral Y, Jentsch S, Mann C. G1 cyclin turnover and nutrient uptake are controlled by a common pathway in yeast. Genes Dev. 1995;9:399–409. doi: 10.1101/gad.9.4.399. [DOI] [PubMed] [Google Scholar]
- Biggins S, Murray AW. Sister chromatid cohesion in mitosis. Curr Opin Cell Biol. 1998;10:769–775. doi: 10.1016/s0955-0674(98)80120-8. [DOI] [PubMed] [Google Scholar]
- Botchan M. Coordinating DNA replication with cell division: current status of the licensing concept. Proc Natl Acad Sci USA. 1996;93:9997–10000. doi: 10.1073/pnas.93.19.9997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carter BLA. The control of cell division in Saccharomyces cerevisiae. In: John PCL, editor. The Cell Cycle. Cambridge, UK: Cambridge University Press; 1981. pp. 99–117. [Google Scholar]
- Chang F, Herskowitz I. Identification of a gene necessary for cell cycle arrest by a negative growth factor of yeast: Far1 is an inhibitor of G1 cyclin, CLN2. Cell. 1990;63:999–1011. doi: 10.1016/0092-8674(90)90503-7. [DOI] [PubMed] [Google Scholar]
- Cho RJ, et al. A genome-wide transcriptional analysis of the mitotic cell cycle. Mol Cell. 1998;2:65–73. doi: 10.1016/s1097-2765(00)80114-8. [DOI] [PubMed] [Google Scholar]
- Ciosk R, Zachariae W, Michaelis C, Shevchenko A, Mann M, Nasmyth K. An Esp1/Pds1 complex regulates loss of sister chromatid cohesion at the metaphase to anaphase transition in yeast. Cell. 1998;93:1067–1076. doi: 10.1016/s0092-8674(00)81211-8. [DOI] [PubMed] [Google Scholar]
- Cohen-Fix O, Koshland D. Pds1p of budding yeast has dual roles: inhibition of anaphase initiation and regulation of mitotic exit. Genes Dev. 1999;13:1950–1959. doi: 10.1101/gad.13.15.1950. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cross FR. DAF1, a mutant gene affecting size control, pheromone arrest, and cell cycle kinetics of Saccharomyces cerevisiae. Mol Cell Biol. 1988;8:4675–4684. doi: 10.1128/mcb.8.11.4675. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cross FR, Tinkelenberg AH. A potential positive feedback loop controlling CLN1 and CLN2 gene expression at the start of the yeast cell cycle. Cell. 1991;65:875–883. doi: 10.1016/0092-8674(91)90394-e. [DOI] [PubMed] [Google Scholar]
- Dahmann C, Diffley JFX, Nasmyth K. S-phase-promoting cyclin-dependent kinases prevent rereplication by inhibiting the transition of replication origins to a prereplicative state. Curr Biol. 1995;5:1257–1269. doi: 10.1016/s0960-9822(95)00252-1. [DOI] [PubMed] [Google Scholar]
- Dasso M, Newport JW. Completion of DNA replication is monitored by a feedback system that controls the initiation of mitosis in vitro: studies in Xenopus. Cell. 1990;61:811–823. doi: 10.1016/0092-8674(90)90191-g. [DOI] [PubMed] [Google Scholar]
- Dawson IA, Roth S, Artavanis-Tsakonas S. The Drosophila cell cycle gene fizzy is required for normal degradation of cyclins A and B during mitosis and has homology to the CDC20 gene of Saccharomyces cerevisiae. J Cell Biol. 1995;129:725–737. doi: 10.1083/jcb.129.3.725. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Descombes P, Nigg EA. The polo-like kinase Plx1 is required for M phase exit and destruction of mitotic regulators in Xenopus egg extracts. EMBO J. 1998;17:1328–1335. doi: 10.1093/emboj/17.5.1328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deshaies R, Chau V, Kirschner M. Ubiquitination of the G1 cyclin Cln2p by a Cdc34-dependent pathway. EMBO J. 1995;14:303–312. doi: 10.1002/j.1460-2075.1995.tb07004.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Di Como CJ, Chang H, Arndt KT. Activation of CLN1 and CLN2 G1 cyclin gene expression by BCK2. Mol Cell Biol. 1995;15:1835–1846. doi: 10.1128/mcb.15.4.1835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dirick L, Bohm T, Nasmyth K. Roles and regulation of Cln/Cdc28 kinases at the start of the cell cycle of Saccharomyces cerevisiae. EMBO J. 1995;14:4803–4813. doi: 10.1002/j.1460-2075.1995.tb00162.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donovan JD, Toyn JH, Johnson AL, Johnston LH. p40SDB25, a putative Cdk inhibitor, has a role in M/G1 transition in Saccharomyces cerevisiae. Genes Dev. 1994;8:1640–1653. doi: 10.1101/gad.8.14.1640. [DOI] [PubMed] [Google Scholar]
- Epstein CB, Cross FR. CLB5: a novel B cyclin from budding yeast with a role in S phase. Genes Dev. 1992;6:1695–1706. doi: 10.1101/gad.6.9.1695. [DOI] [PubMed] [Google Scholar]
- Epstein CB, Cross FR. Genes that can bypass the CLN requirement for Saccharomyces cerevisiae cell cycle START. Mol Cell Biol. 1994;14:2041–2047. doi: 10.1128/mcb.14.3.2041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feldman RMR, Correll CC, Kaplan K, Deshaies RJ. A complex of Cdc4p, Skp1p and Cdc53/Cullin catalyzes ubiquitination of the phosphorylated CDK inhibitor Sic1p. Cell. 1997;91:221–230. doi: 10.1016/s0092-8674(00)80404-3. [DOI] [PubMed] [Google Scholar]
- Felix M-A, Labbe J-C, Doree M, Hunt T, Karsenti E. Triggering of cyclin degradation in interphase extracts of amphibian eggs by cdc2 kinase. Nature. 1990;346:379–382. doi: 10.1038/346379a0. [DOI] [PubMed] [Google Scholar]
- Ferrell JE., Jr Tripping the switch fantastic: how a protein kinase cascade can convert graded inputs into switch-like outputs. Trends Biochem Sci. 1996;21:460–466. doi: 10.1016/s0968-0004(96)20026-x. [DOI] [PubMed] [Google Scholar]
- Ferrell JE, Jr, Wu M, Gerhart JC, Martin GS. Cell cycle tyrosine phosphorylation of p34cdc2 and a microtubule-associated protein kinase homolog in Xenopus oocytes and eggs. Mol Cell Biol. 1991;11:1965–1971. doi: 10.1128/mcb.11.4.1965. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Futcher B. Cyclins and the wiring of the yeast cell cycle. Yeast. 1996;12:1635–1646. doi: 10.1002/(SICI)1097-0061(199612)12:16%3C1635::AID-YEA83%3E3.0.CO;2-O. [DOI] [PubMed] [Google Scholar]
- Goldbeter A. A minimal cascade model for the mitotic oscillator involving cyclin and cdc2 kinase. Proc Natl Acad Sci USA. 1991;88:9107–9111. doi: 10.1073/pnas.88.20.9107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldbeter A, Koshland DE., Jr An amplified sensitivity arising from covalent modification in biological systems. Proc Natl Acad Sci USA. 1981;78:6840–6844. doi: 10.1073/pnas.78.11.6840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hartwell LH, Unger MW. Unequal division in Saccharomyces cerevisiae and its implications for the control of cell division. J Cell Biol. 1977;75:422–435. doi: 10.1083/jcb.75.2.422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hwang LH, Lau LF, Smith DL, Mistrot CA, Hardwick KG, Hwang ES, Amon A, Murray AW. Budding yeast Cdc20: a target of the spindle checkpoint. Science. 1998;279:1041–1044. doi: 10.1126/science.279.5353.1041. [DOI] [PubMed] [Google Scholar]
- Irniger S, Nasmyth K. The anaphase-promoting complex is required in G1 arrested yeast cells to inhibit B-type cyclin accumulation and to prevent uncontrolled entry into S-phase. J Cell Sci. 1997;110:1523–1531. doi: 10.1242/jcs.110.13.1523. [DOI] [PubMed] [Google Scholar]
- Irniger S, Piatti S, Michaelis C, Nasmyth K. Genes involved in sister chromatid separation are needed for B-type cyclin proteolysis in budding yeast. Cell. 1995;81:269–277. doi: 10.1016/0092-8674(95)90337-2. [DOI] [PubMed] [Google Scholar]
- Jackson PK. Cell cycle: cull and destroy. Curr Biol. 1996;6:1209–1212. doi: 10.1016/s0960-9822(96)00697-5. [DOI] [PubMed] [Google Scholar]
- Jaspersen SL, Charles JF, Morgan DO. Inhibitory phosphorylation of the APC regulator Hct1 is controlled by the kinase Cdc28 and the phosphatase Cdc14. Curr Biol. 1999;11:227–236. doi: 10.1016/s0960-9822(99)80111-0. [DOI] [PubMed] [Google Scholar]
- Johnston GC, Ehrhardt CW, Lorincz A, Carter BLA. Regulation of cell size in the yeast Saccharomyces cerevisiae. J Bacteriol. 1979;137:1–5. doi: 10.1128/jb.137.1.1-5.1979. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnston GC, Pringle JR, Hartwell LH. Coordination of growth with cell division in the yeast Saccharomyces cerevisiae. Exp Cell Res. 1977;105:79–98. doi: 10.1016/0014-4827(77)90154-9. [DOI] [PubMed] [Google Scholar]
- King RW, Deshaies RJ, Peters J-M, Kirschner MW. How proteolysis drives the cell cycle. Science. 1996;274:1652–1659. doi: 10.1126/science.274.5293.1652. [DOI] [PubMed] [Google Scholar]
- Knapp D, Bhoite L, Stillman DJ, Nasmyth K. The transcription factor Swi5 regulates expression of the cyclin kinase inhibitor p40Sic1. Mol Cell Biol. 1996;16:5701–5707. doi: 10.1128/mcb.16.10.5701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koch C, Moll T, Neuberg M, Ahorn H, Nasmyth K. A role for the transcription factors Mbp1 and Swi4 in progression from G1 to S phase. Science. 1993;261:1551–1557. doi: 10.1126/science.8372350. [DOI] [PubMed] [Google Scholar]
- Koch C, Nasmyth K. Cell cycle regulated transcription in yeast. Curr Opin Cell Biol. 1994;6:451–459. doi: 10.1016/0955-0674(94)90039-6. [DOI] [PubMed] [Google Scholar]
- Koch C, Schleiffer A, Ammerer G, Nasmyth K. Switching transcription on and off during the yeast cell cycle: Cln/Cdc28 kinases activate bound transcription factor SBF (Swi4/Swi6) at Start, whereas Clb/Cdc28 kinases displace it from the promoter in G2. Genes Dev. 1996;9:129–141. doi: 10.1101/gad.10.2.129. [DOI] [PubMed] [Google Scholar]
- Kotani S, Tugendreich S, Fujii M, Jorgensen P-M, Watanabe N, Hoog C, Hieter P, Todokoro K. PKA and MPF-activated Polo-like kinase regulate anaphase-promoting complex activity and mitosis progression. Mol Cell. 1998;1:371–380. doi: 10.1016/s1097-2765(00)80037-4. [DOI] [PubMed] [Google Scholar]
- Krek W. Proteolysis and the G1-S transition: the SCF connection. Curr Opin Genet Dev. 1998;8:36–42. doi: 10.1016/s0959-437x(98)80059-2. [DOI] [PubMed] [Google Scholar]
- Lahav-Baratz S, Sudakin V, Ruderman JV, Hershko A. Reversible phosphorylation controls the activity of cyclosome-associated cyclin-ubiquitin ligase. Proc Natl Acad Sci USA. 1995;92:9303–9307. doi: 10.1073/pnas.92.20.9303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lanker S, Valdivieso MH, Wittenberg C. Rapid degradation of the G1 cyclin Cln2 induced by CDK-dependent phosphorylation. Science. 1996;271:1597–1601. doi: 10.1126/science.271.5255.1597. [DOI] [PubMed] [Google Scholar]
- Leatherwood J. Emerging mechanisms of eukaryotic DNA replication initiation. Curr Opin Cell Biol. 1998;10:742–748. doi: 10.1016/s0955-0674(98)80117-8. [DOI] [PubMed] [Google Scholar]
- Li FN, Johnston M. Grr1 of Saccharomyces cerevisiae is connected to the ubiquitin proteolysis machinery through Skp1: coupling glucose sensing to gene expression and the cell cycle. EMBO J. 1997;16:5629–5638. doi: 10.1093/emboj/16.18.5629. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lim HH, Goh P-Y, Surana U. Cdc20 is essential for the cyclosome-mediated proteolysis of both Pds1 and Clb2 during M phase in budding yeast. Curr Biol. 1998;8:231–234. doi: 10.1016/s0960-9822(98)70088-0. [DOI] [PubMed] [Google Scholar]
- Lorca T, Castro A, Martinez AM, Vigneron S, Morin N, Sigrist S, Lehner C, Doree M, Labbe JC. Fizzy is required for activation of the APC/cyclosome in Xenopus egg extract. EMBO J. 1998;17:3565–3575. doi: 10.1093/emboj/17.13.3565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lord PG, Wheals AE. Asymmetrical division of Saccharomyces cerevisiae. J Bacteriol. 1980;142:808–818. doi: 10.1128/jb.142.3.808-818.1980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maher M, Cong F, Kindelberger D, Nasmyth K, Dalton S. Cell cycle-regulated transcription of CLB2 gene is dependent on Mcm1 and a ternary complex factor. Mol Cell Biol. 1995;15:3129–3137. doi: 10.1128/mcb.15.6.3129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mendenhall MD, Hodge AE. Regulation of Cdc28 cyclin-dependent protein kinase activity during the cell cycle of the yeast Saccharomyces cerevisiae. Microbiol Mol Biol Rev. 1998;62:1191–1243. doi: 10.1128/mmbr.62.4.1191-1243.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murray A, Hunt T. The Cell Cycle: An Introduction. New York: W.H. Freeman; 1993. [Google Scholar]
- Nash R, Tokiwa G, Anand S, Erickson K, Futcher AB. The WHI1+ gene of Saccharomyces cerevisiae tethers cell division to cell size and is a cyclin homolog. EMBO J. 1988;7:4335–4346. doi: 10.1002/j.1460-2075.1988.tb03332.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nasmyth K. Control of the yeast cell cycle by Cdc28 protein kinase. Curr Opin Cell Biol. 1993;5:166–179. doi: 10.1016/0955-0674(93)90099-c. [DOI] [PubMed] [Google Scholar]
- Nasmyth K. Evolution of the cell cycle. Philos Trans R Soc Lond B. 1995;349:271–281. doi: 10.1098/rstb.1995.0113. [DOI] [PubMed] [Google Scholar]
- Nasmyth K. At the heart of the budding yeast cell cycle. Trends Genet. 1996;12:405–412. doi: 10.1016/0168-9525(96)10041-x. [DOI] [PubMed] [Google Scholar]
- Nasmyth K. Separating sister chromatids. Trends Biochem Sci. 1999;24:98–104. doi: 10.1016/s0968-0004(99)01358-4. [DOI] [PubMed] [Google Scholar]
- Nasmyth K, Adolf G, Lydall D, Seddon A. The identification of a second cell cycle control on the HO promotor in yeast: cell cycle regulator of SWI5 nuclear entry. Cell. 1990;62:631–647. doi: 10.1016/0092-8674(90)90110-z. [DOI] [PubMed] [Google Scholar]
- Nasmyth K, Dirick L. The role of SWI4 and SWI6 in the activity of G1 cyclins in yeast. Cell. 1991;66:995–1013. doi: 10.1016/0092-8674(91)90444-4. [DOI] [PubMed] [Google Scholar]
- Novak B, Csikasz-Nagy A, Gyorffy B, Nasmyth K, Tyson JJ. Model scenarios for evolution of the eukaryotic cell cycle. Philos Trans R Soc Lond B. 1998;353:2063–2076. doi: 10.1098/rstb.1998.0352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Novak B, Toth A, Csikasz-Nagy A, Gyorffy B, Tyson JJ, Nasmyth K. Finishing the cell cycle. J Theor Biol. 1999;199:223–233. doi: 10.1006/jtbi.1999.0956. [DOI] [PubMed] [Google Scholar]
- Novak B, Tyson JJ. Numerical analysis of a comprehensive model of M-phase control in Xenopus oocyte extracts and intact embryos. J Cell Sci. 1993;106:1153–1168. doi: 10.1242/jcs.106.4.1153. [DOI] [PubMed] [Google Scholar]
- Novak B, Tyson JJ. Quantitative analysis of a molecular model of mitotic control in fission yeast. J Theor Biol. 1995;173:283–305. [Google Scholar]
- Novak B, Tyson JJ. Modeling the control of DNA replication in fission yeast. Proc Natl Acad Sci USA. 1997;94:9147–9152. doi: 10.1073/pnas.94.17.9147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nugroho TT, Mendenhall MD. An inhibitor of yeast cyclin-dependent protein kinase plays an important role in ensuring the genomic integrity of daughter cells. Mol Cell Biol. 1994;14:3320–3328. doi: 10.1128/mcb.14.5.3320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peter M, Herskowitz I. Direct inhibition of the yeast cyclin-dependent kinase Cdc28-Cln by Far1. Science. 1994;265:1228–1231. doi: 10.1126/science.8066461. [DOI] [PubMed] [Google Scholar]
- Peters J-M. SCF and APC: the yin and yang of cell cycle regulated proteolysis. Curr Opin Cell Biol. 1998;10:759–768. doi: 10.1016/s0955-0674(98)80119-1. [DOI] [PubMed] [Google Scholar]
- Peters J-M, King RW, Hoog C, Kirschner MW. Identification of BimE as a subunit of the anaphase-promoting complex. Science. 1996;274:1199–1201. doi: 10.1126/science.274.5290.1199. [DOI] [PubMed] [Google Scholar]
- Polymenis M, Schmidt EV. Coupling of cell division to cell growth by translational control of the G1 cyclin CLN3 in yeast. Genes Dev. 1997;11:2522–2531. doi: 10.1101/gad.11.19.2522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Polymenis M, Schmidt EV. Coordination of cell growth with cell division. Curr Opin Genet Dev. 1999;9:76–80. doi: 10.1016/s0959-437x(99)80011-2. [DOI] [PubMed] [Google Scholar]
- Posas F, Takekawa M, Saito H. Signal transduction by MAP kinase cascade in budding yeast. Curr Opin Microbiol. 1998;1:175–182. doi: 10.1016/s1369-5274(98)80008-8. [DOI] [PubMed] [Google Scholar]
- Prinz S, Hwang ES, Visintin R, Amon A. The regulation of Cdc20 proteolysis reveals a role for the APC components Cdc23 and Cdc27 during S phase and early mitosis. Curr Biol. 1998;8:750–760. doi: 10.1016/s0960-9822(98)70298-2. [DOI] [PubMed] [Google Scholar]
- Richardson H, Lew DJ, Henze M, Sugimoto K, Reed SI. Cyclin-B homologs in Saccharomyces cerevisiae function in S phase and in G2. Genes Dev. 1992;6:2021–2034. doi: 10.1101/gad.6.11.2021. [DOI] [PubMed] [Google Scholar]
- Richardson HE, Wittenberg C, Cross F, Reed SI. An essential G1 function for cyclin-like proteins in yeast. Cell. 1989;59:1127–1133. doi: 10.1016/0092-8674(89)90768-x. [DOI] [PubMed] [Google Scholar]
- Salama SR, Hendricks KB, Thorner J. G1 cyclin degradation: the PEST motif of yeast Cln2 is necessary, but not sufficient, for rapid protein turnover. Mol Cell Biol. 1994;14:7953–7966. doi: 10.1128/mcb.14.12.7953. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schneider BL, Yang Q-H, Futcher B. Linkage of replication to Start by the Cdk inhibitor Sic1. Science. 1996;272:560–562. doi: 10.1126/science.272.5261.560. [DOI] [PubMed] [Google Scholar]
- Schwab M, Lutum AS, Seufert W. Yeast Hct1 is a regulator of Clb2 cyclin proteolysis. Cell. 1997;90:683–693. doi: 10.1016/s0092-8674(00)80529-2. [DOI] [PubMed] [Google Scholar]
- Schwob E, Bohm T, Mendenhall MD, Nasmyth K. The B-type cyclin kinase inhibitor p40sic1 controls the G1 to S transition in S. cerevisiae. Cell. 1994;79:233–244. doi: 10.1016/0092-8674(94)90193-7. [DOI] [PubMed] [Google Scholar]
- Schwob E, Nasmyth K. CLB5 and CLB6, a new pair of B cyclins involved in DNA replication in Saccharomyces cerevisiae. Genes Dev. 1993;7:1160–1175. doi: 10.1101/gad.7.7a.1160. [DOI] [PubMed] [Google Scholar]
- Seufert W, Futcher B, Jentsch S. Role of a ubiquitin-conjugating enzyme in degradation of S- and M-phase cyclins. Nature. 1995;373:78–81. doi: 10.1038/373078a0. [DOI] [PubMed] [Google Scholar]
- Shirayama M, Zachariae W, Ciosk R, Nasmyth K. The Polo-like kinase Cdc5p and the WD-repeat protein Cdc20p/fizzy are regulators and substrates of the anaphase promoting complex in Saccharomyces cerevisiae. EMBO J. 1998;17:1336–1349. doi: 10.1093/emboj/17.5.1336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shou W, Dunphy WG. Cell cycle control by Xenopus p28Kix1, a developmentally regulated inhibitor of cyclin-dependent kinases. Mol Biol Cell. 1996;7:457–469. doi: 10.1091/mbc.7.3.457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shou W, Seol JH, Shevchenko A, Baskerville C, Moazed D, Chen ZWS, Jang J, Shevchenko A, Charbonneau H, Deshaies RJ. Exit from mitosis is triggered by Tem1-dependent release of the protein phosphatase Cdc14 from nucleolar RENT complex. Cell. 1999;97:233–244. doi: 10.1016/s0092-8674(00)80733-3. [DOI] [PubMed] [Google Scholar]
- Sigrist S, Jacobs H, Stratmann R, Lehner CF. Exit from mitosis is regulated by Drosophila fizzy and the sequential destruction of cyclins A, B, and B3. EMBO J. 1995;14:4827–4838. doi: 10.1002/j.1460-2075.1995.tb00164.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Skowyra D, Craig KL, Tyers M, Elledge SJ, Harper JW. F-box proteins are receptors that recurit phosphorylated substrates to the SCF ubiquitin-ligase complex. Cell. 1997;91:209–219. doi: 10.1016/s0092-8674(00)80403-1. [DOI] [PubMed] [Google Scholar]
- Smythe C, Newport JW. Coupling of mitosis to the completion of S phase in Xenopus occurs via modulation of the tyrosine kinase that phosphorylates p34cdc2. Cell. 1992;68:787–797. doi: 10.1016/0092-8674(92)90153-4. [DOI] [PubMed] [Google Scholar]
- Sorger PK, Murray AW. S-phase feedback control in budding yeast independent of tyrosine phosphorylation of p34cdc28. Nature. 1992;355:365–368. doi: 10.1038/355365a0. [DOI] [PubMed] [Google Scholar]
- Spellman PT, Sherlock G, Zhang MQ, Iyer VR, Anders K, Eisen MB, Brown PO, Botstein D, Futcher B. Comprehensive identification of cell cycle-regulated genes of the yeast Saccharomyces cerevisiae by microarray hybridization. Mol Biol Cell. 1998;9:3273–3297. doi: 10.1091/mbc.9.12.3273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stuart D, Wittenberg C. CLN3, not positive feedback, determines the timing of CLN2 transcription in cycling cells. Genes Dev. 1995;9:2780–2794. doi: 10.1101/gad.9.22.2780. [DOI] [PubMed] [Google Scholar]
- Su J-Y, Rempel RE, Erikson E, Maller JL. Cloning and characterization of the Xenopus cyclin-dependent kinase inhibitor p27Xic1. Proc Natl Acad Sci USA. 1995;92:10187–10191. doi: 10.1073/pnas.92.22.10187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sudakin V, Ganoth D, Dahan A, Heller H, Hershko J, Luca FC, Ruderman JV, Hershko A. The cyclosome, a large complex containing cyclin-selective ubiquitin ligase activity, targets cyclins for destruction at the end of mitosis. Mol Biol Cell. 1995;6:185–197. doi: 10.1091/mbc.6.2.185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Surana U, Amon A, Dowzer C, McGrew J, Byers B, Nasmyth K. Destruction of the CDC28/CLB mitotic kinase is not required for the metaphase to anaphase transition in budding yeast. EMBO J. 1993;12:1969–1978. doi: 10.1002/j.1460-2075.1993.tb05846.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Surana U, Robitsch H, Price C, Schuster T, Fitch I, Futcher AB, Nasmyth K. The role of CDC28 and cyclins during mitosis in the budding yeast S. cerevisiae. Cell. 1991;65:145–161. doi: 10.1016/0092-8674(91)90416-v. [DOI] [PubMed] [Google Scholar]
- Taylor SS. Chromosome segregation: dual control ensures fidelity. Curr Biol. 1999;9:R562–R564. doi: 10.1016/s0960-9822(99)80355-8. [DOI] [PubMed] [Google Scholar]
- Tinker-Kulberg RL, Morgan DO. Pds1 and Esp1 control both anaphase and mitotic exit in normal cells and after DNA damage. Genes Dev. 1999;13:1936–1949. doi: 10.1101/gad.13.15.1936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tinoco I, Jr, Sauer K, Wang JC. Physical Chemistry. Principles and Applications in Biological Sciences. 3rd ed. Upper Saddle River, NJ: Prentice Hall; 1978. [Google Scholar]
- Tokiwa G, Tyers M, Volpe T, Futcher B. Inhibition of G1 cyclin activity by the Ras/cAMP pathway in yeast. Nature. 1994;371:342–345. doi: 10.1038/371342a0. [DOI] [PubMed] [Google Scholar]
- Tyers M. The cyclin-dependent kinase inhibitor p40sic1 imposes the requirement for Cln G1 cyclin function at Start. Proc Natl Acad Sci USA. 1996;93:7772–7776. doi: 10.1073/pnas.93.15.7772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tyers M, Tokiwa G, Futcher B. Comparison of the Saccharomyces cerevisae G1 cyclins: Cln3 may be an upstream activator of Cln1, Cln2 and other cyclins. EMBO J. 1993;12:1955–1968. doi: 10.1002/j.1460-2075.1993.tb05845.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tyson JJ, Chen KC, Novak B. The eukaryotic cell cycle: molecules, mechanisms and mathematical models. In: Othmer HG, Adler FR, Lewis MA, Dallon JC, editors. Case Studies in Mathematical Modeling: Ecology, Physiology and Cell Biology. Upper Saddle River, NJ: Prentice Hall; 1997. pp. 127–147. [Google Scholar]
- Tyson JJ, Novak B, Chen KC, Val J. Checkpoints in the cell cycle from a modeler's perspective. In: Meijer L, Guidet S, Tung HYL, editors. Progress in Cell Cycle Research. New York: Plenum Press; 1995. pp. 1–8. [DOI] [PubMed] [Google Scholar]
- Tyson JJ, Novak B, Odell GM, Chen K, Thron CD. Chemical kinetic theory as a tool for understanding the regulation of M-phase promoting factor in the cell cycle. Trends Biochem Sci. 1996;21:89–96. [PubMed] [Google Scholar]
- Verma R, Annan RS, Huddleston MJ, Carr SA, Reynard G, Deshaies RJ. Phosphorylation of Sic1p by G1 Cdk required for its degradation and entry into S phase. Science. 1997;278:455–460. doi: 10.1126/science.278.5337.455. [DOI] [PubMed] [Google Scholar]
- Visintin R, Craig K, Hwang ES, Prinz S, Tyers M, Amon A. The phosphatase Cdc14 triggers mitotic exit by reversal of Cdk-dependent phosphorylation. Mol Cell. 1998;2:709–718. doi: 10.1016/s1097-2765(00)80286-5. [DOI] [PubMed] [Google Scholar]
- Visintin R, Hwang ES, Amon A. Cfi1 prevents premature exit from mitosis by anchoring Cdc14 phosphatase in the nucleolus. Nature. 1999;398:818–823. doi: 10.1038/19775. [DOI] [PubMed] [Google Scholar]
- Visintin R, Prinz S, Amon A. CDC20 and CDH1: a family of substrate-specific activators of APC-dependent proteolysis. Science. 1997;278:460–463. doi: 10.1126/science.278.5337.460. [DOI] [PubMed] [Google Scholar]
- Willems AR, Lanker S, Patton EE, Craig KL, Nason TF, Mathias N, Kobayashi R, Wittenberg C, Tyers M. Cdc53 targets phosphorylated G1 cyclins for degradation by the ubiquitin proteolytic pathway. Cell. 1996;86:453–463. doi: 10.1016/s0092-8674(00)80118-x. [DOI] [PubMed] [Google Scholar]
- Wittenberg C, Reed SI. Plugging it in: signaling circuits and the yeast cell cycle. Curr Opin Cell Biol. 1996;6:223–230. doi: 10.1016/s0955-0674(96)80069-x. [DOI] [PubMed] [Google Scholar]
- Wittenberg C, Sugimoto K, Reed SI. G1-specific cyclins of S. cerevisiae: cell cycle periodicity, regulation by mating pheromone, and association with p34CDC28 protein kinase. Cell. 1990;62:225–237. doi: 10.1016/0092-8674(90)90361-h. [DOI] [PubMed] [Google Scholar]
- Wuarin J, Nurse P. Regulating S phase: CDKs, licensing and proteolysis. Cell. 1996;85:785–787. doi: 10.1016/s0092-8674(00)81261-1. [DOI] [PubMed] [Google Scholar]
- Yaglom J, Linskens HK, Rubin DM, Futcher B, Finley D. p34Cdc28-mediated control of Cln3 cyclin degradation. Mol Cell Biol. 1995;15:731–741. doi: 10.1128/mcb.15.2.731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamamoto A, Guacci V, Koshland D. Pds1p, an inhibitor of anaphase in budding yeast, plays a critical role in the APC and checkpoint pathway(s) J Cell Biol. 1996;133:99–110. doi: 10.1083/jcb.133.1.99. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zachariae W, Nasmyth K. Whose end is destruction: cell division and the anaphase-promoting complex. Genes Dev. 1999;13:2039–2058. doi: 10.1101/gad.13.16.2039. [DOI] [PubMed] [Google Scholar]
- Zachariae W, Schwab M, Nasmyth K, Seufert W. Control of cyclin ubiquitination by CDK-regulated binding of Hct1 to the anaphase promoting complex. Science. 1998;282:1721–1724. doi: 10.1126/science.282.5394.1721. [DOI] [PubMed] [Google Scholar]
- Zachariae W, Shin TH, Galova M, Obermaier B, Nasmyth K. Identification of subunits of the anaphase-promoting complex of Saccharomyces cerevisiae. Science. 1996;274:1201–1204. doi: 10.1126/science.274.5290.1201. [DOI] [PubMed] [Google Scholar]