Ensemble-Based Convergence Analysis of Biomolecular Trajectories

Abstract

Assessing the convergence of a biomolecular simulation is an essential part of any careful computational investigation, because many fundamental aspects of molecular behavior depend on the relative populations of different conformers. Here we present a physically intuitive method to self-consistently assess the convergence of trajectories generated by molecular dynamics and related methods. Our approach reports directly and systematically on the structural diversity of a simulation trajectory. Straightforward clustering and classification steps are the key ingredients, allowing the approach to be trivially applied to systems of any size. Our initial study on met-enkephalin strongly suggests that even fairly long trajectories (∼50 ns) may not be converged for this small—but highly flexible—system.

INTRODUCTION

Conformational fluctuations are essential to the functions of proteins, whether they are motor proteins (1), enzymes (2,3), signaling proteins (4–6), or almost any other kind. Different experiments have enabled observation of protein fluctuations over a huge range of timescales, from picoseconds (7) to microseconds (5) to milliseconds (3,6,8) to seconds and longer (9).

Naturally, simulations aim to observe conformational fluctuations as well. A gap remains, however, between the timescale of many biologically important motions (microseconds to seconds), and the timescale accessible to atomically detailed simulation (nanoseconds). To put it another way, some problems are simply not possible to study computationally, since it is so far impossible to run a simulation that is long enough.

For those problems that are at the very edge of being feasible, we would like to know whether we have indeed sampled enough to draw quantitative conclusions. These problems include the calculation of free energies of binding (10,11), ab initio protein folding (12,13), simulation of flexible peptides (14), and conformational changes (15).

Convergence assessment is also crucial for rigorous tests of simulation protocols and empirical force fields; see, e.g., Zaman et al. (16). Many algorithms propose to improve the sampling of conformation space, but quantitative estimation of this type of efficiency is difficult, except in simple cases (17). In the case of force-field validation, it is important to know whether systematic errors are a consequence of the force field, or are due to undersampling.

The observed convergence of a simulation depends on how convergence is defined and measured. It is therefore important to consider what sort of quantity is to be calculated from the simulation, and choose an appropriate way to assess the adequacy of the simulation trajectory (or trajectories). Many relatively simple methods are commonly used, such as measuring distance from the starting structure as a function of simulation time, and calculation of various autocorrelation functions (16,18). Other, more sophisticated methods are based on principal components (19,20) or calculation of energy-based ergodic measures (21).

Many applications, however, require a thorough and equilibrated sampling of the space of structures. All of the methods just listed are only related indirectly to structural sampling. There are many examples of groups of structures that are very close in energy, but very dissimilar structurally. In such cases, we might expect energy-based methods to be insensitive to the relative populations of the different structural groups. It is therefore of interest to develop methods that are more directly related to the sampling of different structures, and see how such methods compare to more traditional techniques.

Daura and co-workers (22,23) previously considered convergence assessment by counting structural clusters, based upon a cutoff in the root mean-square deviation (RMSD) metric. The authors assess the convergence of a simulation by considering the number of clusters as a function of time. Convergence is deemed sufficient when the curve plateaus. This is surely a better measure than simpler, historically used methods, such as RMSD from the starting structure or the running average energy. However, it is worth noting that long after the curve of number of clusters versus time plateaus, the relative populations of the clusters may still be changing. Indeed, an important conformational substate that has been visited just once will appear as a cluster, but its relative population will certainly not have equilibrated.

The method of Daura et al. (22) also suffers from the need to store the entire matrix of pairwise distances. For a trajectory of length N, the memory needed scales as N², rendering the method impractical for long trajectories. At least two groups have developed methods that rely on nonhierarchical clustering schemes, and therefore require memory that is only linear in N. Karpen et al. (24) developed a method that optimizes the clusters based on distance from the cluster center, with distances measured in dihedral angle space. Elmer and Pande (25) have optimized clusters subject to a constraint on the number of clusters, with distance defined by the atom-atom distance root mean-square deviation (26,27).

In this article, we address systematically the measurement of sampling quality. Our method classifies (or bins) a trajectory based upon the distances between a set of reference structures and each structure in the trajectory. Our method is unique in that it not only builds clusters of structures, it also compares the cluster populations. By comparing different fragments of the trajectory to one another, convergence of the simulation is judged by the relative populations of the clusters. We believe the key to assessing convergence is tracking relative bin populations. Our approach can be directly applied to comparing the efficiency of different sampling methods.

In the next section, we present a detailed description of the algorithm and discuss possible choices of metric. We then demonstrate the method on simulations of met-enkephalin, a structurally diverse peptide.

THEORY AND METHODS

We will evaluate sampling by comparing structural histograms, described below. These histograms provide a fingerprint of the conformation space sampled by a protein, by projecting a trajectory onto a set of bins based on distinct reference structures. Comparing histograms for different pieces of a trajectory (or for two different trajectories), projected onto the same set of reference structures, provides a very sensitive measure of convergence. Not only are we comparing how broadly each trajectory has sampled conformation space, but also how frequently each substate has been visited.

Histogram construction

We generate the set of reference structures and corresponding histogram from a trajectory in the following simple way (our choice for measuring conformational distance will be discussed below):

• Step 1. A cutoff distance d_c is defined.

• Step 2. A structure S₁ is picked at random from the trajectory.

• Step 3. S₁ and all structures less than d_c from S₁ are removed from the trajectory.

• Step 4. Repeat Steps 2 and 3 until every structure in the trajectory is clustered, generating a set {S_i} of reference structures, with i = 1,2,….

• Step 5. The set {S_i} of reference structures is then used to build a histogram: every structure in the trajectory is classified according to its nearest reference structure. Note that this classification step generates a unique histogram for a given set of reference structures—unlike the simple clustering that is generated in Step 3.

Such a partitioning guarantees a set of clusters whose centers are at least d_c apart. Furthermore, for a trajectory of N frames, the number of reference structures, M, and therefore the memory needed to store the resulting M × N matrix of distances, is controlled by d_c. For physically reasonable cutoffs (e.g., 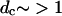Å RMSD), the number of reference structures is at least an order-of-magnitude smaller than the number of frames in the trajectory. The memory requirements are therefore manageable, since the computation of pairwise distances scales as N log N.

There is nothing in principle that prevents the use of a more carefully chosen set of reference structures with our classification scheme. For example, we may consider a set of structures that correspond to minima of the potential energy surface. The cutoff might then be chosen to be the smallest observed distance between any pair of the minimum energy structures, and the set of reference structures so determined could be augmented by the random selection of more reference structures to span the whole trajectory.

However, we expect that the purely random selection used here will naturally include the lowest free-energy substates, since these are the most populated. In either case, any set of reference structures defines a unique histogram for any trajectory.

Trajectory analysis

Once we have a set of reference structures, we may easily compare two different trajectories classified by the same set of reference structures, by comparing the populations of the various bins as observed in the two trajectories: given a (normalized) population p_i(1) for cluster i in the first trajectory, and p_i(2) in the second, the difference in the populations ΔP_i = |p_i(1) – p_i(2)| measures the convergence of substate i's population between the two trajectories.

Note that the two trajectories just discussed may be two different pieces of the same simulation. In this way, we may self-consistently assess the convergence of a continuous simulation, by looking to see whether the relative populations of the most populated substates are changing with time. Of course, this cannot answer affirmatively that a simulation has converged (no method can do so); however, it may answer negatively. In fact, we will see later that our method indicates that structural convergence may be much slower than previously appreciated.

Our approach should also be applicable to some types of noncontinuous trajectories, such as those generated by multiple starts (e.g., (28)) or parallel exchange protocols (e.g., (29,30)). For multiple independent trajectories, one can compare the two histograms generated from 1), the first halves and 2), the second halves of all simulations. If converged, these two histograms should agree. One could also compare histograms generated by grouping entire trajectories into distinct sets. For a parallel exchange simulation, where the ensemble is built from a set of continuous trajectories, histograms from the first and second halves of the simulation can be compared.

The comparison of histograms clearly will not be appropriate when ensembles are generated in a fully decorrelated way. For instance, starting from a single long trajectory, one could generate two ensembles by randomly selecting structures, or perhaps by selecting structures at two different fixed time intervals. So long as the number of structures in each ensemble greatly exceeds the number of reference structures used for classification, it is hard to see how such histograms could be significantly different. In such cases, dynamical correlations have been explicitly discarded, and the histograms can only differ statistically.

Structural metrics

Many different metrics have been used to measure distance between conformations. The choice depends on both physical and mathematical considerations. For example, dihedral angle-based metrics are well suited to capture local structural information (24), but are not sensitive to more global rearrangements of the molecule. Least-squares superposition followed by calculation of the average positional fluctuation per atom (RMSD) is quite popular, but the problem of optimizing the superposition can be both subtle and time-consuming for large, multidomain proteins (31). In addition, RMSD does not satisfy a triangle inequality (32). This is not an issue for the algorithm presented here, but is a consideration for more sophisticated clustering methods (25). We will use RMSD to measure distance here, though we note that distance root-mean-square deviation (or sometimes, distance-matrix error) (26,27) may be appropriate when RMSD is not.

Labeling two structures by a and b, the traditional root mean-square deviation (RMSD) is defined to be the minimum of the root mean-square average of interatomic distances over all possible translations and rotations of x^b—namely,

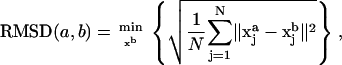(1)

where N is the number of atoms and x_j is the position of atom j.

It is clear that the choice of d_c, together with the choice of metric, determines the resolution of the histogram. Reducing d_c increases the number of reference structures, and reduces the size of the bins. How is d_c chosen? There is no general answer, and a suitable cutoff will depend on the problem under investigation.

The typical RMSD between a pair of structures will depend on the size of the molecule, its flexibility, and the conditions of the simulation. If the magnitude of some important conformational change is known in advance, then this information will guide the selection of an appropriate cutoff. If not, then a series of histograms should be constructed at several values of d_c. The behavior of the histogram as a function of d_c will give a sense of the appropriate value, as we will see below.

RESULTS

We have tested our classification algorithm on implicitly solvated met-enkephalin, a pentapeptide neurotransmitter. By focusing first on a small peptide, we aim to develop the methodology on a system that may be thoroughly sampled and analyzed by standard techniques.

The trajectories analyzed in this section were generated by Langevin dynamics simulations, as implemented in the Tinker v. 4.2.2 simulation package (33). The temperature was 298 K, the friction constant was 5 ps⁻¹, and solvation was treated by the GB/SA method (34). Two 100-ns trajectories were generated, each starting from the PDB structure 1plw, model 1. The trajectories will be referred to as “plw-a” and “plw-b”. Coordinates were written every 10 ps, for a total of 10⁴ frames per trajectory.

Previous methods: RMSD analysis and cluster counting

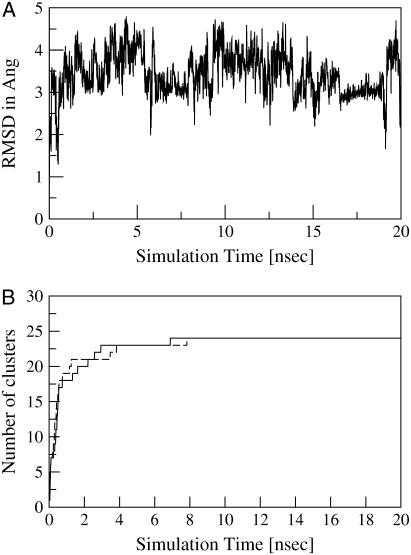
An often-used indicator of equilibration is the RMSD from the starting structure (see Fig. 1 A). Such plots are motivated by the recognition that the starting structure (e.g., a crystal structure) may not be representative of the protein under the simulation conditions—solvent, force field, and temperature. This is the case in Fig. 1 A—the computation was performed with an implicit water model, while the experimental structure was determined in the presence of bicelles (35). The system fails to settle down to a relatively constant distance from the starting structure—rather, it is moving between various substates, some nearer and some farther from the starting structure. Although this is not surprising for a peptide renowned for its floppy character, it also indicates that this method cannot determine when the peptide simulation has converged. Indeed, Fig. 1 A can tell us little about the convergence of the simulation, only that it spends most of its time more than 2.0 Å from the starting structure.

FIGURE 1.

(A) RMSD from starting structure for met-enkephalin trajectory plw-a. (B) Number of populated clusters versus simulation time for the plw-a trajectory. Results are shown for two independent clusterings. After 7 ns, the simulation appears equilibrated. No more clusters appear in the 198-ns plw-ab trajectory.

A perhaps better indication of equilibration is provided by Fig. 1 B, in which we have used the method of Daura et al. (22), albeit with clusters built by the procedure described in Theory and Methods (Histogram Construction). The premise is that convergence is achieved when the number of clusters no longer increases, as this means that the simulation has visited every substate. This analysis suggests that convergence is observed by ∼7 ns, and the curve has the comforting appearance of saturation. However, Fig. 1 B is insensitive to the relative populations of the clusters. To illustrate the problem, consider a simple potential, with two smooth wells separated by a high barrier. By simple cluster counting, a simulation will be converged as soon as it has crossed the barrier once. It is clear, however, that many crossings will be required before the populations of the two states have equilibrated. We will address this question using our ensemble-based method. We find, in fact, that the relative populations of the clusters continue to change, long after their number has equilibrated.

Ensemble-based assessment of trajectories

The use of our systematic approach is much more revealing. We first discuss the selection of an appropriate cutoff. We then demonstrate two different applications of the ensemble-based comparison of trajectories—a comparison between a trajectory and a gold-standard ensemble, and a self-consistent convergence analysis of a single trajectory.

Reference structure generation and cutoff selection

A compound trajectory was formed from trajectories plw-a and plw-b, by discarding the first nanosecond of each trajectory and concatenating the two into a single, 198-ns trajectory (“plw-ab”). We then generated a set of reference structures for the compound trajectory, as described earlier: a structure is picked at random, and it is temporarily discarded along with every structure within a predefined cutoff distance, d_c. The process is repeated on the remaining structures until the trajectory has been exhausted. The result is a set of reference structures that are separated from one another by at least the predefined cutoff distance. Lowering the cutoff (making the reference structures more similar) increases the resolution of the clustering, and increases the number reference structures (see Table 1). Although RMSD is system-size-dependent (36), for a particular system the cutoff defines a resolution.

TABLE 1.

Average number of reference structures generated for various cutoffs (d_c in RMSD)

dc in Å	Number of clusters	σ
1.5	1860.0	14.0
2.0	321.3	6.7
2.5	72.8	3.8
3.0	23.3	2.2
3.5	10.3	0.5

Reported are the average and standard deviation (σ) in the number of reference structures for four independent clusterings of the plw-ab trajectory.

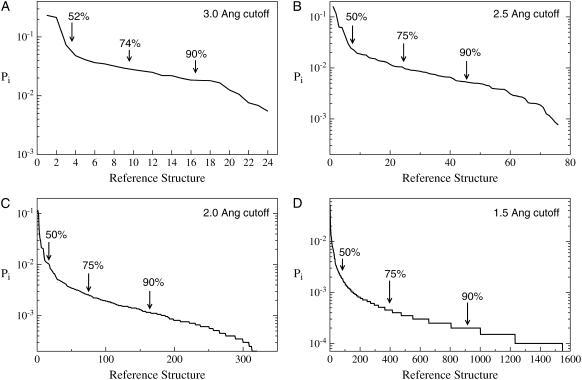
A histogram is then constructed by grouping each frame in the trajectory with its nearest reference structure. The dependence of the histogram on d_c is shown in Fig. 2. With d_c = 3.0 Å, the first three bins already account for >50% of the total population. It might be expected that such a coarse description of the ensemble may not be particularly informative. However, we will see in the next sections that this level is already sufficient to make powerful statements about convergence.

FIGURE 2.

Histograms for the plw-ab trajectory generated for different values of d_c, indicated in the upper-right corner of each plot. P_i is the normalized population of bin i, where i refers to the reference structure.

Lowering the cutoff, the general features of the histogram remain unchanged: a steep slope initially, which accounts for half of the total population, followed by a flatter region. In each case, most (90%) of the population is accounted for by approximately half of all the reference structures. However, a closer inspection reveals that the fraction of bins required to account for the noted percentages of population (50, 75, and 90%) is decreasing with the cutoff. For example, for d_c = 3.0 Å, 16 of 24 bins account for 90% of the trajectory, while for d_c = 2.0 Å, 164 of 331 bins account for 90% of the trajectory. It should be mentioned, however, that this difference between the d_c = 2.0 Å and d_c = 1.5 Å histograms is so small as to be insignificant.

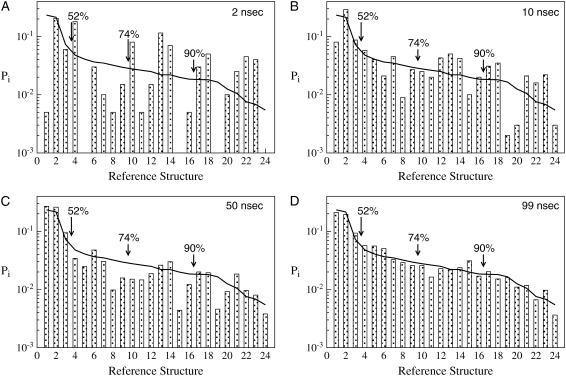
Although it seems obvious that the most revealing cutoff will be system-specific, our histograms are more robust than they first appear. Because reference structures are chosen arbitrarily, the divisions between bins will not reflect basins of the landscape. In other words, many, if not most, bins can be expected to include a number of full and partial local basins. Thus, a lack of convergence in a macroscopic bin, at least in principle, can report on more local, microscopic states. Further, because our approach is so inexpensive compared to the simulation itself, more than one binning of configuration space can and should be considered; see Self-Referential Convergence Assessment and Fig. 4.

FIGURE 4.

Self-consistent convergence analysis of different trajectory lengths for two independent classifications (set 1 and set 2) of the plw-ab trajectory at d_c = 3.0 Å. Each plot compares the first-half (diagonal fill) to the second-half (no fill) of the trajectory for total trajectory lengths of (A) 4 ns, (B) 20 ns, (C) 100 ns, and (D), 198 ns. Percentages indicate the portion of the total trajectory binned to that point.

Based upon the series of histograms in Fig. 2, we continued our study of met-enkephalin based upon d_c = 3.0 Å. At this level of resolution, the main features of the histogram are already present, while the number of reference structures is small enough to make the computation quite inexpensive. We shall see that d_c = 3.0 Å provides sufficient resolution to investigate the convergence properties of our simulation.

Though we do not pursue it here, we note that the tail of the distribution—where half of all the bins account for only 10% of the population—might contain some very interesting structures. Indeed, at the very end of the tail are found bins that sometimes contain a single structure. Might some of these low population bins represent transition states? For now, we set this question aside, and focus instead on convergence assessment.

Comparing trajectories to a gold-standard ensemble

In some applications, we want to compare a trajectory to a gold-standard ensemble. For example, the gold-standard might be the ensemble sampled by a long molecular dynamics simulation, and we may wish to check the ensemble produced by a new simulation protocol against the long molecular dynamics trajectory.

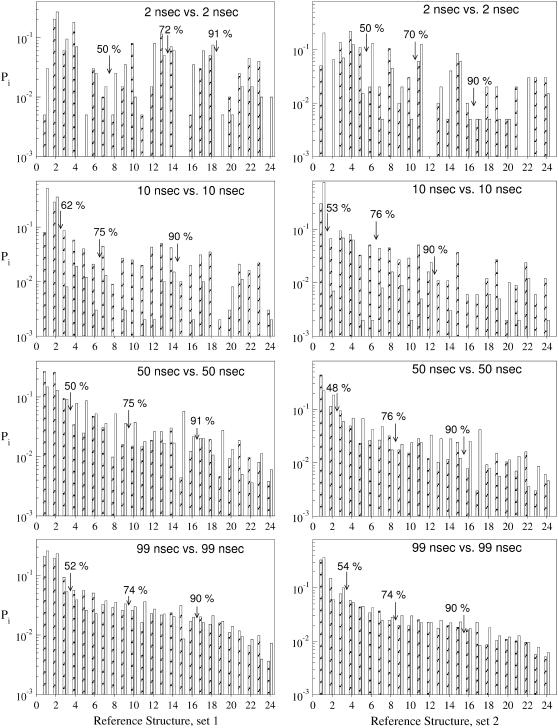
For met-enkephalin, we use our histogram approach to illustrate, in Fig. 3, the evolution of convergence in two long (99 ns) trajectories. The compound trajectory (198 ns) is taken as a gold-standard, from which reference structures are calculated using a cutoff d_c = 3.0 Å. We can then assess the convergence of portions of the trajectory against this full ensemble (see Fig. 3, A–D).

FIGURE 3.

Ensembles for different fractions of trajectory plw-a (bars), compared to the ensemble of the entire 198-ns compound trajectory (solid line): (A) 2 ns, (B) 10 ns, (C) 50 ns, and (D) 99 ns. The value d_c = 3.0 Å RMSD. Note that lnP_i is a free energy-like quantity; hence, on the semilog scale, the difference in populations may be read off in units of k_bT: a factor of 2 on the y axis corresponds to 0.5 k_bT. The percentages indicate the fraction of the 198-ns trajectory binned to that point.

From Fig. 3 A, it is clear that after the first two-nanoseconds, the simulation is far from converged. Many important substates have not yet been visited, and many of the bins are over- or underpopulated by several k_BT. (On a semilog scale, a factor of two in the population represents an error of 1/2 k_BT.) After 50 ns (Fig. 3 C), all clusters are populated, but many important substates have not converged to within 1/2 k_BT of the 198-ns values.

Fig. 3 presents a picture of a very conformationally diverse peptide, especially given the large cutoff (d_c = 3.0 Å) used. The first three substates contain only 52% of the observed structures, while the first nine account for 74%. Indeed, the (experimentally determined) starting structure is located in the second-most populated bin.

We also analyzed the entire set of NMR model structures. These were determined in the presence of bicelles, as it was hypothesized that interaction of the peptide with the cell membrane induces a shift in the conformational distribution (35). We classified the entire set of 80 NMR structures against our set of reference structures. The overwhelming majority of the NMR structures, 75%, were nearest to reference structure 23, the second-least populated bin in our simulation. The next largest group of NMR structures (15 of 80) were nearest to McCallum et al. (2), which held a comparable portion of the simulation trajectory. The remaining five NMR structures were scattered among four different bins. While not conclusive, the comparison between our simulation data and the NMR structures supports the hypothesis that binding to the membrane induces a shift in the distribution of met-enkephalin conformers, relative to the distribution observed in water. Such conformational diversity is not surprising for a peptide, which is known to be a promiscuous neurotransmitter by virtue of its flexibility (35,37,38). However, it will be interesting to revisit the issue in the study of a protein.

Self-referential convergence assessment

We want to assess convergence without the use of a gold-standard. Our previous analysis (Fig. 3) might be used to compare simulation protocols; ensembles from a new protocol may be compared to a gold-standard ensemble. (Here, the gold-standard is the 198-ns compound trajectory.) However, it is not useful as a means of assessing the convergence of a single simulation. After all, given only a 4-ns trajectory, one would like an assessment without reference to the answer.

Fig. 4 therefore demonstrates a purely self-referential scheme for on-the-fly analysis of a continuous trajectory. Fig. 4 A compares, for example, the first two-nanoseconds to the second two-nanoseconds. The series of plots in Fig. 4 shows that the populations of the clusters are still changing significantly, even between the first and second 50-nanoseconds. Presuming we had run only a single 100-ns simulation, we could make Fig. 4 C, and describe the convergence by saying, at a resolution of 3.0 Å RMSD, considering bins containing 75% of the structures, six of nine bins have not yet converged to within 1/2 k_BT. Note the contrast with Fig. 1 B, where it appears convergence is reached after just 7 ns. This contrast is all the more striking considering that d_c = 3.0 Å is a rather conservative choice. At a higher resolution (smaller d_c), the observed convergence is worse.

To test whether our analysis is sensitive to the (random) selection of reference structures, Fig. 4 shows two independent sets of reference structures. There is little difference in the results. Both classifications indicate that >50 ns are required for convergence when d_c = 3.0 Å.

The observed ensembles and corresponding convergence depend on both the metric used and the value of d_c. (This is of course true of any clustering algorithm.) It is therefore important to report this information along with any statements about the convergence of a particular simulation. Indeed, lowering the cutoff, and hence increasing the resolution of the classification, is bound to reduce the observed level of convergence. Instead of Fig. 4, in which each panel is a different length of the trajectory, we could have plotted the same trajectory length at different resolutions. At a high enough resolution, we will always find some substates that are under- or overpopulated. In other words, since all trajectories are finite, a physically acceptable value of d_c must be chosen.

While the choice of d_c is somewhat ad hoc in the present implementation, plots like those in Fig. 4 still can provide valuable, quantitative information. For example, imagine that we wish to calculate the free energy difference between two experimentally known conformations that differ by 3.0 Å RMSD. In this case, Fig. 4 suggests that we cannot expect an accuracy better than 1/2 k_BT. Perhaps more importantly, any fixed choice of cutoff can be useful in comparing different simulation methods—even if the difficult question of absolute convergence is not addressed.

DISCUSSION

We have introduced a structure-based classification approach for the analysis of biomolecular simulation trajectories. The method provides a more rigorous evaluation of convergence than commonly used methods. Our approach is based on a simple intuitive picture—namely, a comparison of the relative populations of different conformational substates. The method is trivially applicable to simulations of proteins of any size.

The results for met-enkephalin indicate that it takes quite some time (>50 ns) for the relative populations of the various substates to equilibrate, even with a fairly promiscuous cutoff (3.0 Å RMSD) that partitions the trajectory into relatively few bins. Because we can expect that many transitions into and out of each substate will be required to equilibrate their relative populations, a simple cluster-counting approach (Fig. 1 B) will present a deceptively optimistic picture of convergence. To carefully assess convergence of a simulation, we must therefore compare the populations of the various substates from different fragments of the trajectory. A simple, fast way to carry out such a comparison is provided by the ensemble method described above. A higher level of rigor can be achieved by comparing multiple pairs of independent blocks of the trajectory.

It must be stressed that—though our method may provide an unambiguous negative answer to the question, Is the simulation converged?—it may only provide a provisionally positive answer. A longer simulation may well reveal longer timescale phenomena, parts of structure space not yet visited.

Our approach should be useful, in its present form, as a means to assess the relative efficiencies of two simulation methods. (The cutoff d_c can always be reduced enough to suggest poorer convergence of at least one of the trajectories analyzed.) Many algorithms have recently generated broad interest by virtue of their potential to enhance the sampling of biomolecular conformation space. Some of these algorithms, notably the various parallel exchange simulations (39), invest considerable CPU time in pursuit of this goal. It is therefore important to ask whether these methods are in fact worth the extra expense, i.e., Does running the algorithm in question increase the quantity: (observed conformational sampling)/(total CPU time)?

In particular, these parallel exchange algorithms should be compared to 1), single, parallelized trajectories, as are possible with NAMD (40), for example; and 2), multiple independent trajectories as suggested by Caves et al. (28). The CPU time is easy enough to quantify, and we hope the present report will aid in evaluating the quality of sampling.

In the future, we will study trajectories of larger proteins, to develop criteria for determining cutoffs in larger systems. On the one hand, the upper bound on RMSD distance between any pair of structures increases with the size of the protein. On the other hand, larger proteins may not be as structurally diverse as small, floppy peptides—at least on the timescale currently accessible to simulation. Work already underway on a G-protein coupled receptor should shed light on these issues (A. Grossfield, personal communication, 2006). Furthermore, the approach should already be able to compare different simulation methods in large systems. The systems that may be treated with our method are not limited to proteins, or even single chains. Indeed, the method is immediately applicable for analyzing simulations of polymers, nucleic acids, or macromolecular complexes.