A Buffering SERCA Pump in Models of Calcium Dynamics

Abstract

Many cells use oscillations in calcium concentration to transmit messages. The oscillations largely result from an influx of calcium into the cytosol from the endoplasmic reticulum (ER), followed by an efflux of calcium from the cytosol back into the ER. The sarcoplasmic/endoplasmic reticulum calcium ATPase (SERCA) pump pumps calcium into the ER. It binds calcium on the cytosolic side and releases it on the ER side and in the delay between binding and release, calcium is buffered by the pump. We developed a model of a buffering SERCA pump and investigated whether including this in a model of calcium oscillations has any significant effects. We found that the oscillations produced when using the SERCA pump, which does not buffer calcium, have a larger amplitude and a slightly smaller period than when using the buffering SERCA pump. We show that the buffering SERCA pump shows adaptation to a stimulus, and we demonstrate that, by using a bidirectional SERCA pump, we are able to eliminate futile cycling of calcium between the cytosol and ER when the cell is at rest.

INTRODUCTION

Calcium oscillations in nonexcitable cells act as a messenger between extracellular stimulation and cell function, such as secretion of enzymes. In many cell types, the oscillations are the result of an influx of calcium into the cytosol from the endoplasmic reticulum (ER) through the inositol trisphosphate receptors (IP₃R) and the ryanodine receptors (RyR), followed by reuptake of calcium into the ER through the sarcoplasmic/endoplasmic reticulum calcium ATPase (SERCA) pumps. Numerous models have been constructed to reproduce calcium oscillations, and all these models contain a model of the SERCA pump. The SERCA pump uses the chemical energy produced from the conversion of adenosine triphosphate (ATP) into adenosine diphosphate (ADP) to transport calcium ions across the membrane from the cytosol to the ER, against a concentration gradient.

Fig. 1 gives an overview of calcium transport in a nonexcitable cell. An agonist binding to a cell membrane receptor stimulates the production of IP₃. The increase in IP₃ levels triggers release of calcium from IP₃R on the ER, which triggers further release of calcium from the ER via the IP₃R as well as the RyR. There is also a small leak of calcium into the cytoplasm from outside the cell. Calcium is removed from the cytosol via pumps in the cell membrane, which take it back outside the cell, and SERCA pumps, which take it back into the ER.

FIGURE 1.

The binding of an agonist stimulates IP₃ production. The agonist activates the membrane-bound enzyme phospholipase C, which hydrolyzes phosphatidylinositol bisphosphate into IP₃ and diacylglycerol. IP₃ activates IP₃R, releasing calcium from the ER. This triggers further release of calcium from the ER through the IP₃R and RyR. There is a positive feedback mechanism whereby calcium can activate phospholipase C. Calcium ions are bound to buffers in the cytosol and ER. Calcium is removed from the ER through the SERCA pump and membrane pump.

In the past, the model of the SERCA pump has been considered less important than models of calcium release from the ER through IP₃R and RyR. Consequently, while detailed models of release mechanisms were developed, less work was done to develop realistic models of calcium uptake. Although complex models of the SERCA pump have been used, such as the six-state model of Yano et al. (1), the SERCA pump has frequently been modeled by a simple Hill equation (2–4) or by the Hill equation with additional terms to account for modulation by ER calcium (5,6). However, the SERCA pump model is as important as models of IP₃R and RyR. A calcium signal cannot be effective unless the cytosolic calcium concentration is able to return to a low level after release, and the mechanism by which this occurs will affect properties such as the amplitude and period of the signal. This then raises the question of how the SERCA pump should be modeled.

When calcium ions are transported into the ER through the SERCA pump, they are bound to pump proteins on the cytosolic side of the membrane. The protein undergoes a change in conformation, which is powered by the energy released from the conversion of ATP to ADP, and the calcium ions are then released on the ER side of the membrane. Although the calcium ions are bound to the pump protein, they do not contribute to the calcium concentration inside the cytosol or to the calcium concentration inside the ER, so the calcium is being buffered by the SERCA pump. Because there is a large amount of pump protein present (Bers (7) estimates 15–75 μmol/L Cyt in a cardiac ventricular cell), the pump is able to bind a large amount of calcium and so the buffering effect of the pump is significant. When the SERCA pump transports calcium, the amount of calcium bound on the cytosolic side of the membrane may not always be equal to the amount released on the ER side, as some calcium remains bound to the pump protein. We have investigated whether a buffering SERCA pump model has a significantly different effect on the calcium transient than the simpler nonbuffering SERCA pump model.

We have compared the effect of using buffering and nonbuffering SERCA pumps in a modified version of the Sneyd et al. (6) model of calcium oscillations in the apical region of pancreatic acinar cells. However, our results are of a general nature and not specific to this type of cell. We have modified the model by Sneyd et al. (6) to include calcium buffers (other than the buffering SERCA pump) in the cytosol and ER. We modeled these endogenous buffers by using one effective buffer in the cytosol and one effective buffer in the ER, rather than modeling the effect of specific buffers. When the buffering SERCA pump is used with the concentration of pump protein, P_t = 15 μmol/L Cyt, the oscillations have a significantly smaller amplitude and slightly larger period compared to the results when using the nonbuffering SERCA pump. As P_t is increased, the amplitude decreases and the period increases, as the pump is able to buffer more calcium. We also show that the buffering SERCA pump is sensitive to changes in the cytosolic calcium concentration, and adapts to a maintained stimulus.

We have also addressed the issue of futile cycling at rest. If the SERCA pump model is based on the Hill equation, such as the model given by Sneyd et al. (6), then when the system is at steady state, calcium is continually pumped into the ER and this is balanced by a leak of calcium out of the ER. However, it has been suggested that this is a waste of energy and the amount of futile cycling should be very low. Other models (8) have incorporated more complex SERCA pumps, enabling them to eliminate futile cycling when the cell is at rest. Using the buffering SERCA pump model presented here, we are also able to achieve zero futile cycling at rest, so that at steady state, there is no SERCA pump activity.

THE SERCA PUMP MODEL

Various models have been proposed for modeling the SERCA pump. Maclennan et al. (9) suggest a reaction cycle involving four transitions. These include the binding of cytosolic calcium, the change of conformation powered by ATP, the release of calcium on the ER side of the membrane, and the return to the original conformation. Others suggest a larger number of reactions in the cycle. For example, Stokes and Green (10) give a scheme involving eight reactions. Dode et al. (11) describe a model with six transitions, which is similar to the reaction cycle from Maclennan et al. (9). In the scheme of Maclennan et al. (9), each change of conformation occurs during the same transition as the phosphorylation or dephosphorylation of the pump, whereas the model of Dode et al. (11) uses two transitions. A. C. Ventura and J. Sneyd (unpublished) have used a four-state model of the same form as that of Maclennan et al., but in their model only one calcium ion is bound during each pump cycle rather than two. The SERCA pump model presented here is based on the four-state diagram given in Fig. 2 A, which contains the same transitions as the reaction cycle given by Maclennan et al. (9).

FIGURE 2.

(A) State diagram of the buffering SERCA pump. The value X₁ gives the concentration of pump protein on the cytosolic side with no calcium bound, X₂ gives the concentration of pump protein on the cytosolic side with two calcium ions bound, and Y₁ and Y₂ are analogous on the ER side. The value c gives the calcium concentration on the cytosolic side and c_e gives the calcium concentration on the ER side. (B) Reduced-state diagram of the SERCA pump, formed by assuming the rate constants k₁, k₋₁, k₃, and k₋₃ are fast. The value X gives the concentration of pump protein on the cytosolic side, and Y gives the concentration on the ER side.

We begin with a four-state model to represent the buffering SERCA pump, and this is reduced to a two-state model, which retains the pump's ability to act as a buffer. The two-state model has been used in the whole cell model. To compare the buffering SERCA pump with a pump that does not have the capacity to buffer, we further reduced the two-state model to obtain a pump model that is an instantaneous function of the cytosolic and ER calcium concentrations. We refer to this model as the “nonbuffering SERCA pump.”

The buffering SERCA pump model

Fig. 2 A shows the state diagram used to derive the equations that govern the flux through the buffering SERCA pump. In this model, two calcium ions bind to the pump protein on the cytosolic side. The pump then changes its conformation from the cytosolic to the ER side using the energy released when ATP is converted to ADP. Two calcium ions are then released on the ER side and the pump changes conformation back to the cytosolic side. There is a delay between the binding and release of the ions, and during this time the bound calcium is not in the ER or the cytosol, so is being buffered by the pump. We denote the cytosolic calcium concentration by c and the ER calcium concentration by c_e. Using the state diagram and the law of mass action, we can write down the system of equations to describe the pump kinetics as

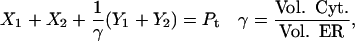(1)

(2)

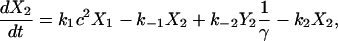(3)

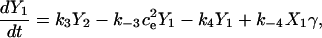(4)

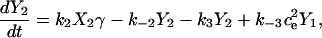(5)

(6)

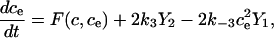(7)

where f(c, c_e) and F(c, c_e) denote all the other reactions. In the model given here, f(c, c_e) includes the flux through the IP₃R, the influx from outside the cell, the efflux through the plasma membrane pump, and binding and release by the endogenous cytosolic buffer. F(c, c_e) includes the flux through the IP₃R and binding and release by the endogenous ER buffer. Note that X₁, X₂, and c are in the units μmoles per liter cytosol (μmol/L Cyt) and Y₁, Y₂, and c_e are in the units μmoles per liter ER (μmol/L ER).

We can simplify the model, but retain the buffering effect of the pump, by assuming the transitions between X₁ and X₂ are fast, and the transitions between Y₁ and Y₂ are fast. Fig. 2 B describes this simplified model. The derivation is given in Appendix A, and results in the following system of differential equations for modeling the SERCA pump,

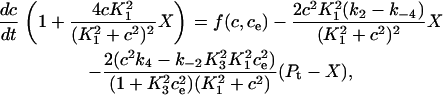(8)

(9)

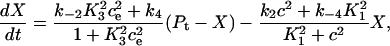(10)

where P_t gives the concentration of pump protein, and .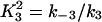

The nonbuffering SERCA pump model

To derive the model for the nonbuffering SERCA pump, we make transitions between the cytosolic and ER sides in the above model occur instantaneously, so at no time is the calcium bound by the pump, and not in either compartment. We do this by taking the limit as the rate constants k₂, k₋₂, k₄, and k₋₄ tend to infinity. We use the parameter s to denote the pump speed, and the above rate constants are all proportional to s. Taking the limit as the rate constants tend to infinity is then equivalent to taking the limit as s tends to infinity. We define the pumping capacity of the SERCA pump as the product of s with P_t, since at steady state the pump flux is proportional to both these quantities. We wish to keep the pumping capacity constant, so as the rate constants tend to infinity, P_t tends to zero, and we keep the product of each of these rate constants with P_t (and therefore the product of s with P_t) fixed. The derivation of the model is given in Appendix B. The model is given by

(11)

(12)

(13)

THE CELL MODEL

We have based our model of calcium oscillations on the model of the apical region of pancreatic acinar cells given by Sneyd et al. (6), but the results are not specific to this cell type. We added endogenous calcium buffering, removed the RyR, and used the simpler IP₃ receptor model given by LeBeau et al. (3). (This was done because the RyR and a more complex IP₃ receptor model are not needed to study the effect of the buffering SERCA pump, and so would increase the complexity of the model unnecessarily.) The model details are given below.

Calcium dynamics

When the nonbuffering SERCA pump is used, the differential equations governing c and c_e are given by Eqs. 12 and 13, where the flux through the SERCA pump, J_SERCA, is given by Eq. 11. If the buffering SERCA pump is used, then the differential equations governing c, c_e, and the pump variable X are given by Eqs. 8–10. In both cases, the functions f(c, c_e) and F(c, c_e), which represent the other reactions involved in the cytosol and ER, respectively, are given by

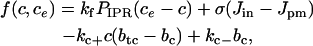(14)

and

(15)

IP₃ receptor

This is the model from LeBeau et al. (3), which is based on the state diagram given in Fig. 3. The parameter p gives the IP₃ concentration:

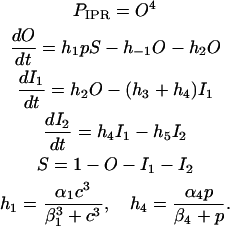FIGURE 3.

The state diagram of the IP₃ receptor model given by LeBeau et al. (3). S is the shut state, I₁ and I₂ are inactive states, and O is the open state.

Endogenous buffering dynamics

The endogenous buffering dynamics in the cytosol and ER are derived from the reaction scheme,

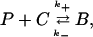(16)

where P is the buffer, C is calcium, and B is buffered calcium. We use the reaction scheme to write models for the buffer concentrations in the ER and cytosol. These are given by

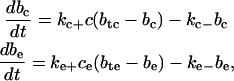where b_tc (b_te) is the total buffer concentration (both bound and unbound) in the cytosol (ER) and b_c (b_e) is the concentration of buffered calcium in the cytosol (ER). These terms also appear in Eqs. 14 and 15, respectively, to model the uptake of calcium by the buffers.

Calcium buffering can be modeled using the fast buffering approximation, in which case the buffering effect is modeled by division by a buffering factor (12). As shown in Appendix C, this does not result in conservation of calcium unless a computationally expensive technique is used when solving the system.

Membrane fluxes

We include two fluxes across the plasma membrane. The value J_in gives the influx from outside the cell and is of the form given by Sneyd et al. (6). The value J_pm gives the flux through the plasma membrane calcium pump and is modeled by a Hill equation with a Hill coefficient of 2. These fluxes are given by

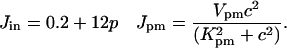Parameter values

The parameters used in the model are given in Table 1. The SERCA pump protein concentration and rate constants are determined as

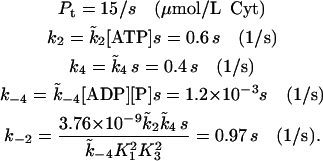TABLE 1.

Parameter values of the model

Parameter	Value (unit)	Parameter	Value (unit)
σ	0.1		0.7 ((μmol/L Cyt)2)
γ	10		0.0002 ((μmol/L Cyt)−1·s−1)
kf	10 (s−1)		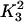1.111111 × 10−5 ((μmol/L ER)−2)
α1	40 ((μmol/L Cyt)−1·s−1)		0.4 (s−1)
β1	0.8 (μmol/L Cyt)		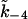4 × 10−8 ((μmol/L Cyt)−2·s−1)
h−1	0.88 (s−1)	[ATP]	3000 (μmol/L Cyt)
h2	0.5 (s−1)	[ADP]	10 (μmol/L Cyt)
h3	0.5 (s−1)	[P]	3000 (μmol/L Cyt)
h5	0.02 (s−1)	kc+	1 ((μmol/L Cyt)−1·s−1)
α4	0.06 (s−1)	kc−	0.25 (s−1)
β4	0.01 (μmol/L Cyt)	ke+	1 ((μmol/L ER)−1·s−1)
Vpm	28.0 ((μmol/L Cyt)·s−1)	ke−	80 (s−1)
Kpm	0.425 (μmol/L Cyt)	btc	100 (μmol/L Cyt)
		bte	375 (μmol/L ER)

The dimensionless parameter s represents the speed of the buffering SERCA pump. The SERCA pump rate constants k₂, k₋₂, k₄ and k₋₄ are each proportional to s. Unless otherwise stated, we keep the pumping capacity (which we defined in The Nonbuffering SERCA Pump Model as the product of s with P_t) constant, so when P_t is given a value, this determines the value of s, which in turn determines the value of the rate constants. When the nonbuffering version of the SERCA pump is used, changing P_t and the rate constants in this manner will not change the flux through the pump. This is because the flux through the nonbuffering SERCA pump is proportional to the product of s and P_t, which does not change. [ATP] is the concentration of adenosine triphosphate, [ADP] is the concentration of adenosine diphosphate, and [P] is the concentration of phosphate.

We have used the Gibbs free energy of hydrolysis of ATP to constrain the SERCA pump rate constants, and this results in the expression for k₋₂ given above. The constraint is given by

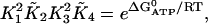(17)

where 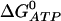is the Gibbs free-energy for the hydrolysis of ATP, R is the universal gas constant, T is temperature, K₂ = k₋₂/k₂, and K₄ = k₋₄/k₄. We use 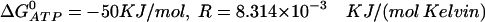, and T = 310 Kelvin. Using these values, the condition becomes

k₋₂ is then .

It is interesting to note that the value of 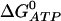determines the ER calcium concentration at steady state (that is, when there is no flux through the IP₃R). As our model does not include a leak of calcium from the ER, the steady-state concentration in the ER must be the concentration that results in zero flux through the SERCA pump. This is given by

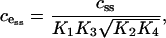where c_ss is the steady-state concentration in the cytosol. The product 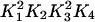is determined by the value of 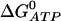, so changing the values of the SERCA pump rate constants will not affect c_ess, provided Eq. 17 holds. Intuitively, it makes sense that the free-energy drop sets that ER steady-state concentration.

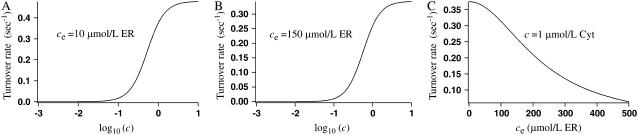
The parameter values for the membrane fluxes were based on those given by Sneyd et al. (6) and the parameter values for the IP₃ receptor are based on those given by LeBeau et al. (3). Minor modifications were made to obtain acceptable oscillations. The parameters for the buffering dynamics and the SERCA pump were chosen so that the model produced calcium oscillations consistent with those given by the model of Sneyd et al. (6). The turnover rate of the nonbuffering SERCA pump (J_SERCA/P_t) as a function of cytosolic calcium concentration (Fig. 4 A), when c_e = 10 μmol/L ER, is compared with the data presented by Dode et al. (11) and Yano et al. (1). They give the cytosolic calcium concentration that results in half-maximum activation of the pump as 0.28 μmol/L Cyt and 0.18 μmol/L Cyt, respectively, whereas in our model half-maximum activation occurs at a cytosolic calcium concentration of 0.53 μmol/L Cyt. Yano et al. (1) also present model data for the turnover rate as a function of ER calcium, when c = 1 μmol/L Cyt. We give the corresponding data from our model in Fig. 4 C. Their data gives a half-maximal inhibition by ER calcium of 176 μmol/L ER where as the corresponding value from our model is 225.8 μmol/L ER. In Fig. 4 B we give the turnover rate as a function of cytosolic calcium when c_e = 150 μmol/L ER, which is a more representative ER calcium concentration for our model than that used in Fig. 4 A. Here, half-maximal activation occurs at a cytosolic calcium concentration of 0.57 μmol/L Cyt, which is close to the value from Fig. 4 A.

FIGURE 4.

The turnover rate of the nonbuffering SERCA pump when the pump speed s = 1. (A) The turnover rate as a function of cytosolic calcium concentration, with c_e = 10 μmol/L ER. This ER calcium concentration is unrealistically low, but is used here so the results can be compared with those of Dode et al. (11) and Yano et al. (1), which use this value. The half-maximum activation occurs at c = 0.53 μmol/L Cyt. (B) The turnover rate as a function of cytosolic calcium concentration, with c_e = 150 μmol/L ER. This is a more representative value for c_e in our model than the value from panel A. Half-maximum activation occurs at c = 0.57 μmol/L Cyt. (C) The turnover rate as a function of ER calcium concentration, when c = 1 μmol/L Cyt. Half-maximum inhibition is at c_e = 225.8 μmol/L ER.

RESULTS

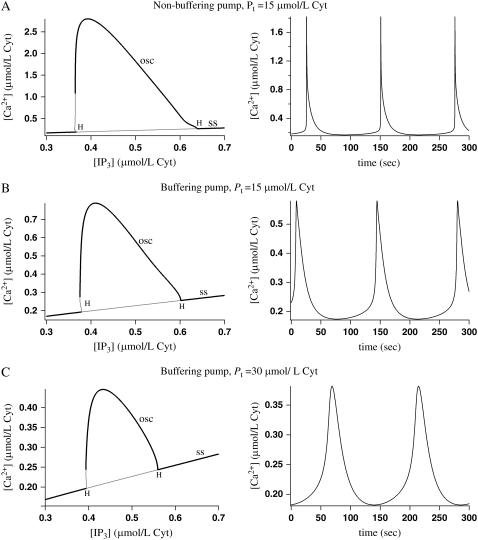
Fig. 5 A shows the bifurcation diagram with IP₃ concentration as the bifurcation parameter, and cytosolic calcium oscillations at IP₃ = 0.5 μmol/L Cyt, where the nonbuffering SERCA pump is used. In Fig. 5 B the buffering SERCA pump is used with P_t = 15 μmol/L Cyt. This means the SERCA pump speed s = 1. We see that using the buffering SERCA pump in place of the nonbuffering SERCA pump has resulted in a significant decrease in oscillation amplitude and a small increase in period, at this value of P_t.

FIGURE 5.

Bifurcation diagrams showing cytosolic calcium concentration with IP₃ concentration as the bifurcation parameter, and cytosolic calcium oscillations when the IP₃ concentration is 0.5 μmol/L Cyt. Shaded lines in the bifurcation diagrams denote unstable branches and H denotes a Hopf bifurcation. The curve of steady states is labeled ss and the maximum value of c over an oscillation is labeled osc. (A) The nonbuffering SERCA pump is used with P_t = 15 μmol/L Cyt and pump speed s = 1. (B) The buffering SERCA pump is used with P_t = 15 μmol/L Cyt and pump speed s = 1. (C) The buffering SERCA pump is used with P_t = 30 μmol/L Cyt and pump speed s = 0.5.

We compared the SERCA pump clearance rate and the amplitude and period of the oscillations with the experimental results given by Dupont et al. (13) from an hepatocyte. We estimated the clearance rate by measuring the rate at which the cytosolic calcium concentration decreases after the peak of an oscillation. From the experimental results we measured a clearance rate of 0.08 μmol/L Cyt/s, an amplitude of 0.93 μmol/L Cyt, and a period of 78.6 s. From our model results, using the nonbuffering SERCA pump, we measured a clearance rate of 0.35 μmol/L Cyt/s, an amplitude of 1.82 μmol/L Cyt, and a period of 125.2 s. Using the buffering SERCA pump (P_t = 15 μmol/L Cyt, s = 1), we measured a clearance rate of 0.02 μmol/L Cyt/s, an amplitude of 0.58 μmol/L Cyt, and a period of 137.9 s. The clearance rate and amplitude from the experimental results fall between the model results when using the buffering and nonbuffering SERCA pump.

In Fig. 5 C we used the buffering SERCA pump and increased the concentration of SERCA pump protein, P_t, to 30 μmol/L Cyt. The pump speed s is decreased to 0.5 so that the product of s with P_t (the pumping capacity of the SERCA pump) is not changed. The amplitude of calcium oscillations decreases as the SERCA pump protein (and thus the buffering capacity of the SERCA pump) increases. This is because when the buffering capacity increases, more calcium will be bound to the buffers during oscillations, lowering the concentration of unbound calcium in the cytosol and ER. When P_t is high enough, the oscillations disappear.

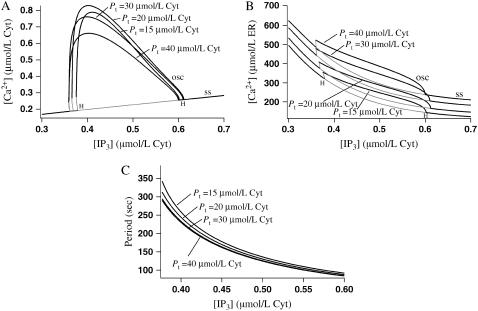
When the buffering SERCA pump is used, increasing the pump protein concentration while keeping the pumping capacity constant (i.e., while decreasing s) has resulted in cytosolic calcium oscillations with a decreased amplitude and increased period. However, if we increase the pump protein concentration and keep the pump speed, s, constant as in Fig. 6, then the amplitude of the oscillations initially increases and then decreases, and the period decreases. The increase in oscillation amplitude as P_t is increased from 15 μmol/L Cyt to 20 μmol/L Cyt is caused by the increased pumping capacity outweighing the buffering effect of the pump. At higher values of P_t, the buffering effect outweighs the increased pumping capacity and the oscillation amplitude decreases. The increased pumping capacity of the SERCA pump has resulted in a higher resting ER concentration as well as higher amplitude calcium oscillations in the ER. These results have been compared to those of Falcke et al. (14) in Discussion.

FIGURE 6.

Bifurcation diagrams showing the effect of increasing P_t from 15 μmol/L Cyt to 20 μmol/L Cyt, 30 μmol/L Cyt, and 40 μmol/L Cyt while keeping s fixed at 1. The buffering SERCA pump is used here. Shaded lines denote unstable branches and H denotes a Hopf bifurcation. The curve of steady states is labeled ss and the maximum value over an oscillation is labeled osc. (A) Cytosolic calcium concentration. (B) ER calcium concentration. (C) Oscillation period.

ADAPTATION

We investigated the reaction of the buffering SERCA pump to a change in cytosolic calcium concentration from 0 to 1 μmol/L Cyt, as shown in the inset in Fig. 7 A. The ER calcium concentration is fixed at 185.9 μmol/L ER and P_t = 15 μmol/L Cyt. The calcium flux from the pump into the ER has been scaled by the factor γ so that it is measured in the units μmol/L Cyt, and is comparable to the flux from the cytosol onto the pump, which is measured in the same units.

FIGURE 7.

The reaction of the buffering SERCA pump to a change in cytosolic calcium concentration. The ER calcium concentration is fixed at 185.9 μmol/L ER. P_t = 15 μmol/L Cyt and the cytosolic calcium concentration is stepped up from 0 to 1 μmol/L Cyt as shown in the inset in panel A. (A) The flux of calcium from the cytosol onto the SERCA pump. (B) The flux of calcium from the pump, into the ER. Note that the units used are μmol/L Cyt/s for comparison with the plot in panel A.

In Fig. 7 A, we give the calcium flux from the cytosol onto the pump, which is given by

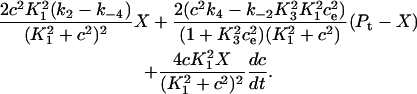In Fig. 7 B, we give the calcium flux from the pump into the ER, which is given by

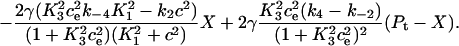When the calcium concentration in the cytosol is stepped up, the pump begins to extract calcium from the cytosol and pump it into the ER. The difference between the rate at which cytosolic calcium is bound to the pump and the rate at which calcium is released into the ER, is the rate at which calcium is being bound to or released from the pump's buffering mechanism. Initially calcium builds up on the pump and the flux from the cytosol is greater than the flux into the ER. Eventually the pump adapts to the changed cytosolic calcium concentration and reaches a new steady state where the fluxes on and off the pump are equal and the amount of calcium bound to the pump remains constant.

FUTILE CYCLING AT REST

When the cell is at rest, the SERCA pump may do work to balance a leak from the ER and maintain a constant calcium concentration inside the ER. This is referred to as “futile cycling at rest”. Various groups (15–17) have presented evidence that this cycling does exist in real cells. Alvarez et al. (15) claim that futile cycling may result in the loss of up to 3% of the cell's energy production. Machaca and Hartzell (17) propose that although the cycle is futile in refilling the ER, it helps maintain elevated calcium levels in the cytosol by slowing the movement of calcium ions toward the plasma membrane. Contrary to these findings, Satoh et al. (18) show that when calcium is removed from the outside of a ventricular cell the SR retains its calcium content for many minutes (18), suggesting the flux of calcium out of the SR is very small. A very low rate of futile cycling seems advantageous because it reduces the energy used by the cell.

Our model does not contain a leak from the ER, so there is no futile cycling at rest. This means that the flux through the SERCA pump is zero at steady state. If the SERCA pump was modeled using a unidirectional pump, such as

(18)

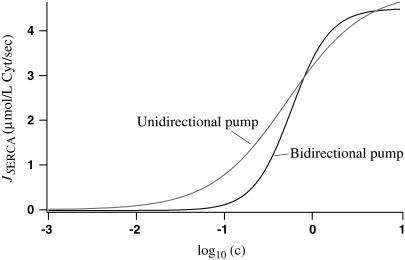
which is given by Sneyd et al. (6), then we could only achieve zero flux if c = 0 or c_e is infinite at steady state, neither of which are realistic conditions. The SERCA pump presented here is bidirectional, so it is possible to achieve zero net flux through the pump at finite and nonzero calcium concentrations. Note that when there is zero net flux, there is also zero net ATP consumption, because the ATP that is consumed due to the inward flux is balanced by the ATP produced due to the outwards flux. If we set the IP₃ concentration to 0 in our model so the calcium concentrations relax to a steady state, we find these steady-state concentrations are c = 0.036 μmol/L Cyt and c_e = 185.9 μmol/L ER. Fig. 8 shows the flux through the nonbuffering SERCA pump (labeled Bidirectional pump) and the pump given by Eq. 18 (labeled Unidirectional pump) as cytosolic calcium concentration varies and ER calcium concentration is fixed at c_e = 185.9 μmol/L ER. Equation 18 was fitted to the nonbuffering SERCA pump over the range c = 0.1 to 10 μmol/L Cyt. We see that our SERCA pump achieves zero flux at a nonzero cytosolic calcium concentration (in fact, at c = 0.036 μmol/L Cyt).

FIGURE 8.

A comparison of the flux through the nonbuffering SERCA pump (which is a bidirectional pump) and the unidirectional pump given by Eq. 18. The value c_e is held constant at 185.9 μmol/L ER. Equation 18 was fitted to our nonbuffering SERCA pump over c = 0.1 to 10 μmol/L Cyt. Note that a log scale is used on the horizontal axis.

DISCUSSION

In the past, the SERCA pump has frequently been modeled using the Hill equation (2–4) or modifications of the Hill equation that account for modulation of the pump flux by the ER calcium concentration (5,6). Equation 18 is an example of such a model. This approach has been taken because a simple model for the SERCA pump has often been regarded as adequate. However, the SERCA pump model may be just as important as the models of ER calcium release and warrants greater attention.

Various models of the SERCA pump have been proposed. Maclennan et al. (9) have described the SERCA pump using a four-state model involving analogous transitions to the model presented here (Fig. 2 A). The transitions involved are as follows. First, calcium is bound on the cytosolic side of the ER membrane. In the next transition, the phosphorylation of the pump as ATP is converted to ADP releases energy and enables the pump to change conformation so that the exposed binding site moves from the cytosolic side to the ER side. Calcium bound to the pump is then released into the ER. Lastly the pump undergoes dephosphorylation and returns to its original conformation. Others have proposed schemes that involve more transitions. Stokes and Green (10) give a table of the reactions involved in calcium transport across the membrane. The mechanism they describe is essentially the same as that described above, with the difference being that the transitions have been broken into a larger number of reactions. Inesi and de Meis (19) give a more complex scheme in which calcium binding and dissociation occurs over a sequence of steps and there is a branched pathway for ADP dissociation. A six-state model describing the pump reactions has been widely used (1,11,20). This again involves essentially the same transitions as the model given by Maclennan et al. (9), but the phosphorylation of the pump and the change of conformation from the cytosolic to the ER side have been separated into two transitions, as have the dephosphorylation of the pump and the change of conformation from the ER to the cytosolic side. For modeling purposes, the four-state model of Maclennan et al. (9) is adequate for representing the pumping and buffering effects of the pump. More complex models are not necessary to reproduce these essential properties of the pump, so have not been used here.

Yano et al. (1) present a model of calcium oscillations in pancreatic acinar cells, which includes a SERCA pump model based on a reaction cycle involving six transitions. Apart from a lesser number of transitions, our model differs from theirs in that our transition rates during calcium binding are proportional to the square of the calcium concentration, since there are two calcium ions being bound. The model of Yano et al. (1) has the transition rates for calcium binding (both on the cytosolic and ER side of the membrane) given as saturating functions of the calcium concentration. The physiological mechanism underlying this approach is not given. Also, the transition rate for the change of conformation from the ER to the cytosolic side in the model of Yano et al. (1) is dependent on the ER calcium concentration, so that an increase in calcium inhibits the transition. Their justification for this is that the main SERCA subtype in pancreatic acinar cells is SERCA2b, but their model was based on that of Dode et al. (11), which was based on experimental data relating to the subtype SERCA1a. They believe that data relating to the SERCA2b subtype (5,21) indicates that SERCA2b responds to the ER calcium concentration using a different mechanism from that of SERCA1a, and they hypothesize that there is another reaction in the cycle that is affected by ER calcium. They then determine that this reaction is most likely the transition from the ER to the cytosolic side. Again, the physiological mechanism underlying the ER calcium dependence of the transition is not given.

Experimental measurements have been made to estimate the concentration of SERCA pump protein present in cells. The results of Bers and Stiffel (22) suggest the concentration in ventricular cells is ∼20 μmol/L Cyt, while Levitsky et al. (23) estimate 14 μmol/L Cyt in Guinea-pig ventricle and Feher and Briggs (24) estimated 47 μmol/L Cyt in dog ventricle. Bers (7) estimates the concentration in ventricular cells to be in the range of 15–75 μmol/L Cyt depending on species. These results all suggest that the amount of SERCA pump protein is large, and therefore the pump could act as a significant calcium buffer. Teucher et al. (25) states that after troponin C, the SERCA pump is the most prominent cytosolic calcium buffer. This raises the question of what effect the inclusion of the buffering effect of the SERCA pump may have in a model.

We have derived a system of equations for modeling a SERCA pump that will act as a calcium buffer. We began with the four-state diagram in Fig. 2 A. We wrote down a system of equations based on the state diagram, using the law of mass action. It is preferable not to use the full four-state model in the whole-cell model, since it slows computations. This is because of the number of additional differential equations involved, and because if the transitions are fast, a small time-step is needed during numerical simulations. We have therefore reduced the four-state model to a two-state model, ensuring that the buffering property of the pump is retained. This is done by assuming that the reactions where calcium binding and release take place are fast. After reducing the model under this assumption, the buffering effect of the pump is now modeled by a buffering factor that modulates the rate at which calcium is transported. To compare the buffering SERCA pump with a pump that does not act as a buffer, we performed a further reduction. This was done by assuming that transitions between the cytosolic and ER sides occur infinitely fast, so the pump speed s tends to infinity. The length of time during which calcium is buffered by the pump then tends to zero. The product of the speed and pump protein concentration is kept constant so that the pumping capacity is not altered.

To illustrate the effect of the buffering SERCA pump, it has been incorporated into a model of calcium dynamics in a nonexcitable cell. Fig. 5 compares the cytosolic calcium oscillations that occur when the nonbuffering SERCA pump is used, with the oscillations that occur when the buffering SERCA pump is used, and the concentration of SERCA pump protein is 15 μmol/L Cyt. We see that using the buffering SERCA pump has resulted in a significant decrease in the amplitude of oscillations, and a small increase in the period.

Falcke et al. (14) have investigated the effect of overexpression of SERCA pumps on the period and amplitude of intracellular calcium waves in Xenopus oocytes. In their model, they use the assumption that increasing SERCA pump density increases the resting ER calcium concentration. Under these conditions they found that an increased SERCA pump density decreased the period and increased the amplitude of calcium waves. These findings are in agreement with experimental results (26). Falcke et al. (14) also found that increasing pump density and keeping the resting ER concentration fixed increased the period and decreased the amplitude of calcium waves.

In the model presented here, increasing the SERCA pump density while decreasing the pump speed does not alter the resting ER calcium concentration because pumping capacity remains constant. Using the buffering SERCA pump, the increased pump density increases the period of cytosolic calcium oscillations, and decreases the amplitude. This is in agreement with the results of Falcke et al. (14), where they keep the resting ER concentration fixed.

If we use the buffering SERCA pump and increase pump density while keeping the pump speed constant, as in Fig. 6, then the resting ER calcium concentration will increase (see Fig. 6 B). In this case, the amplitude of cytosolic calcium oscillations initially increases, but then decreases. This decrease is a result of the increased buffering capacity of the pump outweighing the increased pumping capacity. The oscillation period decreases as the pump density is increased. If the pump density is increased, with pump speed kept constant, using the nonbuffering SERCA pump, then the oscillations have a decreased period and increased amplitude (results not shown), in agreement with the results of Falcke et al. (14).

The model of Falcke et al. (14) does not take into account the buffering effect of the SERCA pump and the results from their model do not agree with the results from ours when the buffering SERCA pump is used, unless the increase in pump density is small. However, their results do agree with experimental results from Xenopus oocytes. The buffering effect of the pump may be less important in oocytes compared to other cells types.

Fig. 7 shows the pump's reaction to a step in the cytosolic calcium concentration. Initially there is a large flux of calcium from the cytosol onto the pump, and a smaller flux from the pump into the ER. The difference between these fluxes is the rate at which calcium is being bound to the pump. The flux from the cytosol and the flux into the ER tend toward the same steady-state value as the pump adapts to the changed environment.

We have looked at the issue of futile cycling across the ER membrane while the cell is at rest. This consists of a leak of calcium out of the ER that is balanced by an influx of calcium through the SERCA pump, requiring the use of energy. This leads to the hypothesis that the amount of futile cycling at rest should be small or even zero, to avoid wasting energy. If the SERCA pump is modeled by a Hill equation, or a modification of the Hill equation such as Eq. 18, then zero futile cycling can only be achieved at unphysiological calcium concentrations. A model such as the one presented here, which is based on a reaction cycle that can operate in both directions, is able to achieve zero futile cycling at rest, without requiring the cytosolic or ER calcium concentrations to be unrealistic.

In Appendix C, we describe the fast buffering approximation. This uses the assumption that the buffering kinetics are fast to reduce the effect of a buffer to division by a buffering factor. The differential equation governing the buffer concentration is then not needed, which simplifies the model. We show that if the discretized equations governing the system are given explicitly, then the fast buffering approximation will not conserve calcium. If the equations are given implicitly conservation can be achieved, but at the expense of a longer computation time. We then show that the loss of conservation does not make a significant difference to the solution in the model presented here.

APPENDIX A: BUFFERING SERCA PUMP MODEL DERIVATION

Here we give the derivation for the buffering SERCA pump model given by Eqs. 8–10. We begin with the system of equations given by Eqs. 1–7 then simplify this model by assuming the transitions between X₁ and X₂ are fast, and the transitions between Y₁ and Y₂ are fast, so that k₁c²X₁ = k₋₁X₂ and 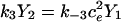. We let X = X₁ + X₂ and Y = Y₁ + Y₂. Then,

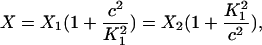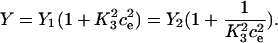Note that 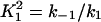and 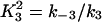. The differential equation for the cytosolic calcium concentration is derived as

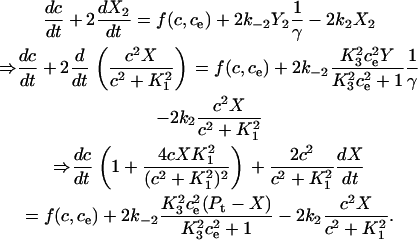Similarly, the differential equation for the ER calcium concentration is derived as

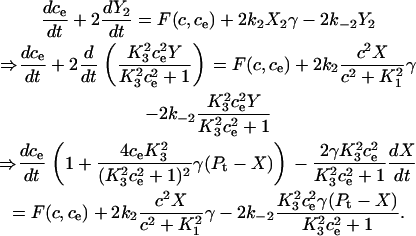The differential equation for the pump variable X is derived as

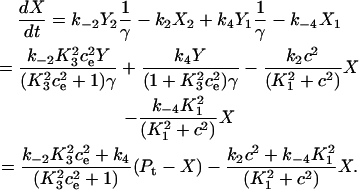We substitute the expression for 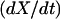into the expressions for 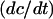and 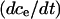to obtain the system of differential equations for modeling the SERCA pump:

(19)

(20)

(21)

APPENDIX B: NONBUFFERING SERCA PUMP MODEL DERIVATION

Here we give the derivation for the nonbuffering SERCA pump model given by Eqs. 11–13. We begin with our model for the buffering SERCA pump, then assume that the speed of the transitions between the cytosolic and ER sides of the membrane are infinitely fast, so the length of time during which calcium is buffered by the pump becomes zero. To do this, we take the limit, since the rate constants k₂, k₋₂, k₄, and k₋₄ tend to infinity all at the same rate. We wish to keep the pumping capacity constant, so the rate constants' products with P_t remains fixed. The value P_t therefore tends toward zero. To perform this process, we first nondimensionalize the system given by Eqs. 19–21 using the dimensionless variables of

We ignore the terms f(c, c_e) and F(c, c_e), because they are not affected by the following process. The system becomes

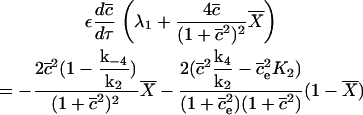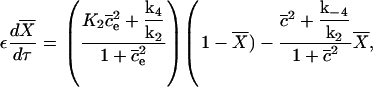where

The values ελ₁ = ψ₁ and ελ₂ = ψ₂ are fixed. We now make k₄, k₋₄, k₂, and k₋₂ tend to infinity with their ratios constant, and P_t tends to zero. This means E becomes small. We expand the solutions as

Now we substitute these expressions into the nondimensionalized equations, and take the limit as E tends to zero, to find the O(1) equations. These are

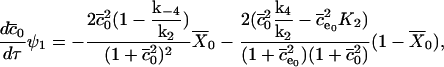(22)

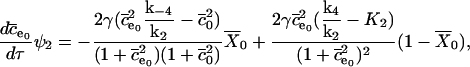(23)

(24)

Note that if we had taken the pump flux out of the cytosol to be

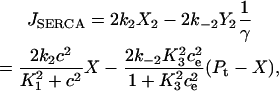and then assumed the transition between X and Y was fast (see Fig. 2 B), so that

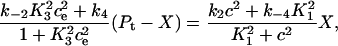then this model gives the same result as solving Eq. 24 for 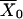, substituting this into Eqs. 22 and 23, then redimensionalizing. Upon adding the terms f(c, c_e) and F(c, c_e) that were ignored during the derivation, the result is

APPENDIX C: CONSERVATION AND THE FAST BUFFERING APPROXIMATION

The chemical reaction for calcium buffering can be described by the reaction scheme given in Eq. 16. If b and c denote the concentrations of buffered and free calcium, respectively, then we can use the reaction scheme to write a general model of calcium buffering as

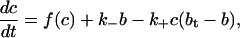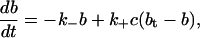where b_t is the total buffer concentration, and f(c) denotes the other reactions involving free calcium.

If we assume that the kinetics are fast (i.e., k₊ and k₋ are large), then we can take b to be in quasi-steady state, and so

Solving for b, we find

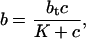where K = k₋/k₊. Then

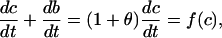where

Then

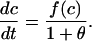So the buffering effect is approximated by division by the buffering factor 1 + θ. However, care needs to be taken when using this approximation once time has been discretized, if total calcium is to be conserved. If

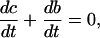where b at time n is determined from c at time n using 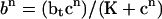(superscripts denote time), then c + b, which is the total amount of calcium, should be conserved. If we use the approximation

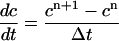and an analogous approximation for , then we can determine the buffering term in the time-discretized model,

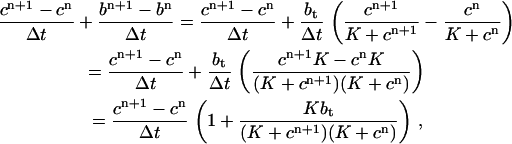so the buffering term is

which contains cⁿ⁺¹. This means that we lose conservation if the equations for determining the solution at the next time-step are given explicitly—that is, if we use a buffering term of the form

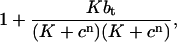where the buffering term contains only c at time n. If conservation is to be achieved, the equations must be given implicitly, and more work must be done to find the solution at each time-step.

We now show that this loss or gain of calcium does not have a significant impact on the system. We use the model presented here with the nonbuffering SERCA pump, but we replace the endogenous buffering terms in the cytosol and ER with the buffering factors that result from the fast buffering approximation. That is, rather than an equation of the form

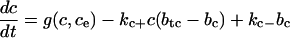for modeling cytosolic calcium, we use the equation

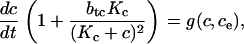where K_c = k_c–/k_c+. The equation for modeling ER calcium is analogous.

Let cⁿ and 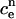denote the concentrations of cytosolic and ER calcium, respectively, at time-step n. If the equation for solving for cⁿ⁺¹ is given explicitly, then it will have the form

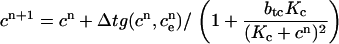If we wish to conserve calcium, then we need to solve the implicit equation

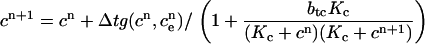The equations for ER calcium are analogous.

Fig. 9 A shows that when using the implicit equations to iterate each time-step, calcium is conserved. That is, the change in the quantity is equal to the input from the cell exterior. When using the explicit equations, there is a loss of calcium. However, from Fig. 9, B and C, we see that this loss has caused very little difference in the calcium oscillations.

FIGURE 9.

Comparison between solutions when solving the model equations explicitly and implicitly, where the fast buffering approximation is used to model the endogenous buffering. The nonbuffering SERCA pump has been used here. (A) The difference between the sum of the cytosolic, ER and buffered calcium, and the input into the cell from the cell exterior. This quantity should be conserved. We give the results when the implicit equations are used and when the explicit equations are used. (B) Cytosolic calcium oscillations. The results from the implicit and explicit equations are plotted on the same axes, but are indistinguishable. (C) The difference between the cytosolic calcium concentrations when using the implicit and explicit equations.