Effects of Intracellular and Extracellular Concentrations of Ca²⁺, K⁺, and Cl⁻ on the Na⁺-Dependent Mg²⁺ Efflux in Rat Ventricular Myocytes

Abstract

Intracellular Mg²⁺ concentration ([Mg²⁺]_i) was measured in rat ventricular myocytes with the fluorescent indicator furaptra (25°C). After the myocytes were loaded with Mg²⁺, the initial rate of decrease in [Mg²⁺]_i (initial Δ[Mg²⁺]_i/Δt) was estimated upon introduction of extracellular Na⁺, as an index of the rate of Na⁺-dependent Mg²⁺ efflux. The initial Δ[Mg²⁺]_i/Δt values with 140 mM [Na⁺]_o were essentially unchanged by the addition of extracellular Ca²⁺ up to 1 mM (107.3 ± 8.7% of the control value measured at 0 mM [Ca²⁺]_o in the presence of 0.1 mM EGTA, n = 5). Intracellular loading of a Ca²⁺ chelator, either BAPTA or dimethyl BAPTA, by incubation with its acetoxymethyl ester form (5 μM for 3.5 h) did not significantly change the initial Δ[Mg²⁺]_i/Δt: 115.2 ± 7.5% (seven BAPTA-loaded cells) and 109.5 ± 10.9% (four dimethyl BAPTA loaded cells) of the control values measured in the absence of an intracellular chelator. Extracellular and/or intracellular concentrations of K⁺ and Cl⁻ were modified under constant [Na⁺]_o (70 mM), [Ca²⁺]_o (0 mM with 0.1 mM EGTA), and membrane potential (–13 mV with the amphotericin-B-perforated patch-clamp technique). None of the following conditions significantly changed the initial Δ[Mg²⁺]_i/Δt: 1), changes in [K⁺]_o between 0 mM and 75 mM (65.6 ± 5.0% (n = 11) and 79.0 ± 6.0% (n = 8), respectively, of the control values measured at 140 mM [Na⁺]_o without any modification of extracellular and intracellular K⁺ and Cl⁻); 2), intracellular perfusion with K⁺-free (Cs⁺-substituted) solution from the patch pipette in combination with removal of extracellular K⁺ (77.7 ± 8.2%, n = 8); and 3), extracellular and intracellular perfusion with K⁺-free and Cl⁻-free solutions (71.6 ± 5.1%, n = 5). These results suggest that Mg²⁺ is transported in exchange with Na⁺, but not with Ca²⁺, K⁺, or Cl⁻, in cardiac myocytes.

INTRODUCTION

The intracellular concentration of Mg²⁺ ([Mg²⁺]_i) regulates numerous cellular functions and is thought to lie in the 0.5–1.0 mM range in many types of cells (see Flatman (1)). The submillimolar [Mg²⁺]_i, below the electrochemical equilibrium of this ion, is thought to be maintained by the balance between passive influx (probably through channels) and active efflux. Although transporter molecules that extrude Mg²⁺ have not been identified in vertebrate cells, functional studies have suggested that Mg²⁺ is transported in exchange with Na⁺ influx (i.e., Na⁺/Mg²⁺ exchange). In Paramecium, an exchanger-like protein with large Mg²⁺ current has been described, which has some similarities with K⁺-dependent Na⁺/Ca²⁺ exchangers (2).

In cardiac myocytes, active Mg²⁺ extrusion from Mg²⁺-loaded cells has been characterized recently. The Mg²⁺ transport critically depends on the extracellular Na⁺ concentration ([Na⁺]_o) with half-maximal activation at 55 mM [Na⁺]_o, and is inhibited by elevation of the intracellular Na⁺ concentration ([Na⁺]_i) with half-inhibitory concentration at ∼40 mM (3). The Mg²⁺ transport is also half-maximally activated by elevation of [Mg²⁺]_i from the resting level (0.8–0.9 mM) to 1.5 mM, and is half-inhibited by high extracellular Mg²⁺ concentration ([Mg²⁺]_o) with half-inhibition at ∼10 mM (4). These results are consistent with the putative Na⁺/Mg²⁺ exchange as the primary transport mechanism for active extrusion of cellular Mg²⁺. Regarding the stoichiometry of the exchange, recent experiments estimated 1 Na⁺/1 Mg²⁺ (37°C (5,6)) or 1–2 Na⁺/1 Mg²⁺ (25°C (7)). However, more complex stoichiometries involving ions other than Na⁺ and Mg²⁺ have also been proposed. First, based on Ca²⁺ dependence of noradrenaline-induced Mg²⁺ efflux observed in rat ventricular myocytes, Romani et al. (8) postulated that the Na⁺/Ca²⁺ exchanger might play a role in the Mg²⁺ transport. Tashiro et al. (9) experimentally showed that Na⁺-dependent Mg²⁺ transport activity developed after overexpression of the Na⁺/Ca²⁺ exchanger in CCL39 cells, suggesting that Mg²⁺ is transported by the Na⁺/Ca²⁺ exchanger at least in some experimental conditions. Later quantitative analysis, however, raised the question of the physiological significance of the Na⁺/Ca²⁺ exchanger for cellular Mg²⁺ transport (10). Second, Rasgado-Flores et al. (11) found that K⁺ and Cl⁻ were involved in extracellular Mg²⁺-dependent Na⁺ efflux in squid giant axons, and proposed a putative Na⁺-K⁺-Cl⁻/Mg²⁺ exchanger which carries 1 Mg²⁺ in exchange for 2 Na⁺, 2 K⁺ and 2 Cl⁻ (also see Rasgado-Flores and Gonzalez-Serratos (12)). This hypothesis, however, has not been confirmed in other cell types.

In this study, we explored possible roles of the Na⁺/Ca²⁺ exchanger and the putative Na⁺-K⁺-Cl⁻/Mg²⁺ exchanger in cellular Mg²⁺ transport in mammalian cardiac myocytes. Experiments were designed to test whether the rate of Mg²⁺ efflux was modified by intracellular and extracellular concentrations of Ca²⁺ (expected for the Na⁺/Ca²⁺ exchanger), and K⁺ and Cl⁻ (expected for the putative Na⁺-K⁺-Cl⁻/Mg²⁺ exchanger). We measured [Mg²⁺]_i of rat ventricular myocytes with the fluorescent indicator furaptra, and estimated the rate of Mg²⁺ efflux from Mg²⁺-loaded cells using the previously established methodology (3,4,7) with varied intracellular and extracellular concentrations of Ca²⁺, K⁺, and Cl⁻. High-affinity Ca²⁺ chelators were used to buffer intracellular Ca²⁺, whereas intracellular concentrations of K⁺ and Cl⁻ ([K⁺]_i and [Cl⁻]_i, respectively) were directly manipulated by intracellular perfusion from the patch pipette.

Preliminary results of this work were previously published in abstract form (13).

METHODS

Male Wistar rats (10–12 w) were sacrificed under deep anesthesia with pentobarbital, in accordance with the procedures approved by the Institutional Animal Care and Use Committee of Tokyo Medical University, and single ventricular myocytes were isolated enzymatically as previously described (14,15). Cells were superfused with normal Tyrode's solution in a bath placed on the stage of an inverted microscope (Nikon, Tokyo, Japan), and intensity of the background fluorescence (cell autofluorescence plus instrumental stray fluorescence) was measured. The normal Tyrode's solution contained (in mM) 135 NaCl, 5.4 KCl, 1.0 CaCl₂, 1.0 MgCl₂, 0.33 NaH₂PO₄, 5 glucose, and 10 HEPES, pH 7.40 (titrated with 5 mM NaOH). The cells were loaded with furaptra by incubation in normal Tyrode's solution containing 5 μM furaptra acetoxymethyl (AM) ester plus (0.5% dimethylsulfoxide (DMSO) for 13–15 min at room temperature. The AM ester was then washed out for at least 10 min with Ca-free Tyrode's solution that contained 0.1 mM K₂EGTA in place of 1.0 mM CaCl₂ of normal Tyrode's solution (Table 1, Extracellular solutions).

TABLE 1.

Composition of solutions

Extracellular solutions (mM)	NaCl	NaMs	KCl	KMs	NMDG-Cl	NMDG-Ms	MgCl2	MgMs2	K2EGTA	Na2EGTA	NaH2PO4	HEPES
Ca-free Tyrode's	135	0	5.4	0	0	0	1.0	0	0.1	0	0.33	10
Mg-loading	0	0	5.4	0	101	0	17.9	6.0	0.1	0	0.33	10
75 K-70 Na	3.5	66.2	5.4	65.3	0	0	1.0	0	0.1	0	0.33	10
0 K-70 Na	69.5	0	0	0	70.3	0	1.0	0	0	0.1	0.33	10
0 K-70 Na-0 Cl	0	69.5	0	0	0	70.3	0	1.0	0	0.1	0.33	10
0 K-0.5 Na	0	0	0	0	135	0	1.0	0	0	0.1	0.33	10
0 K-0.5 Na-0 Cl	0	0	0	0	0	135	0	1.0	0	0.1	0.33	10
Pipette solutions (mM)	KMs	CsMs	NaCl	CsCl	CaCl2	CaMs2	MgCl2	MgMs2	MOPS	[K+]	[Na+]	[Cl−]
135 K-10 Na	130	0	10	0	1.0	0	1.0	0	10	135	10	14
145 Cs	0	130	0	10	1.0	0	1.0	0	10	0	0	14
145 Cs-0 Cl	0	140	0	0	0	1.0	0	1.0	10	0	0	0

Ms, methanesulfonate; NMDG-Cl, N-methyl-D-glucamine titrated by HCl; NMDG-Ms, N-methyl-D-glucamine titrated by methanesulfonic acid. Extracellular solutions also contained 5 mM glucose in common. The pH of the extracellular solutions was adjusted to 7.40 by adding NaOH (Ca-free Tyrode's), NaOH plus HCl (Mg-loading), KOH (75 K-70 Na), HCl (0 K-70 Na and 0 K-0.5 Na) or HMs (0 K-70 Na-0 Cl and 0 K-0.5 Na-0 Cl). Final Na⁺ concentrations were 140 mM (Ca-free Tyrode's), 1.6 mM (Mg-loading), 70 mM (75 K-70 Na, 0 K-70 Na, and 0 K-70 Na-0 Cl) and 0.5 mM (0 K-0.5 Na and 0 K-0.5 Na-0 Cl). The pH of the pipette solutions was adjusted to 7.15 with either 5 mM KOH (135 K-10 Na) or 5 mM CsOH (145 Cs and 145 Cs-0 Cl). The three rightmost columns under Pipette solutions give the final concentrations of K⁺, Na⁺, and Cl⁻.

Experimental protocol and solutions

The extracellular solutions and pipette solutions used during the experimental measurements are listed in Table 1. All modifications of solution composition were made by isosmotic replacement of cations and/or anions to keep solution osmolality constant. For observation of Mg²⁺ efflux, the myocytes were first loaded with Mg²⁺ by incubation in a high-Mg²⁺ and low-Na⁺ solution (Mg-loading solution, Table 1, Extracellular solutions) that contained 24 mM Mg²⁺ and 1.6 mM Na⁺ for 3–5 h. After [Mg²⁺]_i was significantly elevated above 1.2 mM, Mg²⁺ efflux was induced by raising extracellular Na⁺ concentration ([Na⁺]_o) to 140 mM or 70 mM (Table 1, Extracellular solutions); the Mg²⁺-loaded myocyte was superfused with one of the solutions that contained 1 mM Mg²⁺ plus either 140 mM Na⁺ (Ca-free Tyrode's solution) or 70 mM Na⁺ (75 K-70 Na, 0 K-70 Na, and 0 K-70 Na-0 Cl solutions). As an index of the rate of Mg²⁺ efflux, we analyzed the initial rate of change in [Mg²⁺]_i (initial Δ[Mg²⁺]_i/Δt) estimated by linear regression of data points 60–240 s after solution exchange (see Figs. 4, 6, and 8, solid lines). Because the initial Δ[Mg²⁺]_i/Δt values depend strongly on [Mg²⁺]_i levels (4,7), comparison of the initial Δ[Mg²⁺]_i/Δt values was made at comparable initial [Mg²⁺]_i (defined as [Mg²⁺]_i at the first point of the fitted line).

FIGURE 4.

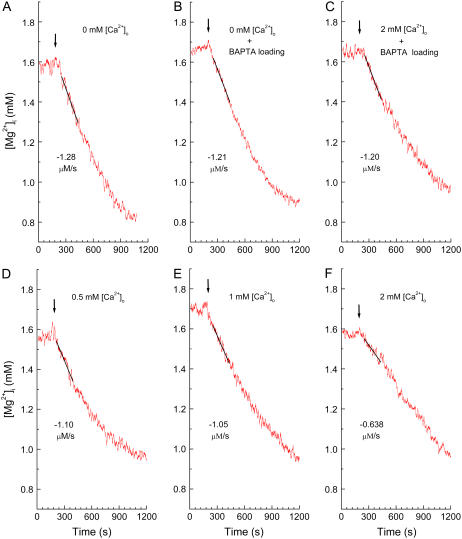
Effects of [Ca²⁺]_i and/or [Ca²⁺]_o on the initial Δ[Mg²⁺]_i/Δt in the Mg²⁺-loaded myocytes. (A–F) Records from six separate experiments in which the Mg²⁺ efflux was induced by addition of extracellular Na⁺ (140 mM) at various [Ca²⁺]_o with or without intracellular BAPTA loading. The cells were loaded with Mg²⁺ in the Mg-loading solution for 3 h with (B and C) or without (A, D–F) concomitant loading of BAPTA, and Tyrode's solution that contained 0–2 mM [Ca²⁺]_o (amounts indicated in the panels) was introduced at the times shown by arrows. In this and subsequent figures (Figs. 6 and 8), [Mg²⁺]_i traces have been smoothed with adjacent averaging of 51 data points (10 s) to reduce noise, whereas a solid line was drawn by the linear least-squares fit to unsmoothed data points for 180 s; the initial Δ[Mg²⁺]_i/Δt estimated from the slope is indicated (μM/s) near the trace. Cells 070904 (A), 070304 (B), 090304 (C), 072104 (D), 081404 (E), and 082704 (F).

FIGURE 6.

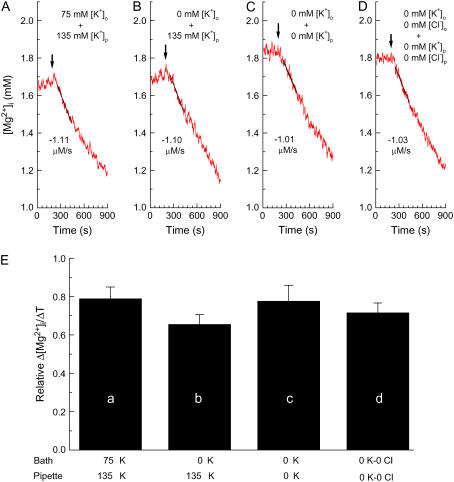
Effects of intracellular and extracellular concentrations of K⁺ and Cl⁻ on the initial Δ[Mg²⁺]_i/Δt. The cells had been loaded with Mg²⁺ in the Mg-loading solution for 3–5 h and were patch-clamped at the holding potential of −13 mV. (A–D) Records from four separate experiments in which the Mg²⁺ efflux was induced (at the times indicated by arrows) by 70 mM extracellular Na⁺ plus either 75 mM K⁺ or 0 mM K⁺. The pipette solution contained either 135 mM K⁺ or 0 mM K⁺. (D) Cl⁻ of the extracellular solution and the pipette solution was omitted by replacement with methanesulfonate. Combinations of [K⁺]_o, [K⁺]_p (pipette K⁺ concentration), [Cl⁻]_o (extracellular Cl⁻ concentration) and [Cl⁻]_p (pipette Cl⁻ concentration) are shown in the panels, and estimated values of the initial Δ[Mg²⁺]_i/Δt (the slopes of solid lines) are indicated (μM/s) near the traces. (A) Cell 021805, series resistance 15.2–14.9 MΩ (during initial Δ[Mg²⁺]_i/Δt measurement); (B) cell 022305, series resistance 18.9–18.6 MΩ; (C) cell 042205, series resistance 15.4–15.2 MΩ; (D) cell 060805, series resistance 11.9–11.6 MΩ. (E) Columns a–d summarize relative Δ[Mg²⁺]_i/Δt estimated from the type of experiments shown in A–D, respectively; combinations of the extracellular solution and the pipette solution are shown below each column. Columns show mean ± SE of 5–11 cells (see Table 2 for numbers of cells).

FIGURE 8.

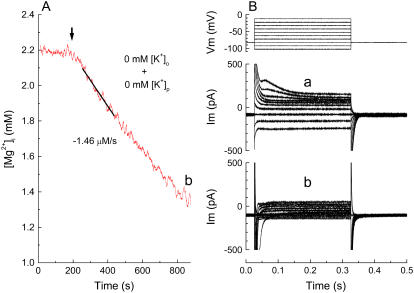
Measurements of initial Δ[Mg²⁺]_i/Δt and membrane currents from the same myocyte. (A) Mg²⁺ efflux induced after intracellular perfusion with the K⁺-free pipette solution (145 Cs solution, Table 1). The cells were loaded with Mg²⁺ in the Mg-loading solution, and patch-clamped with a pipette that contained 145 Cs solution. Extracellular Na⁺ (70 mM) was applied at the time indicated (arrow) in the absence of extracellular K⁺ (see text for details). The holding potential was −13 mV during the fluorescence measurement. (B) Membrane currents recorded shortly after initiation of intracellular perfusion in the Mg-loading solution (a) and just after the fluorescence measurement (shown in A) in the 0 K-70 Na solution (b). The holding potential was −83 mV and 300-ms pulses were applied in 10-mV increments as shown at the top. Cell 040105, cell capacitance 150 pF. Series resistance was 8.5–8.1 MΩ at the time of initial Δ[Mg²⁺]_i/Δt measurement. Similar results were obtained in two other myocytes.

Fluorescence measurements

The optical set-up for the fluorescence measurements from single cells has been described previously (7,16). Cells were illuminated with quasimonochromatic light beams (slit width 5 nm) of 350 nm and 382 nm alternately switched at 100 Hz, and intensity of emitted fluorescence at 500 nm (25 nm full width at half-maximum) was measured from the 150-μm diameter field of a 40× objective (Nikon). Fluorescence signals were low-pass filtered at 1.7 Hz and sampled at 5 Hz.

For each cell, the background fluorescence measured at each wavelength before furaptra loading was subtracted from the total fluorescence measured after furaptra loading to calculate indicator fluorescence intensity. For the patch-clamp experiments, the background fluorescence was not measured before indicator loading from the same cell. We therefore measured the background fluorescence from three to five myocytes with a size (length × width) similar to that used for the experiments, and subtracted the average value at each wavelength from the total fluorescence (3,7). The ratio (R) of the background-subtracted fluorescence intensity at 382 nm excitation, F(382), to that at 350 nm excitation, F(350), was used as the Mg²⁺-related signal (R = F(382)/F(350)).

During the 30-month period of this study, aging of the optical components (and also a renewal of the Xe arc lamp) caused changes in R even with otherwise identical conditions. To correct for the instrumental drift, we occasionally measured R in a Ca²⁺-Mg²⁺-free buffer solution (140 mM KCl, 10 mM NaCl, 1 mM EDTA, 1 mM EGTA, 0.05 mM furaptra, and 10 mM PIPES, pH 7.1) as the standard. All values of the measured R were normalized to the standard R value taken close in time, and the normalized R values were converted to [Mg²⁺]_i with the equation:

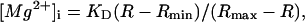(1)

where R_min and R_max are the normalized R values at zero [Mg²⁺]_i and saturating [Mg²⁺]_i, respectively, and K_D is the dissociation constant of furaptra for Mg²⁺. For these parameters, we used the values previously estimated in rat ventricular myocytes at 25°C: R_min = 0.969, R_max = 0.223, and K_D = 5.30 mM (17).

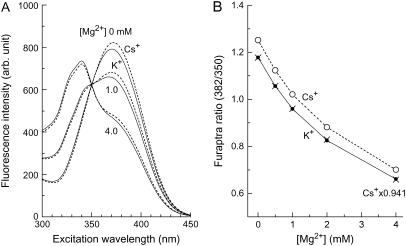
Because some of the experiments included intracellular perfusion with Cs⁺-based K⁺-free pipette solutions, we examined the effects of Cs⁺ on furaptra fluorescence (Fig. 1). As shown in Fig. 1 A, replacement of 135 mM K⁺ plus 10 mM Na⁺ with 145 mM Cs⁺ in the solutions caused changes in the excitation spectra of furaptra; an increase in fluorescence intensity was clearly observed at excitation wavelengths >360 nm, with little alteration in the isosbestic wavelength for Mg²⁺ (350 nm). The plots in Fig. 1 B show a clear displacement of the relation between [Mg²⁺] and furaptra R. When the furaptra R values obtained in the Cs⁺-based solutions are multiplied by 0.941, the scaled R values closely match those obtained in the K⁺-based solutions at any [Mg²⁺] levels between 0 and 4.0 mM. The results of the in vitro measurements suggest that a single scaling factor can be applied to correct for Cs⁺-induced changes in furaptra R at [Mg²⁺] <4.0 mM.

FIGURE 1.

In vitro measurements of furaptra fluorescence in the K⁺-based and Cs⁺-based solutions at 25°C. The solutions contain 135 mM KCl plus 10 mM NaCl (the K⁺-based solution) or 145 mM CsCl (the Cs⁺-based solution), 0.5 mM Na₂EGTA, 0–4.11 mM MgCl₂, 0.5 μM furaptra, and 10 mM MOPS (pH 7.15 by CsOH). Free Mg²⁺ concentration was determined by calculation with the apparent dissociation constant assumed for the Mg²⁺-EGTA reaction: 14.9 mM, at pH 7.15, ionic strength 0.16 M and 25°C (31). (A) Fluorescence excitation spectra measured at 500 ± 10 nm (central wavelength ± half-width) in a 1-cm quartz cuvette with a spectrofluorometer (JASCO, Tokyo, Japan). Solid lines and broken lines were obtained, respectively, in the K⁺-based solutions and the Cs⁺-based solutions, with free Mg²⁺ concentrations indicated near the curves. (B) Values of furaptra R (F(382)/F(350); ordinate) obtained from fluorescence excitation spectra of the type shown in A are plotted as a function of [Mg²⁺] (abscissa). Solid circles (connected with solid lines) and open circles (connected with broken lines) were obtained, respectively, in the K⁺-based solutions and the Cs⁺-based solutions. Points obtained by scaling open circles by a factor of 0.941 are also shown (x's).

Perforated patch clamp

The perforated patch-clamp technique was carried out as described previously (3,7) with the glass pipette filled with one of the pipette solutions containing 145 mM monovalent metal ions (K⁺ + Na⁺ + Cs⁺), 1 mM Ca²⁺, and 1 mM Mg²⁺ (Table 1, Pipette solutions) plus 600 μg/ml amphotericin B. Because a liquid junction potential of −12 to −14 mV was found between the Mg-loading solution and various pipette solutions (Table 1), we corrected all voltage data for a liquid junction potential of −13 mV. After Mg²⁺ loading of the myocytes containing furaptra (above), a GΩ-seal was formed in the Mg-loading solution (Table 1, Extracellular solutions). Voltage pulses of ±5 mV were delivered at 20 Hz from the holding potential, and cell membrane perforation was monitored as an increase in the capacitive currents by an Axopatch 200B amplifier and pCLAMP software (Axon Instruments, Foster City, CA). Current and voltage signals were low-pass-filtered at 5 KHz, and digitized at 20 KHz with a Digidata digitizer (Axon Instruments). As explained in Results, the holding potential was initially −83 mV, but was set at −13 mV when the series resistance approached 20 MΩ. Subsequent fluorescence measurements (below) were carried out with a holding potential of −13 mV. The mean series resistance during the period of analysis was 15.3 ± 0.8 MΩ (mean ± SE) and cell capacitance averaged 174 ± 5 pF in 31 myocytes. The voltage error, calculated as the holding current times series resistance, was at most 3 mV, and was considered insignificant in this study.

Cell shortening

In some experiments, changes in cell length were monitored with a CCD camera system (Aquacosmos, Hamamatsu Photonics, Shizuoka, Japan) with a 20× objective (Nikon). A 5-ms suprathreshold pulse delivered from a stimulator (Nihon Kohden, Tokyo, Japan) every 5 min was passed through a pair of platinum plate electrodes placed on both sides of the bath wall. From cell images taken at 18.6-ms intervals during the evoked twitch contraction, the maximum change in cell length was evaluated for each cell, and was expressed as the percent change relative to the resting length.

Chemicals

Amphotericin B was obtained from Sigma-Aldrich (St. Louis, MO). Furaptra (tetrapotassium salt of mag-fura-2), furaptra AM (mag-fura-2 AM), BAPTA AM, and 5,5′-dimethyl BAPTA AM were purchased from Invitrogen (Carlsbad, CA). Furaptra AM, BAPTA AM, and dimethyl BAPTA AM, were dissolved from their concentrated stock solutions in DMSO. The final concentration of the solvent was 0.1% during fluorescence measurements, which did not affect the [Mg²⁺]_i measurements.

Data analysis

Analysis of fluorescence data was carried out using Origin, Version 7.0 (OriginLab, Northampton, MA). Membrane currents were analyzed with pCLAMP (Clampex version 8.1.0.12, Axon Instruments). Results are expressed as mean ± SE for the indicated number of experiments, and statistical significance was determined at the P < 0.05 level using Student's two-tailed t-test (unpaired).

RESULTS

Intracellular loading of Ca⁺ chelators

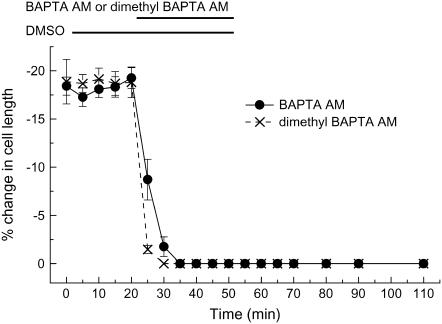
In the initial experiments, we studied the effects of intracellular loading of Ca²⁺ chelators on twitch contraction of the myocytes (Fig. 2). Electrically evoked twitch contraction was quickly abolished (within 15 min) after extracellular application of 5 μM BAPTA AM (but not by 0.1% DMSO). Diminution of twitch occurred even faster (within 10 min) with dimethyl BAPTA AM, which is consistent with dimethyl BAPTA having an affinity for Ca²⁺ four times higher than that of BAPTA. This inhibition by either chelator was not recovered by washout of the AM ester. The results suggest that either BAPTA AM or dimethyl BAPTA AM can be quickly loaded into the myocytes to the extent that the intracellular concentrations of the deesterified and trapped chelator are high enough to keep the intracellular Ca²⁺ concentration ([Ca²⁺]_i) low during normal excitation-contraction coupling.

FIGURE 2.

Effects of intracellular loading of Ca²⁺ chelators on cell shortening expressed as percent change in cell length (ordinate). Cells were superfused with normal Tyrode's solution that contained 1.0 mM Ca²⁺, and field stimulation evoked twitch contraction every 5 min. After the first twitch contraction was recorded at time zero, 0.1% DMSO and then 0.1% DMSO plus either 5 μM BAPTA AM (•) or 5 μM dimethyl BAPTA AM (x's) were added during the periods indicated by horizontal bars at the top. Symbols show mean ± SE of 11 (for BAPTA AM) or 12 cells (for dimethyl BAPTA AM).

To achieve heavy loading of the Ca²⁺ chelator, we applied BAPTA AM (or dimethyl BAPTA AM) for a prolonged time, including the 3-h period of Mg²⁺ loading. A typical protocol began with loading of furaptra AM for 13–15 min, followed by loading of 5 μM BAPTA AM (or dimethyl BAPTA AM) for 20 min in normal Tyrode's solution, and then a further 10 min in Ca-free Tyrode's solution. Subsequent Mg²⁺ loading was carried out in Mg-loading solution in the presence of 5 μM BAPTA AM (or dimethyl BAPTA AM) for 3 h. Because the Mg²⁺-loading solution contained no Ca²⁺ (Table 1, Extracellular solutions), it is expected that the gradual rise in the intracellular concentration of chelator would lower the [Ca²⁺]_i level below the normal value.

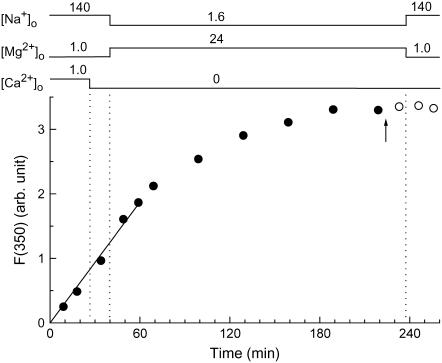
To estimate the intracellular chelator concentrations achieved after this prolonged AM loading (210 min), we used furaptra AM instead of BAPTA AM (or dimethyl BAPTA AM) and monitored furaptra fluorescence during a solution protocol very similar to that described above. Because Zhao et al. (18) reported that the AM-loading rates of the compounds were inversely related to their molecular weight (mol wt), the AM-loading rate of furaptra (mol wt) of furaptra AM, 723) may not be markedly different from those of BAPTA (mol wt of BAPTA AM, 765) and dimethyl BAPTA (mol wt of dimethyl BAPTA AM, 793). Fig. 3 shows an example of such experiments. The rise of F(350) of furaptra (thought to be primarily related to the intracellular concentration of furaptra) was approximately linear in the initial 60 min, and was slowed thereafter to reach a plateau at ∼180 min. In five myocytes, the final plateau level of the fluorescence was 7.9 ± 0.34 times greater than that after the initial 15 min. Under the assumption that BAPTA and dimethyl BAPTA are loaded with similar time courses to that shown here (Fig. 3) for furaptra, the final intracellular concentrations of the chelators may be ∼8 times greater than the levels required to buffer Ca²⁺ during excitation-contraction coupling (see above). The results shown in Fig. 3 also suggest that the chelators, once deesterified, are likely well retained inside the cell, as furaptra F(350) showed little decrease after washout of the AM ester (open circles).

FIGURE 3.

Furaptra fluorescence intensities at 350 nm excitation measured from a single myocyte during and after exposure (solid and open circles, respectively) to 5 μM furaptra AM plus 0.1% DMSO. The arrow indicates the time at which furaptra AM was washed out. [Na⁺]_o, [Mg²⁺]_o, and [Ca²⁺]_o were changed as indicated on top at the times shown by vertical dotted lines. After an initial incubation of the cell in normal Tyrode's solution and the following brief incubation in the Ca-free Tyrode's solution, the bathing solution was changed to the Mg-loading solution that contained 24 mM Mg²⁺ and 1.6 mM Na⁺ for ∼200 min, and then Ca-free Tyrode's solution was reintroduced. A solid line was drawn by linear regression to data points for the initial 60 min, and had a slope of 0.0312/min. Cell 091504-2.

Effects of intracellular and extracellular Ca²⁺ on the Mg²⁺ efflux

The initial Δ[Mg²⁺]_i/Δt was estimated in the myocytes heavily loaded with BAPTA for 210 min. After the myocytes were loaded with Mg²⁺ and BAPTA with the solution protocol described above (Fig. 3) and were superfused with Mg-loading solution in the absence of BAPTA AM for 10 min, Ca-free Tyrode's solution that contained 140 mM Na⁺ and 1 mM Mg²⁺ (Table 1, Extracellular solutions) was introduced to induce Mg²⁺ efflux (Fig. 4). In the myocytes loaded with either BAPTA (Fig. 4 B) or dimethyl BAPTA (not shown), [Mg²⁺]_i rapidly decreased with a rate similar to that observed in the myocytes without chelator loading (Fig. 4 A).

We also examined the effects of extracellular Ca²⁺ concentration ([Ca²⁺]_o) on the initial Δ[Mg²⁺]_i/Δt. The Mg²⁺ efflux was induced in Tyrode's solution containing various [Ca²⁺]_o: 0.5 mM (Fig. 4 D), 1.0 mM (Fig. 4 E), and 2.0 mM (Fig. 4 F). The initial Δ[Mg²⁺]_i/Δt was not markedly different at [Ca²⁺]_o between 0 mM and 1.0 mM (Fig. 4, A, D, and E), but was somewhat reduced at 2 mM [Ca²⁺]_o (Fig. 4 F). However, this reduction of the initial Δ[Mg²⁺]_i/Δt by 2 mM [Ca²⁺]_o was not observed in the myocytes that had been heavily preloaded with BAPTA for 210 min (Fig. 4 C). Table 2 summarizes the initial Δ[Mg²⁺]_i/Δt values obtained at comparable initial [Mg²⁺]_i in various experimental conditions. A comparison of these values is described below.

TABLE 2.

Summary of the initial rate of decrease in [Mg²⁺]_i at 25°C

Experimental conditions	Initial [Mg2+]i	Initial Δ[Mg2+]i/Δt	n
	(mM)	(μM/s)
140 mM [Na+]o
Chelator loading/[Ca2+]o*
–/0 mM	1.50 ± 0.060	−1.16 ± 0.049	8
BAPTA/0 mM	1.46 ± 0.054	−1.32 ± 0.109	7
Dimethyl BAPTA/0 mM	1.49 ± 0.072	−1.26 ± 0.146	4
–/0.5 mM	1.48 ± 0.065	−1.09 ± 0.106	5
–/1.0 mM	1.47 ± 0.050	−1.24 ± 0.098	5
–/2.0 mM	1.47 ± 0.063	−0.75 ± 0.123	5
BAPTA/2.0 mM	1.53 ± 0.047	−1.27 ± 0.115	6
70 mM [Na+]o
[K+]p/[K+]o†
135 mM/75 mM	1.57 ± 0.094	−0.98 ± 0.057	8
135 mM/0 mM	1.57 ± 0.053	−0.85 ± 0.068	11
0 mM/0 mM	1.54 ± 0.081	−0.99 ± 0.117	7
[K+]p-[Cl−]p/[K+]o-[Cl−]o‡
0 mM-0 mM/0 mM-0 mM	1.78 ± 0.048	−1.03 ± 0.075	5

Columns contain mean ± SE values of initial [Mg²⁺]_i (second column) and initial Δ[Mg²⁺]_i/Δt (third column) from n cells (rightmost column) in each experimental condition (leftmost column). For the statistics, we included data only from the cells that were moderately loaded with Mg²⁺ (i.e., initial [Mg²⁺]_i between 1.2 mM and 2.0 mM).

^*Initial Δ[Mg²⁺]_i/Δt values at 140 mM [Na⁺]_o and 5.6 mM [K⁺]_o (cf. Figs. 4 and 5) measured with or without intracellular loading of the Ca²⁺ chelator at indicated [Ca²⁺]_o.

^†Cells were patch-clamped at the holding potential of −13 mV. Initial Δ[Mg²⁺]_i/Δt values were estimated at 70 mM [Na⁺]_o without intracellular chelator loading and in the essential absence of extracellular Ca²⁺ (cf. Fig. 6). [K⁺]_p/[K⁺]_o, combination of K⁺ concentration in the pipette solution ([K⁺]_p) and in the extracellular solution. 135 mM/75 mM, 135 K-10 Na pipette solution and 75 K-70 Na extracellular solution. 135 mM/0 mM, 135 K-10 Na pipette solution and 0 K-70 Na extracellular solution. 0 mM/0 mM, 145 Cs pipette solution and 0 K-70 Na extracellular solution.

^‡Experimental conditions were identical to those described in previous footnote, except that the extracellular solution (0 K-70 Na-0 Cl) and the pipette solution (145 Cs-0 Cl solution) did not contain Cl⁻. [Cl⁻]_p and [Cl⁻]_o, Cl⁻ concentrations in the pipette solution and in the extracellular solution, respectively.

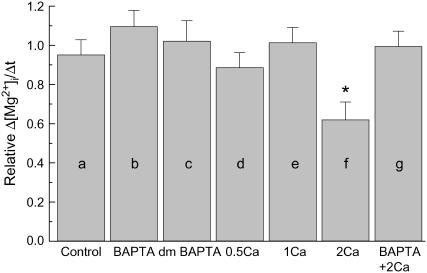
Because the initial Δ[Mg²⁺]_i/Δt value strongly depends on the initial [Mg²⁺]_i level, comparisons of the initial Δ[Mg²⁺]_i/Δt values must be adjusted for variations in the initial [Mg²⁺]_i (4). For a more precise comparison, we therefore utilized the standard relation between the initial Δ[Mg²⁺]_i/Δt and the initial [Mg²⁺]_i constructed previously (solid curve in Fig. 2 of Tursun et al. (4)); any value of the initial Δ[Mg²⁺]_i/Δt was normalized to the standard value on the curve at a given initial [Mg²⁺]_i to calculate relative values of the initial Δ[Mg²⁺]_i/Δt (relative Δ[Mg²⁺]_i/Δt). Relative Δ[Mg²⁺]_i/Δt values thus obtained in various combinations of intracellular chelator loading and [Ca²⁺]_o are summarized in Fig. 5. Neither lowering [Ca²⁺]_i by addition of Ca²⁺ buffers nor elevation of [Ca²⁺]_o up to 1 mM significantly influenced the relative Δ[Mg²⁺]_i/Δt, with average values being close to unity. Raising [Ca²⁺]_o to 2 mM significantly reduced the relative Δ[Mg²⁺]_i/Δt, but this effect was reversed by intracellular loading of BAPTA, suggesting that the intracellular Ca²⁺ overload, rather than 2 mM [Ca²⁺]_o itself, caused the reduction of the relative Δ[Mg²⁺]_i/Δt.

FIGURE 5.

Summary of the initial Δ[Mg²⁺]_i/Δt estimated from the type of experiments shown in Fig. 4. All values of the initial Δ[Mg²⁺]_i/Δt were normalized to those expected for the initial [Mg²⁺]_i to calculate relative Δ[Mg²⁺]_i/Δt (see text for details). Columns a–g show mean ± SE of 4–8 cells (see Table 2 for the number of cells). (a) The initial Δ[Mg²⁺]_i/Δt was estimated without intracellular chelator loading and in the essential absence of extracellular Ca²⁺. (b–c) Cells were loaded with BAPTA (b) or dimethyl BAPTA (c), and the initial Δ[Mg²⁺]_i/Δt was estimated in the essential absence of extracellular Ca²⁺. (d–f) the initial Δ[Mg²⁺]_i/Δt was estimated at 0.5 mM (d), 1.0 mM (e), or 2.0 mM [Ca²⁺]_o (f) without intracellular loading of the chelator. (g) Cells were loaded with BAPTA, and initial Δ[Mg²⁺]_i/Δt was estimated at 2.0 mM [Ca²⁺]_o. *Significantly different from 1.0 (0.01 ≤ P < 0.05).

Effects of intracellular and extracellular K⁺ on the Mg²⁺ efflux

To explore the possibility that the Na⁺/Mg²⁺ exchange involves transport of other ions rather than a simple exchange of Na⁺ and Mg²⁺ (e.g., 2 Na⁺ + 2 K⁺ + 2 Cl⁻ for 1 Mg²⁺ exchange proposed in squid giant axons by Rasgado-Flores et al. (11)), we analyzed the Mg²⁺ efflux in the presence of various extracellular and intracellular concentrations of K⁺ and Cl⁻. To raise the extracellular K⁺ concentration ([K⁺]_o) to 75 mM, [Na⁺]_o was lowered to 70 mM to maintain osmolality of the solution (75 K-70 Na, Table 1, Extracellular solutions). For this reason, the Mg²⁺ efflux was observed in all the extracellular solutions that contained 70 mM Na⁺ (75 K-70 Na, 0 K-70 Na, and 0 K-70 Na-0 Cl, Table 1, Extracellular solutions) throughout this series of experiments. We previously reported that a large depolarization of membrane potential from −80 mV to 0 mV causes a slight but significant facilitation of the Mg²⁺ efflux (7). To minimize any effect of membrane potential change caused by varying [K⁺]_o, we set the membrane potential of the myocytes at −13 mV with the amphotericin-B-perforated patch clamp. The relatively depolarized holding potential of −13 mV was chosen because at high [K⁺]_o (75 mM) and normal [K⁺]_i (135 mM), a large holding current is required with more polarized membrane potentials to cancel the inward rectifier K⁺ current (I_K1), which causes greater voltage error across series resistance. Intracellular perfusion through the patch electrodes was also used to alter [K⁺]_i and [Cl⁻]_i, as amphotericin-B-treated cell membrane is permeable to small monovalent cations and anions (19).

With K⁺ concentration in the pipette ([K⁺]_p) at 135 mM, superfusion of the solution containing 70 mM Na⁺ induced Mg²⁺ efflux in the presence (Fig. 6 A) or absence (Fig. 6 B) of 75 mM K⁺. The initial Δ[Mg²⁺]_i/Δt value was not markedly different at [K⁺]_o between 0 and 75 mM (Table 2). The relative Δ[Mg²⁺]_i/Δt value calculated as described above was, on average, slightly greater, by 20%, at 75 mM [K⁺]_o than that at 0 mM [K⁺]_o, but the difference was not statistically significant (Fig. 6 E, a and b).

Although extracellular K⁺ did not appear to be essential for the Mg²⁺ efflux, it still may be possible that intracellular K⁺ could leak out of the cell and raise the [K⁺]_o of the diffusion-restricted space (e.g., transverse tubules) to a level high enough to activate the exchange, as proposed by Rasgado-Flores and Gonzalez-Serratos (12). To test this possibility, the myocytes were internally perfused with the K⁺-free pipette solution (145 Cs, Table 1, Pipette solutions). Intracellular K⁺ depletion was further facilitated by removal of extracellular K⁺ (0 K-0.5 Na, Table 1, Extracellular solutions).

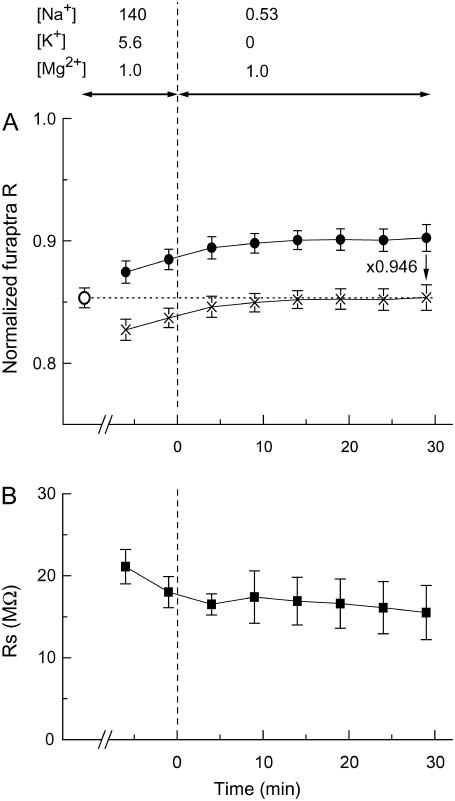
Fig. 7 shows the results of pilot experiments in which fluorescence R of furaptra was measured during the procedure for intracellular K⁺ depletion. After the initial measurement of R from myocytes superfused with Ca-free Tyrode's solution (open circle in Fig. 7 A), a GΩ-seal was formed and internal perfusion of the 145 Cs solution from the patch pipette was initiated. After perforation of the cell membrane, furaptra R gradually rose to higher levels (Fig. 7 A, solid circles). Superfusion of K⁺-free and low-Na⁺ solution (0 K-0.5 Na, Table 1, Extracellular solutions) further increased furaptra R and the quasisteady level was reached in 20 min after exchange of the bathing solution. Because [Mg²⁺]_i is tightly regulated and is generally very stable in resting myocytes (15), we presumed that the increase in furaptra R reflected replacement of intracellular K⁺ with Cs⁺, as found in vitro (Fig. 1), rather than changes in [Mg²⁺]_i. At the end of 30 min superfusion with 0 K-0.5 Na solution, the series resistance dropped to 15.5 ± 3.3 MΩ (Fig. 7 B) in five myocytes, with the average cell capacitance of 186 ± 11 pF. The scaling factor for furaptra R (Fig. 7 A, x's) was, on average, 0.946 to match the mean value obtained before internal perfusion (open circle). Thus, similar scaling factors for K⁺ replacement with Cs⁺ were obtained in the solutions (0.941, Fig. 1) and in the myocytes (0.946). A slight residual difference could be due to the following: 1), incomplete replacement of intracellular K⁺ by Cs⁺; 2), small fluctuation of resting [Mg²⁺]_i, or 3), different interference of Cs⁺ with furaptra R in the myocytes and in the solutions. In any event, the results shown in Fig. 7 strongly suggest that this procedure, which involves internal perfusion through a series resistance of ∼15 MΩ (Fig. 7 B), effectively depletes most, if not all, of the intracellular K⁺.

FIGURE 7.

Changes in normalized furaptra R (A) and series resistance (B) measured in the cells internally perfused with the pipette solution containing 145 mM [Cs⁺] and 0 mM [K⁺] (145 Cs solution, Table 1) through the cell membrane permeabilized with amphotericin B. The indicator-loaded cells were incubated in the Ca-free Tyrode's solution, and a GΩ-seal was formed with the pipette containing amphotericin B. When series resistance dropped and approached 20 MΩ in 10–30 min, the bathing solution was changed from the Ca-free Tyrode's solution to the 0 K-0.5 Na solution (at time zero on the abscissa) as indicated at the top. In A and B, values of normalized furaptra R measured before (○) and after (•) GΩ-seal formation (A) and series resistance values (B, ▪) are plotted as a function of time after extracellular perfusion with the 0 K-0.5 Na solution. The holding potential was initially −83 mV and was set at −13 mV throughout the measurement run. Points obtained by scaling solid circles by a factor of 0.946 are also shown in A (x's). Each symbol represents the mean ± SE from five cells.

The Mg²⁺-loaded myocyte was patch-clamped with the pipette containing 145 Cs solution (Table 1, Pipette solutions) in the Mg-loading solution (Table 1, Extracellular solutions). After the series resistance dropped below 25 MΩ, the 0 K-0.5 Na solution (Table 1, Extracellular solutions) was superfused for 30 min to allow nearly complete exchange between K⁺ and Cs⁺ in the myocyte, as described in the previous paragraph. For the following [Mg²⁺]_i measurements, the interference by Cs⁺ was corrected by multiplying measured values of furaptra R by 0.946 (an average scaling factor in the myocytes; see above) before Eq. 1 was applied. When the superfusate was switched to the 0 K-70 Na solution that contained 0 mM K⁺ and 70 mM Na⁺ (Table 1, Extracellular solutions), [Mg²⁺]_i quickly decreased (Fig. 8 A), as was observed with the pipette solution that contained 135 mM K⁺. When the membrane currents were recorded at the early part of the internal perfusion (Fig. 8 B a), an outward hump was clearly observed upon depolarization from −83 mV to −13 mV, which probably reflected the transient outward K⁺ current (I_to). At the end of the pulses, the steady-state currents were rectified inwardly, as expected for I_K1. These currents (both outward and inward) were abolished after extensive internal perfusion with the K⁺-free pipette solution (145 Cs, Table 1, Pipette solutions) combined with superfusion by the K⁺-free extracellular solution (0 K-70 Na, Table 1, Extracellular solutions), leaving small residual background currents seen at the end of the pulses (Fig. 8 B b). (Note: in Fig. 8 B b, the very fast and large (overscaled) inward current seen immediately after depolarization is probably the Na⁺ current, as the extracellular solution contained 70 mM Na⁺. No such current is evident in Fig. 8 B a, obtained in the Mg-loading solution which contained only 1.6 mM Na⁺ (Table 1, Extracellular solutions).) Thus, the combination of intracellular K⁺ depletion and extracellular K⁺ removal appears to greatly suppress K⁺ currents. Overall, the results strongly suggest that Mg²⁺ can be extruded from the cells even in the absence of extracellular K⁺ and K⁺ flux through channels.

The Δ[Mg²⁺]_i/Δt values, when compared at similar initial [Mg²⁺]_i levels, were not markedly different without or with intracellular K⁺ depletion (Fig. 6, B and C, respectively; also see Table 2). The average relative Δ[Mg²⁺]_i/Δt value was 18% greater after intracellular K⁺ depletion, but the difference was not statistically significant (Fig. 6 E, b and c). The mean series resistance during the period of analysis was 12.8 ± 1.2 MΩ in seven myocytes (cell capacitance 178 ± 9 pF).

Effects of intracellular and extracellular Cl⁻ on Mg²⁺ efflux

The involvement of Cl⁻ in Mg²⁺ efflux was further examined using the same protocol as described in the previous section for removal of K⁺, except for the use of a Cl⁻-free pipette solution (145 Cs-0 Cl) and Cl⁻-free extracellular solutions (0 K-0.5 Na-0 Cl and 0 K-70 Na-0 Cl). The myocyte was internally perfused with the K⁺-free and Cl⁻-free pipette solution (145 Cs-0 Cl), and was superfused with the K⁺-free, low-Na⁺, and Cl⁻-free solution (0 K-0.5 Na-0 Cl) for 30 min. The K⁺-free and Cl⁻-free extracellular solution that contained 70 mM Na⁺ (0 K-70 Na-0 Cl) was then applied to induce Mg²⁺ efflux. Furaptra R was multiplied by 0.946 to correct for the Cs⁺ interference (above). The decrease in [Mg²⁺]_i was clearly observed (Fig. 6 D and Table 2), and the average relative Δ[Mg²⁺]_i/Δt value was comparable to that obtained in the extracellular and intracellular presence of Cl⁻ (Fig. 6 E, c and d). The mean series resistance during the period of analysis was 11.4 ± 0.9 MΩ in five myocytes (cell capacitance 166 ± 9 pF). Table 2 summarizes the initial Δ[Mg²⁺]_i/Δt values obtained at comparable initial [Mg²⁺]_i with various combinations of K⁺ and Cl⁻ concentrations in the pipette solution and in the extracellular solution.

DISCUSSION

Changes in cellular total Mg concentration, a direct measure of Mg²⁺ flux across the cell membrane, cannot be determined experimentally in voltage-clamped cardiac myocytes. In this study, we analyzed the initial rate of decrease in [Mg²⁺]_i (initial Δ[Mg²⁺]_i/Δt) as an index of the Mg²⁺ efflux rate (3,4). Comparison of the initial Δ[Mg²⁺]_i/Δt values obtained at a similar initial [Mg²⁺]_i should provide valid information on the relative changes in total Mg concentration, unless intracellular buffering and/or sequestration of Mg²⁺ are substantially altered (3). Our previous studies have suggested that changes in [Na⁺]_i and [K⁺]_i are unlikely to significantly alter cytoplasmic Mg²⁺ buffering power and [Mg²⁺] in the intracellular organelles (3,4). Interpretation of the initial Δ[Mg²⁺]_i/Δt in terms of Mg²⁺ flux, however, could be complicated by the elevation of resting [Ca²⁺]_i to higher levels (see below).

Effects of intracellular and extracellular concentrations of Ca²⁺

Tashiro et al. (9) reported that overexpression of the Na⁺/Ca²⁺ exchanger (NCX1) in CCL39 fibroblasts results in the appearance of Na⁺-dependent changes in [Mg²⁺]_i, in addition to the expected Na⁺-dependent changes in [Ca²⁺]_i. The results suggested that NCX1 could carry Mg²⁺, at least under some experimental conditions, and raised the possibility that the Na⁺-dependent Mg²⁺ efflux observed in rat ventricular myocytes (15,20) might be carried by NCX1, which is highly expressed in cardiac myocytes. In a later study (10), however, quantitative comparison of the Mg²⁺ transport rates in cardiac myocytes and NCX1-transfected CCL39 cells revealed that the rate of the Na⁺-dependent Mg²⁺ transport found in rat ventricular myocytes was too high (by a factor of 17) to be attributed only to NCX1.

To further evaluate the hypothesis that the Na⁺-dependent Mg²⁺ transporter is distinct from the Na⁺/Ca²⁺ exchanger (10), we examined the effect of intracellular and extracellular Ca²⁺ on the Na⁺-dependent Mg²⁺ efflux in rat ventricular myocytes in this study. Pharmacological inhibitors of the Na⁺/Ca²⁺ exchanger were not used in this study, because most of the known inhibitors are neither potent nor selective; they inhibit other ion transport systems and channels at even lower concentrations than those required to inhibit the Na⁺/Ca²⁺ exchanger (for review, see Bers (21)). It has been established that a certain level of [Ca²⁺]_i is required for the Na⁺/Ca²⁺ exchange activities in both directions (i.e., Ca²⁺ influx and Ca²⁺ efflux). With K_m of this allosteric regulation by Ca²⁺ being near or below the resting [Ca²⁺]_i (22 nM (22); 125 nM (23)), lowering [Ca²⁺]_i to below the resting level (∼100 nM) should inhibit turnover of the Na⁺/Ca²⁺ exchanger. In this study, we superfused the cells with Ca²⁺-free (0.1 mM EGTA) solution and loaded the cells with a large amount of the Ca²⁺ chelator (either BAPTA or dimethyl BAPTA).

The final intracellular concentration of the chelator reached after prolonged incubation with its AM ester could not be directly determined, but it was probably many times greater than that required to buffer Ca²⁺ during normal excitation-contraction coupling, as suggested by the experiments with furaptra (Figs. 2 and 3). Note that the furaptra fluorescence intensity reached after prolonged AM-loading for 210 min was, on average, 7.9 times greater than that at the initial 15 min. Under the assumption that the initial loading rate of furaptra (cf. Fig. 3, solid line) was ∼16 μM/min at 25°C, as previously estimated by Tursun et al. (4), the furaptra concentration at the end of the loading was calculated to be 1.90 ± 0.08 mM (n = 5). Zhao et al. (18) reported that in frog skeletal muscle the AM-loading rates of many indicators depend strongly on their molecular weight; the rate increased steeply as molecular weight decreased below ∼850. From a regression line for the loading rates for furaptra AM (723 mol wt), mag-indo-1 AM (731 mol wt), mag-fura-5 AM (737 mol wt), mag-fura-red AM (810 mol wt), and quin-2 AM (830 mol wt) proposed by Zhao et al. (18; see their Table 2), the loading rates for BAPTA AM (765 mol wt) and dimethyl BAPTA AM (793 mol wt) are estimated to be 80% and 54% of that of furaptra, respectively. Consequently, the final concentrations of intracellular BAPTA and dimethyl BAPTA are estimated to be 1.5 mM (1.90 mM × 0.8) and 1.0 mM (1.90 mM × 0.54), respectively. The high-affinity Ca²⁺ chelator of millimolar concentrations (and removal of extracellular Ca²⁺) should substantially lower [Ca²⁺]_i from 100 nM to much lower levels. Failure of strong Ca²⁺ buffering in reduction of the initial Δ[Mg²⁺]_i/Δt indicates that Mg²⁺ can be transported even under the greatly reduced turnover of the Na⁺/Ca²⁺ exchanger.

Extracellular Ca²⁺ and Na⁺ compete for the external binding site of the Na⁺/Ca²⁺ exchanger with K_m of 1.2 mM for [Ca²⁺]_o (24). The absence of any effect of [Ca²⁺]_o up to 1 mM on the rate of Mg²⁺ efflux also makes it unlikely that a large amount of Mg²⁺ is carried by the Na⁺/Ca²⁺ exchanger, at least in the experimental conditions employed in this study. By raising [Ca²⁺]_o to 2 mM without intracellular loading of the Ca²⁺ chelator, the rate of Mg²⁺ efflux was reduced, on average, by ∼40% probably due to intracellular Ca²⁺ overloading (Figs. 4 F and 5). The apparent decrease in the Δ[Mg²⁺]_i/Δt could be attributed to the allosteric inhibition of the Mg²⁺ transporter by intracellular Ca²⁺, but also could be due to interference of Ca²⁺-related changes of furaptra fluorescence with [Mg²⁺]_i measurements (14). It is also expected that the rise of [Ca²⁺]_i should release Mg²⁺ from cytoplasmic sites that bind both Ca²⁺ and Mg²⁺ (4,25), as well as from intracellular organelles that sequester Mg²⁺, as reported for mitochondria (26). Further experiments are required to determine whether the apparent reduction of the initial Δ[Mg²⁺]_i/Δt truly reflects a decrease in the rate of Mg²⁺ efflux. Overall, our results provide evidence against a large contribution of the Na⁺/Ca²⁺ exchanger (NCX1) to the Na⁺-dependent Mg²⁺ efflux in rat ventricular myocytes.

Effects of intracellular and extracellular concentrations of K⁺ and Cl⁻

Rasgado-Flores et al. (11) reported that intracellular K⁺ and Cl⁻ were essential for extracellular Mg²⁺-dependent Na⁺ efflux in squid giant axons. Based on their results, they proposed the existence of a transporter which carries Mg²⁺ in exchange with Na⁺, K⁺, and Cl⁻. The putative Na⁺-K⁺-Cl⁻/Mg²⁺ exchanger could reverse the direction of the transport to support both Mg²⁺ influx and efflux (12).

In our initial experiments, we simply changed [K⁺]_o between 0 mM and 75 mM to test whether altered K⁺ influx would influence Mg²⁺ efflux. Under voltage-clamp at −13 mV, the average value of relative Δ[Mg²⁺]_i/Δt was slightly greater (by 20%) at high [K⁺]_o (75 mM) than in the absence of extracellular K⁺, but the difference was not statistically significant. The finding presented here may be compared with our previously published results. Tashiro and Konishi (15) loaded rat ventricular myocytes with Mg²⁺ using ionomycin, and reported that the decrease in [Mg²⁺]_i from the Mg²⁺-loaded cells was significantly faster at 56 mM [K⁺]_o than at 6 mM [K⁺]_o, by ∼35% (see their Fig. 7 B). This apparently faster extrusion of Mg²⁺ at high [K⁺]_o observed without control of membrane potential is very likely attributed to cell membrane depolarization by high [K⁺]_o; in voltage-clamped myocytes, a significant increase in the rate of Mg²⁺ efflux (by ∼40%) is associated with depolarization from −80 mV to 0 mV (7). Thus, the effect of extracellular K⁺ on the Mg²⁺ efflux, if any, appears to be minor.

The observation that removal of extracellular K⁺ little influences the Mg²⁺ efflux may not completely eliminate the possibility that intracellular K⁺ leaks out of the cell and activates the Mg²⁺ transporter from the external surface of the membrane (12). However, we internally perfused the myocyte with the K⁺-free pipette solution, in addition to removal of extracellular K⁺, and found that the Mg²⁺ efflux of the fast rate was still present, even when intracellular K⁺ was largely replaced with Cs⁺ (as judged from changes in furaptra R (Fig. 7)) and K⁺ flux across the cell membrane was minimal (as judged from membrane currents (Fig. 8)). The results reported here are inconsistent with the essential role of extracellular K⁺ to activate Mg²⁺ efflux, unless Cs⁺ can substitute for K⁺ to activate the transport (i.e., activation of the transport by Cs⁺ that leaked out of the cell). The possibility that Cs⁺ acts in place of K⁺ is unlikely, however, because 1), no Cs⁺ leakage flux is evident in membrane current recordings (Fig. 8), and 2), Cs⁺ is generally a poor substrate of K⁺ for many known K⁺ transporters, such as Na⁺-K⁺-Cl⁻ cotransporter (27), K⁺-Cl⁻ cotransporter (28), Na⁺/Ca²⁺-K⁺ exchanger (29) and Na⁺/K⁺ pump (30). It is thus unlikely that the Na⁺-K⁺-Cl⁻/Mg²⁺ exchanger proposed in squid axons is primarily responsible for the Na⁺-dependent Mg²⁺ extrusion in rat ventricular myocytes.

Na⁺/Mg²⁺ exchange in cardiac myocytes

The effects of intracellular and extracellular concentrations of Na⁺, Mg²⁺, Ca²⁺, K⁺, and Cl⁻ have been reported previously (3,4) as well as in this study. Among these ion species, the Mg²⁺ efflux appears to require only intracellular Mg²⁺ (4) and extracellular Na⁺ (3) for its activity, whereas clear inhibition of the Mg²⁺ transport is associated only with extracellular Mg²⁺ (4) and intracellular Na⁺ (3). These results do not support complex exchange stoichiometries that involve ion species other than Na⁺ and Mg²⁺ in mammalian cardiac myocytes. The simple Na⁺/Mg²⁺ exchanger appears to be functionally distinct from other known transporters expressed in cardiac myocytes. Further studies are needed to determine the exchange stoichiometry of Na⁺ and Mg²⁺.