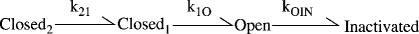Quantitative Analysis of a Fully Generalized Four-State Kinetic Scheme

Abstract

To describe the macroscopic behavior of many ion channels, at a minimum a four-state kinetic scheme is needed to provide for three processes: a delay in activation development, the activation process, and inactivation. I present here an analytical solution for a fully generalized four-state kinetic scheme in which every state can transit to every other state and any initial conditions can be specified. The solution describes the time courses of the probabilities of occupancy of each state during a step change in the rate constants of the scheme and includes closed-form expressions for the relaxation time constants and steady-state probabilities of occupancy as functions of the rate constants. Solutions for several relevant special cases are also included along with demonstrations that the general solution yields the correct behavior for several reduced or special cases where the result is independently known.

INTRODUCTION

Kinetic models are often used to simulate the behavior of both ligand and voltage-gated ion channels. A solution for a two-state kinetic scheme as applied to ion channels was presented in the classic analysis of Hodgkin and Huxley (1). Solutions for fully generalized (i.e., six-rate-constant) three-state schemes have also been presented (e.g., 2). However, to describe the macroscopic behavior of many Na, Ca, and K channels a minimum of four states, or the equivalent produced by some arrangement of subunits, is needed, providing then for three processes: a delay in activation development, an activation process, and inactivation.

A solution for a four-state scheme of sufficient complexity to account for the experimental behavior of ion channels (for example, including inactivation from closed states (3)) does not seem to have been presented. Analytical solutions for four, or any number of states, have been provided (4), but only for the special case that just forward transitions are allowed (i.e., the left-most state can only transit to the second from the left, which can only transit to the third from the left, etc.). This family of solutions is further restricted to the single fixed initial condition that only the left-most state is occupied at time (t) = 0. This special case appropriately described the physical situation being analyzed, sequential irreversible ligand binding, but is not sufficient to simulate the range of behaviors of gated ion channels. A useful analysis showing how to extract values for the rate constants from single channel lifetime distributions for certain four- and even five- and six-state schemes has been provided (5), but this analysis does not yield the full array of information pursued here, and moreover is also restricted to certain special cases.

I present here an analytical solution for a general four-state kinetic scheme. The solution is fully generalized in that every state can transit to every other state, and any initial conditions are allowed. Solutions for several special or reduced cases of interest for gated ion channels are, then, readily obtained from the general solution. All solutions are for the condition that the values of one or more rate constants change instantaneously to a new value at t = 0 owing, for example, to a step change in membrane potential or a sudden change in ligand concentration. The time courses of the probabilities of occupancy of each of the four states during the step are specified, and closed-form explicit expressions for each of the three relaxation time constants as functions of the rate constants of the scheme are presented.

RESULTS AND DISCUSSION

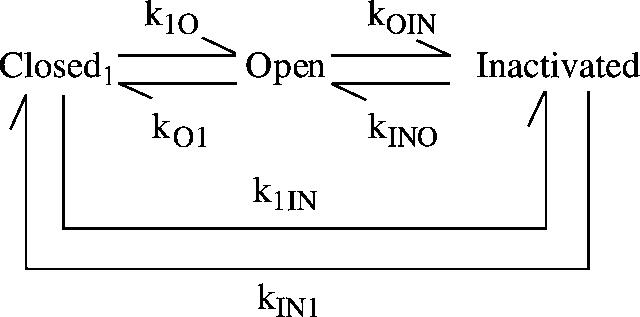
A fully generalized four-state scheme

Scheme 1

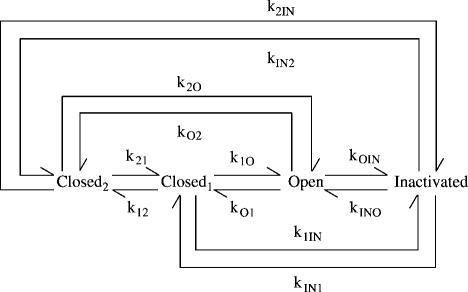
The generalized scheme is presented in Scheme 1. The states are named to emphasize the application of this scheme to voltage-gated ion channels. However, nothing in this analysis specifies the functional nature of any state or restricts the treatment to ion channels.

Figure .

Scheme 1 is described by the four coupled first-order differential equations,

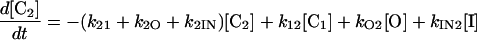(1)

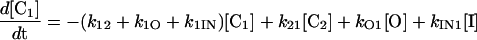(2)

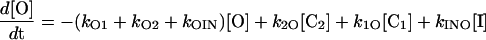(3)

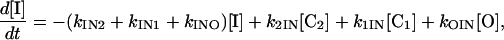(4)

where [C₂], [C₁], [O], and [I] are the concentrations or membrane densities of states closed₂, closed₁, open, and inactivated, respectively. The densities of all the states sum to a constant, N, i.e.,

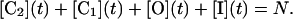(5)

Because of Eq. 5, one of the variables and one of the Eqs. 1–4 is redundant. Eliminating [C₂] and dividing through by N, we have

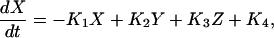(6)

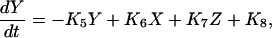(7)

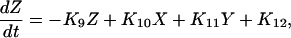(8)

where X, Y, and Z are the probabilities of occupancy of states closed₁, open, and inactivated, respectively. The probability of occupancy of closed₂ is W. The K_i terms are given by

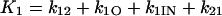(9)

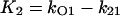(10)

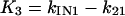(11)

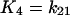(12)

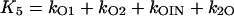(13)

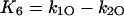(14)

(15)

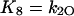(16)

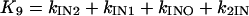(17)

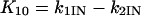(18)

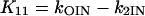(19)

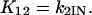(20)

Equations 6–8 may be combined into a single third-order differential equation in either X, Y, or Z. Choosing the probability of occupancy of the open, conducting state

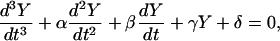(21)

where

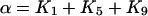(22)

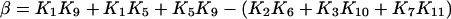(23)

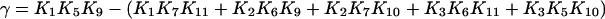(24)

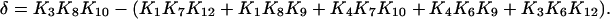(25)

In the steady state 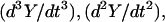and 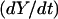are all zero, and Eq. 21 becomes

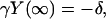(26)

where

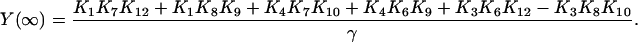(27)

Proceeding similarly, we also have

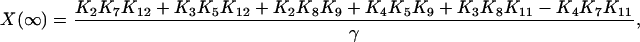(28)

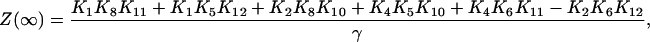(29)

and

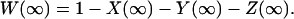(30)

Combining Eqs. 21 and 26, the equation we want to solve is

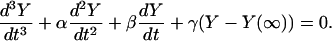(31)

For the three constants α, β, and γ, there always exist three other constants a, b, and c that will satisfy the relations

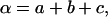(32)

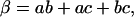(33)

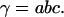(34)

It is shown below (Eq. 36) that a, b, and c are the eigenvalues. Combining Eqs. 31–34, we have

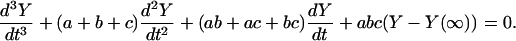(35)

A solution for Eq. 35, obtained using elementary methods, for the condition that the transition rate constants, k_ij, change instantaneously at t = 0, is given by

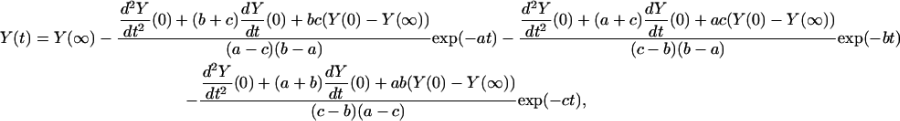(36)

where 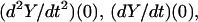and Y(0) are the values at t = 0,

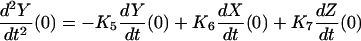(37)

an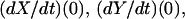d and 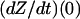are given by Eqs. 6–8 evaluated at t = 0. Expressions corresponding to Eq. 37 for X and Z are similarly obtained by differentiating Eqs. 6 and 8 and evaluating at t = 0. That Eq. 36 is a solution for Eq. 35 may be shown by differentiating.

Solving the algebraic Eqs. 32–34 simultaneously for a, b, and c, we have

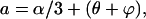(38)

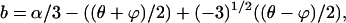(39)

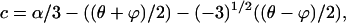(40)

where

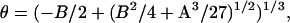(41)

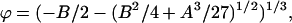(42)

and

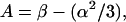(43)

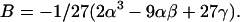(44)

Equations 38–44 together with Eqs. 22–24 and Eqs. 9–20 provide closed-form expressions for the relaxation time constants 1/a, 1/b, and 1/c as functions of the rate constants, k_ij. Direct substitution shows that Eqs. 38–44 are, in fact, a solution for Eqs. 32–34.

Solutions for W(t), X(t), and Z(t) are identical in form to Eq. 36 with identical values for the time constants 1/a, 1/b, and 1/c. Solutions for these other three variables differ only in the values for the steady-state occupancies of these states as specified by Eqs. 27–30 and in the weights given to the initial state occupancies, X(0), Y(0), and Z(0), as specified by Eqs. 6–8. When X(t), Y(t), and Z(t) have been defined, W(t) is also known.

Some special cases of a four-state scheme

No closed₂-open pathway

For many voltage-gated ion channels there is a delay in the development of activation. This means that the closed₂-open pathway cannot be used to any appreciable extent for these channels. For voltage-gated channels, then, a more relevant model would be as in Scheme 1 but with k_2O = k_O2 = 0.

For this and the other special cases of a four-state scheme considered in this section, Eqs. 21–44 are identical to those for the fully generalized scheme. The only differences are in the definitions of the K_i terms (Eqs. 9–20), and all special case results are obtained just by substituting appropriately for the k_ij terms in Eqs. 9–20. The steady-state occupancies are now given by (writing directly in the k_ij terms for this somewhat simpler scheme)

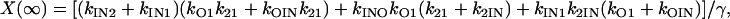(45)

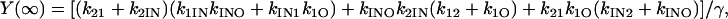(46)

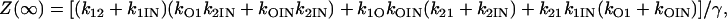(47)

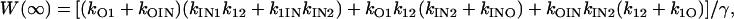(48)

with

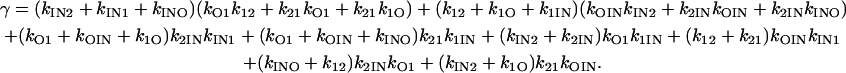(49)

No closed₂-open pathway and identical closed to inactivated rate constants for both closed₁ and closed₂

In a study of Na channel inactivation from closed states (3), it was found that the rate constants governing the transitions from closed to inactivated states have approximately the same value for all closed states (but differ from that for open to inactivated). Incorporating this finding into Scheme 1, we set k_2IN = k_1IN in addition to the k_2O = k_O2 = 0 condition. There are now just nine rate constants as compared to the twelve of the fully generalized scheme.

In this case, Eqs. 22–24 become

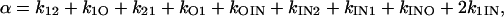(50)

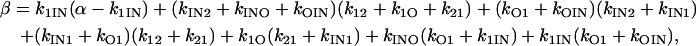(51)

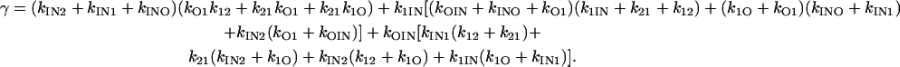(52)

Steady-state occupancies are given by

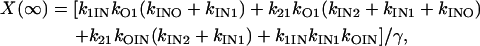(53)

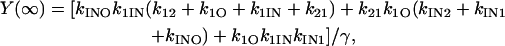(54)

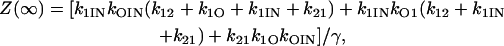(55)

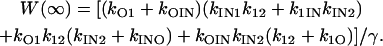(56)

No closed₂-open pathway, identical closed to inactivated rate constants for both closed₁ and closed₂ and an absorbing inactivated state

For Na channels there is typically a range of potentials over which inactivation goes to completion. This behavior can be incorporated as well by setting k_INO = k_IN1 = k_IN2 = 0. For this case,

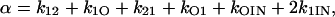(57)

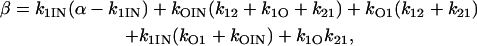(58)

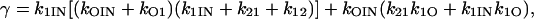(59)

with W(∞) = X(∞) = Y(∞) = 0, and Z(∞) = 1.

Reduction to simpler schemes

The expressions describing the behavior of a generalized four-state scheme are fairly complex. It might be helpful, then, to examine some cases for which the solution is already known and show that the known, correct expressions are, in fact, obtained when the appropriate conditions are applied to the complex equations of the general four-state case. Three such cases with known results are treated: a two-state scheme, a fully generalized three-state scheme, and a four-state scheme in which only forward transitions are allowed (4) as described in the Introduction.

A two-state scheme

Scheme 2

For the two states of Scheme 2, from Eqs. 9–20 and 22–24, β = γ = 0 and

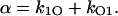(60)

Figure .

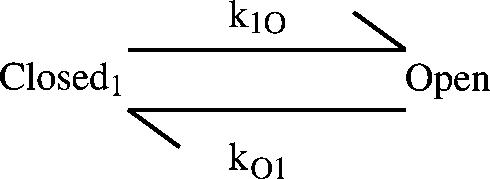
Substituting in Eqs. 38 and 41–44 yields a = α. From the general solution, Eq. 36, noting that for just two states

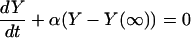(61)

and

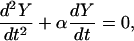(62)

the coefficients on exp(−bt) and exp(−ct) vanish whatever the values of b and c. Now, from Eqs. 39–44, b = c = 0. Substituting in the remaining terms of Eq. 36 yields

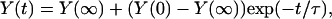(63)

where 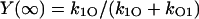and 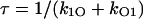, the expected result.

A generalized three-state scheme

Scheme 3

For a general three-state scheme, from Eqs. 9–20 and 22–24,

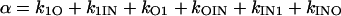(64)

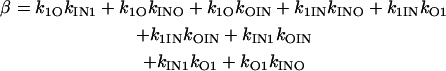(65)

and γ = 0.

Eq. 38 can be written as

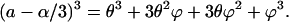(66)

Combining Eqs. 66, 41, 42, and 38 and noting that 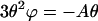and 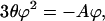we have

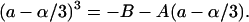(67)

Combining Eqs. 67, 43, and 44 (with γ = 0) yields

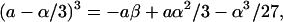(68)

which is satisfied by a = 0. This is not an unexpected result. Summing Eqs. 39 and 40 from the general four-state solution,

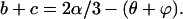(69)

However, from the general three-state solution (2),

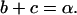(70)

Therefore, for three states, 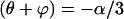and a = 0.

Evaluating the general four-state solution Eq. 36 with a = 0, and noting that for three states (2)

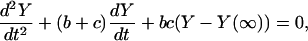(71)

Eq. 36 becomes

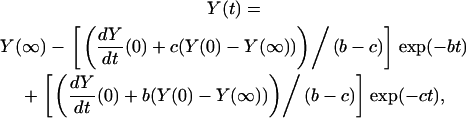(72)

again, just as expected (2).

To evaluate b and c, note that Eq. 39 can be written as

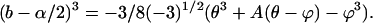(73)

Combining Eqs. 73 and 41–44 and noting γ = 0 for three states yields

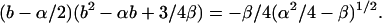(74)

From the general solution for a three-state scheme (2), we have

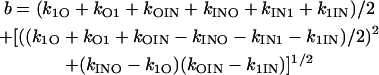(75)

and

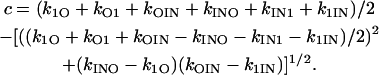(76)

By substituting from Eqs. 64 and 65 it can be seen that the expression under the radical sign in Eq. 75 is just (α²/4–β)^1/2. The remaining term on the right-hand side of Eqs. 75 and 76 is α/2. Hence, Eq. 75 can be written as

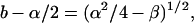(77)

and Eq. 74 becomes

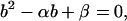(78)

with the roots

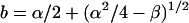(79)

and

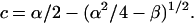(80)

Equations 79 and 80 are just Eqs. 75 and 76. The general four-state solution, then, reduces exactly to the known solution for a three-state scheme just by appropriately setting some of the rate constants to zero.

A four-state scheme with only forward transitions

Scheme 4

From Eqs. 9–20 and 22–24

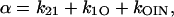(81)

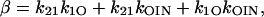(82)

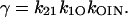(83)

Proceeding as outlined for a general three-state scheme, Eq. 38 becomes

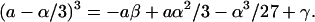(84)

Writing Eq. 84 in terms of the rate constants as specified in Eqs. 81–83, it is seen that Eq. 84 is satisfied by setting a equal to any of the three rate constants. We select a = k₂₁. Again, proceeding as outlined for a general three-state scheme, Eq. 39 becomes

(85)

Combining Eqs. 85, 43, and 44 and again writing in terms of the rate constants as specified in Eqs. 81–83, Eq. 85 can be shown to be satisfied with either b = k_1O or b = k_OIN. Selecting b = k_1O, it is readily shown that Eq. 40 is satisfied by c = k_OIN.

The solution for Scheme 4 presented in Blaustein (4) is restricted to the initial condition that W(0) = 1. Hence, 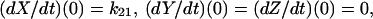and 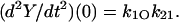Equation 36 becomes

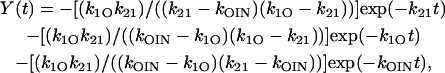(86)

which is exactly the solution for the corresponding state of this special case of a four-state scheme presented in Blaustein (4). A solution for Scheme 4 but now with any initial conditions is given by

(87)

where

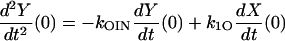(88)

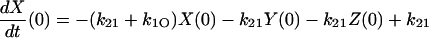(89)

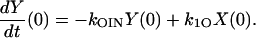(90)

Figure .

With Eqs. 87–90, Scheme 4 can now be evaluated for any number of sequential step changes in rate constants or effective rate constants with each step of any desired duration.

Figure .