“Entropic Traps” in the Kinetics of Phase Separation in Multicomponent Membranes Stabilize Nanodomains

Abstract

We quantitatively describe the creation and evolution of phase-separated domains in a multicomponent lipid bilayer membrane. The early stages, termed the nucleation stage and the independent growth stage, are extremely rapid (characteristic times are submillisecond and millisecond, respectively) and the system consists of nanodomains of average radius ∼5–50 nm. Next, mobility of domains becomes consequential; domain merger and fission become the dominant mechanisms of matter exchange, and line tension γ is the main determinant of the domain size distribution at any point in time. For sufficiently small γ, the decrease in the entropy term that results from domain merger is larger than the decrease in boundary energy, and only nanodomains are present. For large γ, the decrease in boundary energy dominates the unfavorable entropy of merger, and merger leads to rapid enlargement of nanodomains to radii of micrometer scale. At intermediate line tensions and within finite times, nanodomains can remain dispersed and coexist with a new global phase. The theoretical critical value of line tension needed to rapidly form large rafts is in accord with the experimental estimate from the curvatures of budding domains in giant unilamellar vesicles.

INTRODUCTION

It is agreed that cell membranes are nonuniform dynamic structures. However, there is practically no agreement whatsoever as to timescales, nature, or the forces that govern the lateral molecular assemblies that comprise membranes. Estimates of the size of these assemblies, often termed domains or rafts, are approximately tens of nanometers. Putative rafts (1–6) are enriched in cholesterol and sphingolipid. It is difficult to measure their physical properties (3–5,7), perhaps due to their small size or their transitory nature (8,9), but there are proposals that membrane domains play important functional roles in the trafficking and sorting of proteins, cell signaling, viral-induced fusion, etc. (1–3). The mechanism of domain formation in cell membranes remains obscure.

In lipid bilayers (including those having lipid compositions matching that of cell membranes), large domains, of the order of 5–10 μm in diameter, are readily observable by fluorescence microscopy (10–14).

Rafts are thicker than surrounding membrane and represent bilayer structures (13,15,16). Lipids in such domains are in a liquid-ordered state, i.e., the cross-sectional area per lipid molecule is smaller than that of a fluid-disordered membrane (5,10,15). These domains are mobile and grow by their merger. They rapidly resume their circular shape after external perturbations (13), indicating that a significant line tension exists at the raft-bilayer interface. Line tension has been experimentally estimated for multicomponent lipid vesicles (17). Small, nanoscopic domains have also been detected in lipid bilayers (6,18,19). In vesicles, line tension leads to a three-dimensional budding of domains, and theory that accounts for budding has been extensively developed (20,21). We consider phase-separation kinetics for the case of a lipid membrane that is always flat. The results of our calculations, which ignore membrane curvature, are appropriate for and directly applicable to the multitude of experimental studies of rafts that have used planar bilayers and giant unilamellar lipid vesicles.

It is generally thought that for lipid bilayer membranes, domains form as a result of phase separation. In support of this view, domains form upon lowering the temperature of a homogeneous lipid bilayer membrane. However, it is not clear why micrometer-scale domains remain separated from each other for long times. One possibility is that repulsive forces between domains kinetically stabilize them. It is also not understood why nanodomains sometimes remain stable, rather than increasing in size up to complete phase separation. In cell membranes, nanodomains may be created by lipid wetting of proteins (22–24), rather than by phase separation. Obviously, here wetting would not be complete; instead, only a relatively thin lipid film layer would form around the protein molecule and this liquid-ordered layer could have somewhat different physical properties than that of a global liquid-ordered phase. Answering many basic questions regarding domains in model and biological membranes requires understanding kinetics of domain formation, growth, and stability. Unfortunately, even for lipid bilayer membranes, systematic experimental kinetic studies have not yet been undertaken. Theoretical understanding of kinetic phenomena is also lacking. A kinetic theory of phase separation has been quantitatively developed for three-dimensional solid solutions (25–34). However, a lipid bilayer membrane is a two-dimensional system in the liquid state and direct collisions of mobile domains should strongly affect the kinetics of matter redistribution. A rigorous theory that incorporates all pathways of redistribution of matter in liquid, multicomponent membranes, needs to be formulated.

In this study, we approach this problem by utilizing theories that faithfully describe phase separation and domain growth in fields other than membrane biophysics. We modified and/or generalized these theories so that they apply to lipid bilayers and have justified these modifications. Calculations show that domain growth is divided in time and size into two essentially different regions: at short times (approximately milliseconds) and small domain sizes (less than tens of nanometers), the system resembles a solid solution with immobile domains. Here, domains quickly absorb lipid from their supersaturated surrounding milieu. At long times, however, direct interaction of mobile domains to merge, and the budding-off of nanodomains through domain fission, are the dominant means of domain growth. The theory predicts that at low line tension, entropy and boundary energy compete to trap nanodomains in a long-lived state (approximately hours). At somewhat higher line tensions, large domains form, but nanodomains coexist with them. At even higher line tensions nanodomains cease to exist, rapidly merging into micrometer-scale domains. Large energy barriers against close domain contact may kinetically hinder domain merger for larger domains as they progress to form one global phase.

KINETICS OF MATTER REDISTRIBUTION

Setting up the problem

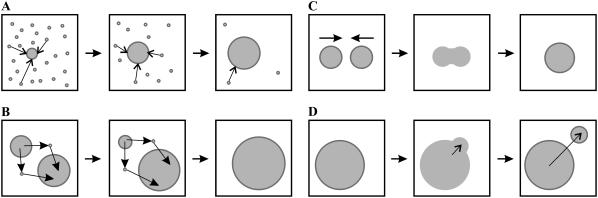
We consider a multicomponent liquid membrane consisting of lipids. We assume that the components are homogenously mixed, but the membrane is initially in a metastable state that can undergo a first-order phase transition. The kinetics of phase separation can be subdivided into stages. In the first stage— nucleation—fluctuations within the homogeneous medium create nuclei of a new phase. If a nucleus enlarges to above a critical size, enlargement continues spontaneously by absorption of supersaturated matter from the surrounding solution. The degree of supersaturation in the surrounding solution decreases as these nuclei enlarge, resulting in the cessation of formation of new supercritical nuclei. The second period of growth is referred to as the independent growth stage, where existing domains continue to grow by accumulating matter from the surrounding membrane.

The original theoretical analysis of the kinetics of phase separation assumed single-component, three-dimensional solid solutions (30,31). This was extended to multicomponent three-dimensional systems (25) under the assumption that the new phase has a well-defined composition that is independent of domain size. This simplifying assumption allows the domain to be assembled from elemental structural units (referred to as quasi-molecules) and domain growth consists of incorporation of additional quasi-molecules. The concept of fixed quasi-molecules imposes equations for the partial fluxes of components from the surrounding membrane to the domains. This approach can be directly applied to a two-dimensional system by using a scaling procedure. To explicitly demonstrate the validity of the approach to a two-dimensional membrane, we combine the scaling approach with direct calculations. In relaxing the condition of solid solutions, the domains are mobile.

Consequently, rafts grow after the independent growth stage continues by two processes in parallel, merger of mobile domains, and Ostwald ripening. Ostwald ripening is a process whereby the equilibrium concentration of domain material within the surrounding solution is higher near a domain of small radius than large radius; material thus diffuses from small to large domains. The small domains disappear as they dissolve their constituents into the surrounding solution; the larger domains accumulate this material to become still larger. This phenomenon is analogous to redistribution of mass from small to large water droplets, mediated by water vapor moving from high to low pressure, the dependence of pressure on radius described by the Laplace law.

These two different modes of matter redistribution superimpose. We calculate each of these rates to determine which mechanism dominates during successive stages of phase separation. To use parameters that explicitly relate to experiment, we choose a standard bilayer consisting of 1:1 DOPC/DPPC + 30% cholesterol. Both micrometer-size and nanoscopic domains have been observed for this mixture and the composition of the liquid-ordered (L₀) and liquid-crystalline (L_α) phases have been derived (18). The L₀ phase consists of 5% DOPC, 53% DPPC, and 42% cholesterol at 20°C; the L_α is 59% DOPC, 14% DPPC, and 27% cholesterol. Cholesterol is only somewhat enriched in the L₀ phase (i.e., the domain); the saturated lipid, DPPC, is more significantly enriched. The unsaturated DOPC is largely excluded from the L₀ domain. For simplicity, we assume that the L₀ domain contains a 1:1 mixture of DPPC and cholesterol and we consider this as the structural unit of the domain. The area fraction of the domain-forming phase φ_∞, found from the lever rule, is φ_∞ ≈ 0.5. Altering the value of the parameter φ_∞ within the range 0.1 < φ_∞ < 0.5, permitted for the phase diagram of our standard bilayer (18), verifies that our conclusions have general validity. Domain ensemble behavior depends strongly on the value of line tension. Unfortunately, in the literature there is only one estimate of the line tension of micrometer-sized domains for phospholipid bilayers, γ ≈ 0.9 pN (17). There is indirect evidence that γ is smaller, and it obviously depends on membrane composition. Therefore, in numerical estimates of the rates of the stages of matter redistribution we varied the value of γ.

Nucleation

We consider nucleation in a two-dimensional metastable multicomponent membrane. Concentrations' fluctuations lead to the formation of small nuclei of new phase. If the nucleus becomes large enough, the decrease in energy resulting from a greater number of favorable interactions within the nucleus exceeds the unfavorable energy necessary to create the one-dimensional circular interface; the nucleus, now supercritical, grows irreversibly. Because we assume that the composition of the evolving nucleus does not depend on its size, the growth of a nucleus is due to addition of structural units that are defined by stoichiometric coefficients {ν_i}. The area per structural unit is

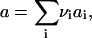(1)

where a_i is the cross-sectional area per molecule of i^th component. Because the subcritical nuclei remain in thermodynamic equilibrium, their size distribution function is described by the equilibrium distribution function. According to classical fluctuation theory (30), the equilibrium distribution function of the nuclei f₀(r) depends exponentially on the minimum work E(r) necessary to create a nucleus of radius r:

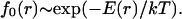(2)

This function is normalized so that f₀(r)dr is the number of the nuclei with radius (r, r+dr) in an area of 1 cm². The area and boundary terms yield

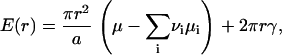(3)

where γ is line tension, μ is the chemical potential of the structural unit within nucleus, and μ_i is the chemical potentials of i^th component in the surround phase. For an ideal solution, μ_i can be expressed as

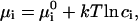(4)

where is the standard chemical potential of i^th component and c_i is the bulk concentration of i^th component measured in 1/cm². E(r) has a maximum at a critical radius r_c, given by

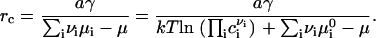(5)

Equations 3 and 5 yield

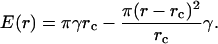(6)

From Eq. 6 we obtain

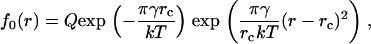(7)

where Q is a pre-exponential factor that cannot be expressed in terms of macroscopic properties of the system. We estimate it by supposing that Q is proportional to the number of nucleation sites (25,26). Q is determined by the number of configurations by which components can arrange into a structural unit, 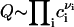. This expression immediately follows from the intuitively appealing hypothesis that the rate of creating a minimal nucleus is proportional to the probability that all components of the structural unit meet. The normalization condition for f₀(r) and the relationship 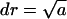yields .

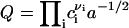In addition to the equilibrium distribution function, we require a kinetic size distribution function f(r, t) to calculate the rate of phase separation. Nuclei growth is described by the Fokker-Planck equation (30,33)

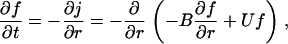(8)

where j is the flux (number of nuclei passing through the critical radius per second, per cm²) in size-space, B is a nuclear size-diffusion coefficient in cm²/s, and U is the nucleus mobility in r-space in cm/s. The relation between B and U can be found at equilibrium, j = 0, as

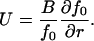(9)

At steady state, j = const, allowing us to rewrite Eq. 8 in the form

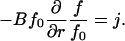(10)

After integration, we obtain

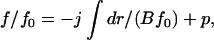(11)

where f₀(r) is defined by Eq. 7. The constants j and p can be found from the boundary conditions that f/f₀ → 1 for r → 0 (because equilibrium is reached in this limit), and that f/f₀ = 0 as r → ∞ (because f₀(r) tends to infinity, whereas f(r) remains finite). Equation 11 has a solution of the form

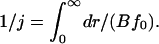(12)

The integrand is sharply peaked at r = r_c. We use Eq. 7 around this point and obtain the stationary solution of Eq. 8 for the flux of nuclei in r-space as

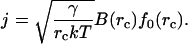(13)

To obtain the flux in terms of measurable quantities, we need to evaluate the diffusion coefficient, B, in r-space. We do so by a macroscopic approach. Consider a supercritical nucleus moving unidirectionally toward large radii. This allows us to ignore diffusion and to write the flux as j = Uf. The coefficient U is a velocity in size-space, dr/dt. A macroscopic nucleus grows by accumulation of structural units diffusing from the bulk to the nucleus interface. The solution of the two-dimensional equation for steady-state diffusion yields the partial flux of i^th component j_i,

(14)

where D is the diffusion coefficient in the membrane, r_* is the cutoff radius (which can be approximated by the size of whole system), and c_ir is the equilibrium concentration of i^th component near a nucleus of radius r. In Eq. 14, we assume that all components have the same diffusion coefficients. To preserve the nucleus composition, it is necessary to impose the condition on partial fluxes of

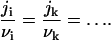(15)

Equation 15 means that the growth of a nucleus proceeds via incorporation of structural units exclusively. Equations 14 and 15 allow us to find the velocity in size-space, dr/dt. The details of the calculations are described in Appendix, where the equation for U is obtained as

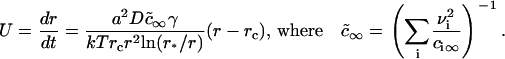(16)

Here, c_i∞ is the equilibrium concentration of i^th component at a straight interface (boundary of domain with infinite radius) and 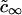is the effective equilibrium concentration. From Eqs. 7, 9, and 16 we obtain B,

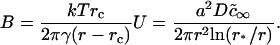(17)

As expected, B is greater for a small nucleus than for a large one. From Eqs. 7, 13, and 17, we obtain the final expression for flux density,

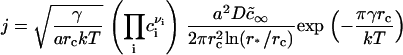(18)

As supersaturation decreases during the nucleation stage, the critical radius increases and the height of the energy barrier against irreversible growth increases. Both effects cause a significant decrease in flux, because j depends exponentially on r_c (Eq. 18). We assume that nucleation ceases when the flux drops 10-fold to estimate the duration of the nucleation stage τ_n, the value of critical radius 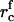at t = τ_n, and the total number of created nuclei N_f. The details of these calculations can be found in the Appendix. Using Eqs. A13–A18 and taking γ = 0.4 pN, φ_∞ = 0.5, and D = 3 × 10⁻⁸ cm²/s (35), we obtain 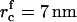, N_f = 6 × 10⁹ 1/cm², and τ_n = 2 × 10⁻⁴ s. For φ_∞ = 0.1, we have 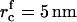, N_f = 2 × 10⁹ 1/cm², and τ_n = 8 × 10⁻⁵ s. Clearly, the nucleation time is very short and is relatively insensitive to variation of φ_∞.

Independent growth stage

At the conclusion of the nucleation stage, N_f supercritical nuclei have appeared in the membrane and, for all practical purposes, additional nuclei are no longer created. The nuclei that already exist continue to grow independently of each other by accumulating matter from the surrounding membrane (Fig. 1 A). This process leads to decreasing supersaturation and thus to declining growth. We estimate the time necessary for this decline (i.e., the duration of this stage, τ_ig) and the average size of the nuclei at t = τ_ig by utilizing the constancy of the total number of nuclei (N_f) during the independent growth stage. The nuclei that were created over time τ_n now migrate in r-space during independent growth. That is, diffusion in r-space is not of consequence during independent growth. Because (as will be shown below) τ_ig > τ_n, the width of the distribution function of the nuclei is determined by diffusion during the brief nucleation phase and thus this width remains rather narrow during independent growth. In fact, the reciprocal dependence of the rate, dr/dt, on r (i.e., mobility decreases with size, Eq. 16) further assures that the distribution remains sharply peaked. Therefore, we can use the average radius 〈r〉 in Eq. A12 to calculate the flux of matter into the nuclei. Using Eqs. A11 and A12, we obtain

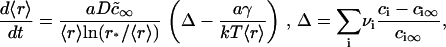(19)

where Δ is the total supersaturation. The condition of mass conservation has the form

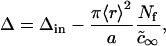(20)

where Δ_in is the initial total supersaturation. Substituting Eq. 20 into Eq. 19, we obtain

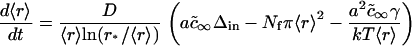(21)

FIGURE 1.

A schematic representation of the main stages of matter redistribution in the course of phase separation: panel A is a stage of independent growth of each domain; panel B is Ostwald ripening; panel C is domain merger; and panel D illustrates two-dimensional budding of nanodomains from a large domain.

We solved this equation numerically using the initial condition .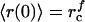

To estimate τ_ig, we compare the rate of growth from Eq. 21 with the Ostwald ripening rate using the obvious condition (d〈r〉/dt)_ig = (d〈r〉/dt)_or at t = τ_ig. The expression for d〈r〉/dt in the case of Ostwald ripening can be easily obtained from Eq. 25 (see below). Letting γ = 0.4 pN and φ_∞ = 0.5, we obtain τ_ig = 6 × 10⁻³ s and 〈r(τ_ig)〉 ≈ 50 nm. For φ_∞ = 0.1, τ_ig = 1.5 × 10⁻³ s and 〈r(τ_ig)〉 ≈ 40 nm. Therefore (as stated above), τ_ig > τ_n. However, τ_ig is rather short and, as we showed to be the case for τ_n, insensitive to the precise value of φ_∞.

Ostwald ripening in the case of immobile domains

During Ostwald ripening, the surrounding medium is only slightly supersaturated. The subcritical domains dissolve and their material is accumulated by the remaining domains, which become larger (Fig. 1 B). Ostwald ripening in a three-dimensional dilute solid solution is quantitatively described by Lifshitz-Slezov theory (30,31), which results in the well-known asymptotic law for domain radius growth,

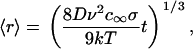(22)

where σ is surface tension, v is the molecular volume of the evolving phase, and c_∞ is the equilibrium concentration at a plane surface. The size-distribution function of domains is narrow and the average radius 〈r〉 is equal to critical radius. The number of domains, N(t), as a function of time (increase of domain size is accompanied by a decrease of the number of domains) is given by

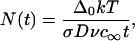(23)

where Δ₀ is the initial supersaturation. At the beginning of Ostwald ripening, supersaturation is small and tends to zero as t^−1/3.

Numerous studies have shown that the cube-root Lifshitz-Slezov law is very general. Lifshitz-Slezov theory can be applied for arbitrary volume fractions (28). It is commonly assumed that Lifshitz-Slezov theory developed for three-dimensional systems can be applied to two-dimensional systems (29). For example, simulating a two-dimensional spin-exchange Ising model (which exhibits a second order, rather than a first-order, phase transition) yields a t^1/3 law (28). This power law has been explicitly demonstrated by Marqusee (36) for a two-dimensional, one-component solid solution. In this case,

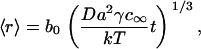(24)

where b₀ is a numerically calculated factor of order one. It is easy to show that Eq. 24 follows from Eq. 22, derived for a three-dimensional system, by scaling σ → γ, ν → a.

It has also been shown that the results obtained for a one-component, three-dimensional system generalize to the case of multicomponent solid solutions (25,32). This can be readily seen by substituting Dc_∞ in Eq. 22 into 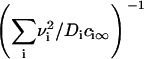. By assuming that all D_i are the same and equal to D, we arrive at the simple substitution, .

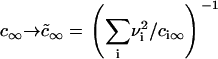We solved the Ostwald ripening problem for a two-dimensional multicomponent system (see Appendix) and proved that the substitution 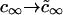is valid for the two-dimensional case. We obtained

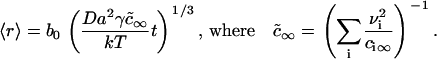(25)

The total number of domains depends on time as

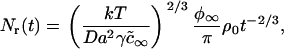(26)

where ρ₀ is a numerically calculated factor of order one. Thus, during Ostwald ripening, the average radius increases slowly and the rate of increase becomes less with time. Any domains of radius less than the critical radius r_c dissolve and those greater than r_c slowly enlarge. In essence, domain radius remains narrowly peaked around 〈r〉 (which is slightly greater than r_c) as domain size slowly migrates in r-space. (Below, we use Eqs. 25 and 26 to estimate the rate of Ostwald ripening.) The dependence of the kinetics of matter redistribution on radius 〈r〉 is readily appreciated from the characteristic time, τ_r, for the number of domains to decrease twofold. Equations 25 and 26 yield

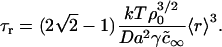(27)

Thus, τ_r does not depend on φ_∞. For our standard bilayer and γ = 0.2 pN, Eq. 27 yields τ_r = 200 s for 〈r〉 = 20 nm; τ_r = 1600 s for 〈r〉 = 40 nm; τ_r = 3000 s for 〈r〉 = 50 nm; τ_r = 24000 s for 〈r〉 = 100 nm; and τ_r ∼ 200 h for 〈r〉 = 1 μm. Clearly, Ostwald ripening is not an effective means for growth of immobile domains for 〈r〉 >50 nm. In fluid membranes, domains are mobile and their merger can readily dominate and determine the rate of matter redistribution.

Merger of mobile domains

We first calculate the rate of domain merger by adapting Smoluchowski's theory of rapid coagulation (37,38) to a two-dimensional system. We then consider the slowing of coagulation due to repulsive forces between approaching domains.

The initial stage of rapid coagulation can be described as a second-order association between two domains (Fig. 1 C)

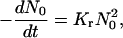(28)

where N₀ is concentration in cm⁻² of the domains of radius r₀ and K_r is the rate constant. In the absence of repulsive forces between approaching domains, domains merge immediately upon contact. The rate K_r is limited by diffusion of domains toward a central domain. Placing the origin of coordinates in the center of this domain, we can write the steady-state diffusion equation as

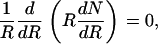(29)

with boundary conditions

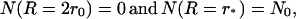(30)

where r_* is the cutoff radius. The solution of Eq. 29 is

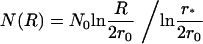(31)

The flux toward the central domain is equal to

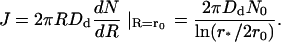(32)

To account for the mobility of the central domain, we need to double the diffusion coefficient (or equivalently the flux) in Eq. 32. Summing up the diffusion flux over N₀ domains, we obtain

(33)

Therefore, we have for the coagulation rate constant

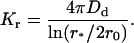(34)

We calculate D_d according to the Saffman-Delbruck equation (39),

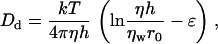(35)

where η is the viscosity of the lipid bilayer, η_w is the viscosity of aqueous solution, h is the thickness of the bilayer, and ɛ is Euler's constant (ɛ ≈ 0.577). Equation 35 is valid for r₀ ≪ ηh/η_w ≈ 1 μm; taking ηh = 6 × 10⁻⁷ g/s and η_w = 10⁻² g/(cm*s), we obtain D_d ≈ 10⁻⁸ cm²/s for r₀ ∼ 50 nm. The same value of D_d can be used for any domain of radius on the order of tens of nanometers, because D_d depends weakly on r₀. For larger domains, the Saffman-Delbruck equation is

(36)

In contrast to Eq. 35, the diffusion coefficient of Eq. 36 is independent of friction between the domain and water. Because this friction should be more consequential as r becomes larger, we explicitly consider it by utilizing the expression for the viscous drag, b, acting on a disk moving along the plane of a membrane (40),

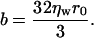(37)

This leads to a diffusion-coefficient D₂,

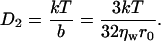(38)

The combination of the Saffman-Delbruck and the viscous drag term yields a net diffusion-coefficient D_d given by

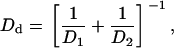(39)

yielding D_d = 3 × 10⁻⁹ cm²/s for r₀ = 1 μm.

It is worth noting that both D_d and K_r depend weakly on r₀. Because the (second-order) rate constant for domain merger is relatively independent of domain size, we set K_r = const and use Eq. 28 to calculate the change of the total domain concentration 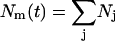(38),

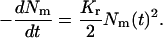(40)

Solving Eq. 40, we come to the time-dependence of the total number of domains,

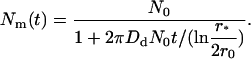(41)

Equation 41 can be easily generalized to the case of slow coagulation,

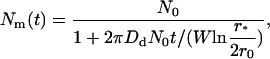(42)

where the inhibition factor W has the form (37)

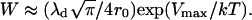(43)

Here, V_max is the height of the energy barrier hindering close contact between two circular domains of radius r₀, and λ_d is the effective width of the barrier.

Repulsive forces between two approaching domains could occur for several reasons. We previously showed that as a consequence of the elastic properties of a membrane, a repulsive force definitely occurs if a height (i.e., thickness) mismatch exists between the domains and the surrounding membrane (41): the height of the elastic deformations at the raft boundary oscillates as it decays and the oscillations cause repulsion between two domains. We obtain V_max according to the Deryaguin approximation (37), yielding V_max ≈ 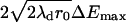, where ΔE_max is the height (per unit length of boundary) of the energy barrier separating two domains. The height and width of the barrier calculated according to the elastic theory of continuous membranes (41) yields λ_d = 3 nm and ΔE_max ≈ 0.1 pN for γ = 0.4 pN. This barrier depends slightly on γ: For γ = 0.2 pN, ΔE_max ≈ 0.07 pN. Because V_max ∝ 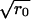, W is inconsequential for small domains, but is huge for large ones. Numerically, W ∼ 1 for r₀ = 50 nm and W ∼ 10⁴ for r₀ ∼ 1 μm.

The characteristic time for domain collisions can be estimated from Eq. 42 as

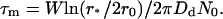(44)

For the number of domains to decrease twofold, we obtain for φ_∞ = 0.5 that τ_m = 0.05 s for r₀ = 50 nm and W ∼ 1, and that τ_m ∼ 1 h for r₀ = 1 μm and W ∼ 10⁴. The importance of the barriers is readily seen by setting W ∼ 1 for r₀ = 1 μm, yielding τ_m ∼ 3 s. As expected, these times are larger if domains occupy a smaller fraction of the membrane area. If φ_∞ = 0.1, we obtain τ_m = 0.2 s for r₀ = 40 nm and W ∼ 1, τ_m ∼ 5 h for r₀ = 1 μm and W ∼ 10⁴, and τ_m ∼ 15 s for r₀ = 1 μm and W ∼ 1.

Domain fission and two-dimensional budding

The increase in domain size that results from merger can, in principle, be reversed if the domains divide. We estimate the characteristic time for a domain of radius R to divide into two domains of radii r and 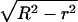(Fig. 1 D), assuming that the bilayer remains flat. That is, we ignore any tendency of a domain to bend out of the plane of the membrane (20). The difference in boundary energies, ΔE, is given by

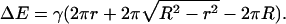(45)

If there is no activation barrier against fission, the characteristic time of division τ_f is

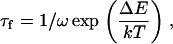(46)

where ω is the characteristic frequency of the oscillation of the boundary. Boundary fluctuations, known as capillary waves, have eigenfrequencies (40) of

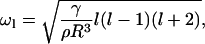(47)

where ρ is the membrane density and l is the eigenvalue for wavelength λ = 2πR/l. We let λ have the size of a domain resulting from fission (i.e., λ ≈ 2r or l = πR/r), to obtain, from Eqs. 45–47,

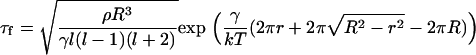(48)

The chance of a large domain dividing into two domains of comparable size (fission) is negligible: for 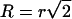and r = 0.1 μm, we obtain that for γ = 0.4 pN, τ_f ≈ 10⁸ s, an impossibly long time. However, a small nanodomain can split off from a large domain (two-dimensional budding). For γ = 0.4 pN and R = 1 μm, it would take τ_f ≈ 0.2 s for an r = 30 nm domain to split off, but τ_f ≈ 200 s for an r = 40 nm domain. Thus, the time-dependence is extremely sensitive to the size of the bud. The likelihood for these nanodomains to split off from a large domain also depends strongly on the line tension. A domain of r = 40 nm would take τ_f ≈ 0.4 s to split from an R = 1 μm domain if γ = 0.2 pN (instead of 200 s for γ = 0.4 pN). Although large domains cannot, as a practical matter, split into two equally sized halves, small domains can split in half if γ is sufficiently low. For γ = 0.4 pN, τ_f ≈ 0.1 s for a small domain to split into two r = 40 nm domains; for γ = 0.2 pN, τ_f ≈ 0.01 s. Because Eq. 45 predicts ΔE → r as r → 0, the maximum rate of two-dimensional budding occurs for pinching off a single structural unit.

The relative contributions of the various stages to matter redistribution

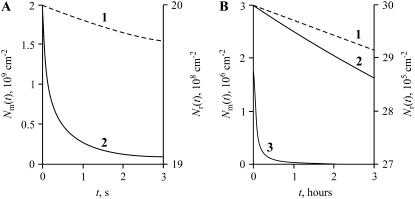
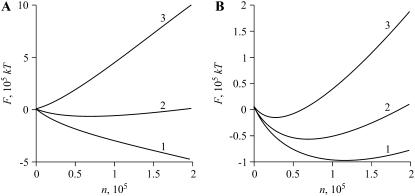
We have estimated the rates at which matter redistributes by all modes and during the various stages. As shown, the nucleation and independent growth stages are very short (10⁻⁴–10⁻³ s). The use of Eq. 42 shows that merger during the independent growth stage leads to a negligible (<1%) decrease in the number of domains. The membrane can thus be considered a solid solution of immobile domains during these early stages. However, for t > τ_ig and r_c > 40–50 nm, the stages of Ostwald ripening and merger/fission proceed in parallel. The rate of merger (Fig. 2 A, curve 2) is clearly much faster than the kinetics of Ostwald ripening (curve 1) for nanodomains (r > 40 nm) over the first few seconds, τ_m/ τ_r ∼ 10⁻⁴. Growth for micrometer-scale domains (Fig. 2 B) is also much faster by merger (curve 3, note timescale of hours) than by Ostwald ripening (curve 1), even though the domains have relatively low mobility. Even when large domains significantly repel each other (Fig. 2 B, curve 2), merger is the dominating process. Quantitatively, dN_m/dt = 10¹⁰ cm⁻² s⁻¹ for r = 40 nm; dN_m/dt = 10² cm⁻² s⁻¹ for r = 1 μm and W ∼ 10⁴; and dN_m/dt = 10⁴ cm⁻² s⁻¹ for r = 1 μm and W ∼ 1.

FIGURE 2.

The decrease in the number of domains caused by Ostwald ripening and domain merger. (A) The domains are initially small, r(0) = 40 nm, and the decreases in domain number are shown over a few seconds. The dotted curve (1) shows the decrease caused by Ostwald ripening (N_r(t), right-hand ordinate). The solid curve (2) illustrates the decrease caused by nanodomain merger (N_m(t), left-hand ordinate). (B) The domains are initially large, r(0) = 1 μm, and the decrease in domain number are shown over the time-course of hours. The dotted curve (1) corresponds to Ostwald ripening and solid curves (2 and 3) illustrate the consequence of microdomain merger. For curve 2, the merger inhibition factor W = 10⁴, and for curve 3, W = 1, accounting for the much slower kinetics of curve 2. A comparison of curves 1–3 demonstrates that domain merger is much more consequential for redistribution of matter than is Ostwald ripening.

These estimates assume that φ_∞ = 0.5 and γ = 0.4 pN. However, as we have shown, the results are not strongly dependent on the value of φ_∞. The mean radius at the end of independent growth is 50 nm for φ_∞ = 0.5 and 40 nm for φ_∞ = 0.1 and the Ostwald ripening characteristic time is completely independent of φ_∞. The characteristic times for merger of nanodomains is also relatively insensitive to φ_∞= τ_m ∼ 0.05 s for φ_∞ = 0.5 and 0.2 s for φ_∞ = 0.1. The value of γ does not affect the characteristic times of merger, but it does affect characteristic times of Ostwald ripening. For instance, τ_r = 1600 s for γ = 0.2 pN (for 〈r〉 = 40 nm), whereas τ_r = 800 s for γ = 0.4 pN.

We are thus led to a general view of domain evolution. At t ∼ τ_ig, the system consists of nanodomains with a narrow size distribution that is peaked at 〈r〉 ∼ r_c ∼ 50 nm. The population of small nuclei (r ∼ a few nm) is in thermodynamic equilibrium with the surrounding membrane and they do not interfere with the subsequent phase separation. For t > τ_ig, supersaturation is very small and asymptotically declines to zero. Phase transition at t > τ_ig is not completed yet and, strictly speaking, the system is not at a state of thermodynamic equilibrium. However, Ostwald ripening is very slow and matter redistribution is overwhelmingly determined by very fast (∼0.1 s) merger and fission of mobile domains. When the merger and fission rates are equal, we can assume that the total area of the domain phase is virtually constant to treat the system of nanodomains as an ensemble of immiscible particles in quasi-equilibrium. Thereby standard approaches of statistical thermodynamics yield calculated domain size distributions for times τ_ig < t < τ_r. (See Discussion for an elaboration of the difference between equilibrium and quasi-equilibrium.)

STABILIZATION OF NANODOMAINS

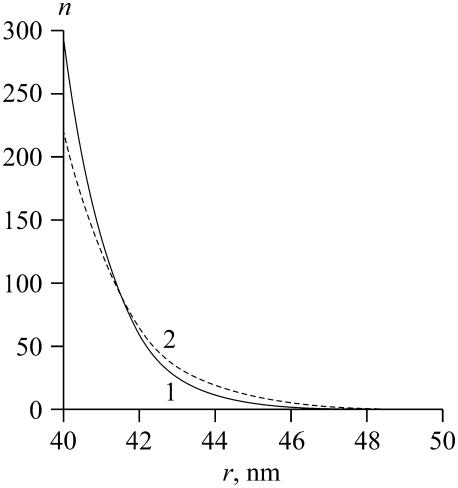
We first calculated the distribution of domain size by considering the ensemble of domains after the independent growth stage (see Appendix). This approach gave the number of domains as a function of domain radius for different values of γ (Fig. 3). The distribution of domain size is very sharply peaked at smaller radii. The characteristic length of the decay of the distribution, ∼3 nm, slightly increases as γ increases. The area, A_r, occupied by the domains, corresponding to curves 1 and 2 in Fig. 3, is independent of γ. Hence, nanodomains are favorable for low line tensions (i.e., γ < 0.18 pN) and they are almost uniform in size, peaked at r = r_min. This peaking occurs because for small γ, the decrease in boundary energy is insufficient to compensate for the decreased entropy that results from domain merger.

FIGURE 3.

The domain size distribution, calculated from Eq. A52 for different values of γ: curve 1 is for γ = 0.04 pN; curve 2 is for γ = 0.16 pN.

In the coexistence region, γ_min < γ < γ_max, the approach described in the Appendix fails (see Appendix), so we formulated the following simplified model. It gives results that are self-consistent over a wide range of parameters.

We assume that the domain-forming phase exists in only two forms: one a monodisperse ensemble of n small domains of radius r = r_min, and the other a single large domain of unknown radius R. The free energy of this system can be obtained directly from Eq. A51, as

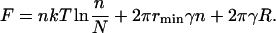(49)

Matter conservation yields

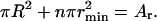(50)

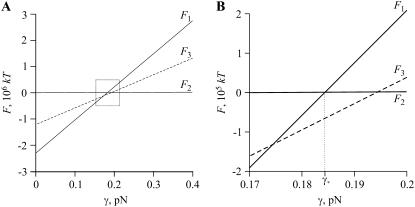
If only small domains of radius r = r_min are present, 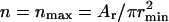and we can obtain the dependence F₁(γ), which is described by the first two terms in Eq. 49. This linear function is shown in Fig. 4 A. At the other extreme, only one domain of radius 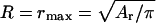is present and here we also have a linear function F₂(γ), which is described by the last term in Eq. 49. However the slope of F₂(γ) is much less than that of F₁(γ), so F₂(γ) is practically parallel to the abscissa in Fig. 4 A. The intersection point of the two curves yields a line tension γ_*. For γ < γ_*, small domains are favorable (F₁ < F₂); for γ > γ_*, only one large domain exists (F₁ > F₂). We now further illustrate why the ensemble of small domains can coexist with one large domain. The total free energy (obtained from Eq. 49) of n = n_max/2 small domains in equilibrium with one large domain of radius R (its radius calculated from Eq. 50) is depicted by the dotted line in Fig. 4 A. For γ close to γ_*, the free energy F₃(γ) lies below F₁(γ) and F₂(γ) (magnified in Fig. 4 B). The difference between F₃(γ) and F₁(γ) or F₂(γ) is significant, ∼10⁵ kT for γ = γ_*. The range of γ for which coexistence is favorable (i.e., F₃(γ) < F₁(γ) and F₃(γ) < F₂(γ)) depends on the number of nanodomains, n. Therefore, determining the values of n that minimize the free energy of Eq. 49 as a function of γ yields the limits of the coexistence region.

FIGURE 4.

The dependence of the free energy of the system F, calculated from Eq. 49, on line tension γ. The value F₁ corresponds to n_max domains of radius r_min, F₂ corresponds to one domain of radius r_max, and F₃ is for n_max/2 domains of radius r_min and one large domain. (A) The entire range of line tensions is used. (B) The dotted rectangle of A is expanded.

Consider the free energy F as a function of n at a line tension γ. Substituting R from Eq. 50 into Eq. 49 yields

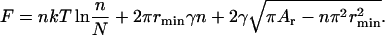(51)

F(n) is depicted at different line tensions γ in Fig. 5 A. At small γ, the system disperses because F(n) decreases monotonically with n (curve 1). For large γ, one large domain forms because F(n) increases monotonically with n (curve 3). For intermediate γ, F(n) exhibits a minimum (curve 2), and so a number of nanodomains coexist with one large domain. The value of n that yields this minimum depends on γ (see Fig. 5 B): as γ becomes larger, the number of minimal domains at equilibrium becomes smaller. Clearly, F(n) exhibits a minimum only in a finite interval of γ (i.e., γ_min ≤ γ ≤ γ_max). We calculate the minimum of F(n) with

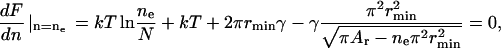(52)

where n_e denotes the number of nanodomains at equilibrium. Substituting n_e = n_max and n_e = 1 into Eq. 52, we obtain

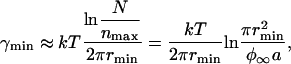(53)

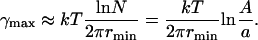(54)

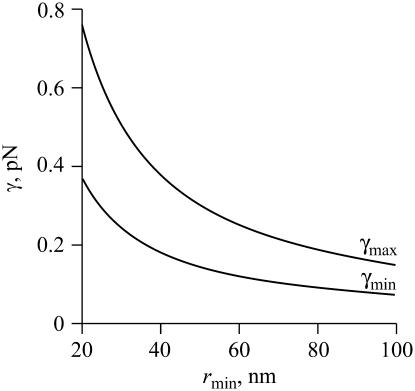
The value γ_min depends on r_min and φ_∞, but is independent of the total area A. For r_min = 40 nm and φ_∞ = 0.1, we have γ_min ≈ 0.18 pN and γ_max ≈ 0.38 pN. As readily seen from Fig. 6, γ_min and γ_max decrease with r_min. Physically, the smaller is r_min, the greater is the increase in entropy when the system disperses. Equivalently, an increase in r_min leads to a decrease in γ_min. Moreover, the difference γ_max–γ_min decreases with r_min, as readily seen from Eqs. 53 and 54. These dependences are of consequence because r_min slowly increases during Ostwald ripening.

FIGURE 5.

The dependence of the free energy F, calculated from Eq. 51, on the number n of domains of minimal radius r_min at different values of γ. (A) An illustration of the three different regimes of γ. Curve 1: γ = 0.16 pN (small γ) yields a system for which domains disperse; curve 2: γ = 0.185 pN (intermediate γ) yields coexistence of small and large domains; curve 3: γ = 0.4 pN (large γ) yields a single large domain. (B) The coexistence of small and large domains for intermediate γ is illustrated for γ = 0.183 pN (curve 1), γ = 0.185 pN (curve 2), and γ = 0.2 pN (curve 3).

FIGURE 6.

The dependence of minimal (γ_min) and maximal (γ_max) line tensions on the minimal radius r_min, calculated from Eqs. 53 and 54, respectively. The area fraction of the domains is φ_∞ = 0.1.

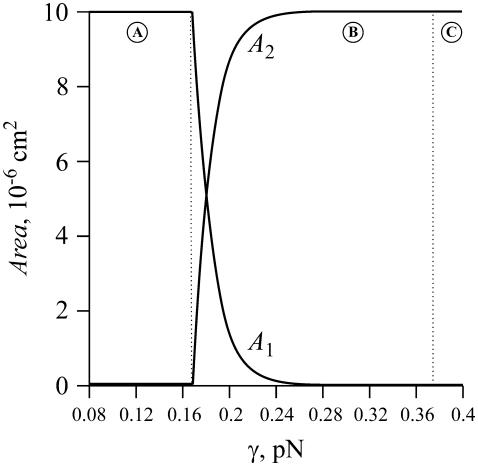
It is useful to consider the fractional area occupied by small and large domains (Fig. 7). We calculated, for each γ, the number of nanodomains at equilibrium (n_e obtained from Eq. 52) and then the equilibrium radius, R, of the large domain (from matter conservation, Eq. 50) to obtain the total area of nanodomains 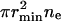(curve A₁) and the area of the large domain (curve A₂). For γ < γ_min, the phase-separated domains maximally disperse into small domains; a large domain is not present (region A). For γ_min ≤ γ < γ_max, nanodomains of minimal size maintain quasi-equilibrium with a large domain of radius R(γ). The greater is the line tension, the fewer are the number of nanodomains. Equivalently, for higher line tension, the total area of nanodomains is less and the area of the large domain is greater (region B). For γ > γ_max, one large domain exists and nanodomains are absent (region C).

FIGURE 7.

The dependence of the total area of nanodomains of radius r_min (curve A₁) and the area of a large domain (curve A₂) on line tension γ. The vertical dotted lines separate region γ < γ_min (A), where only nanodomains exist, from region γ_min < γ < γ_max (B), where nanodomains maintain quasi-equilibrium with one large domain (i.e., a global phase), and region B from region γ > γ_max (C), where one large domain is energetically favorable, and thus nanodomains are not present.

Our simplified model is based on the assumption that the population of domains essentially divides into two distinct groups: the first is the nanodomains of radius r_min; the second is one large domain of R ≫ r_min, which is equivalent to a global phase. However, clearly, this separation does not occur in the vicinity of γ_min because here the gap between small and large domains disappears, i.e., R ∼ r_min. This vicinity of γ_min is, however, exceedingly small. Because the slope of curve A₂(γ) is extremely steep near γ ∼ γ_min, even a seemingly irrelevant change in γ results in a great increase in the area of the large domain: Eqs. 50 and 52 yield that an increase in line tension from γ_min = 0.18 pN to γ = 0.19 pN induces matter to redistribute from the class of nanodomains to one large domain of R ∼ 15 μm ≫ r_min (e.g., see Fig. 7). This illustrates that, except for a rather small region around γ_min, our simplified model is valid for a wide range of γ.

DISCUSSION

Matter redistributes by various modes in the course of phase separation within multicomponent liquid membranes. We have quantitatively considered each of these modes and their superposition. To the best of our knowledge, ours is the first study of nucleation in a two-dimensional multicomponent system; the characteristic time τ_n and the total number of supercritical nuclei created by this mode have now been calculated. The duration of the nucleation stage, τ_n, and the following independent growth phase, τ_ig, are short (approximately milliseconds), and so <1% of the nuclei merge during these stages. Also, at the end of the independent growth stage, i.e., t = τ_ig, almost all the domains are distributed within a narrow interval of radii around 〈r〉 ∼ r_c. After this time, domains enlarge by Ostwald ripening and the balance between collisional-based merger and fission. We treated domains as if they were immobile to calculate the extent and time-course of Ostwald ripening in a two-dimensional multicomponent membrane (see Appendix). Merger of domains does depend upon mobility, and is independent of Ostwald ripening. We describe merger by generalizing the Smoluchowski theory of coagulation to two-dimensional fluid membranes.

At τ_r > t > τ_ig, matter redistribution is dominated by domain merger and two-dimensional budding of nanodomains (Fig. 2, A and B). The resulting distribution of domain sizes depends strongly on line tension, γ. At low γ, nanodomains that have the minimal radius r_min necessary to maintain quasi-equilibrium are stabilized by the balance between the entropy of merger and their boundary energy (Figs. 5 A and 7). At high γ, the nanodomains quickly merge to form micrometer-scale domains; at intermediate γ, nanodomains coexist with large domains (Fig. 5, A and B, and Fig. 7). Merger of large domains is limited by their mobility and any repulsion between them. Nanodomains can split off, via budding, from both large and small domains.

Approximations of the model

We assumed that the composition of a phase is independent of domain size and is homogeneous up to the interface. This assumption is increasingly valid as domain size increases—the focus of the present study—and is consistent with growth via addition of structural units of defined stoichiometry. We described the rate of domain growth by diffusion of components from the bulk surround to the domain. We maintained the composition of domains constant, independent of size, by imposing conditions on the partial fluxes (Eq. 15).

We determined the rate of domain enlargement during the stage of independent growth by neglecting any competition between domains for material from the surround. This approximation should be valid because densities of domains are low. We also assigned a cutoff radius for diffusion, as is always necessary to avoid logarithmic singularities associated with the equations for two-dimensional diffusion (Eq. 14). The cutoff radius may change with the concentration of the components in the surround, but fixing it will not lead to significant errors in calculated rates because logarithms vary slowly. We also introduced a cutoff radius when considering the rate of domain merger (Eq. 30). To be certain that these simplifications were appropriate, we verified that the rate of Ostwald ripening rate in two dimensions under the assumptions was practically the same as that calculated when competition between domains was not neglected and a cutoff radius was not introduced (see Appendix).

The equations of Lifshitz-Slezov theory, originally developed for a one-component system in three dimensions, generalize to a multicomponent system if the diffusing substance is treated as a structural unit (25). This generalization requires only that interfacial kinetics be fast compared to diffusion and that the composition of the domains be well defined and independent of radius. We justify the concept of a structural unit for a two-dimensional system in the Appendix. We used Smoluchowski theory to obtain kinetics of domain merger over an extended time-course (Eq. 42). Although Smoluchowski theory has limitations (38), computer simulations show (27) that the solutions of the Smoluchowski equations are qualitatively applicable (37). An exact analytic theory of coagulation has not yet been developed.

After the independent growth stage, matter redistributes by Ostwald ripening and merger/fission of the domains. Because these two mechanisms have drastically different characteristic rates, it is appropriate to separate them into nonoverlapping stages. However, they do occur simultaneously, and there is some coupling between them. Our formalism partially accounts for the small coupling by allowing r_min to slowly increase in time due to Ostwald ripening.

We can consider domain ensemble evolution as a sequence of quasi-equilibrium states that correspond to different values of r_min. The situation is analogous to an ideal gas in a container with a slowly moving piston. If the piston moves slowly enough, the gas is essentially at equilibrium—defined as quasi-equilibrium—at every time, even though the volume of the container is slowly increasing (in analogy to r_min increasing for our case). We assume that in our quasi-equilibrium states, there is almost no redistribution of monomers between the surround and nanodomains. Eventually, a true equilibrium state—two global phases—of phase separation is reached. We estimate, for γ = 0.2 pN, the time necessary to reach this equilibrium state by noting that γ_min and γ_max decrease with increasing r_min (see Eqs. 53 and 54 and Fig. 6). From Fig. 6, it follows that the nanodomain ensemble is stable for r_min < 40 nm (γ < γ_min), but the system transforms into a global phase for r_min > 100 nm. The time for r_min to enlarge from 40 nm to 100 nm thus provides an estimate for the time to reach equilibrium. From Eqs. 25 and 26, it is ∼3 h. The accuracy of this estimate is limited by our assumption that Ostwald ripening occurs for immobile nanodomains.

In the Appendix, we used the traditional theory of dilute solutions (subject to 1 ≪ n ≪ N) to calculate the distribution of domain size after the independent growth stage (42,43), an approach used for similar membrane problems (23,44). When φ_∞ = 0.1, the ideal gas approximation leads to Eq. A52, which is correct for small line tensions. In the coexistence region, γ_min < γ < γ_max, the condition n ≫ 1 violates an assumption of the approximation, and so we formulated a simplified model, which allowed us to obtain results that were self-consistent over a wide range of parameters. This model is not applicable, however, for a narrow region of line tension around γ = γ_min and it does not describe a gradual transition from small nanodomains to slightly larger domains.

We assumed that the domains were circular for the range of line tensions considered. This approximation is valid because thermal fluctuations do not significantly alter the geometry of the interface; as derived by standard procedures (45,46), the normalized mean fluctuation for large domains is

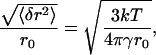(55)

where 〈δr²〉 is the mean-squared fluctuation and r₀ is the radius of domain. Even for a small tension, γ = 0.1 pN, which is less than γ_min = 0.18 pN, the normalized mean fluctuation is only ∼3% for a r₀ = 10 μm domain. Note that long wavelengths are cut off for nanodomains, so there are fewer boundary fluctuations, leading to less entropy for nanodomains compared to larger domains; we neglect this effect. We also note that this article analyzes the metastable initial state between the binodal and spinodal curves and far enough from the critical point, which is very different from an unstable initial state (e.g., near the critical point) where much larger fluctuations are predicted by simulation.

The main parameters that enter our equations are φ_∞, γ, and the diffusion coefficients of lipid molecules, D, and of domains of various sizes, D_d. The value D is known and the Saffman-Delbruck equation allows us to calculate D_d. We used published experimental data for the area fraction φ_∞ (18), but we also varied this parameter. Line tension γ has been estimated as 0.9 pN for a single lipid composition (17). We have shown that our theoretical predictions are not very sensitive to the precise values of φ_∞ and γ, and thus our conclusions should be generally valid.

Stabilization of nanodomains

Colloidal particles can rapidly coagulate if they are not kinetically stabilized (37,38). However, it has also been known for half a century that, at thermodynamic equilibrium, immiscible colloidal particles will remain dispersed if the interfacial tension is sufficiently low (47). However, nanodomains in cellular membranes and lipid bilayers are miscible with their surrounding membrane solution and thus it was possible that miniscule line tensions would make it impossible for entropy to stabilize nanodomains against merger. We have now explicitly determined the conditions necessary for nanodomains to remain dispersed in membranes. If the time interval is not too long (<1 h), our system is effectively a suspension of immiscible two-dimensional domains.

Nanodomains remain in quasi-equilibrium for low line tension (γ < γ_min) at the conclusion of the independent growth stage. At these low line tensions, the nanodomain size distribution is narrowly peaked around r ∼ r_c ∼ r_min (see Fig. 3), because they are effectively arrested in size by an “entropic trap”. Nanodomain growth occurs by Ostwald ripening: for r < r_min = r_c, nanodomains quickly dissolve (see Eq. A20) and this promotes the slow enlargement of nanodomains for r ≥ r_min. For greater line tension (γ_min < γ < γ_max), a fraction of the nanodomains merge and a global, phase-separated region is created. At higher line tension (γ > γ_max), nanodomains quickly merge to micrometer-scale domains, which then slowly evolve. In principle, the rate of merger is limited by relatively low mobility of the domains and any repulsion that kinetically hinders their merger.

The mobility of the domains does not vary appreciably with size (Eq. 35), but the repulsion forces do; these forces are of great consequence only for large domains. We estimated these repulsions by ignoring chemical contributions and assuming that repulsions are caused by the elastic membrane deformations that must occur at the boundary of a domain and surround of different thickness (41). For this elastic model, the height of the repulsive barrier is close to 1, W = 1.2, for r ∼ 40 nm, but is orders-of-magnitude higher, W ∼ 10⁴, for a 1-μm domain (Eq. 43). Undulations of the boundary lower the barrier.

The relation of theory to experiment

In planar lipid bilayers and lipid vesicles (10–13,15), domains are circular and slowly (∼1 h) enlarge through merger for radii greater than several microns. This is in agreement with our estimates for the rate of domain merger (Eq. 42). The estimation of γ ≈ 0.9 pN for large domains in lipid vesicles (17) is in accord with our prediction that micrometer scale domains appear for γ > γ_max ∼ 0.4 pN. Nanodomains have also been detected in lipid model systems (18), but their physical properties, such as line tension and evolution, have not yet been determined.

In cellular membranes, the causes of nanodomain (raft) formation are quite controversial. It is even still debated whether lipid and protein do associate into rafts. Some studies support their existence and stability, and infer their size (26 ± 13 nm) (7), whereas other studies favor transient or nonexistent structures (8). The line tension of rafts in cellular membranes has not yet been measured, and raft dynamics have not been explored. If line tensions are small, this article shows that rafts can be quantitatively described as a system in thermodynamic quasi-equilibrium.

If it should prove that line tension of small rafts is high, several mechanisms may be contributing to their stability. Rafts may not be a product of phase separation, but rather form by a process that is physically equivalent to wetting: if a protein served as a nucleation center for condensing specific lipids around it, a thin film of a lipid phase, different than the surrounding homogeneous membrane, would be created (23). This is analogous to the formation of a thin liquid film on a solid surface exposed to vapor. If a film of lipids caused attraction between proteins, larger lipid/protein domains would result (24). The size distribution of domains that form in this way have been derived by methods of statistical mechanics (23) and are similar to those obtained in this study. Alternatively, rafts may emerge as a consequence of exocytosis and endocytosis (2), particularly if the uptake of rafts depends on the size of the raft. In this way, cells could perpetuate the nanoraft state by removing large rafts from the plasma membrane before the point of global phase change, and delivering monomers that supersaturate the plasma membrane upon mixing with it. More physically, because a cell membrane is an open system (rather than isolated, as we and others assume for convenience) in contact with intracellular pools of membranes, rafts could form as a result of dissipative processes.

Regardless of the physics that underlie cellular membrane domain formation, our study leads us to a novel suggestion. Because of the major result showing that fission and fusion are much faster (and thus more efficient) mechanisms for moving lipids and proteins from one object to another compared to ripening, this major result may be true for the case of bilayer membranes as well. If so, then we can more readily understand why eukaryotic cells use membrane (not domain) fission and fusion for cargo and membrane transport to almost the exclusion of creating carriers within the cytoplasm for shuttling small hydrophobic molecular weight components about. The system of vesicular traffic so widely studied today may have its roots in the physics of colloids.

APPENDIX

The growth law for a macroscopic nucleus in a multicomponent system

Equation 15 provides a means to calculate the growth of a macroscopic nucleus in a two-dimensional multicomponent membrane. However, to evaluate j_i, we must first determine the value of c_ir that appears in Eq. 14. To obtain c_ir, we rewrite Eq. 4 in the form

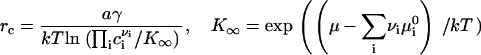(A1)

As described in Slezov and Schmelzer (25), Lifshitz and Pitaevskii (30), and Slezov (32), Eq. A1 leads to

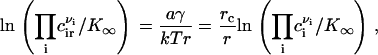(A2)

where c_ir is the equilibrium concentration of i^th component near a nucleus of radius r. Taking the limit r → ∞ in Eq. A2, we obtain

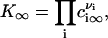(A3)

where c_i∞ is the equilibrium concentration of i^th component at a straight interface. We transform Eq. A2 into a logarithmic form, and for small levels of supersaturation, expand the logarithm and use Eq. A3 to obtain

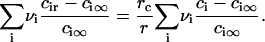(A4)

Equations 15 and A4 yield c_ir for every i.

To calculate the rate of increase of the radius of nucleus, we use Eqs. 1 and 15 to express dr/dt as a function of the partial fluxes j_i,

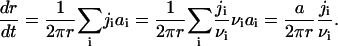(A5)

We multiply both sides of Eq. A5 by 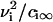, sum over all components, and use Eq. 14 to obtain

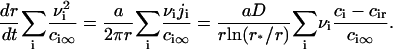(A6)

Using Eq. A4 to exclude c_ir from Eq. A6, we obtain

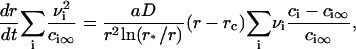(A7)

which yields the equation

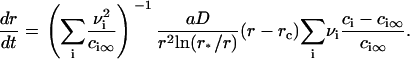(A8)

We introduce the total supersaturation Δ and the effective equilibrium concentration ,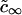

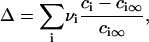(A9)

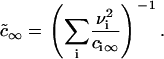(A10)

Equations A1 and A3 yield, for small supersaturation,

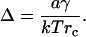(A11)

Equation A8 takes the form

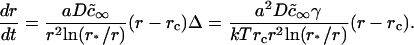(A12)

We use Eq. A12 in the main text to obtain the mobility of nuclei, U, in r-space. The only difference between Eq. A12 derived for a multicomponent system and the equation derived for a one-component system case is the substitution 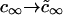. It is of practical importance that the equations of a one-component system readily generalize to multicomponent systems.

Estimating the duration of the nucleation stage

In the main body of text, we assumed that nucleation ceases when the flux decreases by a factor 10. To find the critical radius at the end of nucleation, 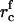, we use Eq. 18,

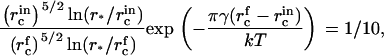(A13)

where the initial critical radius 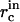can be obtained from Eqs. A9 and A11 for 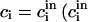are the initial concentrations). Equation A13 defines 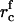as a function of 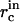and γ, which allows us to use Eqs. A9 and A11 to find the concentrations 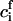at t = τ_n,

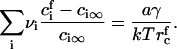(A14)

The composition of the nucleus remains constant during nucleation, allowing us to write (see also Eq. 15)

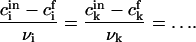(A15)

Multiplying the reduction in concentration by 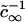and using Eq. A15, we obtain

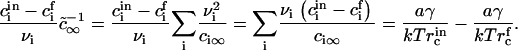(A16)

Hence, the total number of created nuclei N_f is

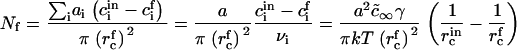(A17)

We estimate the nucleation time τ_n from the ratio of the total number of nuclei created, N_f, Eq. A17, to the average value of the flux. This yields

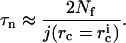(A18)

Eqs. A13, A17, and A18 are used to obtain numerical estimates for 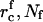, and τ_n as described in the main text.

Dissolution of a subcritical domain

In the main text, we assumed that after a subcritical nanodomain pinches off a large domain, it quickly dissolves and equilibrium is maintained among the ensemble of subcritical nuclei. In fact, fast dissolution is not merely an assumption, but a physically correct assertion.

Diffusion of matter in the background solution limits the rate at which a domain of radius r_d < r_c moves toward smaller radii in r-space. We use Eq. A12 to estimate the dissolution rate of a subcritical nanodomain. Because ln(r_*/r) and r_c do not change appreciably during the nucleation stage, we can consider them constant values and write

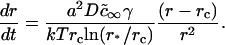(A19)

Equation A19 is easily integrated for r(0) = r_d and r(τ_diss) = 0, yielding the characteristic time of dissolution τ_diss,

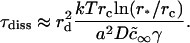(A20)

Using the parameters of our standard bilayer and γ = 0.4 pN, we obtain τ_diss ∼ 2 × 10⁻³ s for r_d = 20 nm and r_c = 40 nm. The value τ_diss is small and independent of φ_∞.

Ostwald ripening in the case of a two-dimensional multicomponent system

We show that the approach of Marqusee for a one-component, two-dimensional system (36) generalizes to the case of a two-dimensional multicomponent membrane. The assumption that the composition of an evolving phase does not depend on nucleus size allows us to introduce fixed stoichiometric coefficients {ν_i}. We describe growth of a nucleus as the addition of structural units where the area per structural unit is

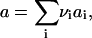(A21)

and a_i is the cross-sectional area per molecule of the i^th component. Rather than introduce a cutoff radius, we consider the ensemble of domains as an effective medium. We assume that the partial flux, j_i, of the i^th component (number of i^th component molecules passing through the interface of a nucleus of radius r per second) has the form of

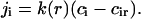(A22)

We introduce k(r) to account for effects of competition between nuclei; this removes the divergences that occur in the two-dimensional steady-state diffusion equation. We now obtain the factor k(r) (Eq. A31). The change of bulk concentration c_i is

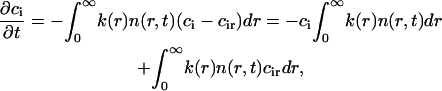(A23)

where n(r, t) is the domain distribution function; n(r, t)dr is thus the number of domains of radius (r, r+dr) per cm². The diffusion equation for the local concentration 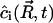can be written as

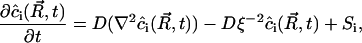(A24)

where D is the diffusion coefficient (equal for all components). The sink term is

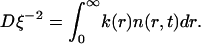(A25)

The source term is

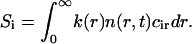(A26)

The balance in the bulk at steady state yields

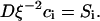(A27)

Moreover, in steady state, 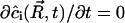. That is, 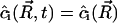. Using Eqs. A24–A27, we obtain

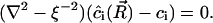(A28)

Here, ξ is effectively a screening length. The obvious boundary conditions for Eq. A28 are 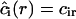and 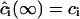. The solution of Eq. A28 for steady-state diffusion is

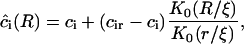(A29)

where K₀(R/ξ) is a modified Bessel function of zero-order. The partial flux is

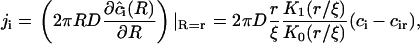(A30)

where K₁(r/ξ) is a modified Bessel function of first-order. A comparison of Eqs. A22 and A30 yields

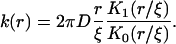(A31)

Using Eq. A25, we obtain

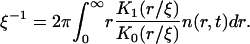(A32)

To obtain the growth law, we invoke constant stoichiometry of components within a domain, independent of size (see Eq. 15). The growth law follows from Eqs. 15, A4, and A22 in a manner similar to that used to derive growth in the first section of the Appendix. The final expression is

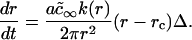(A33)

Using Eqs. A11 and A31, we rewrite Eq. A33 as

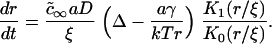(A34)

The domain distribution function obeys the continuity equation in r-space of

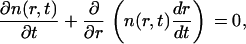(A35)

where dr/dt is defined by Eq. A34. The law of mass conservation for the components has the form

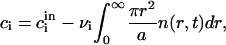(A36)

where 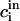is initial bulk concentration of i^th component. Therefore

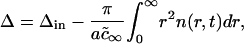(A37)

where Δ_in is initial total supersaturation. In the limit t → ∞, we obtain from Eq. A37 that

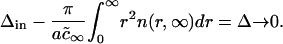(A38)

Hence, the area fraction of new (domain) phase φ_∞ can be expressed as

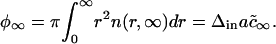(A39)

To find n(r, t) and other characteristics of Ostwald ripening we transform to dimensionless variables and solve the system of Eqs. A32, A34, A35, and A37. The dimensionless radius is

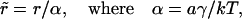(A40)

and dimensionless time and screening length are

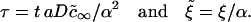(A41)

We used Eq. A39 to renormalize the distribution function n(r, t) as

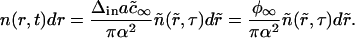(A42)

In dimensionless variables, Eq. A32 yields

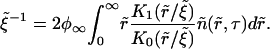(A43)

The growth law is

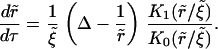(A44)

The continuity equation is

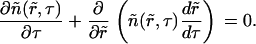(A45)

The mass conservation law is

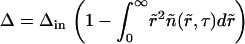(A46)

The system of the dimensionless Eqs. A43–A46 is the same as the system of dimensionless Eqs. 3.11–3.14 from Marqusee (36), although the process we used to make variables dimensionless, Eqs. A40–A42, is different from the one used in Marqusee (36). Therefore, the average dimensionless radius derived from Eqs. A43–A46 is the same as that obtained in Marqusee (36),

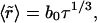(A47)

where b₀ is a factor of order one, as calculated numerically. Using Eqs. A40 and A41 to transform back to the dimensional variables, we obtain

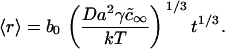(A48)

Similarly, the density of domains is given by

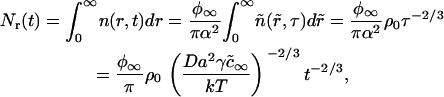(A49)

where ρ₀ is a factor of order one, calculated numerically. We have thus demonstrated that the substitution 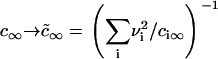allows one to transition from a one-component to a multicomponent system.

Domain size distribution in quasi-equilibrium

Let us consider the regime where Ostwald ripening contributes very slowly and to a modest increase in r_c. According to Eq. 27, the characteristic time τ_r of this process for 〈r〉 ∼ 50 nm and γ ∼ 0.2 pN is ∼1 h. At t > τ_r, the system goes asymptotically into the global phase, which is the true equilibrium state. Therefore, at the time interval τ_ig < t < τ_r we can assume that the system is in a state of quasi-equilibrium. Consequently, standard approaches of statistical thermodynamics can be applied to calculate the domain size distribution for times τ_ig < t < τ_r. (42,43). We consider a domain ensemble with r_min ≤ r ≤ r_max, where r_min = 〈r〉 at t = τ_ig and r_max is defined by the condition that matter is conserved. We assume that the domains have already resulted from the first-order phase transition and each domain has the same composition as the new global phase. We derive the domain size distribution considering discrete, rather than continuous, values of radii. In our model a domain of radius r_m contains m more structural units than does a minimal-sized domain. Quantitatively, 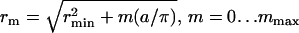, where , a is the area per structural unit, and A_r is the total area occupied by domains. The system is isolated, so matter is conserved as

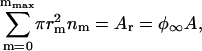(A50)

where n_m is the number of domains with the radius r_m and φ_∞ is the fractional area occupied by domains. The part of the free energy of the system dependent on n_m is given by (23,44)

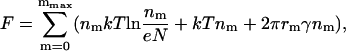(A51)

where N = A/a is the total number of lipid molecules in a monolayer. The first term in Eq. A51 corresponds to the configurational entropy for dilute solutions, the second term is the kinetic energy (kT/2 per degree of freedom, two degrees of freedom per domain) and the last term is the boundary energy of the domain. Equation A51 is valid only if 1 ≪ n_m ≪ N. We neglect interactions between domains and treat the domain ensemble as an ideal gas (23). Minimization of the free energy, Eq. A51, subject to the constraint of Eq. A50, yields the domain size distribution

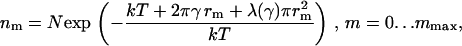(A52)

where λ(γ) is the Lagrange multiplier of the constraint. To determine λ(γ), we substitute n_m of Eq. A52 into Eq. A50 and obtain the equation

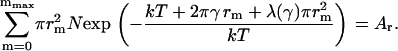(A53)

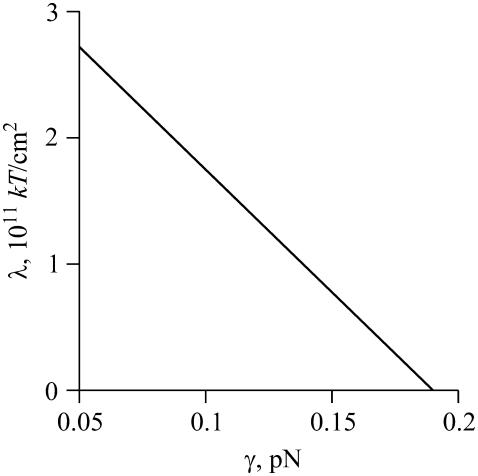
The numerical solution of Eq. A53 for A_r = 10⁻⁵ cm² is shown in Fig. A1. For γ < 0.18 pN, λ(γ) > 0 and the term within the exponential of Eq. A52 monotonically decreases with r_m. From Eq. A52 and the numerically evaluated λ(γ), we obtain the number of domains as a function of domain radius for different values of γ (Fig. 3). As γ increases, the reduction in boundary energy upon merger becomes more significant. Even for a relatively small increase in line tension (γ₂ – γ₁ = 0.12 pN for curves 1 and 2 in Fig. 3), the distribution shifts to large domain sizes. At sufficiently large γ, a single large domain (i.e., a global phase) must exist if the system is to reach minimum free energy. Unfortunately, it was not possible to find the domain size distribution (i.e., n_m, for m = 0…m_max) from Eqs. A51–A53, at λ < 0, because the condition n_m ≫ 1 contradicts n_m ∼ 1, which must hold for a single large domain. We overcame this problem by simplifying the system (see text).

FIGURE A1.

The dependence of the Lagrange multiplier λ, numerically calculated from Eq. A53, on line tension γ.