Abstract
This study compares the rate of denaturation with sodium dodecyl sulfate (SDS) of the individual rungs of protein charge ladders generated by acylation of the lysine 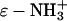 groups of bovine carbonic anhydrase II (BCA). Each acylation decreases the number of positively charged groups, increases the net negative charge, and increases the hydrophobic surface area of BCA. This study reports the kinetics of denaturation in solutions containing SDS of the protein charge ladders generated with acetic and hexanoic anhydrides; plotting these rates of denaturation as a function of the number of modifications yields a U-shaped curve. The proteins with an intermediate number of modifications are the most stable to denaturation by SDS. There are four competing interactions—two resulting from the change in electrostatics and two resulting from the change in exposed hydrophobic surface area—that determine how a modification affects the stability of a rung of a charge ladder of BCA to denaturation with SDS. A model based on assumptions about how these interactions affect the folded and transition states has been developed and fits the experimental results. Modeling indicates that for each additional acylation, the magnitude of the change in the activation energy of denaturation (ΔΔG‡) due to changes in the electrostatics is much larger than the change in ΔΔG‡ due to changes in the hydrophobicity, but the intermolecular and intramolecular electrostatic effects are opposite in sign. At the high numbers of acylations, hydrophobic interactions cause the hexanoyl-modified BCA to denature nearly three orders of magnitude more rapidly than the acetyl-modified BCA.
groups of bovine carbonic anhydrase II (BCA). Each acylation decreases the number of positively charged groups, increases the net negative charge, and increases the hydrophobic surface area of BCA. This study reports the kinetics of denaturation in solutions containing SDS of the protein charge ladders generated with acetic and hexanoic anhydrides; plotting these rates of denaturation as a function of the number of modifications yields a U-shaped curve. The proteins with an intermediate number of modifications are the most stable to denaturation by SDS. There are four competing interactions—two resulting from the change in electrostatics and two resulting from the change in exposed hydrophobic surface area—that determine how a modification affects the stability of a rung of a charge ladder of BCA to denaturation with SDS. A model based on assumptions about how these interactions affect the folded and transition states has been developed and fits the experimental results. Modeling indicates that for each additional acylation, the magnitude of the change in the activation energy of denaturation (ΔΔG‡) due to changes in the electrostatics is much larger than the change in ΔΔG‡ due to changes in the hydrophobicity, but the intermolecular and intramolecular electrostatic effects are opposite in sign. At the high numbers of acylations, hydrophobic interactions cause the hexanoyl-modified BCA to denature nearly three orders of magnitude more rapidly than the acetyl-modified BCA.
INTRODUCTION
Background
Interactions of proteins with surfactants are important in biochemistry, but incompletely understood. Probably the most common example of the use of protein-surfactant interactions in biochemistry is SDS-polyacrylamide gel electrophoresis (SDS-PAGE) (1), a technique used to separate proteins based on their molecular weight. Other examples of the use of surfactants in protein science include the solubilization and reconstitution of membrane-associated proteins by detergents (2–4), and stabilization of drugs (5–7).
The aggregates formed between proteins and SDS have been investigated extensively, but their structures, and the mechanism by which they are formed, still have not been established unambiguously. When fully denatured in SDS, proteins bind ∼1.4 g of SDS per g of protein (or ∼1 SDS molecule per 2 amino acids) (8–11). A wide variety of models has been proposed for the structure of the denatured protein-SDS aggregate (12,13):
In the “rod-like model” (10), the SDS molecules form a shell along the length of the protein backbone.
In the “pearl necklace model” (14), micelle-like structures of SDS are scattered along the chain of the denatured protein. The protein passes through micelles of approximately constant size.
In the “flexible α-helix/random coil model” (15), SDS increases the propensity of cationic residues to form α-helices.
In the “flexible-helix model” (16), the detergent molecules form a flexible, capped cylindrical micelle, around which the hydrophilic segments of the polypeptide associate. The major stabilizing interaction in this model is hydrogen bonding between the oxygen atoms in the SDS molecules and the nitrogen atoms of the polypeptide backbone.
In the “protein decorated micelle model” (12), the protein is located on the outside of micelles of differing sizes.
All these models aim to explain the observation of a constant ratio of SDS molecules to the number of amino acids in the protein-SDS aggregates, but experimental results have not been able to distinguish conclusively between them.
Recent work (17) strongly suggests that molecules of SDS that are associated with the protein are organized into micelles. It appears that either the pearl necklace or protein decorated micelle model is the most accurate of the five models for the protein-SDS aggregate. For bovine serum albumin (BSA), Turro et al. (18) showed, using NMR, that the mobility of the sulfate headgroups was very small and concluded that BSA is coiled predominantly around the exterior of the bound SDS molecules. For this protein, the most likely structure of the protein-SDS aggregate was the protein-decorated micelle. Xu and Keiderling (19) studied the acid-denatured state of cytochrome c and showed that, at high concentrations of SDS (0.5 M), some of the protein was located inside micelles (the pearl necklace model) whereas some of the protein remained on the surface of micelles (protein decorated micelle model).
Regardless of the structure of the aggregate, both the mechanism of denaturation and the contributions of electrostatic and hydrophobic interactions to the denaturation of proteins by SDS remain incompletely understood. Many groups have used equilibrium dialysis and calorimetry (20–23) to demonstrate that at low concentrations of SDS, the average number (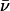 ) of SDS molecules bound to a protein molecule increases sharply as the SDS concentration is raised. The binding then reaches a plateau near values of
) of SDS molecules bound to a protein molecule increases sharply as the SDS concentration is raised. The binding then reaches a plateau near values of 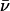 roughly equal to the number of cationic residues in the protein, and increases sharply again as the SDS concentration approaches the critical micelle concentration (cmc) (13). At low concentrations of SDS, the binding is mainly electrostatic, with some simultaneous interaction of the hydrophobic tail with nearby hydrophobic patches on the protein. These initial interactions presumably cause some protein unfolding and expose additional hydrophobic sites. More SDS molecules then bind to the exposed hydrophobic sites in the protein-SDS aggregate (24,25).
roughly equal to the number of cationic residues in the protein, and increases sharply again as the SDS concentration approaches the critical micelle concentration (cmc) (13). At low concentrations of SDS, the binding is mainly electrostatic, with some simultaneous interaction of the hydrophobic tail with nearby hydrophobic patches on the protein. These initial interactions presumably cause some protein unfolding and expose additional hydrophobic sites. More SDS molecules then bind to the exposed hydrophobic sites in the protein-SDS aggregate (24,25).
Although the overall picture described by these theories is probably qualitatively correct, the mechanistic details almost certainly differ among proteins, and the distinction made between the two regimes—primarily electrostatic, and primarily hydrophobic—is probably blurred in many cases. The objective of this study was to distinguish between the effects of charge and of hydrophobicity on the kinetics of denaturation of a model protein, bovine carbonic anhydrase (BCA, E.C. 4.2.1.1), and of derivatives of this protein generated by acylation, having different charges and hydrophobicities.
EXPERIMENTAL DESIGN
BCA is a good model for studying processes involving denaturation
BCA is easy to handle, monomeric, and commercially available; it has no disulfide bonds (26,27). Its structure is well-defined by x-ray crystallography (28,29), and its binding of arylsulfonamide inhibitors is also structurally well-defined (30). A wide range of those inhibitors is commercially available and synthetically accessible. There is an extensive literature describing the denaturation of BCA with other denaturants, i.e., urea and guanidinium chloride (GuHCl) (31–40). These studies showed that the rate of folding of BCA is determined by the isomerization of proline residues (35,41), that BCA is not completely unfolded, even in saturated solutions of GuHCl (39,42, 43), and that BCA, like many proteins that have a large fraction of its structure in β-sheets, is particularly susceptible to aggregation in the partially (un)folded state (44–46).
The denaturation and renaturation of BCA with SDS is well-characterized: it is reversible at low concentrations of SDS (<0.1 mM), and easily followed by capillary electrophoresis (CE) (47,48). Yang et al. (49) synthesized a derivative of BCA, BCA-Ac18 (all 18 lysine groups acetylated), in which the tertiary structure of the proteins is indistinguishable (by catalysis and circular dichroism) from the native structure, but where the external surface of the proteins lacks all 18 of the positively charged lysine 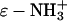 groups present in the native protein. After denaturation with SDS, both BCA and BCA-Ac18 refold with similar rates (11 ± 1 min for BCA and 21 ± 2 min for BCA-Ac18) (50) to the same (native) structure upon complete removal of the SDS.
groups present in the native protein. After denaturation with SDS, both BCA and BCA-Ac18 refold with similar rates (11 ± 1 min for BCA and 21 ± 2 min for BCA-Ac18) (50) to the same (native) structure upon complete removal of the SDS.
In a previous study, we demonstrated that the Zn(II) cofactor of CA does not complicate studies of refolding of CA (48). The Zn(II) cofactor is not required for refolding into a native-like conformation, does not remain associated with the unfolded protein, and does not significantly change the rate of refolding. The presence of the Zn(II) cofactor during refolding, however, does increase the total amount of recovered protein by a factor of 2. All of the solutions used in this study contain 100-μM Zn(II), so that any folded BCA or BCA-derivative contains the Zn(II) cofactor (and therefore binds inhibitors).
Protein charge ladders: systematic variation of protein charge
Reaction of BCA with limited quantities of an anhydride converts some of the 18 lysine-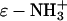 groups to lysine-ɛ-NHCOR groups. The derivatives appear in CE as a set of peaks with regular spacing, a protein charge ladder (51,52). Each “rung” of the charge ladder (with the exception of the native and completely acylated forms) is, we assume, a set of regioisomers with the same number, but different distribution, of modified lysine residues, and therefore, approximately the same net charge. Charge ladders are thus a family of derivatives of a protein, in which the charge can be changed systematically. Using different acylating reagents, we can independently vary another parameter—hydrophobicity—and use the charge to count the number of modifications. Variation in the extent of acylation, and in the structure of the acylating reagent, allow charge and hydrophobicity to be changed independently.
groups to lysine-ɛ-NHCOR groups. The derivatives appear in CE as a set of peaks with regular spacing, a protein charge ladder (51,52). Each “rung” of the charge ladder (with the exception of the native and completely acylated forms) is, we assume, a set of regioisomers with the same number, but different distribution, of modified lysine residues, and therefore, approximately the same net charge. Charge ladders are thus a family of derivatives of a protein, in which the charge can be changed systematically. Using different acylating reagents, we can independently vary another parameter—hydrophobicity—and use the charge to count the number of modifications. Variation in the extent of acylation, and in the structure of the acylating reagent, allow charge and hydrophobicity to be changed independently.
Comparison of rates of denaturation of acetyl- and hexanoyl-charge ladders of BCA
In this study, we compare the rates of denaturation of two charge ladders of BCA, one prepared with acetic anhydride, (CH3CO)2O (BCA-Acn), and one prepared with hexanoic anhydride, (CH3(CH2)4CO)2O (BCA-Hexn). We studied the kinetics of denaturation of both for two reasons: i), because the kinetics of interaction of proteins and surfactants represents an unexplored area; and, ii), practically, because we were unable to measure the equilibrium constants between native and denatured states for BCA and the members of the charge ladders; the rates of denaturation and renaturation are intractably slow at the intermediate (1–2.5 mM) concentrations of SDS that would be required for equilibration (47). In addition, another process, presumably aggregation of partially folded intermediates, occurs at low concentrations of SDS (0.7–2.5 mM) and prevents equilibration of the folded and denatured states (47).
All members of the charge ladders used in this study are stable at room temperature in the absence of denaturant. Each rung of both of the charge ladders used here binds sulfonamide inhibitors (53) (Kd ∼ 0.3–1.3 mM, Fig. S1, Supplementary Material). We conclude that all of the rungs retain a common active-site structure, and, we presume, a common tertiary structure.
For any charge ladder of BCA, as the number of modifications (n) increases, the total charge on the protein becomes more negative, and the surface of the protein becomes more hydrophobic due to conversion of 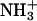 groups to NHCOR groups. Native BCA has a charge of ∼−2.9 at pH 8.4 (50). The charge on the early rungs of the ladder increases linearly with the number of acylations; each rung adds an additional charge of ∼−0.9 (54,55). Therefore, for example, BCA-Ac8 has a charge of ∼−10. The later rungs of the ladder may differ by <0.9 units of charge (56). Using the Linderstrøm-Lang model of cooperativity in proton binding (57), we calculated the charge on BCA-Ac18 to be −19 (50). The mobility of a given rung of BCA-Acn has nearly the same mobility as the corresponding rung of BCA-Hexn. We therefore assume that the charges of the BCA-Hexn are indistinguishable from those of BCA-Acn for a given rung number. (Small deviations in mobility between later rungs of the two ladders may be due either to a change in charge or a change in drag between the two ladders. We assume that any differences in the mobilities are due to additional drag from the hexanoyl groups relative to the acetyl groups.)
groups to NHCOR groups. Native BCA has a charge of ∼−2.9 at pH 8.4 (50). The charge on the early rungs of the ladder increases linearly with the number of acylations; each rung adds an additional charge of ∼−0.9 (54,55). Therefore, for example, BCA-Ac8 has a charge of ∼−10. The later rungs of the ladder may differ by <0.9 units of charge (56). Using the Linderstrøm-Lang model of cooperativity in proton binding (57), we calculated the charge on BCA-Ac18 to be −19 (50). The mobility of a given rung of BCA-Acn has nearly the same mobility as the corresponding rung of BCA-Hexn. We therefore assume that the charges of the BCA-Hexn are indistinguishable from those of BCA-Acn for a given rung number. (Small deviations in mobility between later rungs of the two ladders may be due either to a change in charge or a change in drag between the two ladders. We assume that any differences in the mobilities are due to additional drag from the hexanoyl groups relative to the acetyl groups.)
Hydrophobicity parameters (Hansch π-parameters, log P-values) are often used to quantify the hydrophobicity of modifications to molecules (59). The change in hydrophobicity from 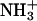 (log P = −2.12) (60) to NHCOCH3 (one modification using acetic anhydride, log P = −1.21) (61,62) is +0.9, that is, more hydrophobic. The change in log P for the change from
(log P = −2.12) (60) to NHCOCH3 (one modification using acetic anhydride, log P = −1.21) (61,62) is +0.9, that is, more hydrophobic. The change in log P for the change from 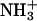 to NH(COCH2)4CH3 (one modification with hexanoic anhydride) is +2.9 (62).
to NH(COCH2)4CH3 (one modification with hexanoic anhydride) is +2.9 (62).
Capillary electrophoresis
We use capillary electrophoresis to monitor the denaturation of charge ladders of BCA. As the negatively charged SDS molecules interact with the proteins, the electrophoretic mobility of the complex increases above that of BCA-Ac18; all of the rungs of both of the ladders have indistinguishable mobilities when they are denatured with SDS. Because the mobilities of the denatured proteins—fully associated with SDS—are much larger than the mobilities of any folded proteins, we can observe all of the rungs of the charge ladder and the denatured protein in the same sample. We detect proteins using absorption at 214 nm; at this wavelength, the amide bonds and aromatic side chains of the protein absorb, but the SDS is transparent. Thus, there is no interference from micelles of SDS, and CE can be used with SDS both above and below the cmc.
Model of the kinetics of the interaction of charge ladders of BCA with SDS
We interpret the kinetics of denaturation using transition state theory (Eq. 1). In this equation, we can relate the experimentally measured rate (k) to the activation energy (ΔG‡), or the
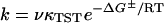 |
(1) |
difference in energy between the folded, starting state, and the conformations in the saddle point of the reaction. In Eq. 1, ν is a characteristic vibration frequency along the reaction coordinate at the saddle point and κTST is a transmission coefficient. For simple chemical reactions, κTST is often assumed to be 1; that is, all of the molecules passing through the transition state proceed to product, and ν = kbT/h (∼6 × 1012 s−1) where kB is the Boltzmann constant, T is the temperature, and h is the Plank constant. For protein folding, however, the transmission through the saddle point is believed to be much less than unity. An empirical estimate for νκTST in the folding of proteins is 106 s−1 (62,63). This number was calculated for cytochrome c (tfolding  400 ms) (64) and is, probably, an underestimate for BCA because it is a larger protein than cytochrome c and folds much more slowly (tfolding
400 ms) (64) and is, probably, an underestimate for BCA because it is a larger protein than cytochrome c and folds much more slowly (tfolding  10 min) (50,65,66). Assuming that νκTST does not change with type or number of acylation, an incorrect estimate for νκTST will affect only the scale of ΔG‡. An underestimate in the value of νκTST will lead to an overestimate in the value of ΔG‡.
10 min) (50,65,66). Assuming that νκTST does not change with type or number of acylation, an incorrect estimate for νκTST will affect only the scale of ΔG‡. An underestimate in the value of νκTST will lead to an overestimate in the value of ΔG‡.
Qualitative description of the model of SDS-protein interaction
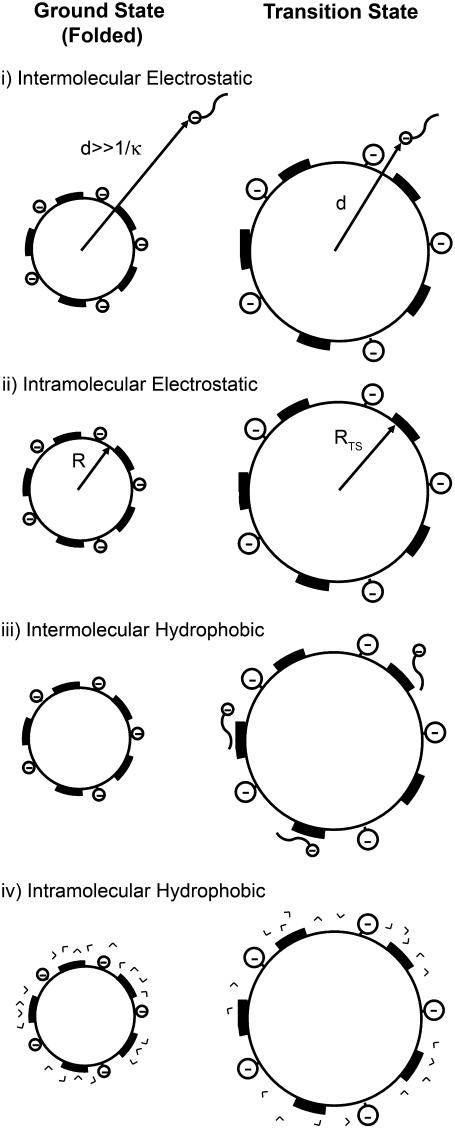
We propose that each acylation influences the activation energy, and thus the rate of denaturation of the rungs of charge ladders of BCA in four ways (see schematic diagram in Fig. 1).
Intermolecular electrostatic interaction. Each acylation increases the electrostatic repulsion between the more negatively charged proteins and the negatively charged SDS relative to the electrostatic repulsion between BCA and SDS. The increased electrostatic interaction increases the stability (and therefore, ΔG‡) of the latter rungs of the charge ladder, relative to unmodified BCA, to denaturation by SDS.
Intramolecular electrostatic interaction. Each acylation decreases the stability of the folded protein, relative to BCA, by increasing the net charge on its surface. The charge-charge repulsion destabilizes the folded state of a protein relative to BCA and makes the latter rungs of the charge ladder less stable than the early rungs to denaturation by SDS. The intramolecular electrostatic repulsion decreases ΔG‡ of each rung of the charge ladder relative to ΔG‡ of BCA.
Intermolecular hydrophobic interaction. Each acylation also increases the exposed hydrophobic surface area and destabilizes the folded protein relative to BCA due to an increase in the interaction between the protein and the hydrophobic tails of the SDS molecules.
Intramolecular hydrophobic interaction. Each acylation destabilizes the folded protein relative to BCA due to an increase in exposed hydrophobic surface area and an increased ordering of water in the folded state relative to unmodified BCA. Both of the effects of increased hydrophobic surface area (effects iii and iv) should make the latter rungs of the charge ladder less stable than the early rungs to denaturation with SDS.
FIGURE 1.
Schematic representation of the four factors discussed in the text for the model of protein denaturation. The protein is represented as a sphere with uniformly distributed negative charge on its surface. The dark patches represent hydrophobic regions on the surface of the protein that result from acylations. The depictions of SDS molecules are wavy lines (dodecanoic chain) with negatively charged headgroups (sulfate group). V-shaped entities represent water molecules.
This model does not account for any specific (local) interactions that are created or destroyed by acylation (e.g., removal of salt bridges between lysine and other anionic residues on the protein, steric interactions caused by increasing the size of the lysine residue, or specific interactions between positively charged residues and molecules of SDS); it treats the protein as a distribution of charges and hydrophobic surface area. A number of groups (67–69) have proposed that positively charged residues on the surface of the protein provide places for the negatively charged SDS molecules to bind and nucleate further unfolding. We neglect any such site-specific nucleation process in our model. Although neglecting local interactions runs the risk of neglecting important specific interactions, we demonstrate that our model replicates the trends in the data without using them. There is thus no need, at least for BCA, to consider local interactions to describe how the rate of denaturation changes with acylation of lysine residues.
We wished to quantify the relative importance of these stabilizing (electrostatic) and destabilizing (hydrophobic and electrostatic) effects as the number of modifications increased. In comparing rungs with the same number of modifications, n, across charge ladders made with different anhydrides, the charge remains the same, but the hydrophobicity differs. We assume that the patterns and regioselectivity of acylation with acetyl and hexanoyl ladders are similar. Thus, we can distinguish the effects of charge and hydrophobicity in one experimental system.
EXPERIMENTAL PROCEDURES
Sources of chemicals and reagents
All chemicals were reagent grade unless stated otherwise. Acetic anhydride, hexanoic anhydride, bovine carbonic anhydrase, 10× Tris-Gly concentrate, HEPBS, dioxane, and dimethylformamide were purchased from Sigma Chemical (Milwaukee, WI). Dialysis cassettes (weight cutoff of 10 kDa) and desalting spin columns were purchased from Pierce (Rockford, IL). SDS (Baker Chemical, Phillipsburg, NJ) was recrystallized in hot ethanol three times, then dried and stored at −20°C until use. SDS was discarded or repurified after 2 months. Tris-Gly buffer was made by diluting 100 mL of the 10× concentrate with 900 mL of freshly distilled, deionized water and filtered with a 0.22-μm filter (Pall, Ann Arbor, MI) before use.
Protein modification using hydrophobic anhydrides
We made solutions of 100 μM of BCA in 500 μL of 0.1M HEPBS buffer, pH 9. Stock solutions of anhydrides were made by diluting 10 μL of anhydride (acetic or hexanoic) into 500 μL dioxane. This stock solution was then diluted with dioxane to make concentrations of anhydride that were 6, 12, and 18 times the concentration of lysines (1.9 mM) in the reaction mixture. These reagents were made immediately before they were used. Twenty-five μL of each of the diluted stocks of anhydride were added to the protein solutions, so that the final ratio of anhydride to lysine was 0.3, 0.6, and 0.9 in each of the reaction mixtures. The mixtures were agitated immediately using a vortex mixer. The reactions were left overnight to ensure complete reaction. The proteins were desalted into 1× Tris-Gly buffer using spin desalting columns. Each reaction mixture was then run on CE to determine the relative concentration of each rung. The reaction mixtures were then combined so that the final concentration of each rung was approximately constant across the ladder.
Denaturation experiments
A charge ladder of BCA (BCA-Acn or BCA-Hexn, 1 mL of 100 μM total protein in Tris-Gly buffer) was placed in a dialysis cassette (MW cutoff of 10 kDa). The dialysis cassette was placed in a 1 L bath of 3 mM SDS in Tris-Gly buffer at room temperature. The buffer was changed every 24 h. At regular intervals of time (approximately every half-hour), 100 μL of the protein solution was removed from the dialysis cassette; ∼7 μL of that aliquot was diluted 10-fold and the absorbance of the diluted sample at 280 nm (ɛ280, BCA = 57,000 M−1cm−1, we assume that the absorption cross section is unchanged by acylation) was measured to determine the total protein concentration. We diluted the aliquot because the absorbance of the 100 μM solution was too high to be read accurately by the ultraviolet spectrometer. This diluted aliquot was discarded. The remainder of the solution was then run on CE. The protein solution, except for the portion diluted for ultraviolet measurement, was returned to the dialysis cassette; the aliquot was outside of the dialysis cassette for ∼5 min.
Capillary electrophoresis conditions
Capillary electrophoresis experiments were carried out in a Beckman (Fullerton, CA) PACE-MDQ system, using a capillary of inner diameter of 50 μm of total length of 110.2 cm, 100 cm to the detector. Tris-Gly in D2O was used as the running buffer, and the applied voltage was 30 kV. D2O was used in place of H2O for the electrophoresis buffer because the viscosity of D2O is higher than that of H2O and the higher viscosity minimizes diffusion. Samples were injected using pressure (20 psi) for 30 s. Each sample contained 0.65 mM dimethylformamide as an electrically neutral marker for electroosmotic flow.
RESULTS AND DISCUSSION
Experimental protocol
The cmc of SDS in the Tris-Gly buffer used in this study is 4.3 mM (50). We chose 3 mM SDS for our studies of denaturation because this concentration of SDS denatures BCA in an interval of time that is convenient for experimental work using CE. In addition, this concentration of SDS is close to the concentration often used in SDS-PAGE (0.1% or ∼3.5 mM) (1). We put 1 mL of a solution of ∼100 μM of a charge ladder of BCA, dissolved in Tris-Gly buffer, into a dialysis cassette (molecular weight cutoff of 10 kDa) and placed the cassette in 1 L of Tris-Gly buffer containing 3 mM SDS. The bath was kept at room temperature (∼22°C) for the duration of the experiment.
SDS molecules pass through the dialysis cassette, but the protein and protein-SDS aggregates and SDS micelles do not. We used the dialysis cassette because we wanted to maintain a constant concentration of free SDS in the solution around the protein. If we assume that BCA and its charge variants, like most proteins, bind SDS at a ratio of ∼1 SDS molecule per 2 amino acids (8–11), each BCA molecule should bind ∼130 SDS molecules. Because BCA binds so many molecules of SDS, it is difficult to keep the concentration of free SDS constant without a large source (here using a dialysis cassette). Without a dialysis cassette, we would be constrained to study denaturation at concentrations of SDS more than 130 times the protein concentration (100 μM in these experiments) i.e., above 13 mM. With the dialysis cassette, we are able to add molecules of SDS to the system without changing the concentration of free SDS, and to study the denaturation of proteins below the cmc of SDS. (We attempted to measure the relative rates of denaturation of rungs of BCA-Acn using buffer containing 10 mM SDS, but the proteins denatured in the time it takes to measure the electropherograms. The experiment, as designed, cannot be done above the cmc because the time it takes to denature some rungs becomes faster than the time of a CE run.)
At regular intervals of time (approximately every half hour), we removed 100-μL aliquots of the solutions containing the charge ladder of BCA from the cassette in a bath of 3 mM SDS in Tris-Gly buffer, measured the total protein concentration in the aliquot using absorbance at 280 nm, and injected a portion (∼10 nL) of the aliquot onto the CE. The unused portions of the aliquots were then returned to the cassette. The aliquots were out of the dialysis cassette for <5 min; this time is shorter than the shortest times for denaturation (∼16 min) measured in our experiments for denaturation, and therefore should not significantly affect our measurements.
Corrections of peak areas
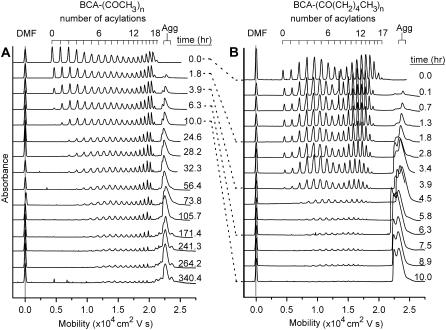
Fig. 2 shows electropherograms as a function of time for the acetyl- and hexanoyl charge ladders of BCA. To quantify the rate of denaturation of each rung of the charge ladders, the peaks were integrated and then corrected for three factors.
FIGURE 2.
Denaturation of hydrophobic charge ladders of (A) BCA-Acn and (B) BCA-Hexn. Dimethylformamide was used as a neutral marker of electroosmotic flow. Each ladder is labeled with the time elapsed after placing the dialysis cassette containing protein in the solution of SDS; the dotted lines match up measurements of BCA-Acn and BCA-Hexn measured at the same amount of elapsed time. The peak corresponding to denatured, aggregated BCA-SDS is labeled (Agg) and has fine structure; this structure may be due to different denatured states of the BCA-SDS aggregate.
Residence time in the detection volume
Proteins that have a higher velocity along the capillary spend less time in the detection volume than proteins that have lower velocity. If two proteins with the same absorptivity were present in a sample in equal concentrations, the protein of lower velocity would have a larger measured peak area than the protein of higher velocity. To correct for this experimental bias, we multiplied the area of each peak by the velocity of the protein (Acorr = Ameasured × LD/tD), where LD is the length of the capillary from the end (where injection occurs) to the detector (100 cm in all of our experiments) and tD is the time it takes for the rung to reach the detector (71).
Initial differences in concentrations of each rung
The areas of each of the rungs in the charge ladder were not all equal before denaturation. To measure the fraction of each rung that has denatured at each time, the velocity-corrected area of each rung in the sample was divided by the velocity-corrected area of that rung in the charge ladder run in the absence of SDS.
Loss of protein due to dialysis
The total protein concentration, as measured by absorbance at 280 nm, decreased by ∼15% over a week of dialysis, presumably through association with the dialysis membrane, and/or leakage out of the dialysis cassette. The correction for total protein concentration assumes that regardless of the mechanism by which protein is lost, each rung is lost equally.
Comparison of the rates of denaturation
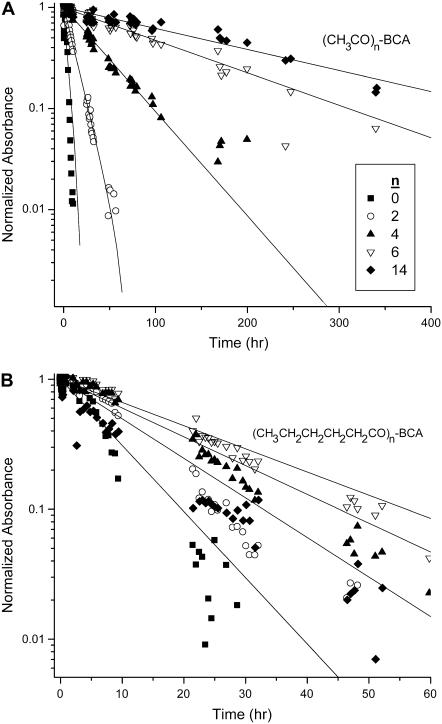
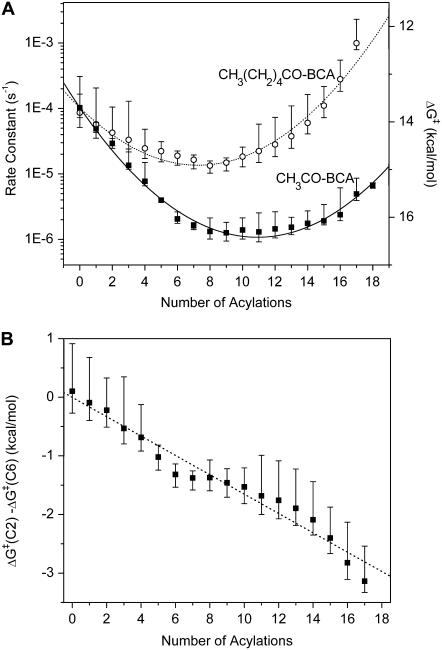
Fig. 3 shows the decrease in corrected peak area as a function of time for representative rungs of the BCA-Acn and BCA-Hexn charge ladders. We fit each of these sets of data to a single exponential decay and plotted the rate of denaturation as a function of rung number (Fig. 4 A). In principle, since every rung (except the native—BCA—and fully functionalized proteins—BCA-Ac18) is a collection of regioisomers, the denaturation profile may not be a single exponential function. We use the single exponential as a measure of the relative rates of denaturation of each rung. The exact functional form is not required for our analysis, and each set of the data in Fig. 3 appears to fit a single exponential well. Fig. 4 A shows that there is a pronounced minimum in the plot of the rates of denaturation versus number of acylations for both charge ladders; the earlier and later rungs denature more rapidly, and the middle rungs denature least rapidly.
FIGURE 3.
Corrected areas (see text for details) as a function of time for representative rungs of (A) an BCA-Acn charge ladder and (B) a BCA-Hexn charge ladder. Deviations from linearity could be due to the fact that each rung of the charge ladder is made up of a mixture of regioisomers that may have different rates of denaturation. The data shown in this figure are from one experiment. (It is difficult to give experimental uncertainties to the points on the graph because the time at which the points were taken differed between repetitions of the experiment.)
FIGURE 4.
(A) Rate constants of denaturation for both (▪) BCA-Acn and (○) BCA-Hexn charge ladders with SDS as a function of the number of acylations. The points are the arithmetic average and the error bars are minimum and maximum values measured in three repetitions for BCA-Acn and four repetitions for BCA-Hexn. The right y axis shows the corresponding ΔG‡ in kcal/mol calculated using Eq. 1. The lines show fits of the equation ΔG‡ = a + bn + cn2 to the data; see text for discussion of this model. (B) A plot of the difference in ΔG‡ between a rung of an acetyl ladder and a hexanoyl ladder as a function of rung number. The data fit a line (slope = 0.17 kcal/mol, R2 = 0.97). The fit of these data to a linear plot (dotted lines) suggests that the difference in ΔG‡ between the two ladders is only due to the difference in the linear term bn; the c coefficient includes only electrostatic contributions to ΔG‡.
Mathematical model of the kinetics of the interaction of charge ladders of BCA with SDS
As we described in the introduction, we propose a model in which there are two types of interactions—electrostatic and hydrophobic—that change the ΔG‡ for denaturation of modified BCA by SDS relative to that of BCA. Each of the two types of interactions has an intermolecular component that describes how the modification changes the interaction between SDS and protein, and an intramolecular component that describes how the modification changes the stability of the modified BCA in the absence of SDS. Here we will construct a mathematical description of the model to fit the data describing rate of denaturation versus the number of acylations (Fig. 4 A).
The four types of interactions should add to give the total activation energy of denaturation for each rung of a charge ladder (Eq. 2), where 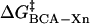 is the activation
is the activation
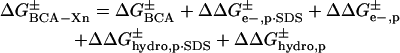 |
(2) |
energy of denaturation for the nth rung of a charge ladder, 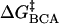 is the activation energy of unmodified BCA, and the other terms are the additional activation energies of unfolding, relative to BCA, due to i), intermolecular electrostatic repulsion between the SDS molecule and the modified BCA
is the activation energy of unmodified BCA, and the other terms are the additional activation energies of unfolding, relative to BCA, due to i), intermolecular electrostatic repulsion between the SDS molecule and the modified BCA 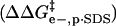 ; ii), intramolecular electrostatic repulsion between the charges on the surface of the modified BCA
; ii), intramolecular electrostatic repulsion between the charges on the surface of the modified BCA 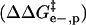 ; iii), intermolecular hydrophobic interaction between the SDS molecules and modified BCA
; iii), intermolecular hydrophobic interaction between the SDS molecules and modified BCA 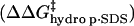 ; and iv), intramolecular hydrophobic interaction due to the additional exposed hydrophobic residues on the surface of modified BCA
; and iv), intramolecular hydrophobic interaction due to the additional exposed hydrophobic residues on the surface of modified BCA 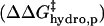 . To write down a functional form for each of these interactions, and to build a tractable model, we must apply a number of approximations to simplify the system composed of the protein, surfactant, and aqueous solvent.
. To write down a functional form for each of these interactions, and to build a tractable model, we must apply a number of approximations to simplify the system composed of the protein, surfactant, and aqueous solvent.
Assumptions in the mathematical description of the model
We approximate both the structure of the folded protein and the structure of the transition state as spheres with net charge uniformly distributed on the surface, and with a uniform dielectric constant inside this shell of charge. The model we propose ignores all molecular-level details of protein, surfactant, and the solvent. The number (and distribution) of the molecules of SDS that bind to the protein in the transition state are also considered to be constant for all rungs of the charge ladders. This assumption concerning the stoichiometry of the transition state is suspect, but required to write an equation for the intermolecular electrostatic repulsion term; we assume a single value for the number of SDS molecules bound in the transition state (m) for all BCA derivatives. We assume the value of dielectric constant of water (ɛw) is 80, and we neglect the change in the dielectric constant that probably occurs near the surface of the protein. Others have shown that the dielectric constant of water is close to 20 over a few layers of water molecules (a few angstroms) due to the reduced mobility of the water molecules next to the surface of the protein (72). The dielectric constant is probably affected by the distribution of charged, polar, and apolar groups in the protein and the net charge of the protein (56). We further assume that the dielectric constant is uniform throughout the interior of the protein (ɛp = 5) (72). In real systems, the dielectric constant is structured on a microscopic scale and may vary with position. The dielectric constant of solvent-exposed regions of the protein is probably higher than the interior due to configurational mobility of polar side chains (73).
Each conversion of a lysine-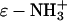 group to a lysine-ɛ-NHCOR group changes the charge (ΔZ) by<1 unit of charge, reflecting charge regulation (54,55). The value of ΔZ is close to −0.9 for the first few acylations in the conditions we used (pH 8.4), and is probably <−0.9 (probably between −0.7 and −0.9) at high numbers of acylation. We will assume that ΔZ = −0.9 for all acylations regardless of the acylating reagent and number of prior acylations (that is, for example, we assume that BCA-Ac5 and BCA-Hex5 have the same net charge and charge distribution). In these calculations, we consider only first-order electrostatic interactions. We will ignore any higher-order electrostatic interactions (for example, charge-dipole and charge-induced dipole effects) between the charged surfactant and protein (assumed to be a dielectric sphere).
group to a lysine-ɛ-NHCOR group changes the charge (ΔZ) by<1 unit of charge, reflecting charge regulation (54,55). The value of ΔZ is close to −0.9 for the first few acylations in the conditions we used (pH 8.4), and is probably <−0.9 (probably between −0.7 and −0.9) at high numbers of acylation. We will assume that ΔZ = −0.9 for all acylations regardless of the acylating reagent and number of prior acylations (that is, for example, we assume that BCA-Ac5 and BCA-Hex5 have the same net charge and charge distribution). In these calculations, we consider only first-order electrostatic interactions. We will ignore any higher-order electrostatic interactions (for example, charge-dipole and charge-induced dipole effects) between the charged surfactant and protein (assumed to be a dielectric sphere).
This model is clearly a draconian simplification, relative to the real proteins. Proteins are not a spherical shell of charges—not all of the charges are uniformly distributed or located at the surface of the protein, and the protein can compensate for additional charges by changing the values of pKa of nearby groups (54,55). Using these assumptions, we can, however, derive equations for each of the terms in Eq. 2.
Intermolecular electrostatic repulsion between SDS and BCA
The repulsion between a negatively charged molecule of SDS and a protein can be described by Coulomb's law in water containing salts (Eq. 3), where qSDS is the charge on SDS (−1 ec), ec is the charge of
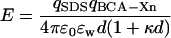 |
(3) |
an electron, qBCA−Xn is the charge on the nth rung of the charge ladder, ɛw is the dielectric constant of water, ɛ0 is the permittivity of free space, d is the distance between the center of the sphere representing the protein and the molecule of SDS, and κ is the inverse Debye length (0.333 nm−1 in Tris-Gly buffer, ionic strength of 10 mM). The  term (the difference between
term (the difference between 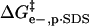 for BCA-Xn and for BCA) is then given by Eq. 4 where qBCA is the charge on
for BCA-Xn and for BCA) is then given by Eq. 4 where qBCA is the charge on
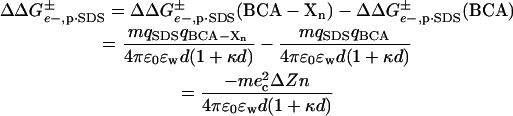 |
(4) |
native BCA (Z0 = −3 ec), and m is the number of molecules of SDS that are bound to the protein in the transition state.
We consider only values of free energy in this calculation. In water, the relative partitioning of the free energy due to Coulombic interactions into enthalpy and entropy is complicated, and the majority of the free energy may be due to entropy (not due to enthalpy—the major portion of the free energy in vacuum) (56). In the interaction of protein with molecules of SDS, it is unclear whether the solvation (entropic effects) or enthalpy is the primary contributor to ΔG.
Intramolecular charge/charge repulsion
The change in energy upon adding a charge to a uniform shell of charge on the surface of a protein is given by Eq. 5, where
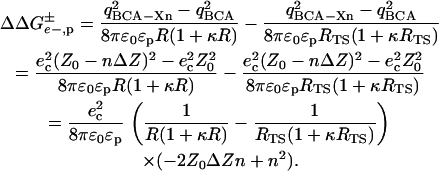 |
(5) |
R is the radius of the protein, ɛp is the dielectric constant in the interior of the protein, and RTS is the radius of the transition state. This equation approximates both the folded protein and the transition state of the protein-SDS aggregate as spheres.
Because we have assumed that ΔZ is the same for acylations in all positions, and because we have assumed that the charge is uniformly distributed on the surfaces of the spherical protein, proteins contained in a given rung of the charge ladder, even though they are regioisomers, should repel a molecule of SDS with the same force. The two equations (3 and 5) that describe how changes in electrostatics affect changes to ΔG‡ will, therefore, be the same for both the acetyl and hexanoyl charge ladders.
Hydrophobic contributions to ΔG‡
Intermolecular hydrophobic interaction between exposed hydrophobic surface area of BCA and molecules of SDS
The additional exposed hydrophobic surface area on the acylated proteins relative to BCA increases the interaction (and hence the equilibrium constant for association) between SDS molecules and the protein. We assume that this increase in interaction is proportional to the additional hydrophobic surface area of the acylated proteins relative to unacylated BCA (Eq. 6); in this equation n is the number of modifications and
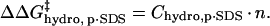 |
(6) |
Chydro,p·SDS is a constant of proportionality that is larger for hexanoyl than for acetyl ladders. The ratio of the π-parameters described in the introduction suggests that each modification with hexanoic anhydride results in a change in hydrophobicity that is similar to three acylations with acetic anhydride, and therefore, that Chydro, p·SDS(BCA-Hexn) ≅ 3 Chydro, p·SDS(BCA-Acn).
Intramolecular destabilization due to additional exposed hydrophobic surface area
The increase in the exposed hydrophobic area on the surface of the acylated BCA relative to BCA should also decrease the stability of the folded protein. The increase in exposed surface area increases the order of the water surrounding the protein, thereby decreasing the entropy in the folded state. The increase in ordered water molecules around hydrophobic residues relative to BCA should be greatest in the folded state; in the denatured state, there is a large exposed surface, and the change due to the chemical modification of lysine residues should be minimal. The ΔΔG°folding between acylated BCA and BCA is, then, primarily due to a destabilization of the ground state; this destabilization should also affect ΔΔG‡ because the transition state should be less affected than the folded state. (The configurational entropy of the modified side chains in the native and transition states may also contribute to the stability of the derivatives. The relative configurational entropy in the ground and the transition state could also increase the rate of denaturation of modified BCA relative to native BCA.)
The free energy required to transfer a hydrocarbon from the pure hydrocarbon phase to water is a linear function of the surface area of the chain (75,76). Zhou and Zhou have generated an empirical stability scale for hydrophobic residues using 1023 point mutations to 35 different proteins (77). They demonstrated that a change in hydrophobic surface area on a protein contributes 12–28 cal mol−1 Å−2 to ΔG°unfolding. Using the stability scale measured by Zhou and Zhou as justification, we assume that the difference in free energy of folding between acylated BCA and BCA (ΔΔG°folding), and also the destabilization of the folded state relative to the transition state (ΔΔG‡), is linear with the number of acylations (Eq. 7); where Chydro,p is a
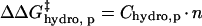 |
(7) |
constant of proportionality that differs between charge ladders and should be proportional to size of the surface area of the acylating reagent used. Because hexanoyl groups are ∼3 times the surface area of acetyl group, Chydro, p(BCA-Hexn) = 3 Chydro, p(BCA-Acn).
We also performed a surface area calculation to determine the change in surface area between the conversion of BCA to BCA-Ac18 and BCA to BCA-Hex18. We calculated that the reaction with acetic anhydride changed the surface area of BCA by 400 Å2 and the reaction with hexanoic anhydride changed the surface area of BCA by 1180 Å2. Since this change is a factor of 2.9, we conclude that our estimate that each modification with hexanoic anhydride adds three times the amount of surface area than modification with acetic anhydride is justified.
Treatment of the changes to hydrophobicity in the model
Because 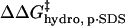 and
and 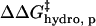 have the same functional form within our model, the same dependence on the number of modifications, and the same dependence on the identity of the anhydride (3·Chydro(Ac) = Chydro(Hex)), we will not be able to distinguish between the intermolecular and intramolecular effects of changes in hydrophobicity. We will only be able to measure the cumulative
have the same functional form within our model, the same dependence on the number of modifications, and the same dependence on the identity of the anhydride (3·Chydro(Ac) = Chydro(Hex)), we will not be able to distinguish between the intermolecular and intramolecular effects of changes in hydrophobicity. We will only be able to measure the cumulative 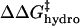 (Eq. 8). Here, Chydro is a proportionality constant and is equal to
(Eq. 8). Here, Chydro is a proportionality constant and is equal to 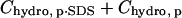 :
:
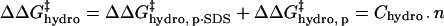 |
(8) |
Combination of electrostatic and hydrophobic terms into a single equation
By substituting Eqs. 3, 4, and 8 into Eq. 2, we can express the activation energy of each rung of the charge ladder as a function of the number of acylations, n (Eq. 9). The nonlinear term in Eq. 9 only depends on intramolecular electrostatic repulsion. Since the data
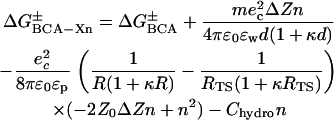 |
(9) |
in Fig. 4 A are clearly nonlinear, we can conclude that the intramolecular electrostatic repulsion is an important factor in the denaturation of proteins, especially when the net charge on the protein becomes large (>10 ec for BCA). Since this repulsion depends only on parameters of the protein (and not the SDS molecules), it may play a role in protein stability and denaturation with other denaturants.
There are four unknown parameters (m, the number of molecules of SDS bound to the protein in the transition state, RTS, the radius of the transition state, d, the distance between the SDS molecules and the protein in the transition state, and Chydro, a constant representing the sum of the hydrophobic interactions) in Eq. 9; it is not possible to measure or estimate these parameters because they depend on the geometry of the transition state. We therefore estimate those parameters using our model and the data in Fig. 4 A, and decide if the calculated values for these parameters seem physically reasonable.
Analysis of the relative rates of denaturation of different rungs to the proposed model
The model predicts that a second-order polynomial describes the rate of denaturation as a function of the number of acylations. We fit the data in Fig. 4 A to a second-order polynomial (a + b n + cn2), where n is the number of acylations. The fits of the two charge ladders were constrained to obtain the best fit for both ladders, with a and c constrained to the same value for both ladders because they describe the electrostatic terms (which we assume to be invariant). Fig. 4 A shows the fits. (If the data for BCA-Acn and BCA-Hexn are fit independently, the values for a and c for each data set are within error of each other.) The coefficients a and c are independent of the kind of acylation because they do not depend on the hydrophobicity of the reagent; they depend only on the electrostatic interactions. As a result, the difference in activation energies between acetyl and hexanoyl ladders (Eq. 10) should be linear (Fig. 4 A). The slope (−0.17 kcal/mol of
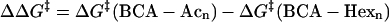 |
(10) |
protein) is equal to ΔChydro, where ΔChydro = Chydro(Ac)-Chydro(Hex) = Chydro(Ac)-3Chydro(Ac) = −2 Chydro(Ac). Therefore, Chydro(Ac) = 0.085 kcal/mol and Chydro(Hex) = 0.26 kcal/mol per acylation.
We found that ΔG‡ for BCA (i.e., the a coefficient) was 14 ± 1 kcal/mol; this value will be directly affected by our estimate that νκTST = 106 s−1. If we underestimated the value of νκTST, the actual ΔG‡ for BCA will be lower.
The c coefficient—due only to intramolecular electrostatic destabilization—was −0.023 ± 0.001 kcal/mol of protein. (The negative sign on the c coefficient indicates that the intramolecular electrostatic repulsion decreases ΔG‡. The negative sign is expected because this repulsion should destabilize the folded state of the protein and decrease the magnitude of the activation energy of denaturation.) Using the model, and assuming a radius of BCA of 2 nm, we calculate RTS to be 2.1 nm. This radius is 5% larger than that of the folded protein, and we speculate that the protein remains relatively compact in the transition state.
The b coefficient for BCA-Acn was 0.50 ± 0.01 kcal/mol of protein; the b coefficient for BCA-Hexn was 0.33 ± 0.01 kcal/mol of protein. This parameter has four components (see Eq. 9): i), electrostatic repulsion between the protein and SDS molecules, ii), the linear portion of the intramolecular electrostatic term, iii), hydrophobic interaction between protein and SDS, and iv), destabilization of the protein due to exposed hydrophobic surface area. From the calculations above, we estimate that Chydro(acetyl) = 0.085 kcal/mol and Chydro(hexanoyl) = 0.26 kcal/mol, and that RTS = 2.1 nm. We then have two remaining unknown parameters, d and m, but only one equation to constrain them. We can, however, make reasonable assumptions about one of these parameters and see if the corresponding value for the other parameter is reasonable. If we assume d is the radius of the protein in the transition state (2.1 nm), we calculate a value for m of ∼7 molecules of SDS bound in the transition state. If we guess that m is ∼10 molecules of SDS, we calculate a value for d of 2.8 nm.
We know that d should not be much larger than the Debye length (3 nm in our buffer) or the interactions should be heavily screened. With the assumptions made in this highly simplified model, we conclude that there are ∼10 molecules of SDS bound in the transition state. Since this number is ∼1 order of magnitude lower than the ∼130 molecules of SDS bound to the protein when completely denatured, we conclude that there are a small number of SDS molecules that interact with the protein and cause changes to the conformation of the protein. The rest of the molecules of SDS thus bind to the denaturing protein in later, nonrate determining steps.
Interpretation of the results of the fitting
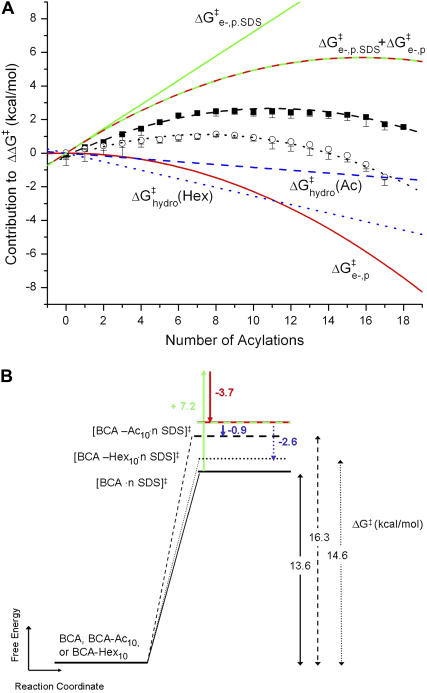
Fig. 5 shows a schematic diagram of how the four effects in the model affect the height of the activation barrier. It also shows a plot of the contributions of 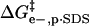 ,
, 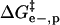 , and
, and 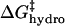 to ΔΔG‡ between BCA and each rung of the charge ladder. For both BCA-Acn and BCA-Hexn, net electrostatics contribute more to ΔG‡ than hydrophobicity. The contribution to ΔΔG‡ due to the changes in net charge of the protein is shown as the dotted red/green line. At low values of n, the
to ΔΔG‡ between BCA and each rung of the charge ladder. For both BCA-Acn and BCA-Hexn, net electrostatics contribute more to ΔG‡ than hydrophobicity. The contribution to ΔΔG‡ due to the changes in net charge of the protein is shown as the dotted red/green line. At low values of n, the 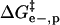 term dominates and the modified proteins have a higher activation energy than the native BCA. At high values of n, the contributions of
term dominates and the modified proteins have a higher activation energy than the native BCA. At high values of n, the contributions of 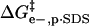 and
and 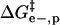 largely offset each other. For BCA-Hexn, the effects of changes in hydrophobicity (dotted blue line) are nearly the same in magnitude as the effects of changes in electrostatics.
largely offset each other. For BCA-Hexn, the effects of changes in hydrophobicity (dotted blue line) are nearly the same in magnitude as the effects of changes in electrostatics.
FIGURE 5.
(A) Contributions to ΔΔG‡ from 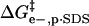 (green line),
(green line), 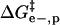 (red line), and
(red line), and 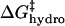 (blue line; dashed line, Acn, and dotted line, Hexn). The sum of the electrostatic contributions is marked as the red-green dashed line. The data for ΔΔG‡—the sum of the four components—are shown for BCA-Acn (▪) and BCA-Hexn (○). The fits to the data (dashed line, BCA-Acn; dotted line, BCA-Hexn) are those given by Eq. 9. See text for details of the model. (B) An example of how the energy of the transition state changes relative to that of the ground state with 10 modifications. The folded states of BCA, BCA-Ac10, and BCA-Hex10 are scaled to the same energy. The arrows (in the same colors as A) indicate how each of the factors changes the relative position of the transition state. The red/green dashed line shows the effects of just the electrostatic terms on the energy of the transition state (i.e., if 10 lysine groups were neutralized with no corresponding change in hydrophobicity).
(blue line; dashed line, Acn, and dotted line, Hexn). The sum of the electrostatic contributions is marked as the red-green dashed line. The data for ΔΔG‡—the sum of the four components—are shown for BCA-Acn (▪) and BCA-Hexn (○). The fits to the data (dashed line, BCA-Acn; dotted line, BCA-Hexn) are those given by Eq. 9. See text for details of the model. (B) An example of how the energy of the transition state changes relative to that of the ground state with 10 modifications. The folded states of BCA, BCA-Ac10, and BCA-Hex10 are scaled to the same energy. The arrows (in the same colors as A) indicate how each of the factors changes the relative position of the transition state. The red/green dashed line shows the effects of just the electrostatic terms on the energy of the transition state (i.e., if 10 lysine groups were neutralized with no corresponding change in hydrophobicity).
The data are consistent with the model presented, but the good agreement between the model and the data are certainly not proof that this model is an accurate description of the molecular processes involved in denaturation. The assumptions discussed earlier are simplifications of a complex biochemical system, and the simplistic model can only begin to identify free energies that may be important in determining how the stability of a protein is changed by chemical modifications to that protein and how surfactants denature proteins. Nonetheless, the model described here offers a first step toward understanding the major components of a very complicated and poorly understood system.
CONCLUSIONS
Hydrophobic charge ladders are a useful tool for determining the relative importance of charge and hydrophobicity in the denaturation of proteins with SDS. Charge ladders provide data in which charge and hydrophobicity vary independently. These data allow us to estimate quantitatively the relative importance of electrostatics and hydrophobicity in the rate of denaturation of BCA (and, in principle, other proteins) with SDS. In particular, the study with acetyl and hexanoyl charge ladders of BCA indicates that both charge and hydrophobicity affect the rate of denaturation of BCA with SDS. We conclude that the effects of charge on denaturation with SDS are ∼5-fold larger than the effects of hydrophobicity for BCA-Acn and of similar size for BCA-Hexn.
To account for the curvature in the data of rate of denaturation versus number of acylations, we must include a nonlinear term that describes intramolecular electrostatic repulsion. The functional form of the model described in this study fits well to the data for BCA-Acn and BCA-Hexn; we conclude that the four terms included in our model—inter- and intramolecular electrostatic repulsion, and inter- and intramolecular hydrophobic interactions—give a plausible description of the major factors in determining the change in the rate of denaturation with acylation. Results suggest that removing small amounts of negative charge (∼1–10 ec) from the surface of a protein may stabilize that protein to denaturation with SDS, but that removing large amounts of charge (>15 ec) will destabilize the protein. There is, therefore, an optimum amount of surface charge to make a protein stable to SDS denaturation and, at least for one protein (BCA), this ideal charge is different from that of the native protein. The strength of using charge ladders is that the effects are averaged over multiple species (regioisomers). The fact that we can describe the denaturation of the set of them represented by each rung of the ladder with a simple, intuitive model, and a common set of numerical constants, implies that the rate of denaturation is dominated by global (nonlocal) effects.
SUPPLEMENTARY MATERIAL
An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.
Acknowledgments
We acknowledge Logan McCarthy, Hongkai Wu, and Chengde Mao for helpful discussions and the National Institutes of Health for research support (GM51559).
References
- 1.Gallagher, S. R. 2005. One-dimensional SDS gel electrophoresis of proteins. In Current Protocols in Molecular Biology. F. M. Ausubel, R. Brent, R. E. Kingston, D. D. Moore, J. G. Seidman, J. A. Smith, and K. Struhl, editors. John Wiley & Sons, New York. 10.2A.1–10.2A.34.
- 2.Rigaud, J. L., M. Chami, O. Lambert, D. Levy, and J. L. Ranck. 2000. Use of detergents in two-dimensional crystallization of membrane proteins. Biochim. Biophys. Acta. 1508:112–128. [DOI] [PubMed] [Google Scholar]
- 3.le Maire, M., P. Champeil, and J. V. Moller. 2000. Interaction of membrane proteins and lipids with solubilizing detergents. Biochim. Biophys. Acta. 1508:86–111. [DOI] [PubMed] [Google Scholar]
- 4.Jones, M. N. 1999. Surfactants in membrane solubilisation. Int. J. Pharm. 177:137–159. [DOI] [PubMed] [Google Scholar]
- 5.Svenson, S. 2004. Controlling surfactant self-assembly. Curr. Opin. Colloid Interface Sci. 9:201–212. [Google Scholar]
- 6.Duro, R., C. Souto, J. L. Gomez-Amoza, R. Martinez-Pacheco, and A. Concheiro. 1999. Interfacial adsorption of polymers and surfactants: implications for the properties of disperse systems of pharmaceutical interest. Drug Dev. Ind. Pharm. 25:817–829. [DOI] [PubMed] [Google Scholar]
- 7.Jones, L. S., N. B. Bam, and T. W. Randolph. 1997. Surfactant-stabilized protein formulations: a review of protein-surfactant interactions and novel analytical methodologies. ACS Symp. Ser. 675:206–222. [Google Scholar]
- 8.Pitt-Rivers, R., and F. S. A. Impiombato. 1968. Binding of sodium dodecyl sulfate to various proteins. Biochem. J. 109:825–830. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Fish, W. W., J. A. Reynolds, and C. Tanford. 1970. Gel chromatography of proteins in denaturing solvents. Comparison between sodium dodecyl sulfate and guanidine hydrochloride as denaturants. J. Biol. Chem. 245:5166–5168. [PubMed] [Google Scholar]
- 10.Reynolds, J. A., and C. Tanford. 1970. Gross conformation of protein-sodium dodecyl sulfate complexes. J. Biol. Chem. 245:5161–5165. [PubMed] [Google Scholar]
- 11.Reynolds, J. A., and C. Tanford. 1970. Binding of dodecyl sulfate to proteins at high binding ratios. Possible implications for the state of proteins in biological membranes. Proc. Natl. Acad. Sci. USA. 66:1002–1003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Ibel, K., R. P. May, K. Kirschner, H. Szadkowski, E. Mascher, and P. Lundahl. 1990. Protein-decorated micelle structure of sodium-dodecyl-sulfate - protein complexes as determined by neutron scattering. Eur. J. Biochem. 190:311–318. [DOI] [PubMed] [Google Scholar]
- 13.Jones, M. N. 1992. Surfactant Interactions with biomembranes and proteins. Chem. Soc. Rev. 21:127–136. [Google Scholar]
- 14.Shirahama, K., K. Tsujii, and T. Takagi. 1974. Free-boundary electrophoresis of sodium dodecyl sulfate (SDS)-protein polypeptide complexes with special reference to SDS-polyacrylamide gel electrophoresis. J. Biochem. (Tokyo). 75:309–319. [DOI] [PubMed] [Google Scholar]
- 15.Mattice, W. L., J. M. Riser, and D. S. Clark. 1976. Conformational properties of the complexes formed by proteins and sodium dodecyl sulfate. Biochemistry. 15:4264–4272. [DOI] [PubMed] [Google Scholar]
- 16.Lundahl, P., E. Greijer, M. Sandberg, S. Cardell, and K. O. Eriksson. 1986. A model for ionic and hydrophobic interactions and hydrogen-bonding in sodium dodecyl sulfate-protein complexes. Biochim. Biophys. Acta. 873:20–26. [Google Scholar]
- 17.Westerhuis, W. H. J., J. N. Sturgis, and R. A. Niederman. 2000. Reevaluation of the electrophoretic migration behavior of soluble globular proteins in the native and detergent-denatured states in polyacrylamide gels. Anal. Biochem. 284:143–152. [DOI] [PubMed] [Google Scholar]
- 18.Turro, N. J., X.-G. Lei, K. P. Ananthapadmanabhan, and M. Aronson. 1995. Spectroscopic probe analysis of protein-surfactant interactions: the BSA/SDS system. Langmuir. 11:2525–2533. [Google Scholar]
- 19.Xu, Q., and T. A. Keiderling. 2004. Effect of sodium dodecyl sulfate on folding and thermal stability of acid-denatured cytochrome c: A spectroscopic approach. Protein Sci. 13:2949–2959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Nielsen, A. D., L. Arleth, and P. Westh. 2005. Analysis of protein-surfactant interactions: a titration calorimetric and fluorescence spectroscopic investigation of interactions between Humicola insolens cutinase and an anionic surfactant. Biochim. Biophys. Acta. 1752:124–132. [DOI] [PubMed] [Google Scholar]
- 21.Moosavi-Movahedi, A. A. 2005. Thermodynamics of protein denaturation by sodium dodecyl sulfate. J. Iranian Chem. Soc. 2:189–196. [Google Scholar]
- 22.Moosavi-Movahedi, A. A., and A. A. Saboury. 1999. Elucidation of binding sites for protein denaturation by surfactant. J. Chem. Soc. Pak. 21:248–259. [Google Scholar]
- 23.Chattoraj, D. K., S. C. Biswas, P. K. Mahapatra, and S. Chatterjee. 1999. Standard free energies of binding of solute to proteins in aqueous medium. Part 2. Analysis of data obtained from equilibrium dialysis and isopiestic experiments. Biophys. Chem. 77:9–25. [DOI] [PubMed] [Google Scholar]
- 24.Andrade, M. I. P., E. Boitard, M. A. Saghal, P. Manley, M. N. Jones, and H. A. Skinner. 1981. Enthalpy of interaction of ribonuclease A and n-alkyl sulfates in aqueous solution. J. Chem. Soc. Faraday Trans. 77:2939–2948. [Google Scholar]
- 25.Tipping, E., M. N. Jones, and H. A. Skinner. 1974. Enthalpy of interaction between globular proteins and sodium n-dodecyl sulfate in aqueous solution. J. Chem. Soc. Faraday Trans. 70:1306–1315. [Google Scholar]
- 26.Colton, I. J., J. D. Carbeck, J. Rao, and G. M. Whitesides. 1998. Affinity capillary electrophoresis. a physical-organic tool for studying interactions in biomolecular recognition. Electrophoresis. 19:367–382. [DOI] [PubMed] [Google Scholar]
- 27.Day, Y. S. N., C. L. Baird, R. L. Rich, and D. G. Myszka. 2002. Direct comparison of binding equilibrium, thermodynamic, and rate constants determined by surface- and solution-based biophysical methods. Protein Sci. 11:1017–1025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Hakansson, K., M. Carlsson, L. A. Svensson, and A. Liljas. 1992. Structure of native and apo carbonic anhydrase II and structure of some of its anion-ligand complexes. J. Mol. Biol. 227:1192–1204. [DOI] [PubMed] [Google Scholar]
- 29.Stams, T., and D. W. Christianson. 2000. X-ray crystallographic studies of mammalian carbonic anhydrase isozymes. In The Carbonic Anhydrases: New Horizons. W. R. Chegwidden, N. D. Carter, and Y. H. Edwards, editors. Birkhaeuser Verlag, Basel. 159–174. [DOI] [PubMed]
- 30.Supuran, C. T., A. Scozzafava, and A. Casini. 2003. Carbonic anhydrase inhibitors. Med. Res. Rev. 23:146–189. [DOI] [PubMed] [Google Scholar]
- 31.Carlsson, U., and B.-H. Jonsson. 1995. Folding of. beta-sheet proteins. Curr. Opin. Struct. Biol. 5:482–487. [DOI] [PubMed] [Google Scholar]
- 32.Carlsson, U., and B.-H. Jonsson. 2000. Folding and stability of human carbonic anhydrase II. In The Carbonic Anhydrases: New Horizons. W. R. Chegwidden, N. D. Carter, and Y. H. Edwards, editors. Birkhaeuser Verlag. Basel. 241–259.
- 33.Bushmarina, N. A., I. M. Kuznetsova, A. G. Biktashev, K. K. Turoverov, and V. N. Uversky. 2001. Partially folded conformations in the folding pathway of bovine carbonic anhydrase II: a fluorescence spectroscopic analysis. ChemBioChem. 2:813–821. [DOI] [PubMed] [Google Scholar]
- 34.Edsall, J. T., S. Mehta, D. V. Myers, and J. M. Armstrong. 1966. Structure and denaturation of human carbonic anhydrases in urea and guanidine hydrochloride solutions. Biochemische Z. 345:9–36. [Google Scholar]
- 35.Fransson, C., P. O. Freskgaard, H. Herbertsson, A. Johansson, P. Jonasson, L. G. Martensson, M. Svensson, B. H. Jonsson, and U. Carlsson. 1992. Cis-trans isomerization is rate-determining in the reactivation of denatured human carbonic anhydrase II as evidenced by proline isomerase. FEBS Lett. 296:90–94. [DOI] [PubMed] [Google Scholar]
- 36.Ko, B. P. N., A. Yazgan, P. L. Yeagle, S. C. Lottich, and R. W. Henkens. 1977. Kinetics and mechanism of refolding of bovine carbonic anhydrase. A probe study of the formation of the active site. Biochemistry. 16:1720–1725. [DOI] [PubMed] [Google Scholar]
- 37.Montich, G. G. 2000. Partly folded states of bovine carbonic anhydrase interact with zwitterionic and anionic lipid membranes. Biochim. Biophys. Acta. 1468:115–126. [DOI] [PubMed] [Google Scholar]
- 38.Ptitsyn, O. B. 1992. The molten globule state. In Protein Folding. T. E. Creighton, editor. 243–300. Freeman, New York.
- 39.Svensson, M., P. Jonasson, P.-O. Freskgaard, B.-H. Jonsson, M. Lindgren, L.-G. Maartensson, M. Gentile, K. Boren, and U. Carlsson. 1995. Mapping the folding intermediate of human carbonic anhydrase II. Probing substructure by chemical reactivity and spin and fluorescence labeling of engineered cysteine residues. Biochemistry. 34:8606–8620. [DOI] [PubMed] [Google Scholar]
- 40.Wong, K.-P., and C. Tanford. 1973. Denaturation of bovine carbonic anhydrase B by guanidine hydrochloride. Process involving separable sequential conformational transitions. J. Biol. Chem. 248:8518–8523. [PubMed] [Google Scholar]
- 41.Semisotnov, G. V., V. N. Uverskii, I. V. Sokolovskii, A. M. Gutin, O. I. Razgulyaev, and N. A. Rodionova. 1990. Two slow stages in refolding of bovine carbonic anhydrase B are due to proline isomerization. J. Mol. Biol. 213:561–568. [DOI] [PubMed] [Google Scholar]
- 42.Henkens, R. W., and T. P. Oleksiak. 1991. Structural elements in unfolded carbonic anhydrase. Carbonic Anhydrase, Proc. Int. Workshop. 44–49.
- 43.Martensson, L. G., B. H. Jonsson, P. O. Freskgard, A. Kihlgren, M. Svensson, and U. Carlsson. 1993. Characterization of folding intermediates of human carbonic anhydrase II: probing substructure by chemical labeling of SH groups introduced by site-directed mutagenesis. Biochemistry. 32:224–231. [DOI] [PubMed] [Google Scholar]
- 44.Ptitsyn, O. B. 1995. Molten globule and protein folding. Adv. Protein Chem. 47:83–229. [DOI] [PubMed] [Google Scholar]
- 45.Wetlaufer, D. B., and Y. Xie. 1995. Control of aggregation in protein refolding: a variety of surfactants promote renaturation of carbonic anhydrase II. Protein Sci. 4:1535–1543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Cleland, J. L., and D. I. C. Wang. 1990. Refolding and aggregation of bovine carbonic anhydrase B: quasi-elastic light scattering analysis. Biochemistry. 29:11072–11078. [DOI] [PubMed] [Google Scholar]
- 47.Gitlin, I., K. L. Gudiksen, and G. M. Whitesides. 2005. Peracetylated bovine carbonic anhydrase (BCA-Ac18) is kinetically more stable than native BCA to sodium dodecyl sulfate. J. Phys. Chem. B. 110:2372–2377. [DOI] [PubMed] [Google Scholar]
- 48.Gudiksen, K. L., A. R. Urbach, I. Gitlin, J. Yang, J. A. Vazquez, C. E. Costello, and G. M. Whitesides. 2004. The influence of the Zn(II) cofactor on the refolding of bovine carbonic anhydrase after denaturation with sodium dodecyl sulfate. Anal. Chem. 76:7151–7161. [DOI] [PubMed] [Google Scholar]
- 49.Yang, J., I. Gitlin, V. M. Krishnamurthy, J. A. Vazquez, C. E. Costello, and G. M. Whitesides. 2003. Synthesis of monodisperse polymers from proteins. J. Am. Chem. Soc. 125:12392–12393. [DOI] [PubMed] [Google Scholar]
-
50.Gudiksen, K. L., I. Gitlin, J. Yang, A. R. Urbach, D. T. Moustakas, and G. M. Whitesides. 2005. Eliminating positively charged lysine
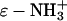 groups on the surface of carbonic anhydrase has no significant influence on its folding from sodium dodecyl sulfate. J. Am. Chem. Soc. 127:4707–4714. [DOI] [PubMed] [Google Scholar]
groups on the surface of carbonic anhydrase has no significant influence on its folding from sodium dodecyl sulfate. J. Am. Chem. Soc. 127:4707–4714. [DOI] [PubMed] [Google Scholar] - 51.Colton, I. J., J. R. Anderson, J. Gao, R. G. Chapman, L. Isaacs, and G. M. Whitesides. 1997. Formation of protein charge ladders by acylation of amino groups on proteins. J. Am. Chem. Soc. 119:12701–12709. [Google Scholar]
- 52.Gao, J., and G. M. Whitesides. 1997. Using protein charge ladders to estimate the effective charges and molecular weights of proteins in solution. Anal. Chem. 69:575–580. [DOI] [PubMed] [Google Scholar]
- 53.Gao, J., M. Mammen, and G. M. Whitesides. 1996. Evaluating electrostatic contributions to binding with the use of protein charge ladders. Science. 272:535–537. [DOI] [PubMed] [Google Scholar]
- 54.Menon, M. K., and A. L. Zydney. 2000. Determination of effective protein charge by capillary electrophoresis: effects of charge regulation in the analysis of charge ladders. Anal. Chem. 72:5714–5717. [DOI] [PubMed] [Google Scholar]
- 55.Gitlin, I., M. Mayer, and G. M. Whitesides. 2003. Significance of charge regulation in the analysis of protein charge ladders. J. Phys. Chem. B. 107:1466–1472. [Google Scholar]
- 56.Gitlin, I., J. D. Carbeck, and G. M. Whitesides. 2006. Why are proteins charged? Networks of charge-charge interactions in proteins measured by charge ladders and capillary electrophoresis. Angew. Chem. Int. Ed. Engl. 45:3022–3060. [DOI] [PubMed] [Google Scholar]
- 57.Linderstrom-Lang, K. 1924. The ionization of proteins. Compt. Rend. Trav. Lab. Carlsberg. 15:1–29. [Google Scholar]
- 58.Reference deleted in proof.
- 59.Fujita, T., J. Iwasa, and C. Hansch. 1964. A new substituent constant, P, derived from partition coefficients. J. Am. Chem. Soc. 86:5175–5180. [Google Scholar]
- 60.Pliska, V., M. Schmidt, and J. L. Fauchere. 1981. Partition coefficients of amino acids and hydrophobic parameters p of their side-chains as measured by thin-layer chromatography. J. Chromatogr. 216:79–92. [Google Scholar]
- 61.Hansch, C., and E. Coats. 1970. α-Chymotrypsin: case study of substituent constants and regression analysis in enzymic structure-activity relations. J. Pharm. Sci. 59:731–743. [DOI] [PubMed] [Google Scholar]
- 62.Fersht, A. R. 1999. Structure and Mechanism in Protein Science. W.H. Freeman, New York.
- 63.Hagen, S. J., J. Hofrichter, A. Szabo, and W. A. Eaton. 1996. Diffusion-limited contact formation in unfolded cytochrome c: estimating the maximum rate of protein folding. Proc. Natl. Acad. Sci. USA. 93:11615–11617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Chan, C. K., Y. Hu, S. Takahashi, D. L. Rousseau, W. A. Eaton, and J. Hofrichter. 1997. Submillisecond protein folding kinetics studied by ultrarapid mixing. Proc. Natl. Acad. Sci. USA. 94:1779–1784. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Semisotnov, G. V., N. A. Rodionova, V. P. Kutyshenko, B. Ebert, J. Blanck, and O. B. Ptitsyn. 1987. Sequential mechanism of refolding of carbonic anhydrase B. FEBS Lett. 224:9–13. [DOI] [PubMed] [Google Scholar]
- 66.Yazgan, A., and R. W. Henkens. 1972. Role of zinc(II) in the refolding of guanidine hydrochloride denatured bovine carbonic anhydrase. Biochemistry. 11:1314–1318. [DOI] [PubMed] [Google Scholar]
- 67.Putnam, F., and H. Neurath. 1945. Interaction between proteins and synthetic detergents. II. Electrophoretic analysis of serum albumin-sodium dodecyl sulfate mixtures. J. Biol. Chem. 159:195–209. [PubMed] [Google Scholar]
- 68.Gelamo, E. L., and M. Tabak. 2000. Spectroscopic studies on the interaction of bovine (BSA) and human (HSA) serum albumins with ionic surfactants. Spectrochim. Acta (A). 56A:2255–2271. [DOI] [PubMed] [Google Scholar]
- 69.Paz-Andrade, M. I., M. N. Jones, and H. A. Skinner. 1978. Enthalpy of interaction between some cationic polypeptides and n-alkyl sulfates in aqueous solution. J. Chem. Soc. Faraday Trans. 74:2923–2929. [Google Scholar]
- 70.Reference deleted in proof.
- 71.Hilser, V. J., and E. Freire. 1995. Quantitative analysis of conformational equilibrium using capillary electrophoresis: applications to protein folding. Anal. Biochem. 224:465–485. [DOI] [PubMed] [Google Scholar]
- 72.Simonson, T. 2003. Electrostatics and dynamics of proteins. Rep. Prog. Phys. 66:737–787. [Google Scholar]
- 73.Simonson, T., and C. L. Brooks III. 1996. Charge screening and the dielectric constant of proteins: insights from molecular dynamics. J. Am. Chem. Soc. 118:8452–8458. [Google Scholar]
- 74.Reference deleted in proof.
- 75.Dill, K. A., and S. Bromberg. 2002. Molecular Driving Forces: Statistical Thermodynamics in Chemistry and Biology. Garland Science, New York.
- 76.Gill, S. J., and I. Wadso. 1976. An equation of state describing hydrophobic interactions. Proc. Natl. Acad. Sci. USA. 73:2955–2958. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Zhou, H., and Y. Zhou. 2002. Stability scale and atomic solvation parameters extracted from 1023 mutation experiments. Proteins. 49:483–492. [DOI] [PubMed] [Google Scholar]