A Model for the Pulsatile Secretion of Gonadotropin-Releasing Hormone from Synchronized Hypothalamic Neurons

Abstract

Cultured gonadotropin-releasing hormone (GnRH) neurons have been shown to express GnRH receptors. GnRH binding to its receptors activates three types of G-proteins at increasing doses. These G-proteins selectively activate or inhibit GnRH secretion by regulating the intracellular levels of Ca²⁺ and cAMP. Based on these recent observations, we build a model in which GnRH plays the roles of a feedback regulator and a diffusible synchronizing agent. We show that this GnRH-regulated GnRH-release mechanism is sufficient for generating pulsatile GnRH release. The model reproduces the observed effects of some key drugs that disturb the GnRH pulse generator in specific ways. Simulations of 100 heterogeneous neurons revealed that the synchronization mediated by a common pool of diffusible GnRH is robust. The population can generate synchronized pulsatile signals even when all the individual GnRH neurons oscillate at different amplitudes and peak at different times. These results suggest that the positive and negative effects of the autocrine regulation by GnRH on GnRH neurons are sufficient and robust in generating GnRH pulses.

INTRODUCTION

Understanding the molecular mechanisms for the pulsatile secretion of gonadotropin-releasing hormone (GnRH) in vivo has been hampered by the low number of GnRH neurons, their scattered distribution, and the poor knowledge of their connectivity (1). The development of cultured GnRH neuronal cell lines (GT1 cells) (2,3) and fetal hypothalamic GnRH neurons (4,5) provided valuable insights into the underlying mechanism. Pulsatile GnRH signals similar to those observed in vivo have been recorded, although the influences from other parts of the brain, the glial cells and non-GnRH neurons, are absent in these cultures (3–5). This suggests that pulsatile release is an intrinsic property of GnRH neurons. It is consistent with the observations showing that lesion but not deafferentation of the medial basal hypothalamus abolishes the pulsatility (6–8). Two conjectures can be drawn from these observations: i), the mechanism for pulsatile GnRH release is robust and capable of surviving the culture conditions; and ii), there exist multiple mechanisms for generating GnRH pulses that operate under different conditions. Both conjectures found their support in numerous observations (9,10). The two are not necessarily mutually exclusive. Both could be indispensable for the GnRH pulse generation. More experiments are required to determine if both of the two conjectures are correct or if only one of them is correct. Mathematical models can serve as a useful tool in determining if a known mechanism is feasible and robust. Here, we provide support for the first conjecture by using a mathematical model.

The autofeedback effect of GnRH had been observed in vivo in the late 1980s (11). However, better understanding has been achieved in recent studies of cultured GnRH neurons. Coherent GnRH pulses were observed in a culture containing two GT1 cell-coated coverslips with no direct cell-to-cell contact (3). This led to the assumption that the GnRH molecules secreted into the extracellular medium may have acted as a “diffusible mediator” that synchronized cells on the two coverslips. The discovery of GnRH receptors on both GT1 cells (12) and fetal GnRH neurons (4) made this assumption compelling. The fact that GnRH agonists potentiate whereas GnRH antagonists suppress the pulsatility (13) suggests that the autocrine regulation is crucial in generating GnRH pulses. The molecular events leading to both the up- and down-regulations of GnRH release have been discovered (3,4,12–15). Based on these experiments, we construct a model of GnRH pulse generator and demonstrate that the autocrine regulations of GnRH provide a sufficient and robust mechanism for episodic GnRH release. The fact that GnRH plays the roles of both a feedback regulator and a synchronizing agent is consistent with all known observations and provides a sensible explanation for the synchronization between sparsely distributed GnRH neurons in vivo.

THE MODEL

Basic assumptions of the model

We summarize the key data collected in culture experiments into the following model assumptions:

• A1. The pulsatile release of GnRH is an intrinsic property of each GnRH neuron. It could potentially occur in a single neuron located in a small liquid droplet (Fig. 1 a) or in a continuously stirred perifusion chamber containing many neurons (Fig. 1 b) (3–8,11).

• A2. GnRH in the extracellular medium plays the roles of a feedback regulator and a synchronizing agent. Direct synaptic or gap-junctional coupling between GnRH neurons is not essential for the pulsatility (3–5,9,11–13).

• A3. The binding of GnRH to its receptors activates three types of G-proteins, G_s, G_q, and G_i. The activated α-subunits of these G-proteins, denoted by α_s, α_q, and α_i, dissociate from their respective βγ-subunits. α_s activates the production of cAMP by adenylyl cyclase (AC) whereas α_i inhibits AC. α_q activates the production of inositol trisphosphate (IP₃) that releases Ca²⁺ from intracellular stores (Fig. 1 c) (3,4,12–15).

• A4. The dependence of the equilibrium concentration of each activated α-subunit on the extracellular level of GnRH (G) follows a Hill function where α stands for S, Q, and I; K_S < K_Q < K_I; n_S = 4 and n_Q = n_I = 2 (Fig. 2 a).

• A5. At equilibrium, the dependence of cytosolic Ca²⁺ concentration (C) on G is sigmoidal (Fig. 2 a), whereas the dependence of cytosolic cAMP concentration (A) on G is biphasic (Fig. 2 b) (see Figs. 1 F, 2 B, and 5 B in Krsmanovic et al. (13)).

• A6. C and A act in synergy to trigger GnRH secretion (Fig. 1 c) (3,5,12,13,15,16).

• A7. The negative feedback through α_i is essential for generating GnRH pulses and for controlling the amplitude and frequency of the pulses (13).

FIGURE 1.

Schematic illustration of a single-cell model (a) and a multi-cell model (b). The volume of the liquid droplet containing the cell in a must be small so that the amount of GnRH secreted by a single cell is enough to cause a big increase in the GnRH concentration. (c) The molecular events triggered by the binding of GnRH to its receptors on GnRH cells. c is adopted and modified from Fig. 6 in Krsmanovic et al. (13).

FIGURE 2.

(a) Dependence of the equilibrium levels of α_s (dashed lines), α_q (dotted lines), and α_i (solid lines) on G. (b) The dependence of the equilibrium levels of Ca²⁺ and cAMP on G. These curves were obtained by fitting the model equations to the data in Figs. 1 F, 2 B, and 5 B in Krsmanovic et al. (13).

FIGURE 5.

Synchronization in a heterogeneous population of 100 cells. In Case A, all the cells are identical. In Case D, all parameters that are assigned a range in Table 1 are randomly chosen from their respective ranges. In Cases B and C, only two parameters (K_I, k_I for B, and K_Q, k_Q for C) are randomly distributed. In these cases, the first 90 cells numbered from 1 to 90 are randomly assigned a value within the oscillatory ranges, whereas the remaining 10 cells (open circles in the middle panels) are randomly assigned a value that is far from the oscillatory range. These ranges are specified in the text. I-max and Q-max refer, respectively, to the maximum values of the variables I and Q during the oscillations.

The model equations

There are six important variables in the model: the GnRH concentration in the extracellular medium (G), the cytosolic concentrations of Ca²⁺ (C) and cAMP (A), and the concentrations of the dissociated α_s, α_q, and α_i in the interior side of the cell membrane denoted by S, Q, and I, respectively. Hereafter, we shall use these notations to refer to the chemicals as well as their concentrations interchangeably. The time evolution of these variables is described by

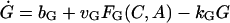(1)

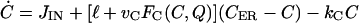(2)

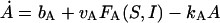(3)

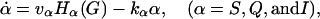(4)

where b_G is the basal rate of G secretion, v_GF_G(C, A) is the rate of C- and A-dependent secretion of G, and k_G is the rate of GnRH removal in the extracellular space. J_IN is the rate of Ca²⁺ influx from the extracellular medium through voltage-gated Ca²⁺ channels on the cell surface. To focus on the autocrine mechanism, we do not attempt a detailed description of the plasma membrane electrical activities. Thus J_IN is assumed to be a small constant. The gradient in Ca²⁺ concentrations across the membrane of the intracellular Ca²⁺ store, endoplasmic reticulum (ER), is C_ER − C, which drives the Ca²⁺ release from the ER. λ is a small nonspecific permeability or leak of the ER membrane. v_CF_C(C, Q) is the rate of Ca²⁺ release through the IP₃-receptor/channels (IP₃R in Fig. 1 c). Ca²⁺ removal occurs at the ER membrane, where Ca²⁺ is pumped back into the ER, and at the plasma membrane where Ca²⁺ is pumped out of the cell. In both places, the pumping rate usually follows a sigmoidal dependence on C. Here, we simplify the two pumps into one single first-order Ca²⁺-removal term, k_CC. b_A is the basal rate of A production. The term v_AF_A(S, I) describes the S- and I-dependent rate of cAMP production by AC, whereas the k_AA is the removal rate of A.

The change in the levels of the three α-subunits, S, Q, and I, is described by Eq. 4. k_αα is the rate for α-removal. The production of these subunits is activated by the binding of G to its receptors. Thus the production rates are dependent on G through the term H_α(G). At steady state, α = (v_α/k_α)H_α(G). The mathematical form for the function H_α(G) can be obtained by fitting a sigmoid curve to the data published in Krsmanovic et al. (13). There are multiple ways to generate a sigmoid curve. We choose the Hill function as explained in assumption A4. We tried other forms of sigmoid functions and found that they worked equally well (data not shown). The Hill functions that yielded the best fit to the experimental data are plotted in Fig. 2 a. They can be regarded as the on and off switches for the production of dissociated α-subunits. Note that the production of S is turned on at very low levels of G with K_S = 0.34 nM. The production of Q is switched on at intermediate levels of G with K_Q = 21 nM, whereas I is turned on at higher levels of G with K_I = 158 nM. The fact that the positive feedback on G-regulated G secretion (via S and Q) occurs at lower levels of G and the negative feedback (via I) occurs at higher levels of G is crucial for generating GnRH pulses in this model.

Q exerts its influence on the secretion of G indirectly through C (see Fig. 1 b). The increase in Q results in higher levels of IP₃, which in turn triggers more Ca²⁺ release from the ER store. This effect is described by the term v_CF_C(C, Q) in Eq. 2. Ca²⁺ release through IP₃Rs is also regulated by C itself. This Ca²⁺ -induced Ca²⁺ release can cause oscillations in C (17). There is no evidence showing that IP₃-induced Ca²⁺ oscillations occur in GnRH cells stimulated by GnRH. We choose not to include this mechanism in this minimal model by assuming F_C(C, Q) = F_C(Q). To obtain a simple form of F_C(Q), we solve for the steady state of C as a function of G and fit it to the observed curve that describes the dependence of C on G (see Fig. 1 F of Krsmanovic et al. (13)). We were able to achieve a good fitting (Fig. 2 b, solid curve) by using F_C(C, Q) = Q.

The regulation of G secretion by S and I is also indirect via A (Fig. 1 b). S and I regulate the production of A by AC in opposite ways, whereas higher S activates AC, elevated I inhibits AC. These effects are described by the term v_AF_A(S, I). Again, we look for the simplest possible form of the function F_A(S, I) that yields a good fit to the observed biphasic dependence of A on G (see Fig. 2, A and B, of Krsmanovic et al. (13)) at equilibrium. Such a fit (Fig. 2 b, dotted curve) is obtained by using F_A(S, I) = Sh_I/(I + h_I). Note that at equilibrium, the inhibition seems to have already saturated at G ∼ 100 nM (Fig. 2 b). This seems to suggest that, at equilibrium, the production of A is completely suppressed even before the curve H_I(G) is fully saturated. This is because h_I is small, which implies that inhibition occurs at low levels of I. During oscillations, however, a similar degree of inhibition occurs at higher levels of G because the response of I to increasing values of G is delayed.

The exact mechanisms through which C and A control the secretion of G is unknown. This makes the choice of the function F_G(C, A) in Eq. 1 difficult. We tested several forms of F_G(C, A) and found that it has to be nonlinear to generate pulsatility. We chose F_G(C, A) = (AC)^m with m = 3. This implies that secretion occurs only in the presence of both C and A signals (assumption A6).

Implicit in the model described by Eqs. 1–4 is the assumption that the rates of the production of dissociated α-subunits is influenced instantaneously by changes in G through H_α(G). Although there is no evidence to either support or reject this assumption, such a dependence is unlikely instantaneous. However, if the time it takes for changed levels of G to influence the dissociation of α-subunits is shorter than a few minutes, this assumption can still be a reasonable approximation since the period of GnRH pulses is very long (∼1 h). The potential problem this assumption may cause is further reduced by the fact that, although H_α(G) changes instantaneously with G, α itself does not. The removal rate constant k_α determines how fast α follows the changes in the value of H_α(G). Therefore the rate constants k_S, k_Q, and k_I are important factors that determine the period of the GnRH pulses.

Based on experimental knowledge, variations in C and A are much faster than changes in the remaining variables of the system. Therefore we can simplify Eqs. 1–4 into the following reduced system by using the quasi steady state approximation for the fast variables C and A:

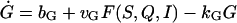(5)

(6)

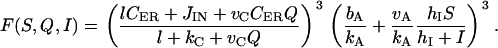(7)

The results in the next section show that such a simplification does not alter the qualitative behavior of the model.

RESULTS

Sequential activation of G-proteins and GnRH pulses

Mechanisms leading to rhythmic oscillations have been studied and modeled in a number of cellular systems (18). It is well known that a positive feedback mechanism can cause oscillations. Due to the existence of the positive autocrine effect of GnRH, oscillations in GnRH are not surprising. Besides showing that the model can reproduce the GnRH pulses with the observed characteristics (Fig. 3), we focus more on the robustness of the mechanism that generates these pulses. We show that the occurrence of GnRH pulses depends on the general properties of the model which are experimentally established. Specific forms of the functions F_G, F_C, F_A, and H_α are not essential. These properties include: i), the autocrine binding of GnRH to its receptors on GnRH cells,; ii), the sequential activation of the three types of G-proteins at increasing doses of GnRH.

FIGURE 3.

Pulsatile GnRH signals generated by the model. a and b are produced by the full model described by Eqs. 1–4; c and d are obtained by the reduced model described by Eqs. 5 and 6. The levels of the α-subunits S (dashed lines), Q (dotted lines), and I (solid lines) are shown in the panels below the time series of G. Effects of α-subunits at different phases of the G signal are shown in the amplified view of a typical pulse in the panels on the right. The thin dotted lines relate the peak values of different α-subunits to different phases of the G signal. Note that in b and d, the level of S is held constant at 2 nM.

This is how GnRH pulses occur based on the model. At low levels of G (e.g., G ≈ 0.24 nM in the interspike intervals (ISIs) in Fig. 3 a), Q ≈ I ≈ 0 and S is small (S_* ≈ 0.52 nM). This is easy to understand based on Fig. 2 a. During this “off phase” of the G cycle, basal G secretion rate, r_b ≡ b_G + v_GF(S_*, 0, 0), determines the level of G (G_* ≈ r_b/k_G). It is obvious G_* cannot be too small for oscillations to occur. If G_* ≥ K_S, the positive feedback through α_s can be switched on at the first thin dotted line in Fig. 3 a2. This propels G to a level that is comparable to K_Q and turns on the second positive feedback through α_q at the second thin dotted line in Fig. 3 a2. As a result, a sharp increase in G is triggered through the autocatalytic process. Around these peak values of G, the negative feedback via α_i is switched on causing a delayed inhibition of G secretion and a sharp decrease in the G value at around the third thin dotted line in Fig. 3 a2.

Fig. 3 a4 clearly shows the sequential on switch of the three G-proteins at the rising phase of the pulse as well as their sequential off switch at the declining phase of the pulse. Note that the decline in the level of I is slow due to the fact that k_I is much smaller than k_S and k_Q. This slow removal of the inhibitory effect of α_i contributes to holding the value of G at a low level for an extended period during the ISI.

It is known that rhythmogenesis can occur if one positive feedback mechanism exists. The existence of two positive feedback G-proteins seems redundant from a mechanistic view point. Fig. 3 b shows that, by holding S at a constant level (the dashed line in Fig. 3, b3 and b4), pulsatile release still occurs. Although the amplitude and the temporal profile of the G signal (see Fig. 3, b2 and b4) are changed, the period is similar. In this case, the activation threshold K_Q for switching on α_q is achieved through a slow accumulation of G during the ISI. This is possible only when r_b/k_G ≥ K_Q. Thus oscillations cannot occur for a constant value of S that is too small. This is because the effects of α_s and α_i on the production of A is assumed to be multiplicative in F_A(S, I). A value of S that is too small will simultaneously block the influence from both S and I. This suggests a way to experimentally verify whether the effects of α_s and α_i are multiplicative. If oscillations can still occur at near zero constant levels of S, this multiplicative assumption should be rejected. Oscillations can also occur when Q is held constant (results not shown). In this case, nonstandard parameter values must be used. In particular, the sensitivity of I to G must be increased enormously, i.e., K_I has to be reduced to a value that is much smaller than the best-fit value.

Fig. 3, c and d, show that the simplified model given by Eqs. 5–7 produces identical results as the full model. This is true both for oscillating S (Fig. 3 c) and constant S (Fig. 3 d). In the remaining part of this article, this simplified model will be used unless stated otherwise.

These results suggest that the sequential activation of the three types of G-proteins that is reflected in the inequalities K_s < K_Q < K_I (Fig. 2) is essential. This comes from the key data (13) on which the model is based. If the order of the sequence is altered, oscillations and other properties of the system will be changed substantially. If this sequential order is maintained, oscillations should naturally occur regardless of the specific functional forms one uses to fit the curves in Fig. 2.

Parameter dependence

Although the sequential activation of the G-proteins provides a robust mechanism for generating GnRH pulses, oscillations with the observed characteristics occur only within reasonably chosen windows of some key parameters. Fig. 4 shows how the period and amplitude of the oscillations change as some parameters change. The inhibitory feedback through α_i is crucial in the termination of each GnRH pulse and in holding the GnRH at a low level during the ISIs. This suggests that parameters that control this inhibitory process should have strong influence on the oscillations. Fig. 4, a and b (for S constant), show that the oscillation amplitude remains almost constant when k_I is changed. However, the period (the inset in each panel) changes several orders of magnitude. When very small values of k_I are used, the period can be extremely long. Fig. 4 b shows that the domain of the oscillation shrinks when S is held constant. This suggests that the existence of two positive feedback mechanisms, although redundant for pulse generation, enlarges the range of parameter values in which oscillations occur.

FIGURE 4.

Bifurcation diagrams versus some key parameters. In each panel, the steady-state values of G in nM are plotted in thick (stable) and thin (unstable) solid lines. The periodic solutions are plotted in thick (stable) and thin (unstable) dotted lines. The oscillation period T in min is plotted in the inset of each panel. Note that logarithmic scales are used for all axes except for the axes of T. Equations 5 and 6 are used in all simulations except for that in b where S = 2 nM. The units of k_I, k_Q, k_G, v_I, and v_Q can be found in Table 1.

The dynamics of I is also influenced by v_I (Fig. 4 c). Oscillations occur for a wide range of v_I values. The oscillation amplitude decreases as v_I increases, consistent with the fact that enhanced amplitude in I results in increased inhibition of G. The oscillation period changes little for most v_I values. The effects of k_Q and v_Q that control the dynamics of Q are shown in Fig. 4, d and e. Both parameters change the period moderately while changing the amplitude by two orders of magnitude. This is because Q is the major autocatalytic agent. Increasing the amplitude of Q (by increasing v_Q or decreasing k_Q) causes an increase in the amplitude of G.

Another important parameter is the removal rate of G, k_G. This parameter can be altered in perifusion experiments, thus a realistic control parameter. Fig. 4 f shows that, when other parameters are fixed at their standard values, oscillations are sensitive to k_G. Within the window in which oscillations occur, higher values of k_G decrease the baseline level of G in the ISIs and leave the peak value unchanged. The change in the period is moderate.

It is interesting to point out that, based on the bifurcation diagrams shown in Fig. 4, the coexistence between a stable steady state and a pulsatile oscillatory state is common in all the diagrams. Fig. 4 f shows that the coexistence between two stable steady states is also possible. Such bistabilities provide potential experimental tests of these bifurcation results. For example, the bistability between a steady state and a periodic state shown in Fig. 4 f can be tested by slowly increasing and decreasing the value of k_G (the removal rate of GnRH in the medium). The model predicts that for a very low value of k_G, G should rest at an elevated plateau level. As k_G is slowly increased in a controlled manner, oscillations in G should occur at values of k_G larger than a threshold value denoted by . Now, one can start from a value of k_G larger than 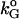where oscillations are observed and slowly decrease it. Oscillations will be replaced by steady states for values of k_G smaller than another threshold value denoted by 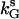. A hysteresis between the steady state and the oscillation exists if .

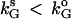A model for a heterogeneous cell population

The model given by Eqs. 1–4 or its simplified version given by Eqs. 5–7 describes either a single cell or a population of identical cells. To study the differences between individual GnRH cells in realistic culture experiments, we extend the single-cell model to the following model of N distinct cells:

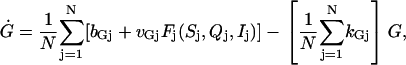(8)

(9)

where 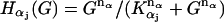, and the function F_j(S_j, Q_j, I_j) is defined as in Eq. 7 for each j, although parameters in this expression differ for different j. The variable G does not carry a subscript because it is the shared signal in the continuously stirred extracellular medium. This model allows us to study how tolerant the pulse-generating mechanism is to the heterogeneity of the cell population.

Fig. 5 shows the behavior of a population of 100 cells for four different levels of heterogeneity. We use three panels to illustrate the behavior of the system in each case. The top panel shows the time series of G. Each individual cell is represented by a dot or circle in the middle and lower panels. In the middle panel, the peak amplitude of a chosen α-subunit is plotted as a function of its peak time for each period. The lower panel is a raster plot of the peak times versus the cell numbers.

The model reduces to a single cell model if all cells are identical. This situation is shown in Case A of Fig. 5. When synchronization is achieved, these identical cells all peak at the same time and with the same amplitude. Thus in each period, all the 100 points land on top of each other in the middle panel and form a vertical straight line in the lower panel. However, such a perfect synchronization will not occur in heterogeneous populations as shown in the other cases of Fig. 5. Therefore a heterogeneous population will be referred to as “synchronized” if a pulsatile G signal is generated and all individual cells peak within the duration of the pulse in each period. Simulations in all the four cases were initiated from random initial conditions. Synchronization emerged after a transient that was shorter than a single oscillation period.

To demonstrate that the coupling mediated by G is strong and robust for generating synchronized pulses, we studied the effects of heterogeneous distributions of some key parameters. We first investigated a uniform random distribution of the parameter K_I within the range 17.4–383.6 nM in which an individual cell is capable of generating oscillations based on the single cell model. We found that synchronization across the population was always achieved (results not shown). In Case B, we further examine the robustness of the synchronization mechanism. For the first 90 cells, numbered from 1 to 90, we randomly chose a K_I value from the above mentioned oscillatory range. These cells are represented by black dots. For the remaining 10 cells (open circles in the middle panel), the K_I values were randomly chosen from the range 3.4–9.7 nM, which does not support oscillations. Their k_I values were also randomly selected from the range 0.0135–0.089 min⁻¹ to eliminate any chance for them to participate actively in rhythmogenesis. Under these conditions, synchronization still occurred, although the amplitudes of individual cells varied significantly and different cells do not peak at the same time. Notice that the 10 “nonoscillatory cells” are forced to “synchronize” with the whole population passively.

A similar study was conducted in Case C in which the K_Q parameter was randomly distributed within the oscillatory range 12.8–88.6 nM for the first 90 cells. For the remaining 10 “nonoscillatory cells”, K_Q was randomly chosen from the nonoscillatory range 230.6–389.6 nM, and k_Q was chosen from the range 1.3–2.7 min⁻¹. Again, synchronization occurred. Notice that random distribution of the parameter K_Q caused little variations in the peak times and amplitudes for the oscillatory subpopulation. This is different from Case B in which the dynamics of I is influenced by the random distribution. This is because the Q variable is much faster than the I variable.

Finally, we tested the effects of heterogeneous distributions in all parameter values. We found that synchrony occurred whenever the ranges are reasonably narrow (not shown). Then, we examined the largest possible ranges for the distributions of many key parameters and found that synchronization was still preserved when almost all the key parameters are uniformly distributed within the ranges given in Table 1. The result is shown in Case D.

TABLE 1.

Standard parameter values

Standard parameter values
Symbol	Standard value	Range	Symbol	Standard value	Range
JIN	0.2 μM/min		KS	0.34 nM	[0.15, 0.3]
bG	0.144 min−1		KQ	21 nM	[15, 40]
ℓ	60 min−1		KI	158 nM	[41, 355]
kG	0.6 min−1	[0.5, 0.8]	kS	9 min−1	[6.4, 9.7]
kA	60 min−1		kQ	9 min−1	[4.8, 111.6 ]
kC	5100 min−1		kI	0.1125 min−1	[0.09, 0.18 ]
vG	324 (nM)−4min−1	[324, 360]	vA	150 min−1	[120, 155]
vC	1.2 (μM)−1min−1		vS	23.4 nM/min	[16.2, 44.1 ]
CER	2.5 μM		vQ	22.5 nM/min	[27.1, 58.4 ]
bA	1.8 nM/min		vI	0.36 nM/min	[0.28, 1.8]
hI	0.036 nM

Parameters in Roman-style symbols are obtained by fitting the curves in Fig. 2 to experimental data in Krsmanovic et al. (13). Ranges within which the parameters are randomly distributed in the study of heterogeneous populations are provided.

Notice that the oscillation period is much shorter in Case D as compared to the period in Cases A–C. This is because in Case D, the values of 12 crucial parameters are randomly assigned from the widest possible ranges provided in Table 1, whereas in Cases B and C, only 2 parameters were randomly assigned a value and the ranges were more restricted. Because the ranges of variation in Case D were so wide, many cells were assigned with parameter values that were very far from the standard values obtained by fitting experimental curves. The number of pulses in Case D was reduced from 8 to 6 when only 1 of the 12 parameters (k_I) was fixed at the standard value, whereas the other 11 were randomly distributed. When 2 out of the 12 (k_I and k_Q) were fixed at their standard values, the number of pulses was reduced to 5. When 3 out of the 12 (k_I, k_Q, b_G) were fixed, the number of pulses in Case D was reduced to 4, similar to the number obtained in Cases B and C (results not shown).

These results demonstrate that coupling through the autocrine regulation by GnRH is a very robust mechanism for achieving synchronization even in highly heterogeneous cell populations. Furthermore, synchronization is still preserved when a fraction of the cells are passive “nonoscillatory” participants.

Effects of some drugs

Important properties of the GnRH pulse generator have been revealed in the study of the effects of drugs that interfere with certain known aspects of the system. A good model should reproduce these effects and provide explanations.

It has been shown that the treatment with the potent GnRH antagonist, SB-75, was capable of abolishing GnRH pulses, causing a sustained and nonoscillatory plateau in G (see Fig. 1 H in Krsmanovic et al. (13)). We assume that SB-75 blocks the activation of all three G-proteins leading to a decrease in v_S, v_Q, and v_I. Decreasing the values of v_S, v_Q, and v_I by 42% to 9.83, 9.45, and 0.3 (nM/min), respectively, we found that the oscillations were abolished reversibly as observed experimentally. However, no elevated plateau in G was obtained. Instead, G stayed at a constant level close to the baseline (results not shown). For this reason, we also assume that the elevated plateau in G is caused by an increase in the value of K_I. Such an increase in K_I signifies that SB-75 not only decreases the activities of the three G-proteins but also reduces the sensitivity of G_i to GnRH. If the decrease in the values of v_S, v_Q, and v_I is combined with an increase in K_I to a value that is >750 nM, a nonoscillatory plateau in G similar to that observed in Fig. 1 H of Krsmanovic et al. (13) is produced (see Fig. 6 a, where K_I = 1000 nM was used). Nonoscillatory GnRH at an elevated plateau could also be observed (results not shown) when the parameters v_S, v_Q, and v_I are decreased at different proportions, provided that they are not reduced by >42% simultaneously.

FIGURE 6.

Response of the pulse-generator model to conditions that mimic the effects of a GnRH antagonist (SB-75) (a), an inhibitor of G_i (PTX) (b), a GnRH agonist (D-Ala) (c), and PTX + D-Ala (d). In all cases, the observed responses are reproduced by the model. The drug effects are turned on and off exponentially following p(t) = p_new + (p_old − p_new)exp(−(t − t₀)/80).

Pertussis toxin (PTX) was shown to abolish the oscillations and cause a sustained increase in G (see Fig. 2 G in Krsmanovic et al. (13)). Since PTX blocks the inhibitory G-protein, we assume that it reduces v_I from the value 0.72 to 0.09 nM/min and increases K_I by the same amount as in Fig. 6 a. In other words, we assume that PTX reduces the activity as well as the sensitivity of G_i to GnRH. The model reproduced the observed response as shown in Fig. 6 b. Thus, blocking the inhibitory feedback is sufficient to eliminate the pulsatility. This suggests that the experiment and the model both support assumption A7. When the GnRH agonist (D-Ala) was applied, an increase in peak amplitude and ISI was observed (see Fig. 1 G in Krsmanovic et al. (13)). We assume that the agonist enhances the activation of all the three G-proteins causing an increase in v_S, v_Q, and v_I from the same values used in Fig. 6 a to 27, 25.2, and 0.81 (nM/min), respectively. These changes caused an increase in the amplitude of the oscillation but left the ISI unchanged (results not shown). We found that a simultaneous increase in both the amplitude and the ISI could be achieved when the increase in the values of v_S, v_Q, and v_I was combined with a slight increase in the values of K_S and K_Q to 0.4 and 23 nM, respectively (see Fig. 6 c). Oscillations with increased amplitude and ISI could also be obtained if the values of v_S, v_Q, and v_I were simultaneously increased by 40%, whereas K_S and K_Q were both increased by 6% (results not shown).

Finally, when both the agonist and PTX are applied simultaneously, the GnRH pulses are eliminated and the sustained increase in G occurs (Fig. 6 d) just as observed experimentally (see Fig. 2 H in Krsmanovic et al. (13)). This was obtained by using the same parameter values as in Fig. 6 c, except that v_I = 0.09 nM/min and K_I = 1000 nM as in Fig. 6 b. Implicit in these parameter choices is the assumption that, as compared to the agonist D-Ala, the action of PTX is further downstream in this signal transduction pathway. This further demonstrates the crucial role of the inhibitory feedback in GnRH pulse generation. A boost in both G_s and G_q cannot compensate the loss of G_i.

DISCUSSION

We developed a mathematical model for the GnRH pulse generator based on the following well-established properties: i), GnRH cells express GnRH receptors allowing GnRH to exert autocrine regulation on its own secretion; ii), the binding of GnRH to its receptors activates sequentially three types of G-proteins: G_s, G_q, and G_i; and iii), the dissociated α-subunits, α_s and α_q, activate GnRH secretion by increasing intracellular levels of cAMP and Ca²⁺, respectively; whereas α_i inhibits GnRH secretion by reducing the production of cAMP. Some key parameter values, such as the activation thresholds, were obtained by fitting the curves in Fig. 2 to experimental data.

Besides reproducing pulsatile GnRH signals with the observed characteristics, we investigated the robustness of this pulse-generating mechanism. This is important since there is insufficient data for us to extract the detailed forms of some key functions and parameter values in the model. Robustness of the mechanism guarantees the occurrence of the same qualitative behaviors when different forms of functions and/or parameter values are used, provided that the well-established properties are retained. Therefore the occurrence of the GnRH pulses in this model is a direct consequence of these properties rather than any specific forms of function and parameter choices. We tried other expressions for the key functions in the model and found that if a good fit to the curves plotted in Fig. 2 was achieved, GnRH pulses were generated.

A number of other biochemical rhythms involving positive feedback regulations have been studied and modeled (18). Of particular interest is the origin of the periodic cAMP signal in cellular amoebae Dictyostelium discoideum (19). In this model, cAMP production and secretion is enhanced by an autocrine regulation of cAMP. This model was later extended to account for the influences of two types of G-proteins (20, 22). The cAMP signaling in D. discoideum and the GnRH signaling in GnRH neurons are similar in the following two aspects: i), in both systems, the signaling molecule plays the roles of both a feedback regulator and a diffusible mediator; and ii), both involve a positive and a negative feedback on the production of cAMP by AC. However, they are also different in two aspects: i), a third G-protein (G_q) is activated by GnRH binding, providing an additional positive feedback mechanism through Ca²⁺ signaling; and ii), in the cAMP models, the negative feedback through G_i is not essential for the oscillations. For the GnRH pulse generator, the positive feedback through G_q and the negative feedback through G_i are both essential for generating GnRH pulses.

The existence of a third feedback pathway mediated by G_q provides a vital connection between GnRH pulse generator and Ca²⁺ signaling in GnRH cells. This allows us to study the mutual interaction between the plasma membrane electrical activities and the secretion of GnRH. A mathematical model of the electrical activities of GnRH cells has been developed (23). A new project for us in the immediate future is to couple the GnRH pulse generator model to this plasma membrane model. This will give a more accurate description of the term J_IN in Eq. 2. This more detailed model can help clarify the puzzle concerning the exact roles of the electrical activities of GnRH pulse generation. In the model presented in this study, we assume that GnRH pulses occur when GnRH neurons are voltage-clamped, provided that there is enough Ca²⁺ influx into the cell. However, synchronization of the electrical activities of GnRH neurons may facilitate and/or strengthen the synchrony mediated by the diffusible GnRH. This type of interaction has been studied in detail in another endocrine cell (21), where the plasma membrane electrical activity was shown to be crucial in controlling the refill of the Ca²⁺ store. Ca²⁺ oscillations generated by plasma membrane electrical activities with a period of ∼8 min were observed in cultured GnRH neurons (24). The mechanism for these oscillations remains unknown. It was found that these asynchronous oscillations in different cells “synchronize” (i.e., all peak at the same time) once every 45 min. Based on our model, we speculate that it is the autocrine mechanism that drives the synchrony of the electrical oscillations but not the converse.

Acting as the feedback regulator, GnRH provides a robust mechanism for the episodic release of GnRH. Acting as the synchronization agent, GnRH also provides a robust mechanism for synchronizing a population of cultured GnRH cells. This has been demonstrated by the heterogeneous population models. We showed that this synchronization mechanism can tolerate strong heterogeneity in the population. Coupling through a diffusible signal in a shared extracellular medium has been studied in a suspension of D. discoideum cells (25) in which shared extracellular cAMP concentration was shown to be very effective in synchronizing heterogeneous populations. In a more recent work (26), a robust synchronization was shown to occur in a diverse and noisy population of Escherichia coli cells through the sensing of a common extracellular signal. A coherent theory of synchronization through a shared diffusive messenger will strengthen our understanding of systems sharing these properties.

This study is based mostly on data collected in cultured GnRH cells in vitro. The multi-cell model, as shown in Fig. 1 b, is basically a continuously stirred chamber of cultured GnRH cells. One should be prudent in extending these results to the GnRH pulse generator in vivo. There are numerous unanswered questions concerning the GnRH pulse generation in vivo. These include: i), What is the role of the electrical activities of the GnRH neurons? ii), Are GnRH neurons in vivo electrically coupled to each other through synapses or interneurons? iii), If electrical coupling exists between GnRH neurons in vivo, does it contribute to the synchronization? iv), If a common extracellular pool of GnRH exists in vivo, is it in the hypothalamic interstitial space or in the hypophysial portal blood? Before these questions are answered, one cannot tell for sure what the actual pulse-generating mechanism in vivo is. However, the robustness of the autocrine mechanism based on in vitro experiments suggests that it can work equally well in vivo provided that GnRH neurons in vivo also express GnRH receptors that are exposed to a common pool of extracellular GnRH and that the binding of GnRH to these receptors sequentially activates G_s, G_q, and G_i in these neurons.