Mechanical Properties of Pore-Spanning Lipid Bilayers Probed by Atomic Force Microscopy

Abstract

We measure the elastic response of a free-standing lipid membrane to a local indentation by using an atomic force microscope. Starting point is a planar gold-coated alumina substrate with a chemisorbed 3-mercaptopropionic acid monolayer displaying circular pores of very well defined and tunable size, over which bilayers composed of N,N,-dimethyl-N,N,-dioctadecylammonium bromide or 1,2-dioleoyl-3-trimethylammonium-propane chloride were spread. Centrally indenting these “nanodrums” with an atomic force microscope tip yields force-indentation curves, which we quantitatively analyze by solving the corresponding shape equations of continuum curvature elasticity. Since the measured response depends in a known way on the system geometry (pore size, tip radius) and on material parameters (bending modulus, lateral tension), this opens the possibility to monitor local elastic properties of lipid membranes in a well-controlled setting.

INTRODUCTION

Since the invention of the atomic force microscope (AFM) in 1986, the spatial analysis of soft biological samples has become a major aim in cellular and molecular biophysics (1). Besides mere visualization of surfaces, the AFM allows one to explore mechanical properties at the nanoscale by means of force-distance curves (2). The two “modes” in force spectroscopy, pulling and indenting, allow one to study force-induced conformational changes of individual macromolecules such as proteins, nucleic acids, and oligosaccharides, and to map elastic properties of cells and membranes with nanometer resolution (1,3,4).

However, quantitative contact mechanics of whole cells or native membrane patches remains cumbersome from an experimental as well as theoretical point of view due to the variable shape of the objects and the complex composition (5,6). The theoretical treatment of the indentation of cells or liposomes is usually based on common contact mechanics according to Hertz or Sneddon, exhibiting only moderate agreement with the measured force curves (1,7–11). Among the few available attempts to model indentation of soft shells with the AFM, Boulbitch recently presented a theory describing the deflection of a cell membrane subject to local forces (12,13), whereas Wan et al. (14) provided an improved model for the indentation of a microcapsule by an AFM tip employing different boundary conditions than Boulbitch and allowing for a change in surface tension. Yao et al. (15) presented an elastic model but neglected the influence of bending.

The determination of mechanical parameters of membranes requires appropriate model systems with defined geometry and composition. Whereas liposomes are well suited for micropipette aspiration experiments (16–19) and solid supported bilayers are frequently used for determining Young moduli (20), no suitable model system is available to study the local bending of membranes with the AFM. Although liposomes have been frequently used for this purpose (5,21–23), the experiments are difficult to reproduce due to variations in vesicle size, interference from adhesion to the supporting surface, which produces severe deformation up to rupture, and inaccurate positioning of the tip. Solid supported membranes, which are stable and easy to prepare, have, however, the drawback of displaying an elastic response that is intricately linked to the elastic properties of the substrate they rest on (20).

Here we present, for the first time, to our knowledge, a method to explore the local mechanical properties of lipid membranes employing pore-spanning bilayers that were recently introduced (24–27). Highly ordered porous alumina with tunable pore size serves as the support to form pore-spanning bilayers attached electrostatically to the functionalized rims of the nanoporous surface. We were able to directly measure the restoring forces of a nearly planar free-standing lipid membrane covering a nanoscopic hole of defined pore size, which is displaced by an AFM tip with a defined normal force. With this technique, it is feasible to infer elastic properties of lipid bilayers from only a few lipid molecules (5,000–30,000 lipids), whereas micropipette suction experiments employing giant liposomes average over as many as ≈10⁸ lipids. To quantify the indentation experiments, we provide the necessary theoretical framework that describes the indentation of a pore-spanning bilayer with a finite-sized tip.

MATERIALS AND METHODS

Preparation of porous alumina

High purity aluminum foils (Goodfellow, Devon, PA; thickness: 0.5 mm) were subject to a two-step anodization process yielding porous alumina with defined pore geometry. The procedure is described elsewhere (see Supplementary Material for detailed information) (24). Employing oxalic acid yields pores exhibiting an average pore radius of (33 ± 2) nm and a porosity of (34 ± 6)% (Fig. 1 A). Anodizing aluminum in phosphoric acid provides larger pores with a mean radius of (90 ± 10) nm and a porosity of (16 ± 5)% (Fig. 1 B).

FIGURE 1.

Scanning electron micrographs of highly ordered gold-coated porous alumina used as the substrate for pore-spanning DODAB and DOTAP bilayers. The average pore radius in A is (33 ± 2) nm with an overall porosity of (34 ± 6)%, whereas in B an average pore radius of (90 ± 5) nm and a porosity of (16 ± 5)% is found.

Preparation of pore-suspending lipid bilayers

Planar pore-spanning bilayers were prepared according to the procedure described previously (24). The gold surface was first functionalized with a monolayer of 3-mercaptopropionic acid followed by an incubation for 4 h at T = 55°C with large unilamellar vesicles composed of either positively charged N,N,-dimethyl-N,N,-dioctadecylammonium bromide (DODAB) or 1,2-dioleoyl-3-trimethylammonium-propane chloride (DOTAP) (0.5 mg/ml in 10 mM Tris, pH 8.6). Large unilamellar vesicles were prepared by the extrusion method using polycarbonate membranes with a mean pore diameter of 1000 nm yielding vesicles with a mean diameter of (600 ± 20) nm as determined by dynamic light scattering.

Atomic force microscopy

Pore-spanning lipid bilayers on porous alumina were imaged in contact mode in aqueous solution with a Dimension 3100 (Nanoscope IIIa+A/D Controller, Veeco, Santa Barbara, CA) and an MFP-3D (Asylum Research, Santa Barbara, CA) AFM using silicon nitride tips purchased from Olympus (Olympus PSA 400, Olympus Biolever, AFFE, Mannheim, Germany) and Veeco Instruments (NP-S) with nominal spring constants between 0.006 and 0.02 N m⁻¹. All images were analyzed using the program SPIP (Scanning Probe Image Processor, Image Metrology, Lyngby, Denmark). Tip radii were characterized by transmission electron microscopy and spring constants of the cantilevers were determined by the thermal noise method (2).

RESULTS AND DISCUSSION

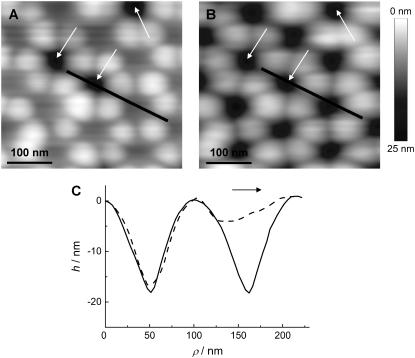
The successful preparation of pore-spanning bilayers on porous alumina substrates was confirmed by means of AFM imaging as illustrated in Fig. 2. Two AFM images obtained from contact mode imaging of a DODAB bilayer covering the highly ordered porous alumina with pore radii of R_pore = 33 nm using a low (0.9 nN, Fig. 2 A) and high (2.7 nN, Fig. 2 B) load force are shown. Each individual pore can be unambiguously assigned and we can clearly distinguish between membrane-covered and uncovered pores by topography images. Fig. 2 A shows that all pores are covered with the lipid bilayer except for three pores, which are labeled with arrows. The uncovered pores can be used as a reference to determine the maximum penetration depth of the AFM tip. At larger forces (Fig. 2 B), the bilayer-covered pores resemble the uncovered porous substrate due to maximal indentation of the membrane into the pores. The height profiles shown in Fig. 2 C, measured along the line drawn in Fig. 2, A and B, show that the variation of the load force influences only the topography of the membrane-covered pores, leaving the profile of the uncovered ones unchanged. The broken symmetry of the bilayer-covered pore imaged at low force (Fig. 2 C) is an artifact arising from the lateral interaction of the tip with the bilayer. The shape depends on the scan direction, which was from left to right as indicated by an arrow.

FIGURE 2.

Visualization of pore-spanning bilayers by AFM (contact mode in aqueous solution). (A) Pores covered by a DODAB bilayer imaged at low forces (0.9 nN). The arrows indicate uncovered pores. (B) Same region imaged at larger forces (2.7 nN). (C) Height profiles along the line shown in A, dashed line, and B, solid line, imaged at two different forces using NP-S cantilevers. Scan direction was from left to right as indicated by the arrow.

Assuming a parabolic tip geometry, the maximum penetration depth 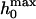can be estimated to be The pore radius R_pore and the tip radius R_tip can be assessed independently from scanning electron microscopy images of the substrate (Fig. 1) and transmission electron microscopy images of the tip (see Supplementary Material).

The goal was now to quantify the elastic properties of these addressable “nanodrums” by employing force spectroscopy at well-defined spots on the surface such as the center of the pore. By performing a cycle of imaging and monitoring force-indentation curves, we were able to control and account for thermal drifts in the x,y plane. Typically, we were capable of recording 10–20 force-indentation curves at 40 different pores repeatedly, providing good statistics.

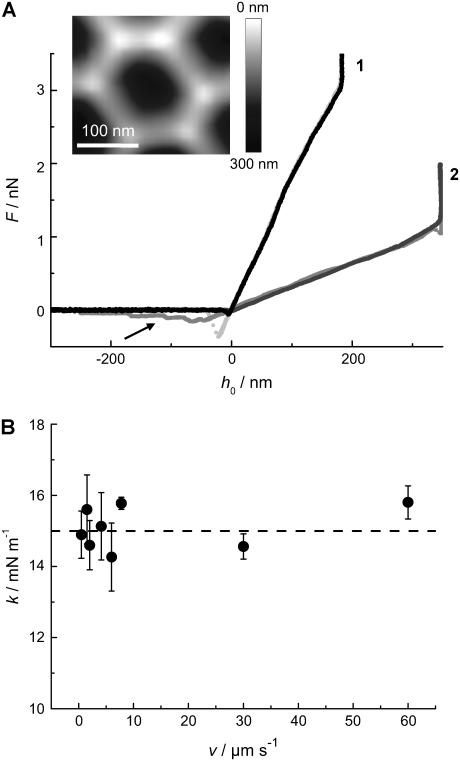
Various force-distance curves are depicted in Figs. 3 and 4. All curves were obtained from the center of the pores at T = 20°C. Fig. 3 A shows trace (indentation) and retrace (relaxation) curves taken on DODAB (curve 1) and DOTAP bilayers (curve 2) covering pores with an average pore radius of 90 nm (inset). We used two different cantilevers for the indentation experiment to account for the different membrane stiffness of the lipids in the gel and fluid phase. The stiffer gel phase (DODAB) was measured with an Olympus PSA 400 (nominal spring constant k ≈ 0.02 N m⁻¹) whereas the softer DOTAP membrane was indented by an Olympus Biolever (k ≈ 0.006 N m⁻¹) matching the corresponding apparent spring constant of the pore-spanning bilayers (see below). This way we could ensure highest possible sensitivity of our measurements. Strikingly, the indentation curves exhibit a linear dependency of the restoring force on the penetration depth for DODAB as well as for DOTAP membranes over the full range. The mean slope, which we will refer to as the apparent “spring constant” of the membrane, depends strongly on the physical state of the bilayer. We found a mean slope for DOTAP bilayers, which are in the fluid phase, of 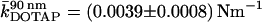and 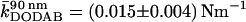for DODAB bilayers, which are in the gel phase. Importantly, both trace and retrace curves lie on top of each other except for the snap-on and snap-off positions, illustrating that under these conditions we are able to assess static, elastic properties, whereas dynamical complications (such as viscous dissipation in the membrane or the solvent) are absent. Further evidence for this claim is that the measured apparent spring constant does not depend on the speed of approach of the AFM tip, see Fig. 3 B. Virtually no dependency of the apparent “spring constant” of the bilayer on the cantilever velocity was monitored up to 60 μm s⁻¹. For our measurements, we used speed between 0.5 μm s⁻¹ and 1.5 μm s⁻¹. This result excludes hydrodynamics as a possible source for additional restoring forces, as well as conceivable complications resulting from compressing the fluid inside the pores that might not permeate the membrane fast enough.

FIGURE 3.

(A) Force-indentation curves taken in the center of a pore (inset) with R_pore = 90 nm (indentation (black) and retraction (light gray) of a DODAB bilayer (1) using an Olympus PSA 400 cantilever with a nominal spring constant of 0.02 N m⁻¹; indentation (black) and retraction (gray) of a DOTAP-bilayer (2) using an Olympus Biolever with a nominal spring constant of 0.006 N m⁻¹). The use of different cantilevers explains the difference in maximal penetration depth. The arrow denotes the occurrence of DOTAP tethers pulled from the surface. (B) Apparent “spring constant” k of a DODAB bilayer spanning a pore with a radius of 90 nm as a function of the vertical cantilever velocity. The dashed line represents the mean value of k. Each data point represents the average of more than 10 force-indentation curves.

FIGURE 4.

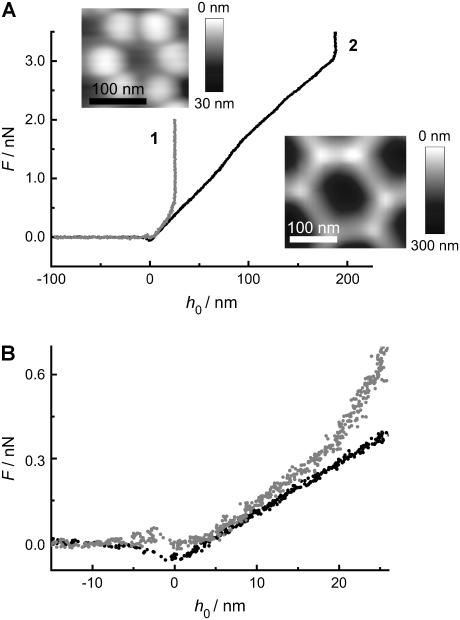
(A) Force-indentation curve of a DODAB bilayer taken in the center of a pore (insets) with (1) R_pore = 33 nm and (2) R_pore = 90 nm. (B) Magnification of figure A emphasizing the different slopes.

Adhesion due to electrostatic attraction between the negatively charged silicon nitride tip and the positively charged bilayer becomes clearly visible in the retraction curve as a snap-off peak. Frequently, we not only observed such a peak upon retraction of the tip, as displayed in the force-distance curve obtained from a DODAB bilayer, but also tether formation when retracting the tip from a DOTAP bilayer. Tether formation is characterized mainly by a force plateau with a value depending on membrane tension and bending rigidity, which has been carefully investigated theoretically and experimentally (28–32). The maximum indentation depth of the tip in the 90 nm pores differs since two different cantilevers with different tip size and geometry were used (see Supplementary Material).

Interestingly, in the case of the force-distance curve obtained from a DOTAP bilayer (curve 2 in Fig. 3 A), a second adhesion peak occurs after reaching the maximum penetration depth at 330 nm, which we tentatively attribute to adhesion of the membrane to the inner pore wall.

Intuitively, the pore size should affect the restoring forces of the membrane such that indentation experiences smaller restoring forces for larger pores. Fig. 4, A and B, show force-indentation curves of DODAB bilayers deposited on pores exhibiting a mean radius of 33 nm and 90 nm. The maximum penetration of the tip is substantially reduced on smaller pores as expected. More importantly, the average slope of the curves denoted as the apparent “spring constant” is significantly larger on the smaller pores. We found an average “spring constant” of the membrane covering the pores with radii of 33 nm of 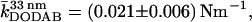which is by a factor of 1.4 larger than that obtained on pores with a radius of 90 nm.

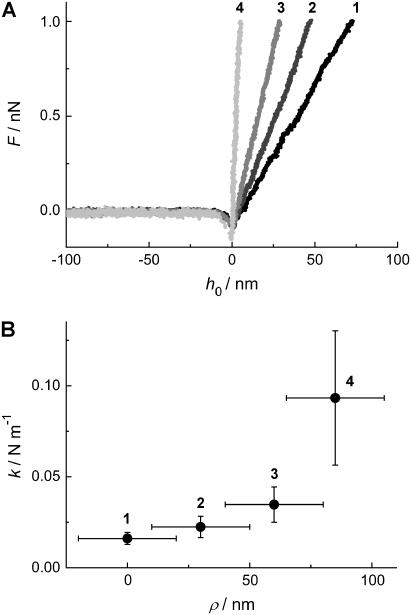
The displacement from the center, i.e., the position, from which the force-indentation curves are obtained, also influences the restoring force. In fact, one expects that the apparent “spring constant” increases if the force-indentation curve is taken closer to the pore rim. To quantify this effect, we took force-indentation curves at different displacements ρ away from the center of a DODAB-covered pore (R_pore = 90 nm). Fig. 5 shows that the measured force-indentation slope increases substantially while positioning the tip closer to the rim. These findings are in accordance with classical thin plate theory (33).

FIGURE 5.

(A) Force-indentation curves of a pore-spanning DODAB bilayer on pores with R_pore = 90 nm taken at different positions starting from the center (1) of the pore to the rim (4). (B) The average slope of more than 10 curves taken at each location as a function of the position ρ from the pore center (1) to the rim (4). The error bars originate from several independent force-indentation curves taken at the same spot.

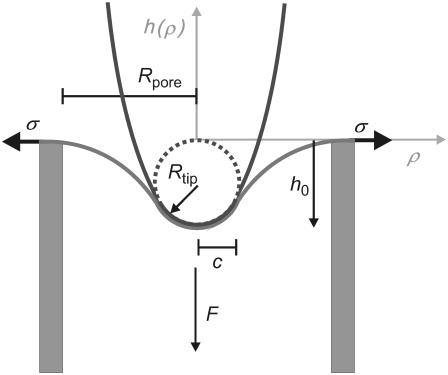
A theoretical model that explains our observations for gel-phase and fluid-phase membranes qualitatively and quantitatively can be developed as follows: the system comprising tip- and pore-spanning membrane is parameterized as shown in Fig. 6. The pore is treated as a circle of radius R_pore, whereas the parabolic AFM tip exhibits a curvature radius R_tip at its apex. The situation is axisymmetric because the tip indents the membrane in the center of the pore.

FIGURE 6.

Illustration of the parameters used for modeling a parabolic tip poking into a membrane spanned over a hole of radius R_pore. c denotes the axial distance of the contact point between membrane and tip, σ the lateral tension, R_tip the radius of curvature of the tip, h₀ the penetration depth in the pore center, F the normal force exerted by the tip, and h(ρ) the shape of the membrane as a function of displacement from the center of the pore.

We model the membrane as a two-dimensional surface. This is a valid approach, provided the lateral extension of the pore-spanning bilayer is much greater than its thickness (∼5 nm). Due to axisymmetry, the membrane shape can then be described by specifying its height h as a function of the radial distance ρ from the axis 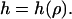In the following, we consider a static situation and calculate the force that corresponds to a given indentation 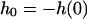(see Fig. 6). In the mesoscopic continuum theory, we want to use the well-known Canham-Helfrich Hamiltonian (34–36):

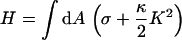(1)

describes the membrane energy as a functional of its shape. Here, σ is the surface tension, κ the bending rigidity, 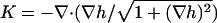twice the local mean curvature, and dA the area element of the curved surface. To get the force for a given indentation, the equilibrium membrane shape has to be found, i.e., the one that minimizes H. This variational problem requires us to solve the corresponding (highly nonlinear) Euler-Lagrange equation, which (a suitable parameterization presupposed) can in principle be done numerically. Let us, however, first consider the so-called small gradient approximation of Eq. 1:

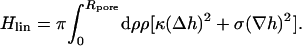(2)

This approximation assumes that the slope of the membrane profile is everywhere small, such that it is permissible to expand both terms in Eq. 1 up to lowest order in 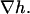It is thus only valid for small indentations. The Euler-Lagrange equation corresponding to the functional Eq. 2 is 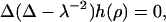where the characteristic length scale 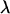is defined as 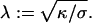Evidently, the general solution to this linear differential equation is a linear combination of the eigenfunctions of the Laplacian corresponding to the eigenvalues 0 and 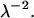For axial symmetry it is therefore given by

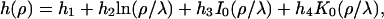(3)

where I₀ and K₀ are the modified Bessel functions of the first and the second kind, respectively (37). The constants h₁,…, h₄ have to be determined from the appropriate boundary conditions: at the rim of the pore the membrane height function has to be flat, 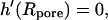and equal to zero 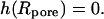One finds three additional conditions at the equilibrium line of contact, where ρ = c. The profile of the tip and the membrane have to touch smoothly: 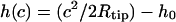and 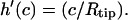Furthermore, the contact curvatures have to balance according to 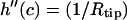(38). Note that the first four boundary conditions can in fact be implemented analytically into the height function (3). Unfortunately, the last one, which determines c, becomes a complicated transcendental equation and can thus only be solved using numerics. For this reason, the final solution cannot be stated explicitly. From the resulting height function, the force F can be obtained in complete analogy to classical elasticity theory (39) by integrating the flux of stress through a closed contour 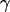around the corresponding source of stress (i.e., the tip in this case) (40–42):

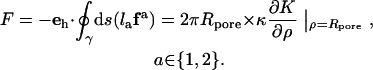(4)

Here, 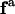is the surface stress tensor, l_a the outward pointing unit normal of the line element ds of 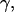and 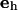is the unit vector normal to the substrate. We chose a contour adapted to the symmetry of the situation: the integral runs along the rim of the pore where 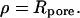Using the height function to calculate the derivative of the curvature at the rim yields the force acting normal on the membrane.

The force obtained this way is only correct for small indentations due to the small gradient approximation we have used. To check the validity of this approach, we have also calculated force-indentation curves in the nonlinear regime using the exact Hamiltonian (1). This requires numerical methods well beyond the ones needed for the small gradient approximation. They rely on techniques that have been used earlier for the study of vesicles (43–47) or tethers (28,29,48). Details of how the nonlinear calculations were done would go beyond the scope of this article but can be found in a forthcoming publication (D. Norouzi, M. M. Müller, and M. Deserno, unpublished). As we will see below, the agreement between these calculations and the experiment is significantly extended to larger indentations; hence the general attempt to use a continuum elastic ansatz is valid. Moreover, since for small indentations both theories coincide, the linear one is perfectly sufficient to match the asymptotic behavior of the force-distance curve. We will thus restrict most of our discussion to the small gradient approximation. Using it for data analysis is also more appropriate for practical fitting purposes, because it is by far easier and faster to calculate the height function (3) from the linear theory than to solve the exact shape equation numerically.

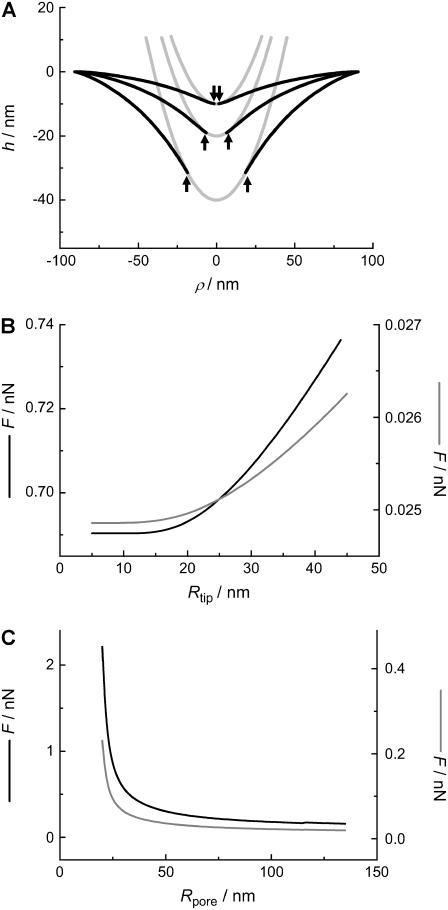
The shapes of the membrane in the fluid state indented by a parabolic tip to reach different penetration depths h₀ are depicted in Fig. 7. The parameters chosen for the fluid system are σ = 1.0 mN m⁻¹, κ = 0.1·10⁻¹⁸ J. The contact radius c increases visibly with increasing penetration depth (arrows).

FIGURE 7.

(A) Calculated membrane shape (small gradient approximation) as a function of maximum penetration depth (10 nm, 20 nm, 40 nm), using the parameters R_tip = 20 nm and R_pore = 90 nm, assuming a fluid membrane (σ_fluid = 1.0 mN m⁻¹, κ_fluid = 0.1·10⁻¹⁸ J). The arrows indicate the point c of detachment between tip and membrane. (B) Force F to maintain a constant penetration depth h₀ = 10 nm as a function of the tip radius R_tip using typical parameters for a membrane in the gel (black line) and fluid phase (gray line); parameters: σ_gel = 5.0 mN m⁻¹, κ_gel = 1.0·10⁻¹⁸ J, σ_fluid = 1.0 mN m⁻¹, κ_fluid = 0.1·10⁻¹⁸ J, and R_pore = 90 nm. (C) Force F at h₀ = 10 nm as a function of the pore radius R_pore for a membrane in the gel (black line) and fluid phase (gray line) using the following parameters: R_tip = 20 nm, σ_gel = 5.0 mN m⁻¹, κ_gel = 1.0·10⁻¹⁸ J, κ_fluid = 0.1·10⁻¹⁸ J, and σ_fluid = 1.0 mN m⁻¹.

The impact of the tip size on the measured restoring force at a penetration depth of 10 nm in the center of the pore is illustrated in Fig. 7 B for membranes in the gel- and fluid-state using the small gradient approximation. The result for the fluid membrane is represented by a gray line (κ = 0.1·10⁻¹⁸ J, σ = 1.0 mN m⁻¹, R_pore = 90 nm, h₀ = 10 nm) and that for a membrane in the gel state by a solid black line (κ = 1.0·10⁻¹⁸ J, σ = 5.0 mN m⁻¹, R_pore = 90 nm, h₀ = 10 nm). Increasing the tip radius has surprisingly little influence on the restoring force of the membrane over a wide range. Generally, the restoring force increases slightly with increasing tip radius, as expected.

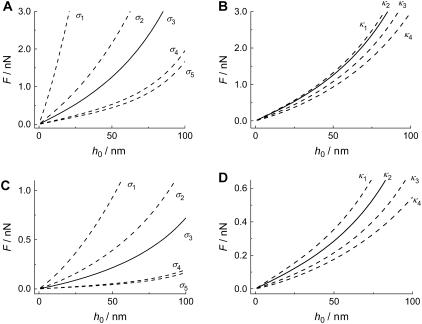
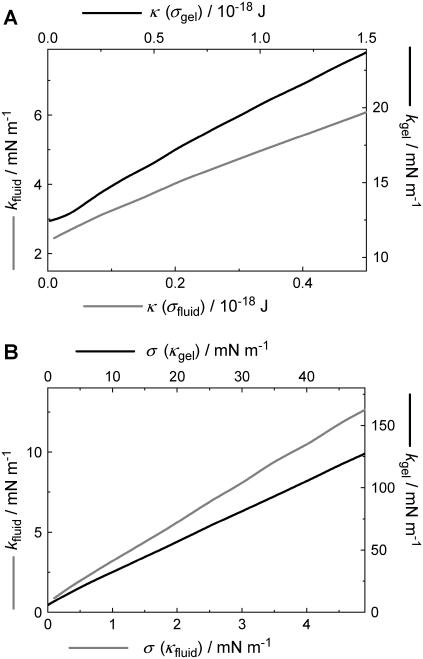
The pore radius, however, has a much stronger influence on the restoring force as illustrated in Fig. 7 C. The force necessary to indent the membrane to 10 nm increases considerably by decreasing the pore size, especially in the small pore regime (<50 nm). The indentation force becomes insensitive to the pore radius for R_pore > 100 nm, which can be explained by the fact that indentation becomes tension-dominated for large length scales. However, one expects the continuum approach to lose validity at smaller pore size since the molecular nature of the bilayer becomes important at smaller length scales. This might also explain our finding that the spring constant of the DODAB-bilayer covering pores exhibiting a mean radius of 33 nm is only by a factor of 1.4 larger than that obtained on pores with a radius of 90 nm (Fig. 4). From our theory, we expect a factor of 2 (see Fig. 7 C). The deviation might be explained by the breakdown of the continuum assumption of the bilayer covering small pores and needs to be elucidated in the future. Therefore, we restrict our modeling to the larger pores. The gray line represents the calculation for a membrane in the fluid phase with κ_fluid = 0.1·10⁻¹⁸ J and a lateral tension of σ_fluid = 1.0 mN m⁻¹ accounting for the adhesion between the membrane and the pore rim. The black line is the result of the calculation for a bilayer in the gel phase (σ_gel = 5 mN m⁻¹, κ_gel = 1.0·10⁻¹⁸ J). A tip size of R_tip = 20 nm was assumed for both cases, and indentation was modeled in the center of the pore. In general, larger forces are needed to displace a membrane in the gel phase than a fluid membrane. To elucidate the impact of σ and κ on the force-indentation curves in more detail, we show parameter curves in Fig. 8 illustrating the situation for membranes with variable lateral tension and bending modulus. The solid line represents the parameters, which are in best accordance with the experiments (see below). Interestingly, the apparent “spring constant” of the membrane estimated from linear regression of the calculated curves between 4 and 10 nm penetration depth shows linear dependency on κ and σ as illustrated in Fig. 9. From the discussion above, we infer that the logical consequence is to adapt values of κ and σ in a physical meaningful range to find best agreement between experimental data and the corresponding model. Since the bending moduli κ for bilayers in the gel phase are in the range of (0.8–1.2)·10⁻¹⁸ J and for membranes in the fluid phase depending on the composition in the range of (0.1–0.6)·10⁻¹⁸ J, we set κ to distinct, typical values for the two systems and optimized solely σ. For DOTAP, a typical value of 1.0·10⁻¹⁹ J was chosen, whereas for DODAB, a bending modulus of 1.0·10⁻¹⁸ J as also found for DPPC was assumed (5,16,50).

FIGURE 8.

(A) Calculated force-indentation plots of a gel phase membrane with a bending modulus of κ_gel = 1.0·10⁻¹⁸ J and varied surface tension (σ_1…5 = 50 mN m⁻¹; 10 mN m⁻¹; 5.0 mN m⁻¹; 1.0 mN m⁻¹; 0.5 mN m⁻¹). (B) Force-indentation plot of a membrane at fixed surface tension (σ_gel = 5.0 mN m⁻¹) and variable bending modulus (κ_1…4 = 1.2·10⁻¹⁸ J; 1.0·10⁻¹⁸ J; 0.5·10⁻¹⁸ J; 0.1·10⁻¹⁸ J). (C) Indentation of a fluid membrane (κ_fluid = 0.1·10⁻¹⁸ J) exhibiting variable surface tension (σ_1…5 = 5.0 mN m⁻¹; 2.0 mN m⁻¹; 1.0 mN m⁻¹; 0.1 mN m⁻¹; 0.05 mN m⁻¹). (D) Indentation of a membrane (σ_fluid = 1.0 mN m⁻¹) with various bending moduli (κ_1…4 = 0.5·10⁻¹⁸ J; 0.3·10⁻¹⁸ J; 0.1·10⁻¹⁸ J; 0.01·10⁻¹⁸ J). All curves were calculated using the small gradient approximation.

FIGURE 9.

Calculated apparent “spring constant” of the membrane, k, as a function of bending modulus and surface tension in two different regimes (k_gel, k_fluid) representing membranes in the fluid and in the gel phase. (A) k as a function of bending modulus with either σ_fluid = 1.0 mN m⁻¹ or σ_gel = 5.0 mN m⁻¹. (B) k as a function of surface tension with either κ_fluid = 0.1·10⁻¹⁸ J or κ_gel = 1.0·10⁻¹⁸ J.

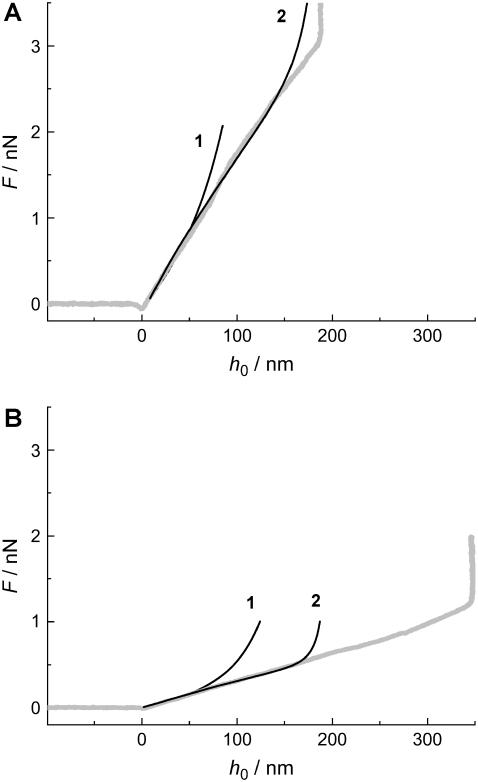
In the following paragraph, modeling of the experimental curves using the small gradient approximation and the exact numerical solution is described. Fig. 10 shows the results of optimizing the lateral tension σ to find best accordance between the experimental indentation curves of DODAB and DOTAP on 90 nm pores employing the small gradient approximation as well as the exact numerical solution of the shape equation. We found good accordance using the small gradient approximation (black line 1) with the experimental curve (gray line) down to an indentation depth of 50 nm for both the membrane in the gel phase (Fig. 10 A) and in the fluid phase (Fig. 10 B). Considerably better agreement between the model and the experimental curve was found for the exact solution describing the force-indentation curve correctly down to a penetration depth of 150 nm (black line 2). We consider the most likely cause for this deviation between the two theoretical models to be a failure of the linearization of the Monge parameterization. Even though very frequently employed, its unphysical divergence of tension and bending energy at vertical slope leads to systematic overestimations of energies and forces already at much smaller slopes. The same has previously been found for the problem of colloidal wrapping (51,52). However, at small enough forces, both solutions coincide with each other, as well as with the experimental curve. Hence, even though the small gradient approximation fails to describe the entire measurement, its asymptotic exactness at small forces can be used to match the experimental data, if parameters are adjusted such as to fit the regime of small forces and not the overall average shape. Deviation of the exact solution from the experimental force-indentation curve at large penetrations could be explained in terms of variable tip geometry deviating from the idealized parabolic indenter (Fig. 10 B).

FIGURE 10.

(A) Force-indentation curve of a membrane in the gel phase (DODAB) covering a pore with a radius of R_pore = 90 nm. 1 represents the solution calculated using the small gradient approximation, whereas 2 shows the exact solution. In both cases, the following parameters were used: R_tip = 20 nm, R_pore = 90 nm, σ_gel = 5.0 mN m⁻¹, and κ_gel = 1.0·10⁻¹⁸ J. (B) The same parameters as in A, but this time for a DOTAP membrane, using the following parameters: R_tip = 20 nm, R_pore = 90 nm, σ_fluid = 1.0 mN m⁻¹, and κ_fluid = 0.1·10⁻¹⁸ J.

The mechanical parameters we obtained from optimizing σ to find best agreement between the model and the data are physically very reasonable. Fluid membranes with low bending rigidity exhibit typically a rupture tension of (5–10) mN m⁻¹, whereas membranes in the gel state should exhibit a considerably higher rupture tension (5). The stability of the membrane can be assessed as follows: the area compression modulus K_a relates to the bending modulus κ and the thickness of the bilayer t_b according to 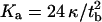(5). The surface tension of the membrane is 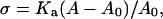with A the actual area and A₀ the area at zero tension. Since the critical lateral strain at lysis is ∼2–5%, one can estimate the rupture tension to be (20–55) mN m⁻¹ for bilayers in the gel phase and (2–5.5) mN m⁻¹ for membranes in the fluid phase. Our values found for σ are well below the rupture tension, thus stressing the fact that pore-spanning bilayers are stable enough to be visualized and indented by atomic force microscopy even if they are in the fluid state. This renders our method a valuable tool to study membranes of arbitrary composition as long as the surface tension is below the critical value of rupture tension.

The results presented in this study agree qualitatively with previous studies from Goldstein and co-workers (28) as well as Derényi et al. (29), who investigated the tether formation of membranes due to pulling with a point load force describing a transition from a linear regime. The authors found that the force grows approximately proportional to the displacement until tethers are formed. Further stretching does result in a constant force. Here we obviously do not enter this regime, which can be attributed not only to the limited penetration depth but also to the finite size of the tip.

Closest to our approach are two recent studies of Boulbitch. In the first one, he scrutinized the impact of a local force on the membrane deflection with the outcome that fluid membranes of the cell exhibit very small spring constants (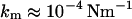) based on bending rigidity and hence would be nearly invisible to AFM (12). The conclusion he draws is that the restoring forces of cells are dominated by the elasticity of the cytoskeleton and osmotic pressure of the cell. In a second publication, Boulbitch (13) reported on the enforced unbinding of a bead adhering to a membrane using a similar approach to ours to determine the force exerted on the membrane by a cylinder. Similar theoretical results treating the indentation of liposomes with more emphasis on stretching of the membrane were obtained by Wan and co-workers (14).

We conclude that contributions from lateral tension and bending rigidity govern the elastic response of pore-spanning DODAB and DOTAP bilayers indented by an AFM tip. Both membranes in the gel state as well as fluid state can be investigated by our method, providing mechanical parameters for either bending rigidity or lateral tension dominated by adhesion to the substrate beyond the pore rim. The indentation is fully reversible, i.e., no hysteresis occurs between indentation and retraction of the tip and the mechanical parameters do not depend on the velocity of the cantilever. We found that the membrane behaves as intuitively expected. The force to indent the membrane to a certain extent increases with increasing tip size, decreasing pore size, larger rigidity, and a position closer to the pore rim. To date, micropipette suction experiments remain the most suitable tool when it comes to measure the bending rigidity of membranes, but at the cost of spatial resolution. AFM in conjunction with membranes covering nanometer-sized pores provides the necessary compromise to study membrane mechanics locally, restricted only by the pore size. It is conceivable to use pore arrays in the future to study the impact of composition and phase separation on the mechanical properties of membranes to map the domain structure of a membrane mechanically.

SUPPLEMENTARY MATERIAL

An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.