Limitation of Cell Adhesion by the Elasticity of the Extracellular Matrix

Abstract

Cell/matrix adhesions are modulated by cytoskeletal or external stresses and adapt to the mechanical properties of the extracellular matrix. We propose that this mechanosensitivity arises from the activation of a mechanosensor located within the adhesion itself. We show that this mechanism accounts for the observed directional growth of focal adhesions and the reduction or even cessation of their growth when cells adhere to a soft extracellular matrix. We predict quantitatively that both the elasticity and the thickness of the matrix play a key role in the dynamics of focal adhesions. Two different types of dynamics are expected depending on whether the thickness of the matrix is of order of or much larger than the adhesion size. In the latter situation, we predict that the adhesion region reaches a saturation size that can be tuned by the mechanical properties of the matrix.

INTRODUCTION

The organization of biological cells is sensitive not only to the biochemical composition of their environment, but also to its mechanical properties. The physical/chemical nature of the external medium (hereafter termed the extracellular matrix; i.e., ECM) and its binding with the transmembrane, integrin proteins responsible for adhesion, allows cells to probe the elastic properties of their environment (1,2). For example, cells migrate to the more rigid part of a surface on which they are placed (3–5). The sensitivity of cells to the mechanical properties of the ECM arises from mechanosensitive nature of cell adhesion (6–8).

Cell/matrix adhesions consist of a complex network of proteins that strongly depends on signaling. The adhesion proteins link the external matrix and the cytoskeleton. In response to cell contractility, substrates with different mechanical properties or thickness (theoretically modeled as two- or three-dimensional) generate different types of adhesion (9–11). Rigid ECM mainly give rise to the formation of focal adhesions, which are large, stable, elongated aggregates of adhesion proteins whose size is of the order of several microns. In contrast, soft matrices result in the formation of transient adhesions. These include initial adhesions (12) and focal complexes that are dynamic, dotlike junctions with typical areas <1 μm² (13). The different types of junctions have different strengths and different consequences on the life of the cell. Focal adhesions are essential to tissue formation since it requires mechanisms that allow for cell proliferation and differentiation. On the other hand, transient focal complexes are associated with increased cell motility (14,15). Thus, the mechanical properties of the extracellular matrix play a key role in the internal life of cells.

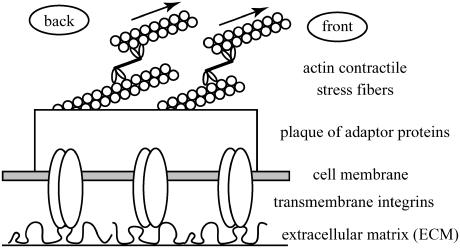
The biochemistry of mechanosensitive cell adhesions has been studied for many years and the precise signaling mechanisms are beginning to be understood (16–19). It is now well established that such junctions consist at least of a cluster of integrins (transmembrane proteins bound to the ECM) that is connected to the actin cytoskeleton (see Fig. 1). Actin-myosin contractility transmits lateral forces to these cell-matrix adhesions. The response of the ECM to the force exerted by the cell allows the cell to probe the physical properties of the ECM. Nonetheless, the question of how the information on the elastic properties of the ECM is then converted into biochemical signaling still remains open. This is the focus of the article.

FIGURE 1.

Schematic view of focal adhesion.

In a previous article (20), we proposed that the dynamics of focal adhesions (FAs) is determined by the activation/deactivation of a mechanosensor located in the adhesion site. The mechanosensor is sensitive to the local elastic stresses in the adhesion zone. We showed that this assumption accounts for many observed features of FA: their sensitivity to local shear forces and their growth in the direction of those forces (21), their apparent motion in stationary cells, and their lack of motion in motile cells (22). Our model has not yet been quantitatively tested by experiments, but there are some recent observations (23) and theories (24) that show that some protein conformational changes in the adhesion are responsible for force transduction.

In this article, we generalize our model that focused on adhesions on rigid substrate, and predict the energetics of FA formation and growth for the case of soft and relatively thin or thick ECM. We show that our model of a mechanosensor located in the adhesion zone combined with the elastic response of the ECM to a localized force that is exerted on the top surface of the FA, predicts behavior that is consistent with experiments performed on various types of elastic substrates. Even more interesting are the predictions of the FA dynamics as a function of the stiffness and thickness of the matrix. We show, for the very first time, that both the elasticity and the thickness of the ECM play a key role in the growth of FA. These aspects were not considered in previous analyses of experiments on soft substrates. In particular, we predict that FA cannot grow on substrates whose stiffness lies below a critical value that depends on the thickness of the ECM. Our second important result is that the dynamics of FA is qualitatively different depending on whether the thickness of the ECM is of order or much larger than the adhesion size. We predict that adhesions grafted to thick ECM reach a saturation size that can be tuned by the mechanical properties of the matrix; this is in contrast to thin ECM where the observed saturation of the adhesion (21,25) might be related to chemical kinetics (26). These predictions should enable direct experimental tests of the model and a more precise identification of the mechanosensing processes that are important in cell/matrix adhesions.

THEORY FOR THE MECHANOSENSITIVITY OF FOCAL ADHESIONS

In this section, we briefly review the theory for the mechanosensitivity of focal adhesions that we presented in Nicolas et al. (20). This background is required for the generalization of the theory to the case of soft ECM in the rest of the article. The interplay between cell adhesion and the elasticity of the extracellular matrix discussed in the section dealing with the results is a direct consequence of this theory.

Theoretical model of mechanosensors in the adhesion

Focal adhesions (FAs) contain both transmembrane integrin proteins that connect the cell membrane with the extracellular matrix (ECM) as well as a large number of other cytoplasmic proteins that form a 100-nm-thick plaque on the intracellular side of the cell (see Fig. 1). Among the plaque proteins are vinculin, talin, or paxillin (27). The plaque is connected to the actin cytoskeleton, which is organized into stress fibers; thus, focal adhesions effectively connect the matrix and the actin cytoskeleton. The latter exerts traction forces on the adhesions (25). Intra- or extracellular stresses were shown to influence the growth dynamics of FA (21,28,29): increased stress leads to growth of the adhesions while reduced force (realized, for example, via myosin II inhibition) results in the shrinking of FA. Since the presence or absence of focal adhesions has an important influence on cell function, the understanding of how intra- or extracellular forces govern FA dynamics is a key issue. The mechanisms underlying the interplay between cell contractility and FA dynamics are far from being understood. Several groups suggest the existence of a mechanosensor (see (7) for a review) but its precise nature and identity have not yet been established. Some physical approaches by other researchers (30) suggested that a mechanism without any mechanosensor but based on force-directed thermodynamic self-assembly could account for the directional response of adhesions to force. As explained in detail in Discussion, their models cannot account for the disappearance or instability of FA on soft or nonreticulated matrices.

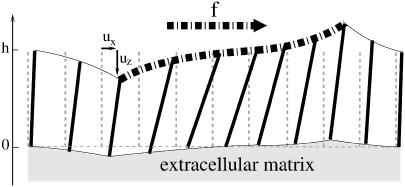
The model we have proposed (20) and that we generalize here to the case of soft ECM, is based on the assumption that the dynamics of focal adhesions depends on the activation/deactivation of a mechanosensor located in the adhesion itself. Since FAs are grafted to the ECM, cytoskeletal stresses induce deformations in the adhesion region. The attachment to the ECM prevents the FA from being translationally displaced by the applied force; indeed, FAs are not stabilized when the ECM is not reticulated and the adhesions can be displaced by the actin force (9). In that case, the force does not deform the adhesion and thus, within our picture, no activation occurs that would lead to the adsorption of additional proteins from the cytoplasm. In our theory, FAs stressed by the actin fibers are modeled as an elastic, thin film bound to a substrate and acted upon by a force on part of its upper surface (Fig. 3). We previously showed that the mechanical response of a sheared elastic medium grafted to a surface is anisotropic (31): the amplitude of the deformation is maximal in the direction of the force and exactly zero in the perpendicular direction. We therefore expect the activation of mechanosensitive molecules that form part of the adhesion to be anisotropic, with activation occurring in the direction of the force. In our model, the parameter that controls the activation/deactivation of the mechanosensor is the relative in-plane variation of density of the proteins of the FA. This quantity is a measure of the relative compression of the mechanosensor between the top and the bottom of the adhesion. If the mechanosensor is modeled as a rod grafted to one end to the ECM and acted upon at its other extremity by the actin force, the relative in-plane variation of density (denoted hereafter as δΦ/Φ), is a measure of the variation of the position of a given rod relative to its neighbors. It takes into account not only the stress resulting from the in-plane compression on the top surface but the relative tilt that originates from the differential compression between the top and bottom surfaces (see Fig. 2). In summary, the mechanosensors are activated in those regions of the adhesion that are more compressed on their top surface than on their bottom surface. In regions where there is a relative dilation, the mechanosensors are deactivated. Activation or deactivation refers to the ability of these molecules to further associate with cytoplasmic proteins for the FAs to grow. Deactivation shrinks the FA while activation favors additional proteins to adsorb, thus increasing the size of the FA. The consequence of the anisotropic stress-induced deformation of the adhesion is the anisotropy of the activation/deactivation: activation occurs primarily in the direction of the force. This results in an anisotropic growth of the FAs as shown in a dynamic model in Besser and Safran (26).

FIGURE 3.

Model for focal adhesions: a sheared elastic thin film of height h grafted to the ECM. The shaded surface on the top of the adhesion represents the finite region that experiences the actin stress.

FIGURE 2.

Schematic view of a stressed FA. The dash-dot line corresponds to the region directly stressed by the surface force. The dashed line indicates the position of the rods and the ECM in absence of force. The rods have no molecular significance but help to visualize the variation of the density in the stressed adhesion.

Adsorption and association of cytoplasmic proteins to stressed FA

When a given region of the adhesion is activated, the adhesion grows, as does the actin stress. Balaban et al. (25) showed that the cytoskeletal pulling forces are proportional to the surface area of the adhesion for forces below 15 nN. This means that FAs grow by addition of new molecules that include not only the plaque proteins, but also links to additional stress fibers. In this manner, the stress applied to the FA (force per unit surface) can be kept constant as the adhesion grows. As the adhesion gets larger in extent, the cell must provide a larger amount of energy to maintain a constant stress since the stressed area becomes larger. At local equilibrium, this contribution must balance the energy cost of the deformation of the adhesion site, Δℰ_elastic. Within our model, the deformation activates the adhesion molecules and initiates the adsorption of new cytoplasmic proteins in the deformed area. However, the adsorption of new proteins and their association with the adhesion molecules involve various energies associated with the new assembly.

Our main assumption is that the growth of FA is a near-equilibrium process, since timescales for adhesion growth are much larger than the diffusion times of molecules. The free energy of adsorption of cytoplasmic proteins to the adhesion site (which includes both their local association energy as well as the elastic deformation energy) determines the probability that proteins in the cytoplasm either bind or unbind to the existing FA. This probability, when included into a kinetic theory, determines the dynamics of the adhesion (see Nicolas et al. (20) for an estimate based on kinetic rates or Besser and Safran (26) for a more detailed theory of adsorption). As we show below, the thermodynamics of the growth process is the crucial ingredient that determines these dynamics, since in our model, the growth of FA is a thermodynamically favorable process (20) (see Appendix A). In this article, we therefore focus on the thermodynamics of FA deformation and growth.

The free energy of adsorption of additional cytoplasmic proteins to the FA includes a contribution from the deformation energy of the FA, Δℰ_elastic,; this deformation occurs because of the localized actin force. In addition, there is a contribution from the association free energy of elastically activated, mechanosensitive molecules in the FA (e.g., the integrins) with cytoplasmic proteins, Δℰ_chemical. From our elastic model, discussed above, the activation of the mechanosensor is related to the local variation of the relative in-plane density 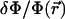of these molecules (or complex of molecules) located at position 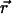(see Fig. 3). We assume that the change in free energy that results from the adsorption of additional protein complexes is proportional to the probability of activation of the mechanosensor. We therefore write the following expression for the free energy of association:

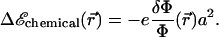(1)

The coefficient −e is the change in free energy per unit area that characterizes the chemical associations required to assemble the FA. When e > 0, the associations are exothermic and the condensation of cytoplasmic proteins in the adhesion releases energy. The value a is the size of the protein complex that associates with the adhesion and causes it to grow. We assume that in addition to the many plaque proteins, this complex contains only one transmembrane integrin protein. We thus estimate a lower bound for a as the minimal distance between integrins at close packing (20 nm). Furthermore, Arnold et al. (32) showed that FAs do not occur when the integrin spacing exceeds a threshold comprised between 58 nm and 73 nm, so we estimate 20 nm < a < 73 nm. The growth of an adhesion depends on the free energy of adsorption of additional cytoplasmic proteins to the FA that includes both the chemical and elastic effects:

Whether the adsorption of additional proteins to the adhesion can proceed as a thermodynamic, self-assembly process or it requires further energy input, depends on the balance between the association free energy discussed above and the elastic deformation energy of the stressed adhesion. Comparison of the predictions of our model to existing experiments makes us conclude that the adsorption of additional proteins to the adhesion is a thermodynamically favorable process (see Appendix A). Except for the presence of the cytoskeletal forces, the growth of adhesions does not rely on any energy input: Δℰ_tot < 0. As a consequence, the limiting factor for FA growth is not the activation rate of the mechanosensor, δΦ/Φ, but the free energy of adsorption of cytoplasmic proteins to the FA as it grows: adhesions only grow when Δℰ_tot < 0. FA are self-assembling, when their growth is thermodynamically favored by a reduction in the total free energy: Δℰ_tot < 0, and when the area of the adhesion, S, increases (ΔS > 0). For this to occur, the total free energy of adsorption of cytoplasmic proteins to the FA must be negative. This analysis leads to the conclusion that:

• The growth of FA reduces the free energy of the system.

• The free energy of adsorption is negative, or equivalently, the adsorption of the additional proteins are, as a whole, exothermic (e > 0).

THEORY FOR AN ELASTIC ECM

In this section, we calculate the elastic response of FA to the forces imposed by their connection to the actin stress fibers. In our model, the coupling of the elastic deformations to the molecular conformations of the molecules in the adhesion region triggers the activation of these molecules to associate with additional cytoplasmic proteins and thus causes the FA to grow. Our calculation relies on several simplifying assumptions that we make to allow a simple, analytically tractable treatment of the problem.

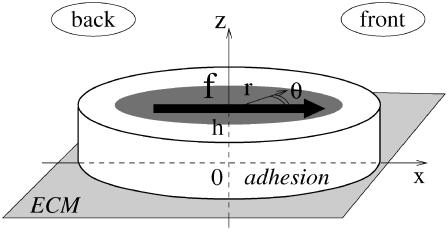
Our first assumption is that focal adhesions can be modeled as thin, elastic films that respond to cytoskeletal forces imposed in a finite region on their top surface (see Fig. 3). The elastic properties of the adhesion are defined by its Young's modulus, Y, and its Poisson ratio, ν (33). To keep the analysis tractable, we analyze the situation for an elastically isotropic thin film (at first glance, the assumption of elastic isotropy is questionable since the integrin layer has a large compression modulus, of order of 1 GPa (35), while the elasticity of the protein plaque is probably similar to that of a gel with a typical Young's modulus, 10 < Y < 10³ Pa. However, we showed in our former work that the elastic symmetry of the material does not qualitatively influence the symmetry of the field of deformation (31)). Refinements can be obtained by adapting the results presented in Nicolas and Safran (31). We next calculate the deformation of an elastic thin film grafted on its bottom surface to an elastic surface (the ECM) and deformed on its top surface by a localized shear stress due to the cytoskeletal forces. As discussed in Nicolas et al. (20), the finite area on which the stress acts is responsible for the symmetry breaking of the deformation. For the sake of simplicity, we model the stress heterogeneity by a gate function: a uniform stress acts on a finite region of the top surface of the adhesion; there is a corona-like region where the top surface is stress-free (see Fig. 3). More realistic distributions of the surface stress distribution could be considered, but our simple model already results in the anisotropic deformation that is the focus of our work. In addition, for analytical simplicity, we treat one focal adhesion as an elastic thin film with infinite lateral extent. As shown below, this approximation is valid once the lateral extent of the stress-free corona of the FA (i.e., the region of the adhesion where the actin force does not act) exceeds the film thickness, which for a typical FA is h ∼100 nm. This length scale is negligible compared to the typical size of a focal adhesion of a few microns. Thus, as long as the FA is several hundred nanometers larger than the region upon which the actin force acts, one can use the simple model described above and treat the FA as infinite in extent in the lateral direction.

We now calculate the deformation of this film of thickness, h, with infinite lateral extent, grafted on its lower side to the ECM and sheared on its upper side by a localized surface force. The elastic deformation of an isotropic medium is obtained by solving the force balance equation (33):

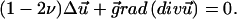(2)

For the thin film described above, this equation must be solved with the boundary conditions

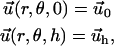(3)

where 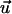is the displacement with respect to the unperturbed film (see Fig. 2). These boundary conditions (Eq. 3) fix the displacements on the bottom (z = 0) and the top (z = h) surfaces of the film (see Fig. 3 for the film geometry). The deformations at the bottom and top surfaces, respectively, are given by and 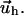The function 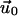depends on the mechanical properties of the ECM layer underlying the adhesion while 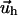is determined by the force, 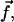due to the stress fibers. We denote Φ_ECM as the deformation energy of the ECM. If the ECM is elastic, Φ_ECM is calculated using the displacements that satisfy Eq. 2 with the boundary conditions 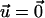on its bottom surface and 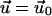on its top surface (which is the bottom surface of the adhesion). This is meaningful when the ECM is grafted to a surface and does not slip nor undergo plastic deformations. We note that the situation where fibronectin (which is a major component of the ECM) is reorganized by the cell cannot be described in this manner. Finally, the field of deformation of the entire system consisting of the ECM and the adhesion, is obtained by solving for the displacements 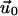and 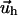that minimize the total free energy for a given surface stress :

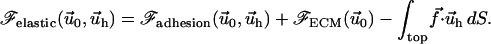(4)

In this equation, Φ_adhesion and Φ_ECM are the elastic energy of the adhesion and the ECM, respectively, integrated along their thickness,

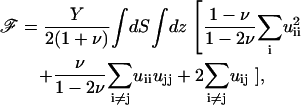where the values of Y and ν are the appropriate ones for the ECM (Φ is then used to calculate Φ_ECM) or the adhesion (Φ is then used to calculate Φ_adhesion). In these formulae, u_ij is the (i, j) component of the strain tensor (33): u_ij = (∂u_i/∂x_j + ∂u_j/∂x_i)/2. Equation 2 is solved by using Fourier transforms, since our model system is taken to be infinite in the x and y directions:

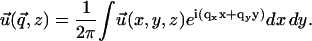Instead of a system of coupled partial differential equations, Fourier transformation in the x and y directions results in a system of three, coupled, second-order, ordinary differential equations in z. Standard techniques of linear algebra allow one to solve for 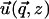as a function of 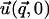and (see Appendix B).

RESULTS

In this section, we begin with a review of a few important results related to the mechanosensitivity of FA on rigid substrates as presented in Nicolas et al. (20); these are needed here to extend our model to the more realistic situation of an elastic ECM with variable thickness. We then focus on the influence of the mechanical properties of the ECM on the energetics of FA and their growth. We show that FA cannot grow on substrates whose stiffness lies below a critical value. We estimate this threshold and predict its dependence on the thickness of the ECM. Two different types of dynamics are expected depending on whether the thickness of the ECM is of the order of or much larger than the size of the FA, which is typically in the micrometer range. In the latter situation, we predict that the growth process can reach a saturation size that can be tuned by the mechanical properties of the matrix.

FA growth in the direction of the applied force

In this section, we analyze the growth of FA in response to cytoskeletal forces using our model. For this part of the discussion, we consider the case of a cell plated onto a very rigid ECM (with infinite shear modulus). The boundary condition of Eq. 2 then becomes one of zero displacement and 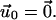Since the experiments of Beningo et al. (11) showed that normal forces do not favor FA growth, we focus here on the effect of a tangential shear stress on the dynamics of FA: 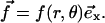The change in the relative in-plane density of the FA determines, in our model, whether a part of the adhesion is activated:

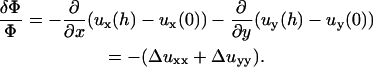(5)

For a rigid ECM, solution of Eq. 2 yields the result for the relative in-plane density change of

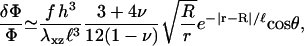(6)

where λ_xz is the shear modulus of the adhesion (λ_xz = Y/(2(1 + ν))), and R is the radius of the stressed region where the force is applied: 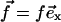if r ≤ R, 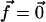otherwise. Equation 6 shows that the effect of the shear stress is localized to the edges of the stressed region and is of short range. The characteristic decay length of the deformation is

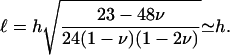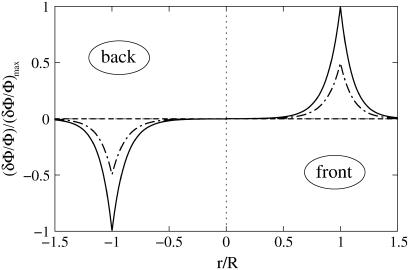
The main result obtained from Eq. 6 is that the activation of the adhesion is anisotropic and occurs mainly in the direction of the force. No activation takes place on the lateral sides where θ = π/2 (see Fig. 4). Our model therefore predicts the local and very directional activation of the adhesion site, consistent with observations.

FIGURE 4.

Profile of the relative in-plane density for an FA grafted to a rigid ECM and stressed by a shear stress The different curves correspond to different directions: 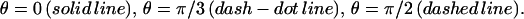Compression occurs mainly in the direction of the force (θ = 0). (R = 10 h, ν = 0.3).

Even when the adhesion is activated, it can only grow if the free energy gain of additional cytoplasmic proteins that adsorb to the adhesion is larger than the cost for the additional deformation of the resulting, larger adhesion (see the discussion above). The total exchange of energy when a free protein complex of size a associates with the front edge of the stressed area of an existing FA, where the activation is the highest, is

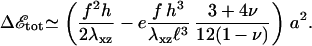(7)

The adhesion grows as long as the addition of the protein complex lowers the total free energy: Δℰ_tot < 0. Experiments have estimated that the average cytoskeletal shear stress is f ≃ 5.5 nN/μm² (25). This allows us to suggest that the lower limit for the value of the chemical free energy of adsorption that allows growth is

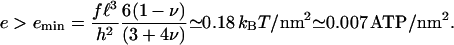(8)

In our picture, a protein complex contains the minimum number of proteins required to grow a FA and is associated with an integrin molecule. Arnold et al. (32) showed that integrin spacing can be as large as 58 nm for a stable FA. Using this order of magnitude for the size of the protein complex, we find that the binding of a protein complex to an activated site releases at least 600 k_BT ≃24 ATP molecules (35) for FAs to grow.

ECM elasticity influences FA growth: case of a thin ECM

FAs are observed to develop and grow only when the stiffness of the ECM exceeds a critical value that is estimated to be between 2 and 10 kPa (3,36). We show here that besides being consistent with these observations, our model predicts that the stiffness threshold is not a fixed quantity but depends on the thickness of the ECM.

We first focus on ECM, the thickness of which, H, is smaller than the size of the FA: H ≪ R. This situation is relevant for cells plated onto glass slides for which the thickness of the ECM is of the order of the thickness of the adhesion: H ∼ h. The system then consists of two coupled elastic layers with different elastic properties. The lower layer (the ECM) is grafted to a rigid surface. The upper layer consists of the integrin layer and the protein plaque whose top surface is stressed by the actin force. The bottom surface of the upper layer and the top surface of the lower layer are in mechanical contact, which implies that their lateral displacements are the same. Surface stress-induced deformations are still expected to be short range, since the deformation must go to zero at the bottom surface of the thin ECM. The stress therefore only induces short-range effects and only those mechanosensors located at the front of the adhesion (in the direction of the force) will be activated, as discussed above. The symmetry of the problem therefore remains unchanged. However, the elasticity of the ECM does affect the energetic balance and thus the kinetics of growth of the FA.

Minimization of the total elastic energy Eq. 4, for a matrix with shear modulus Λ_xz and Poisson ratio Σ, leads to the following variation of the relative in-plane density:

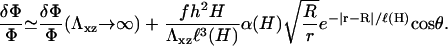(9)

This expression is valid for an elastic matrix where Λ_xz ≫ λ_xz. The first term in this equation is the variation of the in-plane density for a rigid matrix, Eq. 6, while the second term is the contribution of the elastic ECM. Due to the elasticity of the matrix, the deformation decays on a larger range compared with the case of a rigid substrate:

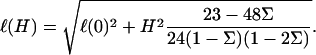In this expression, ℓ(0) is identical to the length of decay ℓ for a rigid ECM (with infinite shear modulus), and α(H) is a prefactor that depends on the Poisson ratios of both the ECM and the adhesion: 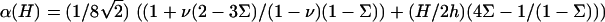Equation 9 shows that an elastic ECM of finite thickness, H, and softer elastic properties increases the relative compression δΦ/Φ at the front of the adhesion for decreasing values of Λ_xz or nonzero values of H. As a result, for H ≫ h (but H ≪ R), the activation energy is more negative (Δℰ_chemical goes like Δℰ_chemical (Λ_xz → ∞) −1/H). Using our assumption that the mechanosensor is activated by compression, we predict that the mechanosensors at the front rim of the FA are more highly activated than on rigid ECM. They will thus be more likely to associate with additional cytoplasmic proteins and the adhesion will preferentially grow from the front, in an asymmetric manner. However, on soft substrates the deformation energy can balance (or even overcompensate) the decrease of Δℰ_chemical since Δℰ_elastic increases with the ECM thickness, H. The balance of the two terms results in a relative increase of the free energy that controls the adsorption of additional cytoplasmic proteins, and hence adhesion growth on soft ECM (see Fig. 6). If this increase is too large—depending on the ECM thickness—the adsorption of additional proteins, even at the front of the adhesion, can be much less probable. This is consistent with the general observation that softer matrices slow down or even completely inhibit FA growth. Considering a protein complex of size a that binds to the lowest energy site in the FA, namely at the front edge of the stressed region, the free energy difference is

(10)

The dependence of Δℰ_tot on the elastic properties of the ECM, Λ_xz, is far from obvious. To predict a decrease in the growth of the adhesion for softer ECM, the theory requires that e < e_max = fℓ³(H)/(2h²α(H)). This fixes an upper limit to the enthalpy for the association of cytoplasmic proteins with the activated integrin molecules, e. Since e_max is an increasing function of H, we estimate it for the minimal relevant thickness: H ≃100 nm (this is the presumed thickness of the cell-synthesized fibronectin fibrils layer (16)). Combined with the lower bound for e-value discussed in the previous section, we estimate that 0.18 k_BT/nm² < e < 0.68 k_BT/nm². For this evaluation we take Σ = 0.45, which is relevant for collagen gels (36). Once e is in the correct range, the total free energy is negative and scales like 1/Λ_xz. As a result, for small values of the Young's modulus, the softening of the ECM can have a significant effect on the probability of binding additional proteins to the adhesion. However, this effect saturates when the Young's modulus becomes larger than λ_xz(H/h). The trend predicted here is consistent with the observation by Engler et al. (36) that FA growth is sensitive to the elasticity of the ECM only when the Young's modulus of the ECM is in the range of few kPa. This is much smaller than the stiffness of the rigid, collagen-covered glass (66 kPa).

FIGURE 6.

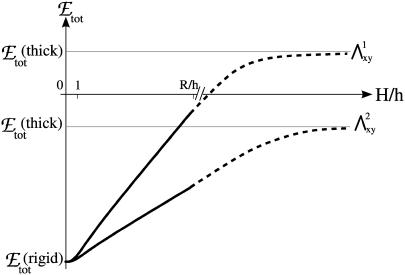
Plot of the free energy of adsorption of additional cytoplasmic proteins to the FA, at the front edge of the adhesion, as a function of the thickness of the ECM. The two curves correspond to two different values of the Young's modulus: 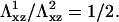The solid curves are calculated from Eq. 10. The shaded lines are the asymptotic values of the free energy for a thick ECM, from Eq. 14. The dashed curves are an interpolation for the regime where H ≫ h, but still finite (not calculated in this work). When the free energy of adsorption is positive, the adhesion does not grow, since the probability for additional proteins to adsorb is vanishingly small.

In addition to the sensitivity of FA to the elasticity of the ECM, we predict the existence of a lower value of the ECM modulus, below which adhesions cannot grow. Adhesions will grow as long as Δℰ_tot < 0 in Eq. 10; this quantity becomes positive when

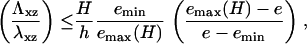(11)

where e_min is defined in Eq. 8. Below this threshold, adhesions will not grow in a deterministic manner; transient, fluctuation-induced adhesions may, however, still exist in this range. As shown by Fig. 5, the shear modulus threshold varies nearly linearly with the thickness of the ECM as soon as H > h. An experimental measurement of the slope on a plot of the ECM elastic modulus Λ_xz as a function of the ECM thickness, H, would give valuable insight about the shear modulus λ_xz of the adhesion.

FIGURE 5.

Variation of the minimal shear modulus for which the FA grows, with the thickness of the ECM (Σ = 0.45, ν = 0.3, h = 100 nm, f = 5.5 nN/μm², e = 0.23 k_BT/nm²).

Thick elastic ECM limit the growth of FA

The previous section demonstrated that there is a threshold value for the Young's modulus of the ECM, below which FAs do not grow. We emphasized that this limit is a function of the thickness of the ECM. The previous calculations were done for matrices whose thickness is small compared to the size of the adhesion. In this section, we focus on the opposite case of ECM whose thickness is much greater than the size of the adhesion zone. This situation is relevant for cells plated onto patterned substrates or embedded into three-dimensional gels. We predict here that the dynamics of FA plated on such substrates is very different from FA grafted onto thin ECM; on thick ECM, the FA reaches a saturation size determined by the elastic properties of the ECM.

The main difference between a thick and a thin elastic substrate is that for infinitely thick ECM, there is no longer a finite, characteristic decay length for the propagation of localized deformations. Deformations in the ECM are long range (33) and displacements created by a point source at the origin decrease as 1/r instead of e^−r/ℓ for the case of finite ECM, where the characteristic decay length, ℓ depends on the thickness. This increases the elastic energy cost that the cell must pay to increase the size of the stressed area (and thus grow the adhesion), since material must be displaced over a large scale even when the stressed region just increases by a small amount. In the limit of a fairly rigid matrix, Λ_xz ≫ λ_xz, with Poisson ratio, Σ = 0.5, the addition of a protein complex of size a to an adhesion of radius R, results in the following change in elastic energy:

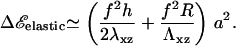(12)

Equation 12 shows that the energy per unit area depends on the radius, R, of the stressed area: the cell must invest more and more energy to maintain a constant stress when the adhesion grows on top of a thick elastic matrix. Of course, these effects also imply that the activation of molecules that favor the association of the additional cytoskeletal proteins with the adhesion zone also occurs over a long range,

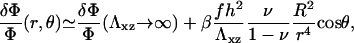(13)

when r > R. The value β is a numerical coefficient determined by the Poisson ratio of the matrix. The adhesion is still activated mainly at the front rim of the stressed region but farther regions also feel the compression and there is no longer an exponential decay of the deformation and hence, of the activation.

Similar to the case of thin ECM, a thick, elastic ECM enhances the activation of mechanosensors in the neighborhood of the stressed area. However, its contribution to the lowering of the adsorption free energy becomes less important for large adhesions, (δΦ/Φ)_ECM ∝ 1/R². The most important effect on the total free energy, Δℰ_tot, is the large increase of the deformation energy, which is proportional to R, as opposed to the enhanced activation energy that goes as 1/R². The deformation term prevents the adhesion from growing indefinitely. For large adhesion sizes, R ≫ h,

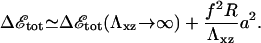(14)

For large enough values of R, Δℰ_tot becomes positive and it is no longer energetically favorable for the adhesion to grow. We therefore predict that FAs do not grow larger than a maximal size that is proportional to the Young's modulus of the ECM (see Eq. 14). This effect might compete with a saturation of adhesion growth based on kinetic effects (26,37), such as a finite reservoir of cytoskeletal proteins or diffusion limitations. We note that FAs in cells plated onto rigid substrates also seem to reach a stationary size. We cannot account for this effect by the elastic mechanism described here that only affects the energetics. (Our model (20) has been extended in Besser and Safran (26) to predict the dynamics of adsorption of cytoplasmic proteins to the adhesion zone.) The results show that the coupling of the nonsymmetric elastic stresses induced by the stress fibers to the protein adsorption dynamics results in different growth velocities for the front and back of the FA, as observed in experiment.) Our predictions should be observable when the ECM is soft enough, and we expect that the saturation size that is energetically determined would be smaller than a saturation size determined by kinetics. The predicted linear dependence of the energetically determined saturation size with the Young's modulus of the ECM might also be a distinctive signature that could be experimentally verified.

DISCUSSION

We have proposed a scenario that allows us to predict how FAs respond to the mechanical properties of the extracellular matrix. Our model relies on the assumption that the dynamics of FA is triggered by the activation/deactivation of a mechanosensor localized in the adhesion itself. We have shown that activation occurs when the mechanosensor is subjected to an anisotropic compression: activation when the top surface molecule is more compressed than the bottom surface. This deformation is characterized by the relative in-plane compression, δΦ/Φ, defined in Eq. 5. Within these assumptions, our model accounts for the following well-known experimental facts:

• FA only respond to local stresses; one adhesion is not affected by stresses localized near a neighboring adhesion.

• When sheared, FA grow in the direction of force.

• FA do not grow on ECM whose elastic modulus is less than a certain value predicted above.

Comparison of our predictions with experiments indicates that the growth of an FA releases energy; no energy input is required to increase the size of an FA. We estimated the global enthalpy of association when the free molecules needed to adsorb to the adhesion bind: −1.7 < −e < −0.4 kJ/mol/nm²; this corresponds to a release of 0.007 < e < 0.027 ATP/nm². Since the protein complex that forms when the adhesion grows has a size between 20 nm and 73 nm (32), the released chemical enthalpy is large and compensates the mechanical energy cost of stressing the adhesion.

Other scenarios can be imagined to explain the asymmetric growth of FA. For example, Shemesh et al. (30) view the FA as a self-assembly of proteins stretched by the actin stress fibers over the entire length of the FA. They assume that the driving force for FA growth is the decrease of density of the proteins when the assembly is stretched by a force. This force results in a reduction of the protein density in the entire FA, which is assumed to be pinned at its back end and pulled at the front. Adding additional proteins to the aggregate restores the equilibrium density and releases the associated stress. Such a mechanism does not require a mechanosensor, but is based on the effect of a tension on a self-assembling aggregate of molecules: additional molecules adsorb to restore the density of the stretched system to its equilibrium value. The difference between our model and that of Shemesh et al. (30) and their very different experimental consequences are discussed in Nicolas et al. (20) and Besser and Safran (26). Both models indeed account for the asymmetric growth of FA but Shemesh et al. (30) only predicts a temporally transient sensitivity to the elastic properties of the ECM. In this model, the steady-state size of the FA is independent of the Young's modulus of the ECM. This prediction does not agree with several experiments (36,39), which leads one to the conclusion that a mechanosensitive process with its attendant activation (as described above) is needed to understand the observed changes in FA growth and steady-state size on soft substrates (see the discussion in Theoretical Model of Mechanosensors in the Adhesion).

However, the molecular origin of the mechanosensor has not yet been identified. We have shown that our model is consistent with many experimental results under the assumption that the deformation that activates the sensor is neither a pure stretching nor compression but rather a type of bending of these molecules (see Appendix C for a further discussion on stretch and flow experiments). The simplest measure of this deformation that accounts for the observed dynamics of FAs is the relative in-plane compression, which is a measure of the differential compression between the top and the bottom of the mechanosensor. Integrins are indeed activated by similar deformations (see (40) for a review) and their activation can trigger the condensation of some plaque proteins (41). They therefore may indeed function as mechanosensors in the sense that we have discussed. Nevertheless, our theory and its predictions are not based upon the identity of a particular molecular species: the essential ingredients are force-induced molecular conformation changes that lead to activation and to association with additional cytoplasmic proteins that result in growth of the FA.

The main prediction of this article that focuses on the case of soft elastic ECM is that the response of FA to stress depends both on the elasticity and on the thickness of the ECM. To our knowledge, the ECM thickness as a controlling parameter, has not yet been considered in experiments. We show here that the free energy for adsorption of additional cytoplasmic proteins to the FA, increases as the ECM becomes thicker (see Fig. 6): the probability that cytoplasmic proteins associate with and adsorb to the adhesion decreases as the thickness of the ECM increases. We conclude that the Young's modulus is not the only parameter that controls FA growth on elastic ECM; the thickness of the ECM also strongly influences FA dynamics. This can also be seen through our prediction that the minimal rigidity of the ECM that allows FA growth varies proportionally to the thickness of the ECM (see Eq. 11 and Fig. 5).

Besides accounting for the observed dependence of FA on the elastic properties of the ECM, our model predicts nontrivial dynamics for stressed adhesions bound to a soft ECM. We have shown that the probability of activating one of the mechanosensors in the adhesion is independent of the size of the adhesion as long as the matrix has a thickness comparable to the size of the stressed area. Dynamic effects as described by Besser and Safran (26) may be responsible for the observed saturation of the size of FA on relatively thin ECM. The mean size of stationary FA is then independent of the thickness of the ECM as long as the matrix is thinner than the size of the FA, which is typically a few microns. This is no longer true for cells plated onto thick ECM. As shown by Eq. 14, the total energy for FA growth on a thick ECM becomes positive when the adhesion exceeds a threshold size. Thus, growth is no longer thermodynamically favorable and the probability of adsorbing new compounds decreases drastically. We predict that the maximal size of the FA is proportional to the elastic modulus of the ECM, Λ_xz. The dependence of the maximal size of FA on the modulus of the ECM might be used to measure the stiffness of the underlying substrate. Measurements of the mean stationary size of the adhesions could thus provide an estimate of the stiffness of the substrate in a nonintrusive or nondestructive manner.

For both thin or thick elastic ECM, our model predicts that the total free energy involved in the absorption of additional cytoplasmic proteins at the front of the FA (where the adsorption is most favorable) varies like 1/Λ_xz, in the limit where Λ_xz ≫ λ_xz (see Eqs. 10 and 14). This free energy determines the probability of adsorption of additional proteins and hence is the major ingredient in dynamical models for adsorption and FA growth (20,26). In general, the more negative the free energy of adsorption, the higher the probability for additional, cytoplasmic proteins to adsorb to the FA and cause it to grow. The variation of Δℰ_tot with the properties of the ECM indicates that the growth of the adhesion is more sensitive to the elasticity of the ECM when the latter is similar to the shear modulus of the adhesion.

From this analysis, coupled with the experimental results of Engler et al. (36), we propose that the Young's modulus of a focal adhesion is of order of 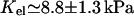(Engler et al. (36)'s notations). We can use this to estimate the maximal variation of density induced by the stress fibers: δΦ/Φ) ≃ 0.57 ± 0.08 (f = 5.5 nN/μm² (25), ν = 0.3). This compression (or dilatation), however, occurs on a length scale ℓ ≃h ≃ 100 nm, which makes it impossible to resolve in a fluorescence experiment. In our model, the region over which the density increases so much is the front edge of the actin-stressed region, since we assumed that the actin stress fibers pull on the adhesion with a force that is uniform but only nonzero in a finite, localized region. Any heterogeneity in the force field would change the geometry of the compressed region (however, it would not modify the asymmetric growth of the FA, since in our model the symmetry is broken by the direction of the force and not by any geometrical properties of the FA itself). Such heterogeneities might explain the variety of the observed distributions of fluorescence intensity when integrin is labeled (ranging from uniform to very noisy or to a smooth gradient; see, for example, pictures in (42–44)).

Recent work by Saez et al. (39) has suggested that the mechanosensitive activity of epithelial cells are controlled by deformations: they observe that the deflection of elastic, micron-scale pillars on which the cell is plated, is independent of the rigidity of the pillars. Their experiment can be thought of in terms of our model of a cell plated onto a thick, elastic ECM; the role of the ECM is here played by the pillar. However, our theory indicates that their conclusion that deformation amplitude, and not stress, controls mechanosensitivity, may be questioned. In our model, we assume that FAs are acted upon by a constant stress due to the actin stress fibers. This stress—for the case of elastic ECM—is also transmitted to the ECM, and we focus on the equilibrium situation, neglecting any transient, viscoelastic effects. Using this model, we have predicted that FAs whose substrates are thick and elastic ECMs reach a saturation size that is proportional to the Young's modulus of the ECM. That is, saturation is dictated by a zero free-energy change so that no additional cytoplasmic proteins adsorb to the FA. Thus, saturation is characterized by Δℰ_tot = 0 in Eq. 14 and this condition leads to R ∝ Λ_xz, the shear modulus of the ECM. Since FAs mainly grow in one direction, the total surface of each adhesion is proportional to R, which implies that the area S ∝ Λ_xz. The total force that each adhesion transmits to the pillar (there is, on average, one FA per pillar in (39)) is the product of the constant stress due to the actin pulling and the surface of the FA. Since that area is proportional to the shear modulus of the ECM, the total force is also proportional to the rigidity of the matrix, as observed by Saez et al. (39). The deformation of the ECM itself (or in the case of the experiments of Saez et al. (39), the pillar that plays the role of the ECM), varies like the force applied by the FA divided by the elastic modulus of the ECM (or pillar). The elastic modulus cancels out and the deformation is therefore constant. Thus, one can explain the experiments of Saez et al. (39), without concluding that the deformation due to the force is the controlling factor in the growth of FA. Their results are consistent with our picture in which the quantity that controls FA growth and mechanosensitivity is the stress (force per unit surface) due to the actin pulling. This results in a constant deformation when the cell is plated on the top of a soft ECM; for rigid, not deformable ECM, the consequences are different (in this situation, the stationary size is determined by the kinetics and not by the energetics).

In conclusion, we have shown that the growth of FA is very sensitive to both substrate stiffness and thickness. This latter point can be checked experimentally by measuring the relationship between the stiffness threshold below which FAs stop growing and the thickness of the ECM. As shown by Eq. 11 and Fig. 5, this threshold increases almost linearly with the thickness of the matrix as long as its thickness remains smaller than the size of the adhesion (less than a few microns; note that the absence of dependence with the ECM thickness would rule out the assumption that a mechanosensor localizes into the adhesion).

APPENDIX A: FA GROWTH RELEASES ENERGY

From the theory of elasticity, we know that Δℰ_elastic ∝ f², whereas displacements, or equivalently the variation of the in-plane density, are linearly proportional to the stress f (33): Δℰ_tot ∝ (f²/Y + αf/Y)ΔS, where Y is the Young's modulus of the adhesion and ΔS the increase of surface area of the adhesion in response to the stress, f. When the ECM is elastic, it participates in the deformation and contributes to the energetic balance. In a simple picture, the ECM can be modeled as an additional spring in series with the adhesion. The net result is that the Young's modulus, Y, of the adhesion can be replaced by an effective Young's modulus 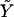of the adhesion plus the ECM. We first consider the case in which the growth of FA does not occur spontaneously since it requires an input of energy, Δℰ_tot > 0, from the cell. Even in this case, nonequilibrium growth could be maintained since cells have a large reservoir of energy in the form of adenosine triphosphate. When the stress on the adhesion is increased, either by external force imposed by the experiment (21) or by additional internal forces (originating, for example, from microtubule disruption (46)), additional energy is required from the cell to increase the area of the adhesion by an amount, ΔS, compared to the situation in the absence of the additional force. In the case that the additional energy is available, one can observe the growth of the adhesion in response to this additional stress, as shown in the experiments of Riveline et al. (21) or Kirschner et al. (46). We now imagine the same situation but on a softer ECM: 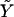is smaller. The energy input needed for the adhesion to grow, Δℰ_tot, is larger than for the case of a rigid ECM. However, we assumed that the cell can provide this amount of energy on a relevant timescale. The parameter that limits the growth of FA is therefore not the cost in energy but the relative, local activation of the mechanosensor, δΦ/Φ. For a soft ECM, this quantity is larger than for a rigid matrix (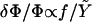). If it were true that adhesions are not self-assembling and require an external input of energy to grow, one would predict that softer ECMs result in larger FAs. This result contradicts experiments that observed that the softer the ECM, the smaller the adhesions (3,36). Thus, the assumption that adhesions require energy input to grow is not consistent with observation. This leads us to formulate a theory in terms of the self-assembly of FA and their stabilization by favorable thermodynamics: Δℰ_tot < 0.

APPENDIX B: SOLUTION OF THE ELASTIC EQUATIONS

We present here the method we used to solve the force balance equation of elasticity Eq. 2 in the case of two adjacent and elastically coupled layers. Since the layers are assumed to be infinite in the x and y directions, we can solve the equations using Fourier transforms:

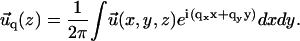In Fourier space, Eq. 2 transforms into a system of three coupled linear differential equations:

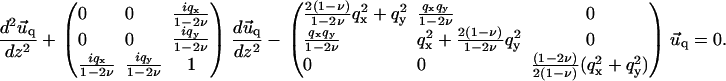(15)

The solution of Eq. 15 is a combination of exponential functions:

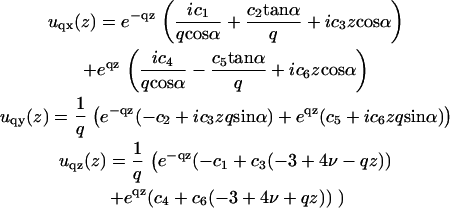(16)

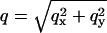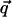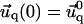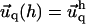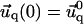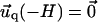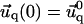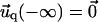In these expressions, and α is the angle between and the q_x axis. The expressions (c_i)_{i ∈ {1..6}} are the constants of integration. Each elastic medium, the adhesion or the extracellular matrix, has its own set of constants. They are fixed by the boundary conditions: and for the adhesion, and for the ECM with finite thickness H, or and for the thick ECM. Equation 16 then gives the deformation in both elastic media as a function of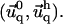

The determination of now results from the minimization of Eq. 4. We therefore need to calculate the elastic energy associated to the deformation of each layer. This is done in the limit where qh ≪ 1. In this limit, only deformations on scales larger than the thickness h of the adhesion are taken into account. The expansion of the energy to second order in qh gives the following result:

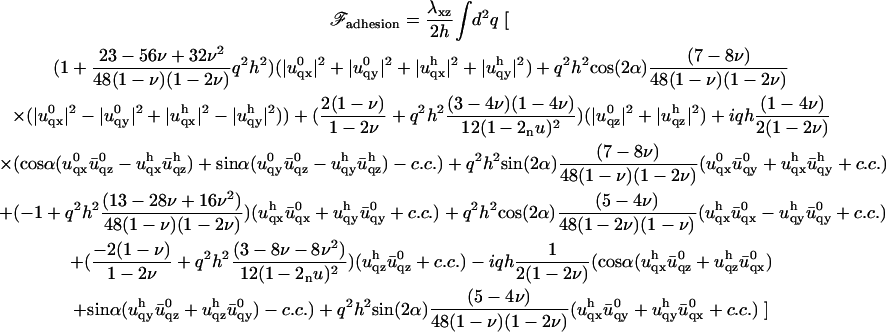(17)

The value 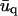is the conjugate of u_q, while c.c. stands for conjugate complex. The expression of the elastic energy of the ECM is much simpler, thanks to the absence of displacement of its bottom surface. In the limit where the ECM is much stiffer than the adhesion, Λ_xz ≫ λ_xz, the elastic energy of the thin ECM with thickness H is

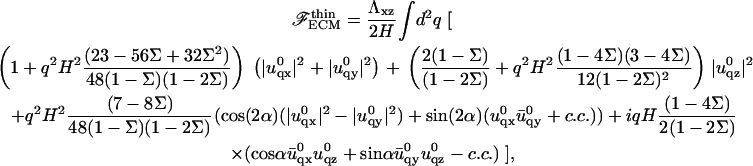(18)

while the elastic energy of the thick matrix is (we assume Σ = 1/2 in this case)

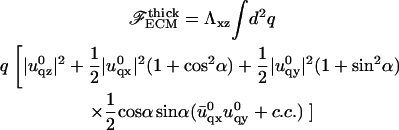(19)

Insertion of the expressions of Φ_adhesion and Φ_ECM into Eq. 4 and its minimization by respect to both and determines 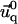and 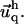Inverse Fourier transformation of both values allows one to calculate the variation of the relative in-plane density, δΦ/Φ (see Eq. 9 for a thin ECM and Eq. 13 for a thick one). Integration of ℱ_adhesion and ℱ_ECM in q-space gives the estimation of the elastic energy for both the adhesion and the ECM (see Eq. 10 for a thin ECM and Eq. 12 for the thick one).

APPENDIX C: COMMENTS ON CYCLIC STRETCH AND SHEAR FLOW EXPERIMENTS

Many experiments show that FAs respond to cyclic stretch and shear flow. We compare here the predictions of our theory to the dynamics of FA that is observed in these experiments.

The situation of cyclic stretch experiments is very different from the case of an external force applied on the top of the cell (21). Stretching the ECM results in applying a force to the bottom surface of the adhesion. The stretching induces a force that acts on the adhesion on its bottom surface and opposes the traction force of the actin fibers. The adhesion therefore undergoes a larger shear than in absence of stretch (see Fig. 7). We therefore predict that in this case, the stretching increases the compression of the mechanosensitive molecules in the stress-free corona, in a direction that is the vectorial difference between the actin force and the stretch force. As a consequence, we would predict that FA and actin stress fibers align parallel to the stretching direction. This prediction is in full agreement with the observations by Kaunas et al. (47): those authors show that the orientation of the stress fibers under uniaxial cyclic stretch depends on both the amplitude of the stretch and the Rho-activity. When the Rho-activity is inhibited, stretch induces the appearance of FA and stress fibers in the direction of the stress. On the contrary, Rho-induced contractility leads to an orientation perpendicular to the stretch. The mechanism at the origin of the perpendicular orientation of the cells under cyclic stretch is unclear, but the results by Kaunas et al. (47) clearly show that the mechanosensitive adhesions are not the only ones involved in the response of the cell in the case of cyclic stretch. Our predictions are also compatible with the experiments by Sawada and Sheetz (48), where they observe that biaxial stretch on triton cytoskeletons induces the accumulation of certain adhesion proteins at the adhesion sites. The stress field in the ECM is not shown, but these are probably the well-oriented adhesions that respond.

FIGURE 7.

Uniaxial stretch of a focal adhesion.

The second situation of cells under shear flow gives an illustration of the response of FA to forces that might oppose the stress fibers. Although the effect of shear flow on cells is still controversial (direct response of FA to the shear flow or response to the flow-induced lamellipod activity?), we here base our argument on the observations by Zaidel-Bar et al. (49). The authors show that FAs are reinforced at the upstream edge of the cell where the lamellipod activity is stopped. On the contrary, FAs disappear at the downstream edge of the cell and give way to focal complexes. Concomitantly, protrusion activity in enhanced at the downstream edge, coupled to an increased Rac activity (confirmed by (50)). Fig. 8 in Zaidel-Bar et al. (49) shows the response of FA localized at the upstream edge to the flow, where our model might be relevant (no Rac activity: lamellipod activity should not interfere with FA dynamics in this region of the cell; the authors also prove that it is not related to any increased contractility or Rho-activation). When stress fibers point parallel to the flow, the upstream adhesion is observed to increase its size; the growth results in a rapid turnover where the growth rate of the front edge of the adhesion exceeds the rate of disassembly at the back (front and back edges of the adhesions are defined by the direction of the stress fiber). The downstream adhesion, on the contrary, decreases in size. The disassembly of the adhesion mainly takes place at its front edge (the front edge still being the one in the direction of the stress fibers). Two situations may be envisioned: 1), The flow-induced force is smaller than the actin stress, and the total force is still oriented in the direction of the stress fibers; the reduction of the size of the FA could then result from the reduction of the compression at the front edge of the adhesion. 2), The flow-induced force is larger and the total force is opposite to the direction of the stress fibers. Our intuition is that in such a situation, FAs cannot grow, since in our vision of FA mechanosensitivity, the growth process involves both adsorption of cytoplasmic proteins and the enlargement of the stress fiber. Such enlargement is only possible if the new actin filament can bind to the existing stress fiber. This intuition is reinforced by micropipette experiments: FAs disappear when stressed in a direction opposite to the stress fibers (D. Riveline, 2006, personal communication). This intuition is also consistent with Fig. 8 A, stripe P, in Zaidel-Bar et al. (49): FAs perpendicular to the flow widen in response to the flow. In this situation, the adhesion is compressed in a direction perpendicular to the stress fiber. The mechanosensor is therefore activated in this direction. Thanks to the proximity of the existing stress fiber, the adhesion can grow in response to mechanosensor activation, which results in a widening.