Analysis of group differences in processing speed: Where are the models of processing?

Abstract

Recently, Myerson, Adams, Hale, and Jenkins (2003) replied to arguments advanced by Ratcliff, Spieler, and McKoon (2000) about interpretations of Brinley functions. Myerson et al. (2003) focused on methodological and terminological issues, arguing that (1) Brinley functions are not quantile–quantile (QQ) plots of distributions of mean reaction times (RTs) across conditions; that the fact that the slope of a Brinley function is the ratio of the standard deviations of the two distributions of means has no implications for the use of slope as a measure of processing speed; that the ratio of slopes of RT functions for older and young subjects plotted against independent variables equals the Brinley function slope; and that speed–accuracy criterion effects do not account for slowing with age. We reply by showing that Brinley functions are plots of quantiles against quantiles; that the slope is best estimated by the ratio of standard deviations because there is variability in the distributions of mean RTs for both older and young subjects; that the interpretation of equality of the slopes Brinley functions and plots of RTs against independent variables in terms of processing speed is model dependent; and that speed–accuracy effects in some, but not all, experiments are solely responsible for Brinley slopes greater than 1. We conclude by reiterating the point that was not addressed in Myerson et al. (2003), that the goal of research should be model-based accounts of processing that deal with correct and error RT distributions and accuracy.

In a typical Brinley function (Brinley, 1965), the mean reaction time (RT) for older subjects for each condition in an experiment is plotted against the mean RT for young subjects for the same condition. The resulting function is usually a straight line, usually with slope greater than 1. Debate has centered on what, if anything, this empirical pattern reveals about age-related changes in information processing (e.g., Cerella, 1994; Fisk & Fisher, 1994; Myerson, Wagstaff, & Hale, 1994; Perfect, 1994). A major problem in the debate is that empirical questions interact with theoretical questions, and they are not always separated in interpretations of experimental results. Such an interaction occurs in Myerson, Adams, Hale, and Jenkins’s (2003) recent reply to an article by Ratcliff, Spieler, and McKoon (2000). Myerson et al. (2003) focused on terminological and methodological issues while neglecting the primary point of Ratcliff et al.’s article—namely, that the empirical patterns revealed by Brinley functions provide only minimal constraint on theoretical explanations of age-related differences in processing (see also Fisher & Glaser, 1996).

Ratcliff et al. (2000) argued that theoretical accounts of aging effects on RT must be developed by fitting explicit models of cognitive processing to the full range of dependent measures for RT—not just the mean RTs that are plotted in Brinley functions but also the full shapes of the RT distributions for both correct and error responses, as well as accuracy values. Any theory that does not account for all of these dependent variables is almost certainly inadequate. Just as one could not have an adequate macroeconomic theory of unemployment rates without considering productivity, interest rates, and so on, so one cannot have an adequate psychological theory of RT without considering accuracy values, error responses, and RT distributions. Fortunately, recent research with sequential sampling RT models (Busemeyer & Townsend, 1993; Ratcliff, 1978, 2002; Ratcliff, Gomez, & McKoon, 2004; Ratcliff & Rouder, 1998; Ratcliff & Smith, 2004; Ratcliff, Van Zandt, & McKoon, 1999; Roe, Busemeyer, & Townsend, 2001; P. L. Smith, 1995, 2000; P. L. Smith & Vickers, 1988; Van Zandt, Colonius, & Proctor, 2000) has shown that the models do a good job of handling all the dependent variables in the RT studies that fall in their domain. Application of these models to the study of aging is beginning to paint a picture of aging effects that, although more complex than any simple slowing account, successfully relates conclusions from studies with RT data to conclusions that have previously been drawn from studies that measure only accuracy or only threshold values.

The Myerson et al. (2003) article has several parts: They pointed out that a Brinley function is not necessarily a quantile–quantile (QQ) plot; they provided an interpretation of the intercept of a Brinley function in terms of two components, a central processing component and a residual component composed of peripheral processes, with the central component slowing more with age than the peripheral component (Cerella, 1985); they claimed that linear regression is an appropriate way to estimate the slope of a Brinley function; they argued that the slope of a Brinley function measures processing speed; and they claimed that the slope of a Brinley function should correspond to the ratios of the slopes of mean RTs plotted as a function of independent variables in experiments.

We begin this article by discussing each of these issues in turn. First, we agree with Myerson et al. (2003) about the terminology of QQ and Brinley functions, that the usual definition of a Brinley function does not fit the technical definition of a QQ function because in a Brinley function, the plotted means are not rank ordered as they would be in a QQ function.

However, in the second section of this article, we stress that it is the case that a Brinley function is a plot of quantiles against quantiles. In Ratcliff et al. (2000), we showed that the condition means of older and young subjects can be understood as quantiles of distributions, one distribution of means for the older subjects and another for the young subjects. When the quantiles are plotted against each other in a Brinley function (i.e., the older subjects’ mean for each condition is plotted against the young subjects’ mean for the same condition), then the slope of the function is the ratio of the standard deviations (SDs) of the two sets of quantiles. Given that the Brinley slope is the ratio of SDs, the slope will have its typical greater than 1 value because the spread of older subjects’ means across experimental conditions is typically larger than the spread of young subjects’ means. Also, given the typical values of older and young subjects’ mean RTs and the SDs in the mean RTs, a negative value for the intercept of the Brinley function falls out of the equation for the relationship between older and young subjects’ quantiles.

Third, we show that linear regression does not provide an appropriate estimator of the slope of a Brinley function. The reason is that there is variability in both of the plotted variables—that is, in both the condition means of the older subjects and the condition means of the young subjects.

Fourth, we discuss two critical problems with Myerson et al.’s (2003) claim that the slope of a Brinley function measures the relative speeds of processing for older versus young subjects: The claim is invalid if the two groups of subjects adopt different response criteria because differences in criteria can be wholly or in part responsible for differences in performance. Also, the claim is consistent with only a small set of models of cognitive processing.

Fifth, we show that Myerson et al.’s (2003) finding that Brinley slopes match the ratio of slopes for older and young subjects’ mean RTs plotted against independent variables can be derived by simple algebra. We also show that their interpretation of this finding is valid only under a restricted range of processing models, and that this analysis is possible only when RT is a linear function of the independent variable.

We end by reviewing applications of a theoretical model, the diffusion model (Ratcliff, 1978, 1981, 1985, 1988, 2002; Ratcliff et al., 2004; Ratcliff & Rouder, 1998; Ratcliff & Smith, 2004; Ratcliff et al., 1999), to experimental paradigms that show various patterns of effects of aging on RT. In the review, we highlight the advantages of a model that fits all the multiple aspects of RT data and allows separate examination of components of processing that might be affected by aging.

Brinley Plots and QQ Plots

A typical Brinley function is constructed by calculating the mean RT for each condition in an experiment for older subjects and young subjects separately. Then the mean RTs are plotted against each other, the mean for the older subjects in each condition plotted against the mean for the young subjects in that same condition.

Ratcliff et al. (2000) showed that each condition mean in an experiment can be treated as representing a quantile point on a distribution of condition means, where the whole distribution would be swept out by all the possible levels of the independent variable, from the easiest possible condition to the most difficult. The particular levels of the independent variable used in an experiment pick out of the distribution the quantiles that are actually measured in the experiment. The levels of the independent variable determine the relative difficulty of the conditions, and if there were no extraneous variability in the data, relative difficulty would order the condition means from shortest to longest. If the relative difficulty of the conditions is the same for older and young subjects, then the rank ordering of the condition means would be the same for older and young subjects and plotting them against each other would yield a QQ plot. However, if the variability in the data is sufficiently large, it will not necessarily be the case that the ordering of the mean RTs from shortest to longest will veridically reflect the ordering of the conditions in terms of difficulty. So when a Brinley function is constructed by plotting, for every condition, the older subjects’ mean from that condition against the young subjects’ mean from the same condition, in order of the conditions’ difficulty, then the ordering of the means will not necessarily be from shortest to longest. Thus, technically speaking, a Brinley function is not a QQ plot because the means do not necessarily reflect a rank ordering of shortest to longest RTs. Myerson et al. (2003) are therefore correct that a Brinley function is not a QQ plot; however, as just explained, a Brinley function is a plot of quantiles against quantiles, where the ordering of the quantiles (i.e., the ordering of the condition means) is determined by the independent variable in the experiment.

While the focus of our original paper (Ratcliff et al., 2000) as well as this reply is not on QQ plots—instead the focus is on the interpretation of Brinley functions as plots of quantiles against quantiles—it is worth mentioning a part of Myerson et al.’s (2003) discussion of QQ plots that could be misleading. Using an example, they showed that a QQ plot can obscure important features of data. In particular, for two sets of data from young and older subjects, one set of data from a visuospatial task and the other from a verbal task, Myerson et al. (2003) showed that a Brinley function divides the two sets into separately observable functions, but a QQ plot obscures this separability (because reordering the condition means fastest to slowest mixes data from the two tasks). While it is correct that the QQ plot obscures important aspects of the data in this case, it should not be concluded that QQ plots generally have this problem. An important aim of exploratory data analysis (EDA), the research area of statistics in which QQ plots were developed and promoted, is to explore data and not to make mistakes such as combining sets of data that show different patterns of results. For example, Chambers, Cleveland, Kleiner, and Tukey (1983), in their text on EDA, gave an example analogous to Myerson et al.’s (2003) and used it to argue that no matter how sensible a single type of analysis might appear to be for some collection of data, there is no excuse for failing to look further for more or different structures in the data. In Chambers et al.’s example, QQ plots are constructed by plotting quantiles of data against quantiles of a theoretical distribution, for amounts of rainfall with and without cloud seeding. With seeding, the QQ plot of amounts of rainfall (log scale) against the quantiles of a normal distribution is nonlinear and the distribution is left skewed. Without seeding, the QQ plot is also nonlinear but the distribution is right skewed. Combining the seeding and nonseeding data produces a linear QQ plot that suggests a normal distribution even though the two components of the distribution are nonnormal. Chambers et al. used this example to illustrate that data should be explored in many ways with many kinds of analyses. For Myerson et al.’s (2003) visuospatial and verbal data, exploring the data by producing separate instead of mixed QQ plots would reveal the same separability of the functions as shown by a Brinley function. As Chambers et al. (p. 212) put it, “The general lesson is important. Theoretical QQ plots are not a panacea and must be used in conjunction with other displays and analyses to get a full picture of the behavior of the data.”

Brinley Functions: Plots of Quantiles Against Quantiles

As stressed in the previous section, Brinley functions are plots of quantiles against quantiles, the mean RTs for older subjects representing quantile points from the distribution of possible mean RTs for them and the mean RTs for young subjects representing quantile points from their distribution. The quantiles of the distributions are ordered by the relative difficulty of the levels of the independent variable in the experiment, and the only assumption necessary for the quantile analysis is that the relative ordering of difficulty be the same for older and young subjects. Note that this same assumption is necessary for the standard slowing interpretation of Brinley plots.

Several of the main findings in the aging literature on Brinley functions can be explained via the analysis of Brinley functions as plots of quantiles against quantiles, as discussed by Ratcliff et al. (2000) and outlined in Table 1. First, it follows from the analysis that if the distributions of quantiles for older and young subjects have about the same shape, then the Brinley function will be approximately a straight line (see Ratcliff et al., 2000), which it usually is (see Chambers et al., 1983, pp. 199–202). Even when the separate plots of older and young subjects’ mean RTs against the independent variable in an experiment are not themselves linear (e.g., Luce, 1986, Figure 2.2), their Brinley function will be approximately a straight line if the distributions have about the same shape (Ratcliff et al., 2000, Equation 4).

Table 1.

Features of Brinley Functions

Feature	Slowing Interpretation	Ratcliff et al. (2000) Interpretation
Slope greater than 1	Cognitive processes are slowed for older subjects relative to young subjects by a factor that is the slope of the Brinley function	The slope of the Brinley function is the ratio of the SD of condition means for older subjects to the SD of condition means for young subjects; the SD for older subjects is typically larger
Linearity	Rarely addressed; if serial or parallel processing is assumed, linearity derives from all processes slowing by a constant amount	A Brinley function will be linear if the distributions of condition means for the older and young subjects have (at least approximately) the same shape
Negative intercept	Processing can be divided into peripheral and central components, and there is more slowing with age in the central components	Intercept = μO −μY(σO/σY); typical values of μs and σs produce negative value of intercept
Negative correlation between slopes and intercepts	Given more slowing with age in the central components, random variation across experiments in central and peripheral components leads to negative correlation	Variation in μs and σs across experiments produces the negative correlation
Target for modeling	Brinley slope	Distributions of mean RTs across conditions, plus all other dependent variables in the task

In contrast, linearity is a characteristic of Brinley functions that has been addressed for only a few tasks by only a handful of the researchers who interpret the slopes of Brinley functions as measures of slowing, in the context of specific serial or parallel processing models (e.g., Cerella, 1991; see also Cerella, 1990). Outside of those tasks, the Brinley plot linearity has not been explained.

Given that the older and young subjects’ condition means are quantiles, the equation for the Brinley function is

$$Q_{\text{O}}=(s_{\text{O}}/s_{\text{Y}})Q_{\text{Y}}+{\mu }_{\text{O}}-{\mu }_{\text{Y}}{s}_{\text{O}}/s_{\text{Y}},$$ (1)

where the subscripts O and Y stand for older and young, μ_O and μ_Y are the means of the condition means, s_O and s_Y are their standard deviations, and Q_O and Q_Y are the quantile values (see Ratcliff et al., 2000, for more detail). Thus, the slope of the line is the ratio of the SDs. As Ratcliff et al. (2000) stressed, the slope shows nothing about the relative speeds of the older and young subjects. The slope (s_O/s_Y) will be greater than 1 if the spread of the older subjects’ means in an experiment is greater than the spread of the young subjects’ means. The slope will be greater than 1 if the older subjects’ spread is greater even if the older subjects’ means are shorter than the young subjects’ means, as they might be, for example, in an experiment in which young subjects were induced to perform as accurately as possible while older subjects were given instructions and practice to respond as fast as possible.

In the literature, the most salient characteristic of Brinley functions is that their slopes are almost always greater than 1, but there are two other characteristics that have received attention. One is that when the slope is greater than 1, the intercept is negative, and the other is that there is a negative correlation between the intercept and slope of Brinley functions across experiments: When the intercepts of Brinley functions are plotted against their slopes for a large number of experiments, the intercepts and slopes fall on a straight line with slope around −500 msec and intercept around 600 msec (Cerella, 1985, 1991).

Both of these findings are directly understandable from the analysis of Brinley functions as plots of quantiles against quantiles. If older subjects’ mean RTs and the SDs in them are greater for older than young subjects in the amounts they typically are, then the intercept (μ_O − μ_Ys_O/s_Y) will have a negative value, as Ratcliff et al. (2000) demonstrated. The value of the intercept depends on the young and older subjects’ mean RTs. In other words, the intercept carries information about the speed of older subjects relative to young subjects (Myerson et al., 2003, claimed we said it directly measures the relative speeds, but this is not the case).

The negative correlation between the intercepts and slopes of Brinley functions from a number of experiments can also be understood from analysis of Brinley functions as plots of quantiles against quantiles. If, across experiments, the linear regression between intercepts and slopes had one true slope and intercept, then with random variation across the experiments, the slope and intercept would be negatively correlated (see Ratcliff & Tuerlinckx, 2002, Figure 5). When there are also differences in mean RTs and the SDs for older and young subjects across experiments, the negative correlation can be understood with Equation 1. In Equation 1, if we let y designate the intercept μ_O − μ_Ys_O/s_Y and x the slope s_O/s_Y, then

$$y={\mu }_{\text{O}}-{\mu }_{\text{Y}}x.$$ (2)

If there are differences across experiments in x—that is, in the SDs, then the intercept of the plot of intercepts against slopes for the experiments’ Brinley functions would be the overall mean RT for older subjects (μ_O) and the slope would be the overall mean RT for young subjects (μ_Y). If there are differences across experiments in the means as well as the SDs, then the slopes and intercepts of the Brinley functions will necessarily be negatively correlated, as we showed by examining systematic changes in means and SDs in Ratcliff et al. (2000; see also Cerella, 1991; Myerson et al., 2003). Here, we show the negative correlation when both means and SDs randomly vary from experiment to experiment by simulation, as follows:

For older subjects, mean RTs were selected from a normal distribution with mean 700 msec and SD 70 msec, and SDs were selected from a normal distribution with mean 150 msec and SD 30 msec. For young subjects, mean RTs were selected from a normal distribution with mean 600 msec and SD 50 msec, and SDs were selected from a normal distribution with mean 100 msec and SD 20 msec. From these distributions, 200 values of older and young subjects’ means and SDs were randomly selected, the Brinley slope and intercept were calculated for each of the 200 sets of values, and they were plotted in Figure 1. Given Equation 2, the intercept of the best fitting line to these points should be the average mean RT for older subjects, μ_O—that is, 700 msec, and the slope of the line should be minus the mean for young subjects, μ_Y—that is, − 600 msec. The obtained values, 704 msec and −604 msec, are very close to these predicted values (and similar to the values obtained by Cerella, 1985, 1991).

Figure 1.

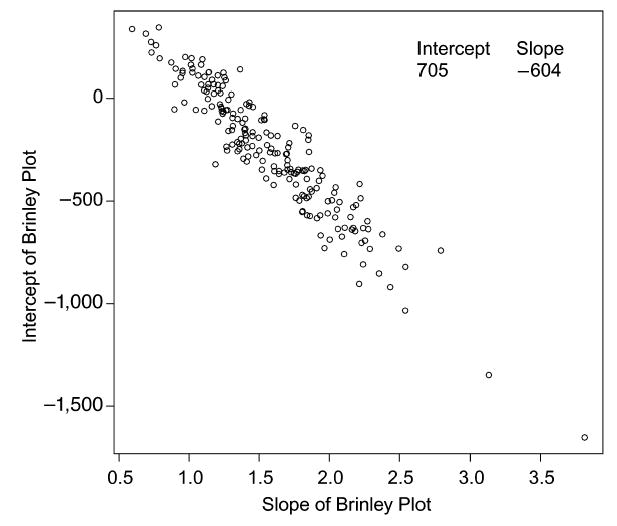
A plot of intercept and slopes from Brinley functions when there is random variation across 200 simulated experiments in the overall means and SDs across conditions. For each simulated experiment, for older subjects, a mean RT was selected from a normal distribution with mean 700 msec and SD 70 msec, and an SD was selected from a normal distribution with mean 150 msec and SD 30 msec. For young subjects, a mean RT was selected from a normal distribution with mean 600 msec and SD 50 msec, and an SD was selected from a normal distribution with mean 100 msec and SD 20 msec. The Brinley slope and intercept were calculated for each of the 200 simulated experiments, and these provide the basis of the plot.

Cerella (1985, 1991; see also Myerson et al., 2003) provided a different account of why the Brinley intercept is negative and why slopes and intercepts are negatively correlated across experiments. They assumed that the cognitive processes examined with Brinley functions can be divided into two parts, central processes and peripheral processes, and they hypothesized that peripheral processes are less affected by aging than are central processes. To the extent that peripheral processing time for older subjects is the same as peripheral processing time for young subjects and given that the slope is greater than 1, the slope will tend to have a negative intercept. To see this, suppose that peripheral processing time is exactly the same for older and young subjects. At this point on the Brinley function, RTs for older and young subjects will be equal and any line through this point with a slope greater than 1 will have a negative intercept. The negative correlation between slope and intercept across experiments is also easily explained: If it is assumed, for the purposes of illustration, that there is no variability in peripheral processing time across experiments but there is variability in slope, then the larger the slope, the more negative will be the intercept. If there is some variability in peripheral processing time across experiments, the negative correlation is still obtained. A limitation of this analysis, as Cerella (1985) made clear, is that central and peripheral processing times cannot be uniquely determined from the data.

Table 1 summarizes the implications of the interpretation of Brinley functions as plots of quantiles against quantiles compared with the interpretation of Brinley functions as measuring the degree of cognitive slowing for older relative to young subjects. Cerella (1985, 1991) and Myerson et al.’s (2003) account of negative Brinley intercepts and negative correlations of slopes and intercepts across experiments assumes two separable components of processing, not an unreasonable assumption, whereas the quantile analysis depends only on the typical values of mean RTs and SDs. The two accounts differ sharply in the targets of their theoretical efforts, with an explanation of the Brinley slope (i.e., the degree of slowing with age) as the target for the standard account with models that are specific to aging, and with an explanation of all the dependent variables in a task as the target for Ratcliff et al. (2000) with models that focus on the processes involved in performing the task.

Myerson et al. (2003) attempted to discredit Brinley functions as measures of quantiles against quantiles by saying that the analysis implies “cognitive psychology’s few quantitative laws [e.g., memory scanning, mental rotation, and visual scanning] would need to be radically reinterpreted” (p. 230). But the Brinley function is not a “quantitative law” (see Briggs, 1974); if it were, then every stable, replicable pattern of data (serial position effects, error gradients, etc.) would have to be called a law. Also, there is no generally agreed upon theoretical account of these “laws,” except perhaps in the case of mental rotation. Moreover, the experimental results to which Myerson et al. (2003) referred—the “laws”—are based on plots of a dependent variable against an independent variable. In contrast, the argument at issue concerns Brinley functions, which are plots of one dependent variable against another dependent variable that usually results in linear functions with slopes that range from near 1 to 3.

The advantages of understanding Brinley functions as plots of quantiles against quantiles are, first, that the properties of Brinley functions listed in Table 1 are automatically obtained, and second, that specific processing models can be focused on predicting the behaviors of all the dependent variables, accuracy values, and the RT distributions for correct and error responses. Then, if a model produces distributions of mean RTs across conditions for older and young subjects that have about the same shape, with the same relative ordering across conditions, and with the means and SDs larger for older subjects, the Brinley plot regularities follow.

Linear Regression Does Not Provide an Appropriate Measure of Brinley Slope

In Myerson et al.’s (2003) view, the slope of a Brinley function measures the relative speeds of cognitive processing for older and young subjects. They claimed that linear regression is the best way to estimate this slope, and in making this argument, they asserted that Equation 1 is a special case of linear regression. Neither of these claims is correct.

If Equation 1 were a special case of linear regression, then the slope of the function would be r(s_O/s_Y) instead of (s_O/s_Y), where r is the correlation coefficient. If there were no variability in the y and x values, then the slope of the linear regression line would be equal to the ratio of the SDs in the y and x values (Myerson et al., 2003, agreed on this point): The ratio of SDs, s_O/s_Y, for the line y = mx + c, is

$$\frac{s_{\text{O}}}{s_{\text{Y}}}=\sqrt{\frac{\mathrm{\Sigma }{(m{x}_i+c-mx-c)}^2}{\mathrm{\Sigma }{(x_i-x)}^2}}=m.$$

However, for a Brinley function, there is, of course, variability in the data, and there is variability in the x values as well as the y values. Given variability in the x values, Equation 1 is not a special case of linear regression (Chen & Van Ness, 1999; Draper & Smith, 1998; Fisk, Fisher, & Rogers, 1992).

As the best estimator of slope, Myerson et al. (2003) advocated use of the “general equation for regression/correlation” (Myerson et al., 2003, Equation 2); however, they do not consider the assumptions underlying it. These are as follows: that there is no variability in x, that there is variability only in y, and that the variability in the y values arises from each value being selected from a normal distribution. Linear regression is robust to violations of normality, but it is not robust to variability in x. If there is variability in x as well as y, the slope is underestimated by linear regression (Fisk et al., 1992) and linear regression should not be used (see also the simulation in the appendix in Ratcliff et al., 2000).

Given that linear regression cannot be used to estimate the slope, what estimator can be used? In the Appendix to this paper, we review statistical research on this question and show that the conclusion is that, when there is variability in both y and x and the number of observations is not large, one recommended estimator is the ratio of the SDs of the y and x values (Draper & Smith, 1998). This is the same as the slope of the Brinley function when the function is analyzed as plotting quantiles against quantiles. In the Appendix, we also discuss other estimators that depend on what is known about the data (e.g., SDs in the individual x and y values) as well as generalized regression that takes into account SDs in mean RTs for both y and x.

Although it is statistically inappropriate to use standard linear regression for estimating the slopes of Brinley plots or for demonstrating that a straight line fits the data, from a practical point of view, it is likely not to be a severe problem if the correlation is high and an accurate value of the slope is not needed. But if the value of the slope is to be used for hypothesis testing, or if the best fitting value of the slope is intended to be meaningful, then the methods outlined in the Appendix are required.

How Well Do Straight Lines Fit Brinley Plot Data?

Before going on to further discuss interpretations of Brinley slopes as measures of slowing, we mention an empirical/statistical problem: A Brinley function is usually presented without any measure of how well the data points are fit by the linear function used to describe them. This contrasts sharply with most model-based approaches (e.g., Ratcliff et al., 2000) in which explicit models are fit to experimental data and goodness-of-fit statistics can be used to determine how accurately the models fit the data. The statistic usually given for Brinley functions is the value of the correlation between the x and y points, but in the usual application this does not provide any information about the extent to which the points actually lie on the fitted straight line. In fact, the usual correlation is not a measure of how well a straight line fits the data; any straight line could be drawn, near to or far from the data, and the value of the correlation would still be the same. For example, there are many ways of fitting straight lines to data, including standard least squares, weighted least squares, several robust methods (e.g., Venables & Ripley, 1996, chap. 8), and methods that accommodate measurement error or variability in the x values (see below). The usual correlation is the same no matter which method of producing a straight line fit is used.

Figure 2, top panel, shows a Brinley function of the data from three experiments from Ratcliff, Thapar, and McKoon (2001, 2003) and Thapar, Ratcliff, and McKoon (2003). The correlation is .941, the slope is 1.46, the intercept is −83 msec, and a straight line appears to fit at least as well as for some data sets in the literature for which data are combined across several experiments (e.g., Cerella, 1990, Figure 3; Faust, Balota, Spieler, & Ferraro, 1999, Figure 2; Nebes & Madden, 1988). The data for two of the experiments shown in Figure 2 include conditions in which instructions stressed the accuracy of responding and conditions in which instructions stressed the speed of responding, and these two data sets are shown with separate symbols. The bottom panel shows the same Brinley function, this time with error bars of ± 2 SE around each data point. On this version of the function, it can be seen that the single straight line does not pass through the confidence regions around the data points. Only with the error bars is it apparent how badly the single line does. With the error bars it is clear that, while the single line fails, separate straight lines fit each data set well (26 out of 30 data points fall within 2 SE). The point is that there is no way to know from the plot of a Brinley function without error bars (like the one in the top panel of the figure) whether or not it misses data points in significant ways.

Figure 2.

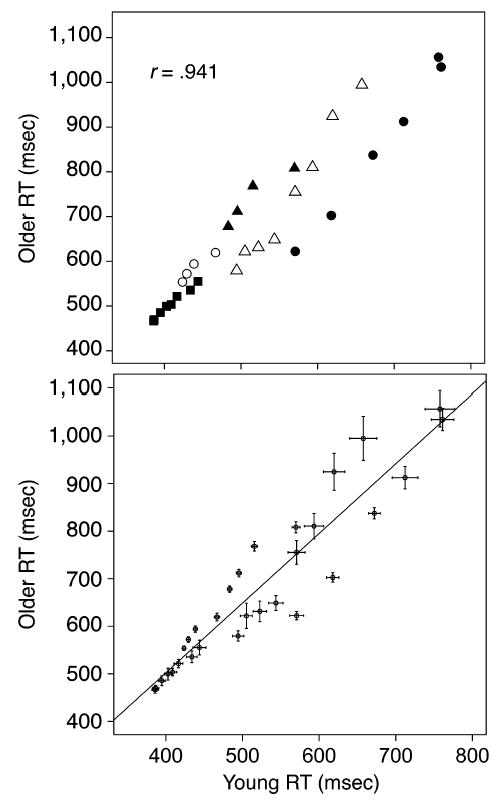
A Brinley function for the data from three experiments in Ratcliff etal. (2001, Experiment1 filled circles, Experiment 2 open triangles and filled squares) and Thapar et al. (2003, open circles and filled triangles). The top plot does not have error bars; the bottom plot is for the same data with ± 2 SE error bars.

Figure 3.

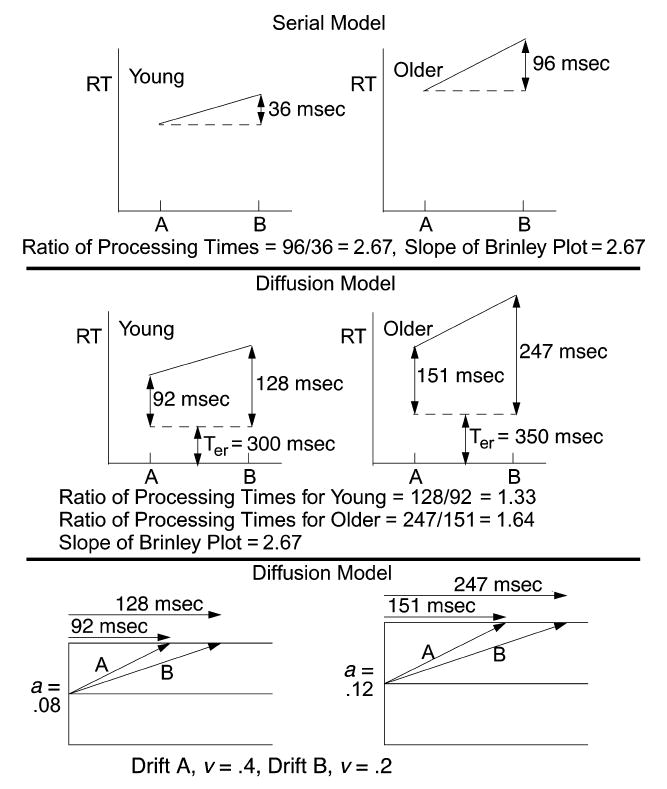
An illustration of predictions from a serial processing model and a diffusion model applied to mean RT. The RT values are derived from a diffusion model with parameters: Condition A, a = 0.08, T_er = 0.3, η = 0.08, S_z = 0.02 drift rates 0.2 and 0.4, and S_t = 0.1; and Condition B, a = 0.12, T_er = 0.35, η = 0.08, S_z = 0.02, drift rates 0.2 and 0.4, and S_t = 0.1. a = boundary separation, T_er = nondecision component of RT, η = SD in drift across trials, S_z = range in starting point across trials, and S_t = and range in the distribution of T_er.

The question of whether the data points are well fit by a straight line is usually not asked in the regression literature (except by assessing quadratic and higher order trends) because the y values are assumed to be single measurements and not means. In standard regression, when the y values are means and there is variability in them (but not in the x values), the question about goodness of fit would translate into determining whether the variability in each mean matched the variability in the means about the regression line—that is, whether it matched the standard error of estimate, s_{est y} (e.g., Stuart, Ord, & Arnold, 1999, p. 502; Draper & Smith, 1966, p. 28). When both the x and y values are means and there is variability in both, one solution for linear regression (Press, Flannery, Teukolsky, & Vetterling, 1992) uses a generalized regression approach and provides a chi-square goodness-of-fit measure (see the Appendix for a full discussion). For the line in the top panel of Figure 2, the chi square value is 1,609.23, p < .05 (df = 28), so the line does not fit the data.

The main point here is that Brinley functions may not be good fits to the data on which they are based. To show how well a Brinley function does fit the data, error bars need to be displayed around the mean RTs (as in the bottom panel of Figure 2) or some other measure of goodness of fit, for example, the chi square, needs to be given. If the function falls outside the error bars or the chi square value is significant, then linear regression is not an adequate description of the data.

The Slope of the Brinley Plot

To reiterate our point about Brinley functions, the slope is the ratio of the SDs of the distributions of condition means for older to young subjects. The slope does not measure the relative speeds of older relative to young, but instead shows the relative spreads of their means across conditions. The distributions of means across conditions are one of many possible meeting points between theory and data. Myerson et al. (2003) interpreted the slope of a Brinley function as measuring relative processing speed: A slope greater than 1 is interpreted as the multiplicative amount by which older subjects are slow relative to young subjects. In this section, we outline three problems with this interpretation.

1. Inconsistent processing speeds

Interpreting the slope of a Brinley function as measuring relative processing speed leads to inconsistent estimates of speed between conditions that differ in terms of whether the instructions to the subjects emphasize speed or accuracy. The inconsistencies come about because of the dependence of a Brinley slope on subjects’ speed–accuracy criterion settings. The problem can be illustrated with data from several experiments in which instructions were used to manipulate speed–accuracy criteria across blocks of trials. For Experiment 2 in Ratcliff et al. (2001), when the older subjects’ means for experimental conditions with speed instructions are plotted against the young subjects’ means for conditions with accuracy instructions, the Brinley function is RT_O = .54RT_Y + 199. When the same thing is done for the speed and accuracy conditions in Thapar et al. (2003) and in Ratcliff et al. (2003), the functions are RT_O = .72RT_Y + 221 and RT_O = .35RT_Y + 308. In all three cases, the slope is less than 1, so if the slope did indeed show relative rates of processing, the conclusion would be that the older subjects were faster than the young subjects. If the plotting of the Brinley function were switched so that the young subjects’ means for speed conditions were plotted against the older subjects’ means for accuracy conditions, the results would be different: The slopes would be much greater than 1.

It might be thought that this problem could be dismissed because differential instructions violate the “correspondence axiom” (Cerella, 1990), but this is not the case. The correspondence axiom states that young and older subjects can be compared via Brinley functions only when they are “performing the same computations” (p. 215). There are two serious difficulties with the axiom. The first concerns a “minimal” condition (p. 215) that data are required to satisfy in order to be consistent with the axiom—namely, that the Brinley function must be monotonic. However, it is not possible to distinguish patterns that are truly not monotonic from patterns for which the underlying functions are monotonic but become distorted by variability in the data.

The second difficulty with the axiom concerns whether differential speed–accuracy instructions actually do violate the axiom. In the original statement of the axiom, equivalence of speed–accuracy criteria was not explicitly required. However, it appears that equivalence is now expected in many current applications (see Cerella, 1990). Unfortunately, if equivalent speed–accuracy criteria are required, it is not possible to determine empirically whether the axiom holds because it is not possible to determine whether criteria are the same across individual subjects or across groups of older versus young subjects. It cannot be stressed too strongly that it is not enough to require accuracy to be equivalent for all the individuals or groups. For example, if the cognitive processes in a task were more difficult for older than young subjects, the older subjects might still attain accuracy levels as high as young subjects by adopting more conservative criteria (i.e., going slower); accuracy would be equivalent between the two groups but their speed–accuracy criteria would be different. It is also not enough if all subjects show very high degrees of accuracy, say above .9. The problem is that a statistically detectable difference in accuracy between, say, 70% and 80% correct, has the same difference in d′ as a difference in accuracy between 95% and 97.5% correct, which is probably not statistically detectable in a typical experiment. The only way to measure speed–accuracy criteria, and therefore the only way to know if they are equivalent across subjects, is through the application of a model that can separate criteria from other components of processing in the task of interest. Ironically, such a model-based demonstration that the correspondence axiom holds is likely to yield more information about age-related differences in processing than the Brinley analysis that requires this condition. In the absence of a model, it is impossible to determine whether the correspondence axiom is violated by differences in speed–accuracy criteria.

Given that there is no way of determining whether speed–accuracy criteria are equivalent or not (at least not in the absence of a model), the correspondence axiom provides no way of determining whether or not equivalence holds, and so the difficulties illustrated with the interpretation of Brinley slopes from Ratcliff et al.’s (2001), Ratcliff et al.’s (2003), and Thapar et al.’s (2003) experiments are germane. For these experiments, if the slope of a Brinley function is taken to measure the relative speed of cognitive processes for older and young subjects, then the relative speeds are not consistent across speed–accuracy instructions. More generally, even when speed–accuracy instructions are not manipulated explicitly in experiments, individual subjects undoubtedly set and vary their criteria themselves. To the extent that older subjects do this differently from young subjects, it can never be known from a Brinley slope by itself that it represents differences in speed of cognitive processes and not differences in criteria, or some combination of the two. The slope can be interpreted only in the context of a model that fully encompasses all the dependent variables of the task.

2. Myerson et al.’s (2003) meta-analysis of Sliwinski and Hall’s (1998) data

Myerson et al. (2003) defended their interpretation of Brinley slopes as representing relative processing speeds with a meta-analysis of data from three “well defined cognitive processes” (p. 231, data from Sliwinski & Hall, 1998)—mental rotation, visual search, and short-term memory scanning. For each task, for young and older subjects separately, Myerson et al. fit a straight line to the function relating RT to the independent variable in the task (number of degrees of mental rotation or visual search set size or memory set size); then they calculated the ratio of the slopes of the best-fitting straight lines for young and old. Also, for each task, they calculated the slope of the Brinley function (fit by linear regression). In each case, the ratio obtained from relating RT to the independent variable was almost identical to the slope of the Brinley function. Myerson et al. (2003) concluded that this identity supports their interpretation of Brinley slopes as measures of the relative processing speeds of young and older subjects.

However, the near-identity of the ratio of the independent variable-RT slopes to the Brinley slope is guaranteed whenever the independent variable-RT slopes are straight lines. The near-identity of the slopes does not provide support for interpreting Brinley slopes as measures of relative processing speeds. It simply falls out of the equations for the independent variable-RT lines (e.g., Ratcliff et al., 2000, Equations 2–4). To see this, consider the following: If the independent variable-RT functions are straight lines and there is no variability in x or y,

$${\text{RT}}_{\text{Y}}=m_{\text{Y}}x+c_{\text{Y}}$$

and

$${\text{RT}}_{\text{O}}=m_{\text{O}}x+c_{\text{O}};$$

eliminating x (e.g., number of degrees of rotation or set size) from the two equations gives

$${\text{RT}}_{\text{O}}=(m_{\text{O}}/m_{\text{Y}}){\text{RT}}_{\text{Y}}+c_{\text{O}}-(m_{\text{O}}/m_{\text{Y}})c_{\text{Y}}.$$

Thus, in the absence of variability in the x and y values, the slope of the Brinley function is guaranteed to be the ratio of the slopes of the individual linear functions. As variability in the data increases, the slope of the Brinley function will diverge from the ratio of the individual slopes. For the data Myerson et al. (2003) analyzed (e.g., their Figure 3), the amount of variability in the data points about the fitted straight line was relatively small, and so the Brinley slope and the ratio of the individual function slopes were almost identical. If there were greater variability in the x and y values, the comparison between the slope of the Brinley function and the ratio of the slopes of the individual functions would be better carried out by systematic Monte Carlo studies in which variance was added to known values of slopes and SDs and recovery of those values could be examined, keeping in mind that there is variability in both the x and the y values (Ratcliff et al., 2000, Appendix A1). However, greater variability would not change the implications of the analysis: Given linear functions for independent variable-RT functions, the ratio of the slopes of these functions will necessarily match the slope of the Brinley function (with the degree of match depending on variability in the data).

It should be stressed that the ratio of the slopes of independent variable-RT functions will match the Brinley slope only when the function for RT versus the independent variable is linear. If the function is nonlinear, the comparison cannot be carried out (e.g., for most variables, such as word frequency, repetitions, study time, contrast, stimulus probability, intensity, stimulus duration, etc., RT is not linear when the independent variable is varied over a large range). However, even when the independent variable-RT functions are nonlinear, the analysis in terms of plots of quantiles against quantiles can be carried out and it does explain the linearity of the Brinley function (see Ratcliff et al., 2000, Equation 4).

3. Model dependence

When Myerson et al. (2003) argued for interpretation of the Brinley slope as a measure of relative speed of processing, they were arguing that their interpretation is a general one: Whatever the task, a Brinley slope measures relative speed of processing. However, this interpretation is valid only under some models, in particular, serial models of cognitive processing and parallel models that mimic the serial models. For example, they talked about the slope of RT against an independent variable as “corresponding to the speed with which they [the subjects] performed a particular cognitive process (e.g., for memory scanning, the number of milliseconds per item in the memory set)” (p. 232). The problem with the argument is that if there are other reasonable models that offer a different interpretation of the Brinley plot slope, then the slope cannot, in general, be said to measure relative speed. Instead, the slope can be interpreted only in the context of whatever model applies to the particular task under study.

In Figure 3, we show how Myerson et al.’s (2003) interpretation of Brinley slopes is most consistent with serial processing. The top panel of Figure 3 shows RT as a function of Experimental Conditions A and B, with RT differences of a size that might be obtained in, for example, a memory scanning task in which Condition A was Set Size 3 and Condition B was Set Size 4. The processing time difference between Conditions A and B is 96 msec for older subjects and 36 msec for young subjects, and in a serial processing model, these times would represent the total time to process one additional item in memory—that is, the time to scan one additional item. The ratio of the differences, 96 msec versus 36 msec, is 2.67, the same value as the slope of the Brinley function that would be derived from these data. The 2.67 slope is understood to represent the factor by which the older subjects’ scanning rate per item is slowed relative to young subjects’ scanning rate. Note that this slope will still be equal to the ratio of standard deviations in a QQ interpretation of the data if the variability in the data is not large.

If processing is not serial and the 96- and 36-msec differences are not measures of the total processing time for each additional item in memory, then the picture is quite different. The middle and bottom panels of Figure 3 show how the RTs might be interpreted in a sequential sampling model, the diffusion model used by Ratcliff et al. (2000). The time T_er is the time taken up by processes other those involved in the decision about whether the test item is or is not in memory, and the remainder of the RT represents the decision process. In this model, the RT differences are not the total processing times for a serial scan of each additional item. For example, for young subjects, suppose that the decision process took 92 msec in Condition A and 128 msec in Condition B; in other words, the 36-msec difference between Conditions A and B is a slowing of 36 msec in a process that took 92 msec to complete for Condition A. In the diffusion model, this difference could come about as shown in the bottom panel of the figure. In this example, evidence accumulates toward the top boundary of the process at a faster rate for Condition A (a larger drift rate in the terms of the model) than for Condition B, so that the boundary is reached in 92 msec for Condition A and 128 msec for Condition B. For older subjects, the decision process takes 151 msec in Condition A and 247 msec in Condition B. In this example, the rate at which evidence accumulates is the same for older and young subjects in each condition and the reason RTs are increased for the older subjects is that their response boundaries are further from the starting point (a= .12) than the boundaries for the young subjects (a = .08); that is, the older subjects are more conservative.

Given the decision times in the example in the figure, the ratio of processing times for the young subjects in the two conditions is 128/92 = 1.33, and the ratio of processing times for the older subjects is 247/151 = 1.64. The ratio of these two ratios is 1.23, quite different from the 2.67 slope of the Brinley function. Thus, in this sequential sampling model, the slope of the Brinley function is not a measure of relative processing speed. In fact, to our knowledge, it is only under the assumption of serial processing (or some kinds of parallel processing including those that mimic serial processing) that a Brinley slope measures relative processing speed.

The serial models required by the interpretation of Brinley slopes as measures of relative processing speed are not currently commonly accepted in cognitive psychology. Perhaps the least controversial task for which serial processing remains relatively unchallenged is mental rotation. But for memory scanning and visual scanning, serial models are clearly inconsistent with serial position effects, repetition effects, the effects of repeated negatives, and so on. In theoretical approaches, processing is not serial (see Bundesen, 1990; Luce, 1986, chap. 12; Murdock, 1971; Ratcliff, 1978; Strayer & Kramer, 1994; Townsend, 1972, 2001; Townsend & Ashby, 1983; Wolfe, 1994). However, perhaps the main problem with serial processing models is that they do not allow predictions to be made about all the dependent variables in an RT task—accuracy values and correct and error RT distributions.

The general point here is that the Brinley interpretation of slopes entails specific assumptions about the applicable models of cognitive processing. We think it is reasonable that researchers arguing for a slowing interpretation of Brinley slopes minimally show support for the cognitive model that makes their favored interpretation possible. The fact that this is rarely done may explain why nicely fitting, linear Brinley plots are often easily assumed to automatically support generalized slowing, even though models that are consistent with generalized slowing are likely to fail to provide a complete and adequate account of data.

Can Theory Take Us Further?

Up to this point in this article, the concern has been with the interpretation of Brinley functions. We have attempted to separate empirical issues about the interpretation of the data, as represented in Brinley functions, from theoretical questions such as how to explain the relative speeds of processing for older and young subjects. The interactions of empirical and theoretical issues have been a major problem in interpreting Brinley functions. Separating the issues is key to understanding the main point that Ratcliff et al. (2000) wanted to make (see also Fisher & Glaser, 1996): Linear Brinley functions are consistent with a variety of different theoretical analyses, and the important questions are what is the range of such models and how can they be tested against each other? The reason these questions do not arise in Myerson et al.’s (2003) article is that they implicitly assumed that a linear Brinley function with slope greater than 1 always implies that processing speed is increased in older relative to young subjects by a factor that is equal to the slope of the Brinley function.

Ratcliff et al. (2000) made the general point that linear Brinley functions can be produced in a variety of ways from a variety of theoretical frameworks. The example in Figure 3 shows the same Brinley function arising from two quite different models, one serial and one parallel. Ratcliff et al. (2000) illustrated the point within the framework of diffusion models by showing that differences between older and young subjects in any of a number of components of the models—for example, drift rates or boundary separation—can produce linear Brinley functions with slopes greater than 1. Fisher and Glaser (1996) also discussed how different serial and parallel processing architectures can account for data that had been taken, on face value, to support some form of a slowing hypothesis.

Generally speaking, Brinley functions have been used to support the hypothesis that cognitive processes slow with age, by the same factor across all tasks (general slowing), by the same factor across all tasks in a domain (domain-specific slowing), or by different factors in different tasks (task-specific slowing). Whatever the context, the Brinley slope is taken as a measure of the difference in the rate of information processing between older and young subjects, and this rate difference is taken to be responsible for the differences in performance between older and young subjects. Our principal point is that any slowing hypothesis is inadequate unless it is an integral consequence of a complete model of processing for whatever task is at issue.

Besides being consistent with a wide variety of theoretical frameworks, an equally important reason that Brinley functions are not diagnostic is that they ignore the necessity of explaining all aspects of the experimental data, correct and error RTs, their distributions, and accuracy rates. Brinley functions only address mean RTs for correct responses (but see G. A. Smith & Brewer, 1995), and so they cannot provide sufficient constraints on theory. Moreover, basing conclusions on only selected aspects of the data, or on theories derived from only those selected aspects, means that the theories will almost certainly make incorrect predictions about the other aspect of the data.

Ratcliff et al. (2001, 2003) and Thapar et al. (2003) illustrated the application to aging research of a model that both accounts for the full range of RT data and allows the various components of processing to be separated. Ratcliff et al. and Thapar et al. have demonstrated the benefits of this approach with three different paradigms.

In the first (Ratcliff et al., 2001), a pair of signal detection–like tasks was used. In one, subjects were asked to judge whether the number of asterisks displayed in a 10 × 10 array was large or small, and in the other, they were asked to judge whether the separation of two dots was large or small. The subjects were given probabilistic feedback: For a large number of asterisks or a large separation, most (but not all) of the time, they were told that “large” was the correct response. Similarly, for a small number of asterisks or a small separation, most (but not all) of the time, they were told that “small” was the correct response. For stimuli in the middle of the range, the probabilities of “large” versus “small” feedback varied; for each stimulus, it was more likely than not to be paired with the appropriate feedback, but it also frequently received inappropriate feedback. Instructions were alternated between blocks of trials, either emphasizing speed or emphasizing accuracy. For all the experimental conditions, the diffusion model gave a good account of all the data: mean RTs, accuracy rates, the shapes of the RT distributions, and the relation between correct and error RTs.

For two-choice tasks like these, the diffusion model separates processing into components: For the decision process, information from a stimulus is accumulated from a starting point toward one or the other of two response boundaries. When the amount of evidence reaches one of the boundaries, a response is initiated. Drift rate is the parameter that captures the rate of accumulation of information, and the distances of the boundaries from the starting point determine how much information must be accumulated before a response is initiated. Components of RT that are outside the decision process (e.g., encoding, response execution) are summarized into another parameter of the model. All of these—the drift rates for the different experimental conditions, the boundary positions, the starting point, and the nondecision component—are assumed to vary in their values across trials.

In the signal detection tasks studied by Ratcliff et al. (2001), the diffusion model fit the data well. Drift rate varied among the conditions, as would be expected (a smaller value of drift rate for more difficult discriminations), but it did not differ significantly between the older and young subjects. According to the model, this means that the quality of the information extracted from the stimuli was the same for the older as for the young subjects. All the subjects adopted more conservative decision criteria (i.e., set their boundaries farther apart) with accuracy instructions than with speed instructions, but the older subjects were more conservative overall. The older subjects were also slower in the nondecision component of RT by a modest amount, about 50 msec (this is similar to the separation between peripheral and central components proposed by Cerella, 1991, but, in contrast, the diffusion model provides an unambiguous estimate of the nondecision components of processing when it is fit to data; see Ratcliff & Tuerlinckx, 2002). The conclusion, through the model, is that in these tasks, the longer RTs and larger SDs of the older subjects relative to the young can be explained by more conservative decision criteria and slower nondecision components of RT. The information upon which the decisions were based is not different between the older and the young subjects.

The second task examined was a masked letter discrimination task (Thapar et al., 2003; see also Ratcliff & Rouder, 2000). On each trial of the experiment, a single letter was presented from 10 to 40 msec; then it was masked and subjects were asked to decide which of two letters it was. The same two choice letters were used for all the trials of a block, and blocks of trials with speed instructions alternated with blocks of trials with accuracy instruction. Again, the diffusion model fit the data well. Drift rate varied with the difficulty of the experimental conditions, and boundary positions were further apart with accuracy instructions than with speed instructions. Just as with the signal detection tasks, the older subjects adopted more conservative decision criteria than the young subjects and the nondecision component of RT was larger for them by about the same modest 50 to 70 msec. However, unlike the signal detection tasks, in this experiment, the quality of the information extracted from the stimuli was not as good for the older subjects as for the young; drift rates were considerably lower for the older subjects.

The third task examined was brightness discrimination (Ratcliff et al., 2003). The stimuli were patches of black and white pixels, and they varied in their proportions of white to black (.525, .575, and .65 white pixels and .525, .575, and .65 black pixels). The patches were masked after 50, 100, or 150 msec. Again, blocks of trials alternated between speed and accuracy instructions. Here, as with the signal detection tasks, the older subjects’ drift rates did not differ significantly from the young subjects’, although the older subjects still adopted more conservative decision criteria (for the speed but not the accuracy instructions) and they were still about 50 msec slower in the nondecision component of RT.

The results for two of the tasks just described, letter discrimination and brightness discrimination with masked stimuli, match the perceptual literature extremely well. According to the diffusion model, older subjects are less able than young subjects to extract information from high spatial frequency stimuli (letters), but they are about equal to young subjects for low spatial frequency stimuli (pixel patches); these differences are reflected in drift rates in the diffusion model. In the perceptual literature, studies have shown declining contrast sensitivity with age for medium and high spatial frequencies but not for low spatial frequencies (Owsley, Sekuler, & Siemsen, 1983), and also decreasing letter identification accuracy with age (Coyne, 1981; Fozard, 1990; Spear, 1993). The drift rates extracted from fits to the data match the results from the perceptual literature.

Both the letter discrimination and brightness discrimination tasks show slopes of Brinley functions greater than 1 in the speed conditions, which match results usually obtained in the Brinley plot literature. In the diffusion model, this is explained by criteria differences in the brightness discrimination task and by both drift rate and criteria differences in letter discrimination. Thus the diffusion model provides an explanation that relates patterns of data in accuracy and RT that were previously evaluated separately.

The conclusion to be drawn from these studies is that age effects cannot be understood simply as slowing of the cognitive processes involved in some task. Rather, components of processing must be examined separately from each other, and when that is done, it appears that some processes (e.g., extracting information from letters presented very quickly) suffer with aging and some (e.g., extracting information about the brightness of pixel displays) do not. Older subjects tend to be more conservative in that they try to avoid making errors (more so in some conditions of some tasks than in other conditions and tasks), and they tend to be slower in at least some nondecision components of processing.

In attributing a part of the RT difference between older and young subjects in their studies to different settings of decision criteria, Ratcliff et al. counter Myerson et al.’s (2003, p. 234) claim that “age differences in time–accuracy tradeoffs have been extensively researched and found wanting as a general explanation for age differences in RTs.” However, applications of the diffusion model show that in some paradigms, differences in speed–accuracy criterion settings are wholly responsible for Brinley function slopes greater than 1 (Ratcliff et al., 2001, 2003). In other paradigms (Thapar et al., 2003), the quality of evidence extracted from the stimulus is lower for older subjects than for young subjects and this, along with more conservative criterion settings in older subjects, produces slopes of Brinley functions greater than 1. Thus, a claim that speed–accuracy criterion settings are not a general explanation of age differences is an oversimplification.

The applications of the diffusion model indicate that there is no single factor that can explain the effects of aging on RT within a single paradigm or across paradigms, at least not for the kinds of paradigms for which the diffusion model is suited—namely, those in which two-choice decisions are reasonably fast and likely made on the basis of a single decision process. For other tasks that produce much longer RTs, models need to be applied and evaluated (e.g., ACT–R, Anderson & Lebiere, 1998; EPIC, Meyer, Glass, Mueller, Seymour, & Kieras, 2001). Interpreting the effects of aging through the diffusion model shows that there are some aging deficits that are common across tasks and others that differ among tasks, and we would expect this also to be the case in tasks for which the decision process is more complex.

CONCLUSION

In the aggregate, we believe that Myerson et al.’s (2003) comments emphasize terminological points at the expense of the more important and central theoretical point of our original article. The empirical patterns exhibited by Brinley functions provide minimal constraint, at best, on any theoretical account of age differences in processing. Brinley functions can be interpreted as showing slowing, but only within a limited range of processing models, serial models, and some parallel models. In order to provide a sufficient account of cognitive processes, models have to explain not only the mean RTs of Brinley functions but also the full distributions of correct and error RTs and accuracy values. Unfortunately, the slowing interpretations usually offered for Brinley function results are rarely accompanied by either a full account of the data or a defense of the slow processing assumption over alternative possibilities. Currently, in the cognitive research domain, the consensus is that elementary processes like retrieval from memory, lexical decision, perceptual discriminations, stimulus identification, and the like involve global accumulation of evidence in sequential sampling processes or highly parallel processes, not serial ones.

In a Brinley function, older subjects’ mean RTs for each condition in an experiment are plotted against young subjects’ mean RTs for the same conditions. The older subjects’ condition means are quantile points from their distribution of possible condition means, and young subjects’ condition means are points from their distribution of possible means. The means are ordered across the range of the distributions by the difficulty of the experimental conditions. From this analysis, as discussed in Ratcliff et al. (2000) and summarized in Table 1, several findings fall out. First, the Brinley function is linear if the distributions of mean RTs for older and young subjects across conditions have the same shape. This answers one of Myerson et al.’s (2003, p. 229) criticisms of our position: “all of which simply begs the question of why there is an orderly, linear relationship between condition means in the first place.” It also allows an understanding of why Brinley functions can be linear when the function relating mean RT and the independent variable is not linear (unlike the examples presented in Myerson et al.’s, 2003, meta-analysis).

Second, if the mean RT across conditions for older subjects is larger than that for young subjects, and the spread in the distribution of condition means is greater for older subjects than young subjects, then the equation for the relationship between quantiles for older and young subjects guarantees that the intercept of the Brinley function is negative and that the slope is greater than 1. Third, in addition, if there is variability across experiments in the means and SDs, the expressions for the slope and intercept of the Brinley function guarantee that there is a negative correlation between the slopes and intercepts.

Fourth, and perhaps most important, because a Brinley function is simply a plot of quantiles against quantiles, it carries no theoretical commitment other than that a theory provides a greater spread of older subjects’ means relative to young subjects’ means. The function does not imply slowing in some or all processes with age, nor does it allow one to choose one or another current model of cognitive processing over others; most current models can produce greater spreads of means for older than young subjects, and they can do so in multiple ways.

We also reviewed applications of the diffusion model to the effects of aging and showed that the effects vary across tasks. In all tasks, there was a modest decrement for older subjects relative to young in the nondecision component of processing (e.g., 40–80 msec), and in most tasks, they set more conservative decision criteria. For one task, there was a decrement in the quality of the information older subjects derive from the stimuli, relative to young subjects, but in two other tasks there was not.

The key to the diffusion model’s ability to separate the effects of age according to components of cognitive processing is that the model provides a good account of all the dependent variables for the data: correct and error RTs and their distributions and accuracy values. It is quite likely that other competing sequential sampling models (e.g., Ratcliff & Smith, 2004) can provide similar interpretations. Competing views in aging research are inadequate if they account for only a fraction of the experimental data. Given the diffusion model’s success in fitting the data, and the analysis of aging effects it provides, the conclusion is that there is not single general, domain-specific, or task-specific factor that underlies the effects of aging on RT. Instead, the multiple components of processing can vary across tasks in whether they are always, usually, or only sometimes affected by aging. Thus the search for a simple model-independent account of the effects of aging on speed of processing is futile. A model-based account will be more complicated, but it will be more comprehensive in its coverage of data and paradigms.

APPENDIX

The problem of fitting linear regression models in the presence of measurement error has rarely been mentioned in the experimental psychology literature (but see Fisk et al., 1992; Myerson et al., 1994). Measurement error occurs when the x values are not fixed values, but are the sum of the true value and an additive error. When there is error in the x values, standard linear regression underestimates the true slope of the regression line. This situation occurs in several domains in psychology, in particular in Brinley functions (the focus here) and in estimating the slope of the z-ROC function in signal detection theory when ROC functions are obtained not from confidence ratings (see Ogilvie & Creelman, 1968), but by manipulating payoffs of probability of the two responses in a yes/no task (see Ratcliff, Sheu, & Gronlund, 1992).

The question then is: When there is measurement error in both x and y, what is the best estimator of the true slope: linear regression, the ratio of the SDs, or some other method (perhaps a correction for measurement error in x values)? It should be stressed that the only aim of the application of linear regression is to estimate the true slope of the function (i.e., linear regression cannot be used to determine anything about the linearity of the fit). Ratcliff et al. (2000, Appendix), using simulated data typical of those found in Brinley functions, provided several Monte Carlo studies of linear regression with measurement error in both x and y, and showed that the ratio of SDs (SD_y/SD_x) is closer to the true value of the slope than is the slope computed from linear regression.

Further examination of the literature on linear regression with measurement error shows that there has been considerable research and that several recommended solutions have been presented, differing in what kinds of information are available from the data. Chen and Van Ness (1999) distinguished between three models that differ in the assumptions about the x values. If the true x values are derived from a single distribution with one mean and a common SD, this is termed the “structural model”; if the x values are different unknown constants, this is termed the “functional model”; if the x values are derived from different unknown constants but with a common SD, this is termed the “ultrastructural model.” The latter model is the one that is most similar to the situation for Brinley functions. Chen and Van Ness then presented maximum likelihood solutions that differ in what information is known. For example, different maximum likelihood estimators are available if the SD of the individual x values is known versus the case in which the ratio in the SDs of the individual x and y values is known. In practice, because mean RT is computed over subjects and replications, the standard error in each x value and each y value is known so that the latter case most closely resembles what is known for Brinley functions. However, although these maximum likelihood estimators have optimal asymptotic properties, Draper and Smith (1998) suggested that, in most applications, the numbers of observations are too small for asymptotic behavior to be obtained.

Draper and Smith (1998) recommended the product of the mean of the slope from regressing y against x and the inverse of the slope of regressing x against y as an estimator of the slope when the number of observations is small. They pointed out that is identical to SD_y/SD_x, the ratio of SDs (see Ratcliff et al., 2000). This estimator is also optimal in some situations (see Chen & Van Ness, 1999, p. 21).

Another method that appears to be well suited for finding the slope and intercept of Brinley functions and z-ROC functions is “generalized least squares,” which can be shown to be the same as orthogonal regression (Chen & Van Ness, 1999, p. 83). In this method, the SD in each of the x and y values is required and a chi square value, ∑(y_i − a − bx_i)²/(σ _y² + b²σ_x² is minimized.

Thus, when there is error in x as well as error in y, the true slope is better estimated either by the ratio of SDs or by generalized least squares rather than by standard linear regression. Which of these methods is better for particular data sets would be best examined by Monte Carlo studies where simulated data used in the Monte Carlo studies matched those in experimental data. For example, for known slope and intercept, similar ranges and SDs in the x values and y values would be used to generate many sets of simulated data, the two methods would be used to estimate slopes and intercepts, and the ability of the methods to recover the true slopes and intercepts, including biases and variability in the estimates across simulations, could be determined.

Standard linear regression in most introductory textbooks assumes that for each x value there is one y value. However, most often when reaction time measures are used, means across many observations serve as the experimental data, which means that standard errors can be computed for the means. This means that the quality of the straight line fit can be assessed by determining whether the standard error of measurement in the y values matches the standard errors in the data points. (Note that the usual correlation coefficient does not assess goodness of fit; this can be seen by drawing any straight line at all that misses the data and noting that the correlation coefficient is the same; see Fisk & Fisher, 1994.) The generalized least squares method presented in Press et al. (1992) uses estimated standard errors in the mean RTs for both older and young subjects and provides an assessment of the quality of the fit based on the chi square function minimized.