Material Properties of the Human Lumbar Facet Joint Capsule

Abstract

The human facet joint capsule is one of the structures in the lumbar spine that constrains motions of vertebrae during global spine loading (e.g., physiological flexion). Computational models of the spine have not been able to include accurate nonlinear and viscoelastic material properties, as they have not previously been measured. Capsules were tested using a uniaxial ramp-hold protocol or a haversine displacement protocol using a commercially available materials testing device. Plane strain was measured optically. Capsules were tested both parallel and perpendicular to the dominant orientation of the collagen fibers in the capsules. Viscoelastic material properties were determined. Parallel to the dominant orientation of the collagen fibers, the complex modulus of elasticity was E* = 1.63MPa, with a storage modulus of E′ = 1.25MPa and a loss modulus of: E″ = 0.39MPa. The mean stress relaxation rates for static and dynamic loading were best fit with first-order polynomials: B (ɛ) = 0.1110 ɛ − 0.0733 and B (ɛ) = −0.1249ɛ 11794-8181 +0.0190, respectively. Perpendicular to the collagen fiber orientation, the viscous and elastic secant moduli were 1.81 and 1.00 MPa, respectively. The mean stress relaxation rate for static loading was best fit with a first-order polynomial: B (ɛ) = − 0.04ɛ − 0.06. Capsule strength parallel and perpendicular to collagen fiber orientation was 1.90 and 0.95 MPa, respectively, and extensibility was 0.65 and 0.60, respectively. Poisson’s ratio parallel and perpendicular to fiber orientation was 0.299 and 0.488, respectively. The elasticity moduli were nonlinear and anisotropic, and capsule strength was larger aligned parallel to the collagen fibers. The phase lag between stress and strain increased with haversine frequency, but the storage modulus remained large relative to the complex modulus. The stress relaxation rate was strain dependent parallel to the collagen fibers, but was strain independent perpendicularly.

Introduction

The facet joint capsule is one of the structures in the lumbar spine that constrains motions of vertebrae during global spine loading (e.g., physiological flexion). It is innervated with mechanically sensitive neurons and is a known source of low back pain [1–6]. It has been suggested that the mechanoreceptors in the facet joint capsule could function proprioceptively [7], similar to afferents from other joint capsules (e.g., knee or shoulder). An approach to studying the lumbar spine and its components that contribute to developing low back pain (LBP) and proprioception, is to develop computational models [e.g., finite element models (FEM)]. These models can be used to predict how the spine and its innervated structures (e.g., the facet joint capsule) would respond to various loading paradigms. However, existing FEMs [8,9] of the human lumbar spine have not used realistic geometry and material properties of the lumbar facet joint capsule (e.g., modeling it as one or more uniaxial springs rather than as an anisotropic, viscoelastic three-dimensional material). Hence, they have not been able to model stress or strain distribution within the lumbar facet capsule during loading.

Despite attempts by previous studies to quantify the load-deformation properties of the human lumbar facet joint capsule [10], a comprehensive analysis of the mechanical and viscoelastic properties of this ligament has not yet been performed. Previous load-deformation studies yielded stiffness values for the lumbar facet capsular ligament, but did not address whether it exhibited nonlinear (exponential or power) stress-strain relationships seen in other ligaments [11]. As it is the reorientation of the fibers that defines the ligament’s extensibility and produces the characteristic nonlinear stress-strain curves [12], it is important to consider the properties of the ligament relative to the orientation of the collagen fibers. Quantification of the relative contribution of the viscous and elastic components in the ligaments is also essential in order to accurately model the stress response of the ligament in more complex motions, which could depend on loading rate or result in stress relaxation-viscoelastic properties observed in other ligaments [13,14].

The aim of this project was to elucidate the static, dynamic, and stress relaxation properties of the facet joint capsule, which could then be incorporated into FEMs of the lumbar spine. In human lumbar facet capsules, collagen fibers have a dominant direction of medial to lateral, with respect to the long axis of the spine [15]. Therefore, capsule specimens were isolated from lumbar spines, and tested parallel and perpendicular to the principal orientation of their collagen fibers.

Materials and Methods

Specimen Preparation.

Intact lumbar spines (n=8; 2 females/6 males; mean age 59±5.3 years), consisting of vertebral level T₁₂ through the sacrum, were procured using an institutionally approved protocol. The protocol specified that all spines come from adults (21–80) who had no history of spine pathology (e.g., fractures, vertebral or disk disease, primary cancer or metastases, arthritis, or degenerative joint disease) and had no spinal deformities (e.g., scoliosis>10, spondylolisthesis, congenital aplasia, etc.), any of which might have altered the biomechanics of the spine leading to altered tissue material properties [16]. All spines had been obtained within 24 h post-mortem and were frozen at −80°C. Anterior-posterior and lateral radiographs were taken of each specimen and assessed by an orthopedist to verify that the spines met the protocol.

To obtain capsule specimens for testing, the spine was thawed overnight and all soft tissues overlying the capsules were carefully dissected free so as not to damage the capsules. An operating microscope was used to facilitate the dissection of superficial fascia adherent to the capsule, as well as to dissect tendons of the multifidi muscles that inserted along the lateral borders of the posterior capsule. The respective laminae of the superior and inferior facets were transected to free the intact joint and capsule from the spine (Fig. 1). Specimens that were not going to be immediately tested were wrapped in gauze soaked in phosphate buffered saline (PBS, pH 7.4), sealed in plastic bags, and refrozen at −80°C. Previously frozen specimens were thawed and brought to room temperature before testing. Care was taken in the planning of experiments to ensure that all specimens were kept well below five freeze-thaw cycles, after which the tissue’s biomechanical properties would have been compromised [17].

Fig. 1.

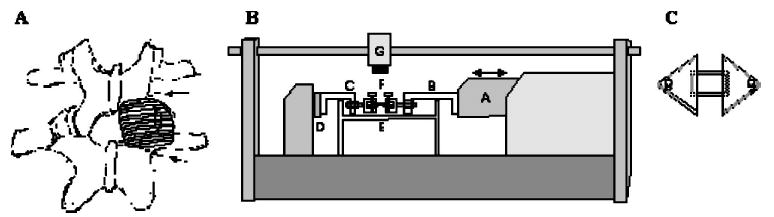
(A) Sketch of two lumbar vertebrae and their left and right facet joints. On the right joint, the posterior aspect of the facet capsule has been drawn. The two dotted lines indicate the locations of the cuts through the laminae of the inferior and superior facet processes of the respective vertebrae to enable producing bone-capsule-bone specimens suitable for testing parallel to the collagen fibers. (B) Side-view drawing of the materials testing apparatus (Tytron 250, MTS, Inc. fitted with a tissue bath. Actuator (A) is fitted with over-the-bath extension arms (B and C) in series with a force transducer (D). The facet capsule (E) is coupled to the extension arms by custom made pin-clamps (F) that attach to the respective trimmed facet processes of the joint. A CCD camera (G) is mounted above the specimen to facilitate optical measurements of strain. (C) Capsules tested perpendicular to the orientation of the collagen fibers were cut free from the facets and mounted acrylic plates glued to both the superficial and deep surfaces. The acrylic mounting plates attached to the locking pin in the pin clamps.

To produce a flat, rectangular capsule geometry suitable for uniaxial testing, the sides of the capsules were cut and trimmed, allowing the facet joint to be opened flat. The geometry of the specimens was controlled to produce specimens with the collagen fiber orientation aligned either parallel or perpendicular to the axis of in-vitro uniaxial loading (henceforth referred to as “parallel” and “perpendicular” capsules, respectively). For parallel capsules, facets were also trimmed to create bone geometry conducive for coupling to the pin clamps of the uniaxial testing apparatus (Fig. 1). Perpendicular capsules were cut free of the facets, and their ends were glued to acrylic mounting plates adhered to both the superficial and deep surface of the capsule. The acrylic mounting plates had holes in the ends, through which the locking pins were placed (Fig. 1).

Width, thickness, and length of the rectangular capsules were measured while the capsules were in the loading apparatus with the preload applied (see Ramp Loading Protocol section). Capsules were measured using a handheld digital micrometer (resolution of 0.01 mm) visualized with an operating microscope at 6× magnification (model OPML, Carl Zeiss, Inc., Thornwood, NY). The length of a capsule, used to define limits of the uniaxial loading, was determined for parallel capsules by measuring the most proximal and distal insertions of the capsule on each side of the respective facets. Visually, most of the insertions occurred proximally, hence, the measure of the endpoint of the capsule was taken as one-third the distance from the most proximal to the most distal insertion, an arbitrary but reasonable estimate. The length of perpendicular capsules was measured as the distances between the edges of the two acrylic mounting plates.

Loading Apparatus.

During testing, specimens were kept in a PBS bath (pH 7.4) at room temperature. The loading apparatus consisted of a commercial materials testing device (model Tytron 250, MTS, Inc., Minn., MN; resolution of 1 μm; repeatability of 5 μm), oriented horizontally, integrated with a custom-made tissue bath (Fig. 1). Force ranges measured using standard transducers were 0.001 to 250 N with a resolution of 1 mN. Data acquisition rates were dependent on the loading rate of the trial (loading rate: sampling rate; 1% strain/s. 6 Hz; 5% strain/s 15 Hz; 10% and 15% strain/s; 30 Hz; 0.2 Hz; 20 Hz; 1 Hz; 60 Hz; 2 Hz; 120 Hz).

Specimens were clamped to the testing apparatus by inserting locking pins in holes drilled through the midpoints of each of the respective bones (for parallel specimens) or acrylic plates (for perpendicular specimens) (Fig. 1). The pin clamps could also be rotated about the loading axis. Hence, the combinations of self-alignment around the pins during loading and manually adjusting the rotary angle of the clamps were used to insure that the specimens were loaded uniaxially and minimizing any planar or rotational shearing.

Optical Strain Measurements.

To facilitate Eulerian plane strain measurements, silicone carbide particles were sprinkled randomly onto the tissue and illuminated with a fiber optic light source to create a stochastic light intensity pattern over the tissue. The light intensity pattern was tracked during loading by recording sequential frames using a CCD camera (model TM-6710CL, Pulnix America, Sunnyvale, CA) mounted over the actuator (Fig. 1). Eulerian plane strains were determined from the images using custom written software [18], which utilized the image correlation function in matlab, v. 6.1 (MathWorks, Inc., Natick, MA), in a method similar to that employed by computer-aided speckle interferometry [19]. The software allowed the user to select a region of interest (ROI) within the images, which was further subdivided into a user-specified (m×n) array of subimages, typically 4×4 (Fig. 2). Each subimage was located in subsequent frames in the series by cross-correlating it with the subsequent image. The new position of the subimage was determined as the region with the highest normalized correlation coefficient. In this manner, the u and ν displacement components in the x and y directions, respectively, of each subimage were calculated throughout a loading cycle (Appendix). Plane strains (ɛ_XX, ɛ_{Y Y}, ɛ_XY) were calculated for each subimage in the array using an FEM approach [20–22]. Principal strains (ɛ1 and ɛ2) and Poisson’s ratio (ν = − ɛ_{Y Y} /ɛ_XX) were computed from the plane strains for each element. Data (strains and ν) for all elements were averaged to yield one mean capsular value.

Fig. 2.

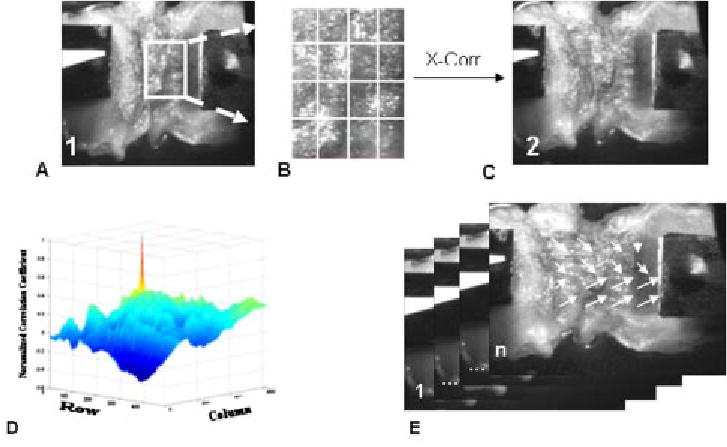
Eulerian plane strain was calculated from a sequence of images in the following manner: User defined a ROI in the first frame of the sequence taken at neutral position (A) ROI was subdivided into (m×n) array, typically 4×4, of elements (B). In custom software utilizing the image correlation function in matlab v 6.5 (MathWorks, Inc), each element of the ROI is cross-correlated (X-Corr.) with the subsequent frame (C). The element’s new position is the location of the highest normalized correlation coefficient (D). In this manner, each element’s u and v displacement vectors, in the x and y directions respectively, were calculated throughout the sequence (1 to n) of images (E). Eulerian plane strain was calculated from the displacement vectors.

Images were matched to their corresponding force-time value by tracking grip displacement in the image. The actuator grip displacement curve determined using image correlation was then iteratively plotted against the actuator displacement data saved in the MTS machine data file by shifting the alignment of the displacement curves and computing the R² of the fit. Proper alignment of the data was taken as the alignment with the highest R² value, as perfectly aligned data would have an R² of 1.0.

Ramp Loading Protocol.

To achieve a common resting length, specimens were stretched until a minimum preload of 0.1 N was obtained. Specimens (parallel: n=25: 5 capsules per joint level; perpendicular: n=10) were then preconditioned to facilitate achievement of reproducible load-displacement curves [23]. Preconditioning consisted of six cycles of ramping up at a rate of 15% strain/s to a strain of 50% of the measured length (i.e., the ramp duration was 3.33 s) that was held for 300 s, ramping down at a rate of 15% strain/s to 0 strain, with a subsequent interramp interval of 3 min. Six cycles were sufficient to reduce the differences between subsequent load-displacement curves to less than 5%, and were on the same order (number and duration) as has been used for other spinal ligaments [24]. The 3-min interval was selected based on published experiments testing the biomechanics of intact lumbar spine specimens [21,22] and is on the same order of magnitude as has been used in other soft tissue experiments [25,26].

Each experimental trial consisted of a ramp displacement to a specified tensile strain (10%, 20%, 30%, 40%, or 50%), which was then held constant for 300 s, followed by a ramp unload (Fig. 3). Preliminary ramp displacement trials were performed sequentially at each of four rates (1%, 5%, 10%, or 15% strain/s) for nine specimens (data not shown). As no significant difference in modulus was found between loading rates at a given tensile strain (p = 0.586, two-factor repeated measures ANOVA (factors: strain rate and strain magnitude); sigmastat v. 2.03 was used for this and all other statistical comparisons), all subsequent specimens were tested only using a loading rate of 15% strain/s. Images were acquired during the ramp phase of the loading cycle and were again acquired during the last 10 s of the hold phase.

Fig. 3.

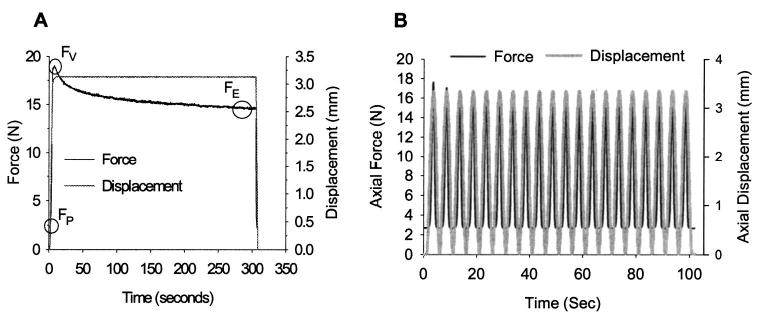
(A) Representative force and displacement data for a single displacement controlled ramp-hold trial to 50% ramp strain. The capsule was preloaded (F_P) to eliminate slack. The capsule was stretched, and the “viscous” uniaxial engineering stress was calculated as (F_V− F_P/A, where A was the measured cross-sectional area. The “elastic” stress ((F_E− F_P)/A) was calculated as the average from the last 5 s of a 300 s hold at peak displacement. (B) Representative force and displacement data for a single displacement controlled dynamic trial at 0.2 Hz to 50% strain. Specimens were dynamically loaded using twenty haversine cycles to 10%–50% strain in 10% increments at 0.2, 1, and 2 Hz. Uniaxial engineering stress was calculated from the mean load from the peaks of the last ten cycles.

Dynamic Loading Protocol.

A subset of the parallel specimens (n = 15) were also tested under dynamic conditions. Specimens were first preconditioned using twenty cycles of loading to 50% haversine strain, i.e., the sine wave oscillated from 0% to 50% strain with a midpoint at 25% strain, at 0.2 Hz. After preconditioning, specimens were tested dynamically using 20 cycles to a specified haversine strain (10%, 20%, 30%, 40%, or 50%), at 0.2, 1.0, and 2.0 Hz (Fig. 2). These frequencies are contained in the range of frequencies employed in the work-related phenomena of whole-body vibration suspected of causing LBP [27,28]. Images were acquired continuously during the cycles.

Extensibility.

After the nondestructive testing was completed, failure strength and extensibility were determined by increasing the strain above 50% in 1% strain increments for 300-s durations. Failure was defined as a decrease in stress with increasing displacement. Differences between parallel and perpendicular failure stress and extensibility were each assessed using a Mann-Whitney rank sum test (α = 0.05).

Data Analysis

Ramp Loading Analysis.

Uniaxial engineering stress was determined from the measured tensile forces and cross-sectional areas of the capsules. Two stress calculations were performed for each ramp loading trial and were designated as the viscous stress (σ_ν) and the elastic stress (σ_E). This nomenclature is analogous to that previously described by Sangeevi [29] and Yahia et al. [24], where for a viscoelastic material undergoing constant deformation, the elastic component is what is left after the viscous component has been exhausted. The viscous stress calculation was made at the peak force, which always occurred at the end of the ramp-up displacement, and the elastic stress was taken from the average of force values during the last 5 s of the 300-s constant displacement, when the capsule had “relaxed” and was in a relative equilibrium (Fig. 3).

Stress-strain relationships (viscous and elastic) were regressed using a linear, exponential (σ (MPa) = A exp^Kɛ) and power function (σ(MPa) = Aɛ^K). To determine the appropriate function, data were first regressed with a linear fit and the correlation coefficient computed. Data were then plotted on a semi-log and a log-log plot, to linearize exponential and power functions, respectively. Regression lines (σ(MPa) = Kɛ + ln[A]) were fit through the linearized data sets and the correlation coefficients computed. The fit with the highest correlation coefficient was used to describe the data set. Differences in the stress-strain relationship across joint levels were assessed using a comparison of linear regression lines (CLRL) [30].

A secant modulus, which passed through (0,0) and the point of interest, was computed at each ramp increment for both the viscous and elastic data (E_V =σ_V /ɛ1 and E_E = σ_E /ɛ1, respectively) to allow for direct comparison between moduli (E_V, E_E, and dynamic) using the same calculation method. Because it includes the nonlinear toe region of the stress-strain curve, E_V computed in this fashion would be smaller than a tangent modulus computed from the linear region of the stress-strain curve. Differences between the E_V and E_E were compared using a Wilcoxon signed rank test (α = 0.05) at each ramp strain increment.

To facilitate comparison to the literature, the capsule stiffness and the tangent modulus were also computed. Stiffness was computed as the slope of the linear region of the load-deformation data for the 50% ramp strain trials only. Differences in stiffness parallel and perpendicular to the collagen fibers were assessed using a Mann-Whitney rank sum test (α = 0.05). The tangent modulus was computed as the slope of the linear portion of the stress-strain curve for all ramp-hold trials (10%–50%). Differences in the tangent modulus resulting from load orientation, i.e., parallel versus perpendicular to the collagen fibers, were determined using a two-factor ANOVA with post-hoc Tukey test (factors: load orientation and ramp strain). The slope of the linear portion of the force-displacement and stress-strain curves was taken from the tenth data point collected (corresponding to 5% strain with a 30 Hz data collection rate) to five points before the max force/stress value, and the linearity of this region was confirmed visually.

Dynamic Loading Analysis.

Specimens typically reached an equilibrium state within the first 10 of the 20 cycles; therefore, only the last ten cycles were analyzed for stress-strain phase differences. Viscoelastic materials exhibit a phase angle (δ), ranging from 0 deg to 90 deg, between stress and strain dynamic peaks. To account for the phase angle, a complex modulus (E*), analogous to E_V from the ramp-hold trials, can be defined as

$$E*=E^{\prime }+E^{″},$$ (1)

where E′ is the storage modulus, which represents the energy stored within the sample and is similar to E_E , Eq. (2):

$$E^{\prime }=\frac{{\sigma }_0}{{\varepsilon }_0}\text{cos}\delta$$ (2)

and E″ is the loss modulus, which represents the energy dissipated per cycle and is similar to (E_V − E_E):

$$E^{″}=\frac{{\sigma }_0}{{\varepsilon }_0}\text{sin\hspace{0.28em}}\delta$$ (3)

The stress and strain data were aligned using the method described in the Optical Strain Measurements section and the phase angles of each were determined using the “Extract Single Tone Information” function in labview v. 7.1 (National Instruments, Austin, TX). Differences in the phase lag, storage, loss, and complex moduli occurring as a result of cycling frequency or haversine amplitude were assessed using a two-factor ANOVA with post-hoc Tukey test (a = 0.05; factors: frequency and amplitude).

Stress Relaxation.

Stress relaxation curves were analyzed for differences in time-dependent behavior as a function of strain. Strain-independent relaxation curves would have the same slope, or relaxation rate, as predicted by the quasi-linear viscoelasticity model of Fung [31]. As shown by Provenzano et al. [32], a strain-dependent relaxation function can be defined as a nonseparable power law (Eq. (4)) for nonlinear viscoelastic materials

$$\sigma (\varepsilon ,t)={\sigma }_V{t}^{B(\varepsilon )}$$ (4)

where σ_V can either be a single value or a function describing peak stress and the function B(ɛ) describes the strain-dependent rate of stress relaxation and can be defined by a polynomial fit to the range of relaxation rates.

For ramp-hold trials, isochronal load data was taken from the peak load for each specimen and was normalized to the peak value (i.e., unity at σ_V). For dynamic trials, load and time values were taken at the peak of each of the 20 haversine cycles and the load was normalized to the first peak value. The load-time relationship was then plotted on a log-log scale and linearly regressed [32]. The slope of the regression line is the relaxation rate. The relaxation rates were then plotted as a function of peak strain and the function B(ɛ) was determined for each data set. The effect of peak strain on the relaxation rate was analyzed for statistical significance for parallel ramp-hold data (a=0.05, repeated measures ANOVA with Tukey), perpendicular ramp-hold data (a=0.05, Friedman’s test with Tukey) and dynamic data (a=0.05, two-factor ANOVA with Tukey (factors: frequency and ramp strain)).

Results

Thirty-five capsules were obtained from eight human lumbar spine specimens. Two of the spine specimens were only intact from L₃ to L₅ . Another two specimens had damage done to the L₅-S₁ joint during harvesting. The other capsules were either damaged during the excision process, excluded from the perpendicular trials due to edge effects from the glue used to adhere the specimens to the acrylic mounting plates, or were too small in length (between facets) to allow for a suitable viewing area for the image correlation. During testing, no evidence was seen of damage when loading to 50% strain or of drying due to air exposure on the superficial surface. Parallel specimens had an average length of 6.08±2.58 mm, width of 11.59±2.87 mm, and thickness of 1.88±0.94 mm. Perpendicular specimens had an average length of 6.83±1.45 mm, width of 7.11±2.45 mm, and thickness of 2.51±1.66 mm.

Image Correlation.

ROI’s were tracked with a high degree of accuracy for all trials. Grips were tracked between subsequent frames with a mean correlation coefficient of R²=0.98 (0.95⩽R²⩾0.99). Alignment of the calculated grip displacement from the images with the MTS actuator displacement reading was also performed with a high degree of accuracy with a mean R² = 0.98 (0.89⩽R²⩾0.99). Elements within the selected ROIs on the capsule surface were tracked through subsequent frames with a mean correlation coefficient of R²=0.96 (0.85⩽R²⩾0.99). Because the specimens were relatively thin, out-of-plane movement, (strain on the z axis) was small and produced minimal error in the calculation of the plane strains (<1%).

Principal angles were large (>10 deg) and varied throughout a loading cycle; therefore, E1 was used for all material property calculations as it was a better representation of total capsular strain. Both plane and principal strains were nonuniform from element to element and varied across the capsule with a mean standard deviation of 13%.

Ramp Loading.

Parallel viscous and elastic stress-strain relationships at all joint levels were exponential in form. No significant differences were determined between the exponential regressions for each joint level in either the viscous or elastic states (CLRL; 0.13⩽p⩽0.59 and 0.06⩽p⩽0.58, respectively). The lowest p-values were associated with comparisons to L_{2 – 3} and were attributed to a larger intercept value at L_{2 – 3} relative to the other levels. For both the viscous and elastic states, data for all joint levels were combined and the exponential stress-strain relationships describing the mean viscous and mean elastic values were determined (Fig. 4; σ_V (MPa) = 0.0034 exp^10.35ɛ1, R² = 0.99; σ_E (MPa) = 0.0030 exp^10.09ɛ1, R² = 0.99).

Fig. 4.

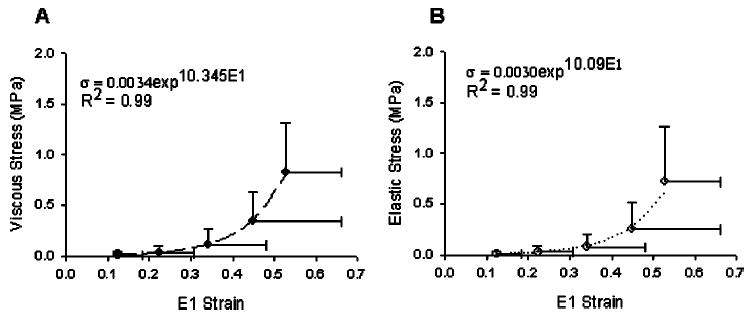
(A) Parallel to the primary axis of the collagen fibers, the mean viscous stress-strain relationship for all joint levels (L_1–2 – L₅-S₁) was exponential in form (regression line shown). The viscous stress was computed as the peak load value that occurred during a ramp-hold trial to a specified uniaxial strain. The peak load always occurred at the end of the ramp up. (B) Parallel to the primary axis of the collagen fibers, the mean elastic stress-strain relationship for all joint levels (L_1–2 – L₅-S₁) was exponential in form (regression line shown). The elastic stress was computed from the average load during the last 5 s of a 300 s hold at incremental ramp strains. Error bars are standard deviations.

Unlike the stress-strain relationship parallel to the collagen fiber orientation, the relationship perpendicular to the fibers was linear in nature from 10%–50% ramp strain (Fig. 5). Due to the small sample size, perpendicular specimens could not be compared for statistical differences among joint levels and are reported as a combination of all joint levels. The mean stress-strain relationship was well correlated in both the viscous and elastic states (σ_ν (MPa) = 2.02ɛ1 − 0.1732, R² = 0.97; σ_E (MPa) = 1.04ɛ1 −0.097, R² = 0.99).

Fig. 5.

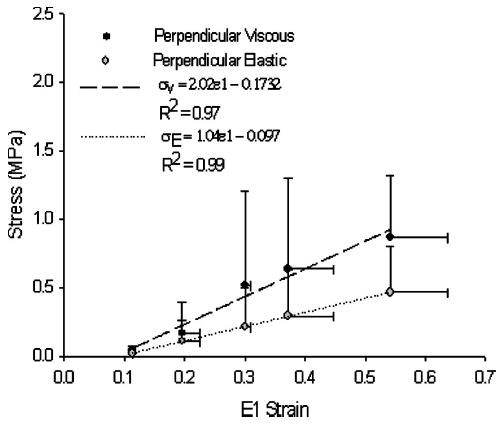
Viscous and elastic stress-strain relationships perpendicular to the collagen fibers were linear in form. Error bars are standard deviations. Mean viscous and elastic data were linearly regressed and fit with coefficients σV = 2.02 ε1 − 0.1732, R 2 = 0.97 and σE = 1.04 ε 1 − 0.097, R 2 = 0.99, respectively.

Parallel to the collagen fibers, E_V was significantly larger than E_E for all ramp strains ( p<0.001, for all comparisons, Table 1), indicating that the specimen had significantly relaxed. Perpendicular to the collagen fibers, E_V was larger than E_E at all ramp strains (Table 1), but statistical significance was not detected (p > 0.05, for all comparisons).

Table 1.

Moduli measured at 10%–50% ramp strain for lumbar facet joint capsules tested parallel (n= 25) and perpendicular (n= 10) to the primary collagen orientation. The tangent modulus (tangent) was computed as the slope of the most linear portion of the engineering stress-first principal strain relationship. The viscous and elastic moduli were calculated as secant moduli from (0,0) to the peak of the ramp when the load was a maximum and to the load 300 s after peak displacement, respectively. Parallel to the collagen fibers, the elastic modulus was significantly smaller than the viscous modulus at all ramp strains (p<0.001, for all comparisons, Wilcoxon signed rank test). Perpendicular to the collagen fibers, the elastic modulus was not significantly different than the viscous modulus at all ramp strains (p>0.125 for all comparisons, Wilcoxon signed rank test.

		Ramp strain
Modulus (MPa)		10%	20%	30%	40%	50%
Parallel	Tangent	0.13±.08	0.40±0.33	1.06±0.73	2.92±1.91	8.08±5.75
	Viscous	0.10±0.09	0.18±0.13	0.33±0.17	0.92±0.49	1.61±0.36
	Elastic	0.10±0.10	0.14±0.11	0.24±0.15	0.73±0.44	1.33±0.49
Perpendicular	Tangent	0.39±0.32	2.51±2.14	3.97±3.66	2.26±1.32	2.76±1.32
	Viscous	0.23±0.20	1.04±0.86	2.57±1.93	2.33±1.19	1.81±0.29
	Elastic	0.12±0.08	0.66±0.57	1.21±0.79	1.23±0.10	1.00±0.27

The tangent modulus was larger parallel to the collagen fibers compared to perpendicularly at 50% grip-to-grip strain (p < 0.001; E_50% (MPa) = 8.08±5.75 and 2.76±1.32, respectively, Table 1). Parallel to the collagen fibers, the tangent modulus increased over the range of strains tested and was similar in magnitude to values previously reported for the cervical spine [33]. Perpendicular to the collagen fibers, the tangent modulus was small at 10% grip-to-grip strain (E_10% (MPa) = 0.39±0.32), but reached a steady state value of approximately 2 MPa from 20%–50% grip-to-grip strain.

The facet joint capsule was significantly stiffer parallel to the collagen fibers compared to perpendicular. The mean stiffness of the capsules parallel to the collagen fibers was 17.95±7.11 N mm⁻¹, which is similar to lumbar joint capsule stiffness previously reported [10,34]. The mean joint capsule stiffness perpendicular to the collagen fibers was 2.29±1.30 N mm⁻¹, which was significantly smaller than the stiffness parallel to the collagen fibers (p<0.001).

Parallel specimens had a smaller Poisson’s ratio compared to perpendicular specimens (0.299±0.15 and 0.488±0.199, respectively), indicating that the perpendicular specimens were more incompressible, exhibiting a smaller volume change, than the parallel specimens.

Stress Relaxation.

The relaxation rate was strain dependent parallel to the collagen fibers, but strain independent perpendicularly. The relaxation rate parallel to the collagen fibers significantly decreased with increasing ramp strain magnitude (rate at % ramp strain versus rate at % ramp strain: p-value; 10%, 20%, and 30% versus 50%: p<0.001; 10% versus 40%: p=0.002; 30% versus 40%: p=0.031; Fig. 6). The mean relaxation rate-strain relationship was best fit with a first-order polynomial (B(ɛ) = 0.1110ɛ1 − 0.0733, R² = 0.87). Perpendicular to the collagen fibers, the relaxation rate was independent of strain magnitude (p = 0.707; Fig. 6). The mean rate data was best fit with a first-order polynomial, in which the strain-dependent coefficient was close to zero and the function was weakly correlated (B(ɛ) = − 0.04ɛ1 − 0.06, R² = 0.34). Relaxation was statistically faster perpendicular to the collagen fibers compared to parallel to the collagen fibers at 40% and 50% ramp strain (p<0.05, Kruskal-Wallis with Dunn’s test).

Fig. 6.

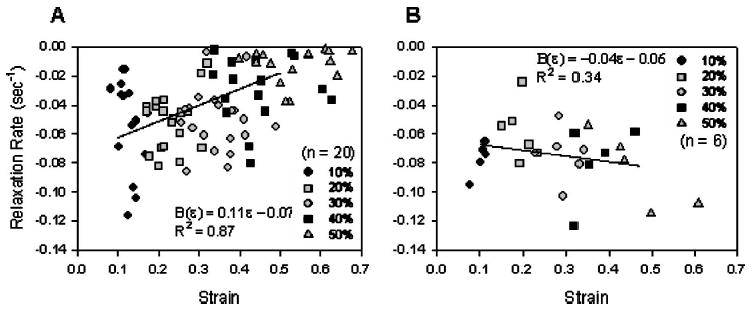
(A) The load relaxation rate parallel to the collagen fibers was dependent upon strain magnitude during ramp-hold trials. The relaxation rate was determined by normalizing relaxation curves to the peak load, then finding the slope of the log (load)-log (time) plot. The relaxation rate significantly decreased with increasing strain magnitude p <0.05 for rate at 10%, 20%, and 30% strain vs rate at 40% and 50% strain, repeated measures ANOVA with Tukey. A strain-dependent relaxation function was defined for mean rate-strain data with coefficients B ( ε) = 0.1110 ɛ − 0.0733, R 2 =0.87. (B) The load relaxation rate perpendicular to the collagen fibers was independent of strain magnitude during ramp-hold trials. A strain-dependent relaxation function was defined for mean rate-strain data with coefficients. B( ε) = −0.04 ɛ − 0.06, R 2 =0.34.

Extensibility.

Parallel specimens had a statistically higher failure stress than did perpendicular specimens (p=0.003). Parallel specimens reached failure at 1.90±0.577 MPa with a mean extensibility of 0.65±0.13. Perpendicular specimens reach failure at 0.951±0.270 MPa with a mean extensibility of 0.60±0.09. There was no difference in extensibility at failure (p=0.517).

Dynamic Loading.

The phase lag between stress and strain was not affected by increases in cycling amplitude (p=0.990), but statistically increased in magnitude with increases in cycling frequency from 0.2 Hz to 2 Hz (p<0.001; Fig. 7). The mean phase lag (combining all ramp strain data) increased from 11.7 ± 9.04 deg at 0.2 Hz to 23.37±9.09 deg at 2 Hz.

Fig. 7.

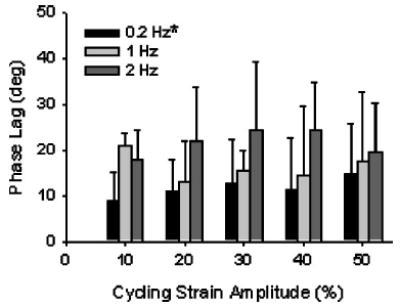
The phase lag (δ) was not affected by increases in cycling amplitude, but did significantly increase with increases in cyclic frequency from 0.2 Hz to 2 Hz (p <0.001, two-factor ANOVA with Tukey). Error bars are standard deviations. * -Statistically different from 2 Hz at all strain amplitudes (p <0.05).

The dynamic moduli (E*, E′, and E″) significantly increased with increasing haversine strain amplitude (p<0.001 for all; Fig. 8). All dynamic moduli were a maximum at 50% strain and were significantly larger than at 10%–40% cycling strain amplitudes (E* and E′: p<0.001; E″: 10%–30%: p<0.001, 40%: p = 0.006). The storage modulus (E′) was also statistically larger at 40% haversine strain than at 10% and 20% (p = 0.007 and p = 0.020, respectively). The dynamic moduli were not significantly affected by increases in cyclic frequency (E*: p=0.294; E′: p = 0.43; E″: p=0.184). Despite the lack of significance, the contribution of the storage modulus to the complex modulus did demonstrate a trend of decreasing with increasing frequency (E′/E*: 0.2 Hz: 85.6±9.4%; 1.0 Hz: 78.48±13.4%; 2.0 Hz: 70.95±14.9%), with a corresponding increase in the contribution of the loss modulus, as expected based on the increase in the phase lag.

Fig. 8.

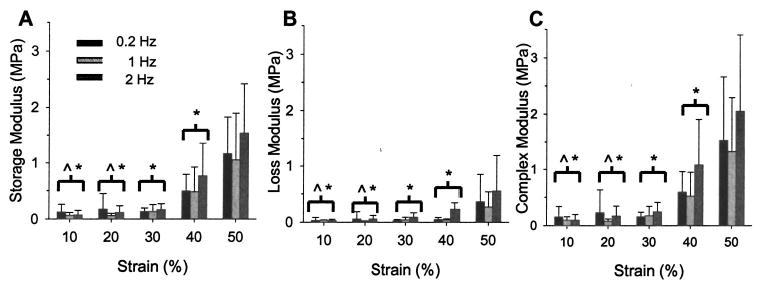
(A) The storage modulus significantly increased as the cycling amplitude increased, but was not affected by changes in cyclic frequency (p <0.001 and p =0.43, two-factor ANOVA with Tukey). (B) The loss modulus significantly increased with haversine amplitude, but was unaffected by cycling frequency (p <0.001 and p =0.184, respectively, two-factor ANOVA with Tukey). (C) The complex modulus significantly increased with haversine amplitude, but was unaffected by cycling frequency (p< 0.001 and p =0.294, respectively, two-factor ANOVA with Tukey). Error bars are standard deviations. ^-Statistically significant (p <0.05) from all frequencies at 40% strain;*-Statistically significant (p <0.05) from all frequencies at 50% strain.

Each of the dynamic moduli was similar in magnitude to its analogous secant modulus. The complex modulus E* was similar in magnitude to the viscous modulus E_V (mean at 50% strain: E* = 1.63 MPa and E_V = 1.61 MPa). The storage modulus E′ was similar in magnitude to the elastic modulus E_E (mean of all frequencies: E′ = 1.25±0.79 MPa; E_E = 1.33±0.49 MPa). As the phase lag was always less than 45 deg, the loss modulus E′ was smaller than E″ and was similar in magnitude to the mean difference between E_V and E_E (mean at 50% ramp strain: E″ = 0.39 MPa and (E_V−E_E) = 0.28 MPa).

Dynamic relaxation rates were not dependent upon cycling frequency (p=0.744), but was dependent upon haversine strain amplitude (Fig. 9). The relaxation rate increased with increasing haversine strain amplitude (10% versus 20%, 30%, 40%, 50%: p < 0.001; 20% versus 40%, 50%: p=0.001; 20% versus 30%: p=0.006; 30% versus 50%: p<0.001; 30% versus 40%: p = 0.001). Data from all frequencies were combined and the strain-dependent rate function was best fit with a first-order polynomial (B(ɛ)= − 0.1249ɛ + 0.0190, R² = 0.92).

Fig. 9.

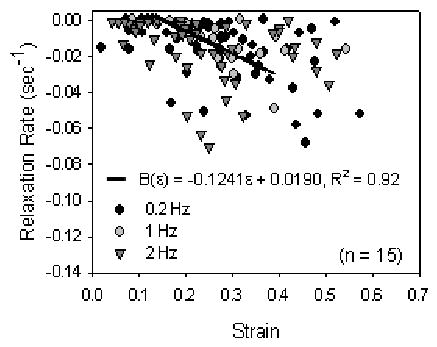
The load relaxation rate parallel to the collagen fibers was dependent upon strain magnitude during dynamic loading trials, but was independent of cyclic frequency (p <0.001 and p =0.744, respectively, two-factor ANOVA with Tukey). The relaxation rate was determined from the load and time values at each peak of twenty cycles, normalized to the maximum load (which was always during the first cycle), then finding the slope of the log (load)-log (time) plot. The relaxation rate significantly increased with increasing strain magnitude 10% vs 30%–50%: p <0.001; 20% vs 40%–50%: p <0.001; 30% vs 50%: p =0.001; 30% vs 40%: p =0.001). Data for all frequencies were combined and a strain-dependent relaxation function was defined for mean rate-strain data with coefficients: B ( ε) = − 0.1249 ε + 0.0190, R 2 =0.92.

Discussion

Like most other soft connective tissues, for example, tendon [35,36], ligament [11,37], and skin [38,39], the mechanical behavior of facet joint capsule was viscoelastic and anisotropic. This was expected given its similarities in composition to other connective tissues and the dominant orientation of its collagen fibers along a medial lateral axis [15]. Similar to human medial collateral [11] and interosseous ligaments [40], the capsule has greater strength parallel to the collagen fibers, and the relationship between stress and strain was nonlinear viscoelastic. Perpendicular to the collagen fiber orientation, the relationship for facet capsule appeared linear viscoelastic in nature.

The nonlinear stress-strain relationship was better fit by an exponential rather than power function, which suggests that the intrinsic waviness (or “crimp” pattern) of the collagen fibers [41] may have relatively low variability in facet joint capsule. This is analogous to predictions of the model by Maksym and Bates [42] for lung viscoelasticity, which was shown to depend on the interactions between elastin, and collagen waviness, and recruitment, and as suggested earlier by Viidik [43–45]. In composite tissues, such as facet joint capsule, elastin tends to dominate load bearing at low strain magnitudes, while the collagen fibers are still being straightened out; whereas, at higher strains, the collagen fibers are largely straight [46] and, being orders of magnitude stiffer than elastin [47,48], bear more of the load. Tissues with low variability in collagen fiber waviness and/or length would have increased recruitment of the fiber bundles over a relatively smaller span of tensile strains compared to tissues with high variability [42], resulting in an increase in the developed stress at large tensile strains. This would appear as a faster rise of the stress-strain relationship, and hence, would tend to be better fit by an exponential than a power function.

The viscous and elastic properties of the specimen were quantified in both the ramp-hold trials and in the dynamic loading trials. The stress-strain relationship parallel to the collagen fibers was found to be non-linear for both the ramp-hold and dynamic trials and the coefficients of the exponential fit describing the relationship were similar in magnitude. The secant moduli used to describe the contributions of the viscous and elastic components of the capsule during the ramp-hold trials were well-matched with analogous dynamic moduli, indicating the accuracy of the individual measurements. In both measurement types, the elastic modulus (E_E and E″) was large compared to the modulus containing both the viscous and elastic components (E_V and E*), indicating that the capsule stores more energy than it dissipates during loading.

The lumbar facet capsule tangent modulus parallel to the collagen fibers was found to be similar in magnitude to the bilinear Young’s modulus of the cervical facet joint capsule reported previously (4.8⩽E₁ (MPa)⩾5, for C2-T1) [33]. This finding indicates that the differences in the mechanical behavior of the facet joint capsule ligament during physiological motion in different regions of the spine [21,22,49] might not be a result of differences in the ligament tissue properties, but from a variety of other reasons, such as differences in the anatomical orientation of the facet joints and the natural kyphosis/lordosis of the spine. As such, the mechanical characterization of the facet joint capsules employed by modelers might be interchangeable from region to region while still producing valid results, as long as care is taken to address other anatomical differences.

Lumbar facet joint capsules exhibited some classic viscoelastic properties, such as stress relaxation. Perpendicular specimens had a consistent stress relaxation rate independent of peak strain magnitude typical of linear viscoelastic materials. Stress relaxation parallel to the collagen fibers was shown to be non-linear, as also seen in the rat medial collateral ligament (MCL) [32]. The rate of relaxation was dependent upon the peak strain magnitude, and could be described well by a polynomial as predicted by the model described by Provenzano et al. [32]. The mechanisms responsible for strain-dependent relaxation in soft tissues are not well known. It is speculated that the decrease in relaxation rate with increased strain could be due to a “wringing out effect,” in which larger strains cause greater water loss and therefore, the tissue behaves more elastically [32].

The lumbar facet joint capsule did not exhibit other viscoelastic tendencies, such as rate dependency. The capsule relaxation data was frequency independent, which is in contrast to the relaxation model that predicts faster relaxation with increased cycling frequency. The lumbar facet joint capsules also did not demonstrate a significant difference in modulus parallel to the collagen fiber orientation with increasing strain rates or increasing cycling frequency. Rate independence has also been observed in tests of isolated collagen fibers from rat tails [29], as well as in the stiffness of cat lumbar facet joints [50], bovine periodontal ligaments [37], and the human MCL under shear loading [11]. It is possible that expanding the range of loading rates used, both static and dynamic, would result in apparent changes modulus. Rate dependence was observed in the cervical alar and transverse ligaments [51] and the anterior longitudinal ligament and ligamenta flava [52]. However, these studies used loading rates which spanned four orders of magnitude, while the loading rates used in the current experiment only spanned one order of magnitude. This is consistent with the idea that within discrete ranges of loading rates the modulus or stiffness would be rate independent. Mechanistically, this could occur if the viscosity response was dependent on the movement of fluid within the tissue. During stretch, fluid would be mobilized, but would be constrained by pore size. Hence, within small ranges of loading rates, there would be no discernable difference in viscosity as the difference in the dispersion rate of the fluid would be small. However, loading rates that span several orders could create noticeably different fluid dispersion rates, resulting in statistically different moduli [53].

Both parallel and perpendicular to the orientation of the collagen fibers, there were large variations from specimen to specimen in stress as a function of strain. However, the overall stress-strain relationships exhibited similar characteristics. The large variability in the stress-strain relationship is consistent with current literature on other ligaments [34,37]. Some of the variability may have been due to the calculation method of each component. Because it was not possible to measure the changes in cross-sectional area throughout a loading cycling, engineering stress was computed over time. This method does not account for any “thinning” of a specimen throughout a loading cycle, which would not necessarily be consistent from specimen to specimen. For instance, a specimen associated with a low peak force value could have thinned more during ramping and have a smaller cross-sectional area at the time of the peak force, thus increasing its peak stress. Strain, however, was calculated using the Eulerian method.

The data from the current study implies that accurately modeling the lumbar spine requires consideration of the viscoelastic material properties of the facet joint capsule. Distinct material properties were seen based on the orientation of the load relative to the collagen fibers. As even simple physiologic motions (e.g., flexion) of the lumbar spine result in complex strain patterns within facet joint capsules [21], it is unlikely that modeling facet joint capsule as a linear elastic isotropic material would accurately predict actual stresses in the capsule during loading. A computational model that could accurately predict the stress state of the facet joint capsules during motion could be highly beneficial in understanding how the biomechanics of the spine and capsular ligament relate to low back pain.

Nomenclature

A = exponential coefficient

B = relaxation function

E = elastic modulus

ɛ1 = first principal strain closest to x axis

E* = complex modulus

E″ = loss modulus

E′ = storage modulus

F_p = preload force

F_E = elastic force

F_ν = viscous force

K = exponential coefficient

t = time

δ = phase angle

ɛ_xx = strain on x axis

ɛ_yy = strain on y axis

ɛ_xy = plane shear strain

η = viscous modulus

σ_E = elastic stress

σ_ν = viscous stress

Appendix: Validation of Image Correlation Software

The strain calculations made using image correlation were validated by comparing results from a dummy specimen to results obtained from a commercial software package (PC Reflex, Qualisys, Inc., Gothenburg, Sweden) collected for the same specimen. PC Reflex tracks infrared reflective markers placed on the surface of the specimen. To accommodate both methodologies of tracking, infrared tape was applied to the surface of the specimen in a 3×3 array and the surface was then coated with silicon carbide particles. The subarray size in the image correlation software was set to 3×3 and each element was individually checked to ensure that it encased an infrared marker. Strain computed using the image correlation software was less noisy over time compared to strain computed from PC Reflex. Strain data calculated from both software packages were not statistically different from one another (p=0.586, two-way repeated measures ANOVA [factors: element number and time]).

The optimal number of subimages to use for surface strain characterization was determined by re-analyzing image sequences (n = 5 at 50% strain), while systematically increasing the number of elements in the subarray. All perfect squares from 4 to 81 were used to define subarray dimensions (e.g., if the number of elements equals 9, the array is 3×3). Mean strain was significantly different when calculated from four subimages compared to calculation from 25 or more subimages (Friedman’s test; results given as number of subimages: p-value; 25: p = 0.005; 36: p = 0.002; 49: p = 0.001; 64: p=0.001; 81: p<0.001). Strain was also significantly different when calculated from nine subimages compared to 81 elements (p=0.007). There was no difference in mean strain when calculated from 16 or more subimages. To save computation time, all further analysis was performed using 16 subimages (4×4 array).