Internal Models of Limb Dynamics and the Encoding of Limb State

Abstract

Studies of reaching suggest that humans adapt to novel arm dynamics by building internal models that transform planned sensory states of the limb, e.g., desired limb position and its derivatives, into motor commands, e.g., joint torques. Earlier work modeled this computation via a population of basis elements and used system identification techniques to estimate the tuning properties of the bases from the patterns of generalization. Here we hypothesized that the neural representation of planned sensory states in the internal model might resemble the signals from the peripheral sensors. These sensors normally encode the limb's actual sensory state in which movement errors occurred. We developed a set of equations based on properties of muscle spindles that estimated spindle discharge as a function of the limb's state during reaching and drawing of circles. We then implemented a simulation of a two-link arm that learned to move in various force fields using these spindle-like bases. The system produced a pattern of adaptation and generalization that accounted for a wide range of previously reported behavioral results. In particular, the bases showed gain-field interactions between encoding of limb position and velocity, very similar to the gain fields inferred from behavioral studies. The poor sensitivity of the bases to limb acceleration predicted behavioral results that were confirmed by experiment. We suggest that the internal model of limb dynamics is computed by the brain with neurons that encode the state of the limb in a manner similar to that expected of muscle spindle afferents.

1. Introduction

To generate reaching movements, the brain appears to compute motor commands based on predicted dynamics of the task (Gottlieb, 1994;Shadmehr and Mussa-Ivaldi, 1994). When the dynamics change unexpectedly, movements exhibit errors. The errors produce unexpected changes in muscle lengths that are transduced by proprioceptive sensors, which in turn evoke short- and long-latency responses that modify the ongoing motor commands. Because of inherent delays in the nervous system, this feedback reduces the error in the ongoing movement but does not eliminate it. To eliminate the error, the brain use the error-driven motor response in one trial to modify the motor commands that initiate the next trial (Thoroughman and Shadmehr, 1999). In theory then, the process of learning the control of limb dynamics is an example of “error-feedback-learning”: reflex circuits transduce the motor error and generate corrective motor commands. These corrections act as the teaching signal for an internal model that computes the subsequent voluntary motor commands (Kawato, 1989; Marsden et al., 1976). The internal model in this case is a sensorimotor map that transforms a desired action (represented in kinematic coordinates) into motor commands (represented as torques), and adaptation is due to supervised learning.

In supervised learning, error signals primarily affect the states in which errors are experienced. However, depending on how states are represented, the effect of error may be local to the state or generalize broadly to neighboring states. For example, if we imagine an internal model as a system that transforms the desired limb position and its derivatives $[{\theta }_d,{\dot{\theta }}_d,{\ddot{\theta }}_d,\cdots ]$ into an estimate of joint torques $\widehat{\tau }$ (Conditt et al., 1997) via a weighted combination of basis elements (Donchin et al., 2003; Thoroughman and Shadmehr, 2000):

$$\widehat{\tau }=\sum _i{w}_i{g}_i\left({\theta }_d,{\dot{\theta }}_d,{\ddot{\theta }}_d,\cdots \right)$$ (1)

Then each basis g_i encodes some aspect of the limb's sensory state and a population code forms a motor command. In this theoretical framework, the tuning of bases determines generalization. For example, broad tuning with respect to limb position θ_d predicts that after one experiences error during reaching in one workspace of the hand (say with the shoulder in a flexed posture), the error will generalize to reaches in another workspace far away (with the shoulder in an extended posture) (Shadmehr and Moussavi, 2000). Indeed, this wide pattern of generalization in terms of limb position is a consistent property of adaptation to novel arm dynamics (Malfait et al., 2002).

If the internal model can be viewed as a population coding via a set of bases, then it is important to predict how the bases encode limb state and how that encoding translates into neuronal discharge. Thus far, the approach has been to measure behavior and then try to find tuning functions that produce generalization patterns that are consistent with the measured data. For example, a previous study suggested that in order to account for the observed patterns of generalization in force fields that depended on both position and velocity of the limb, the bases likely encoded these variables multiplicatively: the bases were directionally tuned, but the depth of tuning was linearly modulated with respect to limb position (Hwang et al., 2003). The result predicted that the bases encoded these two variables in a “gain-field”.

Remarkably, a recent paper found such gain-field coding in the tuning of some cells in the motor cortex (Paninski et al., 2004). Earlier, Bizzi and colleagues had reported that during adaptation, changes in the directional tuning of motor cortical cells paralleled changes in the spatial tuning of task related arm muscles (Li et al., 2001). However, because some cells maintained these changes in tuning even after a washout period, it seemed likely that the motor cortex was involved both in the formation of the internal model and its expression. Therefore, the idea of using patterns of generalization to infer shape of the bases and then testing the predictions in the motor cortex appeared promising.

Unfortunately, there are inherent limitations in this approach. In principle, the bases encode every aspect of limb state, including limb acceleration and possibly higher derivatives. The large state space makes it impossible to design psychophysical experiments that can probe generalization patterns along each dimension of state space.

Here we approached the problem from a different direction. Rather than trying to predict tuning of the bases from generalization patterns in behavioral data, we used a physiologically derived prior assumption on the shape of the bases to predict behavior. If reflex based error-feedback acts as a teaching signal to an internal model, then the states in which the errors are experienced are reported to the central nervous system (CNS) in proprioceptive coordinates. Therefore, we hypothesized that the bases that form the internal model code the desired state of the limb with functions that are similar to the coding found in the neural discharge of muscle-spindle afferents.

This assumption imposes strong constraints on the shape of the bases: the discharge of spindle afferents is a scalar function that nonlinearly encodes all aspects of limb state, including position, velocity, acceleration, and even higher derivatives (Hasan, 1983). Here we simulated adaptive systems that used these bases to learn dynamics of reaching. We compared generalization properties of the system with behavioral data and found that a number of psychophysical results could be accounted for by this new model.

2 Model

2.1 Encoding state of the limb in the peripheral nervous system

Several studies have proposed mathematical models of spindle afferent discharge (Hasan, 1983; Houk et al., 1981; Lin and Crago, 2002; Poppele and Boyd, 1970; Prochazka and Gorassini, 1998; Schaafsma et al., 1991). However, one class of models stands out because first, its components are based on physical properties of muscle fibers (i.e., length-tension relationship), and second, the model can explain neuronal discharge during active motion of freely moving animals (Hasan, 1983; Prochazka and Gorassini, 1998a). In this model (Hasan, 1983), spindle afferent discharge is determined by the impact of the state of the muscle on two physically different zones of the muscle spindle: sensory and non-sensory. These two regions are in series. We label the length of the sensory zone z(t) and the length of the non-sensory zone y(t). Because the zones are in series, the tensions are equal. For the non-sensory zone, tension f(t) is a nonlinear function of y(t) and its first derivative $\dot{y}\left(t\right)$, as shown in Eq. 2. For the sensory zone, tension is assumed to be a simple spring, with the tension proportional to the length of the sensory zone (Eq. 3).

$$f\left(t\right)=k_1\cdot (y\left(t\right)-c)\cdot (1+{\left(\frac{\dot{y}\left(t\right)}{a}\right)}^{1∕3})$$ (2)

$$f\left(t\right)=k_2\cdot z\left(t\right)$$ (3)

Here, k₁ and k₂ are length sensitivities for the non-sensory and sensory zones respectively. Length of a spindle is the sum of the lengths of the sensory and non-sensory zones: x(t) = y(t) + z(t). Substituting this equality into Eqs. 2 and 3, after re-arrangement we arrive at a differential equation that describes the relationship between total muscle spindle length x(t) and the sensory zone length z(t):

$$\dot{z}\left(t\right)=\dot{x}\left(t\right)-a{\left(\frac{bz\left(t\right)-x\left(t\right)+c}{x\left(t\right)-z\left(t\right)-c}\right)}^3$$ (4)

where b = (k₁ + k₂)/k₁. Parameter a is the sensitivity of tension to velocity in the non-sensory zone and parameter b is the ratio of the sum of length sensitivities for both zones and the length sensitivity for the non-sensory zone of the spindle. Parameter c determines the zero length tension and influences the background firing rate.

The receptor potential of the spindle afferent neuron is linearly proportional to the sensory zone length z(t) while the firing rate of the spindle afferent neuron, represented by g(t), is roughly proportional to a linear combination of its potential and its first derivative (Eq. 5). In Hasan's model, the time constant 0.1 was approximated to fit the experimental results (Hasan, 1983).

$$g\left(t\right)=z\left(t\right)+0.1\dot{z}\left(t\right)$$ (5)

From Eq. 4 we see that at any given time, the sensory zone length z(t) depends on the history of spindle length changes -- not just the current length and velocity of the spindle. Thus, if we define the state of the limb as its position and velocity, we see that the spindle discharge at a given “state” will differ as a function of the immediately preceding history by which the limb arrived at that state. For example, although the length and velocity are held at constant values at the end of stretching, the spindle discharge continues to change, converging to the steady state value.

A wide range of spindle afferent discharge characteristics during both passive and active movements can be reproduced by varying the three parameters, a, b, and c in Eq. 4. For active voluntary movements, Hasan (1983) suggested a=100, b=100 and c=−25 for the static-γ neuron activated primary spindle afferents and a=0.1, b=250, c=−15 for the dynamic-γ neuron activated primary spindle afferents. Because we were concerned with modeling voluntary movements, we used these two sets of parameter values to represent the physiologic range. In comparison, for passive movements the term a is about 50% smaller for dynamic-γ and 50% larger for static-γ neuron activated primary spindle afferents.

Note that these parameter values are kept constant during movement. However, γ motoneuron activity changes during a voluntary movement. How does this affect the ability of the model to account for the time course of spindle discharge? For example, a fast movement involves large changes in α motoneuron activity, with correspondingly large changes in γ motoneuron discharge. In contrast, in slow movements one would expect smaller changes in γ motor neuron discharge. Prochazka and Gorassini (1998a) tested the current model, as well as five other models, against the discharge histories of a population of spindle afferents recorded from the hamstring muscle of freely moving cats walking at slow, medium, and fast speeds. Remarkably, this model with its parameters fixed at constant values accounted for the temporal profile of neural discharge exceedingly well in various speeds (with r-squares of 84%, 85%, and 88% for slow, medium, and fast speeds). Prochazka and Gorassini (1998a) noted that “predictions were not improved by adding components of firing rates that mimicked EMG-linked γ motor action.”

2.2 Spindle-like basis set

Eqs. 4 and 5 provide an approximation of how the peripheral nervous system might encode the kinematic state of a muscle during a voluntary movement. Here our intention is to model the encoding of state of an entire arm during reaching movements. To compute the response for a whole arm movement, it is necessary to transform the multi-dimensional movement trajectory to one-dimensional spindle-length history. For a given point-to-point reaching movement, the change of muscle length varies depending on which joint the muscle crosses over. For example, a muscle spindle embedded in the anterior deltoid that crosses over the shoulder joint would respond mostly to shoulder extension whereas a muscle spindle embedded in the brachioradialis that crosses over the elbow joint would respond mostly to elbow extension. Thus, assigning the joint over which the spindle crosses is equivalent to assigning a preferred direction to each muscle in joint space (Fig. 1).

Figure 1.

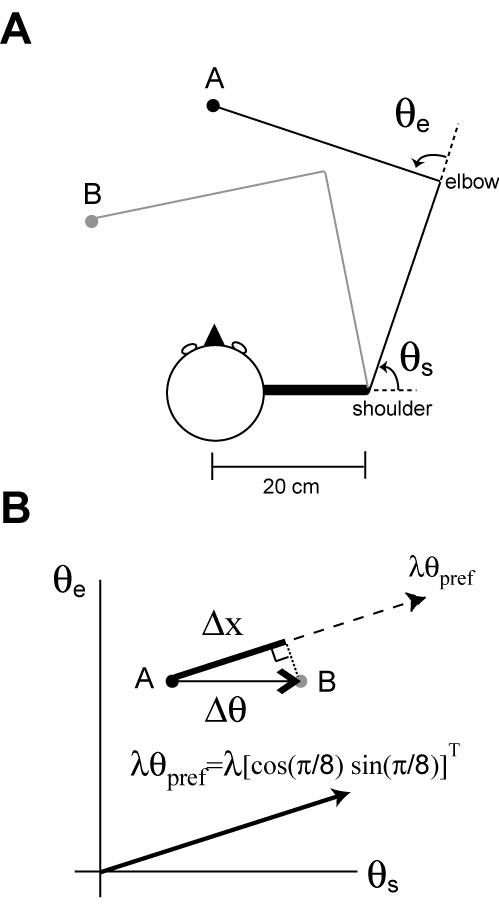
Transformation from a 2D arm movement to muscle length changes. (A) Top down view of the model arm that moves on a horizontal plane. θ_s is a shoulder joint angle and θ_s is an elbow joint angle. Pure shoulder flexion when moving from the point A to B. (B) A movement representation in the joint angle space for the movement in (a). This joint angle change (Δθ) from the point A to the point B induces a length change (Δx) for the muscle that is sensitive to the shoulder joint angle change. For example, the length change of the muscle whose preferred direction is[cos(π / 8) sin(π / 8]and moment arm is λ can be calculated by computing the inner product between Δθ and λθ_pref.

Length changes in a muscle relate to changes in joint angles via a Jacobian matrix that in turn specifies a moment arm. Although this matrix is a function of joint angles, for small amplitude reaching movements the matrix is approximately constant. Eq. 6 describes a simple linearized process to transform a 2D joint displacement to changes in muscle spindle length (Bhushan and Shadmehr, 1999).

$$x\left(t\right)=\lambda {\theta }_{\mathit{pref}}^T\cdot \Delta \theta \left(t\right)=\lambda {\theta }_{\mathit{pref}}^T\cdot (\theta \left(t\right)-{\theta }_0)$$ (6)

θ is a 2×1 vector consisting of shoulder and elbow joint angles. θ₀ is the resting joint position, we used θ₀ = [1.1 2.0]^T radian corresponding to shoulder and elbow angles of 63° and 115° (Fig. 1a), respectively, with a hand position that is 20 cm left and 30 cm in front of the right shoulder point. However, the value for θ₀ does not affect the simulation results presented in this paper. θ_pref is a 2×1 unit vector representing a preferred direction in joint angle space. For example, θ_pref = [1 0]^T corresponds to 0° preferred direction which represents pure shoulder flexion while θ_pref = [0.7 0.7]^T corresponds to 45° preferred direction which responds equally to both shoulder and elbow flexions. The inner product of θ_pref and Δθ computes the change of joint angle in the preferred direction, reducing the dimension from 2D to 1D. Finally, multiplying the inner product by λ , the moment arm, transforms the joint angle into the muscle spindle length (Fig. 1b).

To calculate x(t) for a point-to-point movement, we computed a minimum jerk trajectory. That is, for a movement from point p₁ to point p₂ the trajectory, p(t), was calculated using the following equation, p(t) = p₁ + (p₂−p₁){6(t/T)⁵ − 15(t/T)⁴ + 10(t/T)³} where t is time and T is the total movement time. This trajectory was translated into a joint angle trajectory using a 2D kinematic transformation and finally converted the joint angle trajectory into the spindle length profile according to Eq. 6. For a given x(t), we numerically solved the differential equation in Eq. 4 using forward-Euler method (step size = 1 ms, implemented in Matlab) to obtain the firing rate as a function of time for each basis element.

The important parameters that determine the tuning property of a spindle-like basis element are a, b, c, λ , and θ_pref in Eqs. 3-5. As noted earlier, we used the same values that Hasan (1983) suggested for static and dynamic-γ neuron activated primary endings for parameters a, b, and c. The parameters suggested for the secondary endings were not included because its tuning property was very similar to that of static-γ neuron activated primary endings. For the moment arm λ , there are many possible values as many arm muscles with various lengths are involved. In order to cover the whole range of possible moment arms, we chose two extreme values, the smallest (8 mm) and the largest (80 mm) in the moment arm distribution reported in Murray et al. (1995) Note that the unit for the moment arm is in mm. The preferred direction θ_pref was uniformly distributed in the joint displacement space at π / 8 intervals. Thus the total number of bases (g ) is 2 (two sets of a, b, c) × 2 (two λ 's ) × 16 ( sixteen θ_pref 's ) = 64. Table 1 summarizes values of the five parameters for all 64 basis elements that we used for simulations in this paper.

Table 1.

List of parameters used in simulations

	a	b	c	λ	θ pref ,j ( j = 0, 1, 2,.., 15 )
g1,j	100	100	−25	80	${\theta }_{\mathit{pref},j}={{\displaystyle \left[\cos \left(\frac{j\pi }{8}\right)\sin \left(\frac{j\pi }{8}\right)\right]}}^T$
g2,j	100	100	−25	8	${\theta }_{\mathit{pref},j}={{\displaystyle \left[\cos \left(\frac{j\pi }{8}\right)\sin \left(\frac{j\pi }{8}\right)\right]}}^T$
g3,j	0.1	250	−15	80	${\theta }_{\mathit{pref},j}={{\displaystyle \left[\cos \left(\frac{j\pi }{8}\right)\sin \left(\frac{j\pi }{8}\right)\right]}}^T$
g4,j	0.1	250	−15	8	${\theta }_{\mathit{pref},j}={{\displaystyle \left[\cos \left(\frac{j\pi }{8}\right)\sin \left(\frac{j\pi }{8}\right)\right]}}^T$

3. Results

3.1 Tuning functions

In order to examine the tuning properties of the spindle-like basis elements, we simulated standard center-out reaching tasks and computed the activities of basis elements during reaching.

3.1.1 Task

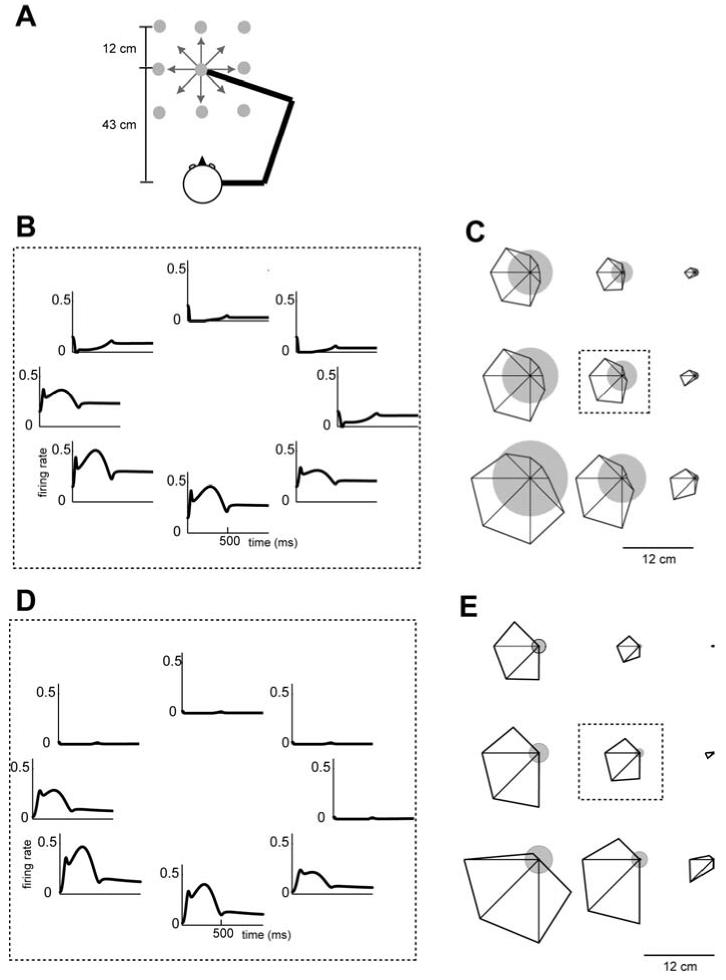
Figure 2a shows the spatial configuration for the reaching simulation. The center-out reaching was made on a horizontal plane at shoulder level. Nine different center positions were located in a 3×3 grid (9 grey dots). The grey dot in the middle was aligned with the body midline and 43 cm away from the center of the head. At each center position, 10 cm reaching was made in 8 different directions (8 arrows). Initially, the arm stayed at the center location and moved to the target in 500 ms. The trajectory of each reaching was assumed to follow a minimum jerk profile. For a given point-to-point reaching, the change of spindle lengths and the corresponding discharge rate was calculated as described in section 2.2.

Figure 2.

A tuning curve of example muscle spindle-like basis elements in a center-out reaching task. (A) Spatial configuration of movements used in tuning curve calculation. Eight directional center-out reaching on a horizontal plane at the shoulder level were simulated in nine different center locations (grey dots). (B) Firing rate of a basis element (a=100, b=100, c=−25, λ =80, θ_pref = [cos(π / 8) sin(π / 8)]^T ) as a function of time when the center position was the middle point in 3×3 grid. (c) Tuning curves at nine different center locations. Size of the circle at each location represents the mean firing rate during the center-hold period (500 ms). Distance from center of circle to vertex of polygon represents the firing rate for reaching in that direction. The direction with the largest distance from the center is the preferred direction of this cell. The plot in the center bounded by a dashed rectangle uses the same data in (a). (D)-(E) The same format as in (B)-(C) for another basis element (a=0.1, b=250, c=−15, λ =80, θ_pref = [cos(π / 8) sin(π / 8)]^T ).

3.1.2 Tuning curves

Figure 2b shows the time course of response for an example basis element with a=100, b=100, c=−25, λ =80, and θ_pref = [cos(π / 8) sin(π / 8)]^T during reaching from a middle center position in 8 different directions. These parameters model a typical static-γ neuron activated primary spindle afferent. The preferred direction π/8 in the joint angle space corresponds to mostly shoulder flexion, thus, the most active direction is down and left in this arm configuration. When the arm moves in the preferred direction of this basis, the response is strongly influenced by hand velocity. However, note the small bump in the response at the beginning, when the hand acceleration in the preferred direction is positive, and the small dip in the response at the end, when the acceleration is negative. These correlations of the basis response are not limited to the hand velocity or acceleration because joint angular velocity and acceleration are approximately linearly related to the hand velocity and acceleration in small amplitude movements. We found that the combined sensitivity to velocity and acceleration produced a response in the simulated spindles that was quite similar to the spindle response recorded during wrist motion (Jones et al., 2001) as well as the discharge of some cells recorded in the somatosensory cortex (area 3a) and motor cortex during foot motion (Wise and Tanji, 1981).

The octagon inside of the dashed rectangle in Fig. 2c displays the data in Fig. 2b as a tuning function. The size of the filled circle represents the mean firing rate during the center-hold period and the distance from the center to each vertex represents the mean firing rate while moving in that direction. To display the effect of limb position on the activity of the bases, the eight other sub-plots in Fig. 2c plot the tuning of this basis when the starting location for the reaching movement was shifted to each of the other 8 positions. The activity during the center-hold period monotonically changes as a function of starting location. However, note that the interaction of position sensitivity and directional tuning is multiplicative since the size of the circles and octagons increase concomitantly. Therefore, the simulations predict that a spindle-like basis will have a tuning curve similar to that of a gain-field.

Figures 2d-e show the tuning properties of a spindle-like basis with a=0.1, b=250, c=−15, and λ =80. These parameters model a typical primary spindle afferent activated by a dynamic-γ motor neuron. This basis displays relatively little sensitivity to changes in the starting position of the reach, but strong sensitivity to hand velocity. Regardless, this basis also shows a gain-field like interaction between position and velocity. Whereas previously we had used psychophysical data during learning to argue for necessity of gain-field coding (Hwang et al., 2003), the current results show that this kind of coding may be a reasonable prior assumption on the tuning of the bases. For bases with a smaller moment arm (k=8), arm position modulates directional tuning by a smaller amount and the tuning remains relatively constant across the workspace.

3.2 Adaptation to a velocity dependent curl field

People tend to reach in roughly a straight path from one point to another with a bell shaped velocity profile (Flash and Hogan, 1985; Morasso, 1981). This tendency continues even when their reaching movements are perturbed by an external force field or by modification of arm inertial properties (Krakauer et al., 1999; Lackner and Dizio, 1994; Shadmehr and Mussa-Ivaldi, 1994). A well studied adaptation protocol is for reaching in velocity dependent curl fields that perturb the hand in the direction perpendicular to the movement. We began by asking if the internal model with the spindle-like bases could adapt to the velocity dependent curl field.

3.2.1 Task

The simulated movement was 10 cm long from the center of the horizontal workspace (the grey dot in the middle of 3×3 grid in Figure 2a) towards the body during 500 ms. The magnitude of the external force was proportional to the hand velocity and the direction was perpendicular to the instantaneous velocity, v(t). That is, $F\left(t\right)=\left[\begin{array}{cc}\hfill 0\hfill & \hfill -13\hfill \\ \hfill 13\hfill & \hfill 0\hfill \end{array}\right]\cdot v\left(t\right)$ where $\stackrel{\rightharpoonup }{F}$ is a 2×1 force vector and $\stackrel{\rightharpoonup }{v}$ is a 2×1 velocity vector.

3.2.2 Representation of the internal model and simulation of arm dynamics

We assumed that the internal model is represented as a population coding via a set of basis elements that have the response function as shown in equation 4. The internal model is:

$${\widehat{\tau }}_{\mathit{env}}\left(t\right)=\sum _{i=1}^{64}{w}_i\cdot g_i\left(t\right)$$ (7)

where ${\widehat{\tau }}_{env}$ is the expected environmental torque, g_i is a firing rate of each basis element, and w_i is a torque vector composed of shoulder torque and elbow torque, corresponding to each basis element. To simulate human arm reaching, we used a simple 2-link system that described the physics of our experimental setup (Shadmehr and Mussa-Ivaldi, 1994).

3.2.3 Adaptation of the internal model

In our simulation, the adaptation of the internal model was implemented by updating weights after each movement so that the squared error of the output from the internal model decreased. The update follows the gradient descent rule, $\Delta w_i=-\eta g_i({\widehat{\tau }}_{env}-{\tau }_{env})$. Here, Δw_i is the amount of weight change for the i-th basis element, η is a learning rate, and τ_env is the actual environmental torque.

3.2.4 Simulation results

Figure 3 displays the simulated hand paths in the early and late phases of training. In the beginning, as the internal model expects zero external (environmental) forces, large movement errors are produced in the field, whereas almost no errors are observed in the null field condition (Fig. 3a). Figure 3c displays the actual external forces and the predicted external forces by the internal model after 200 movements of training. The correlation coefficient between the actual and predicted forces is 0.98. As the predicted forces come to match the actual external forces closely, the movement errors decrease (Fig. 3b). In parallel, errors during catch trials (i.e., trials in which the field is unexpectedly turned off) increase with training. Therefore, the bases can readily approximate a velocity dependent force pattern.

Figure 3.

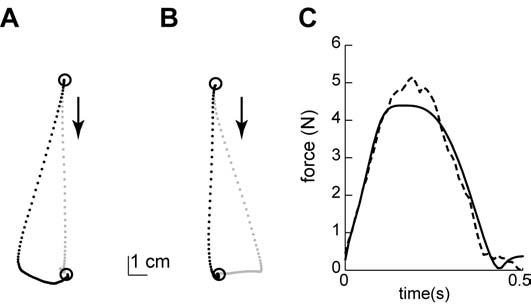
Simulation of adaptation to a velocity dependent curl field using a spindle-like basis set. (A) Hand paths from the early phase of training. Black dots represent a movement in the force field and grey dots represent a movement in the null field (catch trial). (B) Hand paths from the late phase of training. (C) The dotted line represents the velocity dependent forces applied to the simulation arm in the direction perpendicular to the movement direction as a function of time. The solid line represents the predicted forces by the internal model consisting of spindle-like basis elements.

3.3 Transfer of adaptation from reaching to drawing of circles

Mussa-Ivaldi and colleagues (Conditt et al., 1997) observed that when people adapt their reaching in a force field, the internal model that they acquire generalizes to other tasks like drawing of circles. Here, we tested if our spindle-like basis model could reproduce such experimental result.

3.3.1. Task

In their key experiment, they considered two groups of subjects: one group practiced 10 cm point-to-point reaching to 8 directions in a curl field (typically 0.5 s long), and another group trained by drawing circles in the same field (typically 2 s long). The eight directional point-to-point movements spanned a range of 360°. The configuration of reaching and circular movements is displayed in Fig.4a. Mussa-Ivaldi and colleagues noted that the amplitude and the temporal speed of the circular movements were chosen so that the circles passed through the same positions and velocities as the reaching movements.

Figure 4.

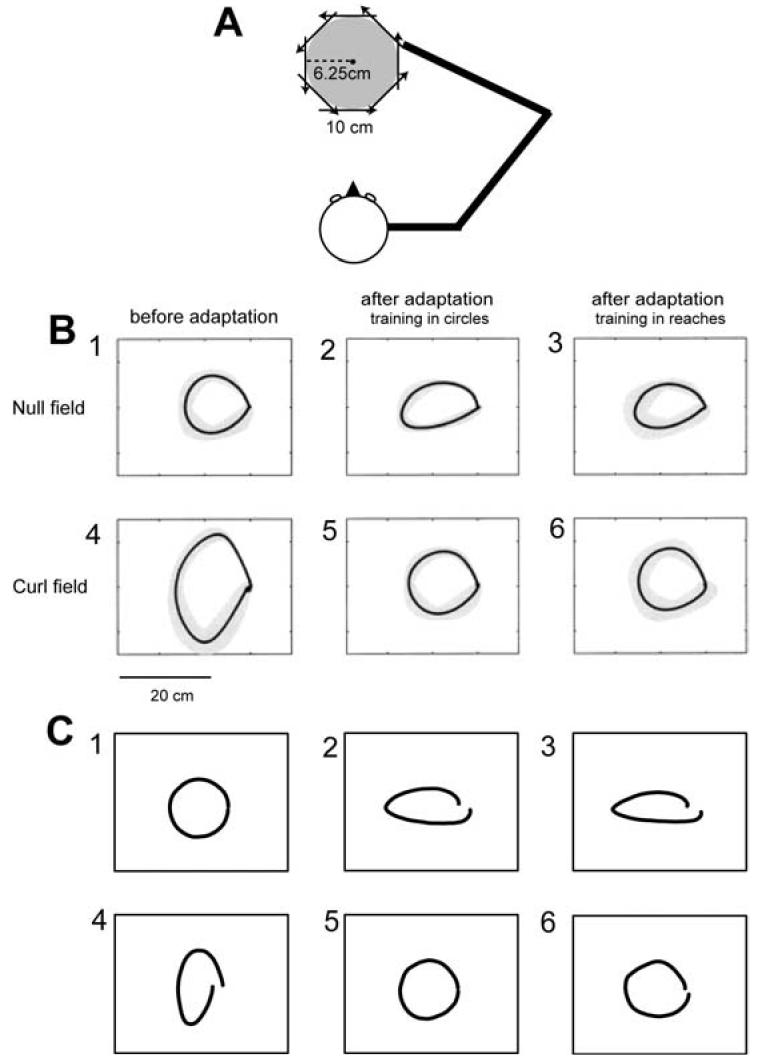
Simulation of adaptation of reaching and transfer to drawing of circles. (A) The configuration of 10 cm reaches in 8 directions and circular movement with a radius of 6.25 cm. (B) Average hand trajectories from subjects recorded by Conditt et al. (1997). (C) Simulation results. (1) Circles made in the null field by the naïve model and naïve subjects. Grey bands represent ±SD. (2) Direct after-effects as a result of adapting to the field by drawing circles. (3) Transferred after-effects as a result of adapting to the field with reaching movements. (4) Trajectories in the force field by the naïve model and subjects. (5) Direct adaptation circles made after adapting to the field directly with circles. (6) Transferred adaptation after adapting to the field with reaching movements.

They then asked the “reach” subjects to draw circles and compared their performance in circular movements to the performance of the group who were originally trained in circular movements. In circle drawing trials, a template of the circle was provided to subjects on the monitor. While the states (e.g., hand position and velocity) were similar in the reach and circle-drawing tasks, the order in which the states were visited and the time-scale of the movements in the two experiments were very different.

Fig. 4b plots some of the trajectories that they recorded in their experiments. They found that when subjects were asked to draw circles, the “reach” group produced circles that looked very similar to the well-trained “circle” group (Fig. 4b-5 and 6). Similarly, when asked to draw a circle, they found that if they turned off the field the trajectoris of the “reach” group looked very similar to the after-effects recorded from the well-trained “circle” group (Fig. 4b-2 and 3). Thus, reaching resulted in a representation that allowed the subjects to draw circles in the field nearly as well as subjects that had trained in circles.

3.2.2 Simulation results

We simulated this experiment with the same bases described above Figs. 4c-1 and 4 show the trajectories produced by the “naïve” model in a null field and in the force field, respectively. The naïve system produced a fairly accurate circle in the null field (Fig. 4c-1) but a distorted circle in the force field (Fig. 4c-4). The similarity in distortions between model system (Fig. 4c-4) and those recorded from naïve subjects (Fig. 4b-4) suggests that the model represented the task's dynamics reasonably well.

We next trained the model to draw circles in the force field (Fig. 4c-5). When the field was removed, the resulting direct after-effect (Fig. 4c-2) was similar to those recorded from subjects (Fig. 4b-2). Finally, we trained the model to reach to 8 target directions in a curl field (movement period was 0.5 seconds, 192 trials) and then fixed the model weights and drew a circle (6.25 cm radius, period of 2 seconds) in the same field. Fig. 4c-6 shows that the resulting trajectory in the field and Fig. 4c-3 shows the resulting transferred after-effect. We observed significant transfer from the reaching to the circle trials both in terms of similarity of after-effects in the direct and transferred conditions (Fig. 4c-2 and 3), and improvement in ability to draw a circle in the field (Fig. 4c-5 and 6). Over all, the model showed much of the transfer characteristics in reaching and circle drawings reported by Conditt et al. (1997).

3.4 Adaptation and generalization in fields that depend on both position and velocity

Spindle-like bases exhibit a gain-field property, i.e., directional tuning is modulated as a function of limb position (Fig. 2). Basis functions with gain-field properties are thought to be able to account for a series of human psychophysical experimental data (Hwang et al., 2003). Here, we tested if our spindle-like basis model could reproduce such experimental data.

3.4.1 Experimental methods and results

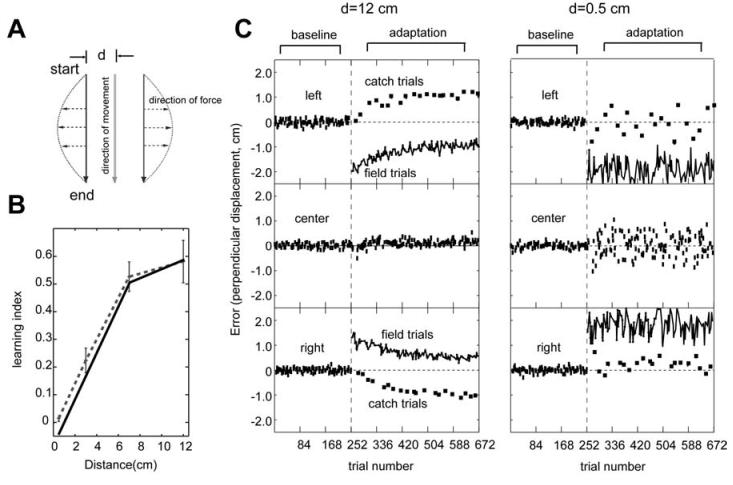
Figure 5a displays the experimental setup. Subjects made movements to the same direction but from three different starting locations, separated by distance d in a horizontal plane. These three different starting locations were randomly intermixed at an equal probability throughout the experiment. Since the direction of these three movements is constant, the joint angular velocity profile of the three movements is identical. A velocity dependent curl force field similar to that in the previous section was applied to the three movements. However, in this experiment, the viscous field was a function of the start location. The coefficient matrices were $\left[\begin{array}{cc}\hfill 0\hfill & \hfill -13\hfill \\ \hfill 13\hfill & \hfill 0\hfill \end{array}\right],0$, and $\left[\begin{array}{cc}\hfill 0\hfill & \hfill 13\hfill \\ \hfill -13\hfill & \hfill 0\hfill \end{array}\right]$ for the left, center and right locations, respectively. The performance of subjects was evaluated by measuring the perpendicular error (p.e.), which is the perpendicular distance from the straight line at 250 ms into the movement. Then, learning index was calculated using $\mathit{Learning}\mathit{Index}=\frac{p.e{.}_{\mathrm{catch}\mathrm{trial}}}{p.e{.}_{\mathrm{catch}\mathrm{trial}}-p.e{.}_{\mathrm{field}\mathrm{trial}}}$. Note that we used the average perpendicular errors across all the catch trials and field trials in the last 84 movement bin for the learning index reported here. When the subject learns this force field completely, the learning index becomes one as the perpendicular error in the field trials becomes zero. The result was that performance in this field improved as the separation distance increased (Fig. 5b, redrawn from Hwang et al. 2003a).

Figure 5.

Simulation of adaptation to a position and velocity dependent force field. (A) The position-velocity dependent force field. (B) The learning performance in the force field described in (a) increases as a function of separation distance. The dotted line is the experimental data excerpted from Hwang et al. (2003) and solid line is the simulation data. (C) Reach errors as a function of trial number in distances of d=12cm and d=0.5cm, respectively (d refers to distance between movements in (a)). Errors for the left, center and right reach trials are plotted in the top, middle and bottom panels, respectively. In the adaptation sets, the squares represent catch trials and the connected lines represent field trials.

3.4.2 Simulation results

The same 64 spindle-like basis functions that were used in the previous simulation were used here. The subplots in Figure 5c display trial-by-trial perpendicular errors produced by the simulation when the separation distance was 12 cm and 0.5 cm, respectively. Note the increased “noise” in the center movement when d was small. This noise is a result of generalization of errors from movements at “left” and “right” to the “center” movement. A very similar pattern of increased noise was observed in reaching of volunteers (Hwang et al., 2003).

As in the actual experiment, at d=12cm errors for the left and right simulated movements gradually decreased with training. On the other hand, at 0.5cm, movement errors remained almost constant throughout training, showing no adaptation. We quantified the learning performance of simulation for each separation distance using learning index. Figure 5b shows that the learning index from the simulation closely matched the previously reported experimental data (Hwang et al., 2003).

There are two key properties in the bases that account for the specific pattern of generalization shown in Fig. 5b. One property is the multiplicative interaction between position and velocity encodings in the basis elements. As the force field in these simulations is a nonlinear function of limb position and velocity, only bases with a nonlinear interaction can properly approximate the force field. The other property is the degree of position sensitivity of bases. About half of our bases had relatively high position sensitivities because their moment arms were long (λ =80 mm), allowing the force output to be monotonically modulated at a large separation distance. The steeper the average gain of the gain field among bases, the easier it is for the system to learn at smaller d. If the average moment arm that we used to build the model was longer (or shorter), the simulated learning would be better (or worse) than the learning that we had observed in our volunteers.

3.5 Generalization of viscous field learning across a large workspace

Shadmehr and Moussavi (2000) described an experiment where subjects trained in a velocity dependent curl field in one workspace (hand to the far left) and were then tested in a different workspace (hand to the far right). We simulated adaptation in this task using the same bases described earlier.

3.5.1 Experimental methods and results

In one group, subjects were trained to reach to 8 directions in a velocity dependent force field $(\stackrel{\rightharpoonup }{F}\left(t\right)=\left[\begin{array}{cc}\hfill 0\hfill & \hfill 13\hfill \\ \hfill -13\hfill & \hfill 0\hfill \end{array}\right]\cdot \stackrel{\rightharpoonup }{v}\left(t\right))$ at the left workspace (shoulder flexed position) and then tested to reach to 8 directions in the same field at the right workspace (shoulder extended position). The distance between these two positions was about 80 cm. The performance of these subjects was compared to the performance of naïve subjects who were tested in the same force field at the right workspace without prior training at the left workspace. Figure 6a shows the performance from these two groups, using perpendicular errors. At the right workspace, the performance of the group with the prior training in the left workspace is significantly better than the performance of the naïve group, suggesting generalization of the force field learning across a large workspace.

Figure 6.

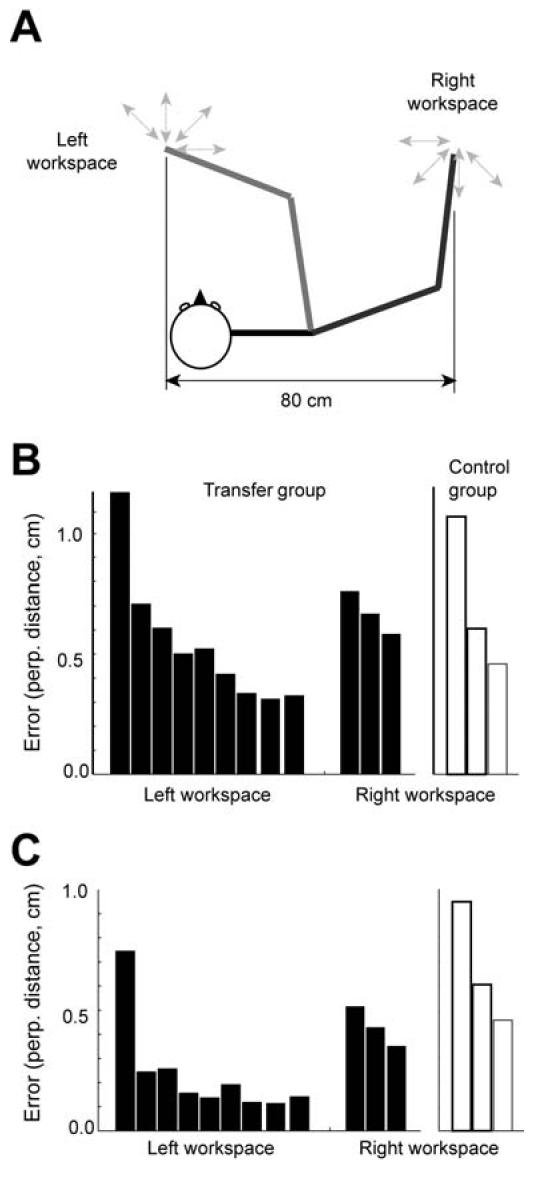
Simulation of viscous field learning and transfer across a large workspace. (A) Subjects trained at the left workspace and then were tested in the right workspace. (B) Experimental data from Shadmehr and Moussavi (2000). Each bar indicates the mean perpendicular error for a 64 movement bin. Black bars are errors for the transfer group and white bars are for the naïve group. After this initial training, the subject was then exposed to the same field at the right workspace (80 cm to the right of the trained workspace). (C) Simulation result. In the transfer group, the model was trained for the viscous field at the left workspace first and then tested at the right workspace. In the naïve group, the model was trained for the viscous field at the right workspace without initial training at the left workspace.

3.5.1 Simulation results

The model was trained to reach to targets at the left workspace and then tested at the right workspace, 80 cm away from the training location. Figure 6b shows errors in the left and right workspaces for the transfer and naïve conditions in the same format as the experimental data. The model showed transfer across a large workspace, reproducing the experimental result.

Note that in this experiment, the bases generalized very broadly across the workspace. Yet, in the results presented above, the same bases under a different training protocol displayed local spatial generalization, allowing adaptation to take place when opposite fields were present at a distance of 12 cm. What property of the basis set allows such flexibility? The important property is the sensitivity of directional tuning to changes in limb position. When the model is trained in a velocity dependent field at the left workspace, all the bases with relatively large activity at the left workspace contribute to adaptation by changing their corresponding weight vectors. However, this change of weight will be generalized only if the activity of the bases does not decrease significantly at the right workspace. Thus, the observed transfer in the simulation was due to the bases that maintained relatively high activity throughout the workspace. These bases had a gain field that was gentle (λ =8 mm). In contrast, these bases with gentle gain fields did not contribute to the adaptation process shown in Fig. 5 because their activity was almost constant at the left, center and right locations, causing the corresponding weight vectors to adapt to nearly zero, which was the average force across the three locations.

These simulations predict that among the neurons that represent the internal model (perhaps in the motor cortex), adaptation in the task of Fig. 5 produces changes in tuning among mostly the cells that have steep gain fields, whereas adaptation in the task of Fig. 6 will produce changes among cells that have gentle gain fields. The proportion of steep to gentle gain field cells is the most important factor that determines how close two movements can be before adaptation to opposite forces becomes difficult.

3.6 Adaptation to an acceleration dependent curl field

In our theoretical framework, the adaptation ability of the system depends on the shape of the bases (Atkeson, 1989). The output of the spindle-like bases during a point-to-point movement is highly correlated with the velocity profile but is less representative of limb acceleration (Fig. 2a). Thus, our simulated adaptive system will adapt more easily to a velocity dependent field than an acceleration dependent one.

3.6.1 Model prediction

To demonstrate this idea, we simulated adaptation to an acceleration dependent curl field, $\stackrel{\rightharpoonup }{F}=\left[\begin{array}{cc}\hfill 0\hfill & \hfill -2\hfill \\ \hfill 2\hfill & \hfill 0\hfill \end{array}\right]\cdot \stackrel{\rightharpoonup }{a}$ where $\stackrel{\rightharpoonup }{a}$ is a 2×1 acceleration vector. The movements were 15 cm long, straight toward the body in 550 ms. Figure 7a and b show simulated hand paths from the early and late training phases. The acceleration dependent curl field switches the direction of perturbation in the middle of a movement as the hand starts decelerating. For example, for the downward movement in Figure 7a, the force pushes the hand to the right while the hand accelerates in the first half of the movement and starts pulling the hand back to the left once the hand decelerates. Because of this change of force direction, this force field causes a large spiral movement when the internal model expects zero external force (Figure 7a). However, with training, the internal model adapts to approximate the external force (correlation coefficient = 0.87). Figure 7c shows that the internal model learned to produce a force profile that was correlated to the external force. Accordingly, simulated movement in the late training phase became straighter and produced a smaller spiral.

Figure 7.

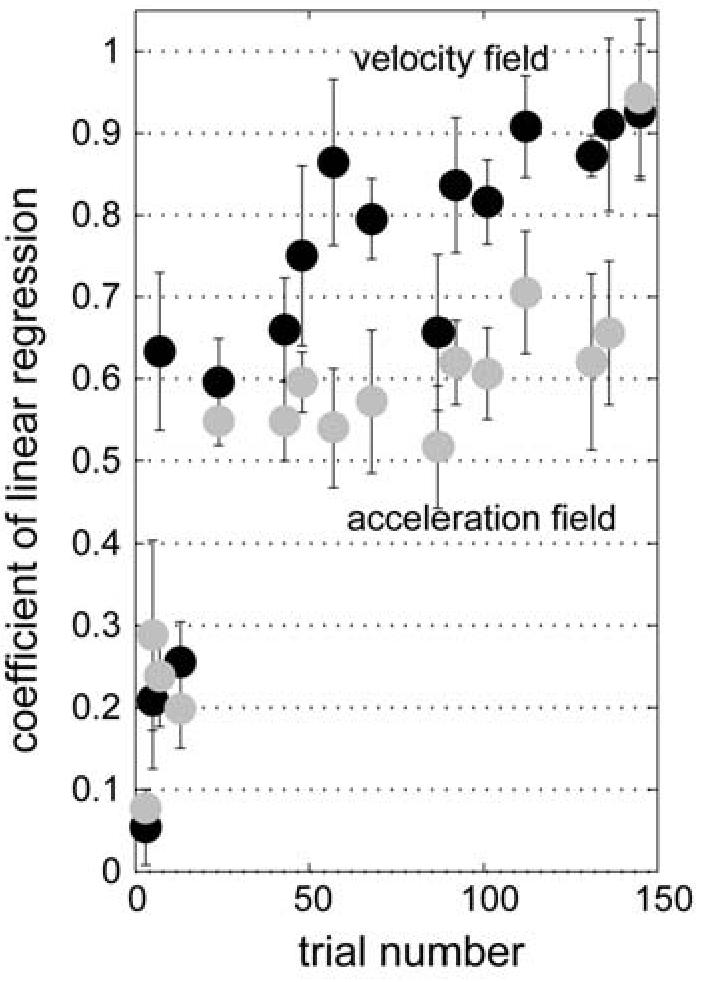
Simulation of adaptation to an acceleration dependent curl field using a spindle-like basis set. (A) Hand paths from the early phase of training. (B) Hand paths from the late phase of training. (C) The grey line represents the acceleration dependent forces applied to the simulated arm in the direction perpendicular to the movement direction as a function of time. The black line represents the predicted forces by the spindle-like basis elements after training.

However, the approximated force for the acceleration dependent field was not as good as the approximated force for the velocity dependent field. This discrepancy occurs despite the fact that training in the acceleration-dependent field (480 trials) lasted more than twice as long as in the velocity dependent field (200 trials). Therefore, although an internal model with spindle-like bases could adapt to an acceleration dependent force, the model predicts that the adaptation rate will be much slower than in a velocity dependent field.

3.6.2 Experimental methods

We tested this prediction by training six subjects to adapt to both a velocity dependent curl field, $\stackrel{\rightharpoonup }{F}\left(t\right)=\left[\begin{array}{cc}\hfill 0\hfill & \hfill -13\hfill \\ \hfill 13\hfill & \hfill 0\hfill \end{array}\right]\cdot \stackrel{\rightharpoonup }{v}\left(t\right)$, and an acceleration dependent curl field, $\stackrel{\rightharpoonup }{F}=\left[\begin{array}{cc}\hfill 0\hfill & \hfill -2\hfill \\ \hfill 2\hfill & \hfill 0\hfill \end{array}\right]\cdot \stackrel{\rightharpoonup }{a}$. The sizes of the matrices were chosen so that for a typical movement, the peak force was similar. Subjects repeatedly made 15 cm movements from the center of the workspace toward a single target in two different sessions; one in a velocity dependent force field and the other in a acceleration dependent force field. We counter-balanced the order of training and compared the adaptation rates.

In order to quantify the degree of adaptation, we measured the force that the subject produced on the handle in a small number of trials where the robot produced a force channel (Scheidt et al., 2000). The robot creates a force channel by exerting a force on the hand of the subject that is equal and opposite to the component of the force the subject exerts on the robot's handle perpendicular to the direction of motion. Therefore, the hand will travel near a straight line to the target. However, the force that the subject produces perpendicular to the direction of motion is precisely the force that the CNS predicts to be required for compensation of the “expected” field. In this way, Scheidt et al. (2000) introduced an elegant way of measuring the output of the internal model.

In each trial, we measured the force temporal profile that the subjects exerted on the handle and linearly regressed that force to the ideal compensation force (which was equal and opposite force to the external perturbation force). For example, if the subject produced the perfect compensation force, these two forces will be identical and the coefficient (the slope) of the linear regression would be one.

3.6.3 Experimental results

Figure 8 shows the coefficient of this linear regression as a function of trial number. To compare subjects' learning performance in the two different fields, we computed a performance index by averaging the linear regression coefficients across trial numbers and subtracted the performance index of the acceleration dependent field from that of the velocity dependent field. The mean difference of the performance indices was 0.15±0.08 (mean ± one standard deviation), suggesting that the subjects learned the velocity dependent field significantly better than the acceleration dependent field (one sided t-test, t=4.72, d.f.=5, p=0.0026). We also measured the time constant of the time series of the linear regression coefficient for each field using an exponential fit: time constant of velocity dependent field, τ = 49.4 ± 7.5 , 95% confidence interval, r² = 0.63; time constant of acceleration dependent field, τ = 71.8 ± 16.8 , r² = 0.53. The significantly slower adaptation rate in the acceleration dependent field is consistent with the poor coding of this signal among the spindle-like bases.

Figure 8.

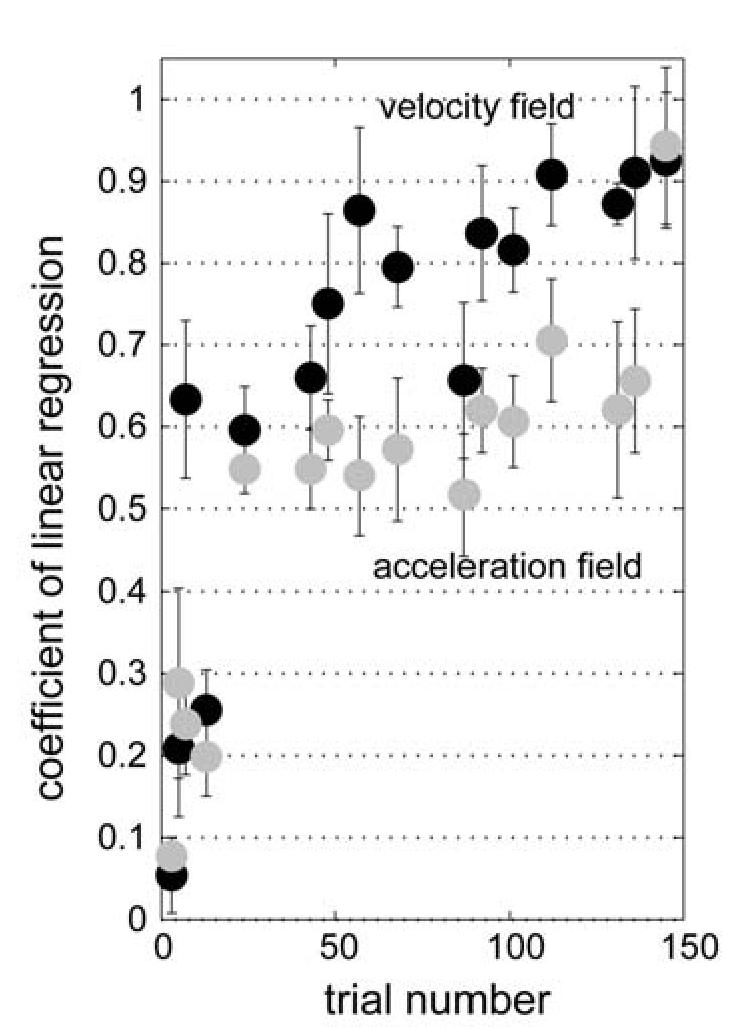
Performance in velocity and acceleration-dependent fields. The figure shows the coefficient of a linear regression between the subject's compensation force and external perturbation force as a function of trial number in the velocity dependent curl field training (black dots) and in the acceleration dependent curl field training (grey dots). Error bars represent S.E.M. for six subjects. The same six subjects trained in both fields in a counter-balanced order. Average performance in the acceleration field was significantly worse than velocity field (t-test, p<0.01).

4 Discussion

We hypothesized that the neural encoding of the internal model of arm dynamics in the brain might be via elements that represent state of the limb with functions that are similar to the coding found in the discharge of muscle spindle afferents. Two ideas motivated this hypothesis: 1) reflex based error-feedback from the spinal cord might act as a teaching signal to an internal model in the brain (Kawato, 1989; Thoroughman and Shadmehr, 1999). In this situation, the states in which errors are experienced are reported to the CNS in proprioceptive coordinates; and 2) the desired sensory state in a sensorimotor transformation may be represented in the CNS in terms of the response that the sensory system transmits when the desired state is actually attained. To test the hypothesis, we formed a basis set in which the response of each basis resembled the response of muscle spindles in whole arm movements. Some of the basis functions showed gain-field like tuning properties, i.e. nonlinear combinations of velocity and position coding. We found that the spindle-like representation could reproduce behavioral results from adaptation studies in velocity and position dependent force fields. Because the spindle-like bases were affected by limb acceleration but this coding was not as significant a factor as the sensitivity to limb velocity, the model predicted and we confirmed poorer ability to learn an acceleration dependent field.

There are a number of short-comings in our model. The spindle model that we used (Hasan, 1983) assumed a constant level of γ motoneuron activity during a movement. This is an oversimplification, of course, yet it is quite remarkable how well the model reproduced the activity of spindle afferents during active movements. For example, Prochazka and Gorassini (1998a) estimated that during free walking of a cat at various speeds, the current model could account for roughly 85% of the variance in the temporal discharge. Neural recordings from human wrist muscle spindle afferents show very similar discharge patterns to that shown in Fig. 1 (Jones et al., 2001). However, the model's ability to predict spindle discharge is not universal. Prochazka and Gorassini (1998b) tested a similar model on the triceps surae muscle of the freely moving cat and found that in case of this muscle, amount of triceps EMG activity that mimicked γ motor action linked to muscle activation did affect the fit of the model, reducing the r-squares by about half (from 0.85 to 0.43). This suggests that the model will improve if it takes into account at least some of the temporal dynamics of γ fusimotor action linked to extrafusal muscle activity (Prochazka and Gorassini, 1998b). Thus, the consideration of γ fusimotor action might change the tuning property and pattern of generalization in some cases.

Spindle afferents are not the only proprioceptive sensors that provide signals regarding muscle states. For example, Golgi tendon organs (GTO) are very sensitive to muscle tension (Gregory et al., 2002; Houk and Simon, 1967). If the desired sensory consequences of limb movement are represented centrally by a neural code that resembles the responses of peripheral sensors, then the representation will include GTO-like bases as well as spindle-like bases. This enriches the bases set to include sensitivity to not only kinematic variables like position and velocity, but also force. For example, a recent report used bias force during reaching as a cue to distinguish between two velocity dependent fields (Kurtzer et al., 2005). The subjects learned the task. The basis set used in the current report cannot learn such a field, but adding GTO-like bases would likely add this ability to the model, and would predict patterns of generalization that can be easily tested.

We used a simple linear conversion from a whole arm movement to a muscle length using a constant moment arm. However, anatomical studies show that the moment arm is not constant and varies as a function of arm orientation (Murray et al., 1995). Furthermore, we distributed the preferred joint displacement uniformly across all directions, but the distribution of preferred directions of cells in the motor cortex depends on arm configuration and is often non-uniform (Scott and Kalaska, 1997). We think that a realistic biomechanical model of the arm could give rise to a spindle-like set of bases that could account for both the behavioral patterns of generalization observed in people and the distribution of preferred directions observed in the motor cortex.

Despite these simplifying assumptions of the spindle model, the idea that adaptation of reaching is largely due to bases that encode limb state in terms of proprioception agrees with much of the current data on behavioral patterns of adaptation. However, there is an important set of data that the model fails to account for. After right-handed individuals train in a force field with their right hand, they exhibit generalization to their left hand (Criscimagna-Hemminger et al., 2003). Of course, spindle-like bases cannot generalize across arms. Interestingly, this generalization is in the extrinsic coordinates of the task. The generalization across arms vanishes when the force field is presented gradually (Malfait and Ostry, 2004), but the gradual presentation does not affect generalization for the trained arm across the workspace (as in Fig. 5). These findings suggest that the generalization across arms may be due to visual cues that arise when large errors are present. Recent results from our lab are consistent with this idea, suggesting that visual cues can lead to awareness of the force patterns (Hwang et al., 2003). Therefore, we believe that the spindle-like bases are a good model of an implicit component of motor learning but cannot account for all aspects of performance. In summary, we report that spindle-like representation of desired limb states in the internal model of arm dynamics appears computationally and physiologically plausible.