Detection of Outbreaks from Time Series Data Using Wavelet Transform

Abstract

In this paper, we developed a new approach to detection of disease outbreaks based on wavelet transform. It is capable of dealing with two problems found in real-world time series data, namely, negative singularity and long-term trends, which may degrade the performance of current approaches to outbreak detection. To test this approach, we introduced artificail disease outbreaks and negative singularities into a real world dataset and applied it and two other algorithms—autoregressive (AR) and Multi-resolution Wavelet Auto-regressive (MWAR) — to this dataset. We compared the performance of these algorithms in terms of sensitivity, specificity and timeliness. The results showed that our approach had similar sensitivity and specificity and slightly better timeliness compared to the other two algorithms. When we introduced negative singularities, its performance did not degrade as much as the other two algorithms' performance. We conclude that our approach to detection, when compared to traditional approaches, may not be as susceptible to degradation of performance caused by negative singularities.

INTRODUCTION

A key research topic in the field of early-warning public health surveillance is the performance of algorithms used to detect outbreaks from surveillance data^1,5. In recent years, several algorithms have been proposed and applied, including AR, ARIMA, SARIMA, CuSUM, RLS, and Serfling.^1–5 Almost all are based on the idea of predicting the present data value from historical data, and then comparing the prediction with the observed value.

Real-world datasets present many challenges to the developers of such algorithms, including noisy data, periodic variations on several scales (which can include daily, weekly, monthly, and/or yearly periodicities), variations due to events other than public-health threats (for example, holidays), and long-term trends that do not vary periodically (for example, if the data are sales of over-the-counter medications, the long-term trend may increase as the number of retailers monitored increases, or as the market share of a single retailer increases). In this paper, we present an approach designed to address a problem in real-world datasets known formally in the signal-processing literature as negative singularity while also taking into account seasonal periodicity in data due to increased incidence of respiratory disease in winter.

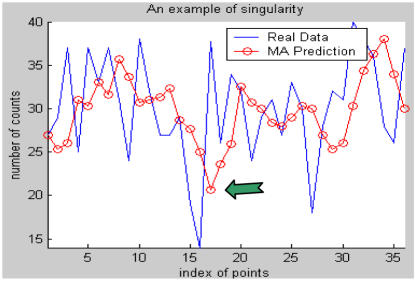
For the purposes of this study, we defined negative singularity in a time series as a data value significantly lower than the values that immediately precede and follow it, causing a discontinuity or a sudden break in the series (For a formal mathematical definition, see [6]). They are often the result of holidays and severe weather, when for example, fewer people go to the store to purchase over-the-counter medications or visit emergency rooms. Another common cause of negative singularities in real-time monitoring systems is network downtime, which may cause an absence of data for a time period. Negative singularities often cause false alarms in sliding window based algorithms (e.g. MA, AR, ARIMA). These abnormal points make the prediction for the data points that follow drop significantly (Figure 1). If the negative singularity lowers the prediction enough, then it will cause the data points that follow—which in the absence of any abnormalities, return to usual levels—to exceed the prediction enough to trigger an alarm.

Figure 1.

An example of singularity problem. At the time point indicated by the green arrow, an alarm sounds, because the actual signal greatly exceeds the prediction (which is depressed by the singularity occurring in the preceding time interval)

In this paper, we introduce a Wavelet-based Anomaly Detector (WAD) that we designed to be robust to the presence of negative singularities. We hypothesized that its performance would be comparable to existing algorithms for outbreak detection in a dataset with no negative singularities, but would remain high when we introduced negative singularities whereas the performance of exiting algorithms would suffer.

METHODS

Wavelet Transform

Wavelet transforms are often applied in the fields of signal and image processing. They transform a signal into different frequency bands by dilating and translating two basis functions.⁷ They derive from the spectral decomposition theorem, which states that any time series can be broken down into multiple statistically independent time series—called resolutions, each representing the contribution of oscillations of different frequencies.¹¹ The lower the frequency, the longer the trend that a given resolution reflects. By summing all the resolutions, we can exactly reconstruct the original data. Furthermore, unlike moving averages, wavelet decomposition does not introduce a time-delay into the signal—the temporal information of the raw data is preserved in each resolution. In other words, the oscillations in each resolution are not phase shifted relative to the original time series.

Using wavelet transform, researchers developed multiresolution-based predictors^7–9. Those predictors first decompose a time series into several resolutions. Then, they make a one-step prediction independently for every resolution. The combination of all the predictions for all the resolutions is then summed to obtain the expected value for the current data point. The model applied to each individual resolution to make predictions can be a neural network ⁸, AR⁹, or any other time series analysis algorithm.

Wavelet-based Anomaly Detector (WAD)

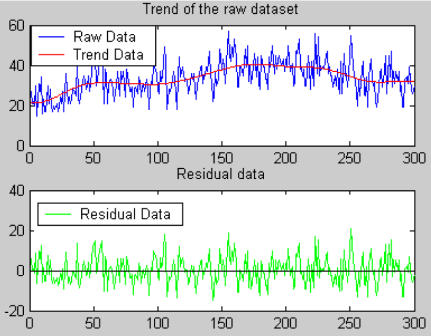
Instead of employing all the wavelet resolutions, we focus on the lowest frequency level (baseline), and developed an algorithm, named Wavelet-based Anomaly Detector (WAD). WAD removes seasonal periodicity by subtracting a long-term trend from a time series. (figure 2) When detecting an outbreak on day_i:

Figure 2.

An illustration of wavelet transform. Subplot 1 presents the raw dataset and its trend, which is the lowest frequency series among 5 levels of wavelet decompositions. The trend subtracted from raw data gives the residual data presented in subplot 2.

1. Use wavelet transform to construct the baseline of the historic time series (from day₁ to day_i−1), which represents the long term trend (Trend Data)

2. Remove long term trend from the time series to obtain residual of day₁ to day_i−1 (Residual Data)

3. Obtian day_i’s residual by subtracting day_i−1‘s trend value from day_i

4. Signal an alarm when day_i‘s residual value exceeds the alarm threshold, which is based on the statistical distribution of historical residual values.

In our experiments, we noted that the residual data for a time series created from emergency department (ED) visits with a respiratory chief complaint (discussed in the next section) roughly follow a normal distribution (Figure 3), so we selected alert threshold values as positive multiples of the standard deviation of the residual time series (we ignore significantly low values).

Figure 3.

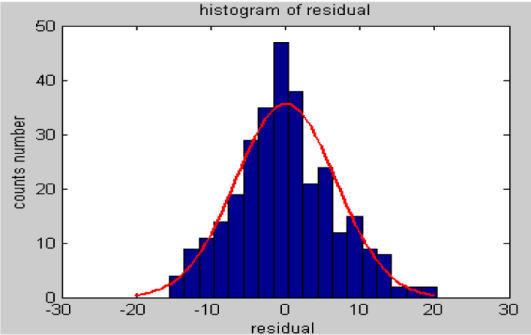
Plot of the residuals, which roughly follow normal distribution.

There are two important differences between WAD and multi-resolution-based predictors. First, instead of decomposing the time series into multiple resolutions, WAD derives only one low-frequency (on the scale of months) resolution, and then subtracts that resolution from the original signal. We detect outbreaks in the residual of the long-term trend. Second, WAD does not apply a complex model to the residual data.

In this study, we used the 5th level of the wavelet transform to remove seasonality with a period more than 32 days, such as the annual wintertime increase in respiratory illness. After this transformation the residual presents a theoretical mean of zero that does not change over time and a variance that does not vary periodically (a mathematical proof can be found in [11]). Note that negative singularities become negative values in the residual.

Dataset

To test the performance of WAD, we compared WAD to AR and a multi-resolution (5 levels) AR predictor (MWAR), both of which used a 3-day slide window, on a real world dataset. The comparison is carried out in a real time mode, which means when detecting a possible outbreak on day_i, the data value beyond this point are unseen for all the algorithms. The dataset was a collection of ED visits of patients with respiratory prodrome from several hospitals in Pittsburgh. The study period was Aug 1, 2000 to May 27, 2001, a total of 300 days. Figure 4 shows a plot of the data. The training period comprises the first 200 days of the study period. The test period comprises the remaining 100 days in the study period (the period after the vertical dashed line in Figure 4). To our knowledge, no significant outbreaks of respiratory disease or negative singularities occurred during the study period.

Figure 4.

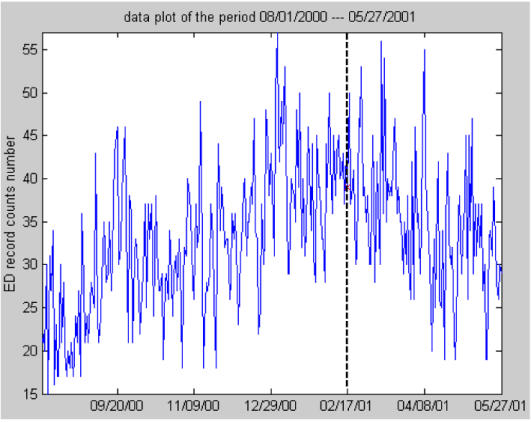
Plot of the whole dataset from 08/01/2000 to 05/27/2001. Training and testing dataset are separated by the dashed line.

Outbreak Simulation

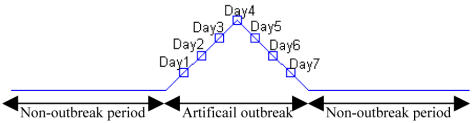
Because there were no known outbreaks during the study period, we assumed artificial outbreaks by adding a certain number of visits with respiratory prodrome to the original data. We modeled the distribution of cases over the 7-day period using the following function: 0.4, 0.8, 1.2, 1.6, 1.2, 0.8 and 0.4 times the standard deviation of the whole dataset from the first day through the 7th day, respectively. The shape of the artificial outbreak is illustrated in Figure 5. We created multiple test datasets by adding the outbreak starting on each day of the test period, resulting in a total of 94 test datasets (each dataset has an artificial outbreak starting on one of the first 94 days of the test period).

Figure 5.

Illustration of the artificial spike with a duration of 7 days, which is multiple times the standard deviation of the whole dataset in respective days.

To test the algorithms’ performance in the presence of negative singularity, we randomly picked 2 days in each dataset, and introduced negative singularities on those days by reducing the counts on those two days to 10% of their original value. Then we recomputed the performance of each algorithm, and compared the results pre and post introduction of those singularities.

Measurements

We defined a true positive alarm to be any alarm within the outbreak time window. Any alarm that occurred outside the 7-day duration is regarded as a false alarm. Accordingly, we computed sensitivity, specificity, and area under the ROC curve as follows:

Sensitivity: number of true alarms within the outbreak period/total number of spikes over all test datasets.

Specificity: number of non-alarm days in each test dataset/total number of days in all test datasets.

We plotted sensitivity and specificity on ROC curves¹² by varying the detection threshold as multiple times standard deviation of the monitor data (from 0 to 5 with a step of 0.1. A threshold out of this range made the sensitivity and specificity of all three algorithms 0 or 1 in the experiments).

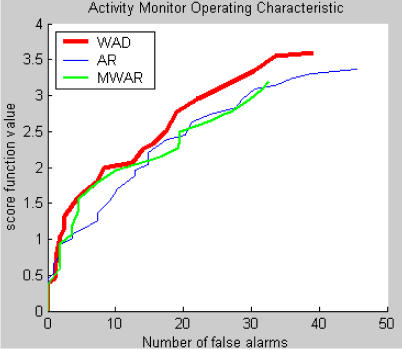
To compare the timeliness of outbreak detection of the three algorithms, we also performed an AMOC (Activity Monitor Operating Characteristic) analysis¹⁰. In an AMOC analysis, the X-axis is the number of false alarms and the Y-axis represents the benefit of a true alarm. For the purposes of this study, we define benefit as the timeliness of a true alarm relative to the 4^th day of the outbreak. Therefore, we computed the benefit score as 5-t, for t<=4, where t is the day when the alarm is signaled. Specifically, if the alarm sounds on day 1, the Y axis will take value 4. If it sounds on day 5 or later, then the benefit score is zero. Note that the higher the score, the earlier the detection of the artificial outbreak.

RESULTS

Figure 6 illustrates the performance of the three algorithms as ROC curves. While MWAR does not show much improvement compared with AR model, WAD’s ROC curve is higher than the other two plots at almost every detection threshold value. The area under the ROC curve for WAD is larger than the areas under the ROC curves for AR and MWAR (Table 1). In the AMOC analysis, WAD obtained a higher score for every detection threshold (Figure 7). In other words, WAD consistently detected the artificial outbreaks earlier than the other two algorithms.

Figure 6.

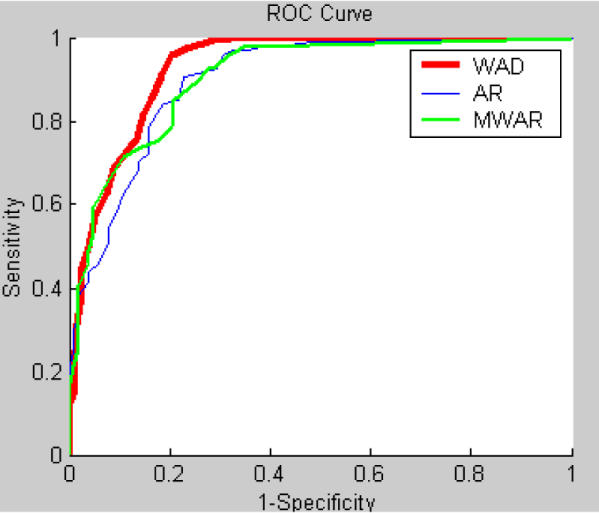
ROC curve of three algorithms

Table 1.

Area under the ROC curve of three algorithms

Algorithms	AR	WMAR	WAD
Area Under Curve	0.9002	0.9049	0.9208

Figure 7.

AMOC curve of three algorithms

When simulated negative singularities were introduced into the test datasets, the performance of the detection algorithms, as measured by area under the ROC curves, decreased (Table 2). The area under the ROC curve decreased by 0.0114 for AR, by 0.0175 for MWAR, and by 0.0052 for WAD.

Table 2.

Area under the ROC curve of three algorithms

Algorithms	AR	WMAR	WAD
Area Under Curve	0.8888	0.8874	0.9156

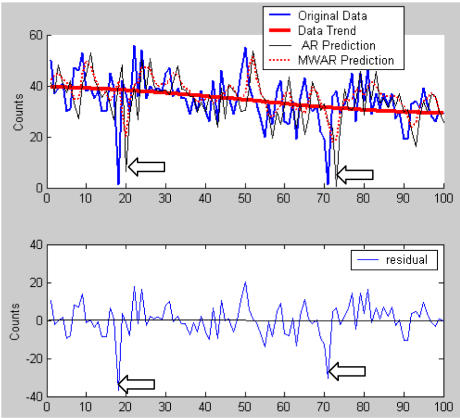
Figure 8 shows how both AR and MWAR models try to exactly reconstruct the real data, and in fact, it did a reasonable job except for an obvious time delay. However, a false alarm was raised because of the negative singularity point. On the contrary, the negative singularity has virtually no effect on WAD’s trend, and it is unable to create a high residual value of the following day in detection stage. As a result, the negative singularity lowers the performance of AR and MWAR to a greater extent than WAD.

Figure 8.

Subplot 1 illustrates the raw dataset with 2 simulated singularities and the prediction values of AR and MWAR, as well as the trend generated by wavelet decomposition. The following days of negative singularities do not present a significant high value in residual data, which is presented in subplot 2, while the prediction values of these days, obtained from AR and MWAR, exceed the monitor value quit a lot.

DISCUSSION

WAD had comparable performance to AR and MWAR for the detection of outbreaks. Notably, it had a slightly, yet consistently, better timeliness of outbreak detection than AR and MWAR. When we introduced just two negative singularities, however, the performance of AR and MWAR—as measured by area under the ROC curve—degraded to a larger extent than WAD. We therefore conclude that the performance of WAD on data with negative singularities may degrade to a lesser extent than the performance of existing algorithms.

The reason that negative singularity points affect WAD’s performance less than AR and MWAR is that those points have little influence on the long-term trend of the time series, and WAD does not signal alarms on the residual points which follow the significantly negative residual values that result from negative singularities. Other methods deal with negative singularities by using a larger moving-average time window to calculate the current prediction value, so that they dilute the singularity point’s effect on the prediction. However, larger windows cause longer time delays (or phase shifts) relative to the original signal, risking delays in outbreak detection (that is, a decrease in timeliness).

We expected WAD to outperform AR when no singularities are present because WAD addresses the problem of long-term trends in time series (mean and variance change with time), but AR does not. The reason that long-term trends in data degrade the performance of AR is that AR typically uses a narrow time window (3 days window in our experiments) to predict a value, so that local fluctuations bias its predictions for the long-term trend. When the long-term trend is increasing, the values predicted by AR are usually lower than the real data. In that case, the algorithm will be more sensitive to noise in the positive direction, causing false alarms. On the other hand, when the long-term trend is decreasing, the predicted values tend to be higher than actual data, so that real increases in the data due to outbreaks are missed, or detected later than they otherwise might have been.

MWAR, on the other hand, does address seasonal trends in time series by applying wavelet transform to generate multiple time series each of which has a mean and variance that do not change with time. Thus, the fact that MWAR did not outperform AR in the absence of negative singularities is surprising. Repetition of this result using different sets of ED data, different data types (such as over-the-counter sales), outbreak sizes and shapes, and so on would be necessary in our future work to conclusively demonstrate that MWAR has no added value over AR, which is unlikely. It could be that the performances were similar due to certain attributes of the dataset, outbreak size and shape, and so on that we used in this study.

WAD does not introduce a phase shift or time delay in the residual relative to the original signal. That is the most likely reason it had improved timeliness of detection over AR and MWAR in the AMOC analysis.

An advantage of WAD over MWAR is computational expense. MWAR requires n+1 wavelet transforms to decompose the raw data into n+1 resolutions, where n is the maximum level of resolution, and it applies AR n+1 times (once per resolution). WAD, on the other hand, only performs one wavelet transform to remove the long-term trend and then applies a simple detection algorithm to the residual data once. Because the wavelet transform computation dominates the overall efficiency of the detection system, WAD is faster than MWAR.

WAD is also characterized by its simplicity in the following two aspects. First, unlike SARIMA or Serfling methods, WAD does not need multiple years of training data. For instance, WAD only needs a minimum of 32 historic points to calculate the standard deviation of the residual for use in setting detection thresholds. The reason we used 200 days of training period was to better train the AR model without possible short-term biases. Second, WAD is a non-parametric model, so the user does not have to do all the adjustments of parameters as in the majority of traditional algorithms.

One potential drawback to WAD is that if the real outbreak lasts for more than 2ⁱ points, where i is the level of wavelet transform (in our study, i is equal to 5), the oscillation caused by the outbreak may be removed by wavelet transform, so that WAD will not detect the outbreak. We expect that a bioterrorism attack will cause a significant increase of short enough duration that this problem will not cause WAD to miss a bioterrorism attack. Nevertheless, it is not a given and thus it is important to be aware of this limitation.