An Analytic Framework for Space–Time Aberrancy Detection in Public Health Surveillance Data

Abstract

Public health surveillance is changing in response to concerns about bioterrorism, which have increased the pressure for early detection of epidemics. Rapid detection necessitates following multiple non-specific indicators and accounting for spatial structure. No single analytic method can meet all of these requirements for all data sources and all surveillance goals. Analytic methods must be selected and configured to meet a surveillance goal, but there are no uniform criteria to guide the selection and configuration process. In this paper, we describe work towards the development of an analytic framework for space–time aberrancy detection in public health surveillance data. The framework decomposes surveillance analysis into sub-tasks and identifies knowledge that can facilitate selection of methods to accomplish sub-tasks.

INTRODUCTION

Public health surveillance is changing. Until recently, the standard surveillance approach was to monitor a single diagnostic indicator, which contained a strong signal for a specific disease. Heightened concerns about bioterrorism are forcing changes to this model. Now, public health departments are under pressure to follow non-specific pre-diagnostic indicators, which are often drawn from many data sources. In addition, there is the expectation that spatial information will be used to facilitate the detection and localization of epidemics.

The requirements of pre-diagnostic surveillance, following multiple non-specific indicators and accounting for spatial structure, cannot be met by a single analytic method for all data sources and surveillance goals. As a simple example, a control chart can quickly detect a large shift in a time series, but a control chart will not perform as well for a slowly increasing shift, which would be better detected by a cumulative sum (cusum) method. Continuing with this example, there are many ways to determine the decision threshold for a control chart or cusum, and different approaches may result in different detection characteristics. This example illustrates two concepts. First, aberrancy detection involves generic tasks (e.g., comparing observed data to a measure of expectation), which can be accomplished by different analytic methods (e.g., control chart, cusum). Second, knowledge exists to guide the selection and configuration of analytic methods for generic tasks.

These two observations – (1) that aberrancy detection involves generic tasks which can be accomplished by different methods; and (2) that knowledge exists to guide the selection of methods – suggest that it may be possible to decompose the task of space–time aberrancy detection into generic sub-tasks, and to model the knowledge used to select appropriate methods for the sub-tasks. When taken together, the task decomposition and the knowledge used to select appropriate analytic methods constitute an analytic framework for space–time aberrancy detection in public health surveillance data.

An obvious role for such a framework is to guide the identification of analytic methods that may be suitable for a specific analysis. A framework of this nature should also help to clarify the similarities and differences of current analytic methods, by providing a “knowledge-level” description [Newell, 1980] of the aberrancy detection process. In this paper, we describe work toward the development of an analytic framework for space–time aberrancy detection in public health surveillance data. This research is part of the BioSTORM (Biological Spatio-Temporal Outbreak Reasoning Module) project, which aims to develop and evaluate knowledge-based surveillance methods [Buckeridge et al., 2002].

TASK ANALYSIS

Our approach to developing an analytic framework builds upon work on task analysis in the artificial-intelligence and knowledge-modeling communities. In 1980 Alan Newell introduced the concept of the “knowledge level” [Newell, 1980]. Roughly speaking, his point was that in developing intelligent systems, one should first consider the task addressed by the system and the knowledge needed to complete the task (i.e., the “knowledge level”) before becoming bogged down in the mechanics of completing the task and representing knowledge (i.e., the “symbol level”).

In the subsequent decades, researchers in the knowledge-acquisition community developed approaches to modeling knowledge-intensive tasks and applied these methods to develop “knowledge level” models of tasks such as diagnosis and design [Chandrasekaran, 1986; Steels, 1990]. These modeling approaches decompose tasks into sub-tasks and then identify a method that either further decomposes a sub-task, or directly accomplishes the sub-task. For example, diagnosis can be decomposed into the sub-tasks of symptom detection, hypothesis generation, and hypothesis discrimination [Benjamins & Jansweijer, 1994]. Symptom detection can either be further decomposed, or directly accomplished by a classification method [Benjamins & Jansweijer, 1994]. The goal of this type of modeling, referred to as task analysis, is to facilitate the acquisition and reuse of knowledge and analytic methods.

The work described in this paper has similarities to and differences from previous work on task analysis. Earlier work focussed on tasks such as diagnosis and design, which can be viewed as search problems with mainly qualitative inputs and outputs. Task analyses of diagnosis and design typically decompose the task into a small number of independent sub-tasks, with each sub-task accomplished by a knowledge-intensive method. While researchers have considered the problem of determining which methods possess the competence to accomplish a sub-task [Benjamins & Jansweijer, 1994], a solution to this problem has been elusive, possibly due to the nature of the methods used for tasks such as diagnosis.

The aberrancy-detection task is most often viewed as a statistical problem with quantitative inputs and outputs. Unlike methods for diagnosis, statistical methods for aberrancy detection are generally not knowledge-intensive in that they do not require qualitative knowledge to operate. As with most statistical problems, the essential knowledge for aberrancy detection is in the selection and configuration of the appropriate method or methods to address a specific situation, and in the interpretation of the results of these methods. A task analysis of aberrancy detection must therefore focus on identifying the knowledge needed to select and configure methods appropriate for sub-tasks, rather than on the knowledge used by methods to accomplish sub-tasks. Ultimately, such a framework should also consider the knowledge used to interpret and possibly to integrate the results of methods, but at the moment we limit our scope to the selection of appropriate methods for a task.

To summarize, previous work in task analysis has focussed on decomposing a generic task into subtasks, and identifying methods that rely upon qualitative knowledge to complete sub-tasks. Little progress has been made in modeling the knowledge used to select methods for a sub-task, and the ultimate goal of the task analysis has traditionally been to facilitate the reuse of knowledge representations and problem solving methods.

As with previous work on task analysis, we aim to identify a decomposition of the aberrancy detection task into sub-tasks, and identify methods that can address these sub-tasks. In contrast with previous work, we also aim to model the knowledge used to select a method for a sub-task. The limited knowledge requirements of statistical methods as compared to qualitative methods should be helpful in addressing this modeling task, which has been problematic for others in the past. Our primary goal is to develop an analytic framework that can guide the selection of methods for a specific surveillance analysis. This framework may enable automated configuration of aberrancy detection methods, but at this stage of our work we do not formalize the framework to the extent necessary for automation.

A DECOMPOSITION OF THE ABERRANCY DETECTION TASK

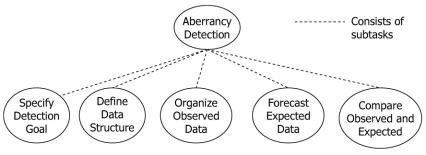
Through a review of surveillance literature and interaction with surveillance practitioners we have decomposed the task of aberrancy detection into five main sub-tasks: (1) specify detection goal, (2) define data structure for analysis, (3) organize observed data, (4) forecast expected data, and (5) compare observation and expectation. The decomposition is shown in Figure 1.

Figure 1.

Task decomposition of aberrancy detection. Ellipses indicate tasks.

Specification of a detection goal elicits knowledge of the expected aberrancy, and selection of a data structure for analysis attempts to structure the data in a manner that will facilitate aberrancy detection. The elicited knowledge and defined data structure both inform the selection of appropriate methods to complete the subsequent three sub-tasks. In the remainder of this section, we describe each sub-task and begin to consider the knowledge used to select methods for sub-tasks.

1. Specify a Detection Goal

The detection goal defines the type of aberrancy one intends to identify and the relative importance of performance characteristics such as sensitivity. In some situations, it may be possible to describe the expected aberrancy in detail, whereas in other situations very little may be known about the aberrancy that one is attempting to detect. Either way, this information helps to select appropriate methods. For example, knowledge of the expected spatial pattern may allow one to select a method optimized to detect that type of pattern [Waller & Jacquez, 1995], whereas limited knowledge of the expected aberrancy would suggest selection of a method with no specific alternate hypothesis [Wong et al., 2002].

Our initial approach to describing the expected aberrancy identifies temporal, spatial and attribute aspects of the aberrancy. The temporal aspect includes the rate and magnitude of change, while the spatial aspect includes the extent and scale of clustering. The attribute aspect of the expected aberrancy refers to those attributes of the data, other than space and time, that may be associated with the aberrancy. For example, the expected aberrancy might be more apparent in a specific set of diagnostic categories, in an age group, or in an occupation.

Performance characteristics of aberrancy detection include sensitivity, timeliness, and predictive value [Frisen, 1992]. Generally speaking, one performance characteristic is enhanced at the expense of another. Depending on the situation it may be possible to identify which performance characteristics are most important, or it may be desirable to weight all characteristics equally.

2. Define a Data Structure for Analysis

Data structure in this context means the stratification over attributes, the temporal resolution, and the spatial resolution of the data. The detection goal should inform the choice of data structure on the premise that knowledge of the expected aberrancy and desired performance characteristics can focus the aberrancy detection task towards specific aspects of the data.

If one is able to clearly define a detection goal, then this goal may strongly suggest a preferable data structure. For example, if the expected aberrancy is known to have a rapid onset, and timeliness of detection is an important performance characteristic, then it would be preferable to organize the data into high resolution temporal categories. Similarly, if the expected aberrancy is known to present as a spatial cluster, then it would be preferable to select a spatial resolution and zoning appropriate to the expected scale of clustering. Stratification over attributes refers to the categorization of data into groups based upon values of one or more variables. At a minimum, the detection goal should suggest stratification according to the main variable of interest (e.g., syndrome, diagnosis, or risk behaviour), but the detection goal may also suggest additional attributes for stratification. Choice of data structure must also take into count the frequency of events. At some combination of stratification and space-time resolution, events will become sparse. This may make it more difficult to detect aberrancy, and will influence the types of analytic methods that can be used.

In cases where the detection goal is not clearly defined, it may not be possible to clearly define a preferable data structure to limit the aberrancy detection task. As a result it may be necessary to use analytic methods that attempt to detect aberrancies over many attribute strata [Wong, Moore et al., 2002] or multiple spatial and temporal resolutions [Kulldorff, 1997].

3. Organize Observed Data

The observed data must be transformed into the structure defined for the analysis. This might be a trivial task that simply requires aggregating individual records into groups using look-up tables. For example, aggregating hospital visit records to syndrome and home address groups on the basis of ICD and ZIP codes. However, if the transformation from the raw data to the desired data structure is not so straightforward, this may require more complex methods. For example, classification of hospital visit records to syndromes using free-text chief complaint or electronic medical record data requires the use of methods more advanced than aggregation. Similarly, classification of home street address to ZIP requires more than a simple look-up function.

If the transformation from raw data to the structure required for analysis is straightforward, then the methods used to accomplish the transformation will likely have little effect on the overall aberrancy detection task. However, if approaches such as classification or georeferencing are required to transform the data, then the choice of methods may influence the overall aberrancy detection by introducing random or systematic error into the data.

4. Forecast Expected Data

Most approaches to aberrancy detection require a measure of expectation to which an observed value can be compared. The expected measure is usually derived from historical data, and often consists of a point estimate and possibly also a measure of variation around the point estimate. For example, time-series methods use moving average and autoregressive models to provide one-step-ahead forecasts and variance estimates. Other forecast methods for aspatial data include calculation of an arithmetic average (and variance) from historical values, and multiplication of a region-wide rate by a local measure of risk such as population.

Forecast methods for spatial data usually rely on one of two approaches. The first approach is to divide the region into tracts, and then use aspatial forecast methods for each tract [Raubertas, 1989]. The second approach is to compute a single statistic of spatial or space-time clustering for the entire region, and then derive a forecast for that statistic [Rogerson, 1997].

Selection of a forecasting method should be influenced by the detection goal, the characteristics of the observed data, and the method that will be used to compare observation and expectation. As an example of the influence of data characteristics on method selection, time-series methods are most appropriately used with data that satisfy a number of conditions (e.g., stationary, Gaussian distribution), and time-series methods are difficult to apply if there are missing values. In terms of the detection goal, it may be important to note that time-series methods incorporate immediately previous observations into the forecast and therefore the forecast value can quickly adjust to changes in the observed value. This adjustment of the expected value may affect detection characteristics.

5. Compare Observation and Expectation

Once observed and expected measures are in hand, there are many possible approaches to identifying aberrancy. The simplest approach, exemplified by the control chart, detects aberrancy if the observed measure exceeds the expected point estimate by some multiple of the variance of the point estimate. A similar approach is also used to compare observed values to expected values obtained through time-series forecasting methods, with the main difference being that the threshold is generally constant over time for a control chart, but varies over time in the time-series approach.

Another approach is to maintain a state variable of aberrancy, which is updated after each comparison of observation to expectation. The state variable accumulates deviation from expectation over time, and following each update, the variable is compared to a decision threshold, which is determined on the basis of desired performance characteristics as defined by the detection goal. A number of methods use this approach including the cumulative sum [Page, 1954], cumulative score [Wolter, 1987], and the sets method [Chen, 1978].

Methods used for spatial data are tightly linked to the approach used to forecast expected values. If a single expected measure of spatial or space-time clustering is calculated for the entire region, then this measure can be compared to the observed measure using a control chart or aberrancy state variable [Rogerson, 1997]. If expected measures are calculated for each tract within a region, then two approaches are possible. The first approach is to apply a separate control chart or aberrancy state method within each tract, and then make an aberrancy decision after correcting for the multiple comparisons made by looking at the tracts separately [Raubertas, 1989]. The second approach is to use a method that identifies focussed clustering of deviation from expectation over space and/or time among the tracts. An aberrancy decision is then made if detected clusters are unlikely to have occurred by chance [Kulldorff, 1997].

The selection and configuration of a method to compare observation to expectation should be based upon the detection goal and the characteristics of the data. For example, the expected aberrancy may be known to exhibit focussed spatial clustering at a known scale but at unknown location. This detection goal suggests that the data should be structured at an appropriate scale, and a spatial method optimized for detection of focussed clustering should be selected. The frequency of the observed events may provide further direction in selection among candidate methods.

DISCUSSION

We have described initial work towards the development of an analytic framework for space-time aberrancy detection in public health surveillance data. The framework includes a decomposition of the aberrancy detection task into sub-tasks, and the knowledge used to select analytic methods that can accomplish sub-tasks. Our initial decomposition identifies five sub-tasks: (1) specify detection goal, (2) define data structure for analysis, (3) organize observed data, (4) forecast expected data, and (5) compare observation and expectation. In this paper, we have described considerations in modeling the knowledge used to select methods, but have not yet begun to model this knowledge.

The analytic framework is intended to facilitate the selection and configuration of methods for a specific analysis. We have given a number of examples of how different aspects of the framework might be used to guide selection of methods for sub-tasks, but have not given an example of how the framework might be used to guide selection of methods for a complete analysis. Such an example will not have much value until we more formally identify the knowledge used to select analytic methods for subtasks, and further define the dependencies between sub-tasks.

The framework is also intended to illustrate and clarify the process of aberrancy detection, and in doing so provide a means for understanding the similarities and differences of analytic methods currently used for aberrancy detection. We have discussed how many methods used for aberrancy detection fit within our task decomposition, and we have used the decomposition to illustrate characteristics of these methods. However, there are many possible approaches to decomposing the task of aberrancy detection, and we do not claim that the decomposition presented in this paper is optimal or that it will encompass all possible methods.

An important consideration is whether sufficient knowledge exists to guide the selection of analytic methods. We have given examples of knowledge about some characteristics of a few methods, but little is known about the competence of many methods that might be used for aberrancy detection. While this will certainly limit the applicability of our analytic framework for method selection, it also creates an opportunity for the framework to be used in order to guide research on the competence of methods. Methods that might be used to address a similar sub-task, but for which there is insufficient knowledge to suggest using one method over the other, are candidates for empirical evaluation (e.g., using simulation studies) to determine the conditions under which one method might be preferable to the other. The knowledge obtained through this type of evaluation could then be used to guide the selection of methods.

Future work will focus on refining our task decomposition, modeling the knowledge used to select methods for sub-tasks, and identifying dependencies between sub-tasks. Once the framework has been more formally defined, we also intend to implement it within a knowledge-based system [O’Connor et al., 2001] in order to allow semi-automated selection and configuration of analytic methods.