Temporal Consistency Checking in Clinical Guidelines Acquisition and Execution: the GLARE’s Approach

Abstract

GLARE (GuideLine Acquisition, Representation and Execution) is a domain-independent system for the acquisition, representation and execution of clinical guidelines. Temporal constraints play an important role within clinical guidelines (e.g. to specify therapies). The treatment of such constraints is one of the distinguishing features of GLARE. During acquisition, GLARE supports (i) the representation and (ii) the checking of the consistency of the temporal constraints. Moreover, it (iii) automatically checks that the times of execution of specific actions respect the general temporal constraints described in the guideline. This treatment of temporal constraints involves the extension of various Artificial Intelligence (AI) techniques.

1 INTRODUCTION

Clinical guidelines are gaining a primary role in the medical field, and the design of computer-based managers of guidelines is becoming a key area of research in Artificial Intelligence (AI) in medicine and in medical decision-making. Many computer-assisted tools for guidelines management have been proposed in the literature (e.g.: Asbru [Shahar et al., 98], EON [Musen et al., 96], GLIF [Peleg & Boxwala, 00], GUIDE [Quaglini et al., 00], PROforma [Fox et al., 98]). In this paper, we describe GLARE [Terenziani et al., 01, 02], a domain-independent system supporting guideline acquisition, representation and execution. In particular we will focus on GLARE’s treatment of temporal constraints.

Temporal constraints play a fundamental role in both the description and the execution of clinical guidelines. As regards description, temporal constraints are an intrinsic part of most guidelines, especially as concerns therapeutic algorithms. In fact, therapies are usually characterized by constraints on the order (e.g., before, after, during) between clinical actions, on their duration, on their repetitions (possibly at periodic times) and on the delay between them. All these constraints must be acquired and represented (through an adequate representation language); moreover, since the set of such constraints tends to increase significantly with the dimension of the guidelines, an automatic way of checking their consistency must be provided. The temporal constraints represented in clinical guidelines are necessarily “general”, in the sense that they impose rules on all possible executions of the given guideline. Specific executions of actions in a guideline are accomplished at specific times (called action-execution times): obviously, action-execution times should be consistent with the general temporal constraints in the guideline itself. Since practical guidelines are usually made of more than one hundred actions, and contain various kinds of temporal constraints, checking temporally consistent executions cannot be performed directly by users. Thus, an automatic tool must be devised to this purpose as well. Although many different approaches in the clinical guideline literature recognized the importance of dealing with temporal constraints (see, e.g., [Keravnou, 96], [Shahar, 98], [Miksch & Kosara, 99]), none of them covered all the above issues. Neither did approaches in the AI field, where no general solution has been proposed to the integration of temporal constraints between classes of actions (such as those in the general guidelines) and instances of actions (such as the specific executions for specific patients), in a context in which also repeated/periodic actions are taken into account (see, e.g., the survey in [Vila, 94]). In this paper, after a brief summary of the system’s main features, we describe GLARE’s approach towards these tasks.

2 MAIN FEATURES OF GLARE

Representation formalism

To guarantee that GLARE can be used also by physicians not expert in Computer Science, we aimed at defining a limited set of clear representation primitives [Terenziani et al., 01]. GLARE distinguishes between atomic and composite actions (plans), where atomic actions represent simple steps in a guideline, and plans represent actions which can be defined in terms of their components via the has-part relation. Control relations establish which actions can be executed next, and in what order. We distinguish between four different control relations: sequence, controlled¹, alternative and repetition. The temporal constraints involved by such relations will be discussed in section 3.

System architecture

GLARE distinguishes between the acquisition phase and the execution phase. The system architecture is therefore composed of two main modules, the acquisition tool and the execution tool. The tools interact strictly with a set of databases, including the clinical database, which provides physicians with standard terminology, and the patient database, which contains the patients’ data (see [Terenziani et al., 01] for details). The graphical interface of the acquisition tool is used to acquire atomic actions, has-part relations and control relations between the components of plans. The guideline is depicted as a graph, where each action is represented by a node, while control relations are represented by arcs. The tool provides different forms of consistency checking, including name and range checking and the checking of several logical design criteria [Terenziani et al., 01]. Temporal consistency checking will be specifically described in the next sections. The execution tool is used for integrating guidelines into clinical practice, by automatically retrieving the patient’s data from the patient database, and by exploiting them. GLARE is available for “off-line” execution too (for education, critical review and evaluation purposes [Terenziani et al., 01]). The execution tool also incorporates a decision support facility, which allows physicians navigating through the guideline to compare alternative paths [Terenziani et al., 02].

GLARE’s representation formalism and acquisition tool have been positively tested by several groups of expert physicians, in different clinical domains.

3 REPRESENTING TEMPORAL CONSTRAINTS IN CLINICAL GUIDELINES

As in most AI approaches to the treatment of time (see, e.g., the survey in [Vila, 94]), in our design of a formalism for representing temporal constraints in clinical guidelines, we carefully took into account the fundamental trade-off between the expressiveness of (temporal) formalisms and the temporal complexity of the correct and complete (temporal) reasoning algorithms operating on them.

While expressiveness is an obvious desideratum (the more a formalism is expressive, the more one can represent a large part of reality in it), we now briefly motivate the second term of the above trade-off.

3.1 Motivating the desiderata

First, it is important to stress that any representation language is meaningless if its intended semantics are not clear and supported (e.g., by an inferential system). In particular, a formalism for temporal constraints is mostly useless if it is not paired with algorithms for temporal reasoning, performing temporal inferences on a set of constraints (expressed in the given formalism) and/or checking their consistency. Consider example Ex.1 in the following, where A and B stand for two actions (and “m” stands for minutes):

(Ex.1)

(1.1) the end of A is equal to the start of B

(1.2) the end of B is equal to the start of C

(1.3) the duration of A is between 10 and 20 m

(1.4) the duration of B is between 10 and 20 m

(1.5) the duration of C is between 10 and 20 m

(1.6) C ends between 30 and 60 m after the start of A

(1.7) C ends between 30 and 50 m after the start of A

(1.8) C ends more than 70 m after the start of A

The constraint (1.6) can be inferred from the set of constraints KB={1.1,1.2,1.3,1.4,1.5}, so that one could correctly assert (1.7) (since (1.7) is consistent with KB), but not (1.8) (which is not consistent). Temporal reasoning is needed in order to support such an intended semantics. With no temporal reasoning, a user can represent any set of constraints, even an inconsistent one (e.g., KB2={1.1,1.2,1.3,1.4,1.5,1.8}) with no reaction by the system.

Of course, temporal reasoning algorithms are computationally expensive. An important desideratum is tractability, i.e. the fact that temporal reasoning is performed in polynomial time (with respect to exponential time). However, temporal reasoning algorithms should also be correct, i.e., such that they only infer constraints that are logically implied by the initial set of constraints (in other words, correctness grants that no wrong inference is made). Completeness (i.e., the fact that all logically implied constraints are actually inferred) is an important desideratum as well, to grant that the system’s answers are fully reliable.

3.2 Temporal constraints in GLARE

Considering the above trade-off, we tried to design a temporal representation formalism as expressive as possible, in order to model most temporal constraints in clinical guidelines. Our formalism allows one to represent the (minimum and maximum) duration of each non-composite action. Temporal constraints can also be associated with control relations between actions. In the sequence and alternative relations, one can indicate the minimum and/or maximum delay between actions. In a controlled relation, one can specify the minimum and/or maximum distance between any pair of endpoints of the actions involved. On the basis of such distances, one can express both qualitative constraints between actions (e.g., constraint (1.1) in Ex.1; however, only continuous pointizable relations can be coped with [Vila, 94]) and quantitative ones (e.g. delays, see (1.6) in Ex.1). Finally, two different ways of specifying repetitions are defined (and can be combined): one can state that the action has to be performed until a given exit condition becomes true, or can specify a duration (frame-time) for the repetitions. In both cases, the frequency of the repetitions in time has to be specified as well; then, several other parameters must/can be provided. For example, in the frequency “3 times every 2 days” it is necessary to provide the granularity for the repetition (days in the example), the grouping (2 in the example), and the number of executions in the given periodicity (3 in the example). Besides these “explicit” constraints, also the implicit constraints implied by the part-of relations between actions have to be taken into account [Terenziani et al., 01].

3.3 GLARE’s internal formalism

While GLARE provides users with an interface high-level language to express such constraints, the temporal reasoning facility maintains a homogeneous internal representation of such constraints, on which the temporal reasoning algorithm operates.

We based the design of our internal representation formalism of temporal constraints on the “classical” bounds on differences approach and on the STP (Simple Temporal Problem) framework [Dechter et al., 91]. This framework takes into account conjunctions (sets) of bounds on the distance between two time points (of the form c≤P1-P2≤d), and has very nice computational properties: correct and complete temporal reasoning (e.g., for consistency checking) can be performed in cubic time by a classical all-to-all-shortest-paths algorithm (such as Floyd-Warshall’s one) [Dechter et al., 91].

Most of the temporal constraints provided by GLARE’s interface formalism can be easily represented by the STP framework. Each action in a guideline (including composite actions) can be represented by its starting and its ending point. Thus, the duration of an action can be modeled as the distance between its endpoints. Delays are directly modeled as distances between points, and also qualitative temporal constraints. For instance, (1.1)’, (1.3)’ and (1.6)’ are the internal representation of constraints (1.1), (1.3) and (1.6) in Ex.1.

(1.1)’ 0≤ End(A)-Start(B)≤0

(1.3)’ 10≤End(A)-Start(A)≤20

(1.6)’ 30≤End(C)-Start(A)≤60

Unfortunately, the STP framework must be significantly extended if one wishes to deal with repeated actions. We propose to represent the constraints regarding repeated actions into separate STP frameworks, one for each repeated plan. Thus, in GLARE, the overall set of constraints in a guideline is represented by a tree of STP frameworks (STP-tree henceforth). The root of the tree is the STP which homogeneously represents the constraints between all the actions (composite and atomic) in the guideline, except repeated actions (which are plans, by our definition). Each node in the STP-tree is an STP, and has as many children as the number of repeated actions it contains. Each arc in the tree connects a pair of points in a STP (the starting and ending point of a repeated action) to the STP containing the constraints between the related subactions, and is labeled with the list of properties describing the temporal constraints on the repetitions (granularity, grouping, etc.).

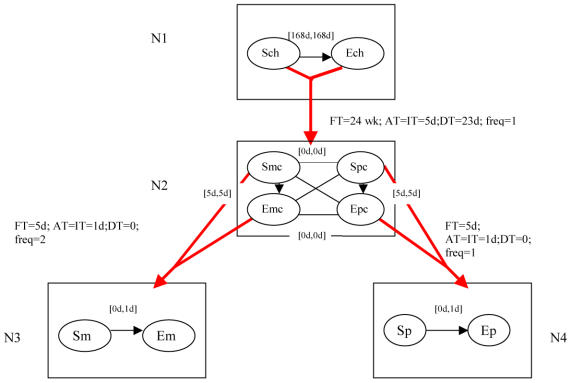
(Ex.2) One possible therapy for multiple mieloma is made by six cycles of 5-day treatment, each one followed by a delay of 23 days (for a total frame time of 24 weeks; the overall therapy is reported as the root of the STP-tree in figure 1). Within each 5-day cycle, 2 inner cycles can be distinguished: the melphalan treatment, to be provided twice a day, for each of the 5 days, and the prednisone treatment, to be provided once a day, for each of the 5 days. These two treatments must be performed in parallel (see the temporal constraints in node N2 in figure 1), and are shown as leaves of the STP-tree (nodes N3 and N4 respectively).

Figure 1:

STP-tree for the multiple mieloma chemotherapy guideline: a naïve graphical representation. Thiny lines and arcs between nodes in an STP represent bounds on differences constraints. Arcs from a pair of nodes to a child STP represent repetitions. Arcs between any two nodes X and Y in an STP of the STP-tree are labeled by a pair [n,m] representing the minimum and maximum distance between X and Y.

4 TEMPORAL REASONING

In GLARE, temporal reasoning can be used both in the acquisition phase, to check that the temporal constraints in the guideline are consistent, and in the execution phase, to check that the times of execution of specific actions respect the temporal constraints in the guideline.

4.1 Checking temporally consistent descriptions

Temporal consistency checking proceeds in a top-down fashion, starting from the root node of the STP-tree. In fact, the root is a “standard” STP, so that Floyd-Warshall’s algorithm can be applied to it to check consistency. Then, we proceed towards the leaves of the tree. For each node in the tree other than the root, we progress in three steps (ALGO1):

ALGO1: temporal consistency of guidelines

1. the consistency of the constraints used to specify the repetition taken in isolation is checked;

2. the “extra” temporal constraints regarding the repetition are mapped onto bounds on difference constraints;

3. Floyd-Warshall’s algorithm is applied to the constraints in the STP plus the “extra” bounds on difference constraints determined at step 2.

While the third step is trivial, the first two steps are performed by ad-hoc specialized algorithms (see [Terenziani et al., 02b] for more details).

Property 1

Our consistency checking algorithm ALGO1 is correct, complete, and tractable (since it operates in O(N³), where N is the number of actions in the guideline).

4.2 Checking temporally consistent executions

When a guideline is executed on a specific patient, actions are performed at specific times. We suppose that the exact times of all the actions in the guideline which have been executed are given in input to our system. Thus, we have to check that they respect (i.e., are consistent with) the temporal constraints imposed by the given guideline. A naïve procedure would be that of checking, for each execution time, whether it is consistent with each one of the (corresponding) constraints in the guideline. However, such an efficient procedure is not complete since execution times may be consistent when taken in isolation, but inconsistent when “combined” all together. Thus, a temporal reasoning algorithm has to be devised to propagate the temporal constraints in the guideline and the execution-times of actions “all together”.

To define such a temporal reasoning algorithm, it is important to notice that an action in a guideline represents a class (set) of instances of actions, in the sense that it will have specific instantiations for specific executions of the guideline itself. On the other hand, while executing (instantiating) a guideline, one has specific instances of the actions in the guideline, which must respect (i.e., be consistent with) the temporal constraints given on their classes. This also means that the (implicit) temporal constraints conveyed by the part-of relations between actions in the guideline must be respected, as well as those involved by periodicity and repetitions.

In a broad sense, periodic events are special kinds of classes of events, i.e., classes whose instances must respect a given periodic temporal pattern. Constraints on the periodicity of repetitions are basically constraints that must be “inherited” by instances. However, it is a “non-classical” form of inheritance. In fact, while constraints about duration, delays and ordering regard single instances (duration) or pairs of instances (delays, precedence), periodicity constraints concern whole sets of instances, imposing constraints on their cardinality and on the temporal pattern they have to respect. Finally, notice that the interplay between part-of relations and periodic events might be quite complex to represent and manage. In fact, in the case of a composite periodic action, the temporal pattern regards the components, which may, recursively, be composite and/or periodic actions.

Finally, notice that, when considering instances, one should also take into account the fact that guidelines have a “predictive” role. E.g., if one has observed a given action E₁ which is an instance of a class of actions E in a guideline, and the class E' follows E in the guideline itself, one expects to observe an instance of E' in a time consistent with the temporal constraints between the classes E and E'. We assume that, as regards the treatment of hospitalized patients, we have complete observability, i.e., that each execution of an action of the guideline is reported in the clinical record of the patient, together with its time of occurrence. Thus the consistency check must consider “prediction”, since not having observed an instance of an action may indicate an inconsistency, unless the temporal constraints in the guideline impose that it may also be executed in a time after NOW. Our temporal reasoning algorithm can be schematized as follows:

ALGO2: temporal consistency on guidelines execution

1. the existence of non-observed instances whose occurrence is predicted by the guideline is hypothesized;

2. all the constraints in the general guidelines are inherited by the corresponding instances (considering both observed and hypothesized instances). This step also involves “non-standard” inheritance of constraints about periodicity;

3. constraint propagation is performed on the resulting set of constraints on instances (via Floyd-Warshall’s algorithm), to check the consistency of the given and the inherited constraints;

4. if constraints at step 3 are consistent, it is further checked that such constraints do not imply that any of the “hypothesized” instances should have started before NOW.

Property 2

Our consistency checking algorithm ALGO2 is correct, complete, and tractable (since it operates in O((N+M)³), where N is the number of actions in the guideline and M the number of instances of actions which have been executed (and observed).

A detailed analysis of our temporal reasoning algorithm, and of Property 2 is outside the goals of this paper, and can be found in [Terenziani & Anselma, 03].

5 COMPARISONS AND FUTURE WORK

In the latest years, many (semi-)automatic approaches to clinical guideline management have been proposed: among them, we consider PROforma [Fox et al., 98] and Asbru [Shahar et al. 98] to be the most similar to GLARE (see [Terenziani et al., 01] for comparisons). As regards temporal constraint treatment specifically, only recently some contributions started to address this issue. For instance, Shahar has proposed a comprehensive approach dealing with temporal abstraction within the clinical procedures [Shahar, 98]. Miksch has focused on a user-friendly tool to show the temporal constraints in a guideline to physicians in a graphical and commonsense way [Miksch & Kosara, 99]. However, to the best of our knowledge, no approach has focused on temporal reasoning to check the consistency of temporal constraints within the (possibly repeated) actions in a guideline. Neither did any contribution consider the checking of consistency between guideline constraints and the times of execution of specific actions, as we did in this work. In the future, we plan to extend our formalism and algorithms to cope also with incomplete observations.