HITON: A Novel Markov Blanket Algorithm for Optimal Variable Selection

Abstract

We introduce a novel, sound, sample-efficient, and highly-scalable algorithm for variable selection for classification, regression and prediction called HITON. The algorithm works by inducing the Markov Blanket of the variable to be classified or predicted. A wide variety of biomedical tasks with different characteristics were used for an empirical evaluation. Namely, (i) bioactivity prediction for drug discovery, (ii) clinical diagnosis of arrhythmias, (iii) bibliographic text categorization, (iv) lung cancer diagnosis from gene expression array data, and (v) proteomics-based prostate cancer detection. State-of-the-art algorithms for each domain were selected for baseline comparison. Results: (1) HITON reduces the number of variables in the prediction models by three orders of magnitude relative to the original variable set while improving or maintaining accuracy. (2) HITON outperforms the baseline algorithms by selecting more than two orders-of-magnitude smaller variable sets than the baselines, in the selected tasks and datasets.

INTRODUCTION

The identification of relevant variables (also called features) is an essential component of construction of decision support models, and computer-assisted discovery. In medical diagnosis, for example, elimination of redundant tests from consideration reduces risks to patients and lowers healthcare costs [1]. The problem of variable selection in biomedicine is more pressing than ever, due to the recent emergence of extremely large datasets, sometimes involving tens to hundreds of thousands of variables. Such datasets are common in gene-expression array studies, proteomics, computational biology, text-categorization, information retrieval, mining of electronic medical records, consumer profile analysis, temporal modelling, and other domains [1–6].

Most variable selection methods are heuristic in nature and empirical evaluations have seldom exceeded domains with more than a hundred variables (see [7–9] and their references for reviews). Several researchers [1, 10, 11] have suggested, intuitively, that the Markov Blanket of the target variable T, denoted as MB(T), is a key concept for solving the variable selection problem. MB(T) is defined as the set of variables conditioned on which all other variables are probabilistically independent of T. Thus, knowledge of the values of the Markov Blanket variables should render all other variables superfluous for classifying T. Technical details about the distributional assumptions underlying this intuition, existence and uniqueness of MB(T), and relations to loss functions and classifier-inducing algorithms were only recently explored however, by the first two authors of the present paper [8]. From a practical perspective, identifying the Markov Blanket variables has proven to be a challenging task as evidenced by the limitations of prior methods. Specifically, the approaches in [1,2] are unsound (i.e., provably do not always return the correct MB(T) even with infinite sample and time); the method of [10] is sound but relies on inducing the full Bayesian network and thus does not scale up to the number of variables; the work in [11] is unsound and has poor average computational efficiency. Notably, two newer families of algorithms [8, 12] are sound and computationally efficient, but require sample exponential to the size of MB(T). In biomedical domains sample sizes are typically limited (and often sample-to-variable ratios are very small), however.

The contribution of the present paper is that it introduces HITON¹, a sound, sample-efficient, and highly scalable algorithm for variable selection for classification, based on inducing MB(T). HITON is sound provided that (i) the joint data distribution is Faithful to a BN, (ii) the training sample is enough for performing reliably the statistical tests required by the algorithm, and that (iii) one uses powerful enough classifiers (i.e., that can learn any classification function given enough data). A distribution is faithful to a BN if all the dependencies in the distribution are strictly those entailed by the Markov Condition of the BN [8]. The vast majority of distributions are faithful in the sample limit [13].

The question that arises is whether the algorithm, and by extension its assumptions, perform well in biomedical data (that, in addition, often involve thousands of variables and limited sample), and the typical classifiers used in practice. To empirically evaluate HITON, a wide variety of domains were selected with different characteristics. In addition, the best algorithms for each tasks were selected as baseline comparisons.

A Novel Algorithm For Variable Selection

The new algorithm is presented in pseudo-code in Figure 1. V denotes the full set of variables and ⊥(T ; X | S ) the conditional independence of T with variable set X given variable set S. HITON-MB first identifies the parents and children of T by calling algorithm HITON-PC, then discovers the parents and children of the parents and children of T. This is a superset of the MB(T). False positives are removed by a statistical test inspired by the SGS algorithm [14]. HITON-PC admits one-by-one the variables in the current estimate of the parents and children set CurrentPC. If for any such variable a subset is discovered that renders it independent of T, then the variable cannot belong in the parents and children set and is removed and not considered again for inclusion [14]. Given assumptions (i) and (ii) HITON-MB provably identifies the MB(T). For proof of correctness the interested reader can see [15] (available from http://discover1.mc.vanderbilt.edu). If k is the maximum number of conditioning and conditioned variables in a test, then because k is bounded by the available sample (seldom taking values > 3 in practice) the average-case complexity is approximately O(|MB|³|V|) or better, which makes it very fast.

Figure 1.

Pseudo-code for algorithm HITON.

METHODS

1. Datasets

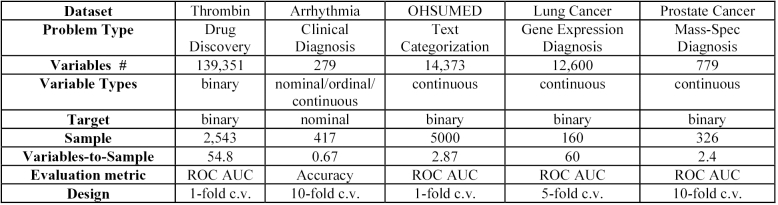
The first task is drug discovery, specifically classification of biomolecules as binding to thrombin (hence having potential or not as anti-clotting agents) on the basis of molecular structural properties [2]. The second task is clinical diagnosis of arrhythmia into 8 possible disease categories on the basis of clinical and EKG data [5]. The third task is categorization of text (Medline documents) from the OHSUMED corpus (Joachims version [6]) as relevant to nenonatal diseases or not [16]. The fourth task is diagnosis of squamus vs. adenocarcinoma in patients with lung cancer using oligonucleotide gene expression array data [17]. Finally, the fifth task is diagnosis of prostate cancer from analysis of mass-spectrometry signal peaks obtained from human sera [18]. Figure 2 summarizes important characteristics of all datasets used in our experiments. We specifically sought datasets that are massive in the number of variables, and with very unfavourable variable-to-sample ratios (as can be seen from the figure).

Figure 2.

Dataset Characteristics

2. Classifiers

We applied several state-of-the-art classifiers: polynomial-kernel Support Vector Machines (SVM) [19], K-Nearest Neighbors (KNN) [20], Feed-forward Neural Networks (NNs) [21], Decision Trees (DTI) [21] and a text categorization-optimized Simple (a.k.a., ‘Naïve’) Bayes Classifier (SBCtc) [21]. We applied SVMs, NNs, and KNN to all datasets with the exception of Arrhythmia where we substituted DTI for SVMs since this domain requires a multi-category classification in which SVMs were not, at the time of experiments, as well-developed as for binary classification. DTI is appropriate for this task (but is well-known to suffer in very-high dimensional and sparse datasets such as the remaining ones in which it was not applied). The text-optimized Bayesian Classifier was used in the text classification task only. For SVMs we used the LibSVM implementation [22] that is based on Platt’s SMO algorithm [23], with C chosen from the set: {10⁻⁸, 10⁻⁷, 10⁻⁶, 10⁻⁵, 10⁻⁴, 10⁻³, 10⁻², 0.1, 1, 10, 100, 1000} and degree from the set: {1, 2, 3, 4}. Thus effectively we examine the performance of linear SVMs as part of the parameterization of polynomial SVMs. For KNN, we chose k from the range: [1,…, number of samples in the training set] using our own implementation of the algorithm. For NNs we used the Matlab Neural Network Toolbox with 1 hidden layer, number of units chosen (heuristically) from the set {2, 3, 5, 8, 10, 30, 50}, variable-learning-rate back propagation, custom-coded early stopping with (limiting) performance goal=10⁻⁸ (i.e., an arbitrary value very close to zero), and number of epochs in the range [100,…,10000], and a fixed momentum of 0.001. We used Quinlan’s See5 commercial implementation of C4.5 Decision Tree Induction and our own implementation of the text-oriented Simple Bayes Classifier described in [21].

3. Variable selection baselines

We compare HITON against several powerful variable selection procedures that have been previously shown to be the best performers in each general type of classification task. These methods are: Univariate Association Filtering (UAF) (for all tasks), Recursive Feature Elimination (RFE) (for bioinformatics-related tasks), and Backward/Forward Wrapping (for clinical diagnosis tasks) [24]. RFE is an SVM–based method; it was employed using the parameters reported in [4]. Univariate Association Filtering is a common and robust applied classical statistics procedure. In text categorization especially, extensive experiments have established its superior performance [25]. UAF: (a) Orders all predictors according to strength of pair-wise (i.e., univariate) association with the target, and (b) Chooses the first k predictors and feeds them to the classifier of choice. Various measures of association may be used. We used Fisher Criterion Scoring for gene expression data [3], X² and Information Gain for text categorization [25], Kruskal-Wallis ANOVA for the continuous variables of Arrhythmia, and G², for the remaining datasets [14]. To maximize the performance of the method we did not select an arbitrary k but optimised it via cross-validation. We used our own implementations of all baseline variable selection algorithms. In the reported experiments we did not include any of the previous methods for inducing MB(T) (most notably the highly-cited Koller-Sahami algorithm [11], but also the ones in [1, 2, 10]) because they are computationally intractable for datasets as large as the ones used in our evaluation. The sound and tractable algorithms of [8, 12] are guaranteed to return worse results than HITON for finite samples due to their theoretical properties and thus were omitted from consideration in these preliminary experiments.

4. Cross-validation

We employed a nested stratified cross-validation design [20] throughout, in which the outer loop of cross-validation estimates the performance of the optimised classifiers while the inner loop is used to find the best parameter configuration/variable subset for each classifier. The number of folds was decided based on sample (Figure 2). In the datasets where 1-fold cross-validation was used, the split ratio was 70/30.

5. Evaluation metrics

In all reported experiments except the Arrhythmia data, we used the area under the Receiver Operator Characteristic (ROC) curve (AUC) to evaluate the classification performance of the produced models. The classifiers’ outputs were thresholded to derive the ROCs. AUC was computed using the trapezoidal rule and statistical comparisons among AUCs were performed using an unpaired Wilcoxon rank sum test. The size reduction was evaluated by fraction of variables in the resulting models. All metrics (variable reduction, AUC) were averaged over cross-validation splits [20].

6. Statistical choices

In all our experiments we apply HITON with a G² test of statistical independence with a significance level set to 5%, and degrees of freedom according to [14].As measure of association in HITON-PC we use the p-value of the G² test (association increases monotonically with the negative p-value).

RESULTS

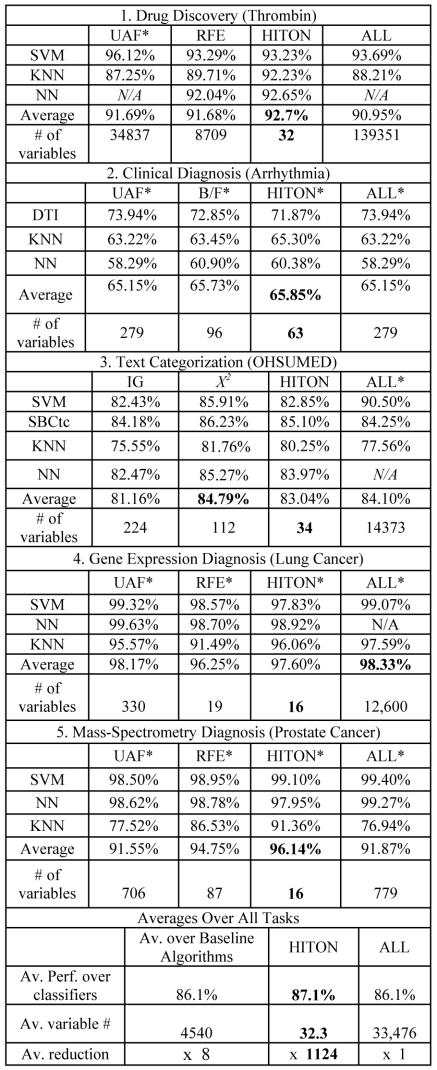
As can be seen in Figure 3, (a) HITON consistently produces the smallest variable sets in each task/dataset; the reduction in variables ranges from 4.4 times (Arrhythmia) to 4,315 times (thrombin); (b) in 3 out of 5 tasks HITON produces the best classifier or a classifier that is statistically non-significantly different from the best (compared to 4 out of 5 for all other baselines combined); (c) in summary (i.e., averaged over all classifiers in each task/dataset), HITON produces the models with best classification performance in 4 our of 5 tasks; (d) averaged over all classifiers and tasks/datasets, HITON exhibits best classification performance, and best variable reduction (~140 times smaller models on the average, than the baseline methods’ average, and ~1100 times on the average smaller models than the average total number of variables). (e) Compared to using all variables, HITON improves performance 2 times out of 5, while maintains performance another two times out of 5 and yields minimally worse performance in the remaining task (text categorization). HITON can be run in a few hours for massive datasets using very inexpensive computer platforms. For example, it took 8 to 9 hours (depending on classifier) to run in the massive thrombin dataset (baselines: 4 to 4.7 hours) using a Intel Xeon 2.4 GHz computer with 2 GB of RAM.

Figure 3.

Task-specific and overall model reduction performance (in bold, best performance per row; asterisks indicate that the corresponding algorithm yields the best model or a non-statistically significantly worse model than the best one).

DISCUSSION

All previous algorithms for soundly inducing the MB(T) condition on the full MB(T) and thus require exponential sample size to the size of the MB(T) [8, 12, 26]. HITON (as close examination of subroutine HITON-PC reveals), conditions on the locally smallest possible variable set needed to establish independence. This yields up to exponentially smaller required sample than [8, 12, 26] without compromising soundness. Any non-members of the Markov Blanket that cannot be excluded due to the small sample are removed by the final (wrapper) phase (which is tractable because it operates in much smaller variable set than the full set).

Algorithms that operate by inducing the full network first [1, 10] although sound, are clearly intractable for large domains. The widely-cited Koller-Sahami algorithm is unsound, cannot be run in datasets as large as the ones used in our experiments, and was recently shown to perform worse than other (sound) algorithms [26]. Thus HITON is the first Markov Blanket – inducing algorithm that combines the following three properties: (a) is sound; (b) is highly-scalable to the number of variables; (c) is sample-efficient relative to the size of the Markov Blanket. Our experimental evaluation suggests that it is applicable to a wide variety of biomedical data, in particular: structural molecular biology, clinical diagnosis, text-categorization, gene expression analysis, and proteomics.

Given that HITON has a well-specified set of assumptions for correctness we can also outline the situations for which its use is expected to be non-optimal as involving: (a) strong violations of faithfulness (e.g., parity functions, noiseless deterministic functions, quantum effects, certain mixtures of distributions [14]), (b) very small samples (in practice <150 instances with binary variables, in our experience), and/or (c) restricted classifiers or uncommon loss functions.

HITON’s power stems from a well-founded theoretical base and because it makes a minimal set of widely-applicable assumptions. Especially with respect to the faithfulness assumption, HITON’s robustness in our experiments implies that either biomedical data do not exhibit severe violations of this distributional assumption, or that such violations are mitigated by currently poorly-understood factors.