A Computer-Based Microarray Experiment Design-System for Gene-Regulation Pathway Discovery

Abstract

This paper reports the methods and evaluation of a computer-based system that recommends microarray experimental design for biologists — causal discovery in Gene Expression data using Expected Value of Experimentation (GEEVE). The GEEVE system uses causal Bayesian networks and generates a decision tree for recommendations.

To evaluate the GEEVE system, we first built an expression simulation model based on a gene regulation model assessed by an expert biologist. Using the simulation model, we conducted a controlled study that involved 10 biologists, some of whom used GEEVE and some of whom did not. The results show that biologists who used GEEVE reached correct causal assessments about gene regulation more often than did those biologists who did not use GEEVE.

INTRODUCTION

Systems biology emphasizes large scale discovery of the interactions of genes, proteins, and other cell elements. Systems biology is confronted with a huge number of interactions, not the least of which is the interaction of genes. There are challenges in designing high throughput experiments, such as cDNA microarrays, and for analyzing the high volume of data generated by those experiments in order to discover gene regulation networks. Intrinsically, these regulation networks are causal in nature.

Microarray technology has opened a new era in the study of gene regulation. It allows a relatively quick and easy way to assess the mRNA expression levels of many different genes. Large time-series datasets generated by microarray experiments can be informative about gene regulation. Microarray data have been analyzed using classification or clustering methods¹ and gene pathway (network) methods^2–4. de Jong⁵ and Smolen, et al.⁶ give good reviews of genetic networks.

Kitano⁷ views systems biology as an endless information exchange between dry experiments (simulation studies and/or data analyses) and wet experiments (actual wet lab experiments). Since high throughput data are relatively expensive to achieve, the role of dry experiments is important in systems biology. Since Fisher⁸ noted that the statistical analysis procedure and experiment design are merely two different aspects of the same whole, much research has concentrated on experiment design itself⁹. Recent notable publications of systems that recommend experiment design includes active learning of Bayesian networks¹⁰ and perturbation recommendation in systems biology studies using Boolean networks¹¹.

In this paper, we use our previously published causal structure search method¹² and introduce a computer system — causal discovery in Gene Expression data using Expected Value of Experimentation (GEEVE) — that recommends which gene-regulation experiments to perform next. Unlike the recently published systems that recommend experiment design^10,11, GEEVE (1) uses a local search method¹²; (2) assumes no ordering among variables; (3) can model the possibility of a hidden common cause; (4) can model an experimenter’s prior knowledge of causal relationships; (5) incorporates a cost model; and (6) can recommend more than one experiment at a time.

To evaluate GEEVE we used a simulation model generated by an expert biologist and conducted a controlled study that involved 10 biologists, some of whom used GEEVE and some of whom did not.

METHODS

A Bayesian network is a directed acyclic graph in which each node represents a variable and each arc represents probabilistic influence. A causal Bayesian network (or causal network for short) is a Bayesian network in which each arc is interpreted as a direct causal influence between a parent node (variable) and a child node, relative to the other nodes in the network¹³. Figure 1 illustrates the structure of a hypothetical causal Bayesian network structure that contains five nodes. The probabilities associated with this causal network structure are not shown.

Figure 1.

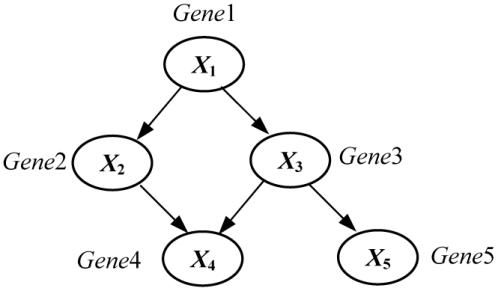
A causal Bayesian network that represents a hypothetical gene-regulation pathway.

The causal network structure in Figure 1 indicates, for example, that the Gene1 can regulate (causally influence) the expression level of the Gene3, which in turn can regulate the expression level of Gene5.

The causal Markov condition gives the conditional independence relationships that are specified by a causal Bayesian network:

A node is independent of its non-descendants (i.e., non-effects) given its parents (i.e., its direct causes).

The causal Markov condition permits the joint distribution of the n variables in a causal Bayesian network to be factored as follows¹³:

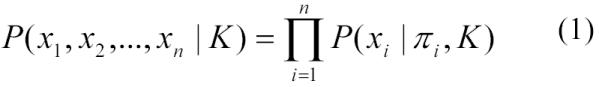where x_i denotes a state of variable X_i, π_i denotes a joint state of the parents of X_i, and K denotes background knowledge.

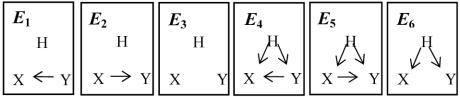
We introduce 6 equivalence classes (E₁ through E₆) among the structures (Figure 2). The causal networks in an equivalence class are statistically indistinguishable for any observational and experimental data on X and Y. We denote an arbitrary pair of nodes in a given Bayesian network B as (X, Y). If there is at least one directed causal path from X to Y or from Y to X, we say that X and Y are causally related in B. If X and Y share a common ancestor, we say that X and Y are confounded in B. We understand that modeling all nodes may better represent the relationship among all the genes, but considering computational tractability, in this paper we concentrate on pairwise relationships between two nodes (X and Y) and a latent variable H.

Figure 2.

Six Local Causal Hypotheses

Let E={E₁, E₂, E₃, E₄, E₅, E₆} and let E_i^XY denote the node pair X and Y with causal relationship E_i. Let us consider the posterior probability that variable X causally influences variable Y given microarray gene expression data D. We can derive the posterior probability of E_i^XY as:

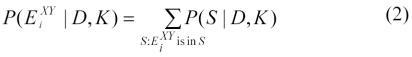where the sum is taken over all causal network structures that (1) contain just the nodes in a structure S, and (2) contain a structure E_i^XY. With appropriate assumptions, we can evaluate P(S|D,K) in Equation 2 in closed form¹⁴.

The GEEVE system.

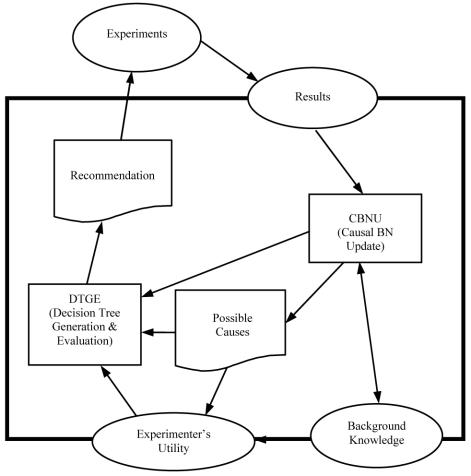
The GEEVE system consists of two modules called the causal Bayesian network update (CBNU) module and the decision tree generation and evaluation (DTGE) module (Figure 3). The CBNU module uses a heuristic scoring method called Local Implicit latent variable scoring Method (LIM)¹² to causally analyze the current microarray data in light of the user’s prior beliefs about causal relationships among the genes under study. The DTGE module evaluates a decision tree that was generated based on the results of the CBNU module and the experimenter’s preferences, which are expressed with GEEVE as a utility function. DTGE also incorporates the cost to analyze a microarray chip. Finally (under assumptions) the best possible experiments are recommended to the experimenter. The experimenter then chooses the next experiment to perform, which may or may not be the one suggested by GEEVE. When the results are available, they can be submitted to the CBNU module for a new round of analysis.

Figure 3.

The GEEVE system. The box with the thick line represents the GEEVE system. Boxes in GEEVE represent system modules. Boxes with wavy lines represent outputs from GEEVE. The Experiments oval is an object that is outside of GEEVE. The ovals on the GEEVE border represent objects that communicate with GEEVE from the outside.

Let the expression U({P(E_i | ξ_j, D′, D, K), {P(E_i | D, K)}), represents the utility of obtaining an update on the probability of each of E₁, E₂, …, and E₆ after performing an experiment ξ_j that has new results D′ in the context of prior results D and background knowledge K.. GEEVE provides a method that allows biologists to assess their utility¹⁵, but due to limited space, we do not explain it in detail. However, we can calculate the expected utility (EU) of ξ_j as:

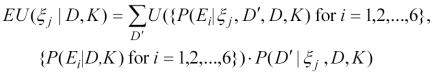where here D′ denotes each possible result of the experiment ξ _j. The optimal experiment is then:

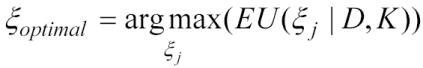Although DTGE limits possible experiments (see the Study Design section), the large number of the experiments and their number of possible outcomes of the experiment make an exact evaluation of the decision tree intractable. Heuristic methods are used to generate D′ and calculate ξ _optimal¹⁵.

High Throughput Data Simulator.

We used the Scheines and Ramsey¹⁶ simulator system (SR Simulator) to generate gene expression data. The SR simulator models genes within multiple cells and incorporates biological variance, such as that due to signal loss or gene mutation, as well as measurement error.

We created a simulator model (Figure 4) using the SR simulator that models a gene regulation pathway based on assessments from a molecular biologist at our university who has many years of research experience related to gene regulation pathways in yeast SNF1 protein kinease¹⁷. Regulation relationships (e.g, CAT8 promotes SIP4) and other parameters of the SR simulator were assessed from the biologist. We estimated the measurement error from published yeast microarray data¹⁸. GEEVE currently models gene expression levels using discrete variables only, although it could be extended to model with continuous variables as well. Thus, we discretized each gene’s expression level into three states (i.e., low, no change, and high) based on each gene’s expression level¹².

Figure 4.

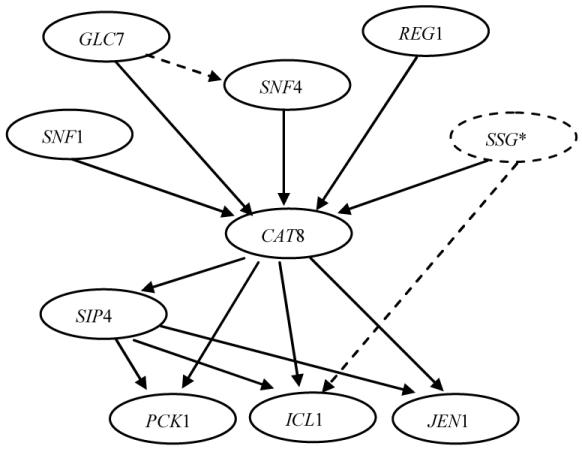
SNF1 simulation pathway model. Dotted lines represent the causal relationships that are biologically plausible, but need further investigation. SSG* represents a group of genes, i.e., SIP1, SIP2, and GAL83. SSG was modeled in the simulator but was hidden to the participants in the control study; i.e., the expression level of SSG was not provided to the participants

Study Design.

Ten biology faculty members, post-docs, and graduate students were recruited for this study and offered $50 per hour of participation. The biologists expressed at least some knowledge of the SNF1 protein kinease pathway. We stratified these study participants into two groups: (1) a control group that did not use GEEVE, and (2) an intervention group that used GEEVE. All participants were able to obtain the gene expressions levels for the nine genes (SSG was hidden from the participants) in Figure 4 under the following experimental conditions¹):

• - a wild-type experiment (i.e., no genes were knocked out);

• - a knock-out experiment for which a single gene (selected from among the nine genes in

• - Figure 4) was deleted.

The participants were asked to finish five phases in this study. Each phase consists of the following steps:

(1) the participant assesses his current beliefs about pairwise causal relationships among a predefined set of genes; (2) the participant requests up to 10 additional microarray experiments; (3) the simulator generates experimental results for the requested experiments; and (4) the participant views the results with or without GEEVE’s analysis and further recommendations for experiments to perform.

Evaluation Metrics.

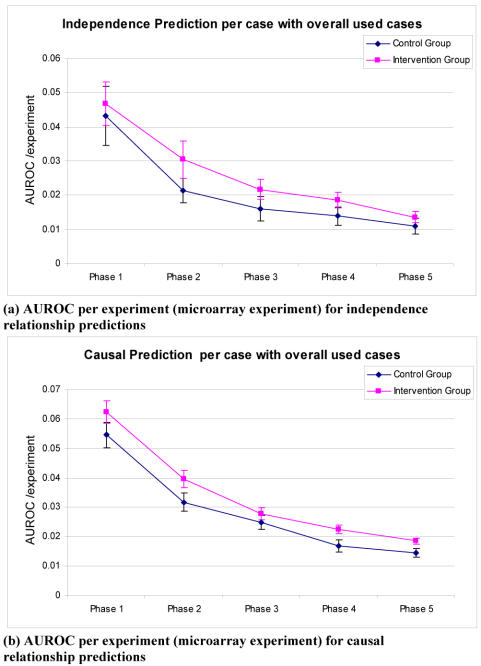
Out of the 36 possible gene pairs (Figure 4), ten gene pairs were preselected based on the preferences of an external expert biologists preference¹⁵. All participants were asked to take the given preferences as if they were their own. We calculated the area under ROC curve (AUROC) for all participants in each phase to characterize their discovery performance. Note that to calculate AUROC in Figure 5, we used non-confounded structures (i.e., relationships between X and Y in Figure 2 are grouped as (1) causally independent for E₃ or E₆; and (2) causally related for E₁ or E₄ (also E₂ or E₅). This is because SR simulator allows us to model microarray’s averaging effect of the mRNA level from millions cells and it is the averaging effect that makes the latent confounded structure discovery difficult if not impossible^15,19. To calculate the AUROC, we measure how well each participant predicts the correct relationships among the ten genes in each phase. Thus (1) if E₃ or E₆ (independence of X and Y) is the true state (according to the generating model) for a given gene pair, then E₁, E₂, E₄, and E₅ are the false states; (2) if E₁ or E₄ (Y → X) is the true state then E₂, E₅, E₃, and E₆ are the false states; or (3) if E₂ or E₅ (X → Y) is the true state then E₁, E₃, E₄, and E₆ are the false states.

Figure 5.

Area under ROC (AUROC) per experiment for the control and intervention groups. Each bar represents a 95% confidence interval.

RESULTS

Table 1 shows more information about the participants in the control and intervention groups. The ten participants were selected based on their knowledge of the SNF1 pathway and cDNA microarray technology. Table 1 shows that participants were equally distributed based on their positions, knowledge of the SNF1 pathway, knowledge of cDNA microarray technology, and their expertise in computers. This is because we stratified the participants into the intervention and control groups in order to balance the dimensions in Table 1, especially focusing on participant’s knowledge in SNF1 pathway. There were three participants (group A) who rated themselves to be more knowledgeable of SNF1 pathway than the other seven participants (group B). Not to give an advantage to the intervention group, we assigned two participants (from group A) and three participants (from group B) to the control group.

Table 1.

Information about the Participants in the Intervention and Control Groups

	Professor	Post doc	Ph.D. student	Others*	Total
Control Group	1	0	3	1	5
Intervention Group	1	1	3	0	5
(a) Positions. *Others is a technician with a Master’s degree in a field other than biology

	Understand Well	Understand Somewhat	Know only the genes	Totally Ignorant	Total
Control Group	0	2	3	0	5
Intervention Group	0	1	4	0	5
(b) Knowledge in SNF1 pathway.

	Understand Well	Understand Somewhat	Totally Ignorant	Total
Control Group	0	5	0	5
Intervention Group	1	4	0	5
(c) Knowledge in cDNA microarray technology

	Average	Std. dev.	p value
Control Group	0.56	0.13	0.34
Intervention Group	0.60	0.16
(d) Subjective self-evaluation of computer expertise using the following values: 0=Novice, 0.5=Intermediate, 1.0=Expert.

Figure 5 plots the comparison of the two groups in each phase considering the number of microarray experiments that the participants in the two groups performed (via the SR Simulator). In particular, it displays the AUROC per microarray experiment (this unit represents the increased fraction of an AUROC that an experimenter would gain per microarray experiment) for each phase for the intervention and the control groups. The intervention group performed statistically significantly better than the control group (p ≤ 0.05) in Phase 2, Phase 4 and Phase 5 in making causal predictions [Figure 5(b)].

SUMMARY

We developed a system called GEEVE that incorporates an experimenter’s preferences regarding which genes to study in order to discover causal relationships among those genes. For genes of interest, GEEVE generates a model of their likely causal relationships, which is based on prior biological knowledge and experimental data.

We showed that most of the time the intervention group (that used GEEVE) performed better — although not always statistically significantly so — than the control group in predicting whether pairs of genes (of interest to the biologist study participant) act independently or have a causal relationship.

Future work includes modeling more general experiments, such as over-expression experiments, as well as multiple gene knock-outs that will allow GEEVE to incorporate more than pairwise relationships into the decision tree. It also will be important to perform more extensive testing of GEEVE using simulated and real microarray data.