Flexible phenylalanine-glycine nucleoporins as entropic barriers to nucleocytoplasmic transport

Abstract

Natively unfolded phenylalanine-glycine (FG)-repeat domains are alleged to form the physical constituents of the selective barrier-gate in nuclear pore complexes during nucleocytoplasmic transport. Presently, the biophysical mechanism behind the selective gate remains speculative because of a lack of information regarding the nanomechanical properties of the FG domains. In this work, we have applied the atomic force microscope to measure the mechanical response of individual and clusters of FG molecules. Single-molecule force spectroscopy reveals that FG molecules are unfolded and highly flexible. To provide insight into the selective gating mechanism, an experimental platform has been constructed to study the collective behavior of surface-tethered FG molecules at the nanoscale. Measurements indicate that the collective behavior of such FG molecules gives rise to an exponentially decaying long-range steric repulsive force. This finding indicates that the molecules are thermally mobile in an extended polymer brush-like conformation. This assertion is confirmed by observing that the brush-like conformation undergoes a reversible collapse transition in less polar solvent conditions. These findings reveal how FG-repeat domains may simultaneously function as an entropic barrier and a selective trap in the near-field interaction zone of nuclear pore complexes; i.e., selective gate.

Nucleocytoplasmic transport describes the exchange of molecular cargo between the nucleus and the cytoplasm across numerous perforations in the nuclear envelope called nuclear pore complexes (NPCs) (1). Each vertebrate NPC is an ≈120-MDa supramolecular complex consisting of ≈30 different proteins called nucleoporins (or Nups) that form an eightfold symmetric central framework embracing a central pore. The cross-section of the central pore reveals an hourglass-like channel that is ≈90 nm long and is narrowest (diameter of ≈40 nm) at the NPC’s midplane (1). Whereas small molecules such as water and ions proceed freely by passive diffusion (2), the NPC poses a barrier to larger molecular cargo (>20 kDa) that do not harbor nuclear localization signals (NLSs) (3). Conversely, the barrier does not seem to hinder the passage of NLS cargo when in complex with a transport receptor (e.g., Karyopherin/Importin) (4). Moreover, because receptor-mediated transport is rapid even for large NLS cargoes (5), it is apparent that the NPC-selective gating mechanism is not solely based on size exclusion.

Presently, an unambiguous understanding of the gating mechanism remains elusive because of a lack of information regarding the mechanical aspects of the molecular components that make up the NPC. Emerging evidence indicates that gating is closely correlated with the interactions and spatial organization of nucleoporins containing phenylalanine-glycine (FG)-repeat domains (called FG domains) (1). Importantly, FG domains exhibit low overall hydrophobicity and are natively unfolded (6). FG nucleoporins account for ≈30% of the NPC and are localized to both the cytoplasmic and nuclear peripheries (7). The flexibility of such FG domains has been largely inferred from immunogold labeling assays, which show that the FG domains of Nup153 and Nup214 can be localized at different locations within the NPC (8, 9).

Several models allege that FG domains form the physical constituents of the underlying barrier. The Brownian affinity gate model (7) proposes that the entropic behavior of peripheral FG domains acts as a substantial barrier to inert cargo while translocation is anticipated for receptor-mediated cargo because of interactions between the FG repeats and the transport receptor (10). The selective phase model (11) predicts that FG domains attract each other via hydrophobic inter-FG-repeat interactions to form a hydrophobic gel or meshwork that obstructs the passage of passive material while allowing hydrophobic cargo complexes to “dissolve” through the sieve-like meshwork. The affinity gradient model (12) suggests that transport complexes “step” through NPCs lined with FG domains that exhibit increasing binding affinities. To add to the ensuing complexity, the asymmetry of FG nucleoporins has been shown to be dispensable for cargo transport to proceed (13). It is even more puzzling that a reduction in permeability is not observed in FG-repeat-reduced, minimal yeast NPCs (14).

To provide insight into how FG domains behave in the NPC near-field, it is beneficial to directly ascertain (i) the nanomechanical response of individual FG domains and (ii) the collective behavior of such surface-tethered FG domains. Here, we have modified the C-terminal FG domain of Nup153 with three cysteine groups at its N-terminal end (Cys-Nup153-C; henceforth known as cNup153) to act as covalent linkages to Au surfaces. Each cNup153 molecule consists of 30 FG-repeat motifs and has a total mass of ≈60 kDa. Using atomic force microscopy (AFM) single-molecule force spectroscopy (SMFS) (15), we have quantified the flexibility of individual cNup153 molecules and mechanically verified that they are unfolded and exhibit entropic elasticity. To ascertain how FG domains can give rise to the barrier effect in the NPC interaction zone, we have fabricated nanometer-sized Au supports (nanodots) to serve as an experimental platform to probe the interaction forces associated with cNup153 clusters by AFM. Under compression, the cNup153 cluster gives rise to an exponentially decaying long-range repulsive force that is characteristic of brush-like molecular conformations.

Briefly, well solvated surface-tethered polymeric molecules dangle out into the solvent and are thermally mobile. At sufficient surface grafting densities, packing constraints between the solvated chains cause them to repel from each other and extend away from the surface in a brush-like conformation. Confining these molecules (i.e., compression) leads to a marked exponentially decaying repulsive entropic force (i.e., steric repulsion) (16). This scenario is unlike the compressive response of bulk polymeric gels, which can be complex [i.e., monotonic, oscillatory, etc. (16)] depending on properties such as molecular structure and the amount of cross-linking (17). Polymer brushes are well accounted for in colloid and surface science and are exploited in technology; e.g., to prevent the aggregation of particle dispersions (18). In biology, steric repulsion is associated with the entropic fluctuations of unstructured microtubule-associated proteins (MAPs) and neurofilament sidearms (19, 20). Such behavior is absent in folded proteins such as BSA, type II histone, IgG, and skeletal muscle myosin (20). Brush-related forces are analyzed by using the theory of Alexander and de Gennes (AdG) (21–24), which relates (or “scales”) the measured steric repulsion to parameters such as the degree of polymerization of the molecules and the grafting distance between neighboring molecules (25). The AdG expression also provides an acceptable fit to the long-range repulsion observed here.

Finally, the cNup153 molecules can be reversibly collapsed after the addition/removal of a less polar solvent from the buffer (i.e., 1,2-hexanediol). Overall, we find that natively unfolded FG domains are entropically dominated and associate less strongly with each other than previously thought. This work provides strong evidence that links the NPC-selective gating mechanism to the presence of an entropic barrier/trap in the local NPC interaction zone (7).

Results

cNup153 SMFS and Worm-Like Chain (WLC) Analysis.

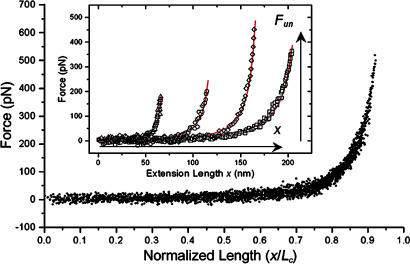
cNup153 molecules were covalently tethered to a Au surface and vertically stretched by the AFM tip. The extension of each molecule is characterized by a force that increases nonlinearly with distance (Fig. 1Inset). Note that each force profile is dominated by a single unbinding peak lacking any unfolding domains, which indicates that cNup153 is structurally similar to an unfolded polymer/polypeptide chain (15). The large variation in the unbinding force (F_un) and extension length (x) arises from the nonspecific binding of the tip to any point along the cNup153 molecular chain.

Fig. 1.

An ensemble of 40 normalized SMFS curves can be superimposed to form a “master curve” which verifies that the elasticity of each cNup153 molecule scales with its contour length [i.e., F(x) ∝ x/L_C]. (Inset) WLC analysis (red) of cNup153. The extension length x and unbinding force F_un are denoted. The values of (x, F_un, l_p, L_C) for each of the four representative extension curves are as follows: triangles, 65.9 nm, 203.9 pN, 0.49 nm, and 73.8 nm; circles, 115.3 nm, 202.1 pN, 0.42 nm, and 128.3 nm; diamonds, 164.7 nm, 457.3 pN, 0.34 nm, and 179.0 nm; squares, 204.1 nm, 373.9 pN, 0.28 nm, and 227.6 nm.

The forced extension of a polymer/polypeptide chain is well characterized by the WLC model of polymer elasticity (15) [also known as the Kratky–Porod chain (26)], which is defined as

[1]

where k_B is Boltzmann’s constant, T is the temperature, l_p is the persistence length, and L_C is the contour length of the chain. By fitting SMFS data to the WLC, we are able to determine the values for l_p and L_C. We find that L_C typically underestimates the full length of cNup153 (≈200 nm) because each molecule can be “picked up” anywhere along its length. l_p provides a measure of the flexibility (i.e., bending rigidity) of the molecular chain (15). After fitting each force curve with the WLC (Fig. 1 Inset), we find (l_p, L_C) to be (0.49 nm, 73.8 nm), (0.42 nm, 128.3 nm), (0.34 nm, 179.0 nm), and (0.28 nm, 227.6 nm) for each curve, respectively.

Although the variability in extension lengths is large, each cNup153 molecule should a priori conform to the same elastic property. By normalizing the extension length of each respective curve by L_C, a “master curve” can be produced that superimposes all of the data onto a single plot (Fig. 1) (27). This analysis indicates that single molecules are being addressed and that the elasticity of each cNup153 molecule scales with its contour length [i.e., F(x) ∝ x/L_C]. Here, the mean persistence length is found to be 3.9 ± 1.4 Å, which is in accordance with the size of a single amino acid residue.

cNup153 Tethered to Au Nanodots.

A 20 × 20 array of nanofabricated Au nanodots on Si is shown in Fig. 2A. Each Au nanodot is spaced ≈1 μm apart to ensure that after binding to the Au, individual clusters of cNup153 remain isolated from each other. A scanning electron micrograph indicates that each nanodot is ≈100 nm in diameter (Fig. 2B). Importantly, the size of each Au nanodot has been specially chosen to mimic the general dimensions of native NPCs (Fig. 2C). The average height and diameter of each nanodot has been measured by AFM to be 27.6 ± 4.6 nm and 97.1 ± 7.4 nm, respectively.

Fig. 2.

Characterization of the Au nanodots. (A) The design consists of a 20 × 20 nanofabricated square array of Au nanodots on a Si substrate, each separated by a distance of ≈1 μm. (Scale bar, 3 μm.) (B) Au nanodots viewed by scanning electron microscopy. (Scale bar, 1 μm.) (C) Three-dimensional AFM image of an individual Au nanodot measuring h = 27 nm and d = 93 nm. A schematic illustrates the general physical dimensions of the NPC. Blue and black boxes represent the cytoplasmic ring and nuclear ring moiety of the NPC, respectively.

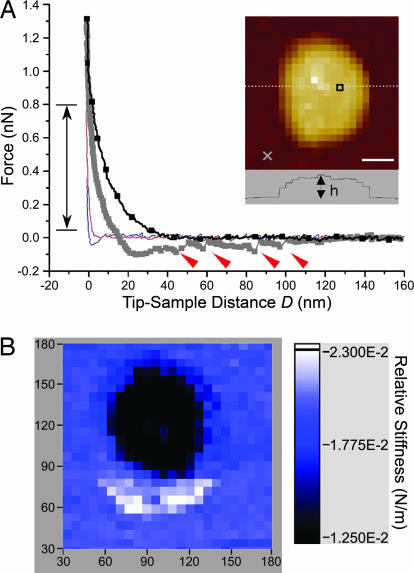
Arrays of force measurements were acquired in force–volume (FV) mode (28) (see Materials and Methods). This way, individual force curves related to specific topographic sites (X, Y) are mapped to reveal the spatial distribution of the measured forces. Experiments conducted in PBS after tethering cNup153 to the Au nanodots show that the force acting between the tip and each Au nanodot is distinct compared with the surrounding area (Fig. 3A). At an approach velocity of 560 nm/s, a repulsive force is detected at a separation distance of D ∼ 40 nm above the surface of the Au nanodot. This is followed by complex hysteretic behavior upon tip retraction. The force curve obtained in the surrounding area shows neither of these characteristics.

Fig. 3.

Representative force curves obtained in a 32 × 32 FV map of a cNup153-tethered nanodot. (A) A long-range, repulsive force (black line with squares) originates at D ∼ 40 nm above the nanodot. Hysteretic behavior results during tip retraction (dark gray squares) after which four stretching–unbinding responses are observed at 47, 60, 86, and 98 nm (red arrows). The average unbinding force is ≈100 pN. The force in the surrounding area does not reflect any of such characteristics on approach (red line) or retraction (blue line). The position of each force curve (square, above the nanodot; cross, in the surrounding area) is indicated in the quasi-topographic image shown in the Inset. (Scale bar, 30 nm.) The dotted line refers to the nanodot cross-section (h = 29 nm). The double-headed arrow denotes the range over which the relative stiffness was calculated. (B) Corresponding FV stiffness map showing the spatial distribution of the long-range repulsion. The relative stiffness (color-coded in the scale bar) shows that a low-stiffness region (≈0.01 N/m) is localized to the nanodot whereas the stiffness in the surrounding area is ≈0.02 N/m and corresponds to hard-wall repulsion. The values along the figure axes are in nanometers.

The in-plane distribution of the measured forces can be deduced from the corresponding FV stiffness map (Fig. 3B), which is generated by calculating the relative stiffness between an applied force range of 0.05 and 0.8 nN for each approach curve (identified in Fig. 3A). Note that in this figure, the long-range repulsion above the Au nanodot gives rise to a lower stiffness as compared with the surrounding area. Observe also that the repulsive zone is strictly localized to the nanodot with an effective radius of 40 nm as evidenced in the dark, low-stiffness area (≈0.01 N/m). The stiffness in the surrounding bright area is ≈0.02 N/m and corresponds to the cantilever spring constant (k_c ≈ 0.02 N/m); i.e., hard-wall repulsion. When cNup153 is absent, hard-wall repulsion is typically observed for both the Au nanodots as well as in the surrounding area (see later, similar to Fig. 5B).

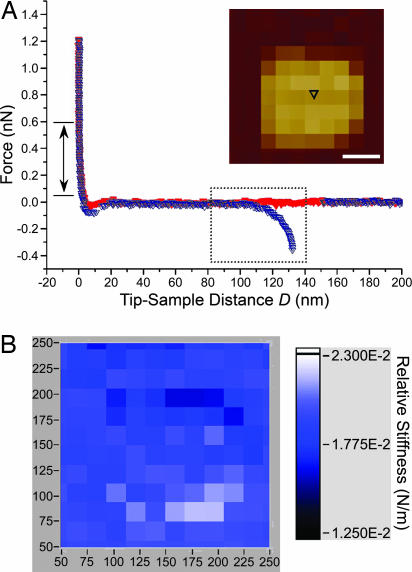
Fig. 5.

Representative force curve obtained over a nanodot in 5% 1,2-hexanediol. (A) The lack of a repulsive force on approach (red symbols) signifies that the entropic barrier has collapsed. Upon retraction (blue symbols), a cNup153 molecule remains bound to the AFM tip and unbinds at D ≈ 130 nm. A WLC fit gives l_p = 0.5 nm for this curve (boxed). The double-headed arrow denotes the range over which the relative stiffness was calculated. The position of the force measurement (black triangle) above the nanodot is indicated in the quasitopographic image shown in the Inset. (Scale bar, 50 nm.) (B) Corresponding stiffness map showing that the relative stiffness (color-coded in the scale bar) is ≈0.02 N/m over the entire area (i.e., the entropic barrier has collapsed). The values along the figure axes are in nanometers. This stiffness map is also similar to control measurements made in the absence of cNup153 (see text).

An important consideration is the origin of the repulsive force associated with each Au nanodot. It is imperative to recognize that it is not an artifact caused by the aggregation of unspecific material on the Au nanodot or the AFM tip. The cross-sectional analysis of the FV map (h = 29 nm; Fig. 3A Inset) fails to indicate any increase in the height of the Au nanodot as one would expect (compare with Fig. 2C). Given that the onset of the repulsive force is detected at D ∼ 40 nm above the Au nanodot surface (Fig. 3A), the cross-sectional height profile of the Au nanodot in this case would be ≈70 nm. Aggregation on the tip would lead to a more homogeneous distribution of force that would be indistinguishable between the nanodot and the surrounding area. Indeed, the lack of endogenous cysteine groups on cNup153 renders non-terminal binding to the Au nanodots unlikely.

Compression of cNup153 Results in a Steric Repulsive Force.

The net force acting on a particle near a polymer-grafted surface is a combination of van der Waals, electrostatic, hydrophobic, and entropic forces (i.e., steric repulsion) (16). The magnitude of the attractive van der Waals force is small compared with the steric repulsion that develops as the molecular chains are compressed and can be neglected. The range of the electrostatic force depends on the ionic concentration of the solution and decays according to the Debye length, κ⁻¹. The relatively high ionic concentration in PBS gives a κ⁻¹ value of 0.76 nm at room temperature and indicates that the electrostatic force is effectively screened at this distance (29). Hydrophobic contributions may be further neglected because the AFM tip is typically covered in a hydrophilic oxide layer.

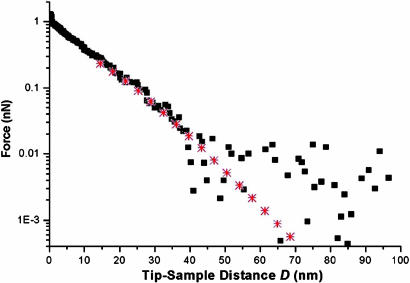
The semilogarithmic plot in Fig. 4(same repulsive force as in Fig. 3A) shows a marked exponential behavior in the measured force that is anticipated for the compression of a polymer brush (21, 22). Accordingly, the AdG theory (25) has been shown to provide a reasonable description of AFM force data of polypeptide (19) and polymer brushes (21, 22), and is used as a qualitative guide in this analysis. The AdG expression equates the measured repulsive force of two brush-bearing surfaces to the osmotic repulsion because of the increase in polymer concentration as the surfaces are brought together, and to the decrease in elastic energy of the polymer chains as they are compressed (see the supporting information, which is published on the PNAS web site). For AFM measurements, the AdG expression can be approximated to account for the compression of a brush on a single wall by a spherical tip (16, 19, 21, 22). Over the restricted distance range 0.2 < D/L < 0.9, the force, F, can be described by

[2]

where D is the distance between the surfaces, s is the average distance between the surface binding sites of cNup153, and L is the effective brush height. The effective radius of curvature is calculated from R_eff = (R_tip× R_dot)/(R_tip + R_dot), where R_tip and R_dot represent the radius of curvature of the AFM tip and the Au nanodot, respectively (16). In some cases, we find that R_tip ≈ R_dot and use R_eff = R_tip/2 for two interacting spheres of equal radii.

Fig. 4.

Semilogarithmic plot of the steric repulsion (from Fig. 3, black squares) and corresponding AdG fit (red stars). From the fit we obtain s = 23.6 nm and L = 39.0 nm. The data collected beyond D ∼ 40 nm is scattered because it is less than the minimum detectable force, which is given by the thermal noise of the cantilever: F_min = (k_BT·k_c)^1/2 ≈ 0.01 nN.

By fitting the curve in Fig. 4 with Eq. 2, we obtain s = 23.6 nm and L = 39.0 nm, using R_tip ≈ R_dot ≈ 40 nm. The averaged values of the fitting procedure obtained over ≈70 force curves (collected over several nanodots) gives s_ave = 23.9 ± 2.8 nm and L_ave = 32.5 ± 7.2 nm. Here, L_ave accurately describes the experimental brush height (D where force increases from zero; see Fig. 3A) of 31.0 ± 6.3 nm. To substantiate s, surface plasmon resonance (SPR) measurements have been carried out for cNup153 end-tethered to flat Au substrates (using the same sample preparation protocols as those described in Materials and Methods), from which we obtain s_SPR ≈ 10 nm for a surface density of 94 ± 10 ng/cm² (data not shown). Here, s_ave compares only moderately well with s_SPR and stems from geometrical differences between the nanodot and the flat Au substrate.

Depending on s, surface-tethered polymer chains can be described as either “mushrooms” or “brushes” (24). Mushrooms form at low surface densities where adjacent chains do not overlap laterally, whereas elongated brushes form at high grafting densities. The mushroom regime is often invoked for s > 2r and the brush regime for s < 2r (24) (see the supporting information). The quantity r is the root-mean-square radius of a WLC and is defined by 〈r²〉 = 2l_pL_C (26). The overall contour length L_C can be calculated by L_C = an = 229.5 nm, where a is the average amino acid backbone length (0.38 nm) and n is the number of residues (604 aa) within the cNup153 chain. Given the experimentally determined value of 0.39 nm for l_p, we find r = 13.4 nm. Taking into account that the cNup153 molecules are extended to L ≈ 3r and that both s_SPR and s_ave are smaller than 2r (= 26.8 nm), we deduce that the cNup153 molecules are brush-like in the weak-overlap regime (23).

cNup153 Undergoes a Reversible Collapse Transition in Hexanediol.

To test the effect of a less polar solvent (11, 30), we have added 5% 1,2-hexanediol to the buffer conditions and observe the long-range repulsion above the nanodot to be completely eliminated and replaced by an attractive force (Fig. 5A). Nevertheless, a cNup153 molecule can bind and be stretched by the retracting tip to a distance of ≈130 nm (Fig. 5A). The corresponding FV stiffness map indicates that the distribution of stiffness is roughly homogeneous and is close to the hard-wall contact stiffness of ≈0.02 N/m (Fig. 5B). It is instructive to note the marked difference between this stiffness map and the one obtained in standard PBS (Fig. 3B). Convincingly, the addition of hexanediol causes the cNup153 molecules to collapse. Upon replacing the 5% 1,2-hexanediol solution with standard PBS, we find that the entropic force is restored (data similar to Fig. 3). Such a reversible collapse transition can be repeatedly driven by consecutively adding/removing the hexanediol (three repetitions attempted only).

Discussion

The mechanical properties of individual cNup153 molecules can be summarized as follows: (i) cNup153 is a single domain exhibiting a flexibility consistent with that of a natively unfolded polypeptide, and (ii) the elasticity of cNup153 is homogeneous over the length of the molecule. These properties are consistent with AFM images obtained of cNup153 (31). Owing to a pronounced flexibility and mobility, it is predicted that natively unfolded proteins are capable of promoting simultaneous interactions with several binding partners at fast molecular association and dissociation rates (32). Interestingly, such characteristics may be manifest in FG domains that can be vital during nucleocytoplasmic transport.

A basic assumption of the selective phase model is that hydrophobic FG–FG interactions occur between FG domains (to give rise to the formation of a hydrophobic meshwork) (11). Given the abundance and proximity of FG domains within the NPC (7), it is reasonable to expect that hydrophobic, intra-FG interactions may also occur within a single FG domain (e.g., cNup153). Moreover, because the measured flexibility of cNup153 is homogeneous over the length of the molecule, intra-FG interactions may drive the molecule to bind to itself. These semistable linkages will ultimately unfold as the molecule is stretched, giving rise to characteristic sawtooth peaks in SMFS force spectra (33). Here, the lack of unfolding peaks in the SMFS data does not show support for such a conjecture. If extrapolated, these findings provide reasonable doubt that inter-FG interactions dominate between FG domains in the NPC to form a sieve-like meshwork (11). Instead, we intuit that FG–FG interactions are weaker than anticipated and dynamic over much shorter time scales. Although molecular dynamics simulations predict that short FG peptides (4 or 12 aa in length) tend to aggregate with each other in the absence of importin β (simulation time of ≈20 ns) (34), the present results (where cNup153 is significantly longer than the simulated FG peptides) show that conformational entropy dominates over such enthalpic interactions.

Our results indicate that the NPC gate-barrier mechanism originates from the entropic fluctuations of the natively unfolded FG domains (i.e., entropic barrier). We emphasize that the calculation of persistence length of cNup153 is key because it shows that the polypeptide chains are flexible and, although entropically elastic, may be extended in a brush-like manner depending only on the spatial constraints within the NPC. During transport, small molecules such as water and ions readily diffuse through such a barrier while larger inert particles are repelled (e.g., AFM tip). It is estimated that at least ≈100 FG nucleoporins are present on either face of a NPC (7), and we anticipate that the high-density FG barrier on each face consists of a repulsive zone large enough to restrict the passage of non-NLS cargo through the central pore. Such entropic behavior suggests also that a smaller number of FG domains is enough to maintain the barrier in native NPCs and may explain why a significant reduction in NPC permeability was not detected in FG-repeat-reduced, minimal yeast NPCs (14).

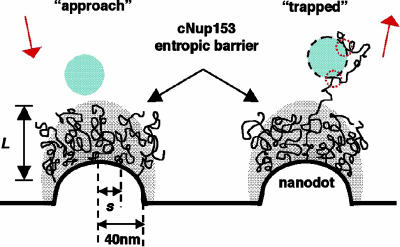
FG-repeat domains may simultaneously trap NLS cargo in the NPC near-field. Here, several retraction force curves that indicate multiple binding interactions between cNup153 and the AFM tip can be identified. Close inspection of the retraction curve obtained above the Au nanodot in Fig. 3A reveals four attractive peaks that are located at 47, 60, 86, and 98 nm, respectively. These peaks are characteristic of molecular stretching and unbinding during SMFS. The multiple peaks result from binding interactions between several cNup153 molecules as well as from several binding sites along the length of an individual molecule, with the AFM tip. Although the binding interactions in this case are nonspecific (unbinding force of ≈100 pN), an analogous situation may occur during nucleocytoplasmic transport. As summarized in Fig. 6, while non-NLS cargo in the NPC near-field are repelled by the entropic barrier, receptor-bound cargo may become trapped because of attractive interactions occurring between the hydrophobic sites of the transport receptor and several FG sites (10).

Fig. 6.

Schematic representation of the entropic barrier. (left) The barrier is formed by the brush-like conformations of the cNup153 molecules that are tethered to the nanodot surface. The gray shaded area emphasizes the stochastic nature of the molecules over large time scales (approximately microseconds). A non-NLS cargo (blue, hatched) is repelled once it is within the near-field of the cNup153 molecules. (right) A receptor-bound cargo (blue, hatched with black dashes) is “trapped” because of attractive interactions that occur between the transport receptor and several FG sites (indicated by red dotted circles).

Further proof of the entropic barrier can be obtained after the reversible collapse transition of cNup153 molecules in hexanediol. In poor solvents, surface-tethered polymer brushes are no longer optimally solvated and collapse into more compact structures (16). Although the overall physics is complex, the addition of a solvophobic (i.e., hydrophobic) solute to a solvophilic (i.e., aqueous) system can give rise to strongly attractive interactions between solvophilic (i.e., hydrophilic) macromolecules or surfaces (35). Polymer brushes can also collapse because of a reduction in temperature (i.e., entropy) (36), which may explain why a disruption in the NPC gating mechanism was caused by chilling (30). Most significantly, our findings are consistent with previous studies which show that a reversible opening/closing of the NPC can be triggered by the addition/removal of hexanediol (11, 30). The reversible collapse of the entropic barrier in different environmental conditions validates the hypothesis that the FG domains form the major constituents of the restrictive barrier in native NPCs.

Overall, these results reveal that the selective gating mechanism is predominantly an interfacial effect arising from the entropic fluctuations of several unfolded FG domains within the peripheral near-field of individual NPCs instead of a bulk-like hydrophobic gel or meshwork.

Conclusions

Nucleocytoplasmic transport is governed by molecular interactions that occur over tens of nanometers. Hence, the key NPC components (e.g., FG nucleoporins) need to be scrutinized and understood on such relevant length scales. This point should be emphasized because the nanoscale properties of a material (e.g., polymer/polypeptide chain conformations at an interface) can differ significantly from its bulk properties (e.g., gel).

This work underscores the functional significance of natively unfolded proteins as they are increasingly being recognized to play important roles in the cell (37). Although the concept of polymer brushes is well established, it is interesting to uncover the functional implications of such phenomena within the context of biology (38). Our multidisciplinary approach has served as a successful experimental platform to study the behavior of FG molecules at the nano scale. These findings suggest that the collective behavior of FG domains gives rise to a repulsive entropic barrier within the peripheral near-field NPC interaction zone. Importantly, this does not preclude the fact that the entropic barrier can also simultaneously serve as a selective gate by “trapping” NLS cargo via specific binding interactions between transport receptors and FG sites.

Nevertheless, the translocation of trapped receptor-bound cargo remains unresolved. Although the geometry of the Au nanodots is unlike the ring-like structure of a NPC, we anticipate that the steric repulsion to be weaker over a hole because the FG domains are less spatially constrained, which provides for a more pronounced “funneling” effect for trapped receptor-bound cargo. Clearly, the overall strength of the entropic barrier is determined by the contour length and an accurate localization of the anchoring site of each FG domain. The present approach may be further useful to study the response of different FG domains to different transport receptors and environmental conditions (e.g., macromolecular crowding) (39).

Materials and Methods

Nanofabrication of Au Nanodots.

Au nanodots were patterned by electron-beam lithography. A 250-nm-thick, 950-kDa polymethylmethacrylate layer was spin coated onto P-type Si wafers passivated with a 500-nm-thick thermal oxide layer and baked at 160°C for 2 h. Designed patterns were exposed at a dosage of 40 fC by using an e-beam with accelerating voltage of 30 kV and a beam current of 22 pA, and developed in 3:1 isopropanol:methyl isobutyl ketone for 70 sec followed by rinsing in isopropanol and deionized water for 20 sec, respectively. Three-nanometer Cr was deposited followed by 25-nm Au on top of the patterned substrates by thermal evaporation. The polymethylmethacrylate resist was lifted off by soaking in acetone for 10 min. The samples were then rinsed in acetone, isopropanol, and deionized water consecutively and dried under N₂.

Cloning and Expression of Recombinant Nup153.

hNup153-C (amino acids 874-1475) was PCR-cloned into the bacterial expression vector pGEX 6P-1 (GE Healthcare), which contains an N-terminal glutathione S-transferase (GST) followed by a precision protease site to cleave off the GST-tag after purification. Three cysteines where added to the N terminus after the vector-encoded precision protease cleavage site. Escherichia coli BL21 expressing the recombinant Cys-Nup153-C were lysed by incubation with lysozyme (30 min, 10 mg/400 ml bacterial culture) in buffer (20 mM Tris, pH 7.8/100 mM NaCl/1 mM DTT) followed by homogenization with a glass potter. Lysates where spun down at 40,000 × g (30 min), and the recombinant protein was purified on a Glutathione Sepharose column (GE Healthcare). The N-terminal GST was cleaved off and the hNup153-C was purified by separation on a sucrose gradient (5–20% sucrose, 218,000 × g, 5 h). The protein was dialyzed against PBS to remove the residual DTT before coupling to Au.

Chemicals.

Ethanolamine hydrochloride, molecular sieves (3 Å), DMSO, 4-(2-hydroxyethyl)piperazine-1-ethane-sulfonic acid (Hepes), and 1,2-hexanediol were purchased from Sigma-Aldrich. The N-hydroxysuccinimidyl ester of methoxy-polyethylene glycol propionic acid (mPEG-SPA; molecular mass of ≈2 kDa) was obtained from Nektar Therapeutics (San Carlos, CA). Methoxy-polyethylene glycol thiol (mPEG-thiol; molecular mass of ≈350 Da) was obtained from Polypure. H₂O (18.2 MΩ·cm⁻¹) was obtained from a NANOpure Diamond water system (Barnstead).

Surface Preparation for SMFS.

Ten-nanometer Pt was deposited followed by 10-nm Au on Si substrates by thermal evaporation. The density of bound Cys-Nup153-C molecules was minimized by first incubating the Au substrates with 2 mM mPEG-thiol dissolved in H₂O (15 min). Excess mPEG-thiol was rinsed off in H₂O. PEG-modified substrates were immersed in 10 μg/ml Cys-Nup153-C in 10 mM PBS (pH 7.4) at 4°C for 48 h. Samples were rinsed in PBS and used immediately. SMFS measurements were made in FV mode with pulling speeds of ≈1 μm/sec.

Binding of cNup153 to Au Nanodots.

Au-patterned Si wafers were immersed in acetone and 2-propanol, dried under N₂, and UV-cleaned for 30 min (UVO cleaner model 42-220; Jelight Company, Irvine, CA). Si was passivated with 2 mM mPEG-SPA by using an established protocol (40) and checked for protein resistance (41). Cys-Nup153-C molecules were covalently attached to the Au nanodots by immersing the PEG-passivated Si in 10 μg/ml Cys-Nup153-C in 10 mM PBS (pH 7.4) at 4°C for 48 h. The samples were then rinsed and stored in PBS buffer at 4°C until use.

AFM Force Volume Spectroscopy.

AFM experiments were carried out in standard PBS buffer (otherwise specified in the text) at room temperature by using a MultiMode NanoScope IIIA controller (Veeco, Santa Barbara, CA) equipped with a 120-μm J-scanner and a standard liquid cell. Measurements were obtained in FV mode of either 16 × 16 or 32 × 32 force measurements of 4,096 data points each. FV data were collected and analyzed by an external PC running a customized labview program with a data-acquisition card (NI6052E; National Instruments, Austin, TX). The relative stiffness (force gradient = ΔForce/ΔZ-piezo distance) was evaluated to produce an additional stiffness map. A maximum value for the tip deflection (i.e., trigger voltage) was set to within ≈1 nN to avoid damaging the tip/sample because of excess loading.

Before each experiment the system was allowed to thermally equilibrate for at least 1 h. Rectangle-shaped Si₃N₄ cantilevers with pyramidal tips were used in all measurements (Microlevers; Veeco). Spring constant calibrations typically fell within a 10% margin of error from the nominal spring constant of 0.02 N/m. All tips were cleaned in oxygen plasma before use. Scanning electron microscopy was used to evaluate the radius of curvature of each tip (R_tip) after each experiment.

Abbreviations

AFM

atomic force microscopy

FG

phenylalanine-glycine

FV

force–volume

NLS

nuclear localization signal

NPC

nuclear pore complex

Nup

nucleoporin

SMFS

single-molecule force spectroscopy.