Membrane protein dynamics and detergent interactions within a crystal: A simulation study of OmpA

Abstract

Molecular dynamics (MD) simulations are used to explore the dynamics of a membrane protein in its crystal environment. A 50-ns-duration simulation (at a temperature of 300 K) is performed for the crystallographic unit cell of the bacterial outer membrane protein OmpA. The unit cell contains four protein molecules, plus detergent molecules and water. An excellent correlation between simulated and experimental values of crystallographic B factors is observed. Effectively, 0.2 μs of protein trajectories are obtained, allowing a critical assessment of simulation quality. Some deficiency in conformational sampling is demonstrated, but averaging over multiple trajectories improves this limitation. The previously undescribed structure and dynamics of detergent molecules in a unit cell are reported here, providing insight into the interactions important in the formation and stabilization of the crystalline environment at room temperature. In particular, we show that at room temperature the detergent molecules form a dynamic, extended micellar structure spreading over adjacent OmpA monomers within the crystal.

Membrane proteins are a key challenge to modern structural biology. They constitute ≈20–30% of genes in most organisms (1), and, yet, only ≈100 unique high-resolution membrane protein structures have been determined (ref. 2; also see http://blanco.biomol.uci.edu/Membrane_Proteins_xtal.html). This small number reflects the difficulties of both membrane protein expression and crystallization. Many membrane protein crystals are obtained in the presence of detergent molecules used to solubilize the protein. [Indeed, relatively few structures, e.g., that of Aqp0 (3), of membrane proteins have been determined at high resolution in a lipid bilayer environment.] Thus, an improved understanding of the nature of protein/detergent interactions within the crystal unit cell is important in aiding crystallization trials and in understanding the relationship between the conformational dynamics of a membrane protein in a crystal relative to in vivo.

Molecular dynamics (MD) simulations have been used for some years to study the structural dynamics of lipid bilayers as well as transmembrane peptides and proteins (4–7). Simulations also have been used to explore the dynamics of (nonmembrane) proteins within crystal unit cells (8–11) to examine, e.g., whether when in a crystal environment the protein exhibits a low degree of conformational drift, thus providing a test of the simulation force field and protocol.

To date, no MD studies of membrane protein crystals have been performed, despite the importance of understanding the nature of protein–detergent and protein–protein interactions within such crystals from the perspective of membrane protein structural biology. Therefore, we performed a 50-ns unit cell simulation of the ≈170-residue N-terminal domain of Escherichia coli OmpA, which consists of an eight-stranded β-barrel, as revealed by crystal structures at resolutions of 2.5 Å (12) and 1.65 Å (13) and by solution NMR studies (14, 15). This small outer membrane protein has been crystallized in the presence of n-octyltetraoxyethylene (C₈E₄), a detergent used in structural studies of a number of membrane proteins, including outer membrane proteins (e.g., OmpA, OmpX, FadL, BtuB, and OmpF), α-helical membrane proteins (e.g., rhodopsin), and monotopic membrane proteins (e.g., squalene hopene cyclase).

The OmpA N-terminal domain is well characterized experimentally, and simulation data are available for this protein in lipid bilayer (16) and detergent micelle (17, 18) environments. The crystal unit cell used in the current simulation contains 4 OmpA molecules, 24 detergent molecules, and water (Fig. 1A). Analysis of a 50-ns MD simulation, performed at a temperature of 300 K, has enabled critical assessment of simulation quality, encompassing analysis of the preservation of crystal contacts, comparison of simulation and experimental B factors, and convergence of protein conformational sampling. Additionally, the equilibrium structure and dynamics of detergent molecules in a membrane protein unit cell is described in atomic detail, providing insight into the protein–protein and protein–detergent interactions important in the formation and stabilization of the crystalline environment.

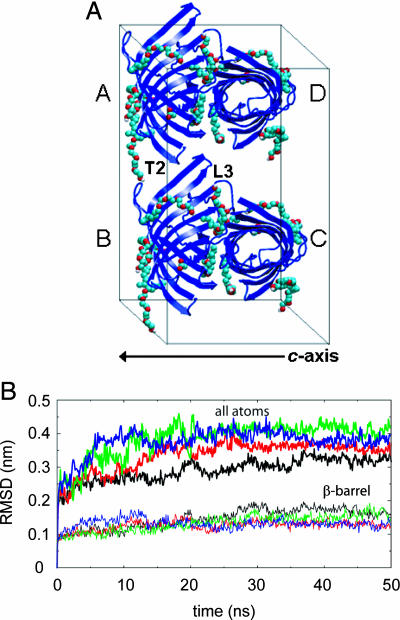
Fig. 1.

Maintenance of protein structure and crystal contacts. (A) The crystallographic unit cell (a = 6.51 nm, b = 7.97 nm, c = 5.02 nm, and β = 94.3°) of OmpA (blue cartoons format), with chain identifiers labeled, and detergent molecules [Corey–Pauling–Koltun (CPK) spacefilling format]. The crystal contact between loop L3 and turn T2 is labeled for one pair of protein molecules. Solvent molecules are omitted for clarity. The c-axis dimension of the unit cell is indicated. (B) C^α rmsd as a function of time for all atoms (upper four lines) and for the β-barrel region only (lower four lines) for OmpA chains A to D (black, red, green, and blue lines, respectively). All structures were fitted to their respective β-barrel region in the simulation starting structure.

Results

Protein Stability and Sampling.

Three types of contact are observed in the crystal (13). Two of these are on a twofold axis and consist primarily of hydrophobic interactions between the β-barrels of pairs of OmpA chains to produce an endless “fiber” along the c-axis, mediated by an annular layer of C₈E₄ detergent molecules (these contacts are between protein pairs A/D and B/C in Fig. 1). The third, smaller crystal contact is more polar and occurs between loop L3 of one OmpA molecule and turn T2 of another (contacts between protein pairs A/B and C/D in Fig. 1) and was aided by the Lys-107 → Tyr mutation in loop L3, which was essential for crystallization. During the 50-ns simulation, these crystal contacts were well maintained throughout, as ascertained by the number of atomic contacts and protein solvent-accessible surface area (data not shown).

Measurement of the C^α rms deviation (rmsd) for the entire protein and for the β-barrel domain provides insight into the conformational stability of each OmpA chain (Fig. 1B). For the β-barrels, after an initial rapid jump, the rmsd plateaued at ≈0.l3 nm after ≈5 ns, with only small subsequent fluctuations and a final value after 50 ns of <0.2 nm. Thus, the barrel was stable in the unit cell, with a rmsd higher than that found for OmpA in a bilayer (16) but comparable with that in a micelle (17). Consistent with this result, the protein secondary structure, analyzed by using dssp (19), remained on average native-like over 50 ns (data not shown). Nevertheless, an occasional loss or gain of a few β-strand residues occurred, as observed during other simulations of OmpA in different environments and also for the solution NMR structure of the OmpA fold in detergent micelles (14). Also consistent with the barrel stability is the maintenance of the internal pore structure. As ascertained by using hole (20), deviations from the crystal structure of <0.5 Å in pore radius were observed, including the region previously proposed to be involved in “gating” the pore (16). As a result, no water molecules traversed the OmpA pores in the 50-ns unit cell simulation.

For the whole protein, which includes the more mobile, unstructured extracellular loops and periplasmic turns of OmpA, after an initial jump in rmsd, subsequent fluctuations were observed, which differed between each chain. Nevertheless, all four of the final rmsds were of the same magnitude with values of ≈0.35 nm. This result compares with values of ≈0.2 nm for OmpA in a bilayer and ≈0.45 nm for the micelle simulation. The loops appear to be less mobile in the unit cell than in the micelle because of the constraining crystal contacts, as revealed by the rmsds for each individual loop, with a final value of <0.1 nm for loop L3. This result is consistent with its involvement in a crystal contact and confirms its high conformational stability, even at 300 K.

Because the unit cell simulation provides four protein trajectories for analysis, the rmsd also was calculated for a trajectory composed of the average structure of all four OmpA chains (i.e., at each point in time, the OmpA structure was averaged across the four monomers within the unit cell; see Fig. 5, which is published as supporting information on the PNAS web site). The rmsd was much smaller than for the individual chains (Fig. 2A), with a final value of just over 0.1 nm for the β-barrel domain. Thus, the random deviations in each of the four simulations tend to compensate through cancellation when multiple trajectories are considered. This finding implies that multiple simulations or additional unit cells may well result in better agreement with experiment, given that the electron density from a crystal structure is both a temporal and spatial average. It also indicates that, to a first approximation, the simulation is stable because no drift in rmsd is seen beyond the initial rise.

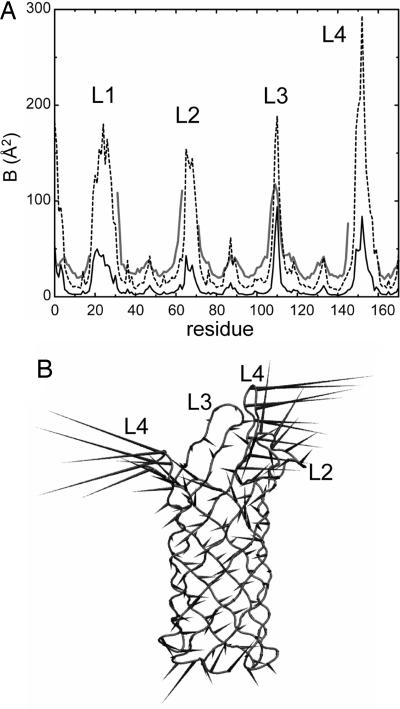
Fig. 2.

Average fluctuations and correlated motions. (A) Time-averaged (excluding the first 5 ns) simulation C^α B factors compared with experimental (i.e., x-ray) B factors. The x-ray B factors are shown as a gray line; the simulation B factors obtained by averaging the four simulation B-factor curves for the individual chains are shown as a broken line; and the simulation B factors derived from a trajectory composed of the average structure of all four OmpA chains at each point in time are shown as a solid black line. (B) Schematic “porcupine plot” diagram of the first principal component of the simulated motion of OmpA chain C (shown in C^α trace format). The cones represent fluctuations, with their orientation indicating the direction of motion of the C^α atom to which they are attached and their length indicating the amplitude of this motion. The figure was made by using dynamite (21).

In addition to simulation stability, it is of interest to analyze the degree of sampling of conformational space within the simulations using block analysis techniques, for example, to establish the convergence of simulated B factors. The average C^α B factors [calculated as (8π²/3)MSF, where MSF is the mean square fluctuation] (22) seem to gradually rise with time, and the patterns of increase are very similar for all four chains (see Fig. 6A, which is published as supporting information on the PNAS web site). Separation of the analysis into just the β-barrel region reveals a fairly flat curve, indicating that the mobile extracellular loops are the main contributors to the lack of convergence. In contrast, the β-barrel is inherently stable and is surrounded by constraining crystal contacts and an annular layer of detergent, which may act in a similar way as a lipid bilayer environment (17).

An alternative approach to assessing conformational sampling is provided by principal components analysis (PCA) and in particular analysis of the average covariance matrix overlap (23). The overlap (which assesses the similarity of all eigenvectors and corresponding eigenvalues describing the motion of a protein) was calculated between equally spaced time windows and the whole simulation, with an overlap value of 0 representing completely dissimilar conformational spaces sampled and a value of 1 representing identical ones (22). A gradual increase in overlap was observed for all four chains over time. For each chain, the mean covariance matrix overlap between the two halves of the simulation and the whole simulation ranged between ≈0.55 for the whole protein and ≈0.70 for the β-barrel only. Thus, it is evident that there is incomplete conformational sampling, particularly for the extramembraneous regions. However, the extent of conformational sampling enables some meaningful conclusion to be drawn and is comparable with/better than that in, e.g., recent simulations of water-soluble proteins for comparison with x-ray data (11).

Protein Mobility.

The local flexibility of each OmpA chain was analyzed by calculating the per-residue simulation B factors, before averaging B factors over all four OmpA monomers in the unit cell for comparison with the crystallographic B factors (Fig. 2A). Clearly, a good residue-by-residue correlation of the simulated with the crystallographic B factors is exhibited, particularly for the β-barrel domain. However, the simulated B factors are generally lower than the x-ray values (except for, e.g., loop L3) as has been observed for other membrane protein simulations [e.g., for the outer membrane transport protein FhuA (24)]. This outcome may in part result from the effects such as static disorder on experimental x-ray B factors (25) and, in particular, from the rapid freezing to 100 K (26). Indeed, theoretical studies suggest that many degrees of freedom in a flash-cooled protein crystal are quenched at temperatures near 200 K (27). The offset also probably reflects incomplete conformational sampling (22); i.e., longer simulation times may sample slower motions, which would increase the simulated B factor. If one extrapolates from the block analysis of average simulated B factors (see Fig. 6A and above) to the average experimental value, then an estimate of 1.2-μs simulation time to obtain full sampling is obtained [for comparison (11) estimate ≈1 μs would be required for convergence of their simulation of a Staphylococcal nuclease crystal]. However, this value is probably an overestimate, and the similar trends in B factors over different time windows for the different domains, and for each chain, suggest that the observed per-residue correlation is reasonable. It is noticeable that the B factors in the lower-resolution structure of OmpA (12) were consistently higher than those for the high-resolution structure. Interestingly, simulations of an extremely high-resolution (0.96 Å) structure of a ≈60-residue scorpion protein toxin [Protein Data Bank (PDB) ID code 1AHO] (28) revealed excellent sampling and agreement between experimental and simulated B factors (>70% correlation), but, again, a constant offset was observed (D. Bemporad and M.S.P.S., unpublished results).

To examine the agreement more quantitatively, correlation coefficients were calculated between experimental B factors and those obtained by averaging per-residue over different time windows of the simulation for all four OmpA chains. Interestingly, the shorter (nanosecond) timescale fluctuations correlate better with the crystallographic B values than the longer-timescale motions do, with coefficients ranging from ≈0.7 for 1-ns windows, down to ≈0.6 for 45 ns. However, B factors calculated for the trajectory composed of the average structure of all four OmpA chains (Fig. 3A) gave a coefficient of 0.71. For comparison, this value is at the upper end of correlation coefficients calculated for crystal structures by using other theoretical methods such as Gaussian network models (29). The improvement in correlation seems to result primarily from averaging of stochastic variations within the mobile, extracellular regions of OmpA. Thus, the variation in B factors for the loops (except loop L3, which participates in a crystal contact) between each chain is much greater than for the stable β-barrel domain (data not shown), highlighting their high mobility and multiple accessible conformational states and potentially explaining the lack of experimental density observed in the crystal.

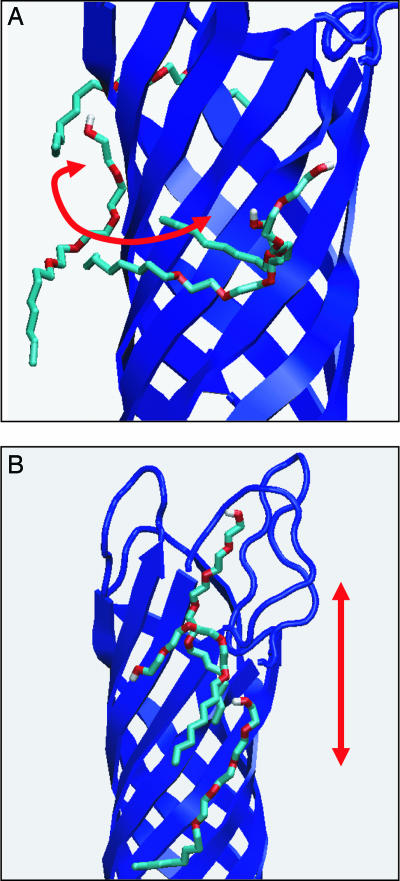
Fig. 3.

Superimposed snapshots of detergent molecules (Corey–Pauling–Koltun bonds format) around OmpA (blue cartoons format). In A, a detergent molecule translates around the barrel surface, perpendicular to the barrel axis, whereas in B, a detergent molecule translates up and down the barrel surface, parallel to the barrel axis.

Given the acceptable agreement between simulated and experimental B factors, we elected to determine the direction and amplitude of the most significant, correlated motions. To this end, principal components analysis was applied to discard the simulation “noise” (30). The C^α covariance matrices for the four OmpA molecules were diagonalized to obtain the eigenvectors and their associated eigenvalues, and the trajectory for each protein then was projected onto the eigenvectors to obtain the principal components. The first eigenvector of each chain accounted for ≈40% of the total eigenvalues (i.e., fluctuations) and thus was analyzed further (Fig. 2B). The high-resolution structure of OmpA includes anisotropic B factors (13). These are consistent with the simulation data in several ways. As expected, the relative atomic motions of the β-barrel are much smaller than those of the turns and loops, consistent also with the analyses above of structural drift and flexibility. Second, the motions in the barrel are primarily perpendicular to the barrel axis and may represent “breathing motions” with consequences for pore formation (16). Interestingly, the small fluctuations in the β-strands seem to steadily increase toward their ends as they reach the loops and turns, so the breathing motions may result from elastic vibrations, transmitted from the loops and/or turns. A gradient of flexibility along the barrel axis also has been observed through NMR dynamics measurements of OmpA (14). Finally, the large fluctuations in the nonbarrel regions are concerted, suggesting that they move as semirigid bodies. Indeed, the loops and turns of OmpA were predicted to move cooperatively on the basis of the anisotropic crystallographic data (13).

Detergent Dynamics.

One of the most significant aspects of the current simulations is that they enable us to examine the room-temperature behavior of detergent molecules within a crystal structure that, at 100 K, diffracts to a high resolution. Over the course of the 50-ns simulation, the 24 C₈E₄ molecules remained bound to the protein surfaces along the c-axis “fiber” (Fig. 1), as indicated by a constant buried solvent-accessible surface area and number of protein–detergent contacts (data not shown). However, they did not retain their bound location and conformation as observed in the x-ray structure; i.e., they behaved differently from the majority of ligands in simulations of protein/ligand complexes (see, e.g., ref. 31). It was possible to quantify the motions of the detergents by calculation of their diffusion coefficients (estimated over the final 10 ns). These diffusion coefficients varied from ≈0, indicating detergent molecules that were effectively stationary within the unit cell, to values of ≈1 × 10⁻⁶ cm²·s⁻¹. The mean value of the diffusion coefficient for all 24 detergents is 0.16 × 10⁻⁶± 0.24 cm²·s⁻¹. This value correlates surprisingly well with lateral diffusion coefficients of ≈0.3 × 10⁻⁶ cm²·s⁻¹ found for 1,2-dimyristoyl-sn-glycero-3-phosphocholine (DMPC) lipids classified as “bound” [i.e., annular lipid (32, 33)] to the surface of OmpA when the protein was simulated embedded in a phospholipid bilayer (34). Thus, at a simple level the detergent molecules within the crystal may substitute for annular lipid within a bilayer environment.

Visual inspection revealed a variety of different types of motion exhibited by the detergent molecules over 50 ns (see Movie 1, which is published as supporting information on the PNAS web site). The primary motions observed were of detergents diffusing around the surface of the β-barrel (Fig. 3A), mimicking annular bilayer lipids. In some cases this diffusion led to a detergent molecule contacting a symmetry-related neighboring OmpA monomer. Additionally, rarer motional modes were observed, which are likely to occur much less frequently in a biological membrane. The first of these was limited one-dimensional diffusion up and down the protein surface (Fig. 3B). The second was a “flip-flop” action with the oxyethylene moiety reversing its polarity with respect to the extracellular or periplasmic side of OmpA. The final motion, which is presumably exclusive to the crystallographic environment, involved the simultaneous movement toward one another of pairs of detergent molecules from neighboring, “nonfiber” OmpA chains along the polar L2–T3 crystal contact (Fig. 1), interacting via their oxyethylene groups. Critically however, complete exchange of detergents between OmpA monomers did not occur.

Overall, the lack of a tightly packed hydrophobic core, combined with the “softer” nature of the uncharged polar section of C₈E₄ compared with membrane lipids, leads to a rather unconstrained detergent annular layer. Fig. 4A shows superimposed snapshots of detergent around the OmpA chain A/D pair over the course of the simulation (similar results were obtained for chains B and C). It is clear that the 12 detergent molecules cover the entirety of the β-barrel surfaces over 50 ns, maintaining a favorable hydrophobic environment while exhibiting high lateral mobility along the c axis. The general picture that emerges is of a fluid micelle-like fiber network. Interestingly, neutron diffraction studies have identified a continuous interconnected network of detergent molecules around crystallographic OMPLA (36).

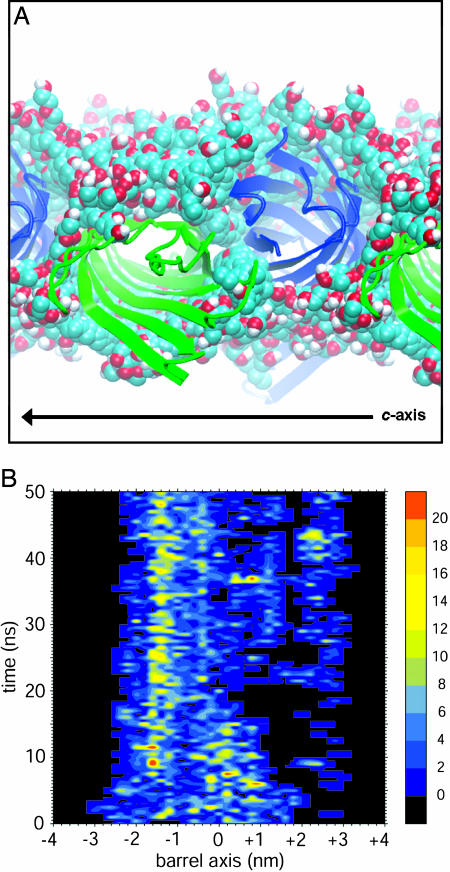
Fig. 4.

Interactions between protein and detergent. (A) Superimposed 0.5-ns snapshots of detergent molecules (Corey–Pauling–Koltun spacefilling format) around adjacent OmpA chains (green or blue cartoons format), observed perpendicular to the c-axis (labeled). (B) Number of interactions (defined as an interatomic distance of <0.4 nm) along the OmpA chain C β-barrel axis with detergent oxyethylene moieties over time. The figure was made by using proximus (S.S.D. and M.S.P.S., unpublished results) and xfarbe 2.5 (35).

To further analyze the behavior of detergent molecules in the crystal lattice, the numbers of contacts between protein and the n-octyl (data not shown) or oxyethylene groups (Fig. 4B) of the detergent molecules were mapped onto the β-barrel axis as a function of time. The n-octyl tails provided a hydrophobic layer around the β-barrel surface over a width of ≈2.5 nm. Interestingly, the more polar oxyethylene moieties also interacted with the barrel region, providing a broader contact width of ≈4 nm (Fig. 4B). This result is in contrast to the more stereotypical patterns of interaction made with OmpA between the tails and headgroups of lipid/detergent molecules in the bilayer (5, 34) and micelle environments (17). This effect is probably because of the mixed nature of the oxyethylene moieties, which are less polar than many detergent headgroups, and thus makes the formation of crystal contacts via detergent easier because of the softer, more flexible nature of interactions. Additionally, the n-octyl and oxyethylene groups showed some intense patches of interaction due to interaction with the two aromatic bands delimiting the hydrophobic girdle of the OmpA barrel, in agreement with their “anchoring” role in the bilayer environment. An additional set of interactions also was observed on the extracellular side because of protein–detergent interactions around the T2–L3 crystal contact (Fig. 1). The detergent motions that led to these interactions involved the mutual contact of sets of detergent molecules via their oxyethylene moieties, bound to the alternative OmpA chains taking part in the contact. These motions were aided by interaction with several anchoring Tyr residues, including the mutated Tyr-107 that was essential for crystallization. Although this residue does not directly take part in the L2–T3 crystal contact, its interaction with detergent suggests that it may have had a role in the initial nucleation or stabilization of this contact, at least before freezing of the crystal. A similar third interaction band has been observed during bilayer simulations of OmpA, and proposed to have a role in binding lipopolysaccharide (LPS) (5, 34).

Discussion

We have presented a previously undescribed MD study of a crystalline membrane protein, which complements simulations of OmpA in a bilayer (16) and micelle (17, 18). This work enables comparison of membrane protein flexibility as a function of environment. Perhaps surprisingly, the β-barrel domain in the crystal simulation was observed to be relatively flexible and, hence, closer to a micelle than to a phospholipid bilayer environment.

Overall, both the unit cell and individual protein monomers were very conformationally stable, with an average C^α rmsd for the β-barrel domain of just 0.5 Å after 50 ns. Good quantitative agreement was obtained between the B factors obtained from simulation (at 300 K) and from experiment (at 100 K), but an offset was observed that may result from the difference in temperature, as well as static disorder in the crystal. Despite the good agreement of simulated and experimental B factors, the demonstrated conformational undersampling (especially for the loops) would be expected to lead to a degree of divergence between simulation and experiment. However, this disparity may result partly also from the lack of experimental electron density for the loops. Indeed, the magnitude of simulation B factors for the loops were rather different from chain to chain, indicating multiple accessible conformational states that may explain the lack of observed density in the crystal. The systematic simulation of multiple unit cells might provide further information on this sampling problem, as well as the effect of static disorder on the average protein structure.

Beyond sampling issues, a major difference between simulation and experiment is in the temperature. Although x-ray data were obtained at ≈100 K, our simulation was at 300 K. This value approximates to the crystallization temperature, thus offering insights into this process. Indeed, we have demonstrated that a mutation (Lys-107 → Tyr) may have led to stabilization of a crystal contact (T2–L3) at room temperature by means of interaction with detergent molecules, rather than by direct protein–protein contacts. It would be of interest to extend our simulations to low-temperature crystals. This study might require some attention to, e.g., water parameters, as suggested by, e.g., simulations of spontaneous ice formation from pure water (37). Nevertheless, it may be possible to “quench” the system to lower temperatures to investigate the instantaneous effect on the dynamics of the system. For example, simulations have been used to explore the dynamics of protein hydration water at temperatures of 150 K (38). Furthermore, theoretical (27) and experimental (26) studies suggest that the process of rapid freezing of protein crystals can have unpredictable effects on the resultant B factors.

The previously undescribed behavior of detergent molecules within a membrane protein crystal environment has been observed. Considerable mobility of the detergent is observed. At 300 K, the detergent molecules produced a well preserved, but dynamic, extended micellar structure around the β-barrels. Of course, it is possible that additional (disordered) detergent molecules may be present, but not resolved, in the crystal structure. However, the integrity of the extended micellar structure of the detergent on a 50-ns timescale lends us some degree of confidence that our model of the detergent organization within the crystal is stable, as indicated by experience with, e.g., self assembly simulations of detergent/protein micelles (18, 39, 40). The observed loosely packed detergent network enabled breathing motions, in agreement with the crystallographic anisotropic B factors and NMR, which were elastically propagated from larger fluctuations in the loops. Although the barrel mobility was comparable with that in a micelle environment (17), deviations from the crystal structure of <0.5 Å in pore radius were observed. The region around the Arg-138–Glu-52 pair hypothesized to gate the central pore remained particularly stable, consistent with the observed lack of water passage in any of the four OmpA trajectories over 50 ns. This closed-gate behavior contrasts with simulations of OmpA in other environments. Whereas simulations of OmpA in a bilayer revealed only small changes in the radius of the pore (16), simulations in a micelle yielded motions in a number of the side chains within the β-barrel, enabling water molecules to traverse the full length of the pore (17). This finding is intriguing, given that the magnitude of fluctuations in the β-barrel domain in the unit cell simulation are more comparable with the flexible micelle than bilayer environment. Indeed, the average β-barrel B factors for OmpA were previously shown to be ≈1.5 times more flexible in a micelle than a bilayer environment (17). This value can be compared with a value of just ≈1.1 times when comparing with the unit cell simulation. However, given the relatively small mobility of the extracellular loops of OmpA in the bilayer and unit cell simulations in comparison with the micelle, it therefore seems likely that mobility of nonbarrel regions may influence pore formation. This hypothesis would be in agreement with the proposal of breathing motions propagated from the loops to the barrel domain (see above).

In terms of contributing to our understanding of the structural biology of membrane proteins, it is of interest to note that the resolution to which the OmpA crystals diffract (better than 1.7 Å) has only been achieved for a handful of membrane proteins (namely, OmpA; PDB ID code 1QJP; bacteriorhodopsin, 1C3W; AmtB, 1U7G; Amt-1, 2B2F; and LeuT_A, 2A65). Of these, AmtB and LeuT_A also have detergent molecules, namely β-octyl glucoside, present within the crystal unit cell. It therefore would be of interest to extend the current simulations to compare the dynamics of this rather different detergent in these well ordered crystals with those of C₈E₄ in OmpA.

Methods

Protein Model.

Initial coordinates for OmpA were taken from the 1.65-Å crystal structure (PDB ID code 1QJP) (13), which was determined at T = 100 K. The simulation model was set up as described in ref. 16, with almost all ionizable side chains in their default state. A total of 34 mobile missing extracellular loop residues and the N-terminal Met were modeled on the basis of the 2.5-Å structure (PDB ID code 1BXW) (12). The final OmpA model consisted of 172 residues, with an overall charge of +1e. The crystal unit cell (space group C2) has one molecule in the asymmetric unit and contains four symmetry-related molecules, with dimensions a = 6.51 nm, b = 79.7 nm, c = 50.2 nm, and β = 94.3° (Fig. 1A). A total of 264 crystal waters and 24 C₈E₄ detergent molecules were included in the simulation unit cell. Additional (noncrystallographic) solvation was performed by superimposition of a box of simple point charge (SPC) waters followed by removal of any waters too close to protein, detergent, or crystallographic water. Four chloride ions were added by random replacement of water molecules to neutralize the system. The system then was energy-minimized (<100 steps of steepest descents) to relax any steric conflicts. A 0.2-ns protein-restrained MD run was performed to relax positions and orientations of water and detergent molecules, during which heavy protein atoms were harmonically restrained with a force constant of 1,000 kJ·mol⁻¹·nm⁻². Subsequently, an unrestrained 50-ns production run was performed.

Simulation Details.

Simulations were performed by using gromacs v3 (41) (www.gromacs.org). An extended, united atom version of the gromos96 force field (42) was used, and C₈E₄ parameters were based on standard gromos96 groups. Long-range electrostatic interactions were calculated by using the particle mesh Ewald method with a 1-nm cutoff for the real space calculation (43). A cutoff of 1 nm was used for the van der Waals interactions. The simulation was performed at constant temperature, volume, and number of particles. The temperatures of the protein, detergent, and solvent were each coupled separately. The Nosé–Hoover thermostat (44, 45) was applied at 300 K with coupling constant τ = 0.5 ps. Coordinates and velocities were saved every 5 ps. The timestep for integration was 2 fs, and the LINCS algorithm was used to restrain bond lengths (46). Molecular graphics images were produced by using vmd (47).

Abbreviations

MD

molecular dynamics

C₈E₄

n-octyltetraoxyethylene

rmsd

rms deviation

PDB

Protein Data Bank.