Fitness cost of LINE-1 (L1) activity in humans

Abstract

The self-replicating LINE-1 (L1) retrotransposon family is the dominant retrotransposon family in mammals and has generated 30–40% of their genomes. Active L1 families are present in modern mammals but the important question of whether these currently active families affect the genetic fitness of their hosts has not been addressed. This issue is of particular relevance to humans as Homo sapiens contains the active L1 Ta1 subfamily of the human specific Ta (L1Pa1) L1 family. Although DNA insertions generated by the Ta1 subfamily can cause genetic defects in current humans, these are relatively rare, and it is not known whether Ta1-generated inserts or any other property of Ta1 elements have been sufficiently deleterious to reduce the fitness of humans. Here we show that full-length (FL) Ta1 elements, but not the truncated Ta1 elements or SINE (Alu) insertions generated by Ta1 activity, were subject to negative selection. Thus, one or more properties unique to FL L1 elements constitute a genetic burden for modern humans. We also found that the FL Ta1 elements became more deleterious as the expansion of Ta1 has proceeded. Because this expansion is ongoing, the Ta1 subfamily almost certainly continues to decrease the fitness of modern humans.

LINE-1 (L1) retrotransposons have had a profound effect on mammalian genomes having generated 30–40% of their mass (1, 2). Modern mammals contain active L1 families, and in Homo sapiens, essentially all of the L1 activity is due to the Ta1 subfamily of the human-specific Ta (L1Pa1) L1 family (3, 4). Here we determined whether the Ta1 subfamily has been deleterious enough to reduce human fitness. An active L1 element could produce three deleterious effects (e.g., ref. 5): First, its replicative products (novel DNA inserts) could act as insertional mutagens. Second, its replicative products could participate in ectopic homologous recombination and cause genetic rearrangements. Third, L1 RNA transcripts or their encoded proteins (or both) could be toxic.

Although L1 replication can generate potentially active, full-length (FL, ≈6 kb) elements, most of its replication products are inactive: these are truncated (TR, mean length, 0.9 kb) L1 elements (6), and members of the SINE (Alu, 0.3 kb) repeated DNA family (1, 7). Here we used a population genetics approach to determine whether the Ta1 subfamily was deleterious. As natural selection against a mutation is expected to keep it at low frequencies within a population, comparing the population frequencies of TR and FL elements should reveal whether natural selection is operating specifically against FL elements. We found that FL Ta1-containing alleles, but not those that contain TR elements or SINE (Alu) inserts, were subject to negative selection. Therefore, some consequence of L1 activity other than generating insertional mutagens, an effect of L1 uniquely related to its length, or both constitute a genetic burden for humans.

Results

Because the Ta1 family continues to expand in present day humans (4), the human genome database (built on pooled DNA from a small number of individuals) provides an incomplete sample of Ta1 insertions that is systematically biased against L1 inserts that are at low frequency in human populations (see ref. 8 and Materials and Methods). To circumvent this bias, we had earlier isolated Ta1-containing alleles from a male of four different ethnic populations (Druze, Biaka pygmy, Chinese, and Melanesian) using a cloning procedure that yielded about the expected number of inserts given the copy number of the Ta1 family (8). We had previously determined the population frequency in 141 individuals of the ≈100 polymorphic elements yielded by our cloning (8). Here we determined the selective constraints on FL and TR element-containing loci by using a previously described maximum likelihood method (9) to analyze the population frequency of 32 FL and 38 TR polymorphic autosomal Ta1 elements (see Materials and Methods for the criteria for selecting this subset of polymorphic elements).

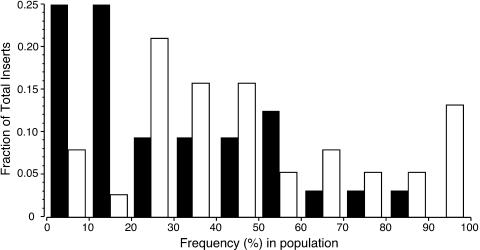
Fig. 1 shows that FL Ta1 elements are present at a significantly lower frequency in humans than TR insertions (P < 0.005, Mann–Whitney U test). Moreover, the shape of the frequency distributions of these two insertion types is significantly different (P < 0.005, Kolmogorov–Smirnov test) (Fig. 1). This observation provides evidence that FL insertions are imposing stronger fitness costs than TR insertions. However, two issues could confound this interpretation of the results.

Fig. 1.

The frequency distribution of polymorphic Ta1 elements. The fractions of FL (filled bars) and TR (open bars) Ta1 inserts are plotted as a function of different polymorphic frequencies. The distribution of FL insertions is significantly skewed toward lower frequencies. Thus, whereas ≈59% of the FL element-containing loci are present in 30% of the population sampled (i.e., 0.25 + 0.25 + 0.09 in the 0–10%, 10–20%, and 20–30% frequency bins respectively), only ≈30.5% (0.08 + 0.025 + 0.21) of the TR elements are present at these low frequencies. In contrast, whereas ≈23% of the TR element-containing loci are present in 70% or more of the population sampled, only ≈6% of the FL element-containing loci are.

First, the low-frequency FL elements could be generated by a very new Ta1 subfamily (hence their low frequency) that uniquely generates mostly FL products. However, all 21 of the 32 polymorphic FL elements for which DNA sequence was available belonged to the known Ta1 subsets (Ta1nd, Ta1d, Ta1dm; oldest to youngest) (3). Furthermore, there was no significant difference between the allele frequencies in these subsets (results not shown).

The second confounding issue is related to the structure of the human populations that we surveyed. For example, systematic different frequencies of FL and TR elements between some subpopulations may lead to an artificially low frequency of FL elements in the overall sample. To control for this and other similar biases associated with population substructure, we compared the polymorphic frequencies of elements within the largest subpopulations: African Americans (n = 40), Caucasians (n = 41), and Asians (Chinese, Japanese, Atayal, Ami, n = 40). All of these subpopulations contained FL Ta1 elements at significantly lower frequencies than TR elements (P < 0.01, P < 0.005, and P < 0.05 respectively, Mann–Whitney U test). These results and the fact that almost all of the polymorphic Ta1 insertions are shared among the major subpopulations indicate that they were generated before subdivision of the ancestral human population.

The preceding analysis indicates that FL elements are more deleterious than TR elements, but provides only relative information about the effects of selection on each class. To quantify the absolute selective effects on Ta1 insertions, we estimated the quantity N_es, (N_e, the effective population size times s, the selection coefficient). This quantity is an important determinant of how transposable elements (TEs) segregate in populations. If |N_es| ≫ 1, allele segregation is largely determined by selection; if |N_es| ≪ 1, allele segregation is similar to that of a neutral allele and is governed primarily by genetic drift. We estimated N_es for the entire set of Ta1 insertions and for the separate FL and TR classes using a maximum likelihood approach (9).

This approach relies on several simplifying assumptions (Materials and Methods) and is based on the mean sojourn time density of selected alleles (10, 11). This procedure compares the likelihood values of two nested models: In the first, the same value of s (the selection parameter) is assumed for both FL and TR elements; in the second, s is allowed to vary for the FL and TR insertions. Table 1 shows that the model with distinct selection coefficients for each class of Ta1 elements, model 2, fits the data significantly better than model 1 (P < 0.01, likelihood ratio test). These results confirm our previous conclusion that FL and TR elements are under different selective constraints. Moreover we estimate that the FL Ta1 insertions have an average N_es value of −1.9 (95% confidence interval, −2.8 to −1.1), an indication of significant negative selection. By contrast the average N_es value for TR Ta1 elements is estimated at −0.28 (95% confidence interval, −1.17 to 0.91), indicating that their population behavior was indistinguishable from that of neutral alleles.

Table 1.

Likelihood estimations for the two nested models

Model	Free Parameters	Best estimate Nes	Support limits	Maximum likelihood
Model 1	s	−1.47	−1.97 to −0.94	−395.81
Model 2	s TR	−0.29	−1.17 to 0.91	−392.31*
	s FL	−1.98	−2.8 to −1.1

*Significant improvement from model 1, P < 0.01, likelihood ratio test.

This procedure is based on several simplifying assumptions about conditions that could affect allele frequency: constant population size, random mating, and the rates of transposition and the strength of selection are constant. Although we know that the human population does not conform to these simplifications, it is unlikely that deviations from these assumptions have affected our estimate of significant negative selection against FL Ta1 elements. This is because any such conditions will similarly affect the population frequencies of both TR and FL insertions. Thus, the fact that TR elements behave like neutral alleles (i.e., that N_es = 0) indicates that purifying selection and not some other factors biased the frequency of the FL-containing alleles. Moreover, the comparison of the observed frequency distributions for TR- and FL-containing alleles (Fig. 1) with those expected based on the estimated selection coefficients for each (Table 1) revealed no significant differences (P < 0.05, both cases, G test, see Fig. 2, which is published as supporting information on the PNAS web site).

The effect of a FL or TR element acting only as an insertional mutagen is not likely to be all that different. Thus, the behavior of TR elements as neutral alleles suggests that insertional mutagenesis is not a major factor responsible for the deleteriousness of FL elements. Therefore, we would expect that the more numerous insertions of the ≈300 bp Alu family of nonautonomous SINE elements, which can also act as insertional mutagens, might also behave as neutral alleles. In agreement with this prediction, the N_es of the currently amplifying Alu Yb lineage in humans is −0.35, a value not significantly different from zero (likelihood ratio test, P > 0.05, Supporting Text, which is published as supporting information on the PNAS web site). Although this analysis used only the Alu inserts present in the database, our finding that these inserts behave as neutral alleles agrees with observations, using different analytical methods, that Alu has not been under negative selection (12, 13).

Polymorphism data, as analyzed for the Ta1 and Alu elements here, reveals the recent (perhaps ongoing) effect of natural selection. However, it has been postulated that TE families reduce host fitness only after reaching some threshold copy number (14–16), an idea supported by recent observations (5). To learn whether the Ta1 amplification fits this pattern, we determined whether purifying selection against FL Ta1 insertions was present from the onset of the Ta1 amplification, which began ≈1 million years ago (3). We compared the number of fixed FL and TR elements (fixed elements representing older insertions) (3, 4) with the number expected based on the strength of selection estimated from the polymorphic Ta1 inserts (Table 1).

Based on the confidence interval of the selection coefficients estimated above for the polymorphic Ta1 inserts, the most conservative estimate for the ratio of polymorphic FL to fixed FL elements (P_fl/F_fl) should be ≈5 times greater than the ratio of polymorphic TR to fixed TR elements (P_tr/F_tr) (Supporting Text). Instead, we found that the P_fl/F_fl ratio is only 1.2 times greater than the P_tr/F_tr ratio (P < 0.01, G test). Thus, the difference in selection coefficients between FL and TR insertions was considerably less in the past then more recently. Assuming that TR elements have always been neutral (or nearly so), it appears that effect of FL Ta1 elements has become progressively more deleterious as the Ta1 family expanded.

Discussion

Fig. 1 and Table 1 show that FL-Ta1 elements but not TR L1 (or Alu inserts, Supporting Text) have been subject to negative selection. The fact that both TR L1 and Alu elements generally behave as neutral alleles suggests that the generation of insertional mutagens is not the major reason why FL-L1 insertions are deleterious. Any strategically located insert could be very deleterious. However, seriously deleterious alleles would be quickly lost from the population and not likely included in the segregating alleles considered here. Thus, the clear distinction between the selective pressure on FL-L1 elements and the shorter L1-generated inserts indicates that one or more properties of FL elements render them generally deleterious, a conclusion consistent with inferences from earlier studies (9, 12, 16–19).

Several explanations could account for selection against FL elements. Because FL elements contain regulatory sequences (6, 20), these inserts could affect gene activity in a number of ways. Additionally, FL elements are potentially capable of autonomously synthesizing L1 RNA and proteins. These L1 products could be directly deleterious, perhaps by binding essential host factors or by effects of their enzymatic activity, e.g., DNA damage by the L1 encoded endonuclease (21, 22).

Finally, FL elements are more likely than TR or Alu inserts to promote deleterious genetic rearrangements due to homologous ectopic recombination between nonorthologous regions, as has been shown for TEs in Drosophila (9, 16, 19), because homologous recombination increases with the length of the homology (23, 24). We could not evaluate this potential contribution to the deleteriousness of FL insertions because we did not have a sufficient number of intermediate length TR elements to determine whether their allele frequency was negatively correlated with their length (Table 2, which is published as supporting information on the PNAS web site). However, the fact that the remarkable lack of L1 elements in recombination hotspots is directly related to their length (25) strongly suggests that the effect of ectopic recombination is a factor in generating the deleterious effect of FL elements.

Assuming that TR elements are neutral, we have estimated that the presence of an FL element generates selective disadvantage of N_es ≈ −2. Given that the estimated effective size of the human population is ≈10⁴ (see Materials and Methods), an N_es ≈ −2 implies a selection coefficient of ≈ −10⁻⁴. It is noteworthy that this value is surprisingly similar to that estimated in Drosophila for a range of active TEs (ref. 9 and references therein), given the vast differences between mammalian and Drosophila genomes.

The exact time at which L1s imposed fitness costs remains uncertain. Their presence in all of the major human subpopulations suggests that most of the studied L1 elements inserted before the spread of modern humans worldwide. This finding suggests that FL L1s were deleterious even in the ancestral African human population. Nevertheless, the fact that the frequencies of FL L1 elements have remained consistently low in each major subpopulation despite considerable neutral drift and the weakening of selection associated with population growth and migration suggests that natural selection continues to act against these elements.

In conclusion, our results indicate that FL Ta1 insertions have imposed a significant cost on human fitness. We also found that FL-Ta1 elements have become more deleterious as the expansion of the Ta1 family proceeded. Understanding what makes FL elements deleterious and how they affect fitness requires a greater understanding of how these genomic parasites affect the human genome. In any event, because the Ta1 amplification is ongoing, it seems likely that the genetic fitness of present humans continues to be reduced.

Materials and Methods

Cloning of Ta1-Containing Alleles.

The human genome database is biased against low-frequency members of the currently amplifying Ta1 family because it was built on the pooled DNA of an unknown number of several individuals. Thus, during assembly, the sequence contributed by low-frequency L1-containing loci will be obscured by the DNA sequence from the non-L1 containing versions of those loci. For example, if the database was compiled from the pooled DNA from five individuals (10 chromosomes), a single L1 element at a particular locus would only contribute 10% of the sequencing signal and thus be missed (or ignored). To obtain an unbiased representation of the Ta1 family in human populations, we devised a method for cloning Ta1-containing alleles from four different ethnic populations (8). Briefly, we amplified Ta1-containing inserts and their 3′ flanking non-L1 genomic sequences by using a Ta1 specific PCR primer and a second primer cognate to an anchor oligonucleotide that we had ligated to random sheared (nebulized) genomic DNA. The purified PCR products were cloned and sequenced.

Ta1-Containing Allele Frequency.

The frequency of each allele in 141 individuals was determined as described by using two PCRs, each with a different pair of PCR primers: one pair flanked the site of the insert, and the other pair used a primer specific for the Ta1 sequence, and a primer cognate to the 3′ flank (8). The ethnic composition of these 141 individuals was as follows: 40 Asians (10 Chinese; 10 Japanese; and 10 each Atayal and Ami, both indigenous to Taiwan); 41 Caucasians from the United States; 40 African Americans; and five each of Druze, Biaka pygmy, Mbuti pygmy, and Melanesian. Chimpanzee DNA was used as a negative control for every set of primers because the Ta1 family is not present in this species. All of the DNA samples were purchased from the Coriell Institute for Medical Research (Camden, NJ).

Selection of Ta1-Containing Alleles for Analysis.

We used only those Ta1 inserts (n = 232) that were both retrieved by our cloning and had flanking sequences represented in the database. We needed the latter to design primers for the PCR, and obtained successful PCRs for 174 of the inserts. Of these, 60% (≈100) were polymorphic and thus useful for the present analysis. After removing those whose size we could not accurately determine by PCR and those that did not reproducibly yield unambiguous PCR patterns, we were left with 70 Ta1-containing loci (32 FL and 38 TR). To confirm the size of the unsequenced Ta1 elements that were too long to efficiently amplify by PCR, we carried out a series of PCRs with a primer cognate to the 5′ non-L1 flanking sequence and a series of primers to the antisense strand of the 5′ end the L1 sequence spaced at 1 kb starting at 96 bp from the 5′ end. All of the TR elements for which we had sequence information were typical 5′ TR L1 inserts, which had been truncated upon insertion.

Maximum Likelihood Modeling.

We make use of a diffusion approximation, and the resulting sojourn time density (10, 11) using equations 4.22–4.26 and 5.47 in ref. 2 to estimate the probability that an element is at frequency y in the population. We assume an infinite number of insertion sites (26). (Charlesworth and Charlesworth also used the diffusion approximation, but with slightly different simplifying assumptions; ref. 27.) We assume that the fitness of individuals who are homozygous for the element is 1+ s; heterozygotes have fitness 1 + s/2; and homozygotes without the element have fitness 1.

Let τ̄[ y, N, s]Δy be the expected amount of time that an allele that is initially present at frequency 1/(2N) spends on the frequency interval I:(y, y + Δy) before it is absorbed at y = 0 or y = 1. Under the standard assumptions of the diffusion approximation,

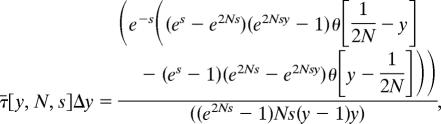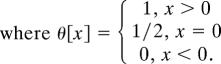Assuming that the number of elements in the population is large, and that the population is at transposition-selection equilibrium, the frequency spectrum of elements is given approximately by F[ y, N, s] = τ̄[ y, N, s]/∫₀¹τ̄[z, N, s]dz. Because we measured the frequencies of elements that were initially identified in the sequenced human genome or were identified in an individual sampled for the clone libraries, the appropriate distribution is not F[ y, N, s] but rather the distribution of element frequency, conditional on the element being present in the first individual sampled. Application of Bayes’ formula, taking F[ y, N, s] as the prior and y as the probability that an element at frequency y in the population is present in the sequenced genome, yields the posterior probability density function F′[y, N, s] = yτ̄[ y, N, s]/∫₀¹ yτ̄[y, N, s]dy. At a given site, j, at which the sequenced genome bears an element, the probability that i of k sequences sampled from the population also bear the element is then P_j = $(\underset{\mathrm{i}}{\overset{\mathrm{k}}{}})$ ∫₀¹F[ y, N, s] yⁱ(1 − y)^k−idy. Because unlinked sites are independent, the likelihood of the data across n separate sites is simply

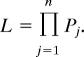The 95% confidence intervals are calculated by using the likelihood ratio test (LRT) to find the values of s at which likelihood gives the LRT values at the 5% cutoff level of the χ² distribution with one degree of freedom in comparison with the maximum likelihood value. For numerical calculation of likelihoods and 95% confidence intervals as a function of s, we assumed N = 10⁴ (28). Qualitative conclusions were unchanged for N = 10⁵.

Comparison of Two Nested Models.

We compared two-nested model to validate the findings that TR and FL elements are subject to different selection regimes. This test works by comparing two nested models of TE-selective effects: (i) model 1 (M1) assumes that all TEs are subject to the equal strength of selection, and (ii) model 2 (M2) allows one selection coefficient for FL elements and a second selection coefficient for TR elements. Using the likelihood ratio test (LRT), we determined whether M2 accounts for the data significantly better than M1 by comparing it to the 5% cutoff value of the χ² distribution with one degree of freedom. If so, this is evidence that selection coefficients of TE insertions are not uniform.

To apply the LRT, the best estimates of parameters for each model must first be obtained. For M1 only the parameter s, the selection coefficient of all TEs, is estimated from the frequency data. For M2 two parameters s_fl for FL elements and s_tr for TR elements are estimated. The parameters for each model are estimated by finding the values for which the likelihood of the data are maximized.

For M1 the likelihood of the data are:

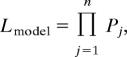where j indexes the sites where an element was identified in the database, and P_j = $(\underset{\mathrm{i}}{\overset{\mathrm{k}}{}})$∫₀¹F′[ y, N, s] yⁱ(1 − y)^k−i as above. For M2,

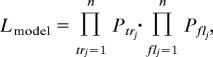where fl_j and tr_j index the sites at which FL and TR insertions are located, respectively. With these equations, it is possible to estimate parameters for both models and to calculate the maximum likelihood of the data under each model. The difference in the log-likelihood between M2 and M1 can then be compared to the χ² distribution with two degrees of freedom to determine whether M2 accounts for the data significantly better than M1.

Abbreviations

L1

LINE-1

FL

full length

TR

truncated

TE

transposable element.