Abstract
Purpose: Recent biochemical and physiological data point to the existence of one or more Ca++-mediated feedback mechanisms modulating gain at stages early in the vertebrate phototransduction cascade, i.e., prior to activation of cGMP-phosphodiesterase (PDE). The present study is a computational analysis that combines quantitative optimization to key data with a qualitative evaluation of each candidate model's ability to capture “signature” features of representative rod responses obtained under a broad range of dark-(DA) and light-adapted (LA) conditions. The primary data motivating the analyses were the two-flash data of Murnick & Lamb. These data exhibited strikingly nonlinear behavior: the period of complete photocurrent saturation (Tsat) in response to a Test flash was reduced substantially when preceded by a less-intense saturating Pre-flash. Depending on the delay between Pre- and Test flashes, the change in Tsat (ΔTsat) could exceed the magnitude of the delay, and could be reduced by as much as ∼50%, corresponding to a large reduction in gain by a factor of 10-15. The overall goal of the study was to evaluate what model structure(s) were commensurate with both the Murnick & Lamb data and the salient qualitative features of rod responses obtained under a broad range of DA and LA conditions.
Methods: Three candidate models were quantitatively optimized to the Murnick & Lamb saturated toad rod flash responses and, simultaneously, to a set of sub-saturated flash responses. Using the parameters from these optimizations, each candidate model was then used to simulate a suite of DA and LA responses.
Results: The analyses showed that: (1) Within the context of a model with Ca++ feedback onto rhodopsin (R*) lifetime (τR), the salient features of the Murnick & Lamb data can only be accounted for if the rate-limiting step is not the Ca++-sensitive step in the early cascade reactions, i.e., if PDE* lifetime, and not τR, is rate-limiting. (2) With τR rate-limiting, the model cannot account for ΔTsat exceeding the delay. (3) The Ca++-dependent reduction in τR required to effect the large gain is incommensurate with the empirical dynamics of dim-flash responses. (4) Regardless of which reaction is rate-limiting, a model using solely modulation of R* lifetime puts strong constraints on the domain of biochemical parameters commensurate with the large gain changes Murnick & Lamb observed. (5) The analyses show that, in principle, the Murnick & Lamb data can be accounted for when τRis both rate-limiting and Ca++-sensitive if, in addition to the feedback onto τR, there is an earlier, stronger Ca++ feedback that does not affect R* inactivation kinetics (e.g., gain at R* activation or transducin (T*) activation). (6) Ca++-modulation of R* activation or T* activation as the sole early gain mechanism can also account for the Murnick & Lamb data, but fails to predict the data of Matthews, and can thus be rejected along with any model of comparable form.
Conclusions: The results imply that the Murnick & Lamb data per se are insufficient to rule out rate-limitation by (Ca++-sensitive) R* lifetime; evaluation of a broader set of responses is required. The analyses illustrate the importance of evaluating candidate models in relation to sets of data obtained under the broadest possible range of DA and LA conditions. The analyses are aided by the presence of reproducible signature, qualitative features in the data since these tend to constrain the domain of acceptable model structures and/or parameter sets. Some implications for vertebrate photoreceptor light-adaptation are discussed.
A recent paper by Murnick & Lamb [1] presented physiological data with striking nonlinear features. Using a two-flash technique, the authors found that a saturating Pre-flash applied to toad rods dramatically reduced the period of complete photocurrent saturation (Tsat) elicited by a second, more intense, saturating Test flash. The interpretation of the data was that the Pre-flash led to a Ca++-dependent reduction in gain early in the phototransduction cascade. The effective gain reduction was substantial. Tsat for the Test flash was reduced by as much as 6-7 s by the Pre-flash, corresponding to an effective reduction in gain by a factor of 10-15, depending on the slope of the Tsat versus ln(I) function. This interpretation receives support from several lines of recent experimental evidence that suggest that one or more steps in the biochemical events leading to activation of cGMP-phosphodiesterase (PDE*) are regulated dynamically by the level of internal calcium [1-11].
The authors suggest that the observed decreases in Test flash Tsat could result from Ca++-sensitive gain modulation at an early phototransduction step. They propose that the Ca++-sensitive process could be Ca++-modulation of the rate of rhodopsin (R*)-inactivation (R* phosphorylation). In this model, a decrease in internal Ca++ pursuant to a flash of light (and cGMP-gated channel closure) accelerates the process of phosphorylation of R* by releasing rhodopsin kinase (RK) from inhibition by the Ca++-binding protein, recoverin (Rec) [4-9].
Murnick & Lamb [1] propose that their data are consistent with PDE*-inactivation being the rate-limiting step in photocurrent recovery, not R* inactivation as proposed by Pepperberg et al. [12-14]. In this model, R* lifetime would be significantly shorter than PDE* lifetime, and would decrease further with light-induced decreases in internal Ca++, reducing the effective gain of photocurrent activation without altering the overall dynamics of photocurrent recovery from saturation controlled by the slower PDE*-recovery. The critical observation supporting this interpretation of the data was that the decrease in Tsat was found to exceed the delay, Δt, between Pre- and Testflashes (e.g., for Δt = 1 s, Tsat was typically reduced by 2 s). Murnick & Lamb reason that within a RecRK model structure, if the light-induced gain reduction is generated at the same step that forms the rate-limiting reaction, this predicts a decrease in Tsat that is, at most, equal to, but never greater than Δt.
Goals of the Present Study: The present article implements and evaluates the model structure (the RecRK model) suggested by Murnick & Lamb [1] to explain their data. In addition, two other candidate models are analyzed. The first alternative model has an early gain mechanism that does not alter the dynamic of photocurrent recovery, i.e., Ca++-modulation of effective R* catalytic gain without a concomitant modulation of R* lifetime (R* activation model). This corresponds to an implementation of a scheme proposed by Lagnado & Baylor [2] to explain their observations that, during the period of light exposure, experimental reduction of Ca++ caused a substantial decrease in transduction gain, but no apparent change in response kinetics. The second alternative model combines the two early gain mechanisms, R* lifetime (RecRK) and R* activation (RecRK-R* activation model).
The models were evaluated in relation to the Murnick & Lamb data, as well as in relation to other key data obtained under a broad range of stimulus conditions. The approach was similar to that used in Hamer [15], i.e., a combination of quantitative optimization of the models to one or more sets of data, combined with qualitative evaluation in which the optimal parameters are used to predict signature qualitative features of a suite of data sets from other experiments under both dark-adapted (DA) and light-adapted (LA) conditions.
The overall goal of the study was to evaluate what model structure(s) are commensurate with both the Murnick & Lamb data and the broader suite of representative DA and LA rod data. The analyses confirm that, within the context of a RecRK model structure in which R* lifetime is Ca++-sensitive, PDE* lifetime indeed must be rate-limiting in order to account for all the features of the Murnick & Lamb data. In addition, the analyses show that rate-limitation by R* lifetime in a RecRK model imposes other fundamental constraints: with τRrate-limiting, the change in τR required to reproduce both the observed gain changes (10-15x) and the empirical intensity-dependence of Tsat [1,12-14] is incommensurate with the dynamics of dim-flash responses. Moreover, it is shown that, if the large gain change implied by the Murnick & Lamb data (10-15x) occurs entirely by means of modulation of R* lifetime, then severe constraints are imposed on some key biochemical parameters and that these constraints occur regardless of which is the rate-limiting inactivation reaction, R* or PDE* lifetime.
The analyses demonstrate that the Murnick & Lamb data can be accounted for by a model in which R* lifetime is both rate-limiting and Ca++-sensitive if, in addition to feedback via RecRK, an early, stronger feedback is present. However, this additional feedback must be such that it does not significantly alter the recovery kinetics of the rate-limiting reaction. This result implies that the Murnick & Lamb data alone are not sufficient to unequivocally identify the rate-limiting reaction in the early cGMP cascade.
Finally, the results show that some model structures can be ruled out despite the fact that they can provide an excellent account of the Murnick & Lamb data, since they fail to account for robust qualitative features of data from other experiments. The latter two results highlight the importance of including as broad a range of data as possible in model evaluation.
METHODS
Analyses: The analyses were similar to those used in [15]. Candidate models were quantitatively optimized (Optimization Toolbox, The Mathworks, Natick, MA) to the Murnick & Lamb [1] saturated toad rod flash responses and, simultaneously, to a set of sub-saturated flash responses from Rieke & Baylor [16]. After the optimization, the optimal parameters were then used to simulate a suite of dark- and light-adapted empirical rod responses under a range of experimental conditions (Empirical Response Suites I and II, described below). The adequacy of each model was then evaluated based on quantitative (optimized) fits to the data, and on the ability of the model to capture salient qualitative (“signature”) features of the broader suite of responses.
Inclusion of the sub-saturated flash response data in the initial optimization turned out to be crucial. Without it, the optimization was not adequately constrained, so that the model could achieve a good fit to the Murnick & Lamb saturated data with parameter values that failed to reproduce essential qualitative features of the Empirical Response Suite, including dim-flash responses and step responses. Inclusion of the sub-saturating responses constrained the optimization such that the model was then more likely to be able to reproduce signature features of the response suite.
Models: The candidate models each have four core sets of phototransduction reactions, elements of which have been implemented in a number of published models [15,17-20].
(1) Simplified R-, PDE activation scheme (Eqs. 1-3 ) . PDE activation is modeled as two sequential first-order reactions [19-21]. In the scheme depicted by Eqs. 1-3, feedback from RecRK has been included (q5RK* in Eqs. 1,2), plus a slow back-reaction from inactive Ri to R* (τb, τRi in Eqs. 1,2; also see Eqs. A6-A8, Appendix 1). RK* in Eq. 1 represents the amount of activated rhodopsin kinase at time t. In Eq. 1, it acts to modulate the rate of R* inactivation. The effect of lowered Ca++ (in response to light) is to increase RK*, increasing the rate of R* inactivation. Both the RecRK feedback reaction and the rhodopsin back-reaction are discussed in Appendix 1.
In Eqs. 1 and 2, (1/τb) and (1/τRi) are the rate-constants for the back-reaction between R and R* and the disappearance of inactivated rhodopsin. q5RK* is a pseudo-first-order rate constant for R* inactivation. Φ is the number of photoisomerizations elicited by a brief flash of light.
In Eq. 3, νrp is the rate of activation of PDE per rhodopsin molecule [20,21], and 1/τE is the rate constant of PDE*-inactivation (i.e., τE is the time constant of PDE*-inactivation).
| (Eq. 1) |
| (Eq. 2) |
| (Eq. 3) |
(2) Dynamic Ca++ reactions (Eqs. 4 and 5 ) . Equations 4 and 5 describe Ca++-influx through the light-sensitive cGMP-gated membrane cation channels (first term, Eq. 4), efflux via the Na+: Ca++, K+ electrogenic exchanger (with rate γCa; second term, Eq. 4), and dynamic Ca++-buffering (cb, third and fourth terms, Eq. 4 and Eq. 5; cf. [17] and [18]). In Eqs. 4 and 5, c is the concentration of free internal Ca++ at time t, and cb is the concentration of Ca++bound to buffer at time t. In the first term in Eq. 4, Jd is the dark circulating current, and F is the fraction of channels open at time t. The Ca++-influx through the channels is set by the factor [FCa/(2FfdVcyto)], which gives fraction of current carried by Ca++ (FCa), converted to concentration units (by the Faraday constant, Ffd, and the cell volume, Vcyto). The Ca++-buffer binds Ca++ with an on-rate of k1, and an off-rate of k2. The parameter eT is the total buffer concentration.
| (Eq. 4) |
| (Eq. 5) |
(3) Hydrolysis and synthesis of cGMP ( Eq. 6 ). PDE* hydrolyzes cGMP (second and third terms, Eq. 6), while Ca++-modulates, in a cooperative fashion (with Hill coefficient, nca), the synthesis of cGMP by guanylate cyclase (Amax; first term, Eq. 6). The hydrolysis terms in Eq. 6 include a light-activated term (βsubE*(t)), and a term to account for basal hydrolysis of cGMP in the dark (βdark; [17,18,20,21]). βsubconverts E* from a unitless number (of molecules) to units of concentration per unit time. Kca is the concentration of Ca++ that yields 1/2-maximal synthesis rate of cGMP (when c = KCa, the first term in Eq. 6 = Amax/2).
| (Eq. 6) |
(4) Closure of membrane cation channels and generation of photocurrent (Eq. 7). The photocurrent elicited by a light stimulus is proportional to the number of membrane cation channels opened by the cooperative action (with Hill coefficient ncg) of free cGMP (g).
To this core set of reactions two forms of additional Ca++
| (Eq. 7) |
feedback have been added, first singly, then in combination.
RecRK Model: This model introduces Ca++-modulation of R* lifetime via RecRK (Eqs. 8,9). The model assumes a cooperative binding (with Hill coefficient, w) of free internal Ca++to Rec that happens rapidly in relation to the time scale of the other reactions. Hence, the interaction between Ca++ and Rec is treated as if it was instantaneous and is quantified by the steady-state solution (Eq. 9) to the differential equations (Eq. A11, Appendix 1). In Eqs. 8,9 below, Rec* symbolizes Rec bound to w Ca++ ions (see Appendix 1, Eqs. A9, A11, A12). KRec,Ca is the Ca++concentration at which half of Rec is bound to Ca++.
Interaction between Rec* and RK (Eq. 8) is treated as a dynamic, reversible reaction. RK* is activated rhodopsin kinase, i.e., RK that has been released from inhibition by recoverin. The feedback gain control is established by an increase in RK* corresponding to a speed-up of the quenching of activated rhodopsin, i.e. an effective decrease in the time constant of recovery, τR. A decrease in Ca++ pursuant to a flash of light (and cGMP-gated channel closure) decreases the amount of bound Rec- Ca++, which reduces Rec's inhibition of RK, thus accelerating the process of phosphorylation of R* and ultimate capping (quenching) by arrestin [4-9]. Eqs. 8-9 are derived in Appendix 1, Section B.
The RecRK model is evaluated for two cases, τE and
| (Eq. 8) |
| (Eq. 9) |
τR*rate-limiting.
R* activation Model: This model replaces the RecRK Ca++ feedback with a feedback that modulates the effective catalytic gain of R* without altering its dynamics. This corresponds to an implementation of a scheme proposed by Lagnado & Baylor [2] to explain their observations that during the period of light exposure, experimental reduction of Ca++ causes a substantial decrease in transduction gain, but no apparent change in response kinetics. Their results imply an early gain mechanism that acts as if it reduced the effective light intensity. The locus of action could be at the “activatability” of rhodopsin, or in the catalytic activity of R* in activating transducin and PDE. However, there is currently no known mechanism for this gain effect, and Lagnado & Baylor's results cannot distinguish between action at R* activation or transducin activation.
Hence, in the present implementation of the Lagnado & Baylor scheme, activation of R* is treated as Ca++-sensitive, such that a reduction in internal Ca++ reduces the number of R molecules activated by a flash. The Ca++-effect is assumed to be rapid, and thus the feedback (denominator of the first term in Eq. 10) is written in the form of a Michaelis-Menten modulation of Φ, the number of R* generated by a brief flash. Kr in Eq. 10 is the K1/2 for the Ca++-effect on R* activation, with Hill coefficient nr.
Here, 1/τR is the first-order rate-constant for inactivation
| (Eq. 10) |
| (Eq. 11) |
of R*, replacing the pseudo-first order rate-constant, q5RK*, of Eqs. 1 and 2. The rest of the Eqs. in this model are as in Eqs. 3 through 7. Again, two cases are examined (τE, and τR rate-limiting).
RecRK-R* activation Model: This model contains both of the additional (non-cyclase) feedback mechanisms: modulation of R* inactivation rate (q5RK*, Eq. 12) and Ca++-modulation of R* activation (denominator of the first term in Eq. 12). Both of these feedback reactions are embodied in Eq. 12.
All other Eqs. in this model are the same as in the RecRK
| (Eq. 12) |
model (i.e., Eqs. 2 through 9).
Four cases are examined for the RecRK-R* activation model. For each of the rate-limiting cases (τE and τR rate-limiting), the analysis is carried out twice, first under the assumption that the RecRK mechanism (modulation of R* lifetime) dominates the early gain control, and then under the assumption that the R* activation mechanism (modulation of R* activation gain) dominates the early gain.
Empirical Response Suite I: After optimization to the Murnick & Lamb saturated two-flash data and the sub-saturated flash responses, the models described above were used to “predict” the responses to a suite of DA and LA stimulus conditions obtained in other studies. These are shown in Figure 1 and Figure 2.
Figure 1.
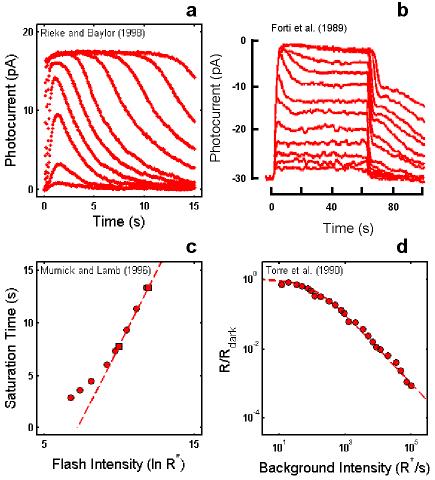
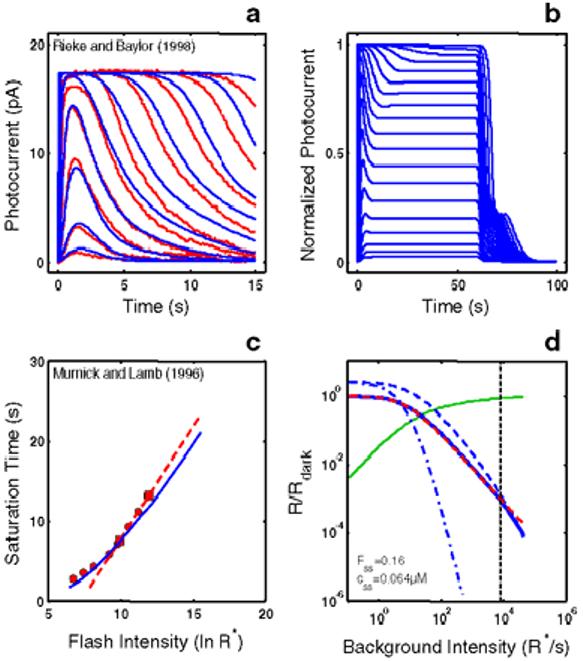
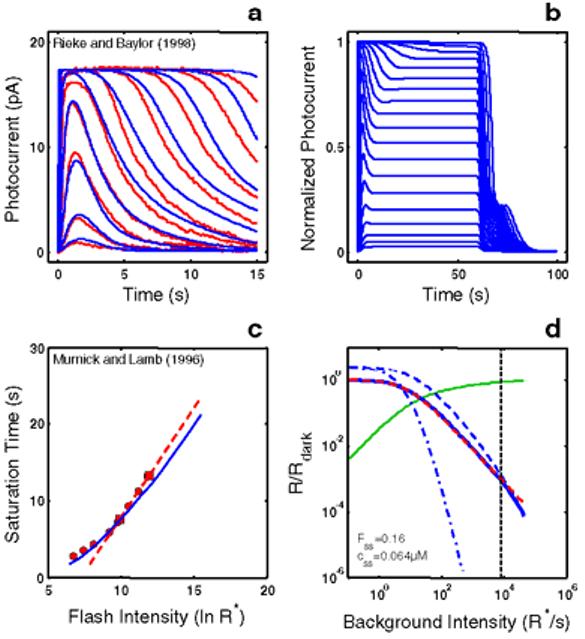
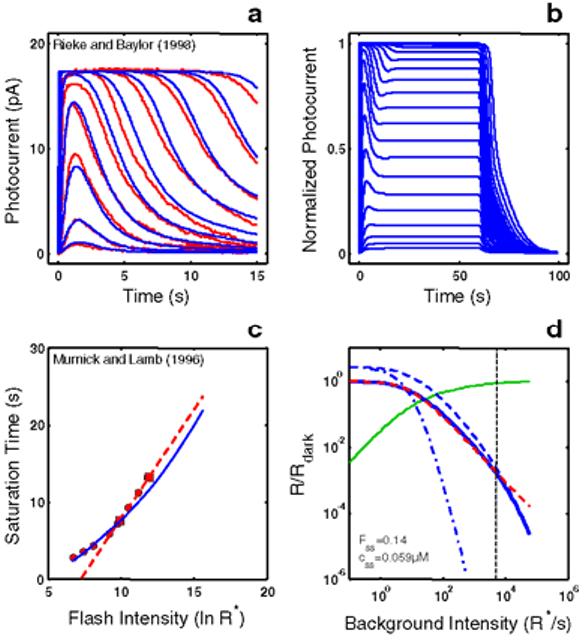
Empirical Response Suite I. A : Sub-saturated flash responses obtained from toad rods obtained by Rieke & Baylor [16]. Each model was simultaneously optimized to a subset of these data and to the Murnick & Lamb saturated data (shown in Figure 3). The sub-saturating responses used for optimization were the responses to the lowest four intensities: 0.10, 0.35, 1.29, and 4.35 photons/m2/10 ms flash, or 2.26, 7.91, 29.15, and 98.3 R*/10 ms flash assuming an effective collecting area of 22.6 m2. B : Step responses obtained from newt rods by Forti et al. [17]. These data have two qualitative, signature features that have been observed in step responses from rods of other species (e.g., salamander [22]; primate [18]). (1) A “nose” on the leading edge of the response that recovers slowly to a steady-state level. (2) A pronounced, multi-phasic response at step-offset, exhibiting a fast recovery phase followed by a slow phase, with some damped resonant behavior in between. C : A summary of the intensity-dependence of saturation period (Tsat) observed by Murnick & Lamb. The signature feature is the slope of the Tsat versus ln(I) function. The thick red dashed line has a slope of 2.8 s/ln unit, the slope for the cell presented in Figure 3 of Murnick & Lamb. The cell presented in their Figure 3 (whose data are analyzed in this paper) only provided two data points on the Tsat function (filled red squares). However, the Tsat slope for this cell closely matches data from another rod presented in their Figure 1 (filled red circles), and is close to the average of the Tsat slopes of seven cells presented in their Table 1 (2.7 s/ln unit). D : The decrease in flash sensitivity as a function of background light intensity (LA flash sensitivity). The data (filled red circles) are from 6 newt rods studied by Torre et al. [23]. The dashed red curve is the Weber-Fechner relation fit to the Torre et al. data: i.e., R/Rdark = (1 + I/Idark 1/2) . The intensity that caused the incremental flash sensitivity to decrease by a factor of 2 (I1/2) was 100R*s-1. The signature feature of note is the relatively large dynamic range over which flash sensitivity obeys the Weber-Fechner relation. In this case, the Torre et al. [23] data obeys the Weber-Fechner relation over a ∼4 log unit intensity range.
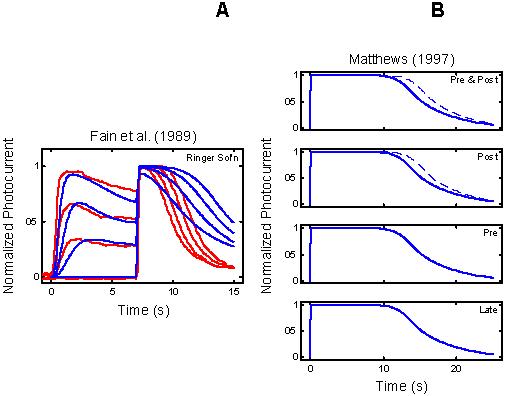
Figure 2.
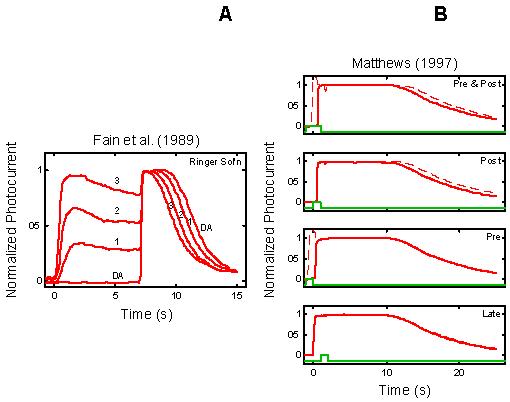
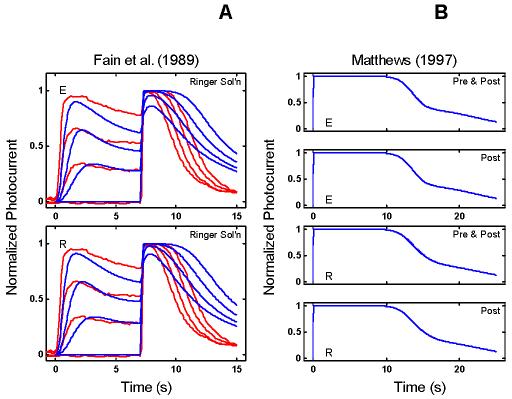
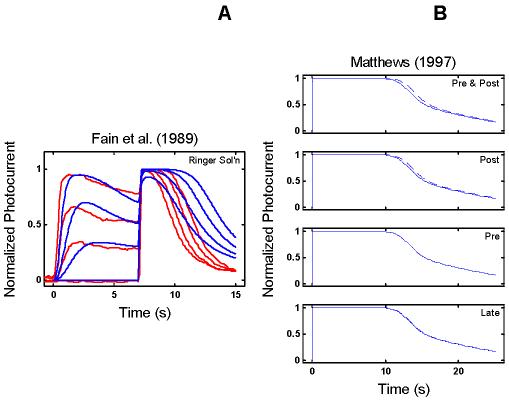
Empirical Response Suite II. A : Results of the Fain et al. [27] step-flash paradigm. A saturating flash was applied after presentation of a 7 s conditioning step of light of increasing intensity (curves labeled 1, 2, and 3). The flash response in the absence of a conditioning step is shown by the curve labeled DA. The signature feature to note is that the period of saturation in response to the flash decreases as the intensity of the conditioning step increases. B : Results of a “Ca++ clamp” experiment by Matthews [2]. Tiger salamander rods were exposed to a 0 Ca++/0 Na+test solution for brief periods around the time of presentation of a super-saturating, 20 ms flash. Removal of external Ca++ minimizes the influx of Ca++ through the outer segment cation channels, while removal of external Na+ prevents Ca++-efflux through the Na+: Ca++, K+ exchanger [22,27-29]. The Ca++ clamp was applied at one of four time periods: from 1 s before, to 1 s after the flash (“Pre & Post” condition); from the time of the flash until 1 s after the flash (“Post” condition); from 1 s before the flash until the time of the flash (“Pre” condition), or from 1 s after the flash until 2 s after the flash (“Late” condition; green trace above abscissa in each panel). The signature qualitative feature to note is that in the “Pre & Post” and “Post” conditions (but not in the “Pre” and “Late” conditions), the period of photocurrent saturation is significantly prolonged under Ca++ clamp (right-most curves in each case).
Figure 1A shows sub-saturated flash responses obtained from toad rods by Rieke & Baylor [16]. Each model was simultaneously optimized to a subset of these data (responses to the lowest four flash intensities) and to the Murnick & Lamb saturated data (shown in Figure 3).
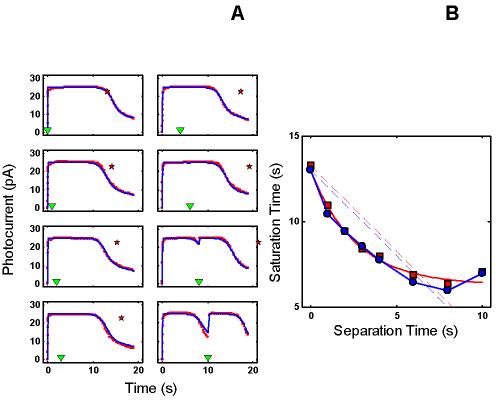
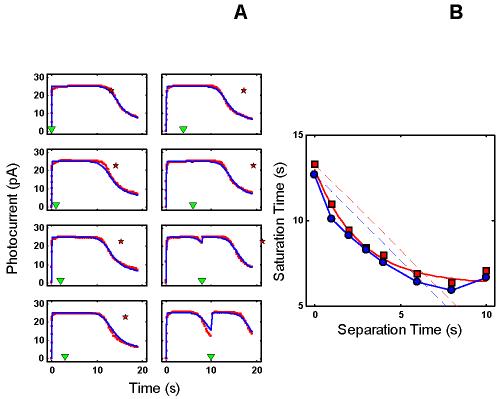
Figure 3.
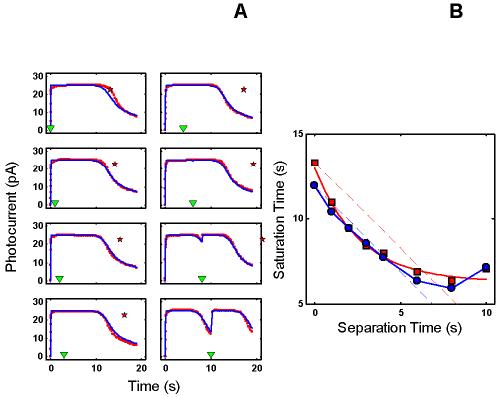
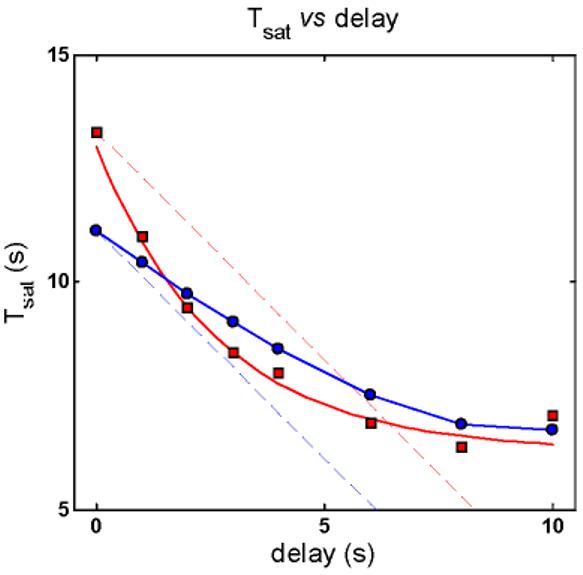
RecRK model accounts for Murnick & Lamb data with τE rate-limiting. A : Murnick & Lamb saturated two-flash data (red) with the model fits (blue) for delays of 0, 1, 2, 3 s (left column of panels), and 4, 6, 8, and 10 s (right column of panels), where delay equals time between saturating Pre-flash and a more intense saturating Test flash. The parameters for the model are given in Table 2. In each panel, the time at which the Test flash was presented is indicated by an inverted green triangle near the abscissa. The red star near the top of each panel marks the time at which the response to the Test flash would have emerged from saturation if the Pre-flash had had no effect. Note that the data remain in saturation for progressively less time as delay increases (the time between the saturated data and the red star increases as delay increases). The model fits the Murnick & Lamb data quite well. B : Plot of Test flash Tsat versus delay for both the data and model (derived from A ). Tsat was defined as the time between application of the Test flash and the time at which the response first recovered from saturation, i.e., fell to less than 90% saturation. The model responses are shown as blue filled circles and the solid blue curve, and the Murnick & Lamb data are shown as red filled squares with a red solid curve. The dashed lines have a slope of −1, and are placed to pass through the first data point (at delay = 0) for both the model results and the data. The data fall below this line out to a delay of 6-7 s, illustrating the signature feature that the change in Tsat can exceed the delay. The model results capture this feature, and also fall below the corresponding blue line of slope −1.
Figure 1B shows step responses obtained from newt rods by Forti et al. [17]. These data have two qualitative, signature features that have been observed in similar recordings from rods of other species (e.g., salamander [22]; primate [18]). (1) A “nose” on the leading edge of the response that recovers slowly to a steady-state level. The relaxation to a steady-state presumably reflects the action of feedback gain mechanisms. (2) A pronounced, multi-phasic response at step-offset, exhibiting a fast recovery phase followed by a slow phase, with some damped resonant behavior in between. The slow phase may reflect a slow back-reaction from inactivated to activated rhodopsin [12,17].
Figure 1C shows a summary of the intensity-dependence of saturation period (Tsat) observed by Murnick & Lamb. The signature feature is the slope of the Tsat versus ln(I) function. The thick red dashed line in Figure 1C has a slope of 2.8 s/ln unit, the slope for the cell presented in Figure 3 of Murnick & Lamb. The cell presented in their Figure 3 (whose data are analyzed in this paper) only provided two data points on the Tsat function (filled red squares). However, the Tsat slope for this cell closely matches data from another rod presented in their Figure 1 (filled red circles), and is close to the average of the Tsat slopes of seven cells presented in their Table 1 (2.7 s/ln unit). Typically, the slope of Tsat versus ln(I) observed in amphibian rods is 2-3 s [1,12-14].
Table 1.
Description of Model Variables & Parameters
| Symbol | Units | Description |
|---|---|---|
| Variables | ||
| R*,R | # | Number of photoactivated, inactive rhodopsin molecules at time t |
| E* | # | Number of activated PDE catalytic subunits per rod at time t |
| g | μM | Concentration of free outer segment (OS) cGMP |
| c | μM | Concentration of intracellular free OS Ca++ at time t |
| cb | μM | Concentration of Ca++ bound to dynamic Ca++ -buffer at time t |
| F | # | Normalized circulated current at time t |
| Rec* | μM | Concentration of recoverin bound to Ca++ |
| RK* | μM | Concentration of activated (disinhibited) rhodopsin kinase |
| Parameters | ||
| Front-End Feedback | ||
| Rectot | μM | Total concentration of recoverin |
| RKtot | μM | Total concentration of rhodopsiin kinase |
| Krec,Ca | μM | Concentration of Ca++ at which 1/2Rectot is bound to Ca++ |
| w | # | Hill coefficient for Ca++ binding to recoverin |
| q3 | sec−1 μM−1 | rate constant for binding of Rec* to RK* |
| q4 | sec−1 | rate constant for unbinding of Rec* to RK* |
| q5 | sec−1 μM−1 | rate constant for interaction between R* and RK* |
| Front-End | ||
| τR | s | Time constant for 1st -order inactivation of R* |
| τE | s | Time constant for 1st -order inactivation of E* (E*=G*PDE*) |
| nrp | s−1 | Rate of production of E* per R* |
| τRi | sec | Time constant for depletion of inactivated rhodopsin |
| τb | sec | Time constant for back reaction from R to R* |
| Ca++, Ca++ -Buffering | ||
| cdark | μM | Dark resting concentration of free intracellular Ca++ |
| c0 | μM | Minimum value of free OS Ca++ (Ca++ floor) |
| γCa | s−1 | Rate constant of Ca++ extrusion by exchanger |
| Vcyto | pL | Effective volume of rod OS |
| FCa | # | Fraction of inward circulating current carried by Ca++ |
| k1 | μM−1 s−1 | On-rate constant for binding of Ca++ to dynamic Ca++ -buffer |
| k2 | s−1 | Off-rate constant for unbinding of Ca++ to dynamic Ca++ -buffer |
| eT | μM | Total Concentration of dynamic Ca++ buffer |
| cGMP, Cyclase | ||
| gdark | μM | Resting cytoplasmic concentration of cGMP in the dark |
| Amax | μM s−1 | Maximum activity of guanylate cyclase |
| βdark | s−1 | Rate constant of cGMP hydrolysis in the dark |
| βsub | s−1 | Rate constant of a catalytic PDE subunit in a well-stirred volume |
| Kc | μM | Concentration of Ca++ at which cyclase activity is half-maximal |
| nca | # | Hill coefficient for Ca++ -modulation of cGMP synthesis via cyclase |
| cGMP-Gated Channel, Photocurrent | ||
| neg | # | Hill coefficient for opening of cGMP-gated channels by cGMP |
| Jdark | pA | Dark circulating current |
The symbold “#” means that the quantity is a unitless number.
Figure 1D shows the decrease in flash sensitivity as a function of background light intensity (LA flash sensitivity). The data are from 6 newt rods studied by Torre et al. [23]. A number of studies have shown that the gain, as measured by the peak amplitude in response to a flash on a background, decreases according to the Weber-Fechner relation over several log units in rods [18,23-25], and over a larger range in cones [26]. The dashed red curve is the Weber-Fechner relation fit to the Torre et al. data [23]. The intensity that caused the incremental flash sensitivity to decrease by a factor of two (I1/2) was 100 R*s−1. The signature feature of note is the relatively large dynamic range over which flash sensitivity obeys the Weber-Fechner relation. In this case, the Torre et al. [23] data obeys the Weber-Fechner relation over a ∼4 log unit intensity range.
Empirical Response Suite II: Figure 2 shows two additional elements of the Empirical Response Suite. The left panel reproduces the results of a step-flash paradigm used by Fain et al. (salamander rods; [27]). A saturating flash was applied after presentation of a 7 s conditioning step of light of increasing intensity (curves labeled 1, 2, 3). The flash response in the absence of a conditioning step is shown by the curve labeled DA. The signature feature to note is that the period of saturation (Tsat) in response to the flash decreases as the intensity of the conditioning step increases.
The right panel in Figure 2B shows the results of a Ca++ clamp experiment by Matthews [2]. Tiger salamander rods were exposed to a 0 Ca++/0 Na+ test solution for brief periods around the time of presentation of a super-saturating, 20 ms flash. The test solution minimizes simultaneously the influx and efflux of Ca++, thus opposing the light-induced fall in Ca++[22,27-29]. Removal of external Ca++ minimizes the influx of Ca++ through the outer segment cation channels, while removal of external Na+ prevents Ca++-efflux through the Na+: Ca++,K+ exchanger.
Matthews applied the Ca++ clamp at four time periods around the time of flash presentation (t=0): the test solution was applied either from 1 s before to 1 s after the flash (“Pre & Post” condition), or from the time of the flash until 1 s after the flash (“Post”), or from 1 s before the flash until the time of the flash (“Pre”), or from 1 s after the flash until 2 s after the flash (“Late”). The signature feature is that the Ca++ clamp significantly prolonged the period of saturation only when the Ca++ clamp was applied within a brief time window around the time of the flash (“Pre & Post” and “Post”), but not if it was applied too early (“Pre”) or too late (“Late”).
The prolongation was interpreted as reflecting a gain increase (relative to the gain with Ringer's solution) at a Ca++-sensitive step early in the phototransduction cascade. By parametric variation of the timing of the application of the Ca++ clamp solution and return to Ringer's solution, Matthews was able to map out a time course for the Ca++-sensitivity of the gain effect (roughly exponential, with a time constant of ∼0.5 s). Matthews proposed that the observed time constant of the Ca++-effect might correspond to RecRK modulation of phosphorylation of R*.
RESULTS
RecRK Model: τE Rate-Limiting: The Murnick & Lamb data can be accounted for with PDE* lifetime rate-limiting: With τE rate-limiting, the RecRK model provides an excellent account of the Murnick & Lamb data. The panels in Figure 3A show the Murnick & Lamb saturated two-flash data (in red) and the model fits (in blue) for delays of 0, 1, 2, 3 s (left column of panels), and 4, 6, 8, and 10 s (right column of panels). The parameters for the model are given in Table 2, and a description of the variables and parameters for all models is given in Table 1.
Table 2.
Parameters for Analysis of RecRK Model
| τE— Rate Limiting (Figs.3-5) | τR— Rate Limiting (Fig. 6) | |||||
|---|---|---|---|---|---|---|
| Value | Lower Bound | Upper Bound | Value | Lower Bound | Upper Bound | |
| “Front-End” Feedback Parameters | ||||||
| q3 | 1.17062 | 0.1 | 10 | 4.77044 | 0.1 | 10 |
| q4 | 0.194099 | 0.1 | 10 | 8.84519 | 0.1 | 10 |
| RKtot | 7 | 7 | ||||
| Rectot | 35 | 35 | ||||
| Kref,Ca | 0.53 | 0.669028 | 0.1 | 1.2 | ||
| w | 2.5 | 1.5 | 2.5 | 2.5 | 1.5 | 2.5 |
| “Front-End” Parameters | ||||||
| 1/τb | 0.05 | 0.005 | 0.05 | 0.00500023 | 0.005 | 0.05 |
| 1/τRi | 0.334905 | 0.05 | 0.5 | 0.5 | 0.05 | 0.5 |
| q5 | 10 | 0.01 | 10 | 0.0497478 | 0.01 | 10 |
| νrp | 1000 | 1000 | ||||
| τE | 2.88 | 0.458034 | 0.2 | 0.6 | ||
| Ca++, Ca++ -Buffer Parameters | ||||||
| fCa | 0.3 | 0.2469 | ||||
| cDark | 0.3 | 0.3 | ||||
| c0 | 0.02 | 0.02 | ||||
| γCa | 96.28 | 50 | 150 | 79.2385 | 50 | 150 |
| k1 | 0.603583 | 0.05 | 5 | 0.703409 | 0.05 | 5 |
| k2 | 0.718945 | 0.05 | 5 | 0.777149 | 0.05 | 5 |
| et | 294.398 | 100 | 1000 | 881.304 | 100 | 1000 |
| cGMP, Cyclase Parameters | ||||||
| βsub | 1.68*10−5 | 1.68*10−5 | ||||
| βd | 0.5 | 0.752485 | 0.2 | 4 | ||
| Amax | 20 | 200 | ||||
| Kc | 0.137747 | 0.05 | 0.24 | 0.0830172 | 0.05 | 0.24 |
| nCa | 2.5 | 3.8 | 1.5 | 3.8 | ||
| gDark | 5 | 2 | ||||
| cGMP-Gated Channel, Photocurrent Parameters | ||||||
| ncg | 2.58614 | 1.5 | 3.5 | 2.36128 | 1.5 | 3.5 |
| Jd | 17.34 | 17.34 | ||||
| Errors | ||||||
| ERRcombo | 0.246417 | 0.515797 | ||||
| ERRml | 0.745378 | 2.58888 | ||||
| ERRflash | 0.081464 | 0.102766 | ||||
Parameters are grouped according to functional elements of the model. All descriptions of parameters are given in Table 1. For each of the two rate-limiting cases analyzed (τE, τR), the columns of numbers show the optimized parameter value, and the lower and upper bounds used in the optimization. The latter are shown only for parameters that were actually optimized. The errors listed at the bottom of the Table are RMS errors for the fits to the Murnick & Lamb [2] saturated two-flash data (ERRM& L'; data from their Figure 3) and to the sub-saturated flash responses from Rieke & Baylor [16] (ERRflash; responses to the 4 lowest flash intensities shown in their Figure 4). The combined error (ERRcombo) was calculated as the square root ofthe product of the two other errors.
In each panel of Figure 3A, the time at which the Test flash was presented is indicated by an inverted green triangle near the abscissa (as this triangle moves to the right on the abscissa, the delay between Pre- and Test flashes increases); the red star near the top of each panel marks the time at which the response to the Test flash would have emerged from saturation if the Pre-flash had not affected Test flash saturation period. Note that the data remain in saturation for progressively less time as delay increases (i.e., the time between the saturated data and the red star increases as delay increases).
The plot of Test flash Tsat versus delay (derived from Figure 3A) is shown in Figure 3B. The model responses are shown as blue filled circles and solid blue curves, and the Murnick & Lamb data are shown as red filled squares with a red solid curve. The dashed lines have a slope of −1, and are placed to pass through the first data point (at delay = 0) for both the model results and the data. The data fall below this line out to a delay of 6-7 s, illustrating the signature feature that the change in Tsat can exceed the delay. The model results capture this feature, and also fall below the corresponding blue line of slope −1.
In addition, after optimization to the Murnick & Lamb data and the sub-saturating flash responses, the RecRK model (with τErate-limiting), using the same set of optimized parameters, reproduces all the salient qualitative features of the DA and LA responses in the Empirical Response Suites shown in Figure 1 and Figure 2. The fits to the sub-saturated toad rod flash responses are shown in Figure 4A. The model is able to provide a reasonable account of the four sub-saturating responses to which it was optimized (four smallest responses in Figure 4A) as well as to responses to five higher intensities (to which the model was not optimized). Figure 4B shows the model step responses, which exhibit the two qualitative features seen in the newt rod responses of Figure 1B, namely the “nose” at step onset and the two-phase response at step offset. The slow phase of the step-offset response is due to the back-reaction between R and R* in the model [17,23]. Figure 4C shows the model Tsat versus ln(I) function (blue solid curve) along with the empirical Tsat data from Murnick & Lamb (dashed red line and red data). The model Tsat versus ln(I) function reproduces the same slope (∼2.8 s/ln unit) as the Murnick & Lamb data. This slope is set by the rate-limiting τE(Table 2).
Figure 4.
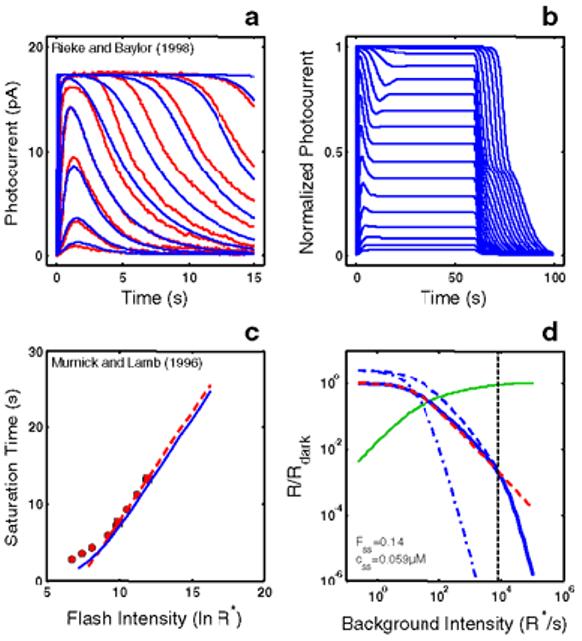
RecRK model accounts for Empirical Response Suite I with τE rate-limiting. A : The RecRK model (with τE rate-limiting) was optimized to both the Murnick & Lamb saturated two-flash data and to four sub-saturating flash responses from toad rods (four smallest responses). The model is able to provide a reasonable account of the 4 sub-saturating responses as well as responses to 5 higher intensities (to which the model was not optimized). B : Model step responses reproduce the “nose” at step onset and the two-phase response at step offset. C : The model Tsat versus ln(I) function (blue solid curve) reproduces the same slope as the Murnick & Lamb data (∼2.8 s/ln unit; red data and dashed line as in Figure 1B). Finally, the model generates a substantial range of Weber's law LA flash sensitivity (∼3 log units; solid blue curve, panel D ). For each of a series of background adaptation levels (Ib), model LA flash sensitivity was defined as the amplitude of the response to a flash of fixed criterion intensity divided by the intensity of the criterion flash. The criterion was the flash intensity eliciting a DA flash response amplitude that was 10% of the full range of circulating current. The dashed red curve is the Weber-Fechner relation from Figure 1D, shifted horizontally to fit the model output below a “cutoff” background intensity (cutoff Ib), marked by a dotted vertical cursor, above which the model was judged to deviate from Weber's law. The cutoff Ib was defined as the highest Ib at which the value of the model deviated from the best-fit Weber-Fechner curve by a criterion amount (0.05 log units). The Weber-Fechner curve was fit (least-squares) to the model over all Ib values up to and including the highest Ib where the model slope was still >= −1. The model slope was estimated by fitting a line to a moving window of 3 adjacent model points (sampling every 20.25 R*/s, or 0.075 log units). Note that the model LA flash sensitivity obeys Weber's law over a significant range (cutoff Ib = 8000 R* s−1. At the cutoff Ib, 14% of the model DA circulating current (Fss) remains, as indicated by the intersection of the vertical cursor line with the green solid curve. The latter plots the fraction that the steady-state current is saturated (i.e., 1 - Fss(Ib)), where Fssis the steady-state circulating current defined to be 1.0 in the dark, and zero when all channels are closed. Also, at the cutoff Ib, the steady-state internal Ca++level (css in inset) has dropped by a factor of 5.1, from a dark value of 0.3 μM to 0.059 μM. Also shown is the LA flash sensitivity of the model under two types of simulated Ca++ clamp conditions: (1) LA flash sensitivity with Ca++ clamped at its dark value (Ca++dark clamp; blue dash-dot curve). Ca++feedback is fully disabled over the entire dynamic range, with only static saturation contributing to flash desensitization. Ca++ was fixed at its dark value in the model, and Ib was adjusted to achieve the same steady-state current as in the unclamped case, ensuring that the steady-state currents were at the same level in relation to static saturation (i.e., cGMP-gated channel). Differences in flash sensitivity then can be ascribed to the differing states of Ca++ in the unclamped and clamped cases. The Ca++ clamp analysis equates steady-state current levels (Fss), but does not equate internal Ca++ levels at the time of presentation of the flash. This is achieved in a second analysis: (2) LA flash sensitivity with Ca++ clamped at the new steady-state level reached in response to each Ib(Cass++ clamp; blue dashed curve). This approach equates the Fss (and hence equates the effect of channel saturation), and equates Ca++ at the time of the flash. Thus, in comparing the unclamped and the Cass++-clamped flash sensitivity, the LA flash response in each case is affected equally by saturation and by the steady-state level of Ca++-mediated gain. The only additional factor shaping the LA flash response in the unclamped case is the dynamic Ca++-mediated gain change evoked by the flash. Note that at high Ib (Ib> cutoff Ib), the unclamped model flash sensitivity falls more steeply than a Weber's law slope of −1, and eventually follows a steep function that parallels the high - Ib behavior of both Ca++ clamped curves. In fact, all 3 curves asymptote to a slope of -(ncg + 1), which is predicted by the instantaneous compressive saturation of the cGMP-gated channels [30].
The model also generates a substantial range of Weber's law LA flash sensitivity (∼3 log units; solid blue curve, Figure 4D). For each of a series of background adaptation levels (Ib), model LA flash sensitivity was defined as the amplitude of the response to a flash of fixed criterion intensity divided by the intensity of the criterion flash. The criterion was the flash intensity eliciting a DA flash response amplitude that was 10% of the full range of circulating current. The dashed red curve is the Weber-Fechner relation from Figure 1D, shifted horizontally to fit the model output below a “cutoff” background intensity (cutoff Ib), above which the model was judged to deviate from Weber's law. The cutoff Ib is marked by the black dashed vertical cursor in Figure 4D, and its definition is given in the legend to Figure 4.
The model LA flash sensitivity obeys Weber's law over a significant range (cutoff Ib = 8000 R* s−1. At the cutoff Ib, 14% of the model DA circulating current (Fss) remains, as indicated by the intersection of the vertical cursor line with the green solid curve. The latter plots the fraction that the steady-state current is saturated (i.e., 1 - Fss(Ib)), where Fss is the steady-state circulating current defined to be 1.0 in the dark, and zero when all channels are closed. Also, at the cutoff Ib, the steady-state internal Ca++ level (css in inset) has dropped by a factor of 5.1, from a dark value of 0.3 μM to 0.059 μM.
Also shown is the LA flash sensitivity of the model under two types of simulated Ca++ clamp conditions: (1) LA flash sensitivity with Ca++ clamped at its dark value (Cadark++clamp; blue dash-dot curve). Ca++-feedback is fully disabled over the entire dynamic range, with only static saturation contributing to flash desensitization. Ca++ was fixed at its dark value in the model, and Ib was adjusted to achieve the same steady-state current as in the unclamped case, ensuring that the steady-state currents were at the same level in relation to static saturation (i.e., cGMP-gated channel). Differences in flash sensitivity then can be ascribed to the differing states of Ca++in the unclamped and clamped cases.
The Cadark++ clamp analysis equates steady-state current levels (Fss), but does not equate internal Ca++ levels at the time of presentation of the flash. This is achieved in a second analysis: (2) LA flash sensitivity with Ca++ clamped at the new steady-state level reached in response to each Ib(Cass++ clamp; blue dashed curve). This approach equates the Fss (and hence equates the effect of channel saturation), and equates Ca++ at the time of the flash. Thus, in comparing the unclamped and the Cass++-clamped flash sensitivity, the LA flash response in each case is affected equally by saturation and by the steady-state level of Ca++-mediated gain. The only additional factor shaping the LA flash response in the unclamped case is the dynamic Ca++-mediated gain change evoked by the flash.
Note that at high Ib (Ib> cutoff Ib), the unclamped model flash sensitivity falls more steeply than a Weber's law slope of −1, and eventually follows a steep function that parallels the high - Ib behavior of both Ca++ clamped curves. In fact, all 3 curves asymptote to a slope of −(ncg + 1), which is predicted by the instantaneous compressive saturation of the cGMP-gated channels [30].
The analyses in Figure 4D (which are recapitulated in all subsequent similar figures) aid in seeing the magnitude of the Ca++-mediated adaptational gain control and the intensity range over which it is exerted. They also help dissect the model sensitivity losses due to dynamic gain mechanisms from those due to static (channel) saturation of the model. For example, the Cadark++ clamp analysis (blue dash-dot curve) shows vividly how much the two Ca++ feedback mechanisms protect the rod from rapidly losing sensitivity (as Ib increases) due to the static saturation of the cGMP-gated channel. Moreover, both Ca++ clamp analyses show that, although the dynamic Ca++-mediated gain mechanisms lead to some absolute loss of sensitivity (especially at low Ib), the rate of decrease of sensitivity with Ib is greatly diminished by the gain mechanisms, permitting Weberian desensitization over a large dynamic range. Finally, it can be seen from the analyses that a significant amount of cGMP-gated membrane channels remain open even at the cutoff Ib where the model begins to fall off more sharply than Weber's law (Fss at the cutoff Ib is 0.14, and is close to this value in all subsequent similar figures).
With the same parameters, the RecRK model with τE rate-limiting also reproduces the signature features of the Fain et al. [27] data; the model saturated flash response emerges out of saturation faster as the intensity of a conditioning step is increased (Figure 5A). Under simulated Ca++ clamp, the model also reproduces the qualitative behavior of the Matthews [3] data (Figure 5B); the period of saturation (blue solid curve) is prolonged (blue dashed curve) by the application of the Ca++ clamp near the time of the flash (“Pre & Post”, “Post”), but not if the flash occurs too early (“Pre”) or too late (“Late”).
Figure 5.
With τE rate-limiting, the RecRK model accounts for the qualitative features of the Fain et al. [27] step-flash data and the Matthews [3] Ca++ clamp data. With the same parameters as in Figure 3 and Figure 4, the RecRK model with τE rate-limiting also reproduces the signature features of the Fain et al. [27] data; the model saturated flash response emerges out of saturation faster as the intensity of a conditioning step is increased (Figure 5A). Under simulated Ca++ clamp, the model reproduces the qualitative behavior of the Matthews [3] data (Figure 5B); the period of saturation (blue solid curve) is prolonged (blue dashed curve) by the application of the Ca++ clamp near the time of the flash (“Pre & Post”, “Post”), but not if the flash occurs too early (“Pre”) or too late (“Late”). Compare with Figure 2.
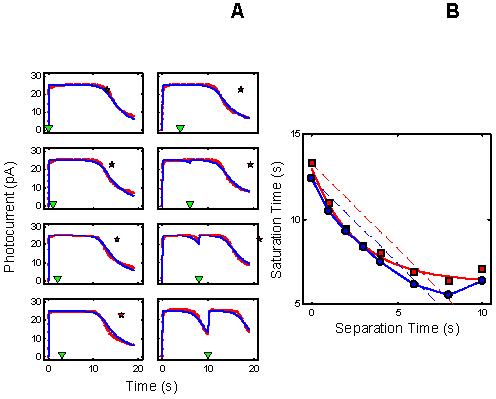
RecRK Model: τR Rate-Limiting: The rate-limiting step cannot also be the Ca++-sensitive step in a RecRK model.:
The analyses show that R* lifetime cannot be rate-limiting in a model in which RecRK is the only early gain mechanism. In simulating the data with the RecRK model, the salient features of the Murnick & Lamb data can only be accounted for if PDE* lifetime, and not R* lifetime is rate-limiting [1]. One critical failure of the model is that, with τR rate-limiting, model Testflash Tsat cannot exceed the magnitude of the delay between Pre- and Test flashes. This is illustrated in Figure 6, which shows Test flash Tsat versus delay for the model (blue) and the Murnick & Lamb data (red). The model results are always above the dashed blue line with slope −1, depicting the fact that the change in model Tsat never equals or exceeds the magnitude of the delay. This failure rules out a model structure in which R* lifetime is rate-limiting and in which early Ca++ feedback occurs solely at R* lifetime (via RecRK; [1]).
Figure 6.
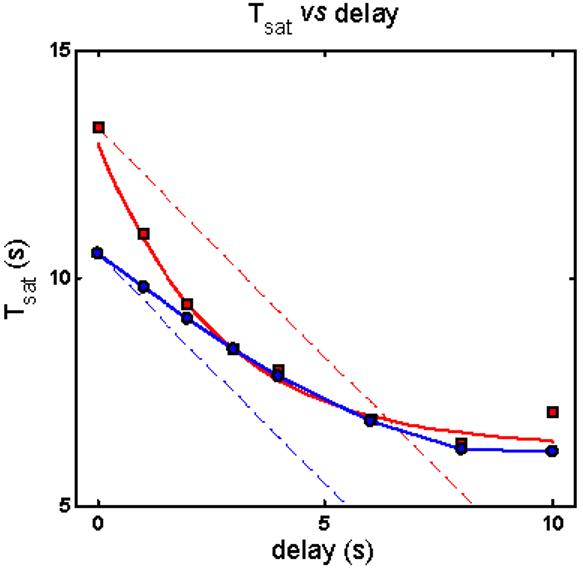
RecRK model does not account for Murnick & Lamb data with τR rate-limiting. With τR rate-limiting in the RecRK model, the reduction in model Testflash Tsat (blue curve) cannot exceed the magnitude of the delay between Pre- and Test flashes; i.e., the model results are always above the dashed blue line with slope −1. This contrasts with the Murnick & Lamb data (red curve versus red dashed line). This failure rules out a model structure in which R* lifetime is rate-limiting and in which early Ca++ feedback occurs solely at R* lifetime (via RecRK; [1]).
Rate-limitation by R* lifetime in a RecRK model is incommensurate with the kinetics of the dim-flash response.: Other fundamental constraints mitigate against R* lifetime being rate-limiting in a model with RecRK as the only early gain mechanism. In order to achieve the gain change observed by Murnick & Lamb (10-15x), the time constant of R* inactivation must decrease by 10-15 times from its dark level to its minimum (τRmin) as Ca++ approaches its physiological minimum (cmin, Eq. 4). Empirical data from measurement of the intensity dependence of Tsat(Tsat versus ln(I); [1,12-14,20]) place bounds on the value of the rate-limiting recovery time constant, i.e., ∼2-3 s. This means that when Ca++ approaches cmin, τR can fall to no less than 2-3 s to remain the rate-limiting reaction with a time constant commensurate with empirical measures of Tsat. Thus, the dark values of τR (τRdark) must be greater than or equal to 20-30 s, forcing the dim-flash flash response to be anomalously prolonged. This problem is illustrated in Figure 7. The top panel shows the relationship between τR and the level of Ca++ as it falls from a dark value of 0.3 μM to a minimum of 0.02 μM. Over this range of Ca++, τR falls from 20 s to ∼2 s. The bottom panel of Figure 7 shows the resulting dim-flash response (blue curve) in comparison to an empirical response (red). The model response was the result of optimizing the RecRK model to the Murnick & Lamb data and to the sub-saturating flash responses with the RecRK parameters set to generate the profile in the top panel of Figure 7. The resulting model dim-flash response can capture much of the early response of the cell due to the influence of Ca++ feedback on recovery, but it has a very prolonged recovery “shelf” reflecting the 20 s (DA) rhodopsin inactivation time constant. This prolonged response profile is not seen in normal, healthy rod responses.
Figure 7.
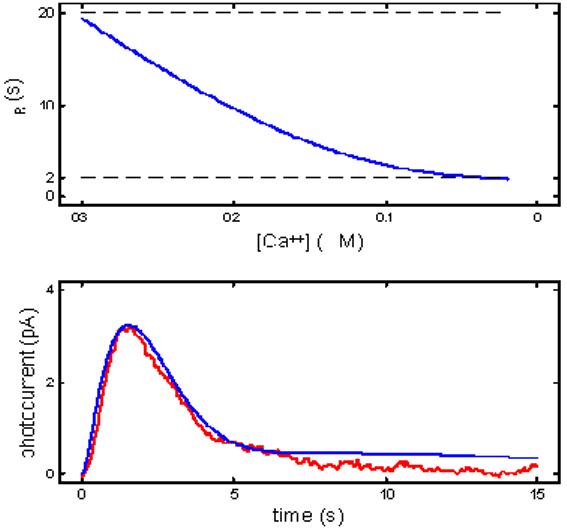
Consequences for the dim-flash response when τR is rate-limiting in a RecRK model. Within the context of a RecRK model structure, rate-limitation by R* lifetime is incommensurate with the kinetics of the dim-flash response. Top panel: The relationship between τR and the level of Ca++ as it falls from a dark value of 0.3 μM to a minimum of 0.02 μM. In this example, parameters in the RecRK model were set such that as Ca++ fell from its dark value to its theoretical physiological minimum, the model τR decreased from 20 s to 2 s. Bottom panel: Resulting dim-flash response from model in top panel (blue curve) in comparison to an empirical dim-flash response (red; curve 2 from Rieke & Baylor [16]; see Figure 1A). The model response was the result of optimizing the RecRK model to the Murnick & Lamb data and to the sub-saturating flash responses with the RecRK parameters set to generate the profile in the top panel. Clearly, with τR being Ca++-sensitive, and the requirement that the change in τR effect a large (10x) gain change, and that, at its minimum, τR remain rate-limiting with a time constant of ∼2 s, the model dim-flash response recovers much too slowly in comparison with empirical rod responses.
RecRK Model: General Considerations: The need for a large front-end Ca++-mediated gain severely constrains RecRK parameters. If the full gain modulation underlying the Murnick & Lamb data (∼10-15x) is assumed to be generated via modulation of τR, this puts strong constraints on some of the biochemical parameters of the RecRK reactions. This is true regardless of which is the rate-limiting reaction, R* or PDE* lifetime.
The model can help to illustrate this problem. Figure 8 shows how the maximum effective “front-end” gain change depends on some of the key biochemical parameters governing the interaction between Rec and Ca++, and between Rec* and RK (here Rec* symbolizes Rec bound to wCa++ ions, the species that inhibits RK).
Figure 8.
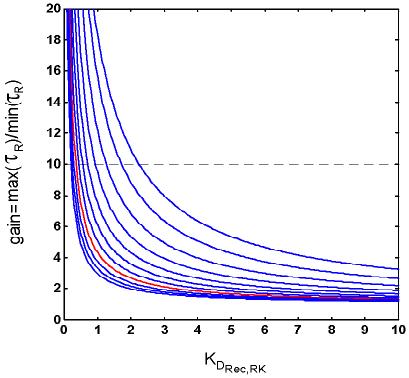
The need for a large front-end Ca++-mediated gain severely constrains RecRK parameters. The relationship between R* lifetime gain change and the dissociation constant for the interaction between Ca++-Rec complex and RK (i.e., KD = q4/q3 in Eq. 8, A10). The gain change (ordinate) is defined as the ratio of τRdark (theoretical value of τR when Ca++ = cdark = 0.3 μM) to τRmin(τR when Ca++ = cmin = 0.02 μM). The curves shown correspond to a family of KRec,Ca values ranging from 0.2 to 1.2 μM (from top to bottom, in 0.1 μM increments). The red curve is for KRec,Ca = 0.9 μM, a value obtained by Klenchin et al. [8]. The horizontal dashed line marks a gain of 10. See text for details. Note that KD must be very small if other RecRK- and Ca++ parameters are set to values estimated in the literature. In this example, Rectot = 34 μM [8] and the Hill coefficient, w = 2 [8]. For KRec,Ca = ∼0.9 μM (red curve) [8], KD must be less than ∼0.25 μM in order to get a gain change of 10x. This value for KD is ∼14 times less than the value estimated by Klenchin et al. (∼3.4 μM; [8]). Analyses show that KD will be even more severely constrained (to even smaller values) if it is assumed that the minimum physiological value for Ca++ is greater than 0.02 μM, as estimated in some studies [33,63-65]. Not only is KD restricted to small values, but, due to the steepness of the functions in the region of high gain values (10x or more), the overall range of permissible values is highly restricted. Hence, for a given KRec,Ca value, only a very restricted range of (small) values for KD are permissible in order to achieve the empirically observed gain changes.
The ordinate in Figure 8 is the maximum, steady-state change in effective R* Gain, defined as the calculated steady-state change in R* lifetime when Ca++ falls from its dark level (0.3 μM in this example; [31]) to its physiological minimum (0.02 μM in this example [32-34]; ΔGain = τR,dark/τR,Ca_min). It can be seen from Eq. 1 that any process that increases RK* effectively increases the rate of inactivation of R* (decreases R* lifetime, τR). From Eq. 8 it can be seen that the steady-state level of RK* will be set by the ratio of q4 to q3, the dissociation constant (KD = q4/q3) for the interaction between RK and Rec* (see Appendix 1, Eqs. A13 and A14). Hence KD is plotted on the abscissa of Figure 8.
The level of RK* is also determined by the parameters governing the interaction of Rec and Ca++. For a given Ca++ level, the amount by which RK* can change depends on the affinity of Rec for Ca++ and the resultant amount of Rec* available. Hence, the different curves in Figure 8 show the Gain versus KD for different values of KRec,Ca. The latter parameter is the K1/2 for the interaction between Ca++ and Rec, i.e., the Ca++ concentration at which 1/2 of the Rec is bound to Ca++(the state in which it inhibits RK, thus slowing R* inactivation). The curves shown correspond to candidate KRec,Ca values ranging from 0.2 to 1.2 μM (from top to bottom, in 0.1 μM increments). The red curve corresponds to a biochemical estimate for this parameter (KRec,Ca=0.9 μM) obtained by Klenchin et al. [8]. The horizontal dashed line occurs at a gain change of 10.
The curves in Figure 8 illustrate that KD must be very small if other RecRK and Ca++ parameters are set to values estimated in the literature. For a value of KRec,Ca = 0.9 μM (the in vivo estimate by Klenchin et al. [8]), KD must be less than ∼0.25 μM in order to achieve a gain change of 10x or more (the gain change implied by the large decreases in Tsat in the Murnick & Lamb data). This value for KD is ∼14 times less than the value estimated by Klenchin et al. (∼3.4 μM; [8]) in an in vitro study with bovine tissue. KD will be even more severely constrained (to even smaller values) if it is assumed that the minimum physiological value for Ca++ is greater than 0.02 μM.
Note that each of the curves is quite steep in the region of high gain values (10x or more). This means that, not only is KDrestricted to small values, but the overall range of (small) KDvalues that are permissible in order to achieve the empirically observed gain changes is highly restricted.
If we knew a priori that the RecRK feedback only generated gain changes on the order of 2-4x, a significantly broader range of values for KD would be permissible. However, in this case, to achieve the an overall gain change of 10x or more, there would need to be an additional feedback mechanism(s) contributing to the overall large gain change, such as a gain affecting R* catalytic activity [2]. Two models that include this kind of gain mechanism are examined in the following sections.
R* activation Model: General Considerations: An R* activation model accounts for the Murnick & Lamb data regardless of what is the rate-limiting reaction: τE Rate-Limiting: A model containing Ca++-modulation of R* activation as the sole early gain mechanism (Eqs. 3-7, 10,11) can account for the Murnick & Lamb data regardless of whether τR or τE is rate-limiting. Figure 9 shows the results for τE rate-limiting. The left panels (Figure 9A) show the excellent fit of the model to the Murnick & Lamb saturated two-flash data. The right panel (Figure 9B) shows the corresponding model Testflash Tsat versus delay along with the Murnick & Lamb data. As was seen in comparable results from the RecRK model (Figure 3B), the model is able to capture the critical feature of the data, i.e., that the decrease model Test flash Tsat in response to the Pre-flash can exceed the delay (blue curve falls below dashed blue line with slope = −1).
Figure 9.
An R* activation model with τE rate-limiting accounts for the Murnick & Lamb data. A : With τE rate-limiting, the R* activation model provides a good fit to the Murnick & Lamb saturated two-flash data. B : The corresponding model Testflash Tsat versus delay along with the Murnick & Lamb data. As was seen in comparable results from the RecRK model (Figure 3B), the model is able to capture the critical feature of the data, i.e., that the decrease model Test flash Tsat in response to the Pre-flash can exceed the delay (blue curve falls below dashed blue line with slope = −1). The format and symbology for this figure is the same as for Figure 3. Parameters for this model are given in Table 3.
Figure 10A shows the model fit to the sub-saturating flash responses, while Figure 10B-D shows the model step responses, Tsatversus ln(I), and LA flash sensitivity, respectively. Clearly the model was able to achieve a reasonable fit to the Murnick & Lamb data, while providing a good account of the sub-saturating flash responses. In addition, the model captures the salient features of the other DA and LA responses, including a relatively large range of LA flash sensitivity adhering to Weber's law (Figure 10B-D).
Figure 10.
An R* activation model with τE rate-limiting accounts for the Empirical Response Suite I. A : With the same parameters yielding a fit to the Murnick & Lamb saturated data, the model provides a reasonable fit to the sub-saturating flash responses, as well as for the signature features of step responses ( B ), Tsat versus ln(I) ( C ). Moreover, it generates a relatively large range of LA flash sensitivity adhering to Weber's law ( D ); cutoff Ib = 12,100 R* s−1. Format and symbology as in Figure 4.
τR Rate-Limiting: When τR is rate-limiting, the R* activation model can achieve a good fit to the Murnick & Lamb data (Figure 11), as well as to the sub-saturated flash responses (Figure 12A).
Figure 11.
An R* activation model also accounts for the Murnick & Lamb data when τR is rate-limiting. A : With τR rate-limiting, the R* activation model provides a good fit to the Murnick & Lamb saturated two-flash data. This is also reflected in ( B ), which shows the corresponding model Testflash Tsat versus delay along with the analogous Murnick & Lamb data. As for the case with τE rate-limiting (Figure 9), as well as the comparable results for the RecRK model (Figure 3B), the model is able to capture the critical feature of the data, i.e., that the decrease model Test flash Tsat in response to the Pre-flash can exceed the delay (blue curve falls below dashed blue line with slope = −1). Format and symbology as in Figure 5. Parameters are given in Table 3.
Figure 12.
An R* activation model with τR rate-limiting accounts for the Empirical Response Suite I. A : The model provides a reasonable fit to the sub-saturating flash responses. B - D : With the same parameters, the model also accounts for the signature features of step responses ( B ), Tsat versus ln(I) ( C ), and generates a relatively large range of LA flash sensitivity adhering to Weber's law ( D ).
These results alone demonstrate that the Murnick & Lamb results can be accounted for by a model in which the rate-limiting step early in the cascade is also Ca++-sensitive, as long as Ca++does not act on the recovery time constant of the target reaction.
With the same parameters, the R* activation model (with τR rate-limiting) also reproduces the salient features of amphibian rod step responses (Figure 12B), the empirical Tsat versus ln(I) function (Figure 12C), as well as a large dynamic range of Weber's law LA flash sensitivity (Figure 12D). In addition, it reproduces the qualitative behavior observed by Fain et al. [27] in their step-flash paradigm, regardless of whether τE (top panel of Figure 13A) or τR (bottom panel Figure 13A) is rate-limiting.
Figure 13.
An R* activation model can be ruled out. A : The R* activation model readily reproduces the qualitative features of the Fain et al. [27] step-flash data regardless of whether τE (top panel) or τR (bottom panel) is rate-limiting. B : However, for neither of the rate-limiting cases (τE: top two panels; τR: bottom two panels) can the model capture the key feature of the Matthews [3] data, i.e., when a Ca++ clamp is applied for a brief period around the time of the flash, the model does not generate any significant extension of saturation period (compare with data, Figure 2B). This failure implies that the R* activation model, and any similar model (with an early Ca++ feed-back up to and including PDE activation) that does not alter the recovery kinetics of the target reaction, can be ruled out.
A pure R* activation model can be ruled out: Despite its ability to account for the Murnick & Lamb data and other representative response profiles, the R* activation model can, nevertheless, be ruled out because it fails to predict the Matthews [3] Ca++ clamp data. This is shown in the right panels of Figure 13B. The top pair and bottom pair of panels are for τE and τR rate-limiting cases, respectively. Note that in both cases, the model does not predict a significant extension of saturation period under Ca++ clamp conditions. This failure implies that the R* activation model, and any similar model (with an early Ca++ feedback up to and including PDE activation) that does not alter the recovery kinetics of the target reaction, can be ruled out.
RecRK-R* activation Model: Dominance by Gain at R* activation: The RecRK-R* activation model combines both early feedbacks, i.e., at R* activation and at R* lifetime (Eq. 12). As was seen with the R* activation model, the analyses show that the Murnick & Lamb data can be accounted for when τR is both rate-limiting and Ca++-sensitive if, in addition to the RecRK feedback, there is an earlier, stronger Ca++ feedback (i.e., Ca++ feedback at R* activation) that does not affect R* inactivation kinetics. This is shown in Figure 14, Figure 15, and Figure 16.
Figure 14.
The combined model with τR rate-limiting can account for the Murnick & Lamb data. With τR rate-limiting, the combined (R*-activation-RecRK) model can provide a good account of the Murnick & Lamb data when the dominant of the two front-end gains is at R* activation (compare with Figure 3, Figure 9, and Figure 11).
Figure 15.
The combined model with τR rate-limiting can account for the Empirical Response Suite I. With τR rate-limiting and R* activation the dominant of the two front-end gains, using the same parameters as in Figure 14, the combined (R*-activation-RecRK) model provides a good account of the sub-saturated flash responses ( A ), reproduces the signature qualitative features of the step responses ( B ), Tsat versus ln(I) ( C ), and generates a relatively large range of Weber's law LA ( D ; cutoff Ib = 5000 R* s−1). Format and symbology as in Figure 4.
Figure 16.
A combined model with τR rate-limiting accounts for Empirical Response Suite II. With τR rate-limiting and R* activation the dominant of the two front-end gains, using the same parameters as in Figure 14, the combined (R*-activation-RecRK) model reproduces the signature qualitative features of the step-flash paradigm of Fain et al. [27] ( A ). As in the Fain et al. data (red), the period of saturation of the model to a saturating flash (blue curves) decreases progressively as the intensity of a prior conditioning step of light in increased. ( B ) With the same parameters, the model also reproduces Matthews' extension of saturation period when a Ca++ clamp is applied near the time of the flash (“Pre & Post” and “Post” conditions; dashed blue curve), but not when it is applied too early (“Pre”) or too late (“Late”) (compare with Figure 2B).
τR is rate-limiting: Figure 14 shows results for the case where τR is rate-limiting. Since the results for τE rate-limiting were virtually the same, and since rate-limitation by τR is the more challenging of the two cases (i.e., when τR was rate-limiting, the RecRK model failed to capture the Murnick & Lamb data; Figure 6), only the results for τR rate-limiting case will be shown.
The model provides a good overall fit to the Murnick & Lamb data (Figure 14A). Moreover, the corresponding plot of Testflash Tsat versus delay (Figure 14B) shows that, in contrast to the RecRK model (Figure 6), with τR rate-limiting, the model can generate a decrease in Testflash Tsat that exceeds the magnitude of the delay (model results fall below the blue dashed line with slope −1).
In addition, the model fits the sub-saturated flash responses (Figure 15A), and accounts for the signature qualitative features of step responses (Figure 15B) and Tsat versus ln(I) (Figure 15C). The model also generates a relatively large dynamic range of LA flash sensitivity adhering to the Weber-Fechner relation (Figure 15D). Finally, the model captures the qualitative features of both the step-flash data of Fain et al. [27] (Figure 16A), and the Ca++ clamp data of Matthews [3] (Figure 16B).
RecRK-R* activation Model: Dominance by Gain at R* lifetime: In contrast to the case where R* activation gain is dominant, if Ca++-modulation of R* lifetime is the dominant of the two early gain mechanisms in the combined model, the large decreases in Testflash Tsat observed by Murnick & Lamb cannot be reproduced (as was seen in the analyses of the RecRK model; Figure 6). This is shown in Figure 17 (Testflash Tsat versus delay). Unlike the data (red), the model never falls below the dashed blue line with slope −1 because the change in Testflash Tsat never exceeds the delay (compare with Figure 3B and Figure 14B). Thus, if both R* activation and R* life-time (RecRK) gains are present, the R* lifetime gain cannot dominate.
Figure 17.
A combined model with τR rate-limiting cannot account for the Murnick & Lamb data if R* lifetime gain dominates. Analogous to what was seen for the RecRK model (Figure 6), when τR is rate-limiting and the stronger of the two front-end gains modulates τR, the combined (R*-activation-RecRK) model cannot account for the Murnick & Lamb [1] data. It cannot generate large enough changes in Test flash Tsat, and the model Tsat versus delay (blue curve) never falls below the slope of −1. This rules out such a model. Thus, if both R* activation and R* lifetime gains are present, the R* lifetime gain cannot dominate.
DISCUSSION
The overall goal of the present study was to evaluate model structure(s) that might be commensurate with both the highly nonlinear data of Murnick & Lamb and a suite of representative DA and LA rod data. A standard model of phototransduction, with only one Ca++ feedback locus at a late stage in the cascade (i.e., cGMP-synthesis), cannot generate the primary observations of Murnick & Lamb's two-flash data [1] or the Fain et al. step-flash data [27]; no combination of parameters will permit such a model to predict a reduction in Testflash saturation period as a result of prior stimulation, nor can such a model account for the Matthews [3] Ca++ clamp data.
In order to account for the striking experimental observations of Murnick & Lamb [1], as well as those of Fain et al. [27] and Matthews [3], at least one additional feedback mechanism is required. Three candidate models were implemented and evaluated: feedback at R* lifetime (RecRK model), feedback at R* activation with no change in R* inactivation kinetics (R* activation model), and a combined model with both early feedbacks (RecRK-R* activation model).
RecRK Model: τR cannot be rate-limiting if it is the only early, Ca++-sensitive gain mechanism: Analysis of the RecRK model confirmed Murnick & Lamb's [1] prediction that when R* lifetime is Ca++-sensitive, PDE* lifetime must be rate-limiting in order to account for all the features of their data (Figure 4, Figure 5, and Figure 6). Ca++-regulation of a rate-limiting τR fails to capture at least one crucial feature of the Murnick & Lamb data: the large change in Tsat that can exceed the magnitude of the delay between Pre- and Test flashes. This failure rules out a model in which Ca++-mediated modulation of a rate-limiting τR is the single early gain mechanism.
With PDE* lifetime rate-limiting (i.e., the dominant early recovery reaction), the effective time constant of the non-dominant recovery reaction (i.e., τR) would be constrained to be less than ∼1 s in the dark, and would have to decrease by 10-15x as Ca++ level dropped to its physiological minimum. Estimates of the non-dominant recovery time constant with Ca++ clamped at its dark level have been reported to be 0.4-0.5 s for amphibian rods [19,20]. This means that τR would have to fall to quite small values (40 to 50 ms) during photocurrent saturation in order to effect the requisite gain change.
The analyses also showed that rate-limitation by R* lifetime in a RecRK model imposes other serious constraints. With τRrate-limiting, the change in τR required to reproduce both the observed gain changes (10-15x) and the empirical intensity-dependence of Tsat (2-3 s/ln unit [1,12,14,22]) is incommensurate with the dynamics of dim-flash responses (Figure 7). In order to be compatible with both empirical Tsatdata and the Murnick & Lamb data, τR would have to transition between 20-30 s in the dark to 2-3 s in complete photocurrent saturation (when Ca++ approaches cmin), thus yielding an inordinately prolonged dim-flash response (Figure 7).
Finally, the analysis of the RecRK model showed that it is difficult to account for the full gain change (∼10-15x) implied by the Murnick & Lamb data by modulation of R* lifetime using parameters in the range of current empirical estimates (Figure 8). This is true regardless of which is the rate-limiting recovery reaction (PDE*- or R* lifetime).
R* activation Model: In principle, τR can be rate-limiting and Ca++-sensitive if the gain occurs at R* activation.:
The limitations of the RecRK model led us to examine an alternative scheme suggested by Lagnado & Baylor [2] (R* activation model; described in Methods, Models). The results showed that when the Ca++-dependent gain change occurs at the locus of effective R* catalytic gain, all the key features of the Murnick & Lamb data can be captured regardless of whether τE or τR is the rate-limiting recovery time constant (Figure 8, Figure 9, Figure 10, and Figure 11). Moreover, the model provides a reasonable account of several of the responses included in the Empirical Response Suites. These results demonstrate that, in principle, the Murnick & Lamb results can be explained by a model in which Ca++feedback modulates effective R* catalytic gain as long as the gain change does not alter R* inactivation kinetics. This same conclusion applies to any reaction prior to PDE activation, as long as the gain change does not alter the inactivation kinetics of the target reaction.
The R* activation model can be rejected: Despite the success at capturing the Murnick & Lamb data as well as many of the salient features represented in the Empirical Response Suites (Figure 9, Figure 10, Figure 11, Figure 12, and Figure 13A), the R* activation model is unable to simulate one key data set, i.e. the extension of saturation period observed by Matthews [3] when changes in internal Ca++ are minimized for a brief period around the time of the saturating flash (Figure 13B). This failure rules out this specific model, and a whole class of models in which the feedback action of a Ca++-decrease is to decrease the gain of any stage up to and including PDE* activation without changing the effective dynamics of the target reaction's inactivation.
Pugh et al. [35] also provide evidence that an R* activation model can be rejected. If Ca++ feedback significantly decreased R* catalytic gain, Pugh et al. reason that it would cause a decrease in the slope of the early rising phase of LA flash responses. However, they present evidence that the early rising phase of the photocurrent of LA flash responses follows an invariant trajectory independent of background intensity. However, several other studies have found evidence that the early rising phase of the LA flash response is not invariant with intensity [10,11,36,37].
If, indeed, the rising phase is invariant with background intensity, this argues against the existence of any decrease in R* catalytic gain, and thus argues against two of the three models analyzed in the present study (either the pure R* activation model or the combined RecRK-R* activation model). However, as discussed in the section above, the remaining model (RecRK) has serious limitations in accounting for all the data using available estimates for key biochemical parameters. This suggests the need to implement other feedback mechanisms. Ca++ feedback onto the affinity or Hill coefficient of the channel for cGMP [38-41] have not been implemented in the present study, but these mechanisms cannot generate the Murnick & Lamb results. Hence, other, as yet unknown mechanisms that can affect early transduction gain may be needed.
Combined RecRK-R* activation Model: A Ca++-sensitive τR can be rate-limiting if gain at R* activation is dominant: When both early Ca++ feedbacks are included (RecRK-R* activation model), the model can account for the Murnick & Lamb data as well as many of the features of the empirical suite of responses regardless of whether τE or τR is rate-limiting, as long as Ca++-modulation of R* activation is the dominant of the two gain mechanisms (Figure 14, Figure 15, and Figure 16). If the gain at τR is dominant, as was seen for the RecRK model (Figure 6), the large decreases in Testflash Tsat observed by Murnick & Lamb cannot be reproduced, thus eliminating this as a viable scheme (Figure 17).
General Considerations: Is PDE* lifetime or R* lifetime rate-limiting? Overall, the models are able to capture a broader range of DA and LA features with parameters in the range of empirical estimates when PDE*-inactivation is the rate-limiting reaction. However, the analyses of the R* activation and RecRK-R* activation models showed that, in principle, the Murnick & Lamb data alone are not sufficient to unequivocally identify the rate-limiting reaction in the early cGMP cascade. The present analyses demonstrated that the Murnick & Lamb data can be accounted for by a model in which R* lifetime is both rate-limiting and Ca++-sensitive if, in addition to feedback via RecRK, an early, stronger feedback is present. The stronger feedback must be such that it does not significantly alter the recovery kinetics of the rate-limiting reaction. Hence, the question of whether τR [12-14] or τE [1,3,19,20,42] is the rate-limiting recovery time constant still remains open.
Role of some key biochemical parameters: In a recent article, Hamer [15] showed that two models (one based on the Nikonov et al. [20] model which used an instantaneous Ca++-buffer, and one with a dynamic Ca++-buffer) failed to be able to capture a suite of rod responses when some key biochemical parameters were held near their current best empirical estimates. One key failure resulted when nCa (the Hill coefficient for Ca++ feedback onto guanylate cyclase) was held to ∼2.2 [43-46]. In this case, the models were able to generate LA flash sensitivity adhering to Weber's law over only a small intensity range. Only when nCa was large (i.e., approaching 4) could the models generate a large dynamic range of Weberian LA similar to that observed by Forti et al. [17].
This result (and other failures using “modern” parameters values) implied that the models analyzed in Hamer [15] lacked one or more important mechanisms. In particular, the failure to reproduce empirical LA behavior using “modern” cyclase Ca++ feedback parameters suggested the possibility that with additional Ca++ feedback, a model might be able to reproduce the empirical LA behavior with nCa held at or near its modern empirical estimate (∼2.2).
The present work has analyzed models with additional feedback mechanisms in place. One finding (not described in the Results) was that with Ca++ feedback at R* lifetime in place (RecRK model), the model was able to fit the Murnick & Lamb [1] data (Figure 3), the sub-saturated flash responses (Figure 4A), and all the other key qualitative features of the Empirical Response Suites (Figure 4B,C and Figure 5), including generation of a large range of LA flash sensitivity adhering to Weber's law (Figure 4D) using a value of nCa = 2.5 instead of ∼4 [15] (see Table 2). Moreover, these results were achieved with 10 other key biochemical parameters set to within ±∼60% (0.2 log units) of their modern empirical estimates (Table 2): Rectot = 35 μM (empirical estimate = 34 μM [8]); RKtot = 7 μM (∼1/5 Rectot [8]); KRec,Ca = 0.53 μM (0.87 μM [8]); w = 2.5 (empirical estimate = 2 [8]); βdark = 0.5 s-1 (empirical estimate = 0.5 - 1 s-1 [16,20,47,48], reviewed in [15]); KCa = 0.14 μM (empirical estimate = 0.1 to 0.2 μM [43-45,49,50], reviewed in [15] and [51]); ncg = 2.59 (empirical estimate = 1.6-3 [24,52-56]); fCa = 0.3 (empirical estimate = 0.10 - 0.25 [17,22,28,57,58] Korenbrot, personal communication); cdark = 0.3 μM (0.2 - 0.7 μM [31,34,59-62]); cmin = 0.02 μM (empirical estimate = ∼0 - 0.05 μM [33,34,63-65]).
Some implications for vertebrate photoreceptor light adaptation: Weber's law and the value of nCa : This paper has evaluated models having one or two Ca++ feedback mechanisms in addition to the more well-studied feedback onto cGMP-synthesis (via Ca++-mediated stimulation of guanylate cyclase). Each model was able to generate a relatively large range of LA flash sensitivity adhering to Weber's law (see Figure 4D, Figure 10D, Figure 12D, and Figure 15D). These results are in contrast to the results of an earlier analysis which found that the Nikonov et al. model [20] was not able to generate a large range of Weberian LA and, with the same set of parameters, capture the features of other DA and LA responses [15]. Moreover, with the Hill coefficient for the cooperative interaction between Ca++ and cyclase held to its modern empirical estimate ∼2(nCa = ∼2; [43-45]), the Nikonov et al. model [20] generates only a modest range of Weber's law LA flash sensitivity.
Addition of a dynamic Ca++-buffer to the Nikonov et al. model [20] conferred the ability to capture a number of signature empirical features and generate a significantly larger range of Weber's law LA flash sensitivity [15]. However, the model had only the one Ca++-feedback (onto cyclase), and the extended range of LA behavior could only be obtained when the Hill coefficient for cooperative action of Ca++ onto cyclase activity (nCa) was high (∼4).
The present results show that, with additional Ca++ feedback, a large range of Weber's law LA flash sensitivity can be generated with a relatively low cyclase Hill coefficient. For example, the combined RecRK-R* activation model (Figure 14, Figure 15, and Figure 16) captures the Murnick & Lamb data as well as the array of signature features of the suite of DA and LA empirical responses with a value of 2.38 for nCa, close to the modern estimates [43-45].
Effects of steady increases in Ca++ feedback on flash sensitivity: Pugh et al. [35] point out that a steady increase in Ca++ feedback (due to a steady Ib) extends the photoreceptor's operating range by “protecting” the cell from sensitivity losses due to the instantaneous saturation imposed by the cGMP-gated channels. In addition, they claim that steady increases in Ca++ feedback will either increase or decrease LA flash sensitivity depending on the specific locus of the feedback.
For example, Pugh et al. [35] claim that a steady increase in cyclase activity will increase flash sensitivity. The analyses of flash sensitivity presented in Hamer [15] argue against this being a general rule. In that paper, in which the models had only one feedback at guanylate cyclase , the Cadark++-clamped sensitivity was higher than the unclamped sensitivity at low to moderate Ib, and lower than the unclamped sensitivity at high Ib. This means that the effect of steady increases in cyclase activity was to decrease flash sensitivity over low to moderate Ib, and to increase flash sensitivity at high Ib. In fact, the relative increase in sensitivity conferred by the steady increase in cyclase activity could be ascribed, in large part, to the extended operating range. Without Ca++ feedback, the Cadark++-clamped sensitivity fell below the unclamped sensitivity due to static saturation of the channels, i.e., when the steady circulating current in the clamped condition began to approach saturation (<∼20% circulating current remaining).
The same pattern can be seen in the present analyses (Figure 4D, Figure 10D, Figure 12D, and Figure 15D). However, in the present models, Ca++ acts at one or more of two additional loci (RecRK or R* activation or both). Pugh et al. [35] point out that steady increases in feedback at these loci will have the effect of decreasing flash sensitivity. Hence, the lower sensitivity of the unclamped function at low/moderate Ib could be due to the effect of Ca++ feedback at RecRK and/or R* activation. Nevertheless, the net combined effect on sensitivity of all the active Ca++ feedbacks in the present models was to decrease sensitivity for all Ib causing less than or equal to ∼15% reduction in (unclamped) circulating current, or ∼75% reduction in current in the Cadark++-clamped condition.
In order to check the relative contribution of RecRK and/ or R* activation gain (versus feedback gain at cyclase), the models were run with the RecRK and/or R* activation feedbacks disabled, (using the same parameters as in Table 2, Table 3, and Table 4), leaving only the feedback at cyclase functional. The result was a small increase in flash sensitivity at low to moderate Ib (as expected). Under these conditions, the effect of a steady increase in cyclase activity was (as in Hamer [15]) to decrease flash sensitivity for all Ib causing less than or equal to ∼70% reduction in current under Cadark++ clamp.This result implies that the relatively lower sensitivity under unclamped conditions at low/moderate Ib was not due simply to a desensitization imposed by decreases in τR and/or R* activation gain. The desensitization must be due to the feedback at cyclase. A more direct demonstration of this was achieved by re-running the models while disabling Ca++ feedback onto cyclase. This resulted in a virtual elimination of the difference between the unclamped and Cadark++-clamped sensitivities at low/moderate Ib.
Table 3.
Parameters for Analyses of R* activation Model
| τE — Rate Limiting (Figs.9,10,13) | τR — Rate Limiting (Figs.11-13) | |||||
|---|---|---|---|---|---|---|
| Value | Lower | Upper | Value | Lower | Upper | |
| Bound | Bound | Bound | Bound | |||
| “Front-End” Feedback Parameters | ||||||
| Kr | 1 | 0.01 | 1 | 0.754487 | 0.01 | 1 |
| nr | 1.75626 | 1.5 | 3.5 | 1.76628 | 1.5 | 2.5 |
| “Front-End” Parameters | ||||||
| 1/τb | 0.00605424 | 0.005 | 0.05 | 0.00506223 | ||
| 1/τRi | 0.276616 | 0.05 | 0.5 | 0.405197 | ||
| τR | 0.724862 | 0.1 | 1 | 2.80803 | ||
| νrp | 1000 | 1000 | ||||
| τE | 2.88 | 0.456273 | ||||
| Ca++, Ca++-Buffer Parameters | ||||||
| fCa | 0.264506 | 0.291954 | ||||
| CDark | 0.3 | 0.3 | ||||
| C0 | 0.02 | 0.02 | ||||
| γCa | 84.8887 | 50 | 150 | 93.6977 | 50 | 150 |
| k1 | 2.71247 | 0.05 | 5 | 3.94229 | 0.05 | 5 |
| k2 | 0.411885 | 0.05 | 5 | 0.223895 | 0.05 | 5 |
| eT | 174.813 | 100 | 1000 | 228.784 | 100 | 1000 |
| cGMP, Cyclase Parameters | ||||||
| βsub | 1.68*10−5 | 1.68*10−5 | ||||
| βd | 0.226277 | 0.2 | ||||
| Amax | 24.4703 | 20 | 200 | 20 | 20 | 200 |
| Kc | 0.105064 | 0.05 | 0.24 | 0.084256 | 0.05 | 0.24 |
| nCa | 3.78534 | 1.5 | 3.8 | 3.06461 | 1.5 | 3.8 |
| gDark | 2 | 2 | ||||
| cGMP-Gated Channel, Photocurrent Parameters | ||||||
| ncg | 2.9839 | 1.5 | 3.5 | 2.8557 | 1.5 | 3.4 |
| Jd | 17.34 | 17.34 | ||||
| Errors | ||||||
| ERRcombo | 0.166388 | 0.197711 | ||||
| ERRml | 0.392868 | 0.542604 | ||||
| ERRflash | 0.0704692 | 0.0720411 | ||||
Table format as in Table 2. Only parameters optimized have lower and upper bounds specified.
Table 4.
Parameters for Analyses of Combined RecRK-R* activation Model τr Rate Limiting
| Δ R* gain dominant (Figs.14-16) | ΔτRgain dominant (Figs.17) | |||||
|---|---|---|---|---|---|---|
| Value | Lower | Upper | Value | Lower | Upper | |
| Bound | Bound | Bound | Bound | |||
| “ Front-End ” Feedback Parameters | ||||||
| Kr | 0.304485 | 0.01 | 0.5 | 0.0212626 | 0.01 | 1 |
| nr | 1.60752 | 1.25 | 2.5 | 1.81912 | 1.5 | 2.5 |
| q3 | 1.51352 | 0.1 | 10 | 4.78438 | 0.1 | 10 |
| q4 | 3.37175 | 0.1 | 10 | 9.34065 | 0.1 | 10 |
| RKtot | 7 | 7 | ||||
| RECtot | 35 | 35 | ||||
| Krec,Ca | 0.833646 | 0.1 | 1.2 | 0.864032 | 0.1 | 1.2 |
| w | 2.06798 | 1.5 | 2.5 | 1.9731 | 1.5 | 2.5 |
| “ Front-End ” Parameters | ||||||
| 1/τb | 0.0149221 | 0.001 | 0.05 | 0.00513759 | 0.001 | 0.05 |
| 1/τRi | 0.312442 | 0.1 | 0.5 | 0.493603 | 0.1 | 0.5 |
| q5 | 0.0753154 | 0.01 | 10 | 0.0494193 | 0.01 | 10 |
| νrp | 1000 | 1000 | ||||
| τE | 0.599617 | 0.2 | 0.6 | 0.395216 | 0.05 | 3 |
| Ca++, Ca++-Buffer Parameters | ||||||
| fCa | 0.302549 | 0.2469 | ||||
| CDark | 0.3 | 0.3 | ||||
| C0 | 0.02 | 0.02 | ||||
| γCa | 97.098 | 79.2385 | ||||
| k1 | 0.507003 | 0.703409 | ||||
| k2 | 0.865133 | 0.781478 | ||||
| eT | 601.726 | 881.304 | ||||
| cGMP, Cyclase Parameters | ||||||
| βsub | 1.68*10−5 | 1.68*10−5 | ||||
| βd | 0.69632 | 0.891205 | ||||
| Amax | 20 | 20 | 200 | 166.197 | 20 | 200 |
| Kc | 0.101011 | 0.05 | 0.24 | 0.085389 | 0.05 | 0.24 |
| nCa | 2.38147 | 1.5 | 3.8 | 3.60063 | 1.5 | 3.8 |
| gDark | 2 | 2 | ||||
| cGMP-Gated Channel, Photocurrent Parameters | ||||||
| ncg | 2.81898 | 1.5 | 3.5 | 2.31204 | 1.5 | 3.5 |
| Jd | 17.34 | 17.34 | ||||
| Errors | ||||||
| ERRcombo | 0.248113 | 0.741438 | ||||
| ERRml | 0.700295 | 4.03937 | ||||
| ERRflash | 0.0879058 | 0.136094 | ||||
Table format as in Table 2 and Table 3. The optimized parameter values and upper and lower bounds are shown for the τR rate-limiting case only, under two conditions: dominance by gain at R* activation (ΔR* gain dominant), and dominance by gain at R*lifetime (ΔτR dominant). Only parameters optimized have lower and upper bounds specified.
The above analyses show that steady-state increases in cyclase activity do not necessarily lead to an increase in LA flash sensitivity as claimed by Pugh et al. [35]. Light adapted flash sensitivity is more complex, with sensitivity depending on the net balance between dynamic sensitivity regulation mechanisms and static saturation influences,including pigment bleaching. It is also important to note that the balance between these is not necessarily a monotonic function of background intensity.
Effects of transient increases in Ca++ feedback on flash sensitivity: Pugh et al. [35] claim that when Ca++ is clamped at its new steady-state level set by each background, the resulting flash sensitivity function has approximately the same shape (intensity-dependence) as the unclamped function. The analyses in the present article and in Hamer [15] show that, strictly speaking, this is not the case. The shape of the Cass++ clamp (blue dashed curves in Figure 4D, Figure 10D, Figure 12D, and Figure 15D) is not the same as either the unclamped model responses (solid blue curves) or the theoretical Weber-Fechner relation (red dashed curves in same Figures); it falls off more quickly with intensity. The only difference between the Cass++-clamped and unclamped conditions is presence or absence of transient increases in Ca++ feedback due to the flash. Hence, the model results serve to illustrate that the effect of these relatively small transient increases in Ca++ feedback can be important for light adaptation, in that they tend to make the flash sensitivity fall off more slowly with background intensity.
Importance of modeling a broad range of data: The results of Murnick & Lamb are reminiscent of some earlier data by Fain et al. [27] reproduced in the present article (Figure 2). Although the reduction in saturation period observed by Fain et al. [27] may be explained by the same mechanism that reproduces the Murnick & Lamb results, the Fain et al. data did not have features that could be used to identify the rate-limiting and Ca++-sensitive reactions within the context of a model of the form of the RecRK model.
The limitations of the Fain et al.data, as well as the results of the present analyses illustrate the importance of evaluating candidate models in relation to sets of data obtained under the broadest possible range of DA and LA conditions. A model may be able to generate an excellent quantitative fit to one or more sets of data (e.g., Figure 9, Figure 10, and Figure 12) and yet fail to capture even qualitative features of other representative responses (e.g., failure of the R* activation model to reproduce the Matthews data; Figure 13B). To the extent that the critical data are truly representative of the cell's response repertoire, such failures can rule out the candidate model.
Hence, the data to be simulated must be carefully chosen, with some attention to reliability. Moreover, analyses are aided by the presence of reproducible signature, qualitative features in the data since these tend to constrain the domain of acceptable model structures and/or parameter sets.
ACKNOWLEDGEMENTS
This work was supported by NEI Grant EY11513 and Smith-Kettlewell Eye Research Institute Grant 0100-10-52. I would like to thank Juan I. Korenbrot, Ph.D. and Norberto M. Grzywacz, Ph.D. for their helpful comments about the physiological data and analyses. In addition, I am grateful for the skillful assistance of my programmer, Spero C. Nicholas, M.S. in carrying out the analyses, and technical assistance of Robert D. Flint, III, B.S.E.
Appendix 1. Equation Derivations
A. Derivation of PDE activation, including an R*<--R Back-Reaction Without Ca++-Feedback Onto R* lifetime
Rhodopsin activation and depletion are treated as first-order process [17,19-21],
| (Eq. A1) |
with a corresponding differential equation,
| (Eq. A2) |
Here Φ represents the number of photoisomerizations elicited by a brief flash of light.
An ordinary differential equation for PDE; activation may be derived from a simplified enzymatic reaction [19,20]:
| (Eq. A3) |
The quantity E represents the number of molecules of a complex of transducin (T) and PDE, [T·PDE] = E, which is activated enzymatically in a single step by R* with rate K.
The corresponding differential equation describing the rate of change of activated E* is given by Eq. A4
| (Eq. A4) |
This scheme assumes that the depletion of E* is a first-order process with rate constant 1/τE. If it is also assumed that the above reaction is not stoichiometrically limited by the amount of E available, then the coefficient governing the accretion of E*, KE, may be approximated as a pseudo-first-order rate constant, νrp, yielding
| (Eq. A5) |
The scheme depicted in Eqs. A1 through A5 is not, strictly speaking, correct. The actual chemistry involves a number of additional steps, including enzymatic activation of the G-protein, or transducin (T). The full PDE activation process may consist of 6-8 “micro-steps” [21,66]. Nevertheless, over the past few years, it has been proposed that the PDE activation process is well approximated by summarizing all the reactions (the internal dynamics of which are, for the most part, unknown) as a two-stage process.
Introduction of R*<--Ri back-reaction
It has been observed in several species that the response to a prolonged step of light has multi-phasic dynamics at step-offset (early fast recovery, followed by a much slower recovery with some occasional resonant behavior in the transition; toad: [67]; salamander: [22,28]; monkey: [18]). One mechanism that can reproduce this behavior is the inclusion of a back-reaction from Ri to R* [17]. Recently, Hamer & Tyler [68] and Hamer [15,69,70] incorporated this back-reaction in computational phototransduction models and were able to capture a number of salient features of amphibian rod responses, including the acceleration of the Tsat versus ln(I) function at high intensities [12] and the multi-phasic step-offset response. The differential equations for accretion and deletion of R* and Ri may be derived from the chemical scheme in Eqs. A6a through A6b (equivalent to scheme by Forti et al. [17]). It is worth noting that this reaction scheme is functionally equivalent to other schemes in which additional forms of inactivated rhodopsin (apoprotein) may continue to activate PDE at a slow rate [71-73].
| (Eq. A6a) |
| (Eq. A6b) |
These may be written in differential equation form as
| (Eq. A7) |
| (Eq. A8) |
B. Derivation of Ca++-Feedback Onto R* lifetime via Rec/RK in the Presence of an R*<--R Back-Reaction
The RecRK model adds Ca-sensitivity to the inactivation of R*. The first reaction is the cooperative binding of Ca++ by Rec:
| (Eq. A9) |
The complex [Rec·wCa++] will be symbolized by Rec*.
The second reaction is a reversible disinhibition of RK to its active form (RK*) by interaction with Rec*:
| (Eq. A10) |
where the complex [Rec*·RK] is the inhibited form of RK. The first reaction (Eq. A9) leads to a differential equation for Rec*:
| (Eq. A11) |
where Rectot = Rec* + Rec, the total amount of Rec in the rod. It was assumed that this reaction reached equilibrium rapidly, such that the formation of Rec* follows the instantaneous level of internal Ca++. Setting Eq. A11 equal to zero and solving for Rec*, we get the steady-state equation
| (Eq. A12) |
where KRec,Ca = (q2/q1)1/w, the Ca++ concentration at which half of Rec is bound to Ca++.
The second reaction (Eq. A10), the disinhibition of RK, can be written in differential equation form as
| (Eq. A13) |
RKtot is the total amount of RK in the cell, and (RKtot − RK*) is the amount of inactive RK.
Eq. A13 has the steady-state solution,
| (Eq. A14) |
where KD = q4/q3, the concentration of Rec* corresponding to 1/2-activation of RK.
For simplicity, it was assumed that RK* leads to R* phosphorylation (-inactivation) in two steps. Step 1 is the interaction between R* and the disinhibited (activated) RK (=RK*) to form a complex, [R*·RK*]
| (Eq. A15) |
Step 2 is incorporation of a number of phosphates (P) onto the [R*·RK*] [74], yielding a new complex [nP·R*] and releasing free RK*. The complex [nP·R*] is treated as inactivated rhodopsin (Ri)
| (Eq. A16) |
Only Step 2 is assumed to be reversible, and q5 is assumed to be rate-limiting in the two forward reactions.
Capping by arrestin, the final mechanism of R* inactivation, is not explicitly modeled [74], but is assumed to be simultaneous with, and stoichiometrically equivalent to the phosphorylation process.
Under these assumptions, the following differential equations result:
| (Eq. A17) |
where q′6 = q6Pn, and Pn is a constant.
Under the assumption that reaction A15 is rate-limiting, phosphorylation will proceed at a rate governed by the instantaneous level of the complex [RK*·R*], and a steady-state solution to Eq. A17 may be used:
| (Eq. A18) |
The differential Eqs. for R* and Ri dynamics may now be written as:
| (Eq. A19) |
| (Eq. A20) |
Substituting Eq A18 into Eq A20, we get
| (Eq. A21) |
In Eq. A19, the Ca++-sensitivity is expressed in the modulation of R* lifetime by RK*.
In addition to decay of R* to Ri (with rate-constant 1/τR; Eq. A6a), depletion of Ri and the back-reaction to R* from Ri are assumed to occur by separate pathways.
| (Eq. A22) |
The back-reaction to R* proceeds with rate 1/τb, and Ri is depleted with rate 1/τRi. The resulting differential equations for R* and Ri with Ca++-modulation by RK are analogous to Eqs. A7-8:
| (Eq. A23) |
| (Eq. A24) |
The quantity (q5RK*) in Eq. A23 corresponds to the R* decay time constant, (1/τR) in Eqs. A2, A7-8. However, in Eq. A23, the rate of decay of R* is a time-dependent function of Ca++. In the presence of light, Ca++ decreases, leading to a decrease in the steady-state amount of Rec* (Eq. A12). A decrease in Rec* leads, in turn, to an increase in the amount of RK* (Eq. A14), which translates to an effective increase in the rate-constant governing the depletion of R* (Eq. A23).
REFERENCES
- 1.Murnick JG, Lamb TD. Kinetics of desensitization induced by saturating flashes in toad and salamander rods. J Physiol. 1996;495:1–13. doi: 10.1113/jphysiol.1996.sp021569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Lagnado L, Baylor DA. Calcium controls light-triggered formation of catalytically active rhodopsin. Nature. 1994;367:273–7. doi: 10.1038/367273a0. [DOI] [PubMed] [Google Scholar]
- 3.Matthews HR. Actions of Ca2+ on an early stage in phototransduction revealed by the dynamic fall in Ca2+ concentration during the bright flash response. J Gen Physiol. 1997;109:141–6. doi: 10.1085/jgp.109.2.141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Kawamura S, Murakami M. Calcium-dependent regulation of cyclic GMP phosphodiesterase by a protein from frog retinal rods. Nature. 1991;349:420–3. doi: 10.1038/349420a0. [DOI] [PubMed] [Google Scholar]
- 5.Kawamura S. Rhodopsin phosphorylation as a mechanism of cyclic GMP phosphodiesterase regulation by S-modulin. Nature. 1993;362:855–7. doi: 10.1038/362855a0. [DOI] [PubMed] [Google Scholar]
- 6.Kawamura S, Hisatomi O, Kayada S, Tokunaga F, Kuo CH. Recoverin has S-modulin activity in frog rods. J Biol Chem. 1993;268:14579–82. [PubMed] [Google Scholar]
- 7.Chen CK, Inglese J, Lefkowitz RJ, Hurley JB. Ca(2+)-dependent interaction of recoverin with rhodopsin kinase. J Biol Chem. 1995;270:18060–6. doi: 10.1074/jbc.270.30.18060. [DOI] [PubMed] [Google Scholar]
- 8.Klenchin VA, Calvert PD, Bownds MD. Inhibition of rhodopsin kinase by recoverin. Further evidence for a negative feedback system in phototransduction. J Biol Chem. 1995;270:16147–52. doi: 10.1074/jbc.270.27.16147. [DOI] [PubMed] [Google Scholar]
- 9.Calvert PD, Klenchin VA, Bownds MD. Rhodopsin kinase inhibition by recoverin. Function of recoverin myristoylation. J Biol Chem. 1995;270:24127–9. doi: 10.1074/jbc.270.41.24127. [DOI] [PubMed] [Google Scholar]
- 10.Jones GJ. Light adaptation and the rising phase of the flash photocurrent of salamander retinal rods. J Physiol. 1995;487:441–51. doi: 10.1113/jphysiol.1995.sp020891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Gray-Keller MP, Detwiler PB. Ca2+ dependence of dark- and light-adapted flash responses in rod photoreceptors. Neuron. 1996;17:323–31. doi: 10.1016/s0896-6273(00)80163-4. [DOI] [PubMed] [Google Scholar]
- 12.Pepperberg DR, Cornwall MC, Kahlert M, Hofmann KP, Jin J, Jones GJ, Ripps H. Light-dependent delay in the falling phase of the retinal rod photoresponse. Vis Neurosci. 1992;8:9–18. doi: 10.1017/s0952523800006441. [DOI] [PubMed] [Google Scholar]
- 13.Pepperberg DR, Jin J, Jones GJ. Modulation of transduction gain in light adaptation of retinal rods. Vis Neurosci. 1994;11:53–62. doi: 10.1017/s095252380001110x. [DOI] [PubMed] [Google Scholar]
- 14.Pepperberg DR, Birch DG, Hofmann KP, Hood DC. Recovery kinetics of human rod phototransduction inferred from the two-branched alpha-wave saturation function. J Opt Soc Am A. 1996;13:586–600. doi: 10.1364/josaa.13.000586. [DOI] [PubMed] [Google Scholar]
- 15.Hamer RD. Computational analysis of vertebrate phototransduction: combined quantitative & qualitative modeling of dark- and light-adapted responses in amphibian rods. Vis Neurosci. 2000;17:679–699. doi: 10.1017/s0952523800175030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Rieke F, Baylor DA. Single photon detection by rod cells of the retina. Reviews of Modern Physics. 1998;70:1027–36. [Google Scholar]
- 17.Forti S, Menini A, Rispoli G, Torre V. Kinetics of phototransduction in retinal rods of the newt Triturus cristatus. J Physiol. 1989;419:265–95. doi: 10.1113/jphysiol.1989.sp017873. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Tamura T, Nakatani K, Yau KW. Calcium feedback and sensitivity regulation in primate rods. J Gen Physiol. 1991;98:95–130. doi: 10.1085/jgp.98.1.95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Lyubarsky A, Nikonov S, Pugh EN., Jr The kinetics of inactivation of the rod phototransduction cascade with constant Ca2+i. J Gen Physiol. 1996;107:19–34. doi: 10.1085/jgp.107.1.19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Nikonov S, Engheta N, Pugh EN., Jr Kinetics of recovery of the dark-adapted salamander rod photoresponse. J Gen Physiol. 1998;111:7–37. doi: 10.1085/jgp.111.1.7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Lamb TD, Pugh EN., Jr A quantitative account of the activation steps involved in phototransduction in amphibian photoreceptors. J Physiol. 1992;449:719–58. doi: 10.1113/jphysiol.1992.sp019111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Nakatani K, Yau KW. Calcium and light adaptation in retinal rods and cones. Nature. 1988;334:69–71. doi: 10.1038/334069a0. [DOI] [PubMed] [Google Scholar]
- 23.Torre V, Forti S, Menini A, Campani M. The Brain: Cold Spring Harbor Symposia on Quantitative Biology, Volume LV. Cold Spring Harbor Laboratory Press; Cold Spring Harbor (NY): 1991. Model of phototransduction in retinal rods; pp. 563–73. [DOI] [PubMed] [Google Scholar]
- 24.Koutalos Y, Nakatani K, Yau KW. The cGMP-phosphodiesterase and its contribution to sensitivity regulation in retinal rods. J Gen Physiol. 1995;106:891–921. doi: 10.1085/jgp.106.5.891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Koutalos Y, Nakatani K, Tamura T, Yau KW. Characterization of guanylate cyclase activity in single retinal rod outer segments. J Gen Physiol. 1995;106:863–90. doi: 10.1085/jgp.106.5.863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Burkhardt DA. Light adaptation and photopigment bleaching in cone photoreceptors in situ in the retina of the turtle. J Neurosci. 1994;14:1091–105. doi: 10.1523/JNEUROSCI.14-03-01091.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Fain GL, Lamb TD, Matthews HR, Murphy RL. Cytoplasmic calcium as the messenger for light adaptation in salamander rods. J Physiol. 1989;416:215–43. doi: 10.1113/jphysiol.1989.sp017757. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Yau KW, Nakatani K. Light-induced reduction of cytoplasmic free calcium in retinal rod outer segment. Nature. 1985;313:579–82. doi: 10.1038/313579a0. [DOI] [PubMed] [Google Scholar]
- 29.Matthews HR, Murphy RL, Fain GL, Lamb TD. Photoreceptor light adaptation is mediated by cytoplasmic calcium concentration. Nature. 1988;334:67–9. doi: 10.1038/334067a0. [DOI] [PubMed] [Google Scholar]
- 30.Matthews HR, Fain GL, Murphy RL, Lamb TD. Light adaptation in cone photoreceptors of the salamander: a role for cytoplasmic calcium. J Physiol. 1990;420:447–69. doi: 10.1113/jphysiol.1990.sp017922. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.McCarthy ST, Younger JP, Owen WG. Dynamic, spatially nonuniform calcium regulation in frog rods exposed to light. J Neurophysiol. 1996;76:1991–2004. doi: 10.1152/jn.1996.76.3.1991. [DOI] [PubMed] [Google Scholar]
- 32.Sampath AP, Matthews HR, Cornwall MC, Bandarchi J, Fain GL. Light-dependent changes in outer segment free-Ca2+ concentration in salamander cone photoreceptors. J Gen Physiol. 1999;113:267–77. doi: 10.1085/jgp.113.2.267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Gray-Keller MP, Detwiler PB. The calcium feedback signal in the phototransduction cascade of vertebrate rods. Neuron. 1994;13:849–61. doi: 10.1016/0896-6273(94)90251-8. [DOI] [PubMed] [Google Scholar]
- 34.McCarthy ST, Younger JP, Owen WG. Free calcium concentrations in bullfrog rods determined in the presence of multiple forms of Fura-2. Biophys J. 1994;67:2076–89. doi: 10.1016/S0006-3495(94)80691-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Pugh EN, Jr, Nikonov S, Lamb TD. Molecular mechanisms of vertebrate photoreceptor light adaptation. Curr Opin Neurobiol. 1999;9:410–8. doi: 10.1016/S0959-4388(99)80062-2. [DOI] [PubMed] [Google Scholar]
- 36.Detwiler PB, Gray-Keller MP. The mechanisms of vertebrate light adaptation: speeded recovery versus slowed activation. Curr Opin Neurobiol. 1996;6:440–4. doi: 10.1016/s0959-4388(96)80047-x. [DOI] [PubMed] [Google Scholar]
- 37.Rispoli G. Calcium regulation of phototransduction in vertebrate rod outer segments. J Photochem Photobiol B. 1998;44:1–20. doi: 10.1016/S1011-1344(98)00083-9. [DOI] [PubMed] [Google Scholar]
- 38.Rebrik TI, Korenbrot JI. In intact cone photoreceptors, a Ca2+-dependent, diffusible factor modulates the cGMP-gated ion channels differently than in rods. J Gen Physiol. 1998;112:537–48. doi: 10.1085/jgp.112.5.537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Hackos DH, Korenbrot JI. Calcium modulation of ligand affinity in the cyclic GMP-gated ion channels of cone photoreceptors. J Gen Physiol. 1997;110:515–28. doi: 10.1085/jgp.110.5.515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Hsu YT, Molday RS. Modulation of the cGMP-gated channel of rod photoreceptor cells by calmodulin. Nature. 1993;361:76–9. doi: 10.1038/361076a0. [DOI] [PubMed] [Google Scholar]
- 41.Hsu YT, Molday RS. Interaction of calmodulin with the cyclic GMP-gated channel of rod photoreceptor cells. Modulation of activity, affinity purification, and localization. J Biol Chem. 1994;269:29765–70. [PubMed] [Google Scholar]
- 42.Sagoo MS, Lagnado L. G-protein deactivation is rate-limiting for shut-off of the phototransduction cascade. Nature. 1997;389:392–5. doi: 10.1038/38750. [DOI] [PubMed] [Google Scholar]
- 43.Gorczyca WA, Gray-Keller MP, Detwiler PB, Palczewski K. Purification and physiological evaluation of a guanylate cyclase activating protein from retinal rods. Proc Natl Acad Sci U S A. 1994;91:4014–8. doi: 10.1073/pnas.91.9.4014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Dizhoor AM, Lowe DG, Olshevskaya EV, Laura RP, Hurley JB. The human photoreceptor membrane guanylyl cyclase, RetGC, is present in outer segments and is regulated by calcium and a soluble activator. Neuron. 1994;12:1345–52. doi: 10.1016/0896-6273(94)90449-9. [DOI] [PubMed] [Google Scholar]
- 45.Calvert PD, Ho TW, LeFebvre YM, Arshavsky VY. Onset of feedback reactions underlying vertebrate rod photoreceptor light adaptation. J Gen Physiol. 1998;111:39–51. doi: 10.1085/jgp.111.1.39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Hodgkin AL, Nunn BJ. Control of light-sensitive current in salamander rods. J Physiol. 1988;403:439–71. doi: 10.1113/jphysiol.1988.sp017258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Cornwall MC, Matthews HR, Crouch RK, Fain GL. Bleached pigment activates transduction in salamander cones. J Gen Physiol. 1995;106:543–57. doi: 10.1085/jgp.106.3.543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Koch KW, Stryer L. Highly cooperative feedback control of retinal rod guanylate cyclase by calcium ions. Nature. 1988;334:64–6. doi: 10.1038/334064a0. [DOI] [PubMed] [Google Scholar]
- 50.Miller JL, Korenbrot JI. Differences in calcium homeostasis between retinal rod and cone photoreceptors revealed by the effects of voltage on the cGMP-gated conductance in intact cells. J Gen Physiol. 1994;104:909–40. doi: 10.1085/jgp.104.5.909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Dizhoor AM, Olshevskaya EV, Henzel WJ, Wong SC, Stults JT, Ankoudinova I, Hurley JB. Cloning, sequencing, and expression of a 24-kDa Ca(2+)-binding protein activating photoreceptor guanylyl cyclase. J Biol Chem. 1995;270:25200–6. doi: 10.1074/jbc.270.42.25200. [DOI] [PubMed] [Google Scholar]
- 51.Pugh EN, Jr, Duda T, Sitaramayya A, Sharma RK. Photoreceptor guanylate cyclases: a review. Biosci Rep. 1997;17:429–73. doi: 10.1023/a:1027365520442. [DOI] [PubMed] [Google Scholar]
- 52.Fesenko EE, Kolesnikov SS, Lyubarsky AL. Induction by cyclic GMP of cationic conductance in plasma membrane of retinal rod outer segment. Nature. 1985;313:310–3. doi: 10.1038/313310a0. [DOI] [PubMed] [Google Scholar]
- 53.Haynes LW, Kay AR, Yau KW. Single cyclic GMP-activated channel activity in excised patches of rod outer segment membrane. Nature. 1986;321:66–70. doi: 10.1038/321066a0. [DOI] [PubMed] [Google Scholar]
- 54.Zimmerman AL, Baylor DA. Cyclic GMP-sensitive conductance of retinal rods consists of aqueous pores. Nature. 1986;321:70–2. doi: 10.1038/321070a0. [DOI] [PubMed] [Google Scholar]
- 55.Watanabe S, Matthews G. Dose-response relation of cyclic GMP-activated channels in the retinal rod photoreceptor. Neurosci Res Suppl. 1989;10:S1–7. doi: 10.1016/0921-8696(89)90003-0. [DOI] [PubMed] [Google Scholar]
- 56.Yau KW, Baylor DA. Cyclic GMP-activated conductance of retinal photoreceptor cells. Annu Rev Neurosci. 1989;12:289–327. doi: 10.1146/annurev.ne.12.030189.001445. [DOI] [PubMed] [Google Scholar]
- 57.Lagnado L, Cervetto L, McNaughton PA. Calcium homeostasis in the outer segments of retinal rods from the tiger salamander. J Physiol. 1992;455:111–42. doi: 10.1113/jphysiol.1992.sp019293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Menini A, Rispoli G, Torre V. The ionic selectivity of the light-sensitive current in isolated rods of the tiger salamander. J Physiol. 1988;402:279–300. doi: 10.1113/jphysiol.1988.sp017204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Ratto GM, Payne R, Owen WG, Tsien RY. The concentration of cytosolic free calcium in vertebrate rod outer segments measured with fura-2. J Neurosci. 1988;8:3240–6. doi: 10.1523/JNEUROSCI.08-09-03240.1988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Korenbrot JI. Ca2+ flux in retinal rod and cone outer segments: differences in Ca2+ selectivity of the cGMP-gated ion channels and Ca2+ clearance rates. Cell Calcium. 1995;18:285–300. doi: 10.1016/0143-4160(95)90025-x. [DOI] [PubMed] [Google Scholar]
- 61.Miller JL, Korenbrot JI. In retinal cones, membrane depolarization in darkness activates the cGMP-dependent conductance. A model of Ca homeostasis and the regulation of guanylate cyclase. J Gen Physiol. 1993;101:933–60. doi: 10.1085/jgp.101.6.933. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Detwiler PB, Gray-Keller MP. Some unresolved issues in the physiology and biochemistry of phototransduction. Curr Opin Neurobiol. 1992;2:433–8. doi: 10.1016/0959-4388(92)90176-l. [DOI] [PubMed] [Google Scholar]
- 63.Sampath AP, Matthews HR, Cornwall MC, Fain GL. Bleached pigment produces a maintained decrease in outer segment Ca2+ in salamander rods. J Gen Physiol. 1998;111:53–64. doi: 10.1085/jgp.111.1.53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Younger JP, McCarthy ST, Owen WG. Weak adapting backgrounds reduce the resting level of cytosolic free calcium in rod photoreceptors. Invest Ophthalmol Vis Sci. 1991;32:907. [Google Scholar]
- 65.Younger JP, McCarthy ST, Owen WG. Light-dependent control of calcium in intact rods of the bullfrog Rana catesbeiana. J Neurophysiol. 1996;75:354–66. doi: 10.1152/jn.1996.75.1.354. [DOI] [PubMed] [Google Scholar]
- 66.Cobbs WH, Pugh EN., Jr Kinetics and components of the flash photocurrent of isolated retinal rods of the larval salamander, Ambystoma tigrinum. J Physiol. 1987;394:529–72. doi: 10.1113/jphysiol.1987.sp016884. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Baylor DA, Lamb TD, Yau KW. Responses of retinal rods to single photons. J Physiol. 1979;288:613–34. [PMC free article] [PubMed] [Google Scholar]
- 68.Hamer RD, Tyler CW. Does the saturation period of vertebrate photocurrent flash response reflect only rhodopsin lifetimes? Invest Ophthalmol Vis Sci. 1996;37:S811. [Google Scholar]
- 69.Hamer RD. Computational modeling of the full flash response dynamics of dark-adapted tiger salamander rod. Invest Ophthalmol Vis Sci. 1998;39:S955. [Google Scholar]
- 70.Hamer RD. How “signature” features in dark- & light-adapted photocurrent responses constrain models of vertebrate phototransduction. Invest Ophthalmol Vis Sci. 1999;40:S208. [Google Scholar]
- 71.Cornwall MC, Fain GL. Bleached pigment activates transduction in isolated rods of the salamander retina. J Physiol. 1994;480:261–79. doi: 10.1113/jphysiol.1994.sp020358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Fain GL, Matthews HR, Cornwall MC. Dark adaptation in vertebrate photoreceptors. Trends Neurosci. 1996;19:502–7. doi: 10.1016/S0166-2236(96)10056-4. [DOI] [PubMed] [Google Scholar]
- 73.Matthews HR, Cornwall MC, Fain GL. Persistent activation of transducin by bleached rhodopsin in salamander rods. J Gen Physiol. 1996;108:557–63. doi: 10.1085/jgp.108.6.557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Bownds MD, Arshavsky VY. What are the mechanisms of photoreceptor adaptation? Behav Brain Sci. 1995;18:415–424. [Google Scholar]


