Abstract
We evaluated the generality of two models of vertebrate phototransduction. The approach was to quantitatively optimize each model to the full waveform of high-quality, dark-adapted (DA), salamander rod flash responses. With the optimal parameters, each model was then used to account for signature, qualitative features of rod responses from three experimental paradigms (stimulus/response, “S/R suite”): (1) step responses; (2) the intensity dependence of the period of photocurrent saturation (Tsat vs. ln(I)); and (3) light-adapted (LA) incremental flash sensitivity as a function of background intensity. The first model was the recent successful model of Nikonov et al. (1998). The second model replaced the instantaneous Ca2+ buffering used in the Nikonov et al. model with a dynamic buffer. The results showed that, in the absence of the dynamic Ca2+ buffer, the Nikonov et al. model does not have sufficient flexibility to provide a good fit to the flash responses, and, using the same parameters, reproduce the salient features of the S/R suite—critical features at step onset and offset are absent; the Tsat function has too shallow a slope; and the model cannot generate the empirically observed I-range of Weber-Fechner LA behavior. Some features could be recovered by changing parameters, but only at the expense of the fit to the reference (Ref) data. When the dynamic buffer is added, the model is able to achieve an acceptable fit to the Ref data while reproducing several features of the S/R suite, including an empirically observed Tsat function, and an extended range of LA flash sensitivity adhering to Weber’s law. The overall improved behavior of the model with a dynamic Ca2+ buffer indicates that it is an important mechanism to include in a working model of phototransduction, and that, despite the slow kinetics of amphibian rods, Ca2+ buffering should not be simulated as an instantaneous process. However, neither model was able to capture all the features with the same parameters yielding the optimal fit to the Ref data. In addition, neither model could maintain a good fit to the Ref data when five key biochemical parameters were held at their current known values. Moreover, even after optimization, a number of important parameters remained outside their empirical estimates. We conclude that other mechanisms will need to be added, including additional Ca2+-feedback mechanisms. The present research illustrates the importance of a hybrid qualitative/quantitative approach to model development, and the limitations of modeling restricted sets of data.
Keywords: Phototransduction, Computational modeling, Vertebrate rods, Light adaptation, Cyclic GMP cascade, Dark-adapted flash responses
Introduction
Much is known about the biochemical steps (the cGMP cascade) linking the absorption of photons and the electrical response of vertebrate photoreceptors. A strong test of our understanding of the phototransduction process is to implement a model of the known and putative underlying biochemical and biophysical mechanisms. In general, the broader the set of data accounted for by a model, the more confidence we have that the model is comprehensive and captures all the essential mechanisms, with realistic, physiologically realizable parameters.
The stoichiometric and, to a lesser degree, kinetic information about the elements of the cGMP cascade in rods is now known in sufficient detail to permit either stochastic molecular modeling (Lamb, 1994) or modeling by explicit differential equations and/or their steady-state counterparts (e.g. Forti et al., 1989; Tranchina et al., 1991; Lamb & Pugh, 1992; Nikonov et al., 1998). In general, despite all that is known about the cascade, models have been evaluated in relation to photoreceptor responses over limited response ranges for a restricted set of stimulus conditions.
Modeling approach
The challenges to development of a comprehensive model of rod phototransduction derive from the complexity of the system—it is simply an inherently difficult problem to accurately simulate the behavior of a complex, nonlinear system like the cGMP cascade over its full operating range, including both dark- (DA) and light-adapted (LA) conditions. One approach to the problem is to use a quantitative optimization algorithm to find a set of parameters yielding a best fit to a representative set of data. However, due to the relatively large number of nonindependent parameters, quantitative optimization of a transduction model to any single set of empirical data, though necessary, may not be sufficient in evaluating candidate models. A good model of the process should provide quantitative account of DA photoreceptor responses to both dim and saturating flashes with the same set of parameters. Moreover, with the same set of parameters, it should be able to capture at least the qualitative features of responses obtained under LA conditions, including dynamic details (so called “signature features”) that reflect the influence of underlying nonlinear mechanisms, or the influence of more than one linear mechanism with distinct dynamics.
Hence, the analyses in the present article combine quantitative optimization and qualitative model evaluation. Such an approach puts stronger constraints on any model, and can thus guide development of a parsimonious, biochemically based model that accounts for a broad range of DA and LA responses.
Two model structures are evaluated. The first is an important model recently proposed by Nikonov et al. (1998). The model implements the major elements of the cyclic GMP (cGMP) cascade—activation/inactivation of rhodopsin and transducin-phosphodiesterase complex, hydrolysis of cGMP by phosphodiesterase, gating of light-sensitive membrane cation channels by cooperative action of cGMP, extrusion of Ca2+ by a Na/Ca2+/K exchanger, Ca2+ feedback via modulation of cGMP synthesis by guanylate cyclase, and Ca2+ buffering. The model provided good quantitative account of dark-adapted, dim-flash responses and (using different parameters) highly saturated flash responses under conditions where internal Ca2+ concentration was held “clamped” at its resting dark level (Nikonov et al., 1998). Hence, it is an important model to evaluate.
The second model structure replaces the instantaneous Ca2+ buffer used in the Nikonov et al. (1998) model with a dynamic Ca2+ buffer.
The overall goal of this research is systematic development of parsimonious models of vertebrate phototransduction that are linked to the known underlying biochemistry, and that are sufficiently complete to account for the broadest possible range of empirically observed responses. Toward that end, the present study evaluates to what extent a reasonable model of the form of the Nikonov et al. (1998) model can account for amphibian rod responses recorded under a range of DA and LA conditions. In addition, we examine the effect of adding a dynamic stage to the control of internal Ca2+ concentration on the generality of the model. Finally, the models are evaluated when some key biochemical/biophysical parameters are held fixed at their recent empirical estimates.
Methods and procedures
Physiological recordings
A set of DA rod flash responses (provided by J. I. Korenbrot, UCSF) served as the reference (Ref) data for the analyses. Whole-cell recordings from larval tiger salamander rods were made under full voltage clamp using tight-seal electrodes in the perforated-patch mode (see Methods in Miller & Korenbrot, 1994). The Ref data set contained seven responses to 20-ms, 520-nM flashes that elicited 13 to 3541 photoisomerizations (R*) in ∼0.3-0.4 log-unit increments. The data were collected using 8-pole Bessel analog filter DC-20 Hz, and digitized at 200 Hz (5 ms per time bin). For efficiency in optimization, four of the seven responses were used, ranging from a quasilinear, near-dim flash response to a fully saturated response (27, 148, 620, and 3541 R*/flash). For calculation of error in the optimization runs, each response was sampled at 25 Hz (40 ms/time bin) starting at time zero (defined as the center of the 20-ms flash), and thus contributed 201 data points.
Quantitative optimization
The models were implemented using Matlab/SIMULINK (The MathWorks, Natick, MA), and optimized to the Ref set of rod flash responses using the Constrained Optimization algorithm provided in the Matlab Optimization Toolbox.
For each optimization, a restricted subset of the model parameters was allowed to vary within upper and lower bounds within a factor of 10 or less of empirical estimates (when available). The remainder of the parameters were either fixed, or “roaming, steady-state” parameters. The latter parameters were not optimized directly, but had to be reset to steady-state values commensurate with the new free-parameter values for each iteration of the optimization. The free, roaming and fixed parameters associated with each model result shown in the figures are identified in Tables 1-3. The output measure of each optimization was relative least-square error (relLSQerr). For each of the seven flash responses, this was calculated by normalizing the model output and the Ref data by the maximum photocurrent for that response, calculating the cumulative squared error between the 201 data points and the corresponding 201 model values. The total relLSQerr was the sum of the relLSQerr values for the seven responses, divided by the total number of error measurements, that is, by 1407 = (201 data points) * (7 flash responses).
Table 1.
Description of model variables and parameters
| Symbol | Units | Description |
|---|---|---|
| Variables | ||
| R* (R) | # | Number of photoactivated (inactive) rhodopsin molecules at time t |
| E* | # | Number of activated PDE catalytic subunits per rod at time t |
| g | μM | Concentration of free outer segment (OS) cGMP |
| c | μM | Concentration of intracellular free OS Ca2+ at time t |
| cb | μM | Concentration of Ca2+ bound to dynamic Ca2+ buffer at time t |
| F | # | Normalized circulating current at time t |
| Parameters | ||
| τR | s | Time constant for first-order inactivation of R* |
| τE | s | Time constant for first-order inactivation of E* (E* = G*·PDE*) |
| νrp | s−1 | Rate of production of E* per R* |
| cdark | μM | Dark resting concentration of free intracellular Ca2+ |
| fse | # | Suction-electrode collecting efficiency |
| Jex | pA | Na+/Ca2+-K+ exchange current |
| Jex,dark | pA | Na+/Ca2+-K+ exchange current in the dark |
| Jex,sat | pA | Saturated magnitude of Na+/Ca2+-K+ exchange current |
| Kex | μM | Cai2+ giving rise to half-maximal exchange current |
| c0 | μM | Minimum value of free OS Ca2+ (Ca2+ floor) |
| γCa | s−1 | Rate constant of Ca2+ extrusion by exchanger |
| Vcyto | pL | Effective volume of rod OS |
| Fca | # | Fraction of inward circulating current carried by Ca2+ |
| b | μMs−1 pA−1 | Converts Ca2+ influx to current. Note: For Vcyto = 1 pL, Fca = 0.193 b |
| BCa | # | Instantaneous Ca2+-buffering power of the rod OS |
| k1 | μM−1 s−1 | On-rate constant for binding of Ca2+ to dynamic Ca2+ buffer |
| k2 | s−1 | Off-rate constant for unbinding of Ca2+ from dynamic Ca2+ buffer |
| et | μM | Total concentration of dynamic Ca2+ buffer |
| gdark | μM | Resting cytoplasmic concentration of free cGMP in the dark |
| Amas | μMs−1 | Maximum activity of guanylate cyclase |
| βdark | s− | Rate constant of cGMP hydrolysis (by E*) in the dark |
| βsub | s−1 | Rate constant of a catalytic PDE subunit in a well-stirred volume |
| Kc | μM | Concentration of Ca2+ at which cyclase activity is half-maximal |
| nca | # | Hill coefficient for Ca2+ modulation of cGMP synthesis via cyclase |
| ncg | # | Hill coefficient for opening of cGMP-gated channels by cGMP |
| Jdark | pA | Dark circulating current |
| Fdark | pA | Normalized circulating current in the dark |
Table 3.
Parameters used for model with dynamic Ca2+ buffer
| (Fig. 7) |
(Fig. 8) |
(Fig. 9) |
(Fig. 10) |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Optimized |
Optimized, τE* = 2 s |
Extended gain control |
"Modern" parameters |
|||||||||
| Parameters | Value | Lower bound | Upper bound | Value | Lower bound | Upper bound | Value | Lower bound | Upper bound | Value | Lower bound | Upper bound |
| "Front-End" Parameters | ||||||||||||
| τR* | 0.416 | 0.1 | 0.99 | 0.391 | 0.100 | 0.990 | 0.99 | 0.1 | 0.99 | 0.99 | 0.050 | 0.99 |
| τE* | 1.195 | 1 | 4 | 2 | 2.174 | 1 | 4 | 1.172 | 1 | 3 | ||
| VRP | 1734.73 | 100 | 10000 | 1161.5 | 100 | 10000 | 2520.5 | 100 | 10000 | 2371.8 | 100 | 20000 |
| R*(0) | 0 | 0 | 0 | 0 | ||||||||
| E*(0) | 0 | 0 | 0 | 0 | ||||||||
| Ca2+, Ca2+-Buffer Parameters | ||||||||||||
| cdark | 0.571 a | 0.568 a | 0.3 | 0.679 a | ||||||||
| Cbdark | 15.31 a | 45.19 a | 55.22 | 45.25 a | ||||||||
| eT | 394.58 | 50 | 1000 | 662.80 | 50 | 1000 | 791.4 | 50 | 1000 | 889.99 | 50 | 1000 |
| b | 0.780 a | 0.486 a | 0.299 | 0.933 | ||||||||
| γCa | 99.67 | 2 | 200 | 62.428 | 50 | 200 | 73.17 | 2 | 200 | 100 | 100 | 300 |
| kl | 0.166 | 0.05 | 5 | 0.1 | 0.2 | 0.142 | 0.05 | 5 | ||||
| k2 | 2.350 | 0.05 | 10 | 0.775 | 0.05 | 10 | 0.8 | 0.1 | 0.7 | 1.801 | 0.05 | 5 |
| c0 | 0.005 | 0.005 | 0.005 | 0.005 | ||||||||
| cGMP, Cyclase Parameters | ||||||||||||
| Kc | 0.219 | 0.1 | 0.22 | 0.22 | 0.1 | 0.22 | 0.1 | 0.1 | 0.22 | 0.2 | ||
| nca | 2.855 | 1.6 | 3.8 | 3.8 | 1.6 | 3.8 | 3.8 | 1.6 | 3.8 | 2 | ||
| Amax | 4.461 a | 9.801 a | 121.4 | 60 | 150 | 20.062 a | ||||||
| βsub | 1.68 × 10−5 | 1.68 × 10−5 | 1.68 × 10−5 | 1.68 × 10−5 | ||||||||
| gdark | 2 | 2 | 2 | 2 | ||||||||
| βd | 0.136 | 0.1 | 2 | 0.130 | 0.1 | 2 | 0.920 | 0.8 | 0.8 | 1.2 | ||
| cGMP-Gated Channel, Photocurrent Parameters | ||||||||||||
| ncg | 2.201 | 1.5 | 3.5 | 3.275 | 1.5 | 3.5 | 2.2 | 2 | ||||
| Jd | 72.296 | 72.296 | 72.296 | 72.296 | ||||||||
| Fdark | 1 | 1 | 1 | 1 | ||||||||
| Rel Err | 0.00224 | 0.0035 | 0.006817 | 0.007386 | ||||||||
Roaming steady-state parameter.
Qualitative evaluation: The stimulus-response suite
After optimization to the Ref data, the optimal (OPT) parameters were held fixed, and three “experiments” were simulated to generate a set of model DA and LA response profiles (stimulus-response suite). Model performance was then evaluated in relation to the accuracy of the fit to the Ref data, as well as to the overall account of the full suite of empirical responses (Fig. 1). The full suite thus includes the fit to the Ref flash series, time-to-peak (Tpk) versus log(I) and peak response amplitude (Rpk) versus log(I), as well as the three simulated experiments—step responses, saturation period (Tsat) as a function of flash intensity (Pepperberg et al., 1992, 1994), and LA relative flash sensitivity as a function of background intensity.
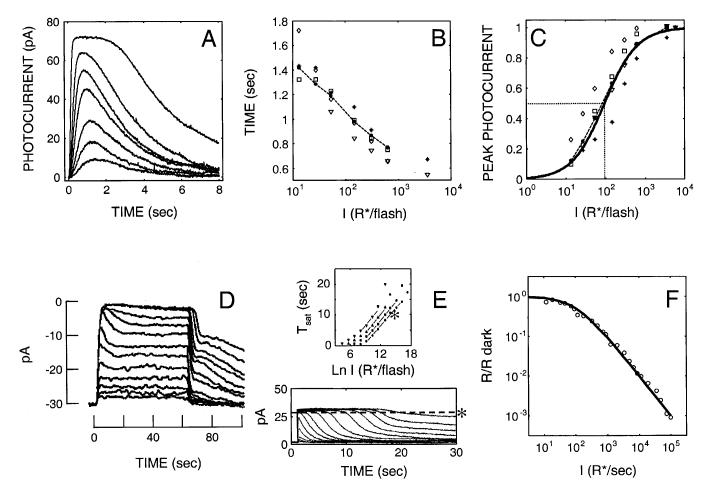
Fig. 1.
Empirical S/R suite of rod responses. (A) Ref flash responses from larval tiger salamander rods (whole-cell, voltage-clamped recordings in the perforated patch mode; data provided by J.I. Korenbrot, UCSF). Stimuli were 20-ms flashes at 520 nm: 13, 27, 54, 148, 310, 620 to 3541 R*/flash. (B) Time-to-peak (Tpk) versus log (R*/flash). Tpk for the Ref flash responses are shown as filled circles with solid lines, along with Tpk data from four other cells recorded under the same conditions. The Tpk of the Ref data decreases by ∼380 ms/log unit from 1400 ms to 760 ms, over the 3-log-unit range of I. All five rods undergo comparable changes in Tpk with intensity (C) Peak response amplitude (Rpk) vs log (R*) for the same 5 rods (Ref data, filled circles). Note that the I1/2 of the Ref rod (95 R*/flash) is representative of the 5 rods shown, and is close to the values reported in Miller and Korenbrot (1994) and Korenbrot (1995). (D) Step responses from newt rods (Forti et al., 1989; Torre et al., 1990).*,† Note the “nose” at step onset that recovers to a steady-state (LA) level, and a multiphasic response at step offset exhibiting a fast recovery phase followed by a slow phase, with some damped resonant behavior in between. (E) Highly saturated, DA responses to 100-ms flashes along with corresponding Tsat functions taken at four recovery criteria (lowest Tsat function corresponds to a 10% recovery criterion, as indicated by the horizontal dashed line through the photocurrent data). Data are from Pepperberg et al. (1992). Flashes ranged from 8 R*/flash to more than 2.9 ×107 R*/flash (>6.5 log10 units). Note that the Tsat functions have a slope of ∼2 s/ln unit, and that the Tsat data accelerate at the highest intensities. (F) LA flash sensitivity versus log (Ib). Flash sensitivity is defined as the peak amplitude of a flash response in the presence of a background, divided by the DA peak flash response amplitude (R/RDA). The data are from six newt rods studied by Torre et al. (1990). Note the data obey the Weber-Fechner relation over ∼4 log units of Ib, and have an I1/2 of 100 R*/s.
Fig. 1A shows the reference flash response series used in the present study. Fig. 1B shows the time-to-peak [Tpk vs. log (R*)] of the Ref flash responses decreasing with flash intensity (filled circles with solid lines), along with Tpk data from four other cells recorded (by J. Korenbrot) under the same conditions. The Tpk of the Ref data decreases by ∼ 380 ms/log unit from 1400 ms to 760 ms, over the 3-log-unit range of I. All five rods undergo comparable changes in Tpk with intensity.
Fig. 1C shows the corresponding Rpk versus log (R*) for the same five rods (Ref data, filled circles). The solid curve is a Hill equation [eqn. (1)] that summarizes the five data sets.
| (1) |
Eqn. (1) was fit to each data set, yielding two parameters— sensitivity (I1/2 = number of R* eliciting a half-maximal peak flash response), and a parameter (nR) analogous to biochemical cooperativity associated with the classical Hill coefficient used in steady-state enzyme analyses. These parameters were then averaged to generate the “mean” Hill equation summarizing the group data. The mean values for I1/2 and nR were 4.21 R*/μ2 (= 95.2 R*/flash) and 1.004, respectively. These values are close to those reported in the literature for salamander rods recorded under comparable conditions (e.g. Miller & Korenbrot, 1994).
Fig. 1D shows step responses obtained from newt rods (Forti et al., 1989; Torre et al., 1990). These responses have several characteristic features, including a “nose” on the leading edge of the response that recovers slowly to a steady-state level, and a pronounced, multiphasic response at step offset exhibiting a fast recovery phase followed by a slow phase, with some damped resonant behavior in between. The slow phase at step offset has a time constant on the order of ∼20 s (Forti et al., 1989; Pepperberg et al., 1992). Similar behavior has been observed in recordings from salamander (Nakatani & Yau, 1988) and primate rods (Tamura et al., 1991).
Fig. 1E shows highly saturated, DA responses to 100-ms flashes ranging from 8 R*/flash to >2.9 × 107 R*/flash (>6.5 log10 units), along with the corresponding Tsat function (Tsat), or period of photocurrent saturation, versus ln(I) taken from Pepperberg et al. (1992). Empirically, the Tsat function tends to be linear with a slope of 2-3 s/ln unit over a dynamic range that varies from cell to cell (Pepperberg et al., 1992, 1994; Hamer & Tyler, 1995; Nikonov et al., 1998). A linear Tsat function is taken to imply dominance of photocurrent recovery by a first-order reaction in the cascade; a slope of 2 s/ln unit implies a rate-limiting time constant of ∼2 s. The rate-limiting reaction has been hypothesized to be either R* (Pepperberg et al., 1992, 1994) or T*·PDE* recovery (Murnick & Lamb, 1996; Sagoo & Lagnado, 1997; Lyubarsky et al., 1997; Nikonov et al., 1998). At high intensities, Pepperberg et al. (1992) have noted that the Tsat function exhibits an acceleration to a steep slope, implying the intrusion of a recovery mechanism with a much slower time constant than 2 s.
Fig. 1F shows the decrease in flash sensitivity traditionally associated with LA. The data in Fig. 1F are from six newt rods studied by Torre et al. (1990). A number of studies have shown that the gain, as measured by the peak amplitude in response to a flash on a background, decreases according to the Weber-Fechner relation over several log units in rods (Torre et al., 1990; Tamura et al., 1991; Koutalos et al., 1995a), and over a larger range in cones (e.g. Burkhardt, 1994). The solid curve is the Weber-Fechner relation fit to these data.* The intensity that caused the incremental flash sensitivity to decrease by a factor of 2 (I1/2) was 100 R*s-1.
Results
The Nikonov et al. (1998) model
The “front-end” of the Nikonov et al. model—the sequence of cGMP-cascade reactions linking a photoisomerization of a rhodopsin molecule (hν + R → R*) to the generation of activated transducin·phosphodiesterase complex (T*·PDE* = E*)—is simulated as two sequential first-order reactions (R* → E* →) with time constants τR* and τE* (Lamb & Pugh, 1992; Lyubarsky et al., 1996; Nikonov et al., 1998). The implementation of the front-end is equivalent to the structure used in Nikonov et al. (1998) and Lyubarsky et al. (1996), except that, in lieu of an analytic expression, explicit differential equations for the two stages were implemented [eqns. (2) and (3)].
Ca2+ dynamics [eqns. (4) and (5)] are determined by the dynamic balance of Ca2+ influx through the cGMP-gated channels [first term in eqn. (4)] and Ca2+ efflux through the Na/Ca2+/K exchanger [second term in eqn. (4)]. Ca2+ feedback is implemented as in a number of other models (e.g., Forti et al., 1989; Tranchina et al., 1991), via modulation of cGMP synthesis by guanylate cyclase [first term in eqn. (6)]. In keeping with some empirical measures and models in the literature, Ca2+ buffering [Bca, eqn. (4)] is treated as an instantaneous process in the outer segment (McNaughton et al., 1986; Lagnado et al., 1992; McCarthy et al., 1996; Tranchina et al., 1991; Miller & Korenbrot, 1993).
All parameter descriptions and values are given in Tables 1 and 2.
Table 2.
Parameters used for analyses of Nikonov et al. (1998) model
| (Fig. 2) |
(Fig. 3) |
(Fig. 4) |
(Fig. 6) |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Nikonov et al. Parameters |
Optimized |
Optimized, τE* = 2 s |
"Modern" parameters |
|||||||||
| Parameters | Value | Lower bound | Upper bound | Value | Lower bound | Upper bound | Value | Lower bound | Upper bound | Value | Lower bound | Upper bound |
| "Front-End" Parameters | ||||||||||||
| τR* | 0.43 | 0.351 | 0.1 | 0.99 | 0.17 | 0.050 | 0.49 | 0.49 | 0.050 | 0.49 | ||
| τE* | 1.4 | 1.051 | 1 | 4 | 2 | 1.292 | 1 | 3 | ||||
| νRP | 6565.8 | 100 | 20000 | 1916.8 | 100 | 20000 | 2567.6 | 100 | 20000 | 5602 | 100 | 20000 |
| R*(0) | 0 | 0 | 0 | 0 | ||||||||
| E*(0) | 0 | 0 | 0 | 0 | ||||||||
| Ca2+, Ca2+-Buffer Parameters | ||||||||||||
| Cdark | 0.385 | 0.250 a | 0.553 a | 0.625 a | ||||||||
| Jex,sat | 18.638 | 26.78 | 4 | 40 | 14.08 | 4 | 40 | 23.17 | 4 | 40 | ||
| Jex,ss | 3.618 | 3.615 a | 3.615 | 6.507 | ||||||||
| Kex | 1.6 | 1.6 | 1.6 | 1.6 | ||||||||
| Fca | 0.1 | 0.1 | 0.1 | 0.18 | ||||||||
| Bca | 15 | 11.74 | 10 | 200 | 55.32 | 2 | 200 | 2 | 2 | 200 | ||
| Vcyto | 1 × 10−12 | 1 × 10−12 | 1 × 10−12 | 1 × 10−12 | ||||||||
| F | 96487 | 96487 | 96487 | 96487 | ||||||||
| fse | 1 | 1 | 1 | 1 | ||||||||
| cGMP, Cyclase Parameters | ||||||||||||
| Kc | 0.1 | 0.0842 | 0.08 | 0.24 | 0.208 | 0.08 | 0.22 | 0.2 | 0.2 | 0.24 | ||
| nca | 2 | 2 | 2.714 | 1 | 4 | 2 | ||||||
| Amax | 30 | 3.254 a | 4.034 a | 17.22 a | ||||||||
| βsub | 1.9 × 10−5 | 1.9 × 10−5 | 1.9 × 10−5 | 1.9 × 10−5 | ||||||||
| gdark | 2 | 2 | 2 | 2 | ||||||||
| βd | 0.948 | 0.166 | 0.1 | 2 | 0.133 | 0.1 | 4 | 0.8 | 0.8 | 1.2 | ||
| cGMP-Gated Channel, Photocurrent Parameters | ||||||||||||
| ncg | 2 | 2 | 1.5 | 1.5 | 3.5 | 2 | ||||||
| Jd | 72.296 | 72.296 | 72.296 | 72.296 | ||||||||
| Fdark | 1 | 1 | 1 | 1 | ||||||||
| Rel Err | 0.0226 | 0.00311 | 0.00696 | 0.01257 | ||||||||
Roaming steady-state parameter.
Activation, inactivation of rhodopsin [R(t)] and PDE [E(t)]
| (2) |
| (3) |
Influx, efflux, buffering of free calcium [c(t)]
| (4) |
| (5) |
Hydrolysis of cGMP [g(t)] and synthesis by guanylate cyclase (A)
| (6) |
cGMP-gated channel, photocurrent [F(t)]
| (7) |
Nikonov model with parameters for suction-electrode recordings
Nikonov et al. (1998) showed that a model of this form was able to capture some important features of suction-electrode recording of DA flash responses, especially in the simulation of a saturating flash series under Ca2+-clamp conditions. In addition, using other parameters, the model was able to provide a good fit to quasi-dim flash responses recorded under nonclamped (Ringer’s) conditions.
Fit to reference voltage-clamped flash responses
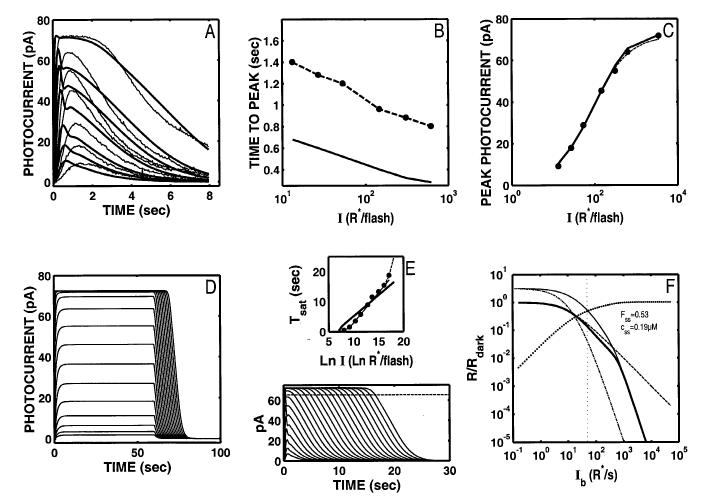
Panel A in Fig. 2 shows the Ref data along with model flash responses (solid curves) using parameters that Nikonov et al. found to provide a good fit to a quasi-dim-flash response (Nikonov et al., 1998; rod a, Ringer’s; see Table 2). With these parameters, the model provides a poor fit to the Ref data (Fig. 2A; relLSQerr = 0.02259), although it does captures I-dependence of the peak amplitude of the Ref flash responses (Fig. 2C). The model flash responses have a distinct “nose” at the peak that becomes more prominent at high intensities. Consequently, the peaks of the model flash responses occur too early and decrease by only ∼500 ms over the 3-log-unit intensity range (solid curve, Fig. 2B). This feature is not generally observed in rod recordings.
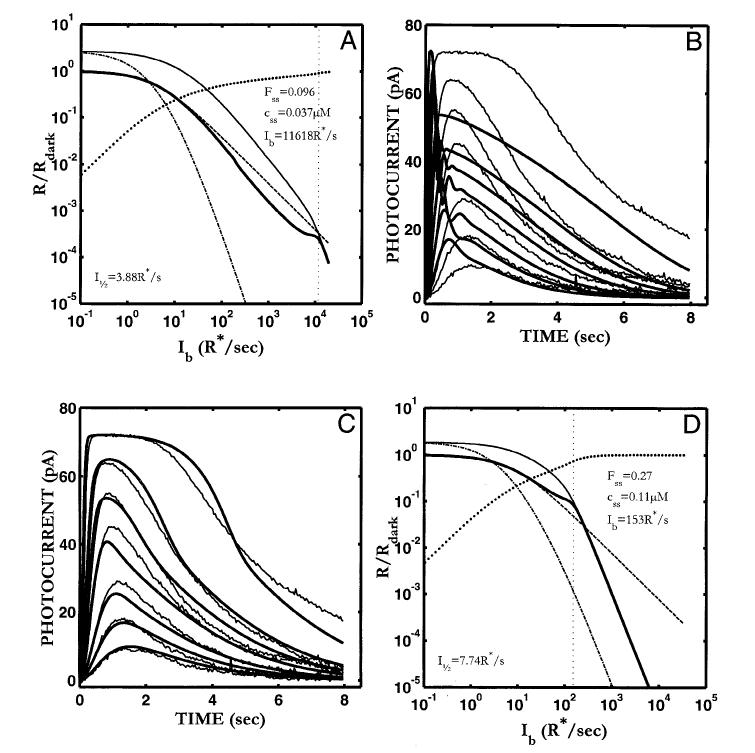
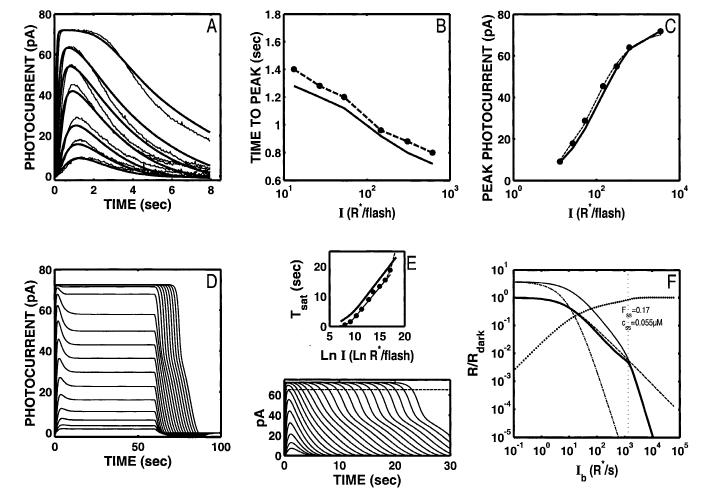
Fig. 2.
The S/R suite is shown for the Nikonov et al. (1998) model using the parameter values that fit the dim-flash response from their rod a (control response in Ringer’s). Parameters are given in Table 2. Model output is shown as solid lines and curves. Data from Fig. 1 are shown by data points and dashed lines and curves. (A) The fit to the Ref data set is poor (relLSQerr = 0.0226), and neither the growth of Tpk nor Rpk with flash I (B,C) match the voltage-clamped Ref data. Note that the model generates an aberrant “nose” at the peak of the flash response (A). This feature is more pronounced at higher intensities. (D) The model step responses are missing the features at step onset and offset (compare with Fig. 1D). (E) The slope of the Tsat function is shallower than the most frequently reported slope (2 s/ln unit). (F) Model LA flash sensitivity (thick, solid curve). The model LA flash sensitivity was defined as the amplitude of the response to a flash of fixed (criterion) intensity in the presence of a background adaptation, divided by the amplitude of the criterion flash presented in the absence of a background. The criterion used was a flash eliciting a DA flash response amplitude that was 10% of the full range of circulating current. The dashed curve is the Weber-Fechner relation from Fig. 1 F, shifted horizontally to fit the model output below a “cutoff” Ib (indicated by the dotted vertical cursor), above which the model was judged to deviate from Weber’s law (see text for details). The I1/2 for the Weber-Fechner curve is 9.85 R* s-1. With the Nikonov et al. dim-flash, suction electrode parameters, the model LA flash sensitivity does not obey Weber’s law over any significant range (cutoff Ib = ∼49 R* s-1). At the cutoff Ib, 53% of the model DA circulating current remains, as indicated by the intersection of the vertical cursor line with a curve plotting the fraction that the steady-state current that is saturated (i.e. 1 - Fss(Ib), shown as solid dots). Here, Fss is the steady-state circulating current defined to be 1.0 in the dark, and zero when all channels are closed. Also, at the cutoff Ib, the steady-state internal Ca2+ level (css in inset) has dropped by slightly more than a factor of 2, from a dark value of 0.385 μM to 0.19 μM. Also shown is the LA flash sensitivity of the model under two types of simulated Ca2+-clamp conditions: (1) L A flash sensitivity with Ca2+ clamped at its dark value (-clamp; dash-dot curve). Ca2+ feedback is fully disabled over the entire dynamic range, with only static saturation contributing to flash desensitization. Ca2+ was fixed at its dark value in the model, and Ib was adjusted to achieve the same steady-state current (Fss) responses as in the unclamped case, ensuring that the steady-state currents were placed at the same level in relation to static saturation (i.e. cGMP-gated channel). Differences in flash sensitivity then can be ascribed to the differing states of Ca2+ in the unclamped and clamped cases. The -clamp analysis equated steady-state current levels (Fss), but did not equate internal Ca2+ levels at the time of presentation of the flash. This was achieved in the second analysis: (2) L A flash sensitivity with Ca2+ clamped at the new steady-state level reached in response to each Ib ( clamp; thin solid curve). This approach equated the Fss (and hence equated the effect of channel saturation), and equated Ca2+ at the time of the flash. Thus, in comparing the unclamped and the -clamped flash sensitivity, the flash response is affected equally by saturation and by the steady-state level of Ca2+-mediated gain. The only additional factor shaping the LA flash response in the unclamped case is the dynamic Ca2+-mediated gain evoked by the flash. Note that at high Ib (Ib > cutoff Ib), the unclamped model flash sensitivity falls more steeply than a Weber’s law slope of -1, and eventually follows a steep function that parallels the high-Ib behavior of both Ca2+-clamped curves. In fact, all three curves asymptote to a slope of -(ncg + 1), which is predicted by the instantaneous compressive saturation of the cGMP-gated channels (Matthews et al., 1990).
Moreover, the model fails to capture other features, as illustrated in Fig. 2, Panels D-F.
Step response
When 60-s steps of light are applied to the model (Fig. 2D), the qualitative behavior does not match that seen in recordings from rods. The response at step onset does not have the “nose” (Nakatani & Yau, 1988; Forti et al., 1989; Fain et al., 1989; Tamura et al., 1991), and the offset response does not exhibit a slow phase (Nakatani & Yau, 1988; Forti et al., 1989; Tamura et al., 1991; see Fig. 1D).
Tsat vs. ln(I)
When supersaturating flashes are simulated, the period of photocurrent saturation (Tsat) increases too slowly with increases in I (Fig. 2E). The solid curve is the model Tsat function, which increases at a rate of 1.4 s/ln unit. This slope reflects the parameter value for the rate-limiting step in photocurrent activation (τE* = 1.4 s) used to fit the dim-flash responses. The filled circles and thick dashed line with a slope of 2 s/ln unit is a typical Tsat function observed by Pepperberg and others (same data as shown in Fig. 1E; Pepperberg et al., 1992; Murnick & Lamb, 1996; Nikonov et al., 1998).
The model also fails to predict the upturn in the Tsat function often seen at high intensities (Pepperberg et al., 1992; Hamer & Tyler, 1996).
LA flash sensitivity
The model does not generate a significant range of Weber’s law behavior in the incremental LA flash responses (thick solid curve, Fig. 2F). The Weber-Fechner relation from Fig. 1F has been reproduced in Fig. 2F (dashed curve), but with the I1/2 adjusted to obtain a least-square fit to the low-I portion of the model flash-sensitivity curve. The I1/2 for the best-fit Weber-Fechner curve was 9.85 R* s-1. This is a factor of ∼10 more sensitive than the newt rod recordings of Torre et al. (1990) shown in Fig. 1F. The portion used to fit the Weber-Fechner curve was chosen using the following procedure.
The fit was obtained by finding a “cutoff” Ib (see Ib in inset, marked by the vertical, dotted cursor line in Fig. 2F) where the model flash-sensitivity function first was judged to fall off steeper than a slope of -1 (the Weber’s law slope).† The Weber-Fechner relation was then fit to the model over the range of Ib values less than or equal to this cutoff Ib.
The cutoff Ib for the Nikonov et al. (1998) model, using their dim-flash, suction-electrode parameters, was 49 R*s-1. At this cutoff Ib, there was 53% of the model DA circulating current remaining, as indicated by the intersection of the vertical cursor line with a curve plotting the fractional saturation of the steady-state current [i.e. 1 - Fss(Ib), shown as solid dots]. Here, Fss is the steady-state circulating current defined to be 1.0 in the dark, and zero when all channels are closed. Also, at the cutoff Ib, the steady-state internal Ca2+ level (css in inset) had dropped by only slightly more than a factor of 2, from a dark value of 0.385 μM to 0.19 μM.
Two additional analyses are shown in Fig. 2F. These will be reproduced in the corresponding panels of all subsequent figures.
-clamp—LA flash sensitivity with Ca2+ clamped at its dark value (dash-dot curve). This analysis represents flash sensitivity with Ca2+ feedback fully disabled over the entire dynamic range, and only static saturation contributing to flash desensitization. This was achieved by clamping Ca2+ at its dark value in the model, and adjusting the Ib values to achieve the same steady-state current (Fss) responses as in the unclamped case. The latter procedure ensured that, in both cases, the steady-state currents were placed at the same level in relation to static saturation (i.e. cGMP-gated channel). Differences in flash sensitivity then can be ascribed to the differing states of Ca2+ in the unclamped and clamped cases.
clamp—LA flash sensitivity with Ca2+ clamped at the new steady-state level reached in response to each Ib (thin solid curve). The approach in the -clamp analysis equated steady-state current levels, but did not equate internal Ca2+ levels at the time of presentation of the flash. This was achieved by clamping Ca2+ at each new steady-state level, not at its dark value. The steady-state current values in this analysis were naturally equated with those of the unclamped case, since Fss was permitted to go to the level it would have in the unclamped case, and then the Ca2+-clamp was applied. This approach equated the Fss (and hence equated the effect of channel saturation), and equated Ca2+ at the time of the flash. Thus, in comparing the unclamped and the -clamped flash sensitivity, the flash response is affected equally by saturation and by the steady-state level of Ca2+-mediated gain. The only additional factor shaping the LA flash response in the unclamped case is the dynamic Ca2+-mediated gain evoked by the flash.
At high backgrounds (Ib > cutoff Ib), the unclamped model flash sensitivity falls more steeply than a Weber’s law slope of -1, and eventually follows a steep function that parallels the high-Ib behavior of both Ca2+-clamped curves. In fact, all three curves asymptote to a slope of -(ncg + 1), which is predicted by the instantaneous compressive saturation of the cGMP-gated channels (Matthews et al., 1990). Such behavior has been observed in a number of recordings of LA photoreceptor flash sensitivity under conditions when Ca2+-mediated feedback is disabled or blocked (Matthews et al., 1988, 1990; Nakatani & Yau, 1988; Tamura et al., 1989, 1991; Schnapf et al., 1990; Nakatani et al., 1991).
Aberrant “nose” at the peak of the model flash response
As noted above, using parameters that fit the control dim-flash response in Nikonov et al. (1998), the model generates flash responses with an aberrant “nose” at the peak, especially prominent at high intensities (compare Figs. 1A and 2A). This feature is not present in the time waveform of the model E* (t) response. It is due to the use of an instantaneous Ca2+ buffer in the model. The “nose” is eliminated from the model photocurrent waveform when Ca2+ is clamped at its dark value, or when Ca2+-buffer power (Bca) is reduced to a relatively small value (< ∼2). The “nose” is not eliminated by optimization of Ca2+-feedback parameters (nca, Kc), or by optimizing these parameters along with the two front-end time constants τR* and τE*.
The model is capable of generating responses that lack the “nose” when large values of Bca are used (up to Bca = 50), but only if other parameters are free to optimize. The most important are βdark and Jex,sat. βdark must be kept near 0.1 s-1, ∼10 times smaller than empirical estimates, and Jex,sat must be permitted to go to 30 pA or more, which exceeds empirical estimates by a factor of 2-3 (Lagnado et al., 1992).
Optimization of the Nikonov et al. (1998) model to DA voltage-clamped flash responses
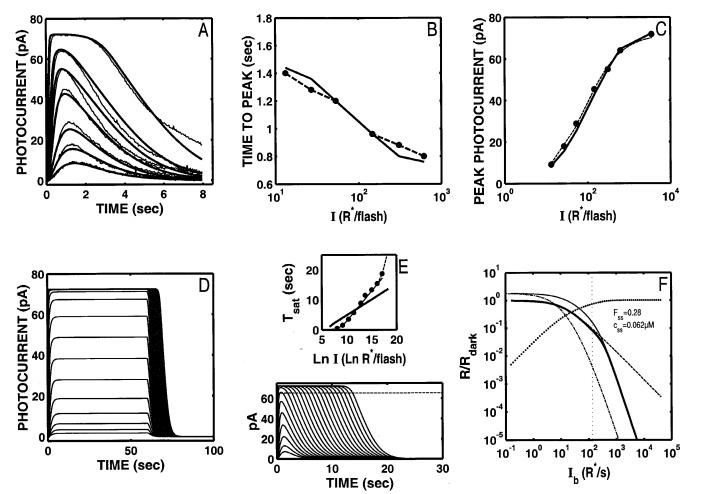
When the model is optimized to the Ref data set (Figs. 3A-3C), using seven free parameters (Table 2), a reasonably good fit is achieved (relLSQerr=0.00311).‡ As implied by the good fit to the data, the optimized model now provides a much improved account of the intensity dependence of Tpk (solid curves, Fig. 3B).
Fig. 3.
S/R suite after optimization of Nikonov et al. model to the Ref voltage-clamped flash responses. (A) When the model is optimized using seven free parameters (Table 2), a reasonably good fit to the Ref data is achieved (relLSQerr = 0.00311). As implied by this fit, the optimized model now provides a much improved account of the intensity dependence of Rpk as well as Tpk (B,C). Note that the “nose” at the peak of the flash response (Fig. 2A) is eliminated from the model response. However, with these parameters, the model still generates step responses (D) that lack the salient features at onset and offset observed empirically (Fig. 1D). (E) The fit to the data required a rate-limiting time constant for PDE inactivation of ∼1 s. Hence, the slope of the Tsat function is too shallow. (F) After optimization, the model now generates a modest range of Weberian LA (thick solid curve; cutoff Ib =136 R*/s); but the range is still almost two orders of magnitude less than observed empirically (see dashed curve, Fig 1F; cutoff Ib predicted to be ∼ 10,000 R*/s; see text for details). At the Ib where the model deviates from Weber’s law, 28% of the circulating current remains. Coding for Fss, -, and -clamped sensitivity in F are as in Fig. 2F.
The value of Bca in the optimal parameters was 11.7, slightly less than the values used in the Nikonov et al. (1998) model (∼15), and 6-28 times less than earlier estimates of the rod’s Ca2+-buffer power (e.g. Lagnado et al., 1992; Korenbrot, 1995; McCarthy et al., 1996). In combination with a low value for βdark (0.14 s-1), and a high value of Jex,sat (27 pA), the resulting model flash responses do not exhibit the aberrant “nose” at the peaks.
Despite the fit to the Ref data after optimization, the model fails to capture several key signature features of both DA and LA responses. For example, the model step responses still lack a “nose” at step onset and a slow phase at step offset (Fig. 3D). Second, the slope of the model Tsat function (solid curve, Fig. 3E) is too shallow (∼1 s/ln unit vs. 2-3 s/ln unit). This is because in order to achieve a fit to the Ref data, the rate-limiting time constant of the front-end reactions could not be any slower than ∼1 s.
Third, after optimization to the Ref data, the model now predicts a modest range of Weberian LA (solid curve, Fig. 3F), but the I-range is almost two orders of magnitude less than observed empirically (see dashed curve, Fig. 1F).§ Note that the model flash sensitivity begins to deviate from Weber’s law at 136 R* s-1, when there is 28% of circulating current remaining and Ca2+ has been driven to 62 nM.
Amelioration of the slope of the model Tsat function
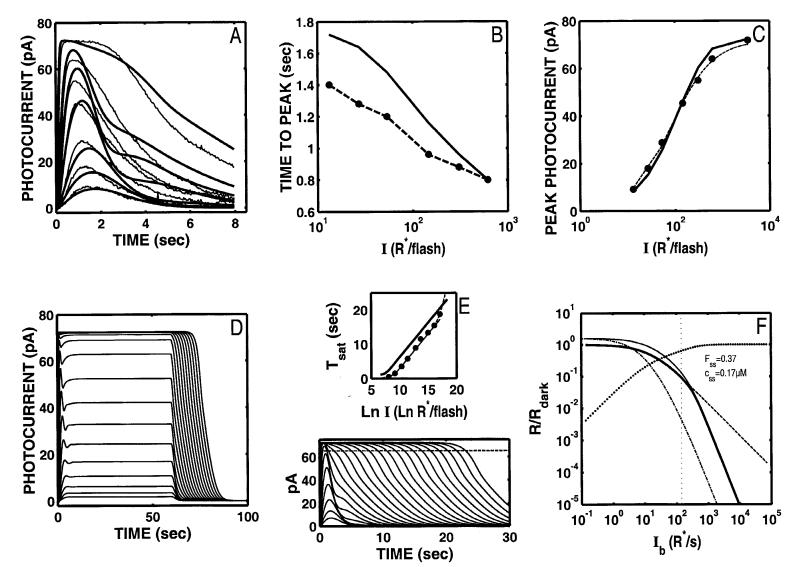
The shallow Tsat function is readily ameliorated by setting either τR* or τE* to 2 s. Fig. 4 shows the result of setting τE* to 2 s and reoptimizing the rest of the eight parameters. Fig. 4E shows that a Tsat function with a slope of 2 was achieved. However, under these conditions, the fit to the Ref data is severely degraded (Fig. 4A; relLSQerr = 0.00696) and cannot be recovered.** In addition, the model Tsat function still lacks the acceleration at high intensities that is observed empirically (compare solid curve in Fig. 4E with the top half of Fig. 1E).
Fig. 4.
S/R suite after optimization of Nikonov et al. model to the Ref data with the rate-limiting “front-end” time constant (τE*) held at 2 s so that a Tsat slope of 2 s/ln unit is generated by the model (solid curve, panel E). However, this feature is achieved at the expense of the model’s ability to achieve a fit to the Ref data (panels A-C). Moreover, the model Tsat function still lacks the acceleration at high intensities that is observed empirically (compare solid curve in Fig. 4E with the top half of Fig. 1E). The range of the model’s Weberian LA is about the same as with the parameters fully optimized (cutoff Ib = 142 R*/s), but is still much smaller than observed empirically. The coding for all the curves in F is as in Fig. 2F.
After optimization with τE* set to 2 s, the time-to peak of the DA model flash responses are delayed relative to the Ref data, and show a hyperintensity dependence (Fig. 4B). The growth of peak amplitude with intensity no longer matches the Ref data (Fig. 4C).
The model 60-s step responses (Fig. 4D) exhibit a rapid, transient “nose” at step onset never seen in amphibian rod responses, and exhibit no slow phase at step offset.
The range of Weberian LA is about the same as when parameters fully optimized (cutoff Ib = 142 R* s-1), but is still much smaller than observed empirically (Fig. 1F).
Amelioration of LA behavior
The modest range of Weberian LA behavior shown in Figs. 3 and 4 is not readily increased to match the data shown in Fig. 1F. When the Hill coefficient, nca, is held at 2, the model cannot generate any significant range of Weber’s law LA behavior. Setting the Hill coefficient for Ca2+ modulation of cyclase to a high value (nca = 4) is, however, not sufficient. When this is done, the model can generate a rough approximation to Weber’s law over an extended intensity range if the ratio of cdark to Kc is set to be large (∼6; solid curve, Fig. 5A). Extended LA behavior was achieved by using the same parameters that yielded an optimal fit to the Ref data (Fig. 3A, Table 2) with the following exceptions: Jex,sat was set (to 15.18 pA) so as to achieve cdark = 0.5 μ M [see eqn. (5)]; nca was set to 4; the latter two changes forced an adjustment of the steady-state value for Amax [eqn. (6)] from 3.25 μMs-1 to 413.833 μMs-1.
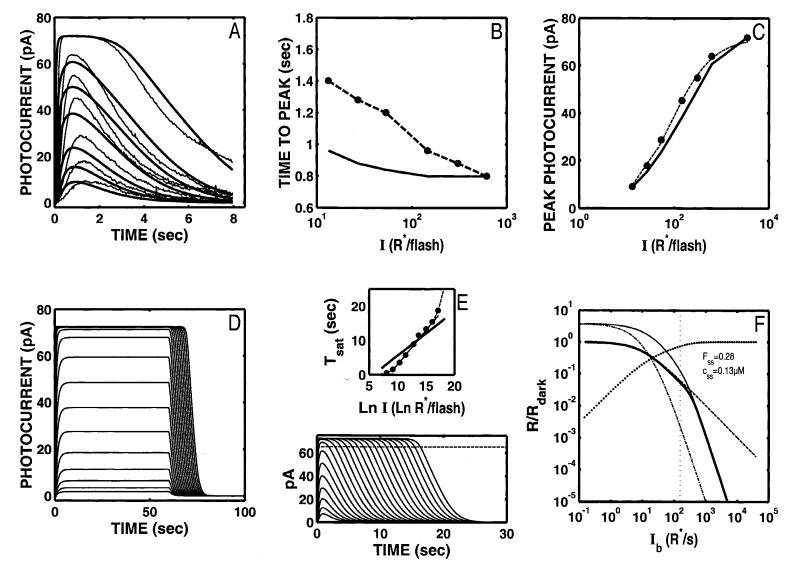
Fig. 5.
(A) The model can generate a rough approximation to Weber’s law adaptation over ∼4 log units of background intensity if nca is set to a high value and the ratio cdark/Kc is also large (∼6). The dashed curve represents the Weber-Fechner relation and has been fit to the model output (thick solid curve) using the same analysis as in Fig. 2F, 3F, and 4F. Based on this analysis, the model roughly adheres to Weber’s law out to a cutoff Ib of 11,600 R* s-1, comparable to the upper I-limit for which the Torre et al. (1990) data adhere to Weber’s law. However, as is evident in panel B, the parameters that support the desired LA behavior are incompatible with a good fit to the Ref data. The model can achieve a reasonable fit to the Ref data with nca held at 4 and the model reoptimized (C), but the resulting parameters will then not support the extended range of LA behavior (cutoff Ib = 153 R* s-1; D). The coding for all the curves in A and D is as in Fig. 2F.
The LA behavior under these conditions is shown in Fig. 5A. The dashed curve represents the Weber-Fechner relation and has been fit to the model output (thick solid curve) using the same analysis as in Fig. 2F, 3F, and 4F. Based on this analysis, the model roughly adheres to Weber’s law out to a cutoff Ib of 11,600 R* s-1, comparable to the upper I-limit for which the Torre et al. (1990) data adhere to Weber’s law.
However, some of the parameters required to achieve this behavior are not physiologically reasonable. For example, the cyclase rate varies by a factor of more than 1000 as Ca2+ goes from its dark value (0.5 μM) to its minimum of 0.037 μM at the cutoff Ib. This is far outside the range of empirical estimates for cyclase modulation, which is likely to be within a range of ∼2-35.††
Moreover, the parameters that support an extended range of LA behavior are incompatible with a good fit to the Ref data (Fig. 5B). An improved fit can be recovered by reoptimizing while keeping nca = 4 (Fig. 5C); but in this case, the large range of Weberian light adaptation is lost (cutoff Ib = 153 R* s-1; Fig. 5D).
Consequence of use of “modern” parameter values
The success of the model in fitting the Ref data (Figs. 3A-3C) is achieved when some biochemical parameters are permitted to deviate from empirical estimates in the literature. It is of interest to evaluate the consequence of holding some key parameters close to their recent empirical estimates.
Dark value for PDE* activity (βdark ≈ 1 s-1)—Nikonov et al. (1998) used βdark = 0.8-1.2 s-1 in modeling both their saturated (Ca2+ clamped) data, and the dim-flash responses. Experimental estimates for this parameter in amphibian rods vary widely: 0.1 s-1 in toad rods (Rieke & Baylor, 1996); 0.3 s-1 (Koutalos et al., 1995a); 0.4-0.8 s-1 in salamander rods (Hodgkin & Nunn, 1988); 0.14-0.72 s-1 in salamander rods (Cornwall & Fain, 1994); and 0.62-0.72 s-1 in salamander rods (Nikonov et al., 1998).
It should be noted, however, that the above estimates are dependent on the available estimates for other parameters. For example, the estimates from Hodgkin and Nunn (1988), Cornwall and Fain (1994), and Nikonov et al. (1998) assume the Hill coefficient for cGMP-gating of the channel (ncg) is 3. If ncg is closer to 2, as some have measured (e.g. Koutalos et al., 1995b; Rebrik & Korenbrot, 1998), then the range of estimates for salamander rod βdark across these three studies is 0.21 to 1.2 s-1. Tamura et al. (1991) estimated βdark = 1.2 s-1 for primate rods (assuming ncg = 2.5) using an approach like that of Hodgkin and Nunn (1988).
There are other estimates of βdark available based on accurate, but less direct measures, utilizing reliable parameter estimates from biochemical studies, in combination with electrophysiological data. The values for βdark can then be derived from a model of the cGMP cascade (e.g. see Miller & Korenbrot, 1994). For example, assuming that 1-3% of channels are open in the dark (biochemical and electrophysiological data from Cameron & Pugh, 1990), one can calculate gdark from the channel Hill equation. This requires an estimate of the K1/2 for the cGMP-gated channel (Kcg) and the Hill coefficient (ncg). Rebrik and Korenbrot (1998) measured Kcg ≈ 35 μ M and ncg ≈ 2.3 in salamander rods, yielding estimates of gdark of 4.8-7.7 μM. Using the range of biochemical estimates of (0.2-0.7 μM; Ratto et al., 1988; Korenbrot & Miller, 1989; Miller & Korenbrot, 1993; Gray-Keller & Detwiler, 1994; McCarthy et al., 1994,1996), and the steady-state equation for guanylate cyclase activity , one can use the estimate of gdark to calculate the dark PDE activity by setting the differential equation d(cGMP)/dt = 0, and solving for βdark. This requires estimates of Kca (0.1-0.26 μ M; Koch & Stryer, 1988; Calvert et al., 1998) and, nca (2-4; Pepe et al., 1986; Koch & Stryer, 1988; Gorczya et al., 1994). Using these ranges of measured values for the relevant parameters, one calculates an enormous range for βdark, that is, 0.005 to 12.3 s-1. With the parameter values set roughly in the middle of their range, one calculates βdark = 0.95 s-1. Hence, I have assumed a reasonable “modern” estimate for βdark to be in the vicinity of 1 s-1 .
Pugh et al. (1999) point out that β(t) (rate of hydrolysis of cGMP by PDE*, both dark- and light-driven activity) is an important parameter and is a dominant (and Ca2+ insensitive!) factor in flash desensitization during light adaptation. βdark is thus important in shaping flash sensitivity mainly at subsaturating intensities where it remains significant in relation to light induced changes in β(t). A perturbation analysis done for the present study revealed that small increases in βdark cause subsaturating flash responses to peak and recover earlier, whereas a decrease in βdark leads to a slowing of the response. Small changes in βdark have no effect on the slope of the Tsat function, but cause a slight expansion of the range of LA flash sensitivity adhering to Weber’s law. The asymptotic slope of the flash-sensitivity function does not change.
Percent circulating current carried by Ca2+ (Fca = 0.18)—Nikonov et al. (1998) adopted a value of Fca = 0.1. This is commensurate with a previous estimates of 10-15% (Yau & Nakatani, 1985; Nakatani & Yau, 1988; Lagnado et al., 1992). However, recent estimates in salamander rods by Korenbrot (personal communication) indicate that Fca is larger, closer to 0.2. At least one phototransduction model has used Fca = 0.25 (Forti et al., 1989), based on empirical estimates from Menini et al. (1988).
In the Nikonov et al. (1998) model, Fca and Jex,sat (maximum rate at which the exchanger can pump Ca2+ out of the rod OS, which occurs when Ca2+ is at its maximum, i.e. in the dark) have complementary influences on the responses (i.e. increases in Jex,sat have the same effect as decreases in Fca, assuming that steady-state Ca2+ is readjusted for each value of Fca or Jex,sat). An increase in Jex,sat means that in the steady state, for example, in the dark, the exchanger is extruding Ca2+ at a higher rate. The result is a lower steady-state Ca2+ level, leading to a decrease in Amax.
A perturbation analysis showed that small increases in Jex,sat (or decreases in Fca) caused LA flash sensitivity to increase at low to moderate Ib, and delayed the time-to-peak for DA flash responses. At high Ib, a small increase in Jex,sat (decrease in Fca) decreased flash sensitivity. Small decreases in Jex,sat (increases in Fca) caused the converse behavior.
Hill coefficient for Ca2+-modulation of guanylate cyclase (nca ≈ 2)—Early estimates of nca were ∼4 (Koch & Stryer, 1988). Several models of the cGMP cascade subsequently used this value (e.g. Forti et al., 1989; Tamura et al., 1991; Tranchina et al., 1991; Miller & Korenbrot, 1993). However, more recent studies indicate that Ca2+ cooperativity at the locus of GCAP-guanylate cyclase is lower, with a Hill coefficient closer to 2 (e.g. Gorczya et al., 1994; Dizhoor et al., 1994; Calvert et al., 1998). Several recent computational implementations of this Ca2+ feedback have adopted this lower value (e.g. Miller & Korenbrot, 1994; Koutalos et al, 1995a; Nikonov et al., 1998; Calvert et al., 1998).
The Hill coefficient, nca, has a strong effect on the range over which Ca2+ can modulate the cyclase rate, especially whenever Kc < . A larger nca causes an extended range of modulation of GC activity over the range of Ca2+ values (light levels). In addition, an increase in nca causes a decrease in time-to-peak of the flash response and a decrease in flash sensitivity for both DA responses, and for LA flash responses at low to moderate Ib. At high Ib, an increase in nca causes an increased flash sensitivity.
Ca2+ concentration at half-activation of guanylate cyclase (Kca ≈ 0.2 μM)—Koch and Stryer (1988) estimated this parameter to be ∼0.1 μM. More recent empirical estimates from both amphibian and bovine rods indicate that Kca is larger (0.2-0.25 μM; Gorczya et al., 1994; Dizhoor et al., 1994; Calvert et al., 1998; see Pugh et al., 1997 for a review). Other values that have been used are 0.087 μM (Koutalos et al., 1995b), 0.2 μM (Miller & Korenbrot, 1994), and 0.15 μM (Ames, 1994).
The empirical range of this parameter is thus only a factor of ∼3. However, the magnitude and dynamics of Ca2+ modulation of cyclase are quite sensitive to Kc (Calvert et al., 1998) depending on its relationship to and the value of the Ca2+ Hill coefficient (nca).
For example, for given values of and nca (assuming , the minimum to which Ca2+ goes in light is 0.02 μM), a decrease in Kc increases the range over which GC activity is modulated by changes in Ca2+: if , GC activity will modulate by only a factor of ∼2 regardless of the value of nca. Assuming nca = 2, if , the range of GC modulation increases to a factor of ∼5; for , the range goes to a factor of ∼10; if Kc = 1/5 , the range increases to a factor of ∼23.
These predicted GC modulation ranges are very sensitive to the value of nca. If nca is 3 and Kc = 1/3 , the modulation range increases from a factor of ∼10 to a factor of ∼28; for Kc = 1/5 , the range increases to ∼122. While a decrease in Kc increases the range over which Ca2+ modulates GC activity, it dramatically slows the GC response to Ca2+ changes. With Kc set equal to , GC activity may reach ∼80% of its maximal rate by ∼1.5 s after onset of a saturating step of light, whereas, if Kc is 1/4 (for the same conditions), GC activity would reach its maximum only after ∼8.5 s.
Hill coefficient for cGMP-gating of light-sensitive membrane cation channels(ncg = 2)‡‡—Values for this parameter range from 1.6 (Koutalos et al., 1995b) to 3 (Fesenko et al., 1985; Haynes et al., 1986; Zimmerman & Baylor, 1986; Watanabe & Matthews, 1989; Yau & Baylor, 1989). Nikonov et al. (1998) found that a value of ncg = 2 fit their subsaturating flash data better than a value of 3.
The Hill coefficient, ncg, controls the steepness with which photocurrent approaches saturation in response to flashes or steps of increasing intensity: a higher ncg causes a steeper Rpk versus log(I) function. An increase in ncg also causes a pronounced decrease in the time-to-peak of subsaturating flash responses, as well as a decrease in slope of the Tpk versus log(I) function. The effects on Tpk are surprising since ncg is a parameter of a static nonlinearity in the model. In addition, increasing ncg causes the flash-sensitivity function to asymptote to a steeper falloff, as expected from theory (see text for Fig. 2F; Matthews et al., 1990).
When the five key parameters above are held to within ∼25% of their modern empirical estimates, allowing five parameters to optimize (νrp, τR*, τE* and Bca and Jex,sat), the model cannot achieve a good fit to the data (Fig. 6A; relLSQerr = 0.01256, a factor of 4 times the error from the optimal fit in Fig. 3A; F(2,7) = 10.665, 0.005 < P < 0.01). The fit to the Ref data is quite sensitive to the parameter βd. The relLSQerr increases by a factor of 4 when βd is changed by only a factor of ∼1.4. If the model is run with the parameters yielding the optimal fit shown in Fig. 3, but with βd increased from 0.17 s-1 to 0.8 s-1 (a factor of 4.7), the fit to the Ref data is degraded by a factor of 41. Qualitatively, the model flash responses in Fig. 6 peak much too early, with Tpk nearly independent of intensity, and the model response amplitudes increase too slowly with intensity (solid curves Figs. 6B and 6C). The model Tsat slope is shallow (Fig. 6E), since the optimal value for the rate-limiting front-end reaction (τE*= 1 s) is ∼1/2 the empirical estimate of 2 s. Finally, the model step response and LA behavior (Figs. 6D and 6F) have the same deficiencies as in Figs. 3-4.
Fig. 6.
S/R suite after optimization of Nikonov et al. model to the Ref data with five key parameters held at or near the best current empirical estimates: βdark = 0.8 to 1.2, Kc = 0.2 to 0.24, nca = 2, ncg = 2, and Fca = 0.18. Five of remaining parameters were allowed to optimize (νrp, Bca, Jex,sat, τE*, τR*). With these “modern” parameter values, the Nikonov et al. model cannot achieve a good fit to the Ref data (A). The times-to-peak (B) are too early for the lower-I flashes, and they do not change with intensity. The peak response amplitudes have the wrong I-dependence (C). The step responses lack the signature features at step onset and offset (D). The best achievable fit to the Ref data required a τE* of 1.3 s, so that the model Tsat function (E) is shallower than 2 s/ln unit. Finally, the model produces only a modest range of Weberian LA (cutoff Ib = 156 R* s-1; F). The coding for all the curves in F is as in Fig. 2F.
Summary of performance of Nikonov et al. (1998) model
Taken together, the results from Figs. 2-6 show that, despite its success in accounting for dim-flash, suction-electrode flash responses and, (with different parameters), saturated responses under Ca2+ clamp (Figs. 4 and 11, Nikonov et al., 1998), the Nikonov et al. model is missing some important mechanisms, and does not have enough flexibility to account for both the full DA Ref flash series and a suite of DA and LA data with a single set of parameters.
Model with dynamic Ca2+ buffer
To expand the domain of response features that can be accounted for, some additional mechanisms must be added to the model. The Nikonov et al. (1998) model assumes that Ca2+ buffering is determined by the instantaneous level of free intracellular Ca2+, as has been assumed in other models (e.g. Tranchina et al., 1991; Miller & Korenbrot, 1994). Although some studies support the idea that Ca2+ buffering is rapid in relation to the time course of the photocurrent responses (e.g. McNaughton et al., 1986; Lagnado et al., 1992; McCarthy et al., 1996), the failures of the Nikonov model led us to revisit the idea of a dynamic Ca2+ buffer, as has been done in some models in the past (e.g. Forti et al., 1989; Tamura et al., 1991). This issue is dealt with in more detail in the Discussion.
Hence, eqns. (4) and (5) were replaced with two explicit differential equations [eqns. (8) and (9)] describing the dynamics of Ca2+ influx through the cGMP-gated channels at a rate determined by the dynamics of photocurrent (F), efflux through the exchanger (at rate γca s-1), as well as Ca2+ sequestration (at rate k1 μM-1 s-1) and release (at rate k2 s-1) by a Ca2+ buffer (cb, with dissociation constant, Kd = k2/k1). Here, cb is the concentration of Ca2+ bound to buffer at any given time. It is also the concentration of Ca2+ buffer bound to Ca2+, since a 1:1 binding is assumed.
Parameters are described in Table 1. All parameter values for the simulations using this model are shown in Table 3.
Calcium influx, efflux, calcium buffer
| (8) |
| (9) |
Here b is proportional to Fca, the fraction of circulating current carried by Ca2+: b = (Fca/2FVcyto) × 10-6, where F is the Faraday constant, and Vcyto is the volume of the rod outer segment in liters, such that the product of b with Jd F, in pA, yields the desired units (μMs-1). The quantity eT is the total Ca2+-buffer concentration. All other equations in this model are as in the Nikonov et al. (1998) model.
The results of addition of a dynamic Ca2+ buffer are shown in Fig. 7A. The two fits (Fig. 3A vs. Fig. 7A) are not statistically significantly different (F4,11 = 1.063, P > 0.1), but the dynamic Ca2+ buffer produces a qualitatively better account of the peak responses and recovery dynamics.
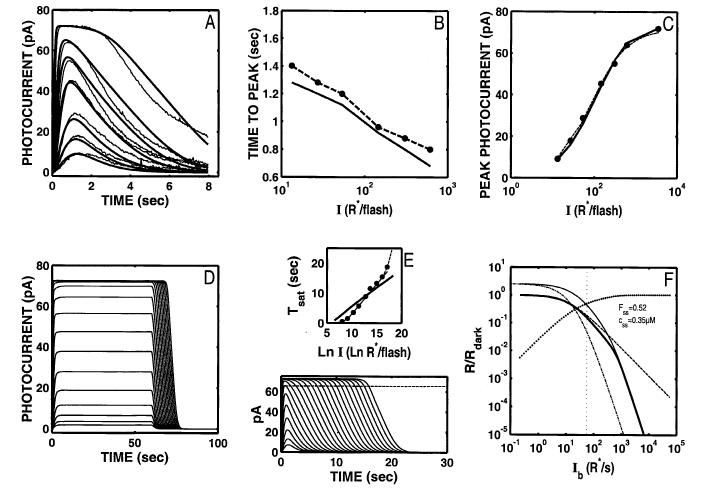
Fig. 7.
S/R suite after a dynamic Ca2+ buffer is added to the model, and the model is optimized to the DA Ref data with 11 free parameters. The model provides an excellent fit to the Ref data (A-C), but with these optimal parameters, fails to reproduce the signature features of the S/R suite: the step responses lack the “nose” at onset, and multiphasic response at offset (D); the Tsat function is too shallow (E), and the model still only generates a modest range of Weberian LA behavior (up to a cutoff Ib of 261 R* s-1; F). The coding for all the curves in F is as in Fig. 2F.
As reflected in the good fit to the Ref data, Rpk versus I and Tpk versus I match the Ref data very well. However, with these optimal parameters, the model step responses (Fig. 7D) and Tsat function (Fig. 7E) suffer from the same deficiencies as the original Nikonov model. The step responses do not exhibit the signature features seen in the Forti et al. (1989) data (Fig. 7D). In addition, since the optimal fit to the Ref data requires a rate-limiting front-end time constant τE* ≈ 1 s, the slope of the Tsat function is still too shallow, and there is no acceleration of the Tsat function at high intensities (Fig. 7E). The model’s light-adaptation behavior (Fig. 7F) is comparable to the original Nikonov model optimized to the Ref data (Fig. 3F). A modest range of Weber’s law LA of the incremental flash response can be accounted for (up to a cutoff Ib of 261 R* s-1). However, the range of adherence to Weber’s law is still ∼1.5 log units less than observed by Torre et al. (1990).
Finally, as with the original Nikonov et al. (1998) model, a good fit to the Ref data is achieved at the expense of some key parameters: nca = 2.85 (vs. ∼2; Gorczya et al., 1994), βdark = 0.136 (vs. 0.8-1.2 s-1; Nikonov et al., 1998), and Amax = 4.5 μMs-1 (vs. 30-100; Forti et al., 1989; Pugh & Lamb, 1990; Tamura et al., 1991; Lamb & Pugh, 1992; Ames, 1994; Nikonov et al., 1998). The ratio of bound to free Ca2+ is 26.8, compared with modern estimates on the order of 74-300 (Lagnado et al., 1992; Korenbrot, 1995; McCarthy et al., 1996).
Improvements conferred by dynamic Ca2+ buffering
Tsat function The desired 2 s/ln unit slope of the Tsat function is readily attained by setting τE* = 2 s, the results of which are shown in Fig. 8. The Tsat slope (Fig. 8E) now matches empirical results (Pepperberg et al., 1992, 1994; Murnick & Lamb, 1996). In contrast to the model with an instantaneous Ca2+ buffer, the addition of the dynamic Ca2+ buffer confers sufficient flexibility for the model to achieve a reasonable fit to the Ref data when τE* is held fixed at 2 s (compare Fig. 4A with Fig. 8A; F(1,9) = 8.897, 0.01 < P < 0.025). In addition, the model step responses now begin to have the “nose” and decay at step onset observed empirically (compare Fig. 8D with Fig. 1D). Moreover, the range of LA flash sensitivity adhering approximately to Weber’s law is extended slightly ( ∼ 0.4 log units, out to a cutoff Ib of ∼ 531 R* s-1; compare Fig. 8F with Fig. 4F). However, this behavior is achieved with some parameters deviating from empirical estimates. For example, the optimal parameters for the model responses in Fig. 8A included nca = 3.8, a value ∼2 times the empirical value (Dizhoor et al., 1994; Gorczya et al., 1994), and βdark = 0.13 s-1, approximately ten times less than empirical estimates.
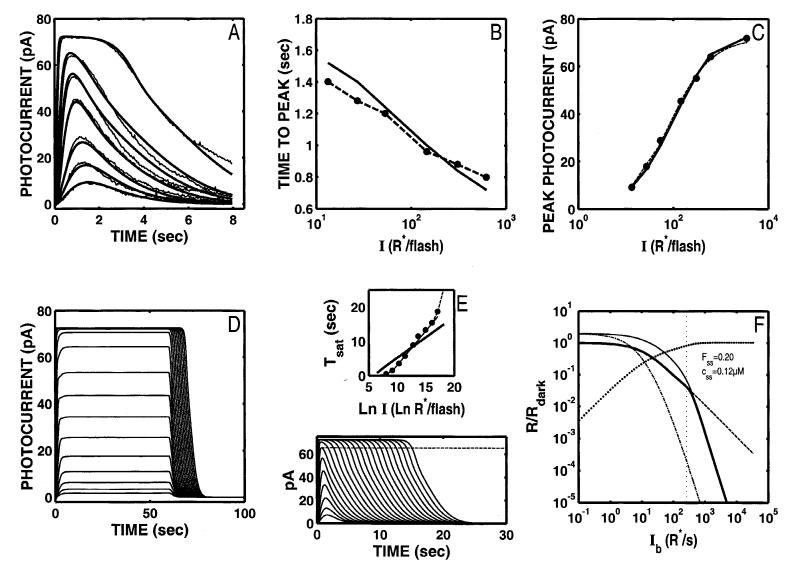
Fig. 8.
S/R suite after optimizing the model (nine free parameters) with a dynamic Ca2+ buffer while holding τE* = 2 s. With the dynamic Ca2+ buffer, the model has sufficient flexibility to maintain a good fit to the DA Ref data (A) even when the rate-limiting recovery stage in the “front-end” reactions is held to a 2-s time constant (E). With these parameters, the step responses begin to show a “nose” at step onset, but still do not have the multiphasic response profile at step offset (D). The model LA flash sensitivity (F) has a slightly extended I-range (∼0.4 log units, out to a cutoff Ib of ∼ 531 R* s-1) in comparison to the Nikonov et al. model with τE* fixed at 2 s (compare with Fig. 4F). The coding for all the curves in F is as in Fig. 2F.
LA flash sensitivity The model with the dynamic Ca2+ buffer has sufficient flexibility so that when parameters are set so that the I-range of Weberian LA is extended (cutoff Ib = 1339 R* s-1; Fig. 9F), the model is capable of achieving a reasonable fit to the data (relLSQerr = 0.00682; Fig. 9A). This is in striking contrast with the Nikonov et al. (1998) model (compare with Figs. 5A and 5B). In addition, the model step responses now have the desired “nose” at step onset (Fig. 9D), and the Tsat function has a ∼2 s/ln unit slope (Fig. 9E). Moreover, these features are attained with several parameters near their empirical estimates (Amax =121.4 μM s-1; τE = 2.17 s; ncg = 2.2; βdark = 0.920; fraction of bound to free Ca2+ = 184.1), while others remain outside empirical estimates (e.g. nca = 3.8; Fca = 0.057).
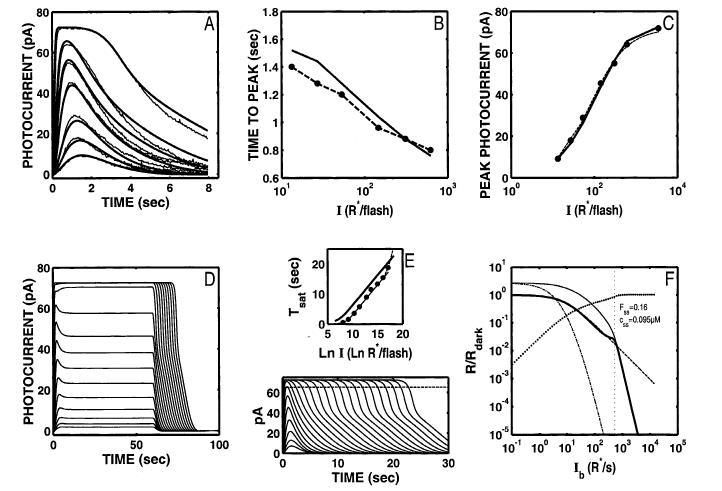
Fig. 9.
S/R suite for the model with a dynamic Ca2+ buffer after adjusting parameters such that an extended I-range of Weberian LA is generated. Nine free parameters were used to optimize, with Amax restricted to be between 60 and 150 μM s-1. The ratio of cdark/Kc was 3.0. The model generates a significantly larger range of LA gain control (cutoff Ib =1339 R* s-1; F), while maintaining a relatively good fit to the Ref DA data (A), and a Tsat function reflecting a 2-s dominant recovery time constant in the “front-end” reactions (E). In addition, the model step responses have the desired “nose” at step onset, though they still lack the multiphasic response at step-offset (D). The fit to the Ref data, though vastly superior than the comparable fit for the Nikonov et al. (1998) model (see Fig. 5A), is significantly poorer than the best the dynamic Ca2+-buffer model can achieve (see the fit when all 11 parameters are optimized, Fig. 7; F(2,10) = 10.22, 0.0005 < P < 0.001). The coding for all the curves in F is as in Fig. 2F.
Although the parameters that yield an extended range of Weber’s law LA are commensurate with a relatively good fit to the DA Ref data, the fit to the Ref data is significantly poorer than that attained when all 11 parameters are free to optimize (compare Fig. 7A vs. Fig. 9A; F(3,12) = 8.172, 0.001< P < 0.005).§§
Consequence of use of “modern” parameter values
As was done in the analysis of the original Nikonov et al. (1998) model, we evaluated the consequence of holding five key parameters at or near their current best empirical estimates. The same five parameters were restricted. When this was done, the best fit to the Ref data was significantly degraded (Fig. 10A) by a factor of 2.1 times the error from the optimal fit in Fig. 7A (relLSQerr = 0.00739 vs. 0.00224; F(3,11) = 8.422, 0.001 < P < 0.005). Moreover, with the parameters yielding a best fit under these constraints, the signature features in the rest of the suite of responses do not match empirical features (Figs. 10D-10F). The step responses no longer exhibit the “nose” at step onset. As in all other simulations shown, the model cannot generate the fast and slow phases at step offset (Fig. 10D). The Tsat function has too shallow of a slope because the optimal rate-limiting decay time constant under these conditions is again ∼ 1 s (Fig. 10E). Finally, the LA flash responses now fail to adhere to Weber’s law over any significant range (Fig. 10F; cutoff Ib = 56 R*/s).
Fig. 10.
S/R suite after adjusting after optimizing the model with a dynamic Ca2+ buffer while holding five key parameters at or near their modern empirical values: βdark = 0.8 to 1.2, Kc = 0.2, nca = 2, ncg = 2, and Fca = 0.18. Seven other parameters were optimized. The best fit to the Ref data is significantly degraded (Fig. 10A) by a factor of 2.1 times the error from the optimal fit in Fig. 7A (relLSQerr = 0.00739 vs. 0.00224; F(3,11) = 8.422, 0.001 < P < 0.005). Moreover, with the parameters yielding a best fit under these constraints, the signature features in the rest of the suite of responses do not match empirical features (D-F). The step responses no longer exhibit the “nose” at step onset. As in all other simulations shown, the model cannot generate the fast and slow phases at step offset (D). The Tsat function (E) has too shallow of a slope because the optimal rate-limiting decay time constant under these conditions is again ∼ 1 s. Finally, the LA flash responses now fail to adhere to Weber’s law over a significant range (cutoff Ib = 56 R* s-1; F). The coding for all the curves in F is as in Fig. 2F.
Discussion
The results of the analyses showed that when key activation, inactivation, and feedback parameters are permitted relatively broad optimization limits, a simple model of phototransduction (Nikonov et al., 1998) can produce a reasonable quantitative account of the reference voltage-clamped flash responses (from dim-flash to fully saturated responses) using a single set of parameters. However, in this case, the optimal model fit is achieved when some key parameters are permitted to deviate (by as much as an order of magnitude) from empirical estimates. When five key parameters are constrained to their empirical estimates, the match to the Ref data is degraded irrevocably (Fig. 6A).
More importantly, even with a set of parameters that yield a good fit to the Ref data, the Nikonov et al. (1998) model cannot reproduce a suite of signature qualitative features of DA and LA responses (Figs. 3B-3F). First, the fit to the Ref flash series does not extend to supersaturating flash intensities; increases in intensity after saturation is reached do not cause saturation period to increase at the empirically observed rate (2 s/ln unit; Fig. 3E). To generate a 2 s/ln unit Tsat slope, (Fig. 4E), at least one of the “front-end” cascade reactions must be set such that the rate-limiting time constant is ∼2 s. But in this case, a fit to the Ref data can no longer be achieved (Fig. 4A). Second, the model cannot simulate a Tsat function with the acceleration observed at high intensities (compare Fig. 1E with Figs. 2E-6E; Pepperberg et al., 1992). Third, despite the fit to the Ref data (Fig. 3A), increasing the stimulus duration to simulate a step response (Fig. 3D) will not produce the signature features observed at the onset and offset of 60-s light steps (compare with Fig. 1D; Forti et al., 1989; Fain et al., 1989).
Finally, the peak amplitude of the LA incremental flash response does not adhere to Weber’s law for more than ∼1 log units unless the Ca2+ cooperativity at cyclase is high (nca = 4), and the ratio of cdark/Kc is relatively large. However, the extended range of light adaptation is achieved at the expense of any reasonable fit to the Ref flash responses (Fig. 5A). Moreover, the LA behavior requires some important parameters to deviate severely from empirical estimates (e.g. βdark = 0.1 s-1, Amax > 400 μ M s-1).
Addition of a dynamic Ca2+ buffer: A working model
Conjoint account of all these features clearly requires more flexibility than the Nikonov et al. (1998) model structure can provide, implying the need for additional mechanisms. One such mechanism was added—replacement of an instantaneous Ca2+ buffer with a dynamic one. With the dynamic Ca2+ buffer, the model was able to account for a broader range of responses. It should be noted that there are some data suggesting that Ca2+ buffers are rapidly equilibrating in relation to the time scale of the rod photoresponse (e.g. McNaughton et al., 1986; Lagnado et al., 1992; McCarthy et al., 1996), and hence the choice to introduce a dynamic Ca2+ buffer into the model warrants some discussion.
An instantaneous Ca2+-buffer model is inadequate
The Ca2+ buffering in the Nikonov et al. (1998) model represents a modern implementation of the experimental evidence favoring rapid Ca2+ buffering. Nevertheless, the present analyses show that, within this sort of model structure, the rapid (instantaneous) Ca2+ buffer in the Nikonov et al. (1998) model is inadequate to account for the broad range of data analyzed. The limitations imposed by instantaneous Ca2+ buffering are not necessarily evident in any given response to a limited set of stimulus conditions. They become evident when one attempts to account for a broader set of responses. Two striking improvements after inclusion of a dynamic Ca2+ buffer are (1) that the model is now able to reproduce a Tsat function with a slope of 2 s/ln unit while maintaining a reasonable fit to the Ref data, and (2) the model is now able to capture some key qualitative features of the LA behavior of rods— namely, the behavior at step onsets, and an extended range of LA gain control—while maintaining a reasonably good fit to the Ref data. By contrast, the Nikonov et al. model cannot simultaneously account for the Ref flash data and the Tsat data of Pepperberg (compare Fig. 4 and 8). In addition, no parameters for the Nikonov et al. model were found that supported both an extended range of Weberian LA and a reasonable account of the Ref flash data (compare Fig. 5 and 9).
The Ca2+ “story” is complex
There are some complexities in the available direct measures of Ca2+ that imply that the full Ca2+ “story” is not yet in. For example, one shortcoming of the direct measurements of Ca2+ dynamics is that they rely on a space average of the Ca2+ response (e.g. aequorin studies like Lagnado et al., 1992; Fura-2 measures, as in McCarthy et al., 1994, 1996; Younger et al., 1996; Indo-dextran measures of Gray-Keller & Detwiler, 1994). Hence, the “true” Ca2+ behavior may be more complex than has been revealed by even the best of the direct methods of measurement.
In addition, two recent studies of Ca2+ dynamics (and concomitant photocurrent recordings) found qualitatively similar Ca2+ behavior, but ascribed the behavior to different mechanisms. Gray-Keller and Detwiler (1994) found that the kinetics of Ca2+ decline during steady illumination followed a time course best described by a sum of two weighted exponentials with “fast” and “slow” components having time constants ≈ 0.6 s and 5.5 s, respectively. Gray-Keller and Detwiler interpreted the components as arising from fast (and low-affinity) and slow (and high-affinity) buffers that are present in approximately equal amounts. The slow time course of Ca2+ decline at high light levels may thus be due to the fast sites having unloaded all their Ca2+, with only the slow buffers remaining.
Using somewhat different methods, McCarthy et al. (1996) obtained qualitatively similar results, but summarized the Ca2+ kinetics by a sum of three weighted exponentials with time constants 0.25 s, 1.35 s, and 6.75 s. After a number of experimental tests, McCarthy et al. (1996) concluded that the data were consistent with Ca2+ equilibrating rapidly (i.e. quasi-instantaneous Ca2+ buffering). The complex Ca2+ dynamics were interpreted as reflecting differential access to the Ca2+ signal due to nonuniformities in its localization and/or mobility within the cell.
Finally, it is worth noting that some of the Ca2+ data dramatically illustrate gaps in our understanding of the full Ca2+ “story.” For example, Gray-Keller and Detwiler (1994) presented data showing that, following a subsaturating flash, the Ca2+ signal outlives the photocurrent response (fully recovered by ∼6 s) by as much as 15 s. Moreover, the dynamic changes in Ca2+ during a step response did not track the photocurrent during the step response. These data cannot be accounted for by any model to date.
Hence, in light of potential limitations of the available Ca2+ data, and divergent interpretations of these data in the literature, a working model structure was adopted that incorporated noninstantaneous Ca2+ buffering, similar to some earlier models of Ca2+ buffering (Forti et al., 1989; Tamura et al., 1991). The overall improved behavior of the model with a dynamic Ca2+ buffer suggests that it is an important mechanism to include in a working model of phototransduction, and that despite the slow kinetics of amphibian rods, Ca2+ buffering cannot be simulated as an instantaneous process.
Need for other mechanisms in the model
Despite the increased generality conferred by addition of the dynamic Ca2+ buffer, the analyses imply that a broad account of the behavior of rod DA and LA responses will require further elaborations of the model.
Accounting for slow phase at step offset, and acceleration of Tsat at high intensities
The slow phase at the offset of long-duration steps reflects some slow decay process that is not readily apparent in the dynamics of dim-flash responses, or even in response to modestly saturating flashes. Forti et al. (1989) were able to simulate this behavior by inclusion of a slow back reaction from inactive rhodopsin (R) to its activated state (R*). A similar result is predictable by assuming that deactivated rhodopsin and/or the raw apoprotein continues to activate the cascade with some slow decay rate on the order of 10-30 s (Cornwall & Fain, 1994; Cornwall et al., 1995; Matthews et al., 1996; Sampath et al., 1998). This same slow process may account for the acceleration of the Tsat function at high intensities (Pepperberg et al., 1992).
Accounting for the full range of LA
In general, the model LA flash-sensitivity results (see cutoff Ib in Figs. 3F-9F) first begin to deviate from a Weber’s law slope of -1 when the background intensity drives the model to within 15-30% of saturation. Above the cutoff Ib, the sensitivity decline begins to be dominated by the channel saturation, and sensitivity falls steeply with a slope determined by the cGMP Hill coefficient of the channel (Matthews et al., 1990).
The range over which the models can adhere to Weber’s law is influenced strongly by Kc, and nca, as illustrated in Figs. 5 and 9. But these analyses illustrated that extending the Weberian LA behavior, in the case of the Nikonov et al. (1998) model, can only be achieved with unrealistic parameters, and sacrifices the fit to the Ref data. The model with a dynamic Ca2+ buffer was able to generate an extended range of Weberian LA with a qualitatively reasonable fit to the Ref data, but the fit was inferior to the optimal fit with all 11 parameters free. In addition, the form of the LA flash-sensitivity function did not adhere strictly to the Weber-Fechner relation over the full I-range (Fig. 9F). This implies that a more comprehensive model will require additional gain control mechanisms.
There are at least three other Ca2+-dependent feedback mechanisms that have not been implemented in the present analyses, but which may provide the model with the needed flexibility to provide a better account of the full range of empirical response profiles, including LA behavior. A number of studies suggest that there is Ca2+-dependent modulation of R* lifetime. This modulation is thought to be mediated by an interaction between the Ca2+-binding protein recoverin (Rec) and the enzyme rhodopsin kinase (RK), which is responsible for phosphorylation (and ultimate quenching by arrestin) of R* (Kawamura, 1993; Klenchin et al., 1995; Chen et al., 1995). The polarity of the modulation is such that a decrease in internal Ca2+ (caused by light) releases RK from inhibition by Rec, and leads to a speedup in the shutoff of R*. In addition, there is evidence that Ca2+ modulates reactions at least two other loci. Changes in internal Ca2+ modulate gain very early in the cascade without modifying the apparent time constant of R* inactivation (Lagnado & Baylor, 1994). Finally, there appears to be Ca2+-dependent modulation of the affinity of the light-activated membrane cation channels for cGMP (Hsu & Molday, 1993; Rebrik & Korenbrot, 1998; Hackos & Korenbrot, 1997). Addition of one or more of these feedback mechanisms, having different sensitivities to internal Ca2+ levels and different dynamics (Koutalos et al., 1995b; Calvert et al., 1998), are likely to be crucial to account for the full range of observed LA behavior.
The effects of incorporating cGMP buffering have not been examined in the present study. Prior studies approximate the cGMP-buffering power of the amphibian rod to be 2 (e.g. Lamb & Pugh, 1992). There is evidence that cGMP buffering may be significantly more powerful (Korenbrot personal communication). The effect of cGMP buffering would be to counteract the effect of light, and hence provide another potentially significant LA mechanism.
The models implemented in this study (as in Nikonov et al., 1998) did not include explicit limitations on total number of rhodopsin, transducin or PDE molecules in the cell. This approach may be adequate for low to moderate light levels. However, the cGMP cascade has a large amount of amplification between R activation and PDE activation. The present understanding of the stoichiometry in salamander rods is 4 × 109 R, 4 × 108 T and 6 × 107 PDE molecules (Pugh & Lamb, 1990, 1993). Estimates of the number of PDE molecules that are activated per R* varies over more than an order of magnitude, from 200-400 s-1 (Gray-Keller et al., 1990) to 1000 s-1 (Vuong et al., 1984; Uhl et al., 1990) to as high as 7000 s-1 (Lamb & Pugh, 1992; Pugh & Lamb, 1993). These values lead to a loose estimate for the number of R* s-1 that will saturate the pool of PDE ranging from 8600 R* s-1 to 300,000 s-1 (assuming a well-mixed system).
Finally, the entire activation sequence has been modeled as a two-stage linear sequence of first-order reactions. However, analyses of the activation dynamics of photoresponses (Penn & Hagins, 1972; Baylor et al., 1974; Cobbs & Pugh, 1987; Hamer & Tyler, 1995) suggest that at least four, and as many as eight or more, stages underlie photocurrent activation. The effect of incorporating a more complete activation scheme remains to be evaluated.
The present study demonstrates the importance of combining quantitative optimization with qualitative evaluation in developing a robust working model of a system as complex as the phototransduction cascade. It also illustrates the limitations of modeling restricted sets of data.
Acknowledgments
The author wishes to thank Juan I. Korenbrot for supplying the flash response data used in the present analyses, and to acknowledge the helpful discussions with Daniel Tranchina, Christopher.W. Tyler, Norberto M. Grzywacz, and Juan I. Korenbrot. The author aslo wishes to thank Spero Nicholas for his expert programming. The research was supported by NEI Grant # EY11513-03, and by The Smith-Kettlewell Eye Research Foundation Grant # 2080-02-00.
Footnotes
Torre et al. (1990) reported an I1/2 of 40 R* s-1. However, using this value, the Weber-Fechner relation does not fit the data shown in their Fig. 4. An I1/2 of 100 R*s-1 fits the data.
The cutoff Ib was found by calculating a slope for the model curve over a 3-point sliding window of Ib values. The window was shifted rightward in 1/4-octave increments, and the cutoff Ib was defined as the highest Ib in the first 3-point data window having a slope at least 10% less than -1 (i.e. ≥ 10% steeper falloff than -1).
The fit to the Ref data is statistically significantly better than that provided by the parameters used in the Nikonov et al. (1998) study [F(6,7) = 7.323, p < 0.01], although this is not surprising since the latter parameters were not optimal for the Ref data used in the present study. Note, for this and all subsequent F tests reported, one free parameter (not shown in Tables 2 or 3) was added to the degrees of freedom (df) used in the calculation of F for each optimization. This additional df was needed to account for the normalization of each flash response used in the calculation of relLSQerr (see Methods and Procedures).
The Torre et al. (1990) flash-sensitivity data adhere to the Weber-Fechner relation out to 105 R*/s. We can use the Torre et al. data to “predict” an equivalent upper limit for Weberian behavior for the model flash-sensitivity functions. Assuming that the salamander rods recorded using the perforated patch, whole-cell technique are ∼10 times more sensitive than the newt rods recorded with suction electrodes, the Torre et al. data “predict” an upper limit for cutoff Ib of ∼104 R*/s.
The fit with τE* fixed at 2 s (Fig. 4A) is significantly worse than the fit after full optimization (Fig. 3A). This was established using a modified F test in which it was assumed that two free parameters had been added to the optimization shown in Fig. 3A, but with no concomitant decrease in error. In reality, adding two free parameters to the optimization would have yielded an error less than or equal to the error obtained in the actual optimization, but never a greater error. Hence, leaving the error unchanged and calculating the F value is a worst-case test of the significance. For this limiting case, the F test yielded a highly significant result [F(1,9) = 11.168, P < 0.01].
A common value reported for the full range of cyclase activity modulation by Ca2+ is 10 (e.g. Dawis et al., 1988; Calvert et al., 1998). The range of 2-35 was derived using ranges of 0.2-0.6 μM for , 0.1-0.2 μM for Kc, 0.02-0.05 for c0, and a value of 2 for nca. The upper estimate for the modulation range depends strongly on the actual value of nca. If a value of 2.5 is used for nca, the estimate for the empirical cyclase modulation range increases to ∼2-87; for nca = 3 (Ames et al., 1999), the range is ∼2-215.
Note that the optimal fit shown in Fig. 3 was achieved with two of the above parameters held at their “modern” values—nca = 2 and ncg = 2. A slightly better, but statistically indistinguishable, fit to the Ref data was achieved when these parameters were permitted to be free. In that case, the optimal values for nca and ncg were 3.21 and 1.52, respectively. However, in both cases, several other key parameters were forced to deviate from their modern estimates to achieve the fit. For example, optimal βd was =< 0.2 s-1, about 3-5 times lower than empirical estimates.
A modified F test was used. It was assumed that one free parameter had been added to the optimization shown in Fig. 7A, but with no concomitant decrease in error. This additional free parameter could only have yielded an error less than or equal to the error obtained in the actual optimization, but not a greater error. Hence, leaving the error unchanged and calculating the F value is a worst-case test of the significance. For this limiting case, the F test yielded a highly significant result [F(3,12) = 8.172, 0.001 < P < 0.005].
References
- Ames A., III Steady state feedback in mammalian phototransduction illustrated by a nomogram. Vision Research. 1994;34:821–827. doi: 10.1016/0042-6989(94)90219-4. [DOI] [PubMed] [Google Scholar]
- Ames JB, Dizhoor AM, Palczewski K, Stryer L. Three-dimensional structure of guanylyl cyclase activating protein-2, a calcium-sensitive modulator of photoreceptor guanylyl cyclases. Journal of Biological Chemistry. 1999;274:19329–19337. doi: 10.1074/jbc.274.27.19329. [DOI] [PubMed] [Google Scholar]
- Baylor DA, Hodgkin AL, Lamb TD. The electrical response of turtle cones to flashes and steps of light. Journal of Physiology. 1974;242:685–727. doi: 10.1113/jphysiol.1974.sp010731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burkhardt DA. Light adaptation and photopigment bleaching in cone photoreceptors in situ in the retina of the turtle. Journal of Neuroscience. 1994;14:1091–1105. doi: 10.1523/JNEUROSCI.14-03-01091.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calvert PD, Ho TW, LeFebvre YM, Arshavsky VY. Onset of feedback reactions underlying vertebrate rod photoreceptor light adaptation. Journal of General Physiology. 1998;111:39–51. doi: 10.1085/jgp.111.1.39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cameron DA, Pugh EN., Jr. The magnitude, time course and spatial distribution of current induced in salamander rods by cyclic guanine nucleotides. Journal of Physiology. 1990;430:419–439. doi: 10.1113/jphysiol.1990.sp018299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen CK, Inglese J, Lefkowitz RJ, Hurley JB. Ca(2+)-dependent interaction of recoverin with rhodopsin kinase. Journal of Biological Chemistry. 1995;270:18060–18066. doi: 10.1074/jbc.270.30.18060. [DOI] [PubMed] [Google Scholar]
- Cobbs WH, Pugh EN., Jr. Kinetics and components of the flash photocurrent of isolated retinal rods of the larval salamander, Ambystoma tigrinum. Journal of Physiology. 1987;394:529–572. doi: 10.1113/jphysiol.1987.sp016884. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cornwall MC, Fain GL. Bleached pigment activates transduction in isolated rods of the salamander retina. Journal of Physiology. 1994;480:261–279. doi: 10.1113/jphysiol.1994.sp020358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cornwall MC, Matthews HR, Crouch RK, Fain GL. Bleached pigment activates transduction in salamander cones. Journal of General Physiology. 1995;106:543–557. doi: 10.1085/jgp.106.3.543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dawis S, Graeff RM, Heyman RA, Walseth TF, Goldberg ND. Regulation of cyclic GMP metabolism in toad photoreceptors. Journal of Biological Chemistry. 1988;263:8771–8785. [PubMed] [Google Scholar]
- Dizhoor AM, Lowe D, Olshevskaya EV, Laura RP, Hurley JB. The human photoreceptor membrane guanylate cyclase, RetGC, is present in outer segments and is regulated by calcium and a soluble activator. Neuron. 1994;12:1345–1352. doi: 10.1016/0896-6273(94)90449-9. [DOI] [PubMed] [Google Scholar]
- Fain GL, Matthews HR, Cornwall MC. Dark adaptation in vertebrate photoreceptors. Trends in Neuroscience. 1996;19:502–507. doi: 10.1016/S0166-2236(96)10056-4. [DOI] [PubMed] [Google Scholar]
- Fain GL, Lamb RD, Matthews HR, Murphy LW. Cytoplasmic calcium as the messenger for light adaptation in salamander rods. Journal of Physiology. 1989;416:215–243. doi: 10.1113/jphysiol.1989.sp017757. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fesenko EE, Kolesnikov SS, Lyubarsky AL. Induction by cyclic GMP of cationic conductance in plasma membrane of retinal rod outer segment. Nature. 1985;313:310–313. doi: 10.1038/313310a0. [DOI] [PubMed] [Google Scholar]
- Forti S, Menini A, Rispoli G, Torre V. Kinetics of photo-transduction in retinal rods of the newt, Triturus cristatus. Journal of Physiology. 1989;419:265–295. doi: 10.1113/jphysiol.1989.sp017873. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gorczya WA, Gray-Keller MP, Detwiler PB, Palczewski K. Purification and physiological evaluation of a guanylate cyclase activating protein from retinal rods. Proceedings of the National Academy of Sciences of the U.S.A.; 1994. pp. 4014–4108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gray-Keller MP, Detwiler PB. The calcium feedback signal in the phototransduction cascade of vertebrate rods. Neuron. 1994;13:849–861. doi: 10.1016/0896-6273(94)90251-8. [DOI] [PubMed] [Google Scholar]
- Gray-Keller MP, Biernbaum MS, Bownds MD. Transducin activation in electropermeabilized frog rod outer segments is highly amplified, and a portion equivalent to phosphodiesterase remains membrane bound. Journal of Biological Chemistry. 1990;265:15323–15332. [PubMed] [Google Scholar]
- Hackos DH, Korenbrot JI. Calcium modulation of ligand affinity in the cyclic GMP-gated ion channels of cone photoreceptors. Journal of General Physiology. 1997;110:515–528. doi: 10.1085/jgp.110.5.515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamer RD, Tyler CW. Does the saturation period of vertebrate photocurrent flash response reflect only rhodopsin lifetimes? Investigative Ophthalmology and Visual Science. 1996;37:811. [Google Scholar]
- Hamer RD, Tyler CW. Phototransduction: Modeling the primate cone flash response. Visual Neuroscience. 1995;12:1063–1082. doi: 10.1017/s0952523800006726. [DOI] [PubMed] [Google Scholar]
- Hodgkin AL, Nunn BJ. Control of light-sensitive current in salamander rods. Journal of Physiology. 1988;403:439–472. doi: 10.1113/jphysiol.1988.sp017258. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hsu YT, Molday RS. Modulation of the cGMP-gated channel of rod photoreceptor cells by calmodulin. Nature. 1993;361:76–79. doi: 10.1038/361076a0. [DOI] [PubMed] [Google Scholar]
- Kawamura S. Rhodopsin phosphorylation as a mechanism of cyclic GMP phosphodiesterase regulation by S-modulin. Nature. 1993;362:855–857. doi: 10.1038/362855a0. [DOI] [PubMed] [Google Scholar]
- Klenchin VA, Calvert PD, Bownds MD. Inhibition of rhodopsin kinase by recovering: Further evidence for a negative feedback system in phototransduction. Journal of Biological Chemistry. 1995;270:16147–16152. doi: 10.1074/jbc.270.27.16147. [DOI] [PubMed] [Google Scholar]
- Koch KW, Stryer L. Highly cooperative feedback control of retinal rod guanylate cyclase by calcium ions. Nature. 1988;344:64–66. doi: 10.1038/334064a0. [DOI] [PubMed] [Google Scholar]
- Korenbrot JI, Miller DL. Ca2+ flux in retinal rod and cone outer segments: Differences in Ca2+ selectivity of the cGMP-gated ion channels and Ca2+ clearance rates. Cell Calcium. 1989;18:285–300. doi: 10.1016/0143-4160(95)90025-x. [DOI] [PubMed] [Google Scholar]
- Korenbrot JI. Cytoplasmic free calcium concentration in dark-adapted retinal rod outer segments. Vision Research. 1995;29:939–948. doi: 10.1016/0042-6989(89)90108-9. [DOI] [PubMed] [Google Scholar]
- Koutalos Y, Nakatani K, Yau K-W. The cGMP-phosphodiesterase and its contribution to sensitivity regulation in retinal rods. Journal of General Physiology. 1995a;106:891–921. doi: 10.1085/jgp.106.5.891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koutalos Y, Nakatani K, Tamura T, Yau K-W. Characterization of guanylate cyclase activity in single retinal rod outer segments. Journal of General Physiology. 1995b;106:863–890. doi: 10.1085/jgp.106.5.863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lagnado L, Baylor DA. Calcium controls light-triggered formation of catalytically active rhodopsin. Nature. 1994;367:273–277. doi: 10.1038/367273a0. [DOI] [PubMed] [Google Scholar]
- Lagnado L, Cervetto L, McNaughton PA. Calcium homeostasis in the outer segments of retinal rods from the tiger salamander. Journal of Physiology. 1992;455:111–142. doi: 10.1113/jphysiol.1992.sp019293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lamb TD, Pugh EN., Jr. A quantitative account of the activation steps involved in phototransduction in amphibian photoreceptors. Journal of Physiology. 1992;449:719–758. doi: 10.1113/jphysiol.1992.sp019111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lyubarsky A, Nikonov S, Pugh EN., Jr. Kinetics of inactivation of the rod phototransduction cascade with constant Journal of General Physiology. 1996;107:19–34. doi: 10.1085/jgp.107.1.19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matthews HR, Fain GL, Murphy RLW, Lamb TD. Light adaptation in cone photoreceptors of the salamander: A role for cytoplasmic calcium. Journal of Physiology. 1990;420:447–479. doi: 10.1113/jphysiol.1990.sp017922. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matthews HR, Cornwall MC, Fain GL. Persistent activation of transducin by bleached rhodopsin in salamander rods. Journal of General Physiology. 1996;108:557–563. doi: 10.1085/jgp.108.6.557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matthews HR, Murphy RLW, Fain GL, Lamb TD. Photoreceptor light adaptation is mediated by cytoplasmic calcium concentration. Nature. 1988;334:67–69. doi: 10.1038/334067a0. [DOI] [PubMed] [Google Scholar]
- McCarthy ST, Owen WG. Highly cooperative, calcium-dependent inhibition of PDE activation in intact rods of the bullfrog. Investigative Ophthalmology and Visual Science. 1994;35:1486. [Google Scholar]
- McCarthy ST, Younger JP, Owen WG. Free calcium concentrations in bullfrog rods determined in the presence of multiple forms of Fura-2. Biophysical Journal. 1994;67:2076–2089. doi: 10.1016/S0006-3495(94)80691-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCarthy ST, Younger JP, Owen WG. Dynamic, spatially nonuniform calcium regulation in frog rods exposed to light. Journal of Neurophysiology. 1996;76:1991–2004. doi: 10.1152/jn.1996.76.3.1991. [DOI] [PubMed] [Google Scholar]
- McNaughton PA, Cervetto L, Nunn BJ. Measurement of the intracellular free calcium concentration in salamander rods. Nature. 1986;322:261–263. doi: 10.1038/322261a0. [DOI] [PubMed] [Google Scholar]
- Menini A, Rispoli G, Torre V. The ionic selectivity of the light-sensitive current in isolated rods of the tiger salamander. Journal of Physiology. 1988;402:279–300. doi: 10.1113/jphysiol.1988.sp017204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller JL, Korenbrot JI. In retinal cones, membrane depolarization in darkness activates the cGMP-dependent conductance. A model of Ca homeostasis and the regulation of guanylate cyclase. Journal of General Physiology. 1993;101:933–961. doi: 10.1085/jgp.101.6.933. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller JL, Korenbrot JI. Differences in calcium homeostasis between retinal rod and cone photoreceptors revealed by the effects of voltage on the cGMP-gated conductance in intact cells. Journal of General Physiology. 1994;104:909–940. doi: 10.1085/jgp.104.5.909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murnick JG, Lamb TD. Kinetics of desensitization induced by saturating flashes in toad and salamander rods. Journal of Physiology. 1996;495:1–13. doi: 10.1113/jphysiol.1996.sp021569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nakatani K, Tamura T, Yau K-W. Light adaptation in retinal rods of the rabbit and two other non-primate mammals. Journal of General Physiology. 1991;97:413–435. doi: 10.1085/jgp.97.3.413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nakatani K, Yau K-W. Calcium and light adaptation in retinal rods and cones. Nature. 1988;334:69–71. doi: 10.1038/334069a0. [DOI] [PubMed] [Google Scholar]
- Nikonov S, Engheta N, Pugh EN., Jr. Kinetics of recovery of the dark-adapted salamander rod photoresponse. Journal of General Physiology. 1998;111:7–37. doi: 10.1085/jgp.111.1.7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Penn RD, Hagins WA. Kinetics of the photcurrent of retinal rods. Biophysical Journal. 1972;12:1073–1094. doi: 10.1016/S0006-3495(72)86145-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pepe IM, Panfoli I, Cugnoli C. Guanylate cyclase in rod outer segments of the toad retina. Effect of light and Ca2+ FEBS Letters. 1986;203:73–76. doi: 10.1016/0014-5793(86)81439-9. [DOI] [PubMed] [Google Scholar]
- Pepperberg DR, Cornwall MC, Kahlert M, Hofmann KP, Jin J, Jones GL, Ripps H. Light-dependent delay in the falling phase of the retinal rod photoresponse. Visual Neuroscience. 1992;8:9–18. doi: 10.1017/s0952523800006441. [DOI] [PubMed] [Google Scholar]
- Pepperberg DR, Jin J, Jones GJ. Modulation of transduction gain in light adaptation of retinal rods. Visual Neuroscience. 1994;11:53–62. doi: 10.1017/s095252380001110x. [DOI] [PubMed] [Google Scholar]
- Pugh EN, Jr., Duda T, Sitaramayya Y, Sharma RK. Photoreceptor guanylate cyclases: A review. Bioscience Reports. 1997;17:429–473. doi: 10.1023/a:1027365520442. [DOI] [PubMed] [Google Scholar]
- Pugh EN, Jr., Lamb TD. Amplification and kinetics of the activation steps in phototransduction. Biochimica et Biophysica Acta. 1993;1141:111–149. doi: 10.1016/0005-2728(93)90038-h. [DOI] [PubMed] [Google Scholar]
- Pugh EN, Jr., Lamb TD. Cyclic GMP and calcium: The internal messengers of excitation and adaptation in vertebrate photoreceptors. Vision Research. 1990;30:1923–1948. doi: 10.1016/0042-6989(90)90013-b. [DOI] [PubMed] [Google Scholar]
- Pugh EN, Jr., Nikonov S, Lamb TD. Molecular mechanisms of vertebrate photoreceptor light adaptation. Current Opinion in Neurobiology. 1999;9:410–418. doi: 10.1016/S0959-4388(99)80062-2. [DOI] [PubMed] [Google Scholar]
- Ratto G, Payne R, Owen WG, Tsien RY. The concentration of cytosolic free calcium in vertebrate rod outer segments measured with fura-2. Journal of Neuroscience. 1988;8:3240–3246. doi: 10.1523/JNEUROSCI.08-09-03240.1988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rebrik TI, Korenbrot JI. In intact cone photoreceptors, a Ca2+-dependent, diffusible factor modulates the cGMP-gated ion channels differently than in rods. Journal of General Physiology. 1998;112:537–548. doi: 10.1085/jgp.112.5.537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rieke F, Baylor TD. Molecular origin of continuous dark noise in rod photoreceptors. Biophysical Journal. 1996;71:2553–2572. doi: 10.1016/S0006-3495(96)79448-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sagoo MS, Lagnado L. G-protein deactivation is rate-limiting for shut-off of the phototransduction cascade. Nature. 1997;389:392–395. doi: 10.1038/38750. [DOI] [PubMed] [Google Scholar]
- Sampath AP, Matthews HR, Cornwall MC, Fain GL. Bleached pigment produces a maintained decrease in outer segment Ca2+ in salamander rods. Journal of General Physiology. 1998;111:53–64. doi: 10.1085/jgp.111.1.53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schnapf JL, Nunn BJ, Meister M, Baylor DA. Visual transduction in cones of the monkey, Macaca fascicularis. Journal of Physiology. 1990;427:681–713. doi: 10.1113/jphysiol.1990.sp018193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tamura T, Nakatani K, Yau K-W. Light adaptation in cat retinal rods. Science. 1989;245:755–758. doi: 10.1126/science.2772634. [DOI] [PubMed] [Google Scholar]
- Tamura T, Nakatani K, Yau K-W. Calcium feedback and sensitivity regulation in primate rods. Journal of General Physiology. 1991;98:95–130. doi: 10.1085/jgp.98.1.95. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Torre V, Forti S, Menini A, Campani M.Model of photo-transduction in retinal rods Cold Spring Harbor Symposium on Quantitative Biology 1990LV563–573.Cold Spring Harbor Laboratory Press; New York: The Brain [DOI] [PubMed] [Google Scholar]
- Tranchina D, Sneyd J, Cadenas ID. Light adaptation in turtle cones. Testing and analysis of a model for phototransduction. Biophysical Journal. 1991;60:217–237. doi: 10.1016/S0006-3495(91)82045-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uhl R, Wagner R, Ryba N. Watching G proteins at work. Trends in Neuroscience. 1990;13:64–70. doi: 10.1016/0166-2236(90)90070-q. [DOI] [PubMed] [Google Scholar]
- Vuong RM, Chabre M, Stryer L. Millisecond activation of transducin in the cyclic nucleotide cascade of vision. Nature. 1984;311:659–661. doi: 10.1038/311659a0. [DOI] [PubMed] [Google Scholar]
- Watanabe S-I, Matthews G. Dose-response relation of cyclic-GMP-activated channels in retinal rod photoreceptors. Neuroscience Research (Suppl.) 1989;10:S1–S8. doi: 10.1016/0921-8696(89)90003-0. [DOI] [PubMed] [Google Scholar]
- Yau K-W, Baylor DA. Cyclic GMP-activated conductance of retinal photoreceptor cells. Annual Review of Neuroscience. 1989;12:289–327. doi: 10.1146/annurev.ne.12.030189.001445. [DOI] [PubMed] [Google Scholar]
- Yau K-W, Nakatani K. Light-induced reduction of cytoplasmic free calcium in retinal rod outer segment. Nature. 1985;313:579–582. doi: 10.1038/313579a0. [DOI] [PubMed] [Google Scholar]
- Younger JP, McCarthy ST, Owen WG. Light-dependent control of calcium in intact rods of the bullfrog Rana catesbeiana. Journal of Neurophysiology. 1996;75:354–366. doi: 10.1152/jn.1996.75.1.354. [DOI] [PubMed] [Google Scholar]
- Zimmerman AL, Baylor DA. Cyclic GMP-sensitive conductance of retinal rods consists of aqueous pores. Nature. 1986;321:70–72. doi: 10.1038/321070a0. [DOI] [PubMed] [Google Scholar]