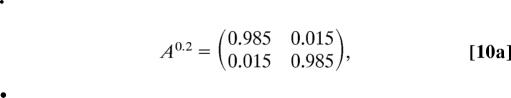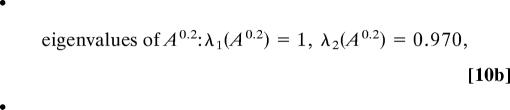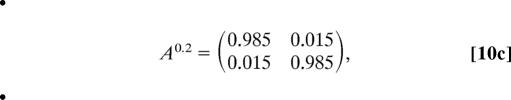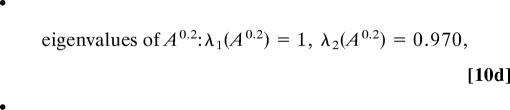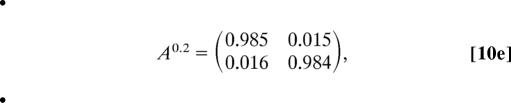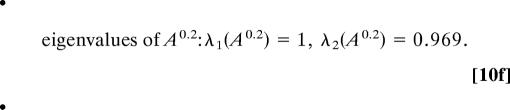Distinct metastable atmospheric regimes despite nearly Gaussian statistics: A paradigm model

Abstract

A controversial topic in the recent climate modeling literature is the fashion in which metastable low-frequency regimes in the atmosphere occur despite nearly Gaussian statistics for these planetary waves. Here a simple 57-mode paradigm model for such metastable atmospheric regime behavior is introduced and analyzed through hidden Markov model (HMM) analysis of the time series of suitable low-frequency planetary waves. The analysis of this paradigm model elucidates how statistically significant metastable regime transitions between blocked and zonal statistical states occur despite nearly Gaussian behavior in the associated probability distribution function and without a significant role for the low-order truncated nonlinear dynamics alone; turbulent backscatter onto the three-dimensional subspace of low-frequency modes is responsible for these effects. It also is demonstrated that suitable stochastic mode reduction strategies, which include both augmented cubic nonlinearity and multiplicative noise, are also capable of capturing the metastable low-frequency regime behavior through a single stochastic differential equation compared with the full turbulent chaotic 57-mode model. This feature is attractive for issues such as long-term weather predictability. Although there have been many applications of HMM in other sciences, this work presents a previously undescribed application of HMM analysis to atmospheric low-frequency variability and points the way for further applications including their use in extended range predictability.

Current evidence utilizing the ≈50-year observational record suggests that much of the low-frequency variability of the Northern Hemisphere midlatitude atmosphere is summarized through a few teleconnection patterns such as the North Atlantic Oscillation (NAO) and the Pacific/North American (PNA) pattern (1, 2). The structure of the low-frequency metastable regime transitions among these patterns is an issue of central importance for both enhanced long-range weather prediction and climate change projection (3, 4). Besides statistical analysis of the observational record, the main current research tools in understanding the above issue are comprehensive atmospheric general circulation models (AGCMs) (refs. 5–8 and references therein) and multilevel quasi-geostrophic models (9–12), which faithfully reproduce many features of the midlatitude low-frequency variability mentioned above.

The statistical observational record from nature necessarily yields a short time series (1, 2, 13), whereas the time series generated by the above numerical models can be extremely long (5–7, 12) or moderate in size (10, 11) according to the resources available; of course, longer time series yield the opportunity for more reliable statistical processing of time series. In this context, a controversy has emerged, which is the central focus of the present work: On the one hand, statistical processing of data is often reported as highly non-Gaussian in the probability distribution function (PDF) of the low-frequency planetary wave patterns with multiple extrema (1, 2, 13). On the other hand, the PDFs of the planetary waves in the numerical models with long integration (5–7, 12) are nearly Gaussian without any multiple extrema even after low-frequency time filtering (5, 6). Starting with the seminal work of Charney and DeVore (14), low-order truncated models have been utilized to predict low-frequency atmospheric regimes as largely dominated by chaotic nonlinear dynamics among the planetary waves (ref. 3 and references therein). Despite the above controversy, a large emphasis has been made on the nonlinear dynamic multimode PDF interpretation of the large-scale circulation (4).

In the present work, a paradigm model is utilized to elucidate and explain a number of scientific issues in the above controversy in an unambiguous fashion. The model used here is a simplified 57-mode model for the angular momentum of the atmosphere (15–19); it has the attractive feature that the low-order truncated model is exactly the 3D Charney–DeVore model without dissipation and forcing, and the low-frequency planetary wave behavior of the 57-mode model resides on the same 3D subspace, which consists of a mean flow and two topographic Rossby waves. The nonlinear statistical dynamics produced by turbulent backscatter on this low-frequency 3D subspace produces time series for long integrations, which are nearly Gaussian as in the AGCMs. Thus, the central issue in the above controversy is exhibited transparently in the above model. The long time series for the low-frequency variability variables are processed statistically here through a hidden Markov model (HMM) analysis; the HMM approach utilized here is a scientifically mature framework to objectively determine simultaneously both the PDFs and metastable regime transitions in a time series (20–24). In the last 30 years HMM analysis has been applied widely from speech recognition (20) to molecular dynamics (24), but this work presents a previously undescribed application of the HMM technique to problems in atmospheric science. Of course, there has been the recent use of other interesting statistical approaches to determine the PDFs of low-frequency variability (2, 6, 11, 25) or given these PDFs the low-frequency regime transitions (11, 26). However, the HMM statistical approach is the only one utilized so far that determines the PDFs and low-frequency regime transitions simultaneously and objectively from the observed time series, with even an objective optimal path.

In outline, the remainder of the work begins with the basic features in the paradigm model and various applications of the HMM analysis to time series in the model. Key issues in the above controversy are elucidated and explained in the paradigm model along the way. The final section deals with the important practical topic of reduced low-order stochastic modeling (5, 6, 15, 16) and the capability of such procedures to capture both nonlinear statistical dynamics and low-frequency metastable regime behavior simultaneously with highly reduced dynamics.

The Paradigm Model

The barotropic quasi-geostrophic equations with a large-scale zonal mean flow U on a 2π × 2π periodic domain are given by

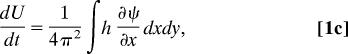where q is the potential vorticity, U is the large-scale zonal mean flow, ψ is the streamfunction, and h is the topography. In Eq. 1, the mean flow changes in time through the topographic stress; this effect is the analogue for periodic geometry of the change in time of angular momentum due to mountain torque in spherical geometry (15–17). Here, as in ref. 16, single-mode, large-scale topography is utilized of the form h(x, y) = h₀[cos(x) + sin(x)]. Substituting the special 3-mode truncated form

yields an exact nonlinear solution of Eq. 1, provided U, a, and b satisfy

It is easy to show that the above equations, after a 45° rotation of a and b, are identical to the equations of Charney and DeVore (14) for nonlinear regime behavior without dissipation and forcing; the integrable phase portrait of solutions of Eq. 3 has either one stable equilibrium or two stable and one unstable equilibrium (19). From Eqs. 2 and 3, U is the amplitude of the zonal mean flow, while a and b are amplitudes of the topographic Rossby waves. The same spectral truncated 57-mode version of the model in Eq. 1 with a magnitude of topography of h₀ = 1.06, with all parameter values corresponding to case c in table 5 and figures 12 and 13 from ref. 16 was integrated numerically in a fully turbulent statistical steady state for the long time of 500,000 time units with a time step 2.5 × 10⁻³ after a spin-up time of 5,000 time units; a long time series sampled every 0.25 time units is utilized in the HMM statistical analysis below. As already reported in ref. 16, most of the statistical mean energy as well as the longest correlation times are concentrated in the zonal mean flow U, and the large-scale topographic Rossby waves with amplitudes denoted by a = ℜψ₁₀ and b = ℑψ₁₀. Thus, these three wave patterns are the analogue of the low-frequency planetary waves in the paradigm model.

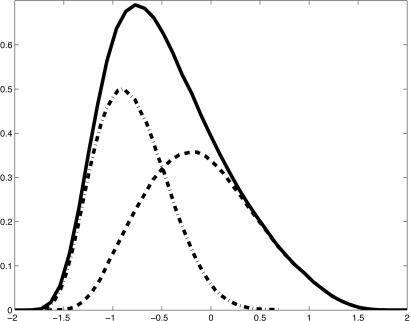
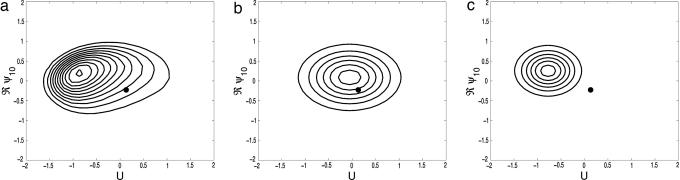
As depicted in Figs. 1 and 2a, the PDF for U and the joint PDF for U and a = ℜψ₁₀ are clearly quasi-Gaussian without any discernible multimode peaks; the same behavior is satisfied for all the other joint PDFs for the 3D subspace that are not displayed here. Clearly, all of these features in the paradigm model transparently mimic the low-frequency statistical behavior of the more comprehensive numerical models when integrated sufficiently long in time (5–7, 12). To compare this statistical behavior with the nonlinear dynamical behavior of the three-mode truncated model in Eqs. 2 and 3 the steady states of the dynamical system in Eq. 3 are evaluated at the mean energy value in these three modes from the full 57-mode system; in this regime, there is only one single stable equilibrium of the truncated system in Eq. 3 and its projection on the U, ℜψ₁₀ subspace is presented in Fig. 2. Clearly, this steady state is distant from the unique PDF maximum and apparently plays no active role in the fully turbulent statistical dynamics of the 57-mode model. As already mentioned above, the equilibrium solutions are for the inviscid case and therefore are different from the dissipative solutions of the original Charney–DeVore model, which includes form-drag.

Fig. 1.

Climatological marginal PDF of U (solid line) and weighted conditional PDFs of hidden states 1 (dashed line) and 2 (dashed–dotted line).

Fig. 2.

Joint PDFs. (a) Climatology. (b) Gaussian PDF of hidden state 1. (c) Gaussian PDF of hidden state 2. The dot denotes the single stable equilibrium state.

All of the above facts demonstrate that the 57-mode model for Eq. 1 is an excellent paradigm model for elucidating the scientific issues in the controversy described in the introduction. An objective analysis of the time series for U, a, and b through HMM analysis is developed next.

HMMs

In a HMM, a given observation sequence Y = Y₁, …, Y_T is explained in terms of a hidden Markov chain X. The Markov chain X has N hidden (i.e., not explicitly observed) states; over time, the chain switches between these N states according to a stochastic matrix A. Each hidden state has an associated output probability distribution B_n for the observed variable Y; distributions of different states can be overlapping (i.e., B_n ∩ B_m ≠ ∅ with n ≠ m). We shall identify atmospheric flow regimes with hidden states that are metastable (i.e., persistent). In this section, we briefly describe HMMs and apply them to the 57-mode model data in the next section.

The conditional independence relations between X and Y are defined by the factorization

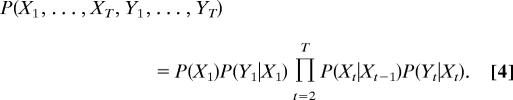A HMM is defined by the following components:

• N hidden states S = s₁, s₂, …, s_N,

• The observation space V ⊂ ℝ^d,

• A (N × N) stochastic transition matrix A = (a_ij),

• A stochastic vector that describes the initial state distribution π⁽¹⁾ = (π⁽¹⁾₁, …, π⁽¹⁾_N), and

• Probability distributions B_n, n = 1, …, N on V.

Since S and V are already implicitly defined, the short-hand notation λ = (A, B, π⁽¹⁾) is used for the model. The tuple (A, π⁽¹⁾) defines the hidden Markov chain X, and the B_n values are output distributions conditioned on the hidden state, i.e., P(Y_t|X_t = s_n) ∼ B_n = 𝒩(μ_n, Σ_n).

We are interested in interpreting a d-dimensional observation sequence Y by a HMM specified by a fixed number of hidden states N and multivariate normal distributions B_n, n = 1, …, N. For the identification of the N² + N + Nd + Nd² parameters, a maximum likelihood approach is used based on the likelihood L(λ|Y). The factorization (Eq. 4) of the joint probability distribution allows for an efficient HMM analysis of Y via the Expectation-Maximization (EM) and Viterbi algorithms.

EM Algorithm.

The EM algorithm is used to fit the HMM parameters to Y. It locally maximizes L(λ|Y) by iterating a fully specified initial model λ⁽¹⁾. Typically, the initial model is set up with equidistributed or random parameters that match the range of Y. A stopping criterion for the iteration is

for some threshold ε (ε = 0.1 here). There is no guarantee to converge to a global maximum in L, nor can it be checked from the iteration alone how close one gets to a global maximum. It is good practice to start EM with different initial models to compare their likelihood and check if they converge to the same or similar λ*.

Viterbi Algorithm.

For given Y and λ, the Viterbi algorithm computes the most probable hidden state sequence Q* = q₁, …, q_T, the Viterbi path, which is defined as

See refs. 20–24 for more details regarding the HMM algorithm described above and used below.

HMM Analysis for Metastable Regimes

As reported in figure 12c of ref. 16, the variable with the longest correlation time is the zonal mean flow U. First, the HMM analysis is applied to every 1.25 time units to decorrelate the observation sequence sufficiently to better reflect an independent output behavior within each hidden state; there are still 4 × 10⁵ time units in the basic times series. Next, the HMM algorithm is applied with a mixture of two Gaussians for the observed data, i.e., N = 2 hidden states in HMM. In this situation, the EM algorithm converges after 26 steps to

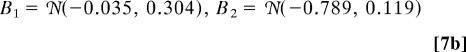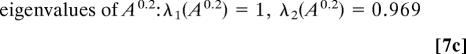The fifth root (every fifth output sample has been used for HMM analysis) of the transition matrix A^0.2 reflects normalization back to the basic sampled time unit, 0.25, of the original system. According to general theory, the unit eigenvalue is associated with the invariant measure, and the value near one, 0.969, for the second eigenvalue indicates the metastability of both states; this is also reflected in the mean residence times of 20 and 15 time units for hidden state 1 and 2, respectively. These mean residence times are much longer than the correlation time of U of ≈5 time units. Also note that the two Gaussian mixture distributions have substantial overlap as reported in Eq. 7 and depicted in Fig. 1. To check robustness of the results, the original HMM analysis is repeated 10 times by chopping up the original time series into 10 equal nonoverlapping pieces; the resulting analysis is remarkable similar with λ₂ = 0.969 ± 0.002 in all 10 cases.

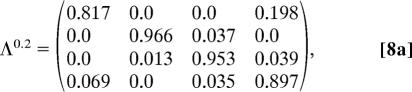
Next, the same time series is analyzed by HMM with four hidden states and yields the following results

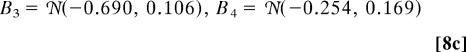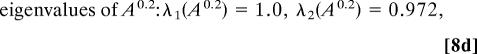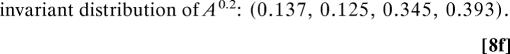Note that there is a pronounced spectral gap between the fourth eigenvalue in Eq. 8e and the others, indicative of metastability. We claim that the metastable behavior of the four-hidden-state model is well approximated by the two-state model reported in Eq. 7 in the sense that states 1 and 4 lumped (added) together from Eq. 8 approximate state 1 in Eq. 7 while states 2 and 3 lumped together approximate state 2 in Eq. 7 (see ref. 24 for more details). First, note that this is true approximately for the invariant distribution in Eq. 8 lumped by the recipe compared with the invariant distribution in Eq. 7. Also, the second metastable eigenvalue from Eq. 8, λ₂ = 0.972, is very close to the metastable eigenvalue λ₂ = 0.969 from Eq. 7.

All these results illustrate that the HMM analysis identifies two hidden states, which provide an excellent description of the metastable regime behavior of the paradigm model. Moreover, the third eigenvalue of Eq. 8 gives rise to further substructure and would lead to a decomposition of the lumped states 2 and 3, which, however, is less metastable. Furthermore, the substructure yields two phase-shifted zonal flow states with similar structure as hidden state 2 in Fig. 3b.

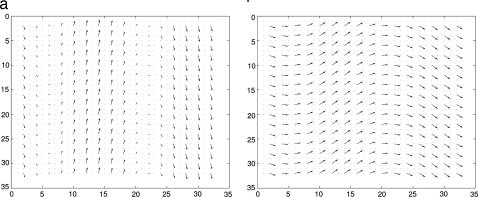
Fig. 3.

Velocity field conditioned on the Viterbi path of a HMM analysis in the subspace U for hidden states 1 (a) and 2 (b). The mountain ridge is at x = 5.

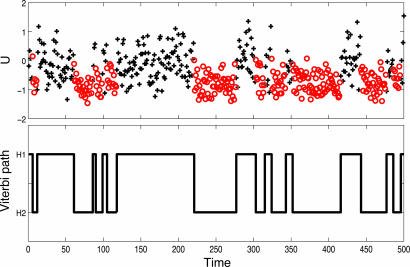
Next, the Viterbi path, the path obtained by assigning each data point to a hidden state, is utilized to supply a physical interpretation of the metastable dynamics. The velocity field conditioned on the Viterbi path of the HMM analysis for U is reported in Fig. 3. Hidden state 1 is clearly a state of topographically blocked flow, whereas hidden state 2 is clearly a state of enhanced stronger westerly zonal flow. The metastability illustrated by the Viterbi path is compared with the actual time series for U over a rather short, randomly selected time interval in Fig. 4to illustrate the coarse-grained significance of the Viterbi path for the time series.

Fig. 4.

U (Upper) and Viterbi path (Lower) of Eq. 7. For U path black crosses and red circles denote states that correspond to hidden states 1 and 2, respectively.

The present HMM analysis establishes unambiguously in the paradigm model that physically reasonable metastable regime transitions between blocked and zonal flows occur in a system with nearly Gaussian PDFs. In the paradigm model there is substantial overlap in the two-state Gaussian mixture distributions, similar to what occurs in the AGCMs (6).

Finally, to gain further confidence in the metastability results reported in Eq. 7, we take the same observation sequence but randomly permute the members before applying the two-state HMM analysis. The algorithm after 116 iterations yields the results

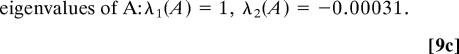Note that the normal distributions in Eq. 9 are nearly identical to those in Eq. 7 because the PDF is approximated well, yet the metastability in the hidden state Markov model has disappeared completely in the randomly shuffled case with second eigenvalue essentially zero with high precision.

Next, results are reported briefly for the HMM analysis applied to 2D time series in the subspace spanned by the low-frequency planetary waves, U, ℜψ₁₀, and ℑψ₁₀. In these cases the HMM analysis yields

• U and ℜψ₁₀

  

  
• U and ℑψ₁₀

  

  
• U and $\sqrt{{{\mathrm{(\Re \psi }}_{10})}^2+{{\mathrm{(\Im \psi }}_{10})}^2}$

  

  

The notable result is the strong stability of the metastable eigenvalue, λ(A^0.2), for all three different 2D time series in Eq. 10 as well as the excellent agreement of this eigenvalue with the two- and four-state hidden models for U alone in Eqs. 7 and 8. Fig. 2 b and c show the joint PDFs conditioned on hidden states 1 and 2 for the Viterbi path for the 2D subspace spanned by U and ℜψ₁₀. Clearly there is substantial overlap of the two conditional PDFs in Fig. 2 b and c, which in combination approximate the nearly Gaussian PDF depicted in Fig. 2a in a fashion like that in the AGCM data (6). Similar to Fig. 3, the hidden state 1 is associated with blocking, whereas hidden state 2 is associated with strong zonal flow; according to the Markov model in Eq. 10, the mean residence times in the blocked and unblocked states are 26 and 29 time units, respectively.

All of these results provide unambiguous evidence for the fact that in the paradigm model, statistically significant metastable regime transitions between zonal and blocked states occur despite the nearly Gaussian PDFs that occur in the time series for the low-frequency variables. Our results imply that there can be atmospheric regimes without multiple extrema in the corresponding PDFs; thus, the association of regimes with multiple extrema, an interpretation put forward by refs. 2 and 13 (and many others), can be misleading. Furthermore, these low-frequency regimes have significant overlap in their conditional distributions and have been demonstrated to exhibit very little relation with the nonlinear dynamics in Eqs. 2 and 3 truncated to the low-frequency subspace.

Low-Order Stochastic Modeling and Metastable Regimes

A topic of wide current interest (refs. 5, 6, 12, 15, and 16 and references therein) is the extent to which the nonlinear dynamics of a low-frequency planetary scale variable such as U can be approximated by a reduced-order stochastic differential equation (SDE)

where B(U) is the drift coefficient, A(U)/2 > 0 is the diffusion coefficient, and W is Brownian motion. Reduced-order stochastic models are interesting in answering the extent to which the turbulent chaotic low-frequency dynamics can be approximated by simpler closed stochastic models with fewer degrees of freedom (5, 6, 12); such reduced atmospheric models also have practical importance for predictability and coupling with the ocean over longer time scales provided they can successfully reproduce the low-frequency variability of the full dynamical model with sufficient accuracy.

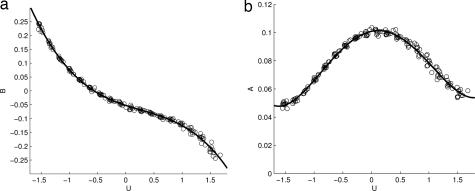
The most popular traditional ad hoc regression strategy in the atmosphere–ocean community involves linear regression fits where B(U) is linear and A(U) is constant (12, 15); in refs. 15 and 16 an a priori stochastic mode reduction strategy has been developed and utilized to predict the coefficients B(U) and A(U) in an a priori fashion for the present 57-mode model as an application of a general stochastic mode reduction theory. In particular, the a priori predictions from equations 4.7 and 4.8 in ref. 16 are an explicit odd nonlinear function for B(U) and an even nonlinear function for A(U); furthermore, these a priori predictions were shown to be superior to those obtained through a purely linear Langevin regression model as regards the correlation functions. This is an example of both multiplicative noise and nonlinearity governing the reduced-order stochastic dynamics for a low-frequency variable. For the two central issues mentioned below (Eq. 11), it is of interest to see whether it is possible to develop a regression fitting strategy for the drift and diffusion coefficients in Eq. 11 from the time series of U, which attempts to capture the low-frequency variability in U. Such a systematic reconstruction method has been developed very recently (27, 28); it focuses on capturing the correct leading eigenmodes of the Fokker–Planck equation associated with Eq. 11. Here it is applied with the simplest implementation of equal relative weights for all eigenvectors and eigenvalues in the cost function. By comparing the actual correlation function of U from the 57-mode model with the correlation functions of the SDE resulting from the approach in refs. 27 and 28 and from the a priori prediction from ref. 16 it is revealed that both methods capture the long-term trends in the correlation function for U, but surprisingly the a priori prediction is a slightly better overall fit at short time scales (data not shown). The strategy from refs. 27 and 28 recovers the PDF of U in Fig. 1 with high accuracy (data not shown). The time series for U was broken into 10 nonoverlapping segments, and the drift and diffusion coefficients for Eq. 11 were determined through the reconstruction procedure (27, 28). The results for the drift and diffusion coefficients for these 10 cases are reported in Fig. 5, respectively. The cubic polynomial nonlinearity for the drift and the quartic polynomial nonlinearity in the diffusion coefficient from Fig. 5 show very little fluctuation among the 10 nonoverlapping time series segments and confirm the general form of the a priori stochastic mode reduction procedure from ref. 16. Furthermore, these examples together with those in ref. 12 show that it is not necessarily possible to model the low-frequency variability of atmospheric variability by a regression strategy based on quadratic nonlinearity alone, as recently proposed in ref. 29.

Fig. 5.

Reconstructed drift B (a) and diffusion A (b) from time series variable U. The open circles are the result of the reconstruction, carried out 10 times on 10 different (nonoverlapping) segments of the time series. The solid line is the 3rd-degree polynomial (for drift) and 4th-degree polynomial (diffusion) curve fitted through all the results.

A much more subtle question is whether the SDE in Eq. 11 with the coefficient from Fig. 5 also captures the metastable regime transitions present in the original 57-mode model and documented in the previous section with reasonable accuracy. This is a question of central importance for the use of such models in extended range predictability. To explore this possibility, a two-state HMM analysis is applied to the time series generated by numerical integration of the SDE in Eq. 11 with the drift and diffusion shown in Fig. 5 with the same sampling interval utilized earlier. The results of the HMM analysis are

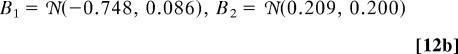The metastable eigenvalue λ₂(A^0.2) from Eqs. 12 and 7 are nearly identical; on the other hand, the Gaussian mixture in the SDE model as reported in Eq. 12 displays somewhat less overlap when compared with the two-state HMM analysis of U from the full 57-mode model in Eq. 7. These are excellent encouraging new results regarding the capability of the regression fit SDE from Eq. 11 with the strategy from refs. 27 and 28 to generate time series that approximate the metastable statistical features of U from the complex 57-mode model. These results suggest the possibility that the reduced stochastic model could be used for long-range predictability studies.

Concluding Discussion

A simple paradigm model for metastable atmospheric regime behavior has been introduced and analyzed here through HMM analysis of the time series of suitable low-frequency planetary waves. The analysis of this model demonstrates how statistically significant metastable regime transitions between blocked and unblocked statistical states can occur despite nearly Gaussian structure for the PDFs of the low-frequency variables. There is no special significant role here for the low-order truncated quadratically nonlinear dynamics alone; it is the stochastic backscatter onto these low-frequency modes that is responsible for the metastable regime transitions. It also was demonstrated here that suitable stochastic mode reduction strategies, which include both augmented cubic nonlinearity and multiplicative noise, are also capable of capturing the metastable low-frequency regime behavior through a single SDE compared with the full turbulent chaotic 57-mode model. This result obviously has implications for the practical use of reduced stochastic models in long-range forecasting.

Abbreviations

AGCM

atmospheric general circulation model

EM

Expectation-Maximization

HMM

hidden Markov model

PDF

probability distribution function

SDE

stochastic differential equation.