Flows driven by flagella of multicellular organisms enhance long-range molecular transport

Abstract

Evolution from unicellular organisms to larger multicellular ones requires matching their needs to the rate of exchange of molecular nutrients with the environment. This logistic problem poses a severe constraint on development. For organisms whose body plan is a spherical shell, such as the volvocine green algae, the current (molecules per second) of needed nutrients grows quadratically with radius, whereas the rate at which diffusion alone exchanges molecules grows linearly, leading to a bottleneck radius beyond which the diffusive current cannot meet metabolic demands. By using Volvox carteri, we examine the role that advection of fluid by the coordinated beating of surface-mounted flagella plays in enhancing nutrient uptake and show that it generates a boundary layer of concentration of the diffusing solute. That concentration gradient produces an exchange rate that is quadratic in the radius, as required, thus circumventing the bottleneck and facilitating evolutionary transitions to multicellularity and germ–soma differentiation in the volvocalean green algae.

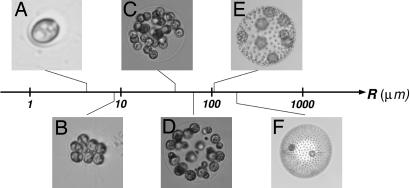
The motility of microorganisms is primarily thought to enable access to optimum environments. Yet some species of colonial motile algae thrive in restrictive habitats such as shallow evanescent puddles, all the while paddling energetically with their flagella. What is the significance, beyond locomotion, of this collective coordinated beating of flagella? Algal metabolism requires exchange, between organisms and water, of small molecules and ions such as CO₂, O₂, and PO₄³⁻. Rapidly growing organisms that are “large” in the sense explained below must augment diffusion with effective modes of transport from remote reaches of their environment (1). The volvocine green algae (2–5) can serve as a model system for understanding how exchange of nutrients and wastes varies with organism size, as in the transition from unicellular to ever-larger multicellular colonies. The Volvocales range from the unicellular Chlamydomonas to large colonies of cells, eventually leading to Volvox, comprising 1,000–50,000 cells (Fig. 1). They include closely related lineages with different degrees of cell specialization in reproductive and vegetative function (germ–soma separation), which seem to represent “alternative stable states” (6). Phylogenetic studies show that these transitions in cell specialization have occurred multiple times, independently (7–9), to geometrically and functionally similar configurations, suggesting that there is a selective advantage to that morphology. The volvocalean range of sizes, >3 orders of magnitude, enables the study of scaling laws; from a theoretical perspective, the spherical form of the Volvocales simplifies mathematical analysis.

Fig. 1.

Volvocine green algae arranged according to typical colony radius R. The lineage ranges from the single-cell Chlamydomonas reinhardtii (A), to undifferentiated Gonium pectorale (B), Eudorina elegans (C), to the soma-differentiated Pleodorina californica (D), to the germ–soma differentiated V. carteri (E), V. aureus (F), and even larger (e.g., V. gigas with a radius of 1 mm). In species in which two cell types can be identified, the smaller are somatic cells and the larger are reproductive cells. Note that the number of cells in Volvox species ranges from 1,000 (e.g., V. carteri) to 50,000 (e.g., V. barberi).

Volvox, the largest colonies in the lineage, are formed by sterile biflagellated Chlamydomonas-like somatic cells, with outwardly oriented flagella, which are embedded at the surface of a transparent extracellular matrix, which also contains the germ cells that develop into flagellated daughter colonies. In some species, germ cells start flagellated, but after their first mitotic division the flagella are absorbed (e.g., V. aureus), whereas in others (e.g., V. carteri) the germ cells are never flagellated. Directional swimming due to the coordinated beating of these flagella also is accompanied by rotation; Volvox is from the Latin “volvere,” to roll (2). Bell (10) and Koufopanou (11) suggested that the extracellular matrix is a storehouse (“source”) of nutrients for the germ cells (“sink”). They interpret this source–sink coupling as a mechanism that increases the uptake of nutrients by the developing germ cells located within the colony. Moreover, they showed (11) that germ cells from Volvox carteri, when liberated from their mother colony and freely suspended in the growth medium, grow more slowly than those embedded in intact colonies. Those experimental studies did not consider the external flow created by collective flagellar beating of the mother colonies. Our studies (3, 4) were designed to investigate the effects of such fluid flows and showed in fact that these flows positively influence germ-cell growth rates. Indeed, externally supplied flows can replace those due to flagella and return germ cells to normal growth rates. Flagella obviously confer motility; we infer that they also play a subtle but crucial role in metabolism. Niklas (1) suggested that as organisms increase in size, stirring of boundary layers, yielding transport from remote regions, can be fundamental in maintaining a sufficient rate of metabolite turnover, one not attainable by diffusive transport alone. Yet there has not been a clear quantitative analysis of this putative connection between flagella-driven stirring and nutrient uptake. Here we investigate the hypothesis that those flows facilitate, even “encourage,” the transition to large multicellular forms. We analyze the idealized problem of the scaling that relates nutrient uptake to body size. Measurements of the actual flow fields generated by colonies confirm the analysis. Because we also aim to understand the physical constraints leading to germ–soma differentiation, we investigate a body plan without such differentiation and examine its failure to deal with those constraints.

Results

Bottleneck Radius.

Consider the case in which only molecular diffusion in the suspending fluid governs transport (uptake or rejection) of a chemical species whose concentration is C(r), where r is the radial distance from the center of the colony. When more than even a few percent of the colony surface is covered by an array of absorbers or emitters, the diffusion-limited rate is well approximated by that of a sphere uniformly covered with absorbers/emitters (12). We now focus, for simplicity, on nutrient acquisition. By Fick’s law, a gradient in concentration yields a flux. We define the uptake rate or current at the surface of the sphere as the integral of the flux over the area of the sphere. Our sign convention is that the current is positive if the sphere takes up nutrients. Therefore, if C_∞ is the concentration far from the colony of radius R, then the steady-state concentration is C(r) = C_∞(1 − R/r). Furthermore, if D is the diffusion constant and dS is the element of surface area of the colony, then the inward current I_d = D∫dS(∂C/∂r) is linear in the colony radius R

The timescale τ_D on which this steady-state profile develops from an initially uniform concentration is τ_D ≃ R²/D. For a typical colony of radius 200 μm and diffusion constant of D = 2 × 10⁻⁵ cm²/s, τ_D ≃ 20 s, which is very long compared with the flagellar beat period but short compared with the life cycle. The current (Eq. 1) can be compared with the metabolic requirements of a colony with surface-mounted cells

where β is the time-dependent nutrient demand rate per unit area, including the requirements of internal “tissue” (e.g., germ cells), and storage by the extracellular matrix. The availability by diffusion can exceed the nutritional requirements at small radii. At sizes greater than the bottleneck radius

at which I_d = I_m, diffusion is insufficient to feed the organism (Fig. 2A). The diffusive rejection of waste products also is limited by a bottleneck radius of the same form as Eq. 3, with β signifying the forced emission rate of waste and C_∞ replaced by the difference between a molecular waste concentration at the surface and at infinity.

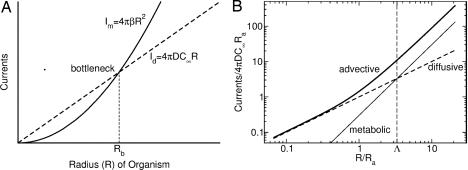
Fig. 2.

Molecular currents (molecules per second) and requirements. (A) A schematic diagram illustrating the existence of the diffusive bottleneck R_b. When the metabolic demand current (solid line), which is quadratic in organism radius R, exceeds the diffusive current (dashed line), which is only linear in R, the metabolism is constrained by diffusion. (B) Log–log plot showing how the advective current (thick solid line) circumvents the diffusive bottleneck for the choice Λ ≡ R_b/R_a = 3.3. At radii greater than the advective radius R_a (Eq. 7), the advective current grows quadratically with R, allowing metabolic needs to be satisfied for any arbitrary size.

Estimation of the bottleneck radius includes several considerations. First, the demand/consumption rate β varies with time and environmental parameters (e.g., light, temperature, nutrient availability) during the life cycle of Volvox. Second, there is uncertainty as to which of the key nutrients is limiting. Third, it is arguable whether the boundary condition for waste rejection at the colony surface involves a specified flux or a concentration. Mindful of these difficulties, we can make a rough estimate using parameters appropriate for either phosphate (13) (D ≃ 10⁻⁵ cm²/s, C_∞ ≃ 6 × 10¹⁴ cm⁻³, and β ≃ 10¹² cm⁻²·s⁻¹) or oxygen (D ≃ 2 × 10⁻⁵ cm²/s, C_∞ ≃ 10¹⁷ cm⁻³, and β ≃ 10¹⁴ cm⁻²·s⁻¹) measured in V. carteri using standard biological oxygen demand (BOD) bottles. We find R_b ≃ 50–200 μm. Intriguingly, the low range of the estimated R_b is comparable with Pleodorina (Fig. 1D), the smallest species where soma differentiation occurs; the high range is comparable with the smallest germ–soma differentiated Volvox colonies (e.g., Fig. 1E). Note that Pleodorina is considerably smaller than Volvox. In the latter, the number of flagellated surface-mounted somatic cells is much higher, and germ cells, which are nonflagellated, lie in the interior of the colony.

As a consequence of the dual role played by the flagellar basal bodies as both anchoring points for flagella and as microtubule organizing centers active in cell division, undifferentiated colonies are subject to the “flagellation constraint” (5, 14), which prevents the use of flagella during cell division. It is therefore appropriate that the largest colonies without true germ–soma differentiation would have a maximum size comparable with the bottleneck radius. For the nonmotile part of the life cycle, which also has the greatest metabolic needs, these colonies would just barely be able to obtain sufficient nutrients by diffusion alone.

Flows, Advection, and Nutrient Uptake.

How does advection, the transport of solutes by flow, modify this picture? The governing advection–diffusion equation is

where u⃗·∇⃗C is the advective rate of change of the concentration field C(r⃗, t), and D∇²C is the diffusive rate of change. Here, the vector u⃗(r⃗, t) is the spatially and temporally varying fluid velocity. The standard measure of the competition between advection and diffusion is the (dimensionless) Péclet number (15), which can be expressed in terms of a typical flow velocity U and the sphere diameter 2R as

Our measurements (4) of the typical fluid velocity near Volvox carteri (Fig. 1E) have shown that Pe can range from 100 to 300, implying that diffusion is negligible compared with advection. For large Pe, the absorption rate I_a generally is a power-law in Pe, as a consequence of the boundary layer that forms near the sphere’s surface. For the no-slip boundary condition at the surface of a solid sphere, Acrivos and Taylor (16) showed that I_a ∼ RPe^1/3 for large Pe. In important recent work, Magar et al. (17, 18) found that the exponent changes when the boundary condition allows slip; with a prescribed tangential flow, the current is I_a ∼ RPe^½.

Because we seek the size dependence of the advective transport, we require a model of the flow field created by the flagella. It is impractical to calculate the detailed flow generated by the array of flagella at the colony surface. Instead, we develop a simple model in which the details of the flagella length, beating frequency, and waveform are subsumed into a single averaged parameter, the force per unit area f⃗ that the spherical surface exerts on the fluid. By using the measured value of the propulsive thrust for V. carteri (3), we estimate f ≃ 0.1 dyne/cm², where we have divided the experimentally determined total thrust force by the area of a colony. Because we prescribe the force per unit area (the shear stress), instead of the tangential flow at the surface of the colony, our flow has crucial qualitative differences from previous work (17, 18). Dimensional analysis shows that the characteristic magnitude of the flow velocity U grows with colony radius

where η = 0.01 g/cm·s is the viscosity of water. When the tangential flow velocity is prescribed, the flow is clearly independent of R. In accord with observations (3), our model predicts that larger colonies with the same average density swim faster than smaller ones. For example, using our estimate of f and a colony radius of R = 100 μm, we find U ∼ 500 μm/s, which is close to observed swimming speeds (3).

For an idealized model, we take the force per unit area to be directed along lines of longitude, f⃗ = f̂θ (see Fig. 3for coordinate system); it is straightforward to include an azimuthal component of f⃗ to allow for rotational motion as well (M.B.S., T.R.P., J.O.K., and R.E.G., unpublished data). Thus, the boundary conditions at the surface of the colony are as follows: vanishing radial velocity and the shear stress condition σ_rθ = −f, where σ_rθ is the stress that the fluid exerts on the surface. Far from the colony, the fluid velocity approaches either the swimming velocity U⃗ = −Uẑ for a freely swimming colony, or zero for a colony held in place. Because inertia is unimportant at the scale of a colony, we find the flow velocity u⃗ by solving the Stokes equation ∇⃗p = η∇²u⃗, where p is the pressure; the velocity field must also be incompressible, ∇⃗·u⃗ = 0. The cylindrical symmetry of the boundary conditions implies that the velocity field and pressure may be represented by an expansion in Legendre polynomials multiplying functions that are linear combinations of powers of r. In a coordinate system moving at the speed of the colony, the radial and polar velocities are u_r = −U[(c − x⁻³)cosθ + A(x, θ)] and u_θ = −U[−(d + x⁻³)sinθ + B(x, θ)], where x = r/R and A(x, θ) and B(x, θ) are infinite sums of terms falling off with distance as x⁻² and higher powers. The precise characteristic velocity whose dimensional scaling was shown in Eq. 6 is found to be U = πfR/8η. The parameters c and d distinguish between free-swimming colonies (c = d = 1) with no net force acting on them and colonies held in place by an anchoring force (c = 1/x, d = ½x).

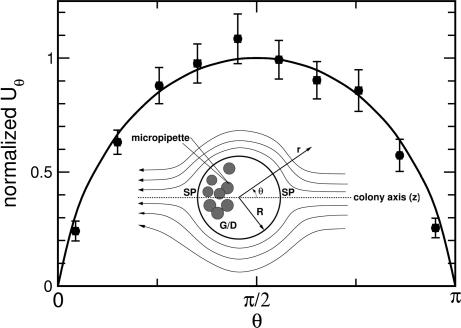
Fig. 3.

Fluid flow near the surface of a colony. Inset shows geometry of the experiment. The organism is held fixed by using a micropipette attached to the posterior region, in the vicinity of the germ cells/daughter colonies (G/D), away from the two stagnation points (SP) of the flow. The fluid flow generated by the colony is measured by using particle imaging velocimetry. Comparison between theoretical (solid curve) and average experimental values (solid circles) of the tangential flow velocity near the organism’s surface is plotted as a function of polar angle θ. Measurements were made on 10 different organisms. For each, a least-squares fit to the theoretical velocity field was performed to determine the single unknown parameter, the maximum tangential velocity. These data then were pooled by normalizing each set to the fitted maximum velocity, ranging from 100 to 600 μm/s for the variously sized colonies measured.

To test this model, we measured the flow fields around colonies using methods described elsewhere (4), building on earlier studies (19, 20) and summarized in Methods. A least-squares fit of each data set was used to determine the velocity scale U for each, and then each data set was normalized to the maximum velocity. Pooling data on 10 colonies, Fig. 3 shows this averaged velocity compared with the suitably normalized theoretical function; the two agree within the standard error of the measurements, validating the idea of surface shear stress supplied by the flagella.

We now examine in detail the nutrient uptake rate. Observe from Eq. 5 that because the flow field in the model has a characteristic velocity U that is proportional to the radius, the Péclet number is proportional to R². Because the Péclet number itself is dimensionless, it can be expressed as the ratio of two radii in the form Pe = (R/R_a)² with

In addition to the bottleneck radius R_b, this “advection radius” R_a serves as a second characteristic length scale in the system, one not previously recognized. It is the length above which advection overtakes diffusion, i.e., Pe > 1. With the estimated parameters described above, we find R_a ∼ 10 μm, similar to the diameter of Chlamydomonas. The ratio Λ ≡ R_b/R_a characterizes the onset of complexity in the Volvocales and is in the range 5–10. Note that R_a is comparable with the length of a flagellum, the “stirring rod,” certainly a curious coincidence.

To understand the role of the advection radius in the rate of molecular nutrient and waste exchange, we used the self-generated flow field calculated above as the velocity u⃗ in the steady-state version of Eq. 4 to find numerically the concentration profile around a model colony. Fig. 4A shows the normalized concentration field C/C_∞ near a swimming colony for a range of Péclet numbers. When Pe ∼ 1, the concentration field is only slightly distorted from spherical symmetry, whereas for Pe ≫ 1, a thin concentration boundary layer forms around the leading edge of the sphere; furthermore, a solute plume, analogous to the “tail” behind sedimenting marine snow (21), the organic detritus falling from the upper layers of the ocean, extends to ever-greater length. This plume of nutrient depletion or waste product accumulation is left behind a swimming colony. As an increasing Péclet number is associated with increasing radius, we may imagine the three frames in Fig. 4A as corresponding to organisms comparable in size with the advective radius, larger, and then much larger. Because R_a is the measure of the size of the boundary layer, the boundary layer width R_a/R, in units of the colony radius, is proportional to Pe^−½. Computations are consistent with this scaling (Fig. 4B), where the boundary layer thickness is taken to be the distance over which the scaled concentration C/C_∞ = 0.1 in front of the colony. The absorption current I_a follows from Fick’s law as an integral, I_a = D∫dS(∂C/∂r), over S, the colony surface. We approximate ∂C/∂r ≃ C_∞/R_a at the surface, yielding

The right-hand side of Eq. 8 also may be expressed as 4πDC_∞RPe^½, the same power law found by Magar et al. (17, 18), whose velocity field included only the first few Legendre polynomial terms. The key point here is that the quadratic dependence of the Péclet number on radius (quite miraculously!) leads to a solute current that scales with the surface area, just as required. Fig. 2B revisits the competition between pure diffusive current and metabolic needs first illustrated in Fig. 2A but now presented on a log–log plot. It shows how the total molecular current crosses over from a diffusion-dominated linear behavior for R < R_a to advection-dominated quadratic scaling for R > R_a. This scaling is the same power as that for the metabolic needs. We therefore conclude that transport by the collective beating of flagella eliminates the diffusion-only inhibition of growth and thus facilitates the transition to enlargement and multicellularity.

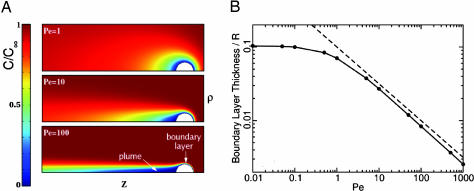
Fig. 4.

Results from numerical calculations of spatial dependence of the concentration field using the theoretically obtained velocity field. (A) Concentration, normalized by C_∞, near a perfectly absorbing [C(R) = 0] swimming spherical colony for various Péclet numbers, illustrating the development of a thin localized anterior boundary layer and long narrow posterior plumes at high swimming speeds. Colors represent the dimensionless concentration C/C_∞. The concentration fields near an immobilized colony are quantitatively very similar. (B) The relationship between boundary layer thickness and Péclet number. The thickness was determined from the computations as the distance from the front surface of the sphere to the point at which C/C_∞ = 0.1. When displayed as shown on a log–log plot (black line), the boundary layer thickness, divided by sphere radius R, is parallel to a line (dashed) proportional to Pe^−½, indicating that it also varies as the −½ power at Péclet numbers greatly exceeding unity.

Discussion

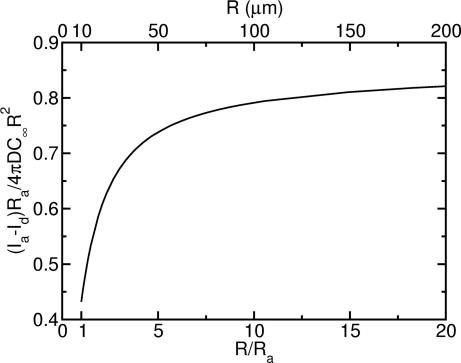
Viewed from a different perspective, the flows we have described enhance the molecular or metabolite exchange rate per unit area of a colony. This advective contribution confers an advantage to increasing size, because it rises precipitously from the smallest organisms up to those whose size is several times the advection radius (Fig. 5). These results suggest that “a greater rate of nutrient acquisition per unit area” is one answer to the often-posed question regarding the advantages of increased size (22), particularly for colonial forms with only a few cells. Significantly, the leveling out of the exchange rate for even larger colonies implies size neutrality in that regime, i.e., that an increase of size in this range no longer affords any greater rate of nutrient acquisition per unit area. Perhaps this characteristic contributes to the polyphyletic origin of the Volvocales.

Fig. 5.

Difference between molecular flux (current/area) with advection and without, plotted as a function of the colony radius R, in units of the advective radius R_a. Numerical results derived using flagella-driven flow show that beyond R_a the advective contribution overpowers pure diffusion. Beyond ≈100 μm = 10R_a, the approximate size where germ/soma differentiation occurs in the Volvocales, that difference saturates, indicating onset of size neutrality, in the sense that increasing size no longer increases the advective advantage in nutrient acquisition per unit area.

It should be emphasized that the details of the boundary conditions for nutrient uptake and/or waste removal can have a large effect on the degree to which advection can enhance these processes. It is also quite possible that the dynamics of waste removal are coupled to those of nutrient uptake.

Although we have focused on the central issue of metabolite exchange in the presence of strong fluid transport by flagella, the solute plumes (Fig. 4A), representing either depletion or waste, also provide spatially and temporally extended signals for the presence of a colony, perhaps significant for intercolony communication, as in sexual induction (23) and quorum sensing (24), and for spatial patterning by means of chemotaxis. In the context of predation, a solute plume increases the probability of detection.

Methods

Colonies of V. carteri f. nagariensis harvested from synchronized populations grown in standard Volvox medium (25) under controlled dark/light cycles (16 h light, 10,760 lux, 28°C/8 h dark, 26°C) were held fixed by micropipette aspiration (Fig. 2), viewed at 4× magnification on the stage of an inverted microscope (Nikon Diaphot 200). Movies were acquired with an analog charge-coupled device camera (SSC-M374; Sony; 480 × 640 pixels) and were typically composed of ≈1,000 images taken at ≈30 frames per s. The resulting flow fields were smoothed by averaging >200 frames. For particle imaging velocimetry (PIV) studies, the medium was seeded with microspheres (Molecular Probes; F8825 carboxylate modified, 1.0 μm, Nile red), viewed by using laser epifluorescence (80 mW, 532 nm) or darkfield illumination. Commercial PIV software (Dantec Dynamics, Skovlunde, Denmark) was used. Averaged velocity fields were used to obtain the tangential velocity component as a function of polar angle θ (Fig. 2), with typically 20 measurements between θ = 0 and θ = π. Apart from minor distortions due to the micropipette, symmetry between the two halves of the profile was observed; we combined those data and partitioned them into 10 bins.