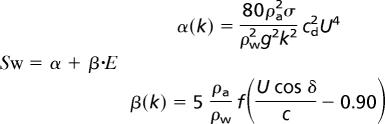Critical bifurcation of shallow microtidal landforms in tidal flats and salt marshes

Abstract

Shallow tidal basins are characterized by extensive tidal flats and salt marshes that lie within specific ranges of elevation, whereas intermediate elevations are less frequent in intertidal landscapes. Here we show that this bimodal distribution of elevations stems from the characteristics of wave-induced sediment resuspension and, in particular, from the reduction of maximum wave height caused by dissipative processes in shallow waters. The conceptual model presented herein is applied to the Venice Lagoon, Italy, and demonstrates that areas at intermediate elevations are inherently unstable and tend to become either tidal flats or salt marshes.

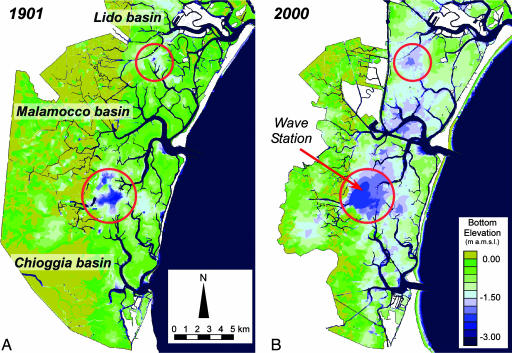
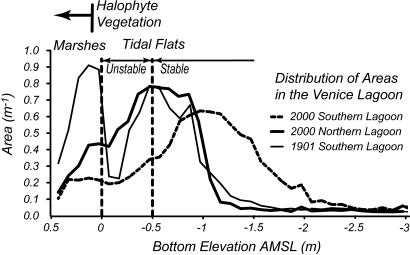
The distribution of elevations in shallow tidal basins such as the Venice Lagoon in Italy (Fig 1, tidal range of 0.7 m) shows that tidal flats have differences in elevation of few tens of centimeters, with an average elevation between −0.50 and −1.00 m above mean sea level (MSL), whereas salt marshes lie at an average elevation higher than +0.20 m, with some variability dictated by local sedimentological and ecological conditions (1–4). Few areas are located at intermediate elevations (i.e., between −0.50 and +0.20 m), suggesting that the processes responsible for sediment deposition and erosion produce either tidal flats or marshes but no landforms located at intermediate elevations. In the relatively pristine northern part of the Venice Lagoon, the most frequent bottom elevation is around −0.50 m (Fig. 2), similar to natural conditions in 1901 in the Southern Lagoon (Fig. 1A). During the last century, anthropogenic causes produced consistent bottom erosion in the Southern Lagoon, leading to a median elevation of approximately −1.00 m above MSL (Figs. 1B and 2). Nevertheless, all three distributions of elevations show a relatively low frequency of elevations between 0 and −0.5 m.

Fig. 1.

Distribution of channels, salt marshes, and tidal flats in the Venice Lagoon in 1901 (A) and 2000 (B). The elevation is expressed in meters above MSL (a.m.s.l.). Areas within the circles are tidal-flat locations away from the channels in which the deposition rates are very low.

Fig. 2.

Distribution of areas within the Venice Lagoon as a function of elevation in 1901 and 2000. The elevation at which the vegetation starts colonizing the landscape was derived from ref. 16. AMSL, above MSL.

Typical conceptual and numerical models of salt-marsh formation envision a gradual transformation of sand flats and mudflats in response to sediment buildup and plant colonization (5–7). However, the evidence points to abrupt transitions to one of two distinct stable outcomes. Salt marshes emerge from tidal flats in locations where sedimentation is enhanced by lower tidal velocities, higher sediment concentrations, or the sheltering effects of splits and barrier islands (1, 8). Alternatively, in areas with consistent sediment resuspension caused by a combination of tidal fluxes and wind waves, tidal flats are dominant. In tidal flats, sediment deposition is balanced by erosion, and the bottom elevation is constantly maintained below MSL (9). Sediment resuspension by wind waves is decisive, because tidal fluxes alone are unable to produce the bottom shear stresses necessary to mobilize tidal-flat sediments (10).

On the basis of a simplified model for wave generation in shallow water (10), we developed a conceptual model to study the distribution of bottom shear stress as a function of elevation. The results are used to explain the bimodal distribution of bathymetry in the Venice Lagoon.

Wind Waves in Shallow Water

Wind waves are created by the transfer of energy from the wind to the water surface. Starting from a flat water surface, wind stresses generate waves that increase in height until the energy dissipation caused by whitecapping, depth-induced breaking, and bottom friction limit the growth process (10, 11). Equilibrium is reached when the energy generated by the wind action equals the energy dissipated. In this situation, the height of the wave is the maximum possible for the particular bathymetry, meteorological forcing, and fetch length (the distance across which the wind can blow without land obstructions). Thus, wave height is largely controlled by depth and increases in deep waters.

To compute wave height in shallow waters we study the local evolution of the wind-wave energy E, directly related to the wave height by the linear theory. Wind-wave energy is described with an equation for the conservation of wave energy, which, for monochromatic waves, reads (10, 11)

where c_g is wave-group celerity and S is a source term. In shallow basins, waves quickly adapt to external forcing (i.e., ∂E/∂t becomes negligible in a short period). In fact, strong dissipation limits advection, so the wave field is essentially controlled by local energy balance. Moreover, the time required to reach equilibrium is short (10), so we can ignore the transient behavior.

The source term S includes wave growth by wind (S_w) and wave decay by bottom friction (S_bf), whitecapping (S_wc), and depth-induced breaking (S_b). Therefore, and as a first approximation, the conservation equation can be reduced to

This equation states that equilibrium is reached when the energy generated by the wind action equals the energy dissipation by bottom friction, whitecapping, and breaking. All terms in the equilibrium equation can be expressed as a function of wave energy (10, 11), and the wave height can be calculated with an iterative algorithm. The terms in Eq. 2 are indicated in Table 1 and were derived from widely adopted wave models (11). In our model we implement Eq. 1 with a finite-elements algorithm. To assess the influence of fetch length on wave generation, the advection term in Eq. 1 was retained. The wave height was then calculated along transects with constant bottom elevation, starting from a flat water surface and using Eq. 1 until steady state was reached.

Table 1.

Formulation for wave generation and dissipation (11)

Process	Formula	Variable
Wind generation		k: wave number;
		σ = 2π/T (T = wave period);
		ρa: air density;
		ρw: water density;
		cd ≅ 0.0012 drag coefficient;
		U: the wind speed in m/s;
		f: wave frequency (f = 1/T);
		δ: angle between wind and wave vector;
		c = σ/k wave celerity
Bottom friction		H: significant wave height;
		Y: water depth;
		cbf = 0.015
White capping		γ integral wave-steepness parameter, (γ = Eσ4/g2);
		γPM = 4.57 × 10−3: theoretical value of γ for a Pearson–Moskowitz spectrum;
		cwc = 3.33 × 10−5
Breaking		Hmax = 0.78 Y, maximum wave height;
		Qb: breaking probability
Wave-induced bottom shear stress		D50 = 20-μm median grain diameter

Bottom shear stresses are directly linked to wave height. In our modeling framework, the bottom shear stress (12) is given as

where f_w is a friction factor and u_m is the maximum horizontal orbital velocity at the bottom associated with the wave. u_m directly depends on wave height H and water depth Y so that, for a given water depth, higher waves produce larger bottom shear stresses. The rate of sediment erosion is supposed to be directly proportional to the difference between bottom shear stress and the critical shear stress for sediment erosion (7, 13):

where R is the erosion rate, A is a constant of proportionality, and α ranges from 1 for cohesive sediments to 1.5 for loose sediments. τ_cr is the critical shear stress for erosion. In our model we set τ_cr = 0.7 Pa after extensive field studies in the Venice Lagoon (14).

Bifurcation of Coastal Landforms

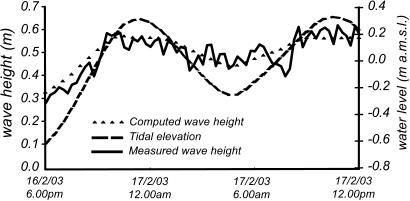
We obtain the shear-stress distribution from our model of wave generation by enforcing a monochromatic wave of period 2 s, the typical value of wind waves in the Venice Lagoon. To test the validity of the model, we compare the wave height generated by a given wind speed with available wave measurements in the Venice Lagoon (Fig. 3). The model well reproduces the measured values and shows a decreasing wave height in shallow water depths caused by the increased energy dissipation. In this simulation, changes in water depth are produced by tidal oscillations in the lagoon.

Fig. 3.

Tidal and wave elevations (both measured and simulated) in the Venice Lagoon (location indicated in Fig. 1B). The simulated waves were computed by using Eq. 1 with measured wind speeds on February 16–17, 2003. a.m.s.l., above MSL.

Wave decay by bottom friction, whitecapping, and depth-induced breaking also affects bottom shear stresses, which are linked to wave height through Eq. 3. However, shear stresses produced by wind waves are not monotonically linked with water depth: they are limited in shallow water because of dissipative processes, but they are also limited in deep water, where wave height can be large but the bottom is too deep to be affected by wave oscillations (i.e., τ_b ≪ τ_cr).

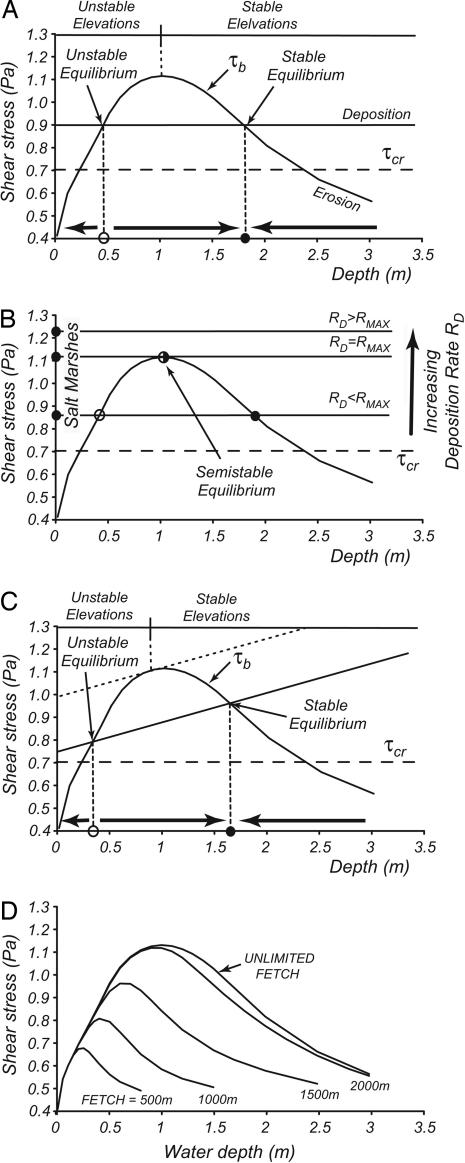
Plotting the equilibrium bottom shear stress as a function of water depth for a given wind speed, we obtain a curve that peaks at an intermediate water depth (Fig. 4A). The curve is obtained without considering the limiting effect of fetch length. This maximum of shear stress bears important consequences for the morphological transition from tidal flats to salt marshes and for the overall redistribution of sediments in shallow tidal basins.

Fig. 4.

Tidal flat equilibrium conditions. (A) Distribution of bottom shear stresses produced by wind waves as a function of elevation. The intersections between the shear-stress curve and the horizontal line (Eq. 6) are the equilibrium tidal-flat elevations. The curves are based on the assumption of constant annual deposition and a geomorphologically significant wind speed of 8 m/s, the typical value for tidal flats in the Venice Lagoon. The equilibrium point on the right is stable because small perturbations in elevation can be recovered by the system, whereas the equilibrium point on the left is unstable. (B) Tidal-flat equilibrium conditions as a function of different deposition rates. (C) Tidal-flat equilibrium conditions for sediment deposition decreasing with elevation. The stable branch of the curve extends to the tangent point with the deposition line. (D) Shear-stress curves as a function of fetch length.

On the basis of the relationship between shear stress and bottom elevation (Fig. 4A), we propose a model for the morphological evolution of salt marshes from tidal flats.

The vertical evolution of tidal flats is governed by the following differential equation:

where y is the tidal-flat elevation, n is the porosity, and R_D is the average annual deposition rate at that location.

The model assumes a prescribed characteristic, geomorphically dominant wind speed with an average annual duration related to that specific wind condition. Following the procedures outlined in ref. 15, the dominant wind speed is obtained by maximizing the product of wave erosion by the frequency of the related wind conditions. Using 50 years of wind data for the Venice Lagoon, we determine a dominant wind speed of 8 m/s blowing from northeast.

An average annual sedimentation rate that is site-dependent but constant during bottom evolution is also assumed. The tidal flat reaches an equilibrium elevation (i.e., dy/dt = 0) when the average annual erosion rate R is equal to the average annual deposition rate R_D. From Eq. 5 we obtain the equilibrium condition:

Thus, the equilibrium depth is the intersection of the shear-stress curve and the horizontal line shown on the right-hand side of Eq. 6 (Fig. 4A).

If the deposition rate is less than the maximum erosion rate, we have two equilibrium elevations, but only the one on the right is stable. In fact, for elevations between the two equilibrium points, the annual erosion rate is higher than the annual deposition rate (the erosion curve is above the deposition curve) and the tidal flat tends to deepen, whereas for elevations below the equilibrium point on the left and above the equilibrium point on the right, deposition dominates erosion and the tidal flat accretes (horizontal arrows in Fig. 4A). Thus, the point on the right is stable, because a small perturbation in elevation can be easily recovered by the system (a lower elevation decreases erosion, producing sediment accumulation, whereas a higher elevation favors erosion and thus deepening). The equilibrium condition on the left is unstable and persists only if the local deposition rate exactly balances the erosion rate; otherwise, the bottom elevation will evolve toward either a stable tidal flat if the annual deposition is smaller than the equilibrium erosion rate or an emergent salt marsh if the annual deposition rate is higher than the equilibrium erosion rate.

For deposition rates higher that the maximum erosion rate R_max, there are not possible equilibrium elevations for tidal flats and the system evolves to salt-marsh elevations (Fig. 4B), whereas for a deposition rate exactly equal to the maximum erosion rate R_max, there is only one semistable equilibrium elevation.

The maximum in shear stress represents the boundary between stable and unstable elevations. In fact, the points on the right-hand branch are the equilibrium elevations that a tidal flat can attain as a function of different deposition rates, whereas the left-hand branch of the curve represents all of the unstable equilibrium conditions. The intertidal landscape is then characterized by tidal-flat elevations belonging to the stable branch of the curve, with different elevations depending on local sediment availability, and few areas having elevations higher than the maximum in shear stress representing tidal flats in transition to salt marshes or vice versa.

In intertidal environments it is common to assume a deposition rate that varies as a function of water depth (16, 17), which is particularly true for salt marshes, in which the inundation period and therefore the time available for suspended sediment to settle decreases with elevation when the marsh becomes emergent. Although this relationship is strictly true for bottom elevations within the tidal range, here we extend this assumption to tidal flats and determine the consequences of a decreasing sedimentation rate on equilibrium conditions. If we assume a constant decrease in sedimentation rate and cohesive sediments (α = 1), the right-hand side of Eq. 6 can be graphically described as a sloping line that intersects the shear-stress curve in two points (Fig. 4C). Again, we can separate the curve into two branches (stable and unstable), but now the boundary between the two branches is defined by the tangent point between the sloping line and the shear-stress curve. Because the line describing Eq. 6 decreases with elevation, the separation point between the two branches is located at a lower elevation than that in the constant-deposition case. Similarly, it is possible to determine the tidal-flat equilibrium conditions for different sediment property (α ≠ 1) and different monotonic relationships between deposition and elevation by substituting the sloping line with the corresponding curve.

Discussion and Conclusions

The presence of an unstable part in the curve of Fig. 4A is a very reasonable explanation for the reduced frequency of areas at intermediate elevations (Fig. 2). However, the unstable region predicted by the model extends to −1.00 m above MSL, whereas field evidence shows that the area frequency decreases only below −0.50 m above MSL. The reasons for this discrepancy are many fold: (i) Short wind fetch limits wave height. The distribution of bottom shear stress as a function of fetch length calculated by using the finite-element model (10) solving Eq. 1 indicates that the peak in shear stress shifts toward shallower depths (as shown in Fig. 4D). The shear stress peaks at −0.5 m for a fetch of 1,000 m, the characteristic value for the Venice Lagoon, where frequent islands and marshes limit the distance over which the wind blows. (ii) Tidal excursions periodically shift the water depth by approximately ±0.35m. (iii) Deposition rates may be affected by water depth (Fig. 4C).

The decoupling of erosion and sedimentation in Eq. 5 is partly justified by the fact that the average path of suspended sediment during a tidal cycle is of the same order of magnitude of the basin dimensions so that only a small fraction of eroded sediments is redeposited at the same location. In general, the deposition rate at each point of the basin depends on sediment redistribution driven by tidal currents, on the distance from the main tidal channels, and on allogenic sediment sources such as rivers and inlets. To determine the evolution of the entire system, our point analysis of tidal-flat evolution must be coupled to a spatial description of sediment transport in the basin so that the local sediment availability and average deposition rate are determined.

It is worth noting (see Fig. 2) that the encroachment of halophyte vegetation on salt marshes starts at +0.05 m in the Venice Lagoon and that the canopy is fully developed only above +0.15 m, as reported in detailed field measurements (18). Thus, halophyte vegetation does not affect the transition from tidal flats to salt marshes for bottom elevations below MSL. Once the tidal flat emerges, the vegetation rapidly colonizes the surface, increasing its elevation by sediment trapping and below-ground organic production. Of particular importance for salt-marsh equilibrium are the feedbacks between vegetation and accretion, including inorganic sediment trapping by vegetation (17, 19, 20). It is then the reduction in wave activity that is ultimately responsible for the bifurcation of tidal landforms.

The bimodal distribution of tidal landforms is well defined for the 1901 Southern Lagoon (see Fig. 2), whereas it is less evident for the 2000 bathymetry, with a less pronounced maximum for salt marshes. This difference is due to the reduction in salt-marsh area occurred in the Venice Lagoon in recent decades but also the presence of different plant species on the marsh platform that expand the possible range of marsh elevations once the vegetation canopy is established (16).

Our model also predicts that wherever sediment supply is negligibly small, any starting elevation on the curve shown in Fig. 4 will evolve to a water depth of 2 to ≈2.5 m, the value at which the curve intersects the horizontal line of critical shear stress. In the Venice Lagoon, a negligible deposition occurs near the divides separating the basins of Chioggia, Malamocco, and Lido, which are away from the large channels carrying the sediments. As expected, these two locations, where wind waves are not fetch-limited, are characterized by large tidal flats that have maintained a constant water depth of 2 to ≈2.5 m in the last two centuries despite the radical morphological changes that occurred in the Venice Lagoon (Fig. 1, circled locations).

The proposed conceptual model indeed can explain and predict evolutionary trends of the Venice Lagoon. In basin locations with high deposition rates, the most frequent tidal-flat elevation is around −0.5 m, because for higher elevations the flat becomes a salt marsh. If sediment availability is reduced (e.g., by removing fluvial supply and promoting sediment loss), the equilibrium condition shifts toward lower elevations, as is happening in the Southern Lagoon, where the dredging of the inlets and the construction of long jetties at the end of the 19th century reduced the median elevation of the flats to −1.00 m above MSL.

Conversely, if we increased the sediment availability (e.g., by rediverting rivers in the Venice Lagoon where they debouched before the 15th century), the lagoon would start silting up but still maintain an average tidal-flat elevation around −0.5 m above MSL. In fact, the lagoon infilling would occur through the formation of new salt marshes rather than by a generalized bottom accretion.

The results of our analysis are valid in microtidal and mesotidal environments away from tidal channels, where the resuspension of bottom sediments is largely due to wind waves rather than tidal currents. In locations with a high tidal excursion or in the channels dissecting the flats, tidal currents and their spatial distribution are instead the chief geomorphic agents (10). Moreover, our analysis is limited to areas within tidal basins or behind barrier islands and splits, which are sheltered from long waves propagating from offshore, but can be also extended to flats lying in lakes and estuaries, where the tidal signal is negligible.

Abbreviation

MSL

mean sea level.