A missing model in reproductive skew theory: The bordered tug-of-war

Abstract

Models of reproductive skew can be classified into two groups: transactional models, in which group members yield shares of reproduction to each other in return for cooperation, and tug-of-war models, in which group members invest group resources in a tug-of-war over their respective reproductive shares. We synthesize these two models to yield a “bordered tug-of-war” model in which the internal tug-of-war is limited (“bordered”) by the requirement that group members must achieve a certain amount of reproduction lest they pursue a noncooperative option leading to group breakup. Previous attempts to synthesize these two models did not allow for the fact that the tug-of-war will affect group output, which in turn feeds back on the reproductive payments required by group members to remain cooperative. The bordered tug-of-war model, which does not assume complete reproductive control by any individual and allows for conflict within groups, predicts that the degree of within-group selfishness will increase as the noncooperative options become less attractive, e.g., as ecological constraints on solitary breeding increase. When the noncooperative option involves fighting for the group resource (e.g., territory) and leaving if the fight is lost, the subordinate's overall share of reproduction is predicted to be independent of its relatedness to the dominant and to increase the greater its probability of winning the fight, the less the value of the territory, and the greater its personal payoff for leaving. The unique predictions of the bordered tug-of-war model may fit skew data from a number of species, including meerkats, lions, and wood mice.

The quest for a unifying model of social evolution has been undertaken with the joint use of evolutionary game theory and kin selection theory to predict how members of social groups should divide up reproduction in an evolutionarily stable way. Models of this reproductive partitioning, i.e., reproductive skew models, seem to have proliferated over the last decade, but most such models can be classified into two broad groups: transactional models, in which group members yield shares of reproduction to each other in return for some cooperative gain, and tug-of-war models, in which group members invest group resources, at the expense of total group output, in a tug-of-war over their respective reproductive shares (1–3).

There have been two main attempts to combine these models into a more general model that incorporates the possibility of both transactions and intragroup conflict occurring within a society (2, 4). Reeve (4) considered that the reproductive payments that subordinates and dominants must provide to each other to maintain group stability set limits to an internal tug-of-war, which occurs within a “window of selfishness” bounded by the minimally required payments. Reeve then went on to analyze the factors that affect the width of the window and thus the scope for conflict. Johnstone (2) took this idea further by explicitly integrating the equations for the minimal payments from transactional theory with the equations of tug-of-war theory to yield a “synthetic” theory.

However, the approach of Reeve (4) and Johnstone (2) is subject to some important problems. The first is that the minimum payments from transactional theory assume that one individual (the dominant in the original concession version of transactional models) has complete control over reproductive shares within the group, whereas tug-of-war models assume incomplete control by both dominants and subordinates. Strictly speaking, if one group member has complete control over the reproductive shares of the others, it follows that the remaining group members have no incentive for trying to increase their shares through a tug-of-war, because the selfish efforts in such a war would by assumption fail to increase their shares and result only in group output reductions. In short, the assumption of complete control rules out intragroup conflict. Thus, the complete-control transactional models cannot be simply conjoined to tug-of-war models.

A mathematical manifestation of the aforementioned inconsistency is that the two previous synthetic models did not allow for the fact that the tug-of-war will affect group output, which in turn should feed back on the reproductive payments required by group members to remain cooperative. The selfish efforts in the tug-of-war and the fractions of reproduction peacefully ceded by the dominant and subordinate to each other are interconnected by the group output and must be solved simultaneously rather than piecemeal, as in the previous synthetic approach. We here attempt to correct this problem and show that the new model makes predictions that are markedly different from either the complete control transactional models or the pure tug-of-war models.

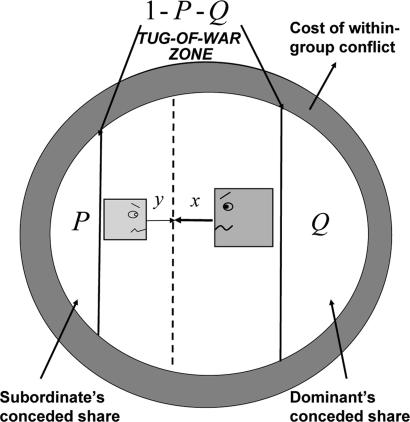
In particular, we develop a “bordered tug-of-war” (BTOW) model in which the internal tug-of-war is limited (“bordered”) by the requirement that group members must achieve a certain amount of reproduction lest they pursue a noncooperative option leading to group-breakup (Fig. 1). The BTOW model may be the most realistic model of reproductive skew in that it does not assume complete reproductive control by any individual and allows for conflict within groups. Indeed, we will argue that it provides a much better fit to existing data on reproductive skew in a variety of species, especially cooperatively breeding vertebrates, than does either the old transactional models or the pure tug-of-war model.

Fig. 1.

The BTOW model. The dominant concedes a fraction P of the group output to the subordinate; the subordinate concedes a fraction Q of the group output to the dominant. There is a tug-of-war in the zone of contested reproductive shares (1 − P − Q) in which the subordinate sacrifices a fraction y of the group output, and the dominant sacrifices a fraction x of the group output, to increase their reproductive shares. The group output is thus reduced by an amount (the shaded region) equal to the sum of these selfish investments.

The Bordered Tug-of-War

In the bordered tug-of war, a dominant individual must yield a fraction P (>0) of the group's actual total reproduction to the subordinate to prevent the subordinate from pursuing its noncooperative option (e.g., leaving the group), and the subordinate must yield a fraction Q (>0) of the group's actual total reproduction to the dominant to prevent the dominant from pursuing its own noncooperative option. We assume that group members monitor their relative reproduction and take the noncooperative option when their reproductive share falls below the critical level. As in all transactional models, this monitoring and ability to pursue the noncooperative option allows group members to extract reproductive concessions from other group members.

To keep the model flexible, at this point, we do not specify what the noncooperative option is for either group member, although it could involve leaving the group, joining another group, fighting to the death, or fighting for sole control of the nest or territory and leaving if the fight is lost. If the subordinate pursues its noncooperative option, it receives a personal payoff of S (payoff to self) and the dominant receives a personal payoff of D (payoff to different individual). If the dominant pursues its noncooperative option, it receives a personal payoff of S′ and the subordinate receives a personal payoff of D′.

We assume incomplete control of reproductive shares. Each party must choose a level of selfish effort that will determine its share of reproduction won in a tug-of-war over the disputed fraction of group reproduction, 1 − P − Q. The subordinate uses up a fraction y of the maximum possible group output G as its selfish effort in the tug-of-war over the disputed fraction, and the dominant uses up a fraction x of the maximum possible group output G as its selfish effort. As in pure tug-of-war models (1), the subordinate's fraction of the disputed share is equal to

where b (≤1) is the competitive efficiency of the subordinate relative to the dominant. The actual group output after the tug-of-war is equal to G(1 − x − y).

Thus, the subordinate's inclusive fitness I, given a symmetrical relatedness r to the dominant, is equal to the actual group output times its total share of reproduction (share conceded by the dominant plus share won in the tug-of-war) plus its relatedness to the dominant times the actual group output times the dominant's total share of reproduction:

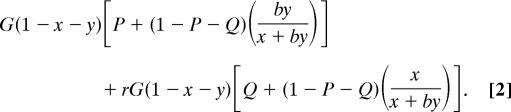Likewise, the dominant's inclusive fitness I′ is equal to

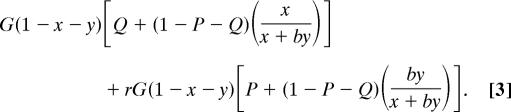Thus, in the BTOW model, there are four targets of selection: P, the share conceded to the subordinate; Q, the share conceded to the dominant; y, the subordinate's selfish effort in the tug-of-war; and x, the dominant's selfish effort in the tug-of-war. We solve for the evolutionarily stable values of these decision variables simultaneously by simultaneously solving the four equations:

The first two equations are the classic tug-of-war equations (1), and the last two equations express the transactional requirement that each party will concede just barely enough reproduction to the other party to prevent the latter from pursuing its noncooperative option.

Although seemingly complex, the raw solutions can be used to derive remarkably simple predictions for the reproductive skew and levels of conflict within groups. The raw solutions are:

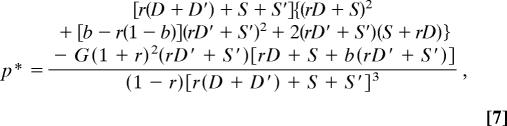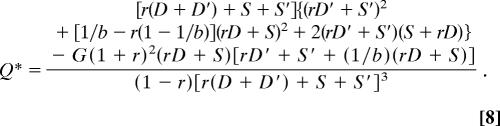We assume that P* and Q* > 0, i.e., both parties have to concede reproduction to each other to prevent collapse of cooperation [cases in which this assumption is violated lead to one-sided bordered tugs-of-war or a pure tug-of-war (unpublished results)]. The solutions for the selfish efforts correspond to inclusive fitness maxima under the condition that the group is stable (see below).

An immediate feature of the raw solutions is that the levels of selfish effort in the BTOW model become functions of the ecologically influenced noncooperative payoffs (S, S′, D, and D′) unlike in the pure tug-of-war model, immediately generating a theory of how ecological parameters and relatedness will determine both skew and the level of conflict within groups. Remarkably, the stable selfish efforts given in Eqs. 5 and 6 do not depend on the relative competitive efficiency b of the subordinate, in striking contrast to selfish efforts in the pure tug-of-war (1). However, as will be seen below, relative subordinate condition may still affect skew and conflict by influencing the noncooperative payoffs S, S′, D, and D′.

From the raw solutions in Eqs. 5–8, we can easily compute the subordinate's overall share of reproduction p* (conceded share plus share won in the tug-of-war) as

In this general model, the overall subordinate share will depend on the ecologically influenced noncooperative payoffs and not on the subordinate's competitive efficiency, as in transactional models, but the role of relatedness depends on the nature of the noncooperative payoffs (as will be seen below).

From the raw solutions in Eqs. 5–8, we can also compute R, the fraction of maximum group output not used up in the tug-of-war, which is equal to 1 − x* − y*. R is an inverse measure of the overall destructiveness of within-group conflict and is given by:

The latter reveals that R increases, i.e., total intracolony conflict decreases as the personal noncooperative payoffs become larger relative to the maximum group output. In other words, the less attractive that the noncooperative option is (e.g., when there are strong ecological constraints on leaving the group), the greater will be the amount of destructive conflict within the group, because the minimal payments decrease and the tug-of-war zone correspondingly expands. The actual group output is just RG, and groups are stable as long as R ≤ 1.

To derive detailed predictions, we next apply the BTOW model to a set of specific noncooperative options that seems to be fairly realistic for many cooperative groups and encompasses the noncooperative options assumed by most previous transactional theories (5).

Fighting and Leaving

We assume that the noncooperative option for a subordinate is to fight for sole possession of the nest or territory and to leave only if it loses the fight. Let f (≤1/2) be the probability that the subordinate wins the fight (which therefore reflects the subordinate's resource holding power). If the subordinate wins the fight, it acquires the nest or territory with personal payoff t. If the subordinate loses the fight (probability = 1 − f), it leaves and receives the solitary breeding payoff s. Thus, S = ft + (1 − f)s and D = (1 − f)t + fs. We assume that the same noncooperative option holds for the dominant, such that S′ = (1 − f)t + fs and D′ = ft + (1 − f)s. This pair of noncooperative options includes as special cases that (i) noncooperation leads to a fight to the death (if s = 0) and (ii) the subordinate simply leaves and the dominant simply ejects the subordinate without cost (f = 0), both of which are noncooperative strategy sets assumed by previous transactional models (5).

Using Eqs. 5–8 above, we solve first for the evolutionarily stable selfish effort by the dominant:

It must be that G > t + s for a stable group (otherwise, 1 − P* − Q* < 0), and it seems likely that t > s (the payoff for sole possession of the nest or territory is greater than the payoff for leaving). If the subordinate is weaker than the dominant (f < 1/2), then the following predictions hold:

1. The dominant's selfish effort will increase with increasing relatedness to the subordinate.

2. The dominant's selfish effort will increase with increasing subordinate fighting ability f.

3. The dominant's selfish effort will increase with increasing maximal group output G.

Using Eqs. 5–8 above, we next solve for the evolutionarily stable selfish effort by the subordinate:

Given that G > t + s, f < 1/2, and t > s (the payoff of the nest or territory is greater than the payoff for leaving), the predictions are:

1. The subordinate's selfish effort will decrease with increasing relatedness to the dominant, oppositely to the case for the dominant.

2. The subordinate's selfish effort will decrease with increasing subordinate fighting ability f.

3. The subordinate's selfish effort will increase with increasing maximal group output G.

All of the above predictions about selfish efforts contrast markedly with predictions of selfish efforts in the pure tug-of-war model (1).

From the raw solutions in Eqs. 5–8, we can easily compute the subordinate's overall share of reproduction p* (conceded share plus share won in the tug-of-war) as simply:

The predictions are:

1. In stark contrast to earlier transactional models, the subordinate's share is independent of relatedness: increasing relatedness decreases its conceded share but increases the share won in the tug-of-war, and these two effects exactly cancel.

2. If f < 1/2, the overall subordinate's share increases with the solitary (leaving) payoff s.

3. If t > s, the overall subordinate's share increases with its fighting ability f.

4. If f < 1/2, the overall subordinate's share decreases with the value of the nest or territory t.

Thus, an important result of the BTOW model with the fighting and leaving option is that reproductive skew no longer depends on relatedness, but only on ecological factors and relative fighting ability.

From the raw solutions in Eqs. 5–8, we can also compute R, the fraction of maximum group output not used up in the tug-of-war, which is equal to 1 − x* − y*. R is an inverse measure of the overall intensity of within-group conflict and here becomes simply:

The latter reveals that the level of cooperation R increases, i.e., total intracolony conflict decreases, as the total payoff for two noncooperative group members becomes larger relative to the maximum group output if they cooperate (independently of relatedness). In other words, when there are strong ecological constraints against breaking up the group, the greater will be the amount of destructive conflict within the group. Groups that are more stable will have higher levels of internal conflict. An important corollary of Eq. 14 is that the actual group output in a BTOW is just (actually slightly above) t + s.

Finally, there is an interesting connection between the subordinate's share in Eq. 13 and level of cooperation R in Eq. 14: the dominant's share (i.e., the reproductive skew) is equal to 1 − p*, which is equal to f + (1 − 2f)/RG. In other words, reproductive skew and intragroup conflict will be positively related if f < 1/2.

Asymmetrical Relatedness

The above model assumed symmetrical relatedness between the dominant and subordinate. We briefly consider what happens when there is asymmetrical relatedness to each other's offspring, as when the dominant is the parent of the subordinate (and there is no extra-pair paternity). In this case, the r in Eq. 2 for the subordinate's inclusive fitness becomes equal to 1.0, because it will be as closely related to siblings as to its own offspring; the r in Eq. 3 for the dominant's inclusive fitness becomes equal to 1/2. The selfish effort for the subordinate in this case drops to zero, which then leads to an infinitesimal selfish effort by the dominant, and P* becomes 0, with the result that there is predicted to be complete skew and no intra-group conflict.

Conclusions and Possible Relevance to Empirical Skew Data

Thus, in the fight-and-leave case of the BTOW, the overall fraction of reproduction captured by the subordinate increases the greater its probability f of winning the fight, the greater its leaving payoff s, and the less the payoff t for sole possession of the nest or territory (Table 1). The maximal group output G and the genetic relatedness r have no net effect on the subordinate's share, making the skew predictions of the BTOW strikingly different from those of either the pure transactional or the pure tug-of-war models (1, 5). As we shall see below, these predictions mesh well with reproductive skew data in a number of species (including meerkats, lions, and wood mice) that have resisted accommodation by either transactional or pure-tug-of-war frameworks.

Table 1.

Comparison of model predictions for changes in the subordinate's share as each parameter changes (other parameters held constant)

	Pure transactional (complete dominant control with transactions)	Pure tug-of-war (incomplete control)	BTOW (incomplete control with transactions)
Leaving payoff s increased	+	0	+
Payoff for sole possession of nest or territory t increased	+	0	− (f < 1/2)
Relatedness increased	−	0	0
Subordinate's fighting ability increased	+	+	+
Maximal group output G increased	−	0	0

We assume (i) the fighting and leaving noncooperative option and (ii) the payoff for winning the fight to retain the nest or territory t is greater than the payoff s for having to leave if the fight is lost. 0, the model predicts no effect on the subordinate's share; −, there is a predicted decrease; +, there is a predicted increase.

It is important to note that the form of the subordinate's share allows us to determine when this share (and thus the reproductive skew) will be determined primarily by an intrinsic factor (the subordinate's fighting ability) versus the ecological factors s and t. To see this point, suppose that we measure the degree of ecological constraint on group living as X = s/t, where decreasing X corresponds to harsher ecological constraints as in previous transactional models (5). The subordinate's share then is simply equal to [f(1 − X) + X]/(1 + X). Under harsh ecological constraints, i.e., as X approaches 0, then the subordinate's share is just equal to its probability of winning a fight, f. Under weaker ecological constraints, i.e., as X approaches 1, the subordinate's fighting ability has little or no effect on its share, which now is determined primarily by ecological factors: the subordinate's share equals X/(1 + X) if constraints are weak enough and f is low enough. Thus, reproductive skew will be more strongly coupled to resource holding power under strong ecological constraints and more strongly coupled to ecological factors under weaker constraints.

In the fight-and-leave variant of the BTOW, the fraction of the total group output that is not used up in the tug-of-war is just (s + t)/G. In other words, the magnitude of the group-level destruction due to the conflict should be worse when group members have worse options for breaking up the group. The subordinate's fighting ability f and the genetic relatedness r have no net effect on magnitude of the conflict, making the BTOW conflict predictions completely different from those of the pure tug-of-war model of intragroup conflict (Table 2).

Table 2.

Comparison of model predictions for changes in total within-group conflict (measured as proportion of group output expended in the tug-of-war) as each parameter changes (other parameters held constant)

	Pure transactional (complete dominant control)	Pure tug-of-war (incomplete control)	BTOW (incomplete control with transactions)
Leaving payoff s increased	0	0	−
Payoff for sole possession of nest or territory t increased	0	0	−
Relatedness increased	0	−	0
Subordinate's fighting ability increased	0	+	0
Maximal group output G increased	0	0	+

We assume (i) the fighting and leaving noncooperative option and (ii) the payoff for winning the fight to retain the nest or territory t is greater than the payoff s for having to leave if the fight is lost. 0, the model predicts no effect on total conflict; −, there is a predicted decrease; +, there is a predicted increase.

The BTOW model seems to be compatible with reproductive skew data from a variety of species for which complete control transactional and/or pure tug-of-war models seem relatively poor fits. We briefly consider three cases, all of which should be the focus of more quantitative discriminating tests.

Meerkats.

Clutton-Brock et al. (6) conducted an extensive study of reproductive skew and conflicts in meerkats and presented evidence that dominants have incomplete control over reproduction, apparently supporting the pure tug-of-war model. Relatedness did not affect the reproductive skew, subordinates in better condition reproduced more, and subordinates produced relatively more offspring in years of higher rainfall, all of which are compatible with the BTOW model predictions with regard to r, f, and s, respectively. The finding that ecological factors such as rainfall affect reproductive skew is not predicted by pure tug-of-war models without adding special assumptions about how the subordinate's relative competitive ability is affected by those factors. Thus, the BTOW model currently seems the best fit to the data.

Lions.

Packer et al. (7) found that female lions have a very low reproductive skew and low levels of internal conflict (reflected in the weak expression of dominance behavior), despite having high values of within-group relatedness, which they argued supported a pure tug-of-war over transactional models of reproductive skew. These findings are also compatible with the fight-and-leave version of the BTOW model. To see this point, note that, in lions, the payoff for sole possession of nest site t may be similar to the leaving payoff s because there is no fixed territory containing long-lasting resources in this species. If s equals t, the BTOW model predicts even sharing of reproduction regardless of relatedness. (The latter also is predicted if the noncooperative option is just to leave without a fight for both group members, i.e., S = S′ = s.)

Wood Mice.

Gerlach and Bartmann (8) found that reproductive skew, subordinate output, and total pair reproductive output did not differ between pairs of unrelated females and pairs of sisters, which they pointed out contradict both the pure tug-of-war and the complete control transactional models. However, all these results are predicted by the BTOW model with the fighting-and-leaving option. Moreover, they found that greater reproductive skew in favor of the dominant was associated with greater aggression by the dominant, also as predicted by the BTOW model. Finally, mother–daughter associations exhibited relatively high total outputs and subordinate nursing times, which is the BTOW prediction for asymmetrical relatedness.

The applicability of the BTOW model to such systems and perhaps many others may be due to the enhanced realism of its assumptions. First, it allows for incomplete control by dominant individuals, the degree of control being continuously varying. Importantly, it allows for both internal conflict and reproductive concessions (transactions) required to maintain group stability, making it the most complete model of the balance of social cooperation and conflict that yet exists. We have termed the model the “bordered tug-of-war,” but we might equally well have labeled it an “incomplete control transactional model,” because both terms capture the model's hybrid nature. The model also incorporates features of “pay-to-stay” models of reproductive skew (9), because the selfish investments in the tug-of-war can be viewed as the inverse of “work payments” made to the other party. In other words, each party (not just one, as in current pay-to-stay models) must decide how much to contribute to the group output by restraining its selfish effort. Although these “payments” are distinct from, and additional to, the shares of reproduction that each party concedes to the other as incentives for cooperation, the BTOW model predicts how they should be optimally adjusted in the face of the threat that the other party will choose its noncooperative option.

Although the BTOW is a hybrid model, it generates entirely new predictions (such predictions are not a mere “averaging” of the predictions of the pure tug-of-war and complete control transactional models; see Tables 1 and 2). Another novel prediction is that the actual group output will be close to sum of the separate outputs of the dominant and subordinate if the group breaks up. In other words, the model predicts that there may often be no clear-cut advantages to group living when group reproductive output is compared with the sum of reproductive outputs of solitary individuals. Thus, the model may even illuminate puzzling cases in which groups are not obviously more productive than an ensemble of solitary breeders. The next theoretical challenge is to determine under what general conditions the BTOW, pure tug-of-war, and transactional models with one-way payments each will apply. These conditions are closely tied to the ecological circumstances under which the required payments to the dominant Q* and the subordinate P* are (i) both >0; (ii) both 0; and (iii) 0 in one case but >0 in the other (unpublished results), respectively.

Abbreviation

BTOW

bordered tug-of-war.