Coarse-grained normal mode analysis in structural biology

Abstract

The realization that experimentally observed functional motions of proteins can be predicted by coarse-grained normal mode analysis has renewed interest in applications to structural biology. Notable applications include the prediction of biologically relevant motions of proteins and supramolecular structures driven by their structure-encoded collective dynamics; the refinement of low-resolution structures, including those determined by cryo-electron microscopy; and the identification of conserved dynamic patterns and mechanically key regions within protein families. Additionally, hybrid methods that couple atomic simulations with deformations derived from coarse-grained normal mode analysis are able to sample collective motions beyond the range of conventional molecular dynamics simulations. Such applications have provided great insight into the underlying principles linking protein structures to their dynamics and their dynamics to their functions.

Introduction

Recent advances in sequencing and structural genomics indicate that the canonical sequence-to-structure-to-function paradigm is insufficient for understanding and controlling the mechanisms of biomolecular interactions and functions. Because molecular structures are dynamic rather than static, information regarding their dynamics is required to establish the link between structure and function. Normal mode analysis (NMA) has re-emerged in recent years as a powerful method for elucidating the structure-encoded dynamics of biomolecules. NMA has been applied to proteins since the early 1980s [1,2]. However, its usefulness in structural biology has been exploited only recently, after the observation that the collective motions predicted by NMA for folded structures are highly robust and bear functional significance [3,4,5••]. Although the actual motions of macromolecules in solution are very complex, involving transitions among innumerable conformations, the success of NMA hinges upon the fact that motions near native state conditions are much simpler and more robust. Structural changes are dominated by the inter-residue contact topology of the folded state, implying that the most probable deformations are those requiring the smallest energy ascent in the multidimensional energy landscape.

It is plausible that the motions NMA predicts are functional if one considers that each protein functions only if it is folded into its equilibrium/native structure and that each equilibrium structure encodes a unique equilibrium dynamics. Furthermore, NMA yields a unique analytical solution of the modes of motion accessible at equilibrium (near a global energy minimum). Thus, the equilibrium dynamics predicted by NMA, and the structure-encoded collective motions in general, ought to be functional, based on the premise that each protein has evolved to optimally achieve its biological function.

This review centers on the use of coarse-grained NMA methods to refine experimental data and predict biological functional features from macromolecular structures. The merits of several related methods are discussed, as well as recent successes in identifying the intrinsic motions of proteins and future prospects. Special attention is given to applications in which these models are used to predict motions, dynamics, and critical residues for function or folding.

EN models and coarse-grained NMA

Building upon the ability of NMA to predict the most probable cooperative motions of biomolecular structures, much of the increased utilization of NMA in recent years has resulted from the introduction of computationally simpler elastic network (EN) models. These EN models replace detailed atomic potentials with uniform harmonic potentials between interacting atom or residue pairs [6-8]. These and subsequent studies have demonstrated that the large-scale collective motions predicted by NMA are insensitive to both the model and the details of the force-fields used, provided that the topology of inter-residue contacts in the native structure is accurately modeled [6-11]. Given the computational efficiency of coarse-grained NMA, a convenient methodology has been to map the protein structure onto its EN model, perform a coarse-grained NMA using an EN model of suitable resolution to generate ‘alternative’ structures sampled during equilibrium fluctuations, and use the NMA-generated ‘alternative’ forms to characterize the natural dynamics or reconstruct structures at their atomic-level representation. This three-step procedure and associated applications are summarized in Figure 1. Below, we briefly describe the tasks indicated in the figure and discuss the various applications to structural biology.

Figure 1.

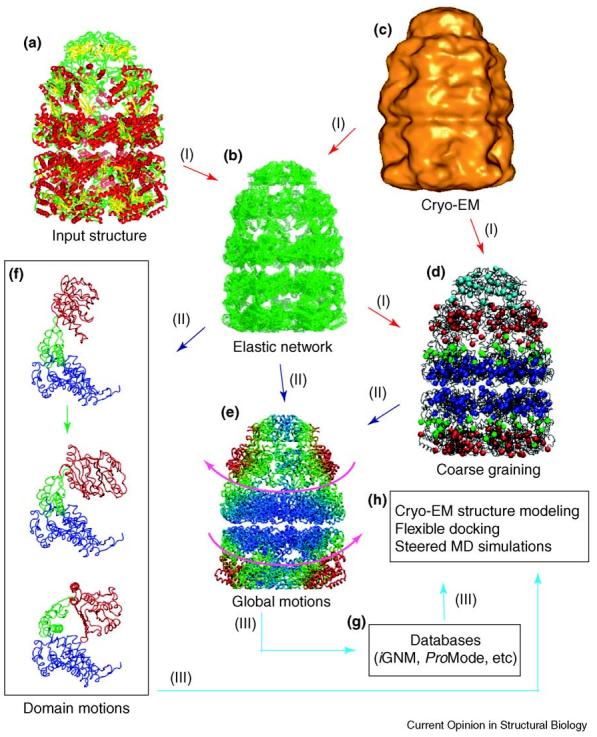
Overview of various methodologies and applications to the GroEL–GroES complex of EN models. The EN model (b) requires an initial input structure, typically an atomic-resolution structure such as in (a), colored according to secondary structure elements. As noted in the text, a lower-resolution structure, such as a cryo-EM map (c), can also be used as input for constructing an EN model. In order to process supramolecular assemblies, further coarse graining (d) is adopted. A low-resolution EN model in which only every 20^th residue is used to define the nodes is shown. Once the EN model is constructed, various motions are calculable by NMA, ranging from the level of the entire molecule to domains and individual residues. (e) The global motions computed for the GroEL–GroES complex (PDB code 1gru) [68], revealing a counter-rotation of the GroES-bound (trans) ring with respect to the lower (cis) ring (as shown by the magenta arrows). The structure has been colored by increasing mobility from blue to red, showing that the mobility increases with increasing distance from the interface between the cis–trans rings and from the cylindrical axis of symmetry. (f) The motions of the individual subunits, each composed of three domains (apical, red; intermediate, green; equatorial, blue), obtained from analysis of the EN model. The top diagram shows the ATP-bound form of a subunit in the trans ring and the lowest diagram is its unliganded counterpart in the cis ring. Applying the deformations from the first (slowest) mode calculated by NMA to the trans ring monomer produces the middle structure, demonstrating the intrinsic (structure-encoded) ability of the subunit to reconfigure into the closed form assumed in the cis ring. This is consistent with successive interchange of the subunit conformations between the two forms upon binding of the cap to either ring and cap dissociation during the chaperonin cycle. From these calculations, (g) databases of global motions have been constructed, and (h) several important additional applications of these motions and deformations have been indicated.

Mapping the structure onto reduced models that maintain contact topology

The most common model adopted in coarse-grained NMA involves a single site per residue representation, in which the sites are identified by the Cα atoms and connected by uniform springs. The dynamics of such an interconnected bead-and-spring model can be described by the Gaussian network model (GNM) or an EN model using potentials of the form:

$$V=\frac{\gamma }{2}\left[\sum _{i,j}^N\left({\mathit{R}}_{\mathit{ij}}-{\mathit{R}}_{\mathit{ij}}^0\right)•\left({\mathit{R}}_{\mathit{ij}}-{\mathit{R}}_{\mathit{ij}}^0\right)f\left(R_{\mathit{ij}}^0\right)\right]$$ (1)

$$V=\frac{\gamma }{2}\left[\sum _{i,j}^N{\left(\mid R_{\mathit{ij}}\mid -\mid R_{\mathit{ij}}^0\mid \right)}^{2}f\left(R_{\mathit{ij}}^0\right)\right]$$ (2)

for the GNM and the EN model, respectively. Here, γ is the uniform spring constant, ${\mathit{R}}_{\mathit{ij}}^0$ and R_ij are the original and instantaneous distance vectors between residues i and j, $R_{\mathit{ij}}^0$ and R_ij are the corresponding magnitudes; the summation is performed over the pairs of residues/nodes filtered through the function $f\left(R_{\mathit{ij}}^0\right)$, which selects the interacting pairs. $f\left(R_{\mathit{ij}}^0\right)$ is either the Heaviside function based on an interaction cut-off distance of R_c[$f\left(R_{\mathit{ij}}^0\right)=-1$ if $R_{\mathit{ij}}^0\le R_c$ and zero otherwise] [10,11] or an exponentially decaying function of distance [9].

Lower resolution models have been adopted in order to examine larger biomolecular assemblies, whereby groups of residues are clustered into unified sites [12,13] or rigid blocks (such as the rotations and translations of blocks [RTB] and block normal mode [BNM] methods) [14,15]. Related methods effectively quantize the shape of the structure without directly identifying specific residues or groups of residues [16,17]. A reduction in the number of nodes by one order of magnitude increases the computation speed by three orders of magnitude, as NMA computing time scales with N³. Notably, the global motions computed by such coarse-grained NMA maintain their fundamental characteristics and can be related to functional mechanisms [13].

Performing NMA with EN models: functional deformations and critical sites

NMA depends upon the eigenvalue decomposition of the Hessian matrix — a 3N × 3N matrix composed of the second derivatives of the potential (V ) with respect to residue fluctuations. Thus, for an EN model potential (Equation 2), one obtains 3N–6 normal mode vectors describing anisotropic deformations. In the case of the GNM, the Hessian is replaced by the N × N Kirchhoff matrix (Γ), which describes the inter-residue contact topology, such that N–1 isotropic modes are obtained. The B-factors computed by the GNM yield good agreement with X-ray crystallographic data [18] and NMR order parameters [19]. However, the mechanisms of deformations cannot be characterized unless a 3N-dimensional Hessian is used in NMA.

An exciting contribution of NMA to structural biology is its ability to provide insight into large-scale and long-time conformational motions of proteins, which tend to be inaccessible to standard molecular dynamics (MD) techniques. Recent applications to very large supramolecular assemblies include the ribosome [20,21] and viral capsids [22,23]. In general, a few of the low-frequency modes (u_j) predicted by NMA exhibit a large degree of overlap:

$$I_j=\frac{\mid {\mathit{U}}_j•\Delta \mathit{r}\mid }{{\mid \sum _i^{3N}{u}_{\mathit{ij}}^2\mid }^{1∕2}{\mid \sum _i^{3N}\Delta r_i^2\mid }^{1∕2}}$$ (3)

with the vector describing the displacement between two known conformations (Δr) [11]. Overlap values exceeding 80% suggest that the structures (open and closed) have an intrinsic tendency to reconfigure along a small set of low-frequency modes, even if the fully evolved conformational change might involve passage over a conformational energy barrier. Recently, it has been shown that only minimal information about the target structure is required to drive one structure into the other through a linear combination of low-frequency normal modes [24].

The usefulness of NMA becomes particularly significant when combined with experimental data. Notable applications that provide insights into functional mechanisms include the study of muscle myosin ATPase regulation [25] and flexibility [26,27•], the modulation of protein flexibility during the RNA polymerase cycle [28] and the elucidation of the ribosomal machinery [20,21].

Although these coarse-grained Cα-based NMA methods lack any sequence specificity, there is increasing evidence of their ability to identify functional and structural roles of individual residues. Many studies have identified residues that impart inherent stability and are critical for folding [29-31], as well as residues that form binding ‘hot spots’ [32], catalytic residues [33•] and deformable residues [34].

Applications to structural biology: use in predicting structure and dynamics

Flexible docking

A major application of NMA is the identification of potential conformational changes (e.g. of enzymes upon ligand binding) [11,35]. In particular, it has been shown that over half of 3800 known protein motions (inferred from different conformations of the same protein) can be approximated by perturbing the original structures along the direction of their two lowest-frequency normal modes [36]. Such results suggest that protein structures may have evolved to accommodate or facilitate biologically functional conformational changes. Among the alternative mechanisms of motion accessible near the folded state, those along the smoothest ascent directions are the most readily explored. The biological functions will then be more readily achieved, provided that the associated motions coincide with those smoothest ascent directions (i.e. those along the lowest-energy modes). The fact that the observed changes coincide with those predicted by the slowest NMA modes should not be a coincidence, but a design principle favored by nature. Building on the notion that NMA can be used to identify potential motions induced by binding, a computationally tractable way to generate a set of docking targets has been proposed [35].

Cryo-EM structure modeling

Recently, there have been several applications of NMA to low-resolution cryo-electron microscopy (cryo-EM) structure modeling. Such experimental data are naturally low resolution, being reconstructed by averaging over multiple images of many molecules from several different angles. Additionally, the imaged molecules often undergo structural changes together with vibrations, making it very difficult to extract high-resolution structural information. Several groups [16,17,37•] have constructed EN models of pseudo-atomic representations for a given cryo-EM map and calculated the resulting distortions due to normal modes as an aid in the refinement of the raw cryo-EM data to produce higher resolution structural information. Alternatively, a procedure for the flexible docking of atomic or residue-level structures into cryo-EM maps has been suggested, using the NMA mode shapes calculated for either the pseudo-atomic EN models or homology-based structures [37•,38•,39,40••].

Domain identification

Because elastic networks quickly identify coupled motions, it is possible to partition a protein into various domains [9]. Recently, this idea of decomposing proteins into domains based on their structural topology has been automated [41], and applied to identifying domains that have been recombined or swapped during evolution [42].

Steering MD simulations and exploring non-equilibrium dynamics

As discussed above, the low-frequency modes from NMA are able to capture the collective dynamics of proteins. This fact has recently been applied to steer MD simulations along these dominant modes of motion using hybrid methods that combine MD and harmonic modes [43••,44,45]. Specifically, a hybrid MD/NMA simulation protocol has been implemented, whereby motions along the direction of the slowest few modes are coupled to a temperature bath and thus amplified to study the unfolding and large-scale domain motions of peptides and proteins [43••,44]. The inverse of this approach, namely that the normal modes of a protein can be extracted from an applied driving force in an MD simulation [46], has also recently been shown.

Drawing on similar insight, it has been suggested that one can minimize steric clashes and interpolate between two conformations of a protein using the modes from an EN model [47] to characterize this transition. Because the harmonic approximation of NMA remains valid only near the equilibrium structure, an alternative method for escaping the local minima surrounding the native state involves the iterative calculation of successive EN models deformed along one or several low-frequency modes [48]. This method allows ‘cracking’ or partial unfolding of the underlying EN structure, suggesting that such unfolding or ‘proteinquakes’ may be coupled to collective motions [49,50•].

High-throughput examination of families of proteins

Fold families, such as globins [51], and protein super-families [52••] in general have been compared using NMA-based methods to identify common and distinctive structural and dynamic features. For the test case of proteases, salient dynamic features derived from GNM calculations, combined with data-mining methods in an unsupervised learning technique, have been shown to identify the highly conserved catalytic triad [53]. More recently, the minima in the slowest modes (global hinge centers) have been shown to be co-localized near catalytic residues in a representative set of enzymes [33•]. These results indicate that a great deal of information about functional residues can be extracted from the comparative coarse-grained NMA of protein family members.

How are NMA predictions verified by experiments?

Inherent to many of these computational predictions is assignment of correlated or collective motions. Several experimental techniques, including hydrogen-deuterium (H/D) exchange, FRET probes and labeled NMR, have the capacity to verify such predictions by identifying pairs of residues that experience coupled motions. Key residues predicted to act as functional hinges or ligand-binding sites [33•], or critical to folding [29,30] are tested by site-directed mutagenesis (e.g. correlated mutations), H/D exchange data and other biochemical (e.g. cross-linking) experiments. The free energy changes associated with H/D exchange of individual amino acids measured near native state conditions for a series of proteins have been correlated, for example, with the entropic costs predicted by the GNM [54]; the experimentally observed structural changes of enzymes between their open and closed forms have been shown, in several applications, to correlate with the low-frequency motions predicted by coarse-grained NMA [11,19,33•,55]. As mentioned above, NMA results are particularly useful in providing insights into molecular mechanisms of biological function when interpreted in conjunction with experimental data [21,25,26,27•,28-32,33•].

Databases and servers of molecular motion

The logical extension of family analysis is the compilation and maintenance of web-accessible databases housing NMA-based calculations for all available protein structures. Several such databases have been constructed, including iGNM [56], ProMode [57], ElNémo [58], WEBnm [59] and MolMovDB [60], which allow the user to browse precalculated data and/or submit structures for NMA.

Conclusions and perspectives

The past five years have seen a renewed interest in NMA-inspired methods because they provide a biologically relevant and unique analytical solution of the equilibrium dynamics of biomolecules. The successes of NMA indicate that three-dimensional structures contain the requisite information to determine functional motions. The most collective, or global, modes of motion predicted by NMA are insensitive to the details of models and energy parameters, and instead depend on the topology of inter-residue contacts at equilibrium; this justifies the widespread use of the more efficient coarse-grained EN models described here. Such approaches are now being used, in conjunction with experimental studies, to unravel the supramolecular dynamics and long timescale motions of large structures that are otherwise inaccessible via conventional simulations.

These studies lead to emerging paradigms for a dual role for key structural elements in both chemical and mechanical activities of enzymes [33•,61], or in both folding and signaling properties of membrane proteins [30,62]. More recently, applications to membrane proteins have provided insights into their gating mechanisms [63,64]. The major future directions of this type of computational research and also the anticipated impact on structural biology lie in the elucidation of the functional dynamics of quaternary structures or supramolecular assemblies, as already suggested by the applications to the ribosome, viral capsids and motor proteins [20-23,25,26,27•,28]. Also, the development of hierarchical coarse-graining algorithms that reduce the complexity of the systems while maintaining their functional features will become increasingly important [65].

The utility of coarse-grained NMA partially stems from the use of EN models for analyzing structure-encoded dynamics. An important area of future research is deciphering the networks of communication in biomolecular systems and, in particular, understanding the allosteric mechanisms of signal transduction [66••]. EN-based models, combined with NMA and machine learning algorithms, appear to be promising tools for quantifying allosteric effects [65,67].