The group covariance effect and fitness trade-offs during evolutionary transitions in individuality

Abstract

Transforming our understanding of life is the realization that evolution occurs not only among individuals within populations but also through the integration of groups of preexisting individuals into a new higher-level individual, that is, through evolutionary transitions in individuality. During evolutionary transitions (such as during the origin of gene networks, bacteria-like cells, eukaryotic cells, multicellular organisms, and societies), fitness must be reorganized; specifically, it must be transferred from the lower- to the higher-level units and partitioned among the lower-level units that specialize in the fitness components of the new higher-level individual. This paper studies the role of fitness trade-offs in fitness reorganization, the evolution of cooperation, and the conversion of a group into a new individual during the origin of multicellular life. Specifically, this study shows that the fitness of the group is augmented over the average fitness of its members according to a covariance effect. This covariance effect appears to be one of the first emergent properties of the group and a general aspect of groups with multiplicative properties that are themselves averages of properties of lower-level units. The covariance effect allows groups to break through the constraints that govern their members, and this effect likely applies to group dynamics in other fields.

Transforming our understanding of life is the realization that evolution occurs not only among individuals within populations but also through the integration of groups of preexisting individuals into a new higher-level individual, that is, through evolutionary transitions in individuality (1–5). These evolutionary individuals constitute the familiar hierarchy of life: gene networks, bacteria-like cells, eukaryotic cells, multicellular organisms, and certain societies of organisms such as social insects. How does a group become an individual? This is the central question motivating this study. The premier example of the process of individuation of groups is the evolution of multicellular individuals from unicellular and colonial ancestors. The hypothesis explored here is that specialization of reproductive and vegetative viability-enhancing functions, termed germ–soma specialization, is a major factor in the conversion of cell groups into true multicellular individuals. Once cells specialize in fitness components, they cannot survive and reproduce on their own, and the group becomes indivisible and, hence, an individual.

The fitness of any evolutionary unit can be understood in terms of its two basic components: fecundity (reproduction) and viability (survival). As embodied in current theory, trade-offs between these fitness components drive the evolution of diverse life-history traits in extant organisms (6, 7). Fitness trade-offs gain special significance during the transition from unicellular to multicellular life for several related reasons: (i) fitness trade-offs often create a covariance effect at the group level so that group fitness is augmented beyond the average fitness of component cells; (ii) fitness trade-offs based on preexisting life-history variation provide a basis for the emergence of cooperative interactions within the group; and (iii) fitness trade-offs select for germ–soma specialization. These ideas are further developed in the study reported here.

Although kinship has long been appreciated as a necessary precondition for the transition to multicellularity (1, 3–5), there are colonial species with high degrees of kinship that have not evolved true individuality (i.e., germ–soma specialization). For example, in the volvocine green algae (8), all cells in a colony are clonally derived from a single cell, often by just a few cell divisions, yet true individuality based on germ–soma specialization emerges only in the larger colonies. To understand what other factors are needed for germ–soma specialization, the model studied here assumes high kinship among cells (it assumes no genetic variation or selection within groups).

The model studied here is motivated in part by the biology of volvocine algae. These algae are flagellated photosynthetic eukaryotic organisms that range from unicellular (i.e., Chlamydomonas) and multicellular forms with no cell differentiation (e.g., Gonium and Eudorina; 8–32 cells) or incomplete germ–soma differentiation (e.g., Pleodorina; 64–128 cells) to multicellular forms with complete germ–soma separation (Volvox; 500–50,000 cells) (8). We use the terms “germ” and “soma” to refer to cells specialized at reproduction and viability functions. Although in some lineages (e.g., Volvox carteri) this specialization is complete and occurs early in development, in other lineages (e.g., Volvox aureus), specialization is not complete and reproductive cells differentiate late in ontogeny from undifferentiated cells or even somatic cells. Flagellar action is important for viability in the volvocines because it provides for motility and mixing of the surrounding medium (9, 10). However, volvocine cells cannot divide to reproduce while flagellated, and this constraint underlies the trade-off between reproduction and viability in this group.

Results

A simple reproductive effort model is developed below to study the evolution of specialization by cells at reproduction and viability (11–13). The phenotype of cells is described by their effort at reproduction (fecundity) with the remainder of effort put into the viability. The viability, V, and fecundity, B, of the group are assumed to be simple additive functions of the cell efforts at viability, v, and fecundity, b. The first result of this model is the group covariance effect given in Eq. 1, showing that the fitness of the cell group, W (taken as the product of V and B), is greater than the average fitness of member cells, w̄, by an amount equal to the negative covariance of the fitness components at the cell level (viability, v, and fecundity, b).

If the covariance between fitness components is itself negative, as is the case when fitness components trade off with one another, then there is an enhanced fitness at the group level from what would be expected from the average of the contributions of single cells. The covariance effect given in Eq. 1 translates the negative covariance of fitness components of group members into a benefit at the group level.

The particular mathematical representation of the covariance effect given in Eq. 1 depends on additivity of fitness effects as described in the Model and Methods. Additivity of fitness effects is the simplest assumption possible, and it likely applies early in the group-formation process. For example, in the volvocine green algae, flagellar action is the main adaptive capacity underlying viability. The forces contributed by cells to group motility are additive initially as cells start forming groups (9, 10). Nevertheless, the assumption of additivity of the contributions of cells to the viability of the group may be relaxed, and the general points below still hold (12).

Indeed, the covariance effect does not depend on additivity, and it is more general than the explicit mathematical form given in Eq. 1. What is required is that, if one cell has a high reproductive effort (and hence a low viability and a low cell fitness), this may be compensated for by another cell with high viability (and hence a low fecundity and also a low cell fitness) (12). Consequently, even though each of these cells by themselves would have a low fitness, together they can bring a high fitness to the group, especially under conditions of convexity of the trade-off (see Model and Methods and Fig. 3). This kind of joint effect, whereby multiple cells may contribute more to the group than could each alone, does not require additivity (12). Also, this kind of joint effect would not be possible if group fitness were simply assumed to be the average of the cell fitnesses (Eq. 4).

Fig. 3.

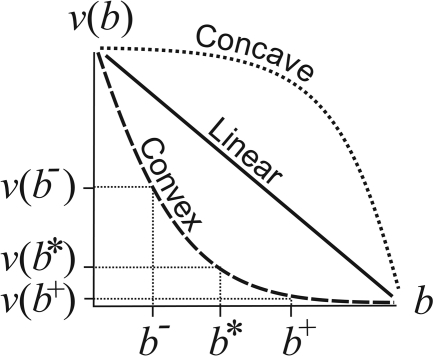
Trade-off relations between viability, v, and fecundity, b. For a strictly convex (concave) function v(b), if we take a particular point, say b*, and two points equidistant below and above b*, say b⁻ and b⁺, respectively, then v(b⁻) + v(b⁺) > (<) 2 v(b*). If b is fecundity and v(b) is viability, then convexity of v implies that there is an advantage to specializing in the two components of fitness, whereas concavity implies there are diminishing returns on investment in either component.

The covariance effect assumes coloniality and the existence of groups. The next result shows how fitness trade-offs and the covariance effect underlie the emergence of altruism and specialization among group members. This result may be illustrated simply by randomly drawing an initial distribution of reproductive effort of cells in cell groups and observing the self-organization of the groups according to the model described in Model and Methods (see Eqs. 2 and 3). In these simulations, groups were reformed each generation by randomly sampling cells across parent groups according to their group fitnesses (Eqs. 2 and 3). These simulations are not intended to represent real development but rather to capture the role of fitness trade-offs in the process of self-organization of groups.

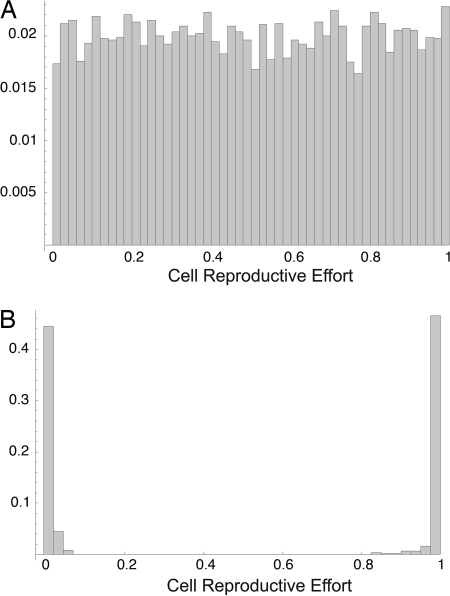
In Fig. 1 we see a typical result after 100 generations for an initially uniform distribution of reproductive effort and convex fitness function. Nearly identical final results are observed for other initial distributions of reproductive effort (e.g., normal distributions). As seen in Fig. 1, cells within groups eventually specialize completely either at reproduction or at viability. By so doing, the group obtains the benefits of convexity, that is, the benefit of increasing returns on cell effort expended at either of the fitness components. Simulations of cells living alone never specialize and attain the intermediate effort which maximizes w = vb. For the parameter values of the simulation in Fig. 1, this intermediate fecundity is b = 0.25, and the maximal cell fitness at this point is w = 0.092, which is approximately half the fitness groups may obtain by specialization (Fig. 2).

Fig. 1.

Initial (A) and final (B) distributions of cell reproductive effort. Total number of cells = 10,000; group size = 6; and v = e^−4b using Eqs. 2 and 3 for group fitness as described in Model and Methods. There are certain issues not fully explored here having to do with finite sampling effects which become stronger as groups get smaller. For example, specialization is more difficult in groups with a group size of two because some groups will only have one specialized cell type and hence have low fitness.

Fig. 2.

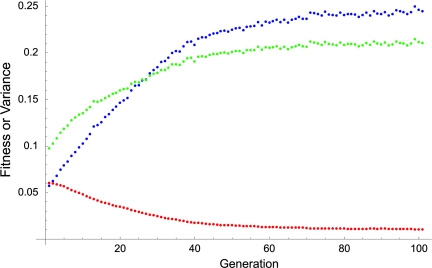
Cell specialization benefits the group and costs the cells within the group. Average group fitness (green) was found by using Eqs. 2 and 3 described in Model and Methods. Average cell fitness, using Eq. 4, is shown in red. Note that both kinds of specialized cells (germ and soma) are altruists. Variance in reproductive effort of cells is shown in blue. The simulation is described in Fig. 1.

Fig. 2 plots the average group fitness, average cell fitness, and the variance in cell reproductive effort during the simulation shown in Fig. 1. As cells specialize, the variance in reproductive effort (blue) reaches its maximal value of 0.25, and the covariance of fitness components reaches its maximum negative value (the covariance of the fitness components of cells within the group follows a similar curve to the variance in reproductive effort in Fig. 1). The average group fitness (green) increases, and the fitness of individual cells within the group declines to near zero (red). As cells specialize, the variance and covariance of fitness components become maximal, leading to an advantage of groups over individual cells as expressed in Eq. 1.

For mathematically concave or linear trade-off functions (see Model and Methods and Fig. 3), cell specialization does not pay (12) and therefore is not observed in the simulations. Although a covariance effect may arise by random events (with some groups by chance having cells with large and small reproductive efforts), the covariance of fitness components eventually declines to zero along with the declining cell variance in reproductive effort. In the end, without convex curvature of the trade-off function, all of the cells living in groups attain the same reproductive effort as do cells living alone, and there is no group benefit. This uniform reproductive effort is the value which maximizes cell fitness w = vb (12).

Discussion

Natural selection at any level requires heritable variation in fitness. During evolutionary transitions in individuality, the heritability of fitness for the new higher level must increase, while, at the same time, it must decrease for the lower-level units. This requires the reorganization of fitness (Table 1), which refers to the transfer of fitness from the lower level to the new higher level (as shown in Fig. 2) and the specialization of lower-level units in the fitness components of the higher-level unit (as occurs in Fig. 1).

Table 1.

Reorganization of fitness during evolutionary transitions in individuality

Fitness components	Viability (vegetative/somatic functions)
	Fecundity (reproductive functions)
Definition of fitness reorganization	Transfer of fitness from lower to higher level
	Lower levels specialize in fitness components of higher level
	Heritability of fitness emerges at higher level
Means of fitness reorganization	Covariance effect
	Fitness trade-offs
	Germ-soma specialization
	Cooperation
	Conflict and conflict mediation
Consequences of fitness reorganization	Individuality at the new higher level
	Increased functionality and complexity
	Evolvability at new level

The fitness of any evolutionary unit can be understood in terms of its two basic components: fecundity (reproduction) and viability (survival) (Table 1). By specializing in these essential components, cells relinquish their autonomy in favor of the group; as a result, fitness and individuality are transferred from the level of the cell to the level of the group. The cell group, by virtue of the specialization of its member cells, becomes integrated and indivisible and, hence, a true individual.

The evolution of cooperation (Fig. 2) is fundamental to this process because cooperation exports fitness from the lower level (e.g., its costs to cells) to the higher level (its benefits to the cell group) and in this way may create new levels of fitness. As with all cases of altruism, there is a selective advantage for cooperative cells to defect and cooperate less. Hence, there is the need (from the group perspective) for mechanisms that reduce conflict and competition among cells and by so doing enhance cooperation for the benefit of the group. A variety of features of modern multicellular organisms can be understood as mediators of conflict because they reduce selection within the organism and increase selection between organisms (5, 14, 15). The most basic conflict mediator in multicellular groups is probably passing the life cycle through a single cell stage (so that all of the members of the group are clonally descended from a single cell) (4, 16, 17). The model studied here assumes high degrees of kinship among cells by assuming that there is no selection among cells within groups, and as a result, selection is at the cell group level. Although fundamental to the origin of multicellularity, high degrees of kinship are not sufficient for the emergence of individuality involving the specialization of cells at reproductive and vegetative functions, as the example of the volvocine algae mentioned previously illustrates.

What factors in addition to kinship are required for the evolution of individuality of cell groups? The factors studied here involve the nature and structure of the fitness effects that underlie the costs and benefits of cooperation. Reproduction and survival trade off with one another, leading to an intermediate effort at both activities when selection occurs at the cell level. It would be costly for cells to depart from this intermediate investment in both fitness components, even when it would benefit the group for them to do so (for example, under conditions of convex curvature of the trade-off, as shown in Fig. 3). For this reason, both kinds of specialized cells, germ and soma, are altruists because for both cell types the specialization costs the cell but benefits the group (Fig. 2). The convex curvature of the trade-offs at the cell level creates an opportunity for the group to capitalize on the increasing returns on efforts that cells may expend on the two fitness components according to the magnitude of the covariance between fitness components (Eq. 1), this effect being maximal when cells specialize in one component or the other (Fig. 2). The covariance effect given in Eq. 1 converts the negative covariance of fitness components into a group benefit, and this benefit in turn selects for increased specialization of cells in the fitness components of the group (Fig. 1). In this way cooperation may emerge from existing life-history trade-offs and the group may break through the trade-off constraints that govern life as a single cell. We have recently presented evidence in the volvocine algae that a somatic (reproductive altruism) gene in the multicellular V. carteri had its origins in a life-history trade-off gene in Chlamydomonas-like unicellular ancestors (18).

Without convex curvature of the trade-off function relating fitness components, there is no advantage to specialization. For example, groups of genetically identical cells would not specialize under a concave trade-off, and there would be no tendency toward cooperation or increased individuality as observed in Fig. 2. The factors in nature underlying a convex curvature of the trade-offs are likely diverse. In the volvocine green algae, we have argued that the curvature is initially concave in unicells but becomes increasingly convex as colonies increase in size because of the increasing cost of reproduction (9, 12, 19). We believe it is for this reason that germ–soma specialization and individuality emerge in only the larger members of this lineage.

The covariance effect is one of the first emergent properties of the group and likely applies to other properties of group structured and nested collectives, where the output or performance of the group is a product of characteristics which are themselves additive functions of contributions of group members. In addition to the examples considered above, to a first approximation whole organism energy use is the sum of the number of mitochondria per cell over the cells in the organism. If there were a trade-off between the amount and efficiency of energy processing by cells, then a beneficial covariance effect would ensue at the whole organism level with respect to the product of energy use and efficiency. In the case of the eukaryotic cell, a covariance effect may underlie the specialization of the mitochondria at energy use and the specialization of the nucleus at reproduction. In a social insect colony we may expect reproduction and viability of individual insects to trade off with one another. The ensuing covariance effect could select for specialization of insect casts at one function or the other. The covariance effect may occur in situations other than evolutionary transitions in individuality. In ecology, ecosystem energy flux is taken to be the summation of flux across individuals within size classes (20). Within each size class, the flux is the product of organismal metabolism and a measure of abundance such as number or mass of the organisms. If there were trade-offs between mass and metabolic rate associated with life history or population performance (21, 22) then there could be an enhanced energy flux at the system level related to the covariance of these organismal properties. The covariance effect is likely relevant to the emergence of new properties in these and other collectives.

Model and Methods

We employ a simple reproductive effort model similar to those used in life-history theory (11–13). Consider groups of N cells, with cells indexed i = 1, 2, …, N. Let e₁, e₂, …, e_N be the reproductive effort for each cell, and let b₁, b₂, …, b_N be the resulting contribution to the fecundity of the group. We assume the contribution to fecundity is an increasing function of reproductive effort, so, for simplicity, we work in terms of fecundity instead of reproductive effort. Let v₁, v₂, …, v_N be the vegetative, viability enhancing, capabilities of each cell. As more effort is put into reproduction, less is available for vegetative functions, resulting in a trade-off between the contributions of the cell to the fitness components of the group. We consider a discrete generation life cycle, which is appropriate for the volvocine green algae (9) and other simple colonial groups, so that the fitness of the group is the product of viability and fecundity as given in Eq. 2.

Furthermore, we assume that the viability and fecundity of the group, V and B, respectively, are simple arithmetic averages of the cell properties as given in Eq. 3.

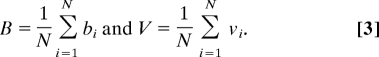An alternative formulation would be to regard the group fitness as the average of the cell fitnesses as in Eq. 4.

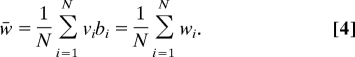For the group of organisms we have in mind, volvocine algae, and the underlying characters involved in their fitness components, such as flagellar action, Eq. 4 would be inappropriate. Flagellar action of the cell group is composed out of flagellar actions of the cells, and this composition occurs before cell division and the production of offspring. We think such an unfolding of events is likely to be the general situation biologically; activities taken by cells are composed before their expression in terms of fitness of the cell group. As a result, averaging components (Eq. 3) before multiplying (Eq. 2) is more biologically meaningful then multiplying first and then averaging (Eq. 4). Using the definition of covariance and Eqs. 2 and 3, it can be seen that the fitness of the group is greater than the average fitness of component cells by an amount equal to the negative covariance of the fitness components at the cell level (Eq. 1).