Myosin-V is a mechanical ratchet

Abstract

Myosin-V is a linear molecular motor that hydrolyzes ATP to move processively toward the plus end of actin filaments. Motion of this motor under low forces has been studied recently in various single-molecule assays. In this paper we show that myosin-V reacts to high forces as a mechanical ratchet. High backward loads can induce rapid and processive backward steps along the actin filament. This motion is completely independent of ATP binding and hydrolysis. In contrast, forward forces cannot induce ATP-independent forward steps. We can explain this pronounced mechanical asymmetry by a model in which the strength of actin binding of a motor head is modulated by the lever arm conformation. Knowledge of the complete force–velocity dependence of molecular motors is important to understand their function in the cellular environment.

Class-V myosins are two-headed linear molecular motors involved in various intracellular transport processes that move processively and directionally toward the plus end of actin filaments (1–4). The energy required for forward motion is supplied by hydrolysis of ATP (1, 5). During each forward step both heads of a myosin-V motor undergo a coordinated chemomechanical cycle, which results in a hand-over-hand stepping mechanism (6, 7). After release of ADP in the trailing head, ATP can bind, and this head detaches from the filament. Now, the leading head can perform the power stroke of its lever arm (8). Subsequently, the now-forward head can rebind to the filament. The mechanism that prevents premature ADP release from the leading head in a two-head-bound myosin is believed to be based on intramolecular strain (9–11).

Apart from myosin-V, forward motion has been studied extensively for many linear and rotary motors (12–19). For most of these motors tight coupling of forward motion to ATP hydrolysis has been reported (6, 20, 21). In contrast, the modes of force-induced backward motion seem to be quite diverse in the different motor systems. Whereas for the F₁-ATPase the hydrolysis cycle is completely reversible, and forced backward rotation can lead to ATP synthesis (22, 23), backward steps of the linear motor kinesin have been shown to be tightly coupled to ATP binding (24, 25). In kinesin, backward forces lead to a decrease of the intrinsic forward bias of a step. In the present study, we investigate force-driven motion of myosin-V by using an optical trap with force feedback control in which we observe a force-induced mode of backward motion distinct from kinesin and completely independent from the ATP cycle.

Results

In a first set of experiments we tested motor velocities under various high loads in forward and backward direction at 1 μM ATP. Forces in the direction of unloaded movement (forward) of myosin-V and forces opposing the unloaded movement (backward) of a motor attached to a trapped polystyrene bead were applied by moving a piezo-driven microscope stage parallel to a surface-anchored actin filament and switching between the two directions (26). Once a motor bound to the actin filament, a feedback cycle adjusted the position of the microscope stage to keep the bead stationary and thereby follow the steps of myosin-V. With this method, loads of 3, 5, and 10 pN in forward (negative force values) and backward directions (positive force values) were applied. We tested the orientation of the actin filament before each experiment by recording the unloaded direction of motion of the motor. After the application of high backward loads, the motor was still able to step forward against low forces, proving the motor is undamaged and functioning (see sample trace in Fig. 5, which is published as supporting information on the PNAS web site).

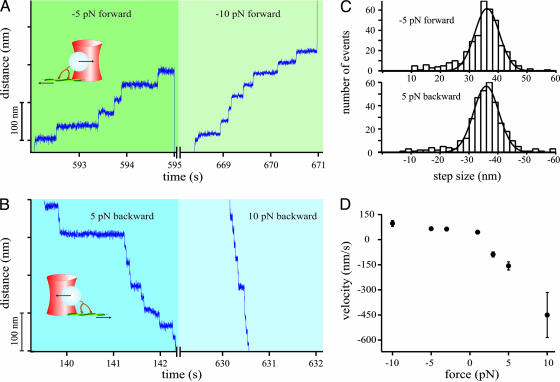
Sample traces of a single myosin-V motor at −5 and −10 pN forward loads and 1 μM ATP are shown in Fig. 1A. The molecule steps along its track until the force set-point is changed or the motor detaches and the bead is pulled rapidly toward the center of the trap. Fig. 1B shows the same molecule stepping in the backward direction at 5- and 10-pN backward loads. This behavior was observed routinely (>60% of all trials). In all other cases backward force application led to immediate detachment of the motor. Additional examples of backward steps at various backward forces and ATP concentrations are shown in Fig. 6, which is published as supporting information on the PNAS web site. The step size of the motor is distributed around 36 nm in both directions (Fig. 1C) and independent of load and ATP concentration (data not shown). Changes in overall motor velocity are therefore entirely attributable to changes in the stepping rate. The average velocities in forward and backward directions exhibit a drastically different load dependence, as can be seen from Fig. 1D. Whereas forward motion is only marginally influenced by load (movement at −10 pN is 1.5 times faster than at −3 pN), the motor is accelerated in the backward direction by a factor of 5 from −90 nm/s at 3 pN up to −450 nm/s at 10 pN. This is even significantly faster than the unloaded motion of myosin-V under saturating ATP conditions.

Fig. 1.

Response of myosin-V to high forces at 1 μM ATP. (A) Sample trace of forward steps at −5 and −10 pN forward loads. (B) Sample trace of backward steps of the same motor molecule as in A at 5 and 10 pN backward loads. (Insets) Experimental scheme of force application. (C) Step size distributions of forward and backward steps at ±5 pN and 1 μM ATP, fitted by a Gaussian curve. Mean values are (36.1 ± 1) nm in forward direction and (−36.0 ± 1) nm for backward steps. (D) Motor velocity as a function of force. Velocities were calculated by dividing the constant step size of 36 nm through average dwell times (see Methods).

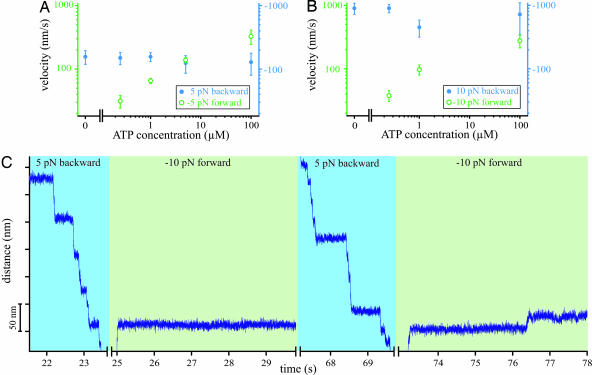
In the next set of experiments we explored the influence of ATP concentration on backward motion at forces greater than stall force (superstall force, F > 3 pN). Fig. 2A and B shows the average velocity of both forward and backward steps as a function of the ATP concentration at forces of 5 and 10 pN, respectively. Under forward loads, the average velocity decreases with decreasing ATP concentration as expected from Michaelis–Menten behavior. At low ATP concentrations, velocity increases with increasing load, indicating that at least one load-dependent transition affects the rate of ATP binding. Similar behavior was observed for kinesin (27). At saturating ATP concentrations (100 μM) the maximum velocity is independent of force within the error bars. This result is in accordance with earlier results that found ADP release insensitive to force if the motor is bound with both heads to the filament (26). In contrast, the average velocity of backward steps remains constant at all applied ATP conditions. This behavior clearly shows that backward stepping does not require ATP binding or hydrolysis. The discrepancy between forward and backward motion becomes most obvious in the absence of ATP (see Fig. 2C). Under these conditions the myosin-V molecule almost entirely resists forward motion even at the highest loads (green-shaded regions), whereas backward motion (blue-shaded regions) is indistinguishable from that observed at higher ATP concentrations. We observed very few forward steps at −10 pN, which sets a lower limit of 4 s for the average dwell time of forward steps. Under zero ATP conditions the directionality could not be determined directly from the unloaded stepping direction of the motor. However, the strong asymmetry of load dependence made it easy to infer forward and backward directions. Fig. 2C demonstrates that in the absence of ATP the myosin-V motor acts as a mechanical ratchet, a mechanical analog of a diode, by rectifying mechanical loads into the backward direction.

Fig. 2.

Dependency of myosin-V stepping on ATP concentration. (A) Motor velocity as a function of ATP concentration at −5 pN forward load (open green circles, left green axis) and 5 pN backward load (filled blue circles, right blue axis). (B) Motor velocity as a function of ATP concentration at −10 pN forward load (open green circles, left green axis) and 10 pN backward load (filled blue circles, right blue axis). (C) Sample traces showing asymmetric stepping of myosin-V without ATP. At 5 pN backward load the motor performs rapid processive backward steps (blue background). At −10 pN forward load, almost no forward steps occur (green background).

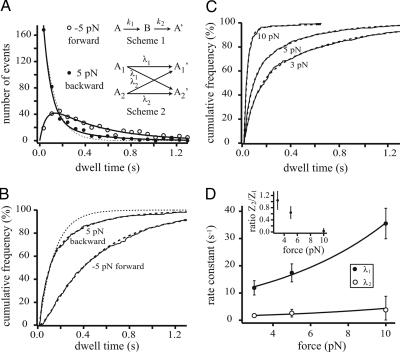
Our results so far show very different kinetic behaviors under forward and backward loads. To further investigate the underlying kinetic schemes for force-induced stepping in both directions, we analyzed dwell-time distributions of the individual steps. Fig. 3A shows the histograms of dwell times for both forward (open circles) and backward steps (filled circles) within a processive run at 5 pN and 1 μM ATP. To get a binning-independent representation for the dwell-time distributions allowing for a more robust analysis, we chose to analyze cumulative frequency plots of dwell-time distributions (for details, see Methods and Supporting Text, which is published as supporting information on the PNAS web site). Fig. 3B shows the cumulative frequency plots of the same data sets as the one in Fig. 3A. Forward steps follow the well known tightly coupled kinetic scheme of two serial transitions with rate constants k₁ and k₂ in the chemomechanical cycle of the motor (6, 26):

[Scheme 1]

A′ denotes the same state as A after one forward step.

Fig. 3.

Stepping kinetics at high forces and load dependence of backward steps. (A) Dwell-time histograms of forward steps (open circles, −5 pN) and backward steps (filled circles, 5 pN) at 1 μM ATP. Forward steps could be fit by assuming two sequential irreversible transitions (Scheme 1 Inset) (6). Backward steps follow a different kinetic scheme. The most elementary model succeeding to fit the dwell-time distribution is shown in Scheme 2 Inset (for details see Results). (B) Binning independent cumulative frequency plots of the same data as in A. The dashed lines are best fits using the kinetic schemes shown in A. The dotted lines in A and B are fits of a single-exponential curve to the dwell-time distribution of backward steps. (C) Cumulative frequency plots of dwell-time distributions for backward steps at 3-, 5-, and 10-pN backward loads. Data from experiments with 0, 0.25 and 1 μM ATP were pooled. (D) Influence of force on the rate constants λ₁ and λ₂ according to Eq. 1. (Inset) Influence of force on the amplitude ratio Z₂/Z₁.

The cumulative frequency plots could be fit by using a slow rate of ATP binding ((2.2 ± 0.2) s⁻¹ at 1 μM ATP and −5 pN) in series with a fast rate constant of (17.6 ± 3.7) s⁻¹ associated with ADP release (see Eq. 3 in Supporting Text), which is similar to the previously measured value at saturating ATP (26). In contrast, backward steps seem to follow single-exponential kinetics (dotted line in Fig. 3 A and B). However, at longer dwell times we observe a population of slower steps that indicates the existence of an alternative slower pathway. The most elementary kinetic scheme explaining such a biphasic behavior is given in Scheme 2 (see also Methods, Eq. 2). A backward step proceeds from two distinct mechanical starting states A₁ and A₂ into either of both states by a single transition λ₁ and λ₂:

[Scheme 2].

In this model, A₁ and A₂ do not interconvert at the time scales of λ₁ and λ₂. Applying Scheme 2 to the data at 1 μM ATP and 5-pN backward load, we find that 60% of the steps occur at a fast rate of (14.5 ± 3.8) s⁻¹ and 40% at a slow rate of (2.9 ± 1.9) s⁻¹ (Eq. 5 in Supporting Text; continuous lines in Fig. 3A and dashed lines in Fig. 3B). At the same force and ATP condition, the dwell times of the first backward step after application of the backward load, which had not been included in the analysis so far, average to a value of (0.37 ± 0.05) s with a corresponding rate constant of (2.7 ± 0.4) s⁻¹.

Cumulative frequency plots of dwell-time distributions at 3-, 5-, and 10-pN backward forces are shown in Fig. 3C. Because backward stepping kinetics apparently did not depend on ATP concentration, we pooled data over ATP concentrations ranging from 0 to 1 μM to improve statistics. The rate constants obtained by fitting Scheme 2 to the data are summarized in Table 1. The plots in Fig. 3C show that dwell times are strongly force dependent. In accordance with this dependence we find that both rate constants λ₁ and λ₂ of the two pathways are force dependent (see Fig. 3D) and follow the exponential equation (28):

where λ_0i denotes a transition rate extrapolated to zero load; d_i, the distance along the direction of force application from the ground state to the transition state for the respective transition in the corresponding energy landscape; k_B, the Boltzmann constant; and T the absolute temperature. We obtain values of λ₀₁ = (8 ± 2) s⁻¹ and d₁ = (0.6 ± 0.1) nm for the rate constant λ₁, and λ₀₂ = (1.2 ± 0.9) s⁻¹ and d₂ = (0.5 ± 0.4) nm for the rate constant λ₂. Care has to be taken in interpreting the values for the rate constants extrapolated to zero load. At smaller forces, rates other than the detachment rate of the forward head may become rate limiting, and hence the rate of backward stepping is likely slower than those extrapolated values. In addition, the population of the two pathways shifts with force. Pathways are equally probable at 3 pN, whereas at high forces (10 pN) the fast pathway is populated almost exclusively (Fig. 3D Inset).

Table 1.

Statistics of superstall backward stepping

Force, pN	Steps within a backward run*				First backward step after a forward step†
	Rate constant λ1, s−1	Rate constant λ2, s−1	Amplitude ratio Z2/Z1	n	Rate constant, s−1	n
3	11.9 ± 2.6	1.7 ± 0.7	1.04	395	1.6 ± 0.2	78
5	17.4 ± 3.3	2.6 ± 1.4	0.64	675	2.6 ± 0.3	82
10	35.5 ± 5.6	3.8 + 5/−3.7	0.03	198	6.3 ± 2.4	20

*Data include experiments with 0, 0.25, and 1 μM ATP (displayed in Fig. 3D).

^†Data include experiments with 0.25 and 1 μM ATP. The rate constant is calculated as the inverse of the average dwell time.

Discussion

Our data show a clear asymmetry in the response of double-headed myosin-V to high forward and backward forces. Previous studies have demonstrated that forward steps at low forces are tightly coupled to ATP hydrolysis with one step per ATP (3, 6). Our data show that this relationship holds true even at larger forward forces (<−5 pN) (see Figs. 2 and 3B). In the forward direction, an additional mechanical pathway for steps induced by mechanical load and uncoupled from ATP binding can be excluded within our experimental limits. This finding becomes obvious in Fig. 2C (green-shaded regions), where the motor almost completely resists forward forces of −10 pN without moving.

For superstall backward loads (F > 3 pN), however, the motor velocity is independent of ATP across the whole range of applied concentrations ranging from 0 to 100 μM. The only realistic explanation for this observation is that forced superstall backward steps do not require ATP binding or hydrolysis. Trying to explain the finding of ATP-independent velocity with a model tightly coupled to hydrolysis would require ATP-binding rate constants beyond the diffusion limit (>10⁹ M⁻¹·s⁻¹) at the lowest ATP concentrations. We therefore postulate another, entirely mechanical, pathway not requiring ATP binding for superstall backward stepping of myosin-V. Its main aspects are (i) backward stepping occurs in a hand-over-hand manner; (ii) backward motion is limited by force-induced detachment of the leading head from actin; and (iii) after detachment of the leading head, conformational changes in the trailing head associated with the power stroke (henceforth also referred to as reversal of the power stroke) are reversed by high backward forces. Several pieces of evidence support this model.

Although a hand-over-hand motion for load-induced backward stepping has not been shown directly there is some evidence favoring this stepping model over detachment of both heads and rapid reattachment at the next binding site. First, the continuous stepping distance of 36 nm in long processive runs and the absence (<10% at 10 pN in this study) of step sizes corresponding to two or more binding sites render unbinding and rapid reattachment unlikely (26). Moreover, application of lateral loads of up to 8 pN in addition to superstall backward loads still leads to long processive runs (a sample trace at 8 pN sideward force and 3 pN backward force is given in Fig. 7, which is published as supporting information on the PNAS web site). Under these conditions the bead would be rapidly forced toward the trap center upon detachment of the motor, and thus prevent the motor from rebinding.

Association of the force-dependent rate-limiting transition for backward stepping with forced detachment of the forward head is supported by calculations done by Vilfan (29), who found that force applied to the junction of the two lever arms of a double-headed motor does not lead to considerable torques on the motor domains if both heads are bound simultaneously to the actin filament. Large applied loads will hence act predominantly on the actin–myosin binding interface. Therefore, unbinding of the forward head from the actin filament is likely the rate-limiting transition in backward stepping. Supporting this interpretation, the measured transition-state distance d of ≈0.6 nm that the center of mass of the double-headed molecule has to be moved for the limiting transition to occur (see Fig. 3D) is comparable to the distances measured for breaking molecular interfaces in proteins or antibody–antigen interactions (30, 31).

After detachment of the leading head, conformational changes associated with the power stroke in the trailing head, in particular rotation of the lever arm, are reversed rapidly. This step is supported by recent results with single-headed myosin-V constructs, which indicated that such a reversal is possible in constructs with six light-chain binding sites (IQ repeats) (10). In the same study the authors found that power stroke reversal did not seem to occur in shortened levers with one IQ repeat, possibly because of the smaller torque transmitted through a short lever arm (10). Moreover, even in myosin-II with two IQ repeats Takagi et al. (32) proposed force-induced power-stroke reversal. These observations render force-induced power-stroke reversal in double-headed wild-type myosin-V likely when only one head is attached to actin.

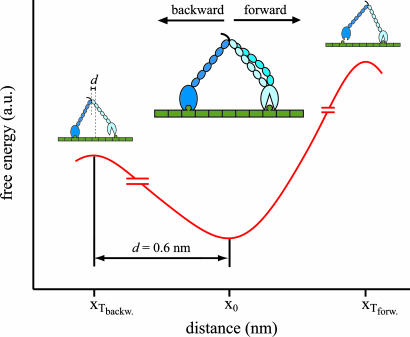
Can our model for force-induced stepping explain the pronounced asymmetry between forward and backward loads? A priori, forward forces act on the trailing head similar to the way backward forces act on the leading head. However, an asymmetry is naturally inherent in a two-headed motor bound to a polar filament (see Fig. 4). Electron microscopy images of working myosin-V bound with both heads to actin suggest that the trailing head (dark blue in Fig. 4) will always be in a post-power-stroke conformation. In contrast, the leading head (light blue) will be predominantly in a pre-power-stroke conformation because of intramolecular strain (33, 34). Kinetic studies have shown pronounced differences for the binding affinity of single-headed myosin-V constructs to actin depending on their state in the chemomechanical cycle (5, 35, 36). Pre-power-stroke states show a much lower affinity than post-power-stroke and rigor states (5, 9, 35). Crystal structures of single-headed myosin-V constructs representing different states of the chemomechanical cycle directly relate the position of the lever arm to the state of the actin binding site of myosin-V (37, 38). Release of nucleotide products is accompanied by a successive rotation of the lever arm and correlated to closure of the 50-kDa cleft and thus successively stronger binding to the actin filament. Therefore the leading head occupying a pre-power-stroke conformation will be much more prone to mechanical detachment under backward load than the trailing post-power-stroke motor domain under forward load.

Fig. 4.

A model for the asymmetric stepping of myosin-V. The double-headed molecule experiences an asymmetric energy landscape where the conformation of the lever arm determines the affinity of the respective head to actin. The head in post-power-stroke lever arm conformation (dark blue, trailing head) is strongly bound to actin. The leading head can adopt a weakly and a strongly bound pre-power-stroke conformation (blue and light blue). Backward force applied to the motor can induce detachment of the leading head, whereas a forward force does not lead to detachment of the trailing head. a.u., arbitrary units; x_Tbackw. and x_Tforw., position of transition state in backward and forward direction.

The sequence for long processive backward runs as observed in our experiments will then be as follows: after rate-limiting detachment of the leading head the conformational changes associated with the power stroke will be reversed in the trailing head. This head will now become the leading head and switch from the high-affinity post-power-stroke state to a low-affinity pre-power-stroke-like state. The detached head reverts to the post-power-stroke state in the absence of intramolecular strain and rebinds strongly to the filament. Processive backward steps hence demonstrate that mechanical forces applied to the lever arm of a myosin-V molecule with just one head bound can directly alter the affinity of the polymer-binding interface. This transition is purely mechanical in the sense that it seems to take place in both the presence and the absence of the appropriate nucleotide. Experiments in the presence of fluorescently labeled nucleotides may help to clarify possible correlations with the specific nucleotide state.

Our experiments show that there is a pathway for backward stepping uncorrelated to ATP binding. It is interesting to note that for the microtubule-based linear motor kinesin, Nishiyama et al. (24) and more recently Carter and Cross (25) reported strong coupling of backward steps to ATP hydrolysis or binding. Obviously, the underlying chemomechanical pathway for backward steps is completely different from that of myosin-V. It is important to note that occasional backward steps occurring at loads smaller than stall, when myosin-V moves forward, may follow a different pathway. In this regime, a detached leading head will likely bind to the same forward position on actin. However, we find that at low backward loads, the ratio of backward steps to forward steps decreases with increasing ATP concentration from 1:6 at 0.25 μM ATP to 1:28 at 100 μM ATP, indicating that at least a fraction of the backward steps at low load have to be independent of ATP. Our experiments further show that force-induced myosin-V backward stepping at our experimental conditions can occur uncoupled from ATP synthesis. Further experiments are needed to show whether a pathway of backward stepping coupled to ATP synthesis exists at appropriate nucleotide conditions similar to what has been observed for F₁-ATPase (22, 23).

In conclusion, myosin-V is an example of how an asymmetric ratchet potential can be realized by a two-headed motor and a polar filament. Certainly the term ratchet as we use it here strictly refers to the response of the motor under a load. It must not be confused with Brownian ratchet models sometimes used to describe the motion of molecular motors (39, 40).

The hand-over-hand model for force-induced backward stepping as discussed so far captures many important aspects of our experiments. However, the statistical analysis of dwell-time distributions as shown in Fig. 3 suggests a more refined picture of the weakly bound conformation present in the leading head. We consistently find a double-exponential dwell-time distribution with a fast phase and a slow phase. We can rule out nonspecific interactions of motor or bead to surface or filament as a possible source for the observed biphasic behavior: a similar slow phase is absent in forward motion, and a directional asymmetry of nonspecific interaction does not appear likely. Moreover, experiments with beads in the absence of motors showed no binding interactions. A similar slow detachment phase was also observed in a recent study with single-headed myosin-V constructs by Purcell et al. (10). They reported an ATP-independent release rate of 1.5 s⁻¹ under low backward forces of 2 pN. The biphasic behavior rather suggests the presence of two alternative states from which detachment of the leading head can proceed. In the elementary model we use here (Scheme 2), isomerization between both detachment states can occur only on a slow time scale (≪λ₁ and λ₂). Other, more complex, models involving reversible transitions may allow faster interconversion. Possible candidates for the two states A₁ and A₂ are a weakly and a strongly bound pre-power-stroke conformation. A variety of actin-bound states of myosin-V with differing binding strength have been reported in kinetic studies (35, 36), consistent with our interpretation. The relative amplitude by which the two release kinetics are populated (Z₂/Z₁) depends strongly on force (Fig. 3D). Whereas at moderate backward forces of 3 pN the slow release rate occurs in 50% of the cases, we almost exclusively find the fast release rate at the highest forces of 10 pN. Hence, at higher forces, reversal of the conformational changes associated with the power stroke of the attached head ends more likely in a prestroke state exhibiting less affinity to actin than the one populated at lower forces. This interpretation is further supported by the dwell-time distribution of the first force-induced backward step directly after force application when the motor has just finished a forward step. According to our model under substall backward forces or forward forces the lead head should predominantly populate a strongly bound pre-power-stroke state after finishing a forward step. The dwell times of this population should therefore reflect directly the kinetics of the strongly bound state. The agreement with this prediction is in fact very good, as can be seen in Table 1. As a consequence the fast phase of backward stepping will be suppressed in forward runs at substall forces. While the strongly bound prestroke conformation likely reflects an on-pathway conformation, the exact nature of the weakly bound prestroke state has yet to be determined. It may be even off the regular pathway of forward stepping.

At first sight it may not seem straightforward to relate our results to the physiological function of myosin-V as an organelle transporter in a cell. However, in melanosome transport myosin-V colocalizes on the melanosomes with much stronger kinesins that can exert forces up to 7 pN (27, 41, 42). Tug-of-war scenarios are therefore likely to occur and for future modeling of melanosome transport our data may be an important piece of evidence. Our results suggest that in such a case myosin-V will follow the kinesin motion in backward steps using no ATP while still staying attached to the actin filament. Full knowledge of the force–velocity relation for an individual molecular motor is an important prerequisite for modeling large-scale cellular motions involving forced backward stepping of motors. Recently Grill et al. (43) have put forward a tug-of-war model to explain large-scale oscillations of the mitotic spindle during cell division of Caenorhabditis elegans embryos.

In conclusion, we could show that a double-headed myosin-V motor exhibits a pronounced asymmetric, ratchet-like response to high loads. Superstall backward stepping does not require ATP binding. Further experiments are needed to show whether such a mechanically induced backward stepping pathway is present also in other linear molecular motors.

Methods

Sample Preparation.

Chick brain myosin-V and rabbit skeletal F-actin were purified and processed as described in refs. 26 and 44–46. Myosin-V (30 pM) was adsorbed on polystyrene beads (diameter: 535 nm, 2.5% solid; Polysciences, Eppelheim, Germany) preblocked with 10 μg/ml BSA and diluted 1/100 in assay buffer (25 mM imidazole·HCl, pH 7.4/25 mM KCl/1 mM EGTA/10 mM DTT/4 mM MgCl₂). Motility buffer additionally contained an oxygen-scavenging system to retard photobleaching (6 mg/ml glucose oxidase, 1 mg/ml catalase, and 1% glucose) and various amounts of nucleotides. More details are given in Supporting Text.

Experimental Procedures.

Experiments were performed in a custom-built optical trap as described in ref. 26. Beads, sparsely covered with motor protein, were positioned over tetramethylrhodamine-phalloidin-labeled and aligned actin filaments attached to a coverslip by myosin-II treated with N-ethylmaleimide (26, 47). Before each experiment the trap stiffness was calibrated for the trapped bead from the amplitude of the thermal diffusion (48). Typically, values between 0.06 and 0.12 pN/nm were used. Constant forces up to 10 pN in forward (assisting) and backward (resisting) motor directions could be applied to an attached motor by clamping the distance between bead and trap center with a feedback-controlled piezo-driven microscope stage (26). If the motor detached, the piezotable was rapidly driven toward the end of the feedback range (±750 nm). See Supporting Text for more details.

Data Analysis.

Data were analyzed by using igor pro 4.0 (WaveMetrics, Portland, OR). For better temporal resolution, signals of piezotable and photodiode were summed. Dwell times (duration of a level) and step sizes (distance between two successive levels) were tabulated. Velocities (mean ± 2SEM) were calculated as (36 nm)/(average dwell time). Forward steps were described by Scheme 1 (see Supporting Text for more details) (6, 26). Backward steps could be described by Scheme 2. The normalized probability density P_b(t) of dwell times predicted by this model is

with rate constants λ₁ and λ₂ and amplitudes Z₁ and Z₂ = (1 − Z₁). Rate constants and amplitudes (mean ± SEM) were obtained by fits according to Scheme 1 and Scheme 2, respectively, to cumulative frequency plots of dwell-time distributions of forward and backward steps, respectively (see Supporting Text for a detailed description).