Scaling the metabolic balance of the oceans

Abstract

Oceanic communities are sources or sinks of CO₂, depending on the balance between primary production and community respiration. The prediction of how global climate change will modify this metabolic balance of the oceans is limited by the lack of a comprehensive underlying theory. Here, we show that the balance between production and respiration is profoundly affected by environmental temperature. We extend the general metabolic theory of ecology to the production and respiration of oceanic communities and show that ecosystem rates can be reliably scaled from theoretical knowledge of organism physiology and measurement of population abundance. Our theory predicts that the differential temperature-dependence of respiration and photosynthesis at the organism level determines the response of the metabolic balance of the epipelagic ocean to changes in ambient temperature, a prediction that we support with empirical data over the global ocean. Furthermore, our model predicts that there will be a negative feedback of ocean communities to climate warming because they will capture less CO₂ with a future increase in ocean temperature. This feedback of marine biota will further aggravate the anthropogenic effects on global warming.

The role of the oceans in the CO₂ budget of the biosphere depends largely on the balance between the uptake of carbon by phytoplankton photosynthesis and its remineralization by the respiration of the whole planktonic community (1). For large areas of the epipelagic ocean, planktonic community respiration (CR) exceeds gross primary production (GPP), resulting in net heterotrophy and a source of CO₂ (2–4). The solution of the contentious debate over the extent of such heterotrophic areas (5–7) is hindered by the limited spatiotemporal coverage achievable by traditional incubation methods (8, 9). Here, we tackle this question from a different perspective based on the metabolic theory of ecology (MTE) (10). The flux rates within an ecosystem are the result of the sum of the individual rates of all its constituent organisms (11, 12), which, in turn, are governed by the combined effects of body size and temperature (13–15). Although MTE suggests a universal scaling of metabolic rate as the 3/4 power of body size, it predicts a differential temperature-dependence of heterotrophic processes (driven by ATP synthesis) and autotrophic rates (controlled by Rubisco carboxylation) (12). Following the MTE, the respiration of a heterotrophic planktonic organism B_i can be estimated if we know its body size M_i and the ambient absolute temperature T:

where b₀ is a normalization constant independent of body size and temperature, e^−E_h/kT is Boltzmann’s factor, where E_h is the average activation energy for heterotroph respiration (13), and k is Boltzmann’s constant (8.62·10⁻⁵·eV·K⁻¹), and α_h is the allometric scaling exponent for body size (14, 15).

For the metabolic rates of marine autotrophs, things are complicated by the dependence of photosynthetic activity, not only on body size and temperature, but also on light (10, 16). Accordingly, we have extended the quantitative theory to account for the relationship between individual gross photosynthesis P_i and photosynthetic active radiation (PAR).

where p₀ is a normalization constant independent of body size, temperature, and light, E_a is the average activation energy for photosynthetic reactions (12), α_a is the allometric scaling exponent for autotroph body size, and PAR/(PAR + K_m) is the Michaelis–Menten photosynthetic light response (16, 17), where K_m is the half-saturation constant that represents the amount of quanta at which half the maximum photosynthetic activity is reached. This formulation for the relationship between photosynthesis and light was selected over other equations (18) because, being mathematically more simple, it provided an equally good fit.

Hence, the rate of net primary production (NPP) of a plankton community is equal to the sum of the individual rates of all its autotrophic organisms

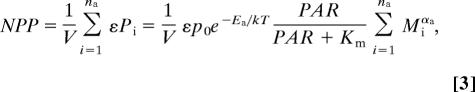where n_a is the number of autotrophic organisms in the volume V, and ε is the fraction of photosynthesis allocated to growth (i.e., the carbon-use efficiency). MTE provides evidence that this carbon-use efficiency is independent of body size and environmental temperature (12); here, we assume that it is also independent of light (19).

Together, Eqs. 1–3 lead to an expression for CR,

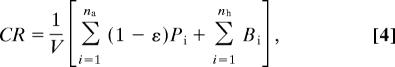where (1 − ε)P_i is the respiration rate of a phytoplankton individual, and n_h is the number of heterotrophic organisms in the volume V.

In this article, we first evaluate these equations at both the organism and population levels, using the most comprehensive compilation of plankton metabolism to date. The coefficients in these equations as predicted by the MTE (10, 12–15) are validated against experimental data. We then use Eqs. 3 and 4 to provide a theoretical framework for the evaluation of the metabolic balance of the oceans and use them to better understand the effects of temperature on oceanic carbon cycling.

Results

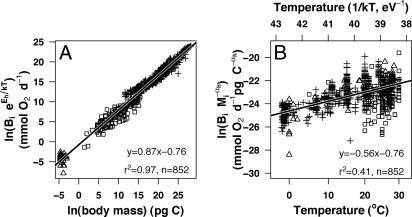
To test Eqs. 1 and 2, we first compiled data on respiration of individual plankton species B_i and (1 − ε)P_i and on phytoplankton net production rates εP_i, as a function of body size, temperature, and PAR. From our analysis, the respiratory rates of planktonic organisms from heterotrophic bacteria to zooplankton and the production rates of phytoplankton follow metabolic theory (Figs. 1 and 2). Although the temperature-corrected respiration rates of heterotrophs (bacteria and zooplankton; Fig. 1A) and autotrophs (Fig. 2A) and the temperature-corrected net photosynthetic rates of phytoplankton (Fig. 2D) scale allometrically with body carbon, with exponents somewhat higher than the expected 3/4 power (Table 1), this difference is mainly because planktonic organisms do not have a uniform constant density. Theories to explain the 3/4 power scaling are based on the designs of resource-distribution networks. These theories require a proportional scaling between the volume of fluid within the network and the mass of the organism (14, 20, 21). Although this assumption of a uniform constant density probably holds true when mass is expressed as the wet mass of the organism, body or cell mass is usually expressed in carbon units in marine plankton studies. Because mass in carbon units (M_i) and biovolume (v) are not proportional but scale allometrically (e.g., M_i ≈ v^0.712) (22), when we use biovolume as a measure of body size, the allometric exponents become closer to 3/4 (0.72 for heterotroph respiration and 0.74 for εP_i and 1 − εP_i; see Fig. 5, which is published as supporting information on the PNAS web site), which gives support to the 3/4 scaling theories.

Fig. 1.

Effects of body size and temperature on individual-level heterotrophic respiration. (A) Effect of body mass on temperature-corrected respiration rates of bacteria (triangles) and micro- and mesozooplankton (squares and crosses). (B) Effect of the temperature function 1/kT (upper x axis); the corresponding temperatures in degrees Celsius are presented (lower x axis) on bacteria (triangles) and micro- and mesozooplankton (squares and crosses), respiration rates corrected for the effects of body size. See Table 1 for parameter estimates used in the temperature and size corrections.

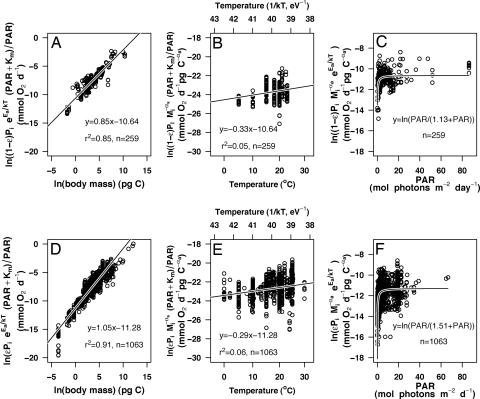
Fig. 2.

Effects of body size, temperature, and light on individual-level phytoplankton respiration (A–C) and net photosynthesis (D–F). (A and D) Effect of body mass on light- and temperature-corrected metabolic rates. (B and E) Effect of temperature on metabolic rates corrected for the effects of body mass and light. (C and F) Michaelis–Menten light-saturation curve for body-size- and temperature-corrected phytoplankton metabolism. Parameter estimates used for the corrections are the separate models for respiration and growth presented in Table 1.

Table 1.

Individual-level physiological rates of marine plankton

Rate	ln(Nc)	α	−E	Km	df	r2
Heterotroph respiration	−0.76 (0.94)	0.87 (0.0051)	−0.56 (0.024)		849	0.97
Autotrophs
Respiration	−10.64 (3.54)	0.85 (0.023)	−0.33 (0.089)	1.13 (0.289)	255	0.85
Net production	−11.28 (1.44)	1.05 (0.011)	−0.29 (0.036)	1.51 (0.173)	1,059	0.92
Combined model
Respiration	−13.18 (1.35)	1.02 (0.010)	−0.28 (0.034)	1.52 (0.159)	1,317	0.91
Net production	−11.56 (1.25)
Gross production	−11.38

Data shown are the parameter estimates and standard error (in parentheses), degrees of freedom (df) and coefficient of determination (r²). Models fit were ln(Rate) = ln(Nc) + α × ln(M_i) − E × (1/kT) + ln(PAR/(Km + PAR)), where Nc is the respective normalization constant, α is the allometric exponent, E the activation energy, and Km the Michaelis–Menten half-saturation constant (this last term is not used for heterotrophs), Rate is the metabolic rate in mmol of O₂·d⁻¹, M_i is the organism mass in pgC, T the absolute temperature, and PAR the daily irradiance in mol photons·m⁻²·d⁻¹. In the combined model for autotrophs, α, −E, and, Km are the same for respiration and net and gross production, but each rate has a different normalization constant. This combined model was used in our calculations of phytoplankton community rates.

Our data also support the MTE prediction of a differential temperature scaling of heterotrophic processes and autotrophic rates (12). Heterotrophic respiration scales with temperature, with an activation energy close to the predicted value of E_h = 0.65eV (Table 1 and Fig. 1B). Phytoplankton respiration and net production show a weaker temperature dependence than heterotrophic respiration, with exponents similar to the expected activation energy for autotrophic processes of E_a = 0.32 eV (Table 1 and Fig. 2 B and E). Hence, and despite the differences in the kinetics of Rubisco carboxylation between land and aquatic plants (19), the resemblance between the activation energies for marine phytoplankton (Fig. 2 B and E) and those predicted based on terrestrial plant photosynthesis (12) suggests that terrestrial and aquatic plants have remarkably similar temperature dependence.

Finally, phytoplankton production is a rapidly saturating function of light irradiance well fitted by a Michaelis–Menten photosynthetic response (Fig. 2 C and F). The fact that phytoplankton respiration is also affected by the incident irradiance (Fig. 2C and Table 1) provides further evidence that autotroph respiration is ultimately constrained by photosynthesis. Furthermore, because the allometric exponent α_a, effective activation energy E_a, and Michaelis–Menten parameter K_m are similar for phytoplankton net production and respiration, the carbon-use efficiency of marine phytoplankton ε is essentially independent of body size, temperature, and light availability, as it was assumed in the development of Eq. 3. This finding has fundamental implications for global-change modeling of the world’s oceans and enables us to combine phytoplankton respiration and net production into a single model of phytoplankton metabolism. In this model (see Methods and Table 1), gross and net photosynthesis and phytoplankton respiration have the same temperature, size, and light dependence, but the respective normalization constants p_o, εp_o, and (1 − ε)p_o differ. From this analysis, we can directly derive a value for the carbon-use efficiency ε of 83%, which lies within the range of reported phytoplankton net growth efficiencies (23, 24). Also, because photosynthesis scales isometrically with body carbon (Table 1), the term

is well approximated by the total phytoplankton biomass (in carbon units)

without the problems associated with the use of allometric equations and the “fallacy of the averages” (25) that also facilitates modeling global phytoplankton production.

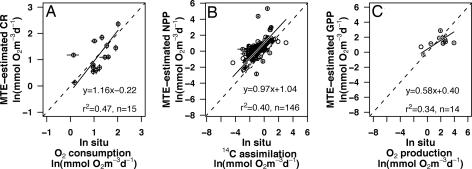
The next step in evaluating the feasibility of using MTE to estimate the metabolic balance of the oceans is to compare the estimates of community respiration and production, obtained by combining the equations in Table 1 and plankton size–structure information with concurrent direct measurements of the amount of oxygen consumed and carbon assimilated by natural communities incubated in situ. Although there is considerable scatter in the relationships, the correlation between measured and estimated values is highly significant in both cases (Fig. 3 A and B). The respiratory rates obtained by both methods are not significantly different (paired t test, t = 0.43, df = 14, P = 0.68), but NPP estimated by using the MTE approach is significantly higher than production estimates based on ¹⁴C uptake (paired t test, t = 13.36, df = 145, P ≪ 0.001), not surprising, because ¹⁴C uptake is usually lower than NPP and seems to approximate net community production, depending on how much heterotrophic activity is occurring (26) (see Supporting Text, which is published as supporting information on the PNAS web site). To estimate the metabolic balance of a planktonic community, we need to compare CR with the GPP and not with NPP. When we estimate GPP using our combined model (Table 1; see also Supporting Text) and compare the obtained rates to gross primary O₂ production estimated by in situ light–dark bottle incubations, there is no significant difference between the two methods (Fig. 3C, paired t test, t = −1.35, df = 13, P = 0.12), albeit the number of paired observations is small.

Fig. 3.

Predicted versus in situ estimates of plankton CR and production. Scatter plots of the in situ-measured CR (A), net (B), and gross (C) primary production versus the estimates based on MTE. Data were log-transformed to normalize variances. The lines fit are the structural (reduced major axis) relationship. Dashed lines are the 1:1 relationship. Error bars indicate the 95% confidence intervals for the mean (see Supporting Text). No error bars are shown when these were not available from in situ data.

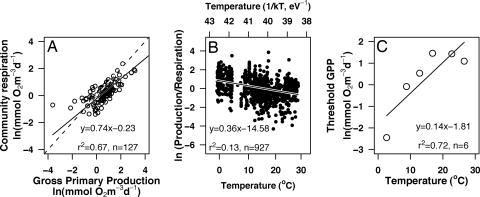
Encouraged by the good agreement of Eqs. 1–4, at both the organism and community levels, we estimated the metabolic balance of planktonic communities, using all of the information available on plankton population size–structure during Atlantic meridional transect (AMT) cruises 1–6 (Fig. 6, which is published as supporting information on the PNAS web site). The threshold of GPP that separates heterotrophic and autotrophic communities obtained, following our macroscopic view of the metabolic balance in the Atlantic Ocean, is 0.4 mmol of O₂·m⁻³·d⁻¹ (Fig. 4A), which lies within the lower range of threshold GPP reported from data on incubation measurements (2–7, 9, 27). When respiration and production rates were depth-integrated, our complementary approach suggests that net heterotrophy prevails in the oligotrophic regions of the Atlantic Ocean, whereas more productive regions are usually net autotrophic (Fig. 7, which is published as supporting information on the PNAS web site).

Fig. 4.

The metabolic balance of the oceans. (A) Relationship between GPP and CR, estimated based on MTE. Solid line is the reduced major axis relationship. Dashed line is the 1:1 relationship. The GPP where both lines intersect is the threshold GPP for metabolic balance (GPP = CR). (B) Temperature-dependence of the GPP/CR ratio obtained by using the global data set (27). (C) Relationship between the threshold GPP and temperature obtained by dividing the global data set into 5°C temperature intervals.

Discussion

In addition to allowing high spatiotemporal resolution of community rates from size–structure information, the application of metabolic theory provides great opportunities to disentangle the possible causes for the imbalance and to study the determinants of its variability at the level of organism physiology and population composition. For example, our model allows simple predictions of the effects of global warming on the metabolic balance of the oceans. Because phytoplankton production scales as e^−E_a/kT and heterotrophic respiration as e^−E_h/kT, with E_a < E_h (Table 1 and Figs. 1B and 2 B and E), both community production and respiration will increase in a possible scenario of sea temperature rise, but respiration will increase relatively more than production. The effect of a greater increase in respiration than in production renders a picture in which an increase in temperature would shift points in Fig. 4A upwards more than to the right and move the cloud of points toward heterotrophy. Because plankton CR is mainly driven by heterotrophic respiration (27, 28), the true, more complex, nonexponential decrease in the production–respiration ratio with increasing temperature is well approximated by e^E_a:h/kT, where E_a:h = E_h − E_a is the difference between the activation energies for heterotrophs and autotrophs, which has a theoretical value of 0.33 eV (for the full model, see Supporting Text; and see Fig. 8, which is published as supporting information on the PNAS web site). We tested these predictions using an independent global data set of respiration and production measurements consisting of almost 1,000 measurements spread around the oceans (27). As predicted by metabolic theory, the ratio between community production and respiration increases as the temperature function 1/kT increases, with a slope of 0.36 V (Fig. 4B, 95% confidence interval: 0.30 to 0.42 eV), almost indistinguishable from the predicted value for E_a:h of 0.33 eV.

Our model also predicts an increase in the threshold of GPP that separates heterotrophic and autotrophic communities with temperature. The threshold of GPP for metabolic equilibrium depends on the functional relationship between production and respiration. With a change in temperature, this functional relationship becomes steeper because of the higher increase in CR than in GPP at the same time that the cloud of points is moved toward higher rates. Therefore, the theoretical form for the relationship between the threshold of GPP and temperature depends on both Boltzmann’s factor and the intrinsic functional relationship between CR and GPP. When the production and respiration data from the global data set (27) are grouped into 5°C temperature intervals, the threshold GPP increases with temperature, as our theory predicts (Fig. 4C). The threshold GPP, therefore, strongly depends on ambient temperature going from <1 mmol of O₂·m⁻³·d⁻¹ in cold environments to >4 mmol of O₂·m⁻³·d⁻¹ at temperatures >15°C.

Accordingly, if sea temperature increases as a result of human activity (29), the threshold primary production for metabolic equilibrium increases, and the pelagic surface waters would capture relatively less CO₂. Our predicted response of the metabolic balance of marine biota to an increase in temperature is not taken into account by current coupled climate/carbon-cycle models. Combining our model with current global estimates of photic layer plankton respiration and production (1) and with ocean temperature warming scenarios enables us to understand the relevance of the predicted change in the metabolic balance of the oceans (see Supporting Text; and see Fig. 9, which is published as supporting information on the PNAS web site). Our first-order calculation suggests that the biota of the epipelagic ocean will capture 4 gigatons of C per yr⁻¹ less by the end of this century, representing a reduction of 21% less CO₂ captured. This amount is equivalent to one-third of current worldwide CO₂ emissions by industrial activities and would significantly aggravate the anthropogenic effects on climate change.

Global warming has profound effects on plankton composition, production, and community dynamics (30–33). These changes are not taken into account in the above calculations but could be of great relevance. The fact that the effect of temperature on the metabolic balance of the oceans can still be clearly perceived even under the diverse community composition and physical forcing conditions covered by the global production–respiration data set (Fig. 4 B and C) suggests that our predicted response to climate warming would also be apparent if community composition and ocean physical forcing are modified by climate. Furthermore, the strength of the model we propose is that, because it is based on individuals, changes in community composition and physical forcing could be easily included in future prediction scenarios. There is great demand for an improved knowledge of ocean biology to evaluate the feedback between climate and the oceanic carbon cycle (30). We have shown that putting metabolic theory into practice is a way forward.

Materials and Methods

Individual Physiological Rates.

We searched the primary literature for studies providing concurrent reports of body size, temperature, and respiration rates of marine plankton. Because the available data on marine heterotrophic protist respiration was scarce, we included the full data set compiled in ref. 34 for aquatic protists. We also constructed a database of phytoplankton production rates from published literature estimates, providing accompanying information on cell size, temperature, and incubation irradiance. Data were extracted from tables or digitized from figures reported in the original papers (see Tables 2 and 3, which are published as supporting information on the PNAS web site).

Combined Model of Phytoplankton Photosynthesis.

Because phytoplankton growth and respiration exhibit essentially identical size, light, and temperature dependencies, we performed a multiple regression analysis of metabolism versus size, temperature, light, and an extra categorical variable that coded whether a datum referred to growth or respiration. By doing this, we were able to calculate the best overall estimates for the size, light, and temperature dependencies of phytoplankton metabolism as well as the normalization constants for growth and respiration, εp_o and (1 − ε)p_o (Table 1). With these values, we then calculated the normalization constant for gross photosynthesis p_o and the carbon-use efficiency ε.

AMT Data.

Samples were collected and analyzed for the determination of the size–abundance distributions of pico-, phyto-, and zooplankton (35–38) (Fig. 6). The mesozooplankton biomass for three size-fractions (0.2–0.5 mm, 0.5–1 mm, and >1 mm) was divided by the average body carbon per organism in each size fraction to obtain an estimate of abundance. Average body carbons for each size fraction of 0.0041, 0.011, and 0.041 g, calculated from AMT6 data, were used for all cruises. To estimate community rates by using the MTE method, at least pico- and phytoplankton abundance data, together with heterotrophic protists, were required.

Environmental temperature was measured at the time of sampling with vertical profiles by using a conductivity–temperature–depth (CTD) device. Although incident surface PAR was continuously measured throughout the cruises, light-attenuation coefficients were estimated from measurements of down-welling irradiance made with a SeaOPS sensor (Satlantic, Halifax, Nova Scotia, Canada) at 490 nm wavelength.

Epipelagic simulated in situ community production and respiration were measured by incubations for the determination of ¹⁴C uptake and changes in dissolved oxygen concentrations in light–dark incubations (36, 37).

Further details about the AMT program can be obtained from the web site www.pml.ac.uk/amt.

Global Respiration Data Set.

To further validate the predictions of metabolic theory, we used a recently compiled global respiration and production data set (27). Because temperature was reported in only 58% of the paired respiration–production measurements, with few reports at low temperature, we estimated temperature for each location, date, and depth from data in the World Ocean Atlas (39). The use of only those entries in the original data set that reported temperature or of a subset of the global data set consisting of data from surface waters (to avoid any possible interaction with the variation of the production respiration ratio with depth) resulted in similar patterns for the relationships presented.

Abbreviations

AMT

Atlantic meridional transect

CR

community respiration

GPP

gross primary production

MTE

metabolic theory of ecology

NPP

net primary production

PAR

photosynthetic active radiation.