DIFFERENTIATION AMONG POPULATIONS WITH MIGRATION, MUTATION, AND DRIFT: IMPLICATIONS FOR GENETIC INFERENCE

Abstract

Populations may become differentiated from one another as a result of genetic drift. The amounts and patterns of differentiation at neutral loci are determined by local population sizes, migration rates among populations, and mutation rates. We provide exact analytical expressions for the mean, variance, and covariance of a stochastic model for hierarchically structured populations subject to migration, mutation, and drift. In addition to the expected correlation in allele frequencies among populations in the same geographical region, we demonstrate that there is a substantial correlation in allele frequencies among regions at the top level of the hierarchy. We propose a hierarchical Bayesian model for inference of Wright's F-statistics in a two-level hierarchy in which we estimate the among-region correlation in allele frequencies by substituting replication across loci for replication across time. We illustrate the approach through an analysis of human microsatellite data, we show that approaches ignoring the among region correlation in allele frequencies underestimate the amount of genetic differentiation among major geographical population groups by approximately 30%, and we discuss the implications of these results for the use and interpretation of F-statistics in evolutionary studies.

Sewall Wright pointed out more than 70 years ago that isolated populations tend to diverge from one another as a result of genetic drift and that the amount and pattern of divergence among populations reflects the extent of migration between them (Wright 1931). In particular, individuals belonging to the same population are expected to be more similar to one another than those belonging to different populations, and individuals from different populations within the same geographical region are expected to be more similar to one another than are individuals from different geographical regions. As a result, evolutionary biologists have commonly used statistics that describe patterns of population differentiation as an indication of the extent to which populations are genetically isolated from one another. Wright's F-statistics, and statistics related to them like Nei's G-statistics (Nei 1973), have been the most widely used descriptors of population differentiation for more than fifty years (Malécot 1948; Wright 1951).

While F-statistics are intended to measure the amount of differentiation among populations, they are implicitly based on Wright's island model (Wright 1931), a pseudo-spatial model in which all populations are equally likely to exchange migrants. Much work in theoretical population genetics has been directed towards understanding the patterns of genetic differentiation that arise when more realistic models of migration are incorporated into the models (e.g., Malécot 1948; Kimura and Weiss 1964; Nei and Feldman 1972; Felsenstein 1975; Nagylaki 1976; Maruyama 1977; Crow and Aoki 1984; Slatkin 1991; Notohara 1990; Epperson and Li 1997). Many investigators now calculate pairwise F-statistics to provide an indicator of the amount of differentiation between those populations (e.g., Dyer and Nason 2004).

Another aspect of Wright's model has been less widely appreciated. His model implies that allele frequencies among populations at any given point in time are uncorrelated when the number of populations exchaning genes is very large. As a result, the variance in allele frequency among contemporaneous populations is equivalent to the variance in allele frequency within any one population over time. Surprisingly, this result no longer holds when a small to moderately large number of populations are exchanging genes.

Fu et al. (2003) show that substantial among-population correlations in allele frequency are expected even for mutation rates as large as 10⁻³ unless more than 100 populations are exchanging genes. Their results re-emphasize an obervation made by Nei (1973): When a finite number of populations is involved in gene exchange, the entire set of populations “drifts” together. The mean allele frequency changes from generation to generation, and the resulting correlation in allele frequencies among populations may be substantial unless the number of populations exchanging genes is very large. As a result, the variance in allele frequency among contemporaneous populations may be substantially smaller than the variance in allele frequency within any one population over time.

We explore two questions raised by these results: (1) How is the magnitude of among population correlation affected by hierarchical structure in the migration process? How does the magnitude of the within region correlation compare with the magnitude of the among region correlation? By hierarchical structure we mean that there is a higher rate of migration among populations within a region than among populations in different regions. (2) Given that the number of populations actually exchanging genes is larger than the number of populations from which samples are available and is generally unknown, can an approximate estimator that does not depend on the number of populations provide a reasonable estimate of the expected amount of differentiation among populations? After exploring these questions, we illustrate the importance of accounting for among population correlations in estimates of population genetic structure through analysis of a human population data set (Rosenberg et al. 2002) with a hierarchical Bayesian model, and we discuss the implications of our results for genetic analyses of population structure.

PROCESS MODEL RESULTS

Analysis of population genetic data must incorporate two aspects of sampling: the usual statistical sampling associated with the sampling of alleles or genotypes within populations and the genetic sampling associated with sampling population allele or genotype frequencies from an underlying stochastic evolutionary process (see Weir 1996, pp. 15–17 for additional discussion). We use the modeling framework introduced in Fu et al. (2003) for the stochastic evolutionary process.

Briefly, we focus on a single locus with A allele types, b ₁, b ₂, ⋯, b _A, and assume that there are P populations indexed by i (refer to Table 1 for a summary of notation used in the process model). Let V_A×A, be a general mutation matrix which has a element, v _rs, the probability of mutation from allele type b _r to allele type b _s. Let M_P×P be a general (backward) migration matrix, i.e., ${\mathrm{M}}_{\mathit{ij}}={\stackrel{\leftharpoonup }{m}}_{\mathit{ij}}$ is the probability that the allele in population i came from population j. Backward migration rates are generally used for analysis of migration in population genetic models (see, for example, Nagylaki 1982; Rousset 1999, 2001).

Table 1.

Notation used in the single locus process model.

Parameter	Definition
A	Number of alleles
S	Number of populations in each geographical region
k	Number of geographical regions
P	Total number of populations. P = kS
V	An A × A matrix of mutation rates. v rs is the mutation rate from the rth allele to the sth allele
M	A P × P matrix of backward migration rates. m ij is the probability that an allele in population i came from population j in the preceding generation
B	The Kronecker product of M and V
N ij	Number of individuals in population j of geographical region i
${\mathrm{p}}_{\mathrm{ij}}^{\left(\mathrm{t}\right)}$	The vector of allele frequencies in population j of geographical region i at time t. $p_{\mathit{ij},r}^{\left(t\right)}$ is the frequency of the rth allele.
Properties when the process has reached stationarity.
uij	The mean vector of allele frequencies in population j of geographical region i.
Σij,ij	The variance-covariance of allele frequencies within population j of geographical region i.
Σij,i′j′	The covariance of allele frequencies between population j of geographical region i and popogulation j′ of geographical region i′.
Finite island model
m 0	Probability that an allele came from the same population in the preceding generation.
m 1	Probability that an allele came from a different population in the same geographical region in the preceding generation.
m 2	Probability that an allele came from a different geographical region in the preceding generation.
F-statistics
$F_{ST}=\frac{{\sigma }_p^2}{{\mu }_p(1-{\mu }_p)}$	Wright's F ST, where ${\sigma }_p^2$ is the variance of allele frequencies and μp is the mean allele frequency.
θ	An interpretation of F ST that arises when μp is taken as the mean allele frequency and ${\sigma }_p^2$ is taken as the allele frequency variance in a single population over time.
$\theta (p_{11}^{\left(t\right)},\dots ,p_{\mathit{kS}}^{\left(t\right)})$	An interpretation of F ST that arises when μp is taken as the mean allele frequency and ${\sigma }_p^2$ is taken as the allele frequency variance across populations at a single time.

A multi-level hierarchy arises naturally when migration occurs more frequently among populations within the same geographical region than among populations in different geographical regions. Consider a 2-level hierarchy in which there are S populations nested within each of k geographical regions (kS = P). Assume that population j in geographical region i is of size N _ij, and let ${\mathrm{p}}_{\mathit{ij}}^{\left(t\right)}$ be the A × 1 vector of allele frequencies in that population at generation t. We concatenate the population allele frequency vectors within geographical region i to an SA × 1 vector ${\mathrm{p}}_i^{\left(t\right)}$ and concatenate the k resulting cluster vectors to a kSA × 1 vector p^(t). We define

$${\mathrm{p}}^{\ast \left(t\right)}=(\mathrm{M}\otimes {\mathrm{V}}^{\prime }){\mathrm{p}}^{\left(t\right)},$$ (1)

where M ⊕ V′ denotes the Kronecker product of M and V′. Given N _ij, we assume that the population is diploid (so that the number of allele copies is 2N _ij) and that the ${\mathrm{p}}_{\mathit{ij}}^{(t+1)}$ are conditionally independent. Thus,

$$2N_{\mathit{ij}}{\mathrm{p}}_{\mathit{ij}}^{(t+1)}\sim \mathcal{M}(2N_{\mathit{ij}},{\mathrm{p}}_{\mathit{ij}}^{\ast \left(t\right)}),$$ (2)

where M denotes a multinomial distribution.. Through (1) and (2), we pass from p ^(t) → p*^(t) → p ^(t+1).

Stationary equations for means and covariances

The Markov Chain defined through (1) and (2) has a finite state space. If all entries of V′ are nonzero for some t ≥ 1, then this chain has no absorbing states. In fact, it is aperiodic and irreducible and thus has a unique stationary distribution (see Ewens 1979 for an introduction to stationary distributions in population genetic models). The stationary mean vector is identical in all populations and is given by the unique left eigenvector of V corresponding to an eigenvalue of 1. The stationary variance-covariance matrix is given by the solution of the following set of equations:

$$\begin{array}{cc}\hfill {\Sigma }_{\mathit{ij},\mathit{ij}}& =\left(1-\frac{1}{2N_{\mathit{ij}}}\right){\left(\mathrm{B}\Sigma {\mathrm{B}}^{\prime }\right)}_{\mathit{ij},\mathit{ij}}+\frac{1}{2N_{\mathit{ij}}}[\mathit{Diag}\left({\mathbf{u}}_{\mathit{ij}}\right)-{\mathbf{u}}_{\mathit{ij}}{{\mathbf{u}}^{\prime }}_{\mathit{ij}}]\hfill \\ \hfill {\Sigma }_{\mathit{ij},i^{\prime }{j}^{\prime }}& ={\left(\mathrm{B}\Sigma {\mathrm{B}}^{\prime }\right)}_{\mathit{ij},\mathit{ij}},\hfill \end{array}$$ (3)

where B = M ⊕ V′ (see Appendix A for details of the derivation, which follows Fu et al. 2003).

Results for a Finite Island Model

To make further analytical progress we consider a special case of the general structured migration model presented in the preceding section. The finite island model studied in Fu et al.(2003) imagined that a single backward migration rate applied to all populations. A natural generalization is to consider a hierarchical model in which migration occurs among populations within a single geographical region at the same rate but in which migration occurs among populations in different geographical regions at a different (and smaller) rate. For notational simplicity, we consider a 2-level hierarchy in which there are S populations within each of k geographical regions. We specify the migration matrix, M as follows:

$$\mathrm{M}=\left(\begin{array}{cccc}\hfill {\mathrm{M}}_1\hfill & \hfill {\mathrm{M}}_2\hfill & \hfill \dots \hfill & \hfill {\mathrm{M}}_2\hfill \\ \hfill {\mathrm{M}}_2\hfill & \hfill {\mathrm{M}}_1\hfill & \hfill \dots \hfill & \hfill {\mathrm{M}}_2\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill {\mathrm{M}}_2\hfill & \hfill {\mathrm{M}}_2\hfill & \hfill \dots \hfill & \hfill {\mathrm{M}}_1\hfill \end{array}\right),$$ (4)

where

$${\mathrm{M}}_1=\left(\begin{array}{cccc}\hfill m_0\hfill & \hfill \frac{m_1}{S-1}\hfill & \hfill \dots \hfill & \hfill \frac{m_1}{S-1}\hfill \\ \hfill \frac{m_1}{S-1}\hfill & \hfill m_0\hfill & \hfill \dots \hfill & \hfill \frac{m_1}{S-1}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill \frac{m_1}{S-1}\hfill & \hfill \frac{m_1}{S-1}\hfill & \hfill \dots \hfill & \hfill m_0\hfill \end{array}\right)$$ (5)

and

$${\mathrm{M}}_2=\left(\begin{array}{cccc}\hfill \frac{m_2}{S(k-1)}\hfill & \hfill \frac{m_2}{S(k-1)}\hfill & \hfill \dots \hfill & \hfill \frac{m_2}{S(k-1)}\hfill \\ \hfill \frac{m_2}{S(k-1)}\hfill & \hfill \frac{m_2}{S(k-1)}\hfill & \hfill \dots \hfill & \hfill \frac{m_2}{S(k-1)}\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill \frac{m_2}{S(k-1)}\hfill & \hfill \frac{m_2}{S(k-1)}\hfill & \hfill \dots \hfill & \hfill \frac{m_2}{S(k-1)}\hfill \end{array}\right),$$ (6)

with m ₀ = 1 − m ₁ − m ₂, and m ₁ > m ₂. The remainder of the formulation is unchanged.

Lengthy calculations (outlined in Appendix B) provide exact expressions for the stationary mean vector and for the stationary variances and covariances. To illustrate the properties of this specialization we consider an example with two alleles and asymmetric mutation.

Example

With two alleles at a locus, the mutation matrix is given by

$$\mathrm{V}=\left(\begin{array}{cc}\hfill v_{11}\hfill & \hfill v_{12}\hfill \\ \hfill v_{21}\hfill & \hfill v_{22}\hfill \end{array}\right),$$

where v ₁₁ = 1 − v ₁₂ and v₂₂ = 1 − v ₂₁. This mutation matrix leads to the stationary mean vector u = (μ_p, 1 − μ_p), where μ_p = ν₂₁/(ν₁₂ + ν₂₁). In addition,

$${\sigma }^2=\frac{\frac{1}{2N}{\mu }_p(1-{\mu }_p)}{1-(1-\frac{1}{2N}){\delta }_v^2[(1-r_{1,S}-r_{2,k}+r_{3,k,s})+(r_{1,S}-r_{3,k,S}){\rho }_1+r_{2,k}{\rho }_2]},$$

where δ_v = v ₁₁ − v ₂₁ = 1 − (ν₁₂ + v ₂₁), σ² is the variance in allele frequency within any one population over time, ρ₁ is the allele frequency correlation for populations in the same geographical region, and ρ₂ is the allele frequency correlation for populations in different geographical regions. ρ₁ and ρ₂ are given by

$$\begin{array}{cc}\hfill {\rho }_1& =\frac{{\delta }_v^2(r_{1,S}-r_{3,k,S})\left[1-{\delta }_v^2\left(1-\frac{r_{2,k}}{k-1}\right)\right]}{c(S-1)}+\frac{{\delta }_v^4{r}_{2,k}^2}{\mathit{cS}(k-1)}\hfill \\ \hfill {\rho }_2& =\frac{r_{2,k}{\delta }_v^2\left[1-{\delta }_v^2\left(1-\frac{r_{1,S}-r_{3,k,S}}{S-1}-r_{2,k}\right)\right]}{\mathit{cS}(k-1)}+\frac{(r_{1,S}-r_{3,k,S})r_{2,k}{\delta }_v^4}{\mathit{cS}(k-1)}\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill c& =\left[1-{\delta }_v^2\left(1-\frac{r_{2,k}}{k-1}\right)\right]\left[1-{\delta }_v^2\left(1-\frac{r_{1,S}-r_{3,k,S}}{S-1}-r_{2,k}\right)\right]-\frac{(S-1){\delta }_v^4}{S(k-1)}{r}_{2,k}^2\hfill \\ \hfill r_{1,S}& =2m_1-\frac{S}{S-1}{m}_1^2\hfill \\ \hfill r_{2,k}& =2m_2-\frac{k}{k-1}{m}_2^2\hfill \\ \hfill r_{3,k,S}& =2m_1{m}_2-\frac{S-1}{S(k-1)}{m}_2^2.\hfill \end{array}$$

In the case where each geographical region contains only a single population, i.e., S = 1, these results reduce to those presented in Fu et al. (2003) for the finite island model.

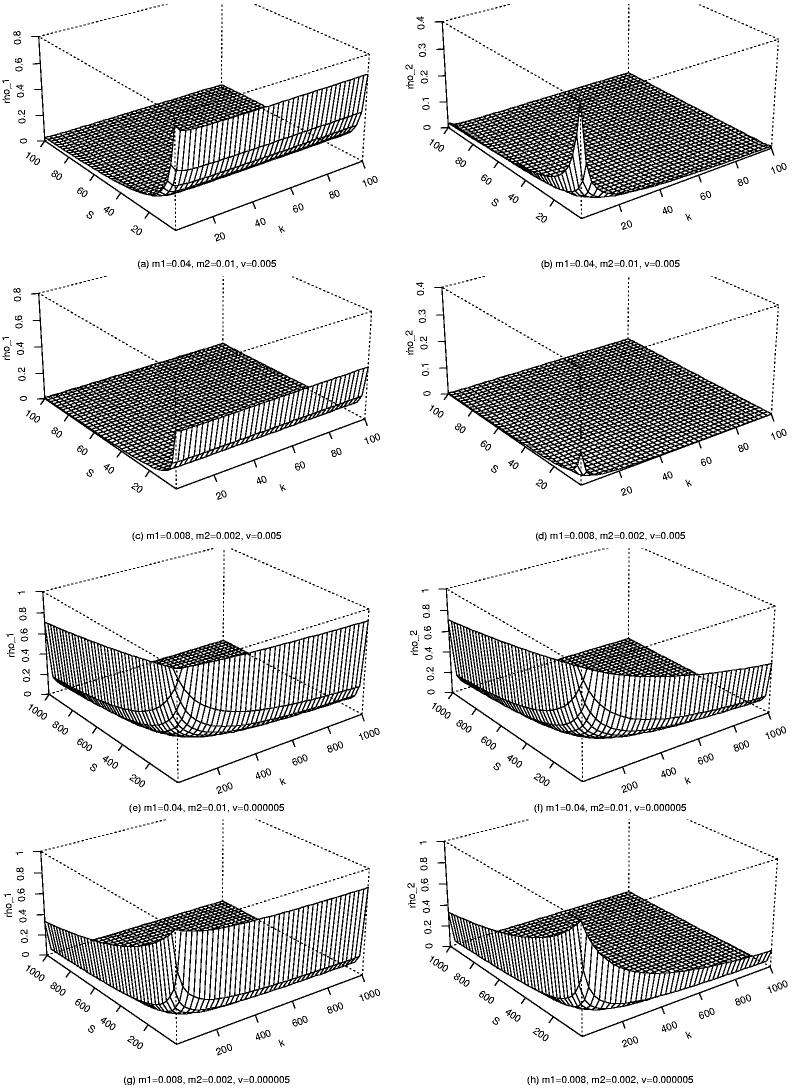
Figure 1 illustrates the magnitude of ρ₁ and ρ₂ for several parameter combinations. Notice that with mutation rates that may be typical of protein-coding loci (v = 5 × 10⁻⁷), both the correlation of allele frequencies among populations within a geographical region, ρ₁, and the correlation among geographical regions, ρ₂, are very high unless either the number of populations within each region, S, or the number of regions K is on the order of 200 or more. Moreover, the correlation decays more slowly as a function of increasing numbers of populations and regions when migration is common (m ₁ = 0.04, m ₂ = 0.01) than when it is rare (m ₁ = 0.008, m ₂ = 0.002). Notice also that the within-region correlation is relatively insensitive to the number of regions. It depends largely on the number of populations within each region. Similarly, the among-region correlation depends primarily on the number of regions and less on the number of populations within regions. Finally, with mutation rates that may be more typical of microsatellites (v = 0.005) the within-region correlation remains substantial with as many as 40 populations per region and the among-region correlation is small only when migration is rare (m ₁ = 0.008, m ₂ = 0.002).

Figure 1.

Plots of the correlation among populations within the same geographical region, ρ₁, and among geographical regions, ρ₂, as a function of the number of geographical regions, k, and the number of populations within each region, S, for several choices of migration rate with two mutation rates in the two-allele model.

INTERPRETATION FOR F-STATISICS

In general, the expressions for the stationary variance depend on the stationary mean. We can, however, calculate a scaled variance,

$$F_{\mathit{ST}}=\frac{{\sigma }_{p\left(t\right)}^2}{{\mu }_{p\left(t\right)}(1-{\mu }_{p\left(t\right)})},$$ (7)

that removes this dependence. In this case F _ST can be regarded as an intraclass correlation coefficient (Cockerham 1969; Weir and Cockerham 1984). In fact, Wright (1969, p.294) defined F _ST as “the correlation between random gametes within populations, relative to gametes of the total set of populations.” Since it was first introducted by Wright (1951) and Malécot (1948), F _ST has been the most widely used statistic for describing hierarchical structure in genetic data.

For a finite set of populations evolving according to (1) and (2) there are two quantities that might correspond with (7). (Refer to Table 2 for a summary of notation used in relation to F-statistics.) One of these quantities, which we will denote θ, takes ${\sigma }_{p\left(t\right)}^2$ to be the allele frequency variance in a single population across time (or equivalently as the allele frequency variance in a single population associated with different realizations of the stochastic evolutionary process). The second takes ${\sigma }_{p\left(t\right)}^2$ to be the allele frequency variance across populations at a single point in time, i.e.,

$$\theta (p_{11}^{\left(t\right)},\dots ,p_{\mathit{kS}}^{\left(t\right)})=\frac{\sum _{i=1}^k\sum _{j=1}^S{(p_{\mathit{ij}}^{\left(t\right)}-{\mu }_{p\left(t\right)})}^2∕\mathit{kS}}{{\mu }_{p\left(t\right)}(1-{\mu }_{p\left(t\right)})},$$ (8)

where ${\mu }_{p\left(t\right)}={\sum }_{i=1}^k{\sum }_{j=1}^S{p}_{\mathit{ij}}^{\left(t\right)}∕\mathit{kS}$.

Table 2.

Notation used in the two-allele, multiple locus hierarchical beta model.

Parameter	Definition
θ(I)	An estimate of θ
θ(II), θ(III)	Alternative estimates of $\theta (p_{11}^{\left(t\right)},\dots ,p_{\mathit{kS}}^{\left(t\right)})$
I	Number of loci (two alleles per locus)
K	Number of geographical regions
S k	Number of populations in geographical region k
p iks	Frequency of allele A 1 at locus i in population s of geographical region k
πik	Mean allele frequency at locus i in geographical region k
πi	Mean allele frequency at locus i
π	Mean allele frequency across loci
πik(1 − πik)θx	Variance in allele frequency at locus i within geographical regions
πi(1 − πi)θy	Variance in allele frequency at locus i among geographical regions
π(1 − π)θv	Variance in allele frequency across loci
ρ1	Allele frequency correlation among populations within geographical regions
ρ2	Allele frequency correlation among geographical regions

We use θ in our notation to emphasize that both quantities treat populations as random effects, as in Cockerham's random-effects model for θ-statistics (Cockerham, 1969; Weir and Cockerham, 1984; Weir, 1996; Weir and Hill, 2002). In particular, θ in our formulation has precisely the same interpretation as θ in the Cockerham random-effects model (Weir, personal communication; Holsinger in press). Moreover, θ is the parameter most directly related to features of the allele frequency distribution associated with the process model described above, as well to allele frequency distributions arising from the pure isolation model underlying evolutionary interpretations of Weir and Cockerham's θ-statistics (Weir and Cockerham 1984; Weir 1996; Weir and Hill 2002). Thus, we regard θ as the quantity that corresponds to Wright's F _ST. Notice that $\theta (p_{11}^{\left(t\right)},\dots ,p_{\mathit{kS}}^{\left(t\right)})$ corresponds to a random effects interpretation of Nei's G _ST (1973).

Estimation of θ is straightforward. Given a sample of genetic data from some set of populations we estimate μ_p(t) and ${\sigma }_{p\left(t\right)}^2$ from the data, and the estimate corresponding to θ is ${\theta }^{\left(I\right)}=\frac{{\widehat{\sigma }}_{p\left(t\right)}^2}{{\widehat{\mu }}_{p\left(t\right)}(1-{\widehat{\mu }}_{p\left(t\right)})}$. Notice that if the number of populations and population clusters is very large, then the allele frequency correlations illustrated in Figure 1 are negligible, and $\theta \approx \theta (p_{11}^{\left(t\right)},\dots ,p_{\mathit{kS}}^{\left(t\right)})$ (see also Fu et al. 2003). Recalling that k and S in (8) refer to the number of population clusters and populations among which migration is occurring, not the number of populations included in the sample, an estimate of θ^(I) might also be regarded as an estimate of $\theta (p_{11}^{\left(t\right)},\dots ,p_{\mathit{kS}}^{\left(t\right)})$ when ρ₁ and ρ₂ are small.

Estimation of $\theta (p_{11}^{\left(t\right)},\dots ,p_{\mathit{kS}}^{\left(t\right)})$ is less straightforward. Let Num denote the numerator on the right hand side of (8), and Denom the corresponding denominator. θ^(III) = E(Num/Denom) would correspond precisely with the definition of $\theta (p_{11}^{\left(t\right)},\dots ,p_{\mathit{kS}}^{\left(t\right)})$. To estimate θ^(III), however, would require knowledge of k and S, and they are generally unknown. An alternative is to estimate $\theta (p_{11}^{\left(t\right)},\dots ,p_{\mathit{kS}}^{\left(t\right)})$ with θ^(II) = E(Num)/E(Denom), which is is relatively insensitive to k and S for moderate values. In fact, we can show that θ^(II) → θ^(III) in probability as k and S tend to infinity. Furthermore, by using θ^(II) to estimate $\theta (p_{11}^{\left(t\right)},\dots ,p_{\mathit{kS}}^{\left(t\right)})$, we can provide an approximate expression for θ^(II) that does not depend on k or S (see equation (10)).

Tables 3 and 4 provide comparisons among θ^(I), θ^(II) and θ^(III) for 2N = {100, 1000}, v = v ₁₂ = v ₂₁ = {5 × 10⁻³, 5 × 10⁻⁶}, and several choices of m ₁ and m ₂ with m ₁ + m ₂ = 0.05. We calculate the expectations for θ^(III) from simulations using the process model in (1) and (2) conditional on $0<(1∕\mathit{kS}){\Sigma }_{\mathit{ij}}{p}_{\mathit{ij}}^{\left(t\right)}<1$; efficiency refers to the fraction of simulated samples satisfying this condition. We calculate θ^(I) and θ^(II) from the corresponding analytical expressions. Notice that θ^(I) can be two orders of magnitude greater than θ^(II) and θ^(III) under model (1) and (2). Notice also that θ^(II) and θ^(III) are quite similar, except when the population size, N is small. These patterns also hold with larger local population sizes (results not shown). For large mutation rates (5 × 10⁻³) the differences among θ^(I), θ^(II), and θ^(III) are fairly small. For smaller mutation rates (5 × 10⁻⁶) the differences between θ^(II) and θ^(III) are negligible, except when local populations are small (N = 50), but the differences between either of them and θ^(III) can be substantial. With N = 500, k = S = 5, m ₁ = 0.04, and m ₂ = 0.01, for example, θ^(II) ≈ θ^(III) = 0.01, but θ^(I) = 0.67.

Table 3.

Comparison of statistics related to F _ST under models (1) and (2) with migration rate = 5 × 10⁻² and mutation rate = 5 × 10⁻³. θ^(I) measures the variance in allele frequency over time. θ^(III) measures the variance in allele frequency among populations at one time. θ^(II) is an approximation of θ^(III) that does not require the number of populations and geographical regions involved in gene exchange to be known.

2N	k	S	m1	m2	θ(I)	θ(II)	θ(III)	SD	efficiency
100	5	5	0.04	0.01	0.104857	0.088287	0.088165	(0.0261710)	1.0000
			0.045	0.005	0.114985	0.098791	0.098595	(0.0319790)	1.0000
	25				0.092199	0.075152	0.075144	(0.0196840)	1.0000
	2	25	0.04	0.01	0.087076	0.078536	0.078344	(0.0143560)	1.0000
			0.045	0.005	0.088258	0.079740	0.079580	(0.0149500)	1.0000
	5	10	0.04	0.01	0.092473	0.084034	0.084032	(0.0166960)	1.0000
			0.045	0.005	0.097628	0.089286	0.089035	(0.0190960)	1.0000
	10	5	0.04	0.01	0.102506	0.094253	0.094415	(0.0196310)	1.0000
			0.045	0.005	0.113911	0.105868	0.105622	(0.0236580)	1.0000
	25	2	0.04	0.01	0.136095	0.128451	0.128495	(0.0259200)	1.0000
			0.045	0.005	0.164526	0.157379	0.157060	(0.0323100)	1.0000
	50				0.086341	0.077787	0.077586	(0.0140480)	1.0000
	2	50	0.04	0.01	0.083761	0.079480	0.079537	(0.0102010)	1.0000
			0.045	0.005	0.084353	0.080078	0.080110	(0.0105510)	1.0000
	5	20	0.04	0.01	0.086417	0.082161	0.082202	(0.0109240)	1.0000
			0.045	0.005	0.089016	0.084784	0.084727	(0.0120320)	1.0000
	10	10	0.04	0.01	0.091266	0.087055	0.087153	(0.0123930)	1.0000
			0.045	0.005	0.097070	0.092913	0.093262	(0.0140960)	1.0000
	20	5	0.04	0.01	0.101417	0.097300	0.097387	(0.0144150)	1.0000
			0.045	0.005	0.113428	0.109421	0.109984	(0.0174510)	1.0000
	50	2	0.04	0.01	0.135132	0.131318	0.131391	(0.0185340)	1.0000
			0.045	0.005	0.164123	0.160562	0.160681	(0.0230060)	1.0000
	100				0.083398	0.079114	0.079003	(0.0100390)	1.0000
1000	5	5	0.04	0.01	0.011475	0.009505	0.009551	(0.0031180)	1.0000
			0.045	0.005	0.012712	0.010747	0.010740	(0.0039037)	1.0000
	25				0.009964	0.007988	0.007989	(0.0022913)	1.0000
	2	25	0.04	0.01	0.009364	0.008376	0.008370	(0.0016830)	1.0000
			0.045	0.005	0.009502	0.008514	0.008566	(0.0017697)	1.0000
	5	10	0.04	0.01	0.009997	0.009010	0.009026	(0.0019700)	1.0000
			0.045	0.005	0.010608	0.009622	0.009587	(0.0022499)	1.0000
	10	5	0.04	0.01	0.011192	0.010207	0.010233	(0.0024105)	1.0000
			0.045	0.005	0.012579	0.011598	0.011605	(0.0029496)	1.0000
	25	2	0.04	0.01	0.015372	0.014395	0.014389	(0.0033988)	1.0000
			0.045	0.005	0.019142	0.018173	0.018133	(0.0044631)	1.0000
	50				0.009278	0.008290	0.008299	(0.0016529)	1.0000
	2	50	0.04	0.01	0.008978	0.008484	0.008504	(0.0012243)	1.0000
			0.045	0.005	0.009047	0.008553	0.008571	(0.0012423)	1.0000
	5	20	0.04	0.01	0.009287	0.008793	0.008808	(0.0013060)	1.0000
			0.045	0.005	0.009591	0.009097	0.009090	(0.0014191)	1.0000
	10	10	0.04	0.01	0.009855	0.009361	0.009374	(0.0014759)	1.0000
			0.045	0.005	0.010541	0.010049	0.010038	(0.0017295)	1.0000
	20	5	0.04	0.01	0.011061	0.010569	0.010607	(0.0017637)	1.0000
			0.045	0.005	0.012520	0.012029	0.012027	(0.0021845)	1.0000
	50	2	0.04	0.01	0.015248	0.014760	0.014780	(0.0024704)	1.0000
			0.045	0.005	0.019087	0.018602	0.018633	(0.0031901)	1.0000
	100				0.008936	0.008442	0.008445	(0.0011957)	1.0000

Table 4.

Comparison of θ^(I), θ^(II), and θ^(III) under models (1) and (2) with migration rate = 5 × 10⁻² and mutaion rate = 5 × 10⁻⁶.

2N	k	S	m1	m2	θ(I)	θ(II)	θ(III)	( SD )	efficiency
100	5	5	0.04	0.01	0.953072	0.118488	0.035089	( 0.054724 )	0.4755
			0.045	0.005	0.953208	0.164943	0.033850	( 0.065785 )	0.5904
	25				0.953047	0.087227	0.062394	( 0.041973 )	0.1781
	2	25	0.04	0.01	0.910622	0.092072	0.028777	( 0.042559 )	0.7901
			0.045	0.005	0.910662	0.095906	0.042092	( 0.047543 )	0.7554
	5	10	0.04	0.01	0.910761	0.105795	0.059872	( 0.052400 )	0.5814
			0.045	0.005	0.911008	0.130219	0.043044	( 0.059456 )	0.8211
	10	5	0.04	0.01	0.911023	0.131652	0.045810	( 0.061431 )	0.8369
			0.045	0.005	0.911657	0.188210	0.085297	( 0.091228 )	0.6027
	25	2	0.04	0.01	0.911899	0.208303	0.108143	( 0.102550 )	0.5364
			0.045	0.005	0.913652	0.330517	0.157490	( 0.159240 )	0.4574
	50				0.910719	0.090522	0.072460	( 0.037416 )	0.3946
	2	50	0.04	0.01	0.837299	0.092947	0.062259	( 0.043739 )	0.8353
			0.045	0.005	0.837358	0.094857	0.054165	( 0.046723 )	0.7797
	5	20	0.04	0.01	0.837517	0.099732	0.072560	( 0.044300 )	0.7544
			0.045	0.005	0.837927	0.112247	0.050154	( 0.054560 )	0.9811
	10	10	0.04	0.01	0.837939	0.112617	0.063899	( 0.054699 )	0.8844
			0.045	0.005	0.838983	0.143004	0.091877	( 0.065587 )	0.7936
	20	5	0.04	0.01	0.838831	0.138653	0.086329	( 0.066072 )	0.9120
			0.045	0.005	0.841123	0.200321	0.129833	( 0.090874 )	0.7485
	50	2	0.04	0.01	0.841685	0.214397	0.130166	( 0.103500 )	0.8935
			0.045	0.005	0.847488	0.339170	0.227145	( 0.155290 )	0.8039
	100				0.837453	0.092185	0.079117	( 0.033759 )	0.6879
1000	5	5	0.04	0.01	0.668069	0.013146	0.010830	( 0.006217 )	0.9823
			0.045	0.005	0.668735	0.019198	0.014646	( 0.010087 )	0.9840
	25				0.667938	0.009381	0.008466	( 0.003690 )	0.9079
	2	25	0.04	0.01	0.502417	0.009950	0.009753	( 0.002385 )	0.9998
			0.045	0.005	0.502523	0.010403	0.010242	( 0.002637 )	0.9982
	5	10	0.04	0.01	0.502824	0.011588	0.011166	( 0.003502 )	0.9985
			0.045	0.005	0.503594	0.014620	0.013987	( 0.005088 )	0.9996
	10	5	0.04	0.01	0.503639	0.014802	0.014242	( 0.004560 )	0.9988
			0.045	0.005	0.505597	0.022460	0.021450	( 0.008391 )	0.9987
	25	2	0.04	0.01	0.506344	0.025410	0.024043	( 0.008184 )	0.9958
			0.045	0.005	0.511859	0.046643	0.044096	( 0.015554 )	0.9992
	50				0.502703	0.009767	0.009523	( 0.002418 )	0.9921
	2	50	0.04	0.01	0.337740	0.010053	0.010058	( 0.001463 )	1.0000
			0.045	0.005	0.337842	0.010279	0.010240	( 0.001674 )	1.0000
	5	20	0.04	0.01	0.338100	0.010859	0.010784	( 0.001838 )	1.0000
			0.045	0.005	0.338776	0.012375	0.012261	( 0.002633 )	1.0000
	10	10	0.04	0.01	0.338797	0.012420	0.012385	( 0.002337 )	1.0000
			0.045	0.005	0.340523	0.016267	0.016259	( 0.003926 )	1.0000
	20	5	0.04	0.01	0.340267	0.015701	0.015694	( 0.003031 )	1.0000
			0.045	0.005	0.344113	0.024223	0.023941	( 0.006016 )	1.0000
	50	2	0.04	0.01	0.345061	0.026333	0.026123	( 0.005173 )	1.0000
			0.045	0.005	0.355126	0.048401	0.047733	( 0.010099 )	1.0000
	100				0.337997	0.009963	0.009929	( 0.001447 )	1.0000

INFERENCE UNDER A HIERARCHICAL BETA MODEL

Results presented in the preceding sections refer to variation at a single locus observed across time, but as evolutionary biologists we more commonly have samples from several or many different genetic loci collected from populations at the same time. If we regard the genetic sample as having been drawn from populations at stationarity with respect to the same underlying stochastic evolutionary process, then the samples at each locus can be regarded as (approximately independent) samples from the stationary distribution of this process. In fact, even if the populations are not at stationarity it may be reasonable to regard samples from different loci as (approximately independent) samples from a common underlying process, provided that the relevant evolutionary parameters (mutation, migration, and population size) are shared across the loci.

Assuming a common N and m across loci seems reasonable, because these parameters refer to demographic features of the populations from which the samples are drawn. It may seem problematic to assume common mutational parameters, but notice that in the example studied above, the scaled variance and correlations depend only on the total mutation rate, ν₁₁ − ν₂₁ = 1 − (ν₁₂ + ν₂₁). Similarly, in a multiallele model, the scaled variance and correlations depend only on the total mutation rate, provided that all alleles are equally likely to mutate (see equations (12) and (13) in Fu et al. 2003). Thus, we need not assume a common mutational bias across loci, only that the total mutation rate at each locus can be regarded as an independent sample from the same underlying distribution of mutation rates. In short, we propose to substitute replication across loci for replication across time. Weir (1996, pp. 174–175) justified bootstrap resampling across loci to obtain the sampling distribution for a method-of-moments estimate for θ using a similar argument (see also Weir and Hill 2002).

We assume that our sample consists of data from K population clusters, each of which has S _k populations, k = 1, … , K, and that the genotype of each individual is determined at I loci, each with two alleles A ₁ and A ₂. Let p_IKS×1 denote the allele frequencies of A ₁, i.e., p _iks is the allele frequency of A ₁ in s ^th population of the k ^th population cluster at locus i, i = 1, … , I; k = 1, … , K; s = 1, … , S _k. Notice that this structure corresponds to the stochastic evolutionary process illustrated in our example. Classical results (summarized in Crow and Kimura 1970 and in Ewens 1979) suggest that the stationary distribution of allele frequencies among populations is well-approximated by a Beta distribution when only two alleles are segregating. Griffiths (1979; see also Ewens 1979) extends these results to show that the distribution of allele frequencies is well-approximated by a Dirichlet distribution when mutation is equally frequency among all alleles at a multi-allelic locus. Moreover, Balding (2003) has shown that a Dirichlet distribution arises naturally in population genetics whenever alleles are regarded as exchangeable, regardles of whether the underlying stochastic evolutionary process has reached stationarity. Several authors have used Beta or Dirichlet distributions to construct likelihood or Bayesian methods for analysis of genetic structure (e.g., Balding and Nichols 1995; Roeder et al. 1998). Thus, we assume a hierarchical beta model for the allele frequency distribution:

$$\begin{array}{c}\hfill p_{\mathit{iks}}\mid {\pi }_{\mathit{ik}},{\theta }^x\sim \mathit{Beta}\left(\frac{1-{\theta }^x}{{\theta }^x}{\pi }_{\mathit{ik}},\frac{1-{\theta }^x}{{\theta }^x}(1-{\pi }_{\mathit{ik}})\right),\hfill \\ \hfill {\pi }_{\mathit{ik}}\mid {\pi }_i,{\theta }^y\sim \mathit{Beta}\left(\frac{1-{\theta }^y}{{\theta }^y}{\pi }_i,\frac{1-{\theta }^y}{{\theta }^y}(1-{\pi }_i)\right)\hfill \end{array}$$ (9)

and

$${\pi }_i\mid \pi ,{\theta }^v\sim \mathit{Beta}\left(\frac{1-{\theta }^v}{{\theta }^v}\pi ,\frac{1-{\theta }^v}{{\theta }^v}(1-\pi )\right).$$

It follows that

$$\begin{array}{c}\hfill E\left(p_{\mathit{iks}}\right)=\pi ,\hfill \\ \hfill {\sigma }^2=\mathit{Var}\left(p_{\mathit{iks}}\right)=\pi (1-\pi )\{{\theta }^v+{\theta }^y(1-{\theta }^v)+{\theta }^x(1-{\theta }^y)(1-{\theta }^v)\},\hfill \\ \hfill {\sigma }^2{\rho }_1=\mathit{Cov}(p_{\mathit{iks}},p_{{\mathit{iks}}^{\prime }})=\pi (1-\pi )\{{\theta }^v+{\theta }^y(1-{\theta }^v)\}\hfill \end{array}$$

for s ≠ s′,

$${\sigma }^2{\rho }_2=\mathit{Cov}(p_{\mathit{iks}},p_{{\mathit{ik}}^{\prime }{s}^{\prime }})=\pi (1-\pi ){\theta }^v$$

for k ≠ k′ and s ≠ s′ and

$$\mathit{Cov}(p_{\mathit{iks}},p_{i^{\prime }{k}^{\prime }{s}^{\prime }})=0$$

for all k, k′, s and s′ but i ≠ i′. Extension of this modeling framework to multiple alleles per locus is straightfoward, but tedious (see Holsinger 1999 for an outline of the approach). Fu et al. (2005) describe an alternative approach with the same variance-covariance properties based on a mixture of beta random variables. We assume the prior distribution for the parameters is given by independent uniform densities. Posterior inference is done through Markov Chain Monte Carlo (MCMC) simulation with the Metropolis-Hastings algorithm (Gilks et al., 1996).

F_ST in the Hierarchical Beta Model

Natural estimates of θ and $\theta (p_{111}^{\left(t\right)},\dots ,p_{\mathit{IKS}}^{\left(t\right)})$ arise from this model. Specifically,

$$\begin{array}{cc}\hfill {\theta }^{\left(I\right)}& =\frac{{\sigma }_{p\left(t\right)}^2}{{\mu }_{p\left(t\right)}(1-{\mu }_{p\left(t\right)})}=\frac{{\sigma }^2}{\pi (1-\pi )}\hfill \\ \hfill & ={\theta }^v+{\theta }^y(1-{\theta }^v)+{\theta }^x(1-{\theta }^y)(1-{\theta }^v),\hfill \end{array}$$

corresponds directly with the definition of θ as a function of the temporal mean and variance in allele frequencies. Notice also that

$$1-{\theta }^{\left(I\right)}=(1-{\theta }^v)(1-{\theta }^y)(1-{\theta }^x).$$

Thus, θ^(I) exhibits the conventional mathematical properties of F-statistics in hierarchically structured populations (Wright 1969, p. 295; Weir 1996). θ^v corresponds to the scaled allele frequency variance across loci, θ^y to the scaled allele frequency variance across geographic regions within a locus, and θ^x to the scaled allele freqency variance across populations within a geographic region.

An estimate of $\theta (p_{111}^{\left(t\right)},\dots ,p_{\mathit{IKS}}^{\left(t\right)})$ corresponding to θ^(II) arises from noticing that as the number of populations and geographical regions tends to infinity, for i = 1, … , I,

$$\frac{E[\sum _{k=1}^K\sum _{s=1}^{S_k}{(p_{\mathit{iks}}-\overline{p}...)}^2∕K\overline{S}]}{E[\overline{p}...(1-\overline{p}...)]}$$

converges in probability to

$${\theta }^{\left(\mathit{II}\right)}=\frac{{\theta }^{\left(I\right)}[1-(w_1{\rho }_1+w_2{\rho }_2)]}{1-{\theta }^{\left(I\right)}(w_1{\rho }_1+w_2{\rho }_2)},$$

with $w_1={\sum }_{k=1}^K{S}_k^2∕K^2{\overline{S}}^2$, w ₂ = 1 − w ₁ and $\overline{S}={\sum }_{k=1}^K{S}_k∕K$ where the expectation is across the stochastic evolutionary process. Notice that ${\sum }_{k=1}^K{S}_k^2={\sum }_{k=1}^K{(S_k-\overline{S})}^2+K{\overline{S}}^2$. Thus, w ₁ tends to 0 as K tends to infinity, provided that there exists ε in (0, ∞) such that ${\sum }_{k=1}^K{(S_k-\overline{S})}^2<\epsilon$ for all K. As a result,

$$\begin{array}{cc}\hfill {\theta }^{\left({\mathit{II}}^{\ast }\right)}& =\frac{{\theta }^{\left(I\right)}(1-{\rho }_2)}{1-{\theta }^{\left(I\right)}{\rho }_2}\hfill \\ \hfill & ={\theta }^y+{\theta }^x(1-{\theta }^y)\hfill \end{array}$$ (10)

provides a reasonable estimate of E(Num)/E(Denom) when the number of populations and geographical regions is unknown but large (compare Holsinger in press). Finally,

$${\theta }^{\left(\mathit{III}\right)}=E\left[\frac{\sum _{i=1}^I\sum _{k=1}^K\sum _{s=1}^{S_k}{(p_{\mathit{iks}}-\overline{p}...)}^2∕\left(IK\overline{S}\right)}{\overline{p}...(1-\overline{p}...)}\right]$$

where the p _iks are replaced with samples from the posterior distribution and the expectation is calculated across the joint posterior corresponds directly with the definition of $\theta (p_{111}^{\left(t\right)},\dots ,p_{\mathit{IKS}}^{\left(t\right)})$, if K and S _k are known. For completeness, we note that

$${\rho }_1=\frac{{\theta }^v+{\theta }^y(1-{\theta }^v)}{{\theta }^v+{\theta }^y(1-{\theta }^v)+{\theta }^x(1-{\theta }^y)(1-{\theta }^v)}$$

and

$${\rho }_2=\frac{{\theta }^v}{{\theta }^v+{\theta }^y(1-{\theta }^v)+{\theta }^x(1-{\theta }^y)(1-{\theta }^v)}.$$

Decomposition of $\theta (p_{111}^{\left(t\right)},\dots ,p_{\mathit{IKS}}^{\left(t\right)})$

In the formulation just presented $\theta (p_{111}^{\left(t\right)},\dots ,p_{\mathit{IKS}}^{\left(t\right)})$ summarizes the population structure while ignoring the hierarchy. As is clear from the discussion of θ^(I), however, it is natural to consider the partitioning of variation at each level of the hierarchy. There we pointed out that θ^x corresponds to the scaled allele frequency variance among populations within geographical regions and θ^y to the scaled allele frequency variance among geographical regions. In this section we consider an approach to decomposing $\theta (p_{111}^{\left(t\right)},\dots ,p_{\mathit{IKS}}^{\left(t\right)})$. Specifically, let

$$\begin{array}{cc}\hfill {\theta }_K^{\left({\mathit{II}}^{\ast }\right)}& =\frac{E[\sum _{k=1}^K\sum _{s=1}^{S_k}{S}_k{({\overline{p}}_{\mathit{ik}}.-{\overline{p}}_i..)}^2∕K\overline{S}]}{E[\overline{p}...(1-\overline{p}...)]}\hfill \\ \hfill & =\frac{{\theta }^{\left(I\right)}({\rho }_1-{\rho }_2)}{1-{\theta }^{\left(I\right)}{\rho }_2}\hfill \\ \hfill & ={\theta }^y\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill {\theta }_E^{\left({\mathit{II}}^{\ast }\right)}& =\frac{E\left[\sum _{k=1}^K\sum _{s=1}^{S_k}{(p_{\mathit{iks}}-{\overline{p}}_{\mathit{ik}}.)}^2\right]∕K\overline{S}}{E[\overline{p}...(1-\overline{p}...)]}\hfill \\ \hfill & =\frac{{\theta }^{\left(I\right)}(1-{\rho }_1)}{1-{\theta }^{\left(I\right)}{\rho }_2}\hfill \\ \hfill & ={\theta }^x(1-{\theta }^y),\hfill \end{array}$$

where the expectations are taken across the stochastic evolutionary process. Then ${\theta }_K^{\left({\mathit{II}}^{\ast }\right)}$ and ${\theta }_E^{\left({\mathit{II}}^{\ast }\right)}$ correspond to the scaled allele frequency variance among contemporeneous geographical regions and among contemporaneous populations within geographical regions, respectively. Notice that

$${\theta }^{\left({\mathit{II}}^{\ast }\right)}={\theta }_K^{\left({\mathit{II}}^{\ast }\right)}+{\theta }_E^{\left({\mathit{II}}^{\ast }\right)}.$$

Thus, ${\theta }_K^{\left({\mathit{II}}^{\ast }\right)}$ and ${\theta }_E^{\left({\mathit{II}}^{\ast }\right)}$ provide a readily interpretable additive decomposition of θ^(II*). Specifically, ${\theta }_K^{\left({\mathit{II}}^{\ast }\right)}={\theta }^y$ is the proportion of contemporaneous genetic variation attributable to allele frequency differences among regions, and ${\theta }_E^{\left({\mathit{II}}^{\ast }\right)}$ is the proportion of contemporaneous genetic variation attributable to allele frequency differences among populations within regions. θ_x and θ_y retain the multiplicative relationship with θ^(II*) characteristic of Wright's F-statistics:

$$1-{\theta }^{\left({\mathit{II}}^{\ast }\right)}=(1-{\theta }^x)(1-{\theta }^y).$$

APPLICATION

Human Population Data

Cann et al.(2002) describe the HGDP-CEPH Human Genome Diversity Cell Line Panel. We analyze the genetic diversity at 377 autosomal microsatellite loci in 1056 individuals included in the panel. These individuals represent 52 worldwide populations, and the genotypes are derived from those used in a related analysis reported in Rosenberg et al. (2002). Using an individual-based Bayesian classification algorithm (Pritchard et al. 2000), Rosenberg et al. (2002) were able to gather the 52 populations into 5 geographically coherent groups. We treat these groups as geographical regions (K = 5) in our analysis: Eurasia (21 populations, i.e., S ₁ = 21), Africa (6 populations, i.e., S ₂ = 6), East Asia (18 populations, i.e., S ₃ = 18), America (5 populations, i.e., S ₄ = 5) and Oceania (2 populations, i.e., S ₅ = 2). To illustrate analysis within the framework developed above, we designate the most frequent allele type at each locus as A ₁ and group all other allele types into a pseudo-allele type A ₂. Analyses in which we designated the second most frequent allele type at each locus A ₁ and grouped the remainder into a pseudo-allele class produced results concordant with those described below (results not shown).

Results

Results from analysis of these data are presented in Table 5. To illustrate the effect of ignoring the region-level allele frequency correlation Table 5 includes estimates from a model in which we assume independent uniform (0,1) prior distributions for π_i. Specifically, the hierarchical model developed above uses

$${\pi }_i\mid \pi ,{\theta }^v\sim \mathit{Beta}\left(\frac{1-{\theta }^v}{{\theta }^v}\pi ,\frac{1-{\theta }^v}{{\theta }^v}(1-\pi )\right),$$

while the reduced model uses

$${\pi }_i\sim \mathit{Unif}(0,1).$$

Because the actual number of population clusters and populations is unknown, we present values for θ^(III) in which we assume that the actual numbers of population clusters and populations are equal to those in our sample.

Table 5.

Parameter estimates for the human microsatellite data. See the text for an explanation of the difference between the two models.

	Hierarchical beta model		Reduced model
Parameter	Mean	(2.5%, 97.5%)	Mean	(2.5%, 97.5%)
π	0.3401	(0.3301, 0.3506)	n.a.1
θx	0.0294	(0.0283, 0.0306)	0.0293	(0.0283, 0.0305)
θy	0.0784	(0.0729, 0.0845)	0.0760	(0.0704, 0.0818)
θv	0.0298	(0.0237, 0.0370)	n.a.
ρ1	0.8010	(0.7869, 0.8149)	0.7371	(0.7191, 0.7552)
ρ2	0.2253	(0.1847, 0.2708)	n.a.
θ(I)	0.1322	(0.1254, 0.1395)	0.1031	(0.0979, 0.1087)
θ(II*)	0.1055	(0.1000, 0.1115)	0.1031	(0.0979, 0.1087)
${\theta }_K^{\left({\mathit{II}}^{\ast }\right)}$	0.0784	(0.0729, 0.0845)	0.0760	(0.0705, 0.0818)
${\theta }_E^{\left({\mathit{II}}^{\ast }\right)}$	0.0271	(0.0260, 0.0282)	0.0271	(0.0261, 0.0282)
θ(III) 2	0.1046	(0.1031, 0.1060)	0.1052	(0.1039, 0.1067)

¹Parameters not estimated in the reduced model are reported as not applicable.

²θ^(III) based on the observed number of population clusters and populations.

Notice that in the hierarchical model θ^(II*) = 0.1055 is quite similar to θ^(III) = 0.1046, suggesting that our estimate of $\theta (p_{11}^{\left(t\right)},\dots ,p_{\mathit{kS}}^{\left(t\right)})$ is little affected either by uncertainty about the actual number of population clusters and populations or by approximating E(Num/Denom) by E(Num)/E(Denom). Similarly, notice that in the reduced model, θ^(I) = θ^(II*) = 0.1031 is quite similar to θ^(III) = 0.1046 in the hierarchical model. More importantly, notice that θ^(I) = θ^(II*), because the allele frequency correlation among geographical regions is neglected. As a result, the estimate of θ^(I) = 0.1031 from the reduced model is about 30% smaller than the estimate of θ^(I) = 0.1322 in the hierarchical model. Method of moments estimates for the full, multi-allele data set (reported in Rosenberg et al. 2002) give an estimate quite similar to those reported here for the variance component among populations within regions: 0.025 versus θ^x = 0.0294. The smaller value reported for the variance component among regions, 0.043 versus θ^y = 0.0784, probably reflects the effect of grouping less frequent alleles into a single pseudo-allele class.

The discrepancy between estimates of F _ST in the hierarchical and reduced models (θ^(I) = 0.1322 versus θ^(I) = 0.1031, respectively) illustrates that analyses of F-statistics must either incorporate among region correlations or interpret the results in terms of differentiation relative to an unknown set of geographcial covariances (see Weir and Hill 2002 for similar results in an analysis of variance context). In these data, the price for ignoring the population covariances is a 30% underestimate of F _ST . In a similar analysis of data from Platanthera leucophaea, an orchid, Holsinger (in press) showed that neglecting the among population correlations would lead to an estimate of F _ST less than half of the best estimate (0.2122 versus 0.4837).

These data also show that there are substantial correlations among both populations (ρ₁ = 0.8010) and geographical regions (ρ₂ = 0.2253). Moreover, the additive partitioning of θ^(II*) indicates that 75% of the total allele frequency variation is a result of differences among geographic regions while 25% is a result of differences among populations within geographical regions $({\theta }_K^{\left({\mathit{II}}^{\ast }\right)}=0.0784,{\theta }_E^{\left({\mathit{II}}^{\ast }\right)}=0.0271)$. Notice both models lead to the same additive partitioning, because it is done relative to the set of geographical covariances.

Alternatively, we can use the traditional multiplicative partitioning of F-statistics and note that there is more than twice as much allele frequency differentiation among population clusterss than among populations within population clusters (θ^y = 0.0784 vs. θ^x = 0.0298). For these data, the two partitionings produce similar numerical results. For data sets in which θ^y is large, however, the differences may be substantial. Which partitioning is to be preferred will depend on whether interest centers on describing the contribution of each level of the hierarchy to contemporaneous variation in allele frequency (${\theta }_K^{\left({\mathit{II}}^{\ast }\right)}$ and ${\theta }_E^{\left({\mathit{II}}^{\ast }\right)}$) or on describing the magnitude of allele frequency variance at each level across replicates of the stochastic evolutionary process (θ^y and θ^x).

DISCUSSION

Wright's F-statistics have been the most widely used tool for describing the genetic structure of populations since they were first introduced more than fifty years ago (Malécot 1948; Wright 1951). Unfortunately, they paid little attention to the distinction between population and sample frequencies. Cockerham (1969) clearly understood the distinction between population and sample frequencies and the additional role of genetic sampling, but Nei's gene diversity statistics (1973) were the first widely used method that recognized some of the sampling properties. Unfortunately, Nei's statistics accounted only for the statistical sampling associated with sampling from actual populations and did not consider the genetic sampling associated with sampling the populations from an underlying stochastic evolutionary process (Weir 1996). To address these shortcomings, Weir and Cockerham (1984) introduced what is now the most widely used approach for characterizing population structure, a method-of-moments approach that accounts for both statistical and genetic sampling.

While the Weir and Cockerham (1984) approach is satisfactory in many ways, it suffers from several important limitations. First, interval estimates of the parameters either depend on asymptotic convergence of mean squares calculated from Bernoulli random variables to a chi-squared distribution (Li 1996) or on bootstrapping of samples across loci. In contrast, interval estimates are easily derived from the MCMC sample produced during analysis of our hierarchical model. Second, the chi-squared approximation depends on the assumption that the correlation among populations is zero, while the results in section 2 clearly show that the among-population correlation can be very large for reasonable mutation and migration rates, unless the number of populations and population clusters is very large. Third, as Weir and Hill (2002) point out, the estimate of θ provided by Weir and Cockerham's method estimates F _ST only when the correlation among populations is zero. When the correlation is non-zero, then the estimate provided is

$$\beta =\frac{\theta -{\theta }_A}{1-{\theta }_A},$$

where θ is equivalent to F _ST and π(1 − π)θ_A is the covariance in allele frequencies among populations. If samples at each locus are independent samples from a common underlying stochastic evolutionary process, however, then θ_A is equivalent to our θ^v and β is equivalent to our θ^(II*). Specifically,

$${\theta }^{\left({\mathit{II}}^{\ast }\right)}=\frac{{\theta }^{\left(I\right)}-{\theta }^v}{1-{\theta }^v},$$

where θ^(I) is our estimate of F _ST. In short, the parameters of the hierarchical statistical model we develop have direct, natural interpretations in terms of parameters related to the underlying stochastic evolutionary process, θ and $\theta (p_{11}^{\left(t\right)},\dots ,p_{\mathit{kS}}^{\left(t\right)})$, even in the face of substantial among population correlations. Ours is not the only approach that can account for these correlations, but existing alternatives depend on approximating the among population allele frequency distribution with a normal distribution (Nicholson et al. 2002; Weir and Hill 2002) or use a mixture approach whose interpretation is less natural (Fu et al. 2005). Of course, a normal approximation will work well only when allele frequency distributions are unimodal, roughly symmetric, and have little mass near 0 or 1, conditions satisfied only when min $[((1-\theta )∕\theta )p,((1-\theta )∕\theta )(1-p)]\gg 0$.

Applying our method to human microsatellite data illustrates that the among population correlation in allele frequencies can be substantial, even in species like humans with large, highly dispersive populations. The estimated allele frequency correlation among geographical regions (Eurasia, Africa, East Asia, America, and Oceania), ρ₂, is greater than 20%. The estimated allele frequency correlation among populations, ρ₁, is even greater, about 80%. As a result of the correlation among major population groupings our best estimate of F _ST, θ^(I), is about 30% greater than estimate of F _ST that ignore the region-level correlation..

While the numerical difference betewen θ^(I) and θ^(II*)) (0.13 vs. 0.10) may not seem great, one reason for interest in estimates of θ is their possible relationship to evolutionary process parameters. For example, if we were to treat the data as coming from a 1-level hierarchy, assume that mutation rates are much smaller than migration rates, and neglect the among population correlation in allele frequencies, then F _ST = θ ≈ 1/(4Nm + 1) (Crow and Kimura 1970). Thus, we might estimate Nm as $\widehat{Nm}=(1∕f-1)∕4$. Using θ^(I) as our estimate of F _ST we would obtain $\widehat{Nm}=2.25$, while using θ^(II*) we would obtain $\widehat{Nm}=1.67$.

As the results in Tables 3 and 4 show, however, we might vastly overestimate the extent to which gene flow is responsible for retarding population differentiation when the actual number of population clusters and populations is small or the migration rates are large or both. In the case of Platanthera leucophaea, for example, ignoring the correlation among populations would lead to an inferred estimate of Nm of about 0.98 with a 95% credible interval of 0.73-1.20, while a better estimate would be that Nm is only 0.27 with a 95% credible interval of 0.19-0.37 (Holsinger in press). In short, because existing methods for analysis of population structure typically neglect among population correlations in allele frequency and because such correlations may be substantial, past inferences about migration derived from F-statistics may substantially overstate the importance of gene exchange in preventing differentiation of partially isolated populations.

APPENDIX A

At stationarity, the distribution for p^(t) is the same for all t. Thus, let u_kSA×kSA denote the stationary mean vactor, i.e., E[p^(t)|M, V, N] where N is the vector of population sizes.

Since $E[{\mathrm{p}}_{\mathit{ij}}^{(t+1)}\mid {\mathrm{p}}_{\mathit{ij}}^{\left(t\right)},\mathrm{M},\mathrm{V},\mathrm{N}]={\mathrm{p}}_{\mathit{ij}}^{\ast \left(t\right)}$,

$$\begin{array}{cc}\hfill E[{\mathrm{p}}^{(t+1)}\mid \mathrm{M},\mathrm{V},\mathrm{N}]& =\mathit{EE}[{\mathrm{p}}^{(t+1)}\mid {\mathrm{p}}^{\left(t\right)},\mathrm{M},\mathrm{V},\mathrm{N}]\hfill \\ \hfill & =E[{\mathrm{p}}^{\ast \left(t\right)}\mid \mathrm{M},\mathrm{V},\mathrm{N}]\hfill \\ \hfill & =(\mathrm{M}\otimes {\mathrm{V}}^{\prime })E[{\mathrm{p}}^{\left(t\right)}\mid \mathrm{M},\mathrm{V},\mathrm{N}]\hfill \\ \hfill & =\mathrm{B}(\mathrm{M},\mathrm{V})E[{\mathrm{p}}^{\left(t\right)}\mid \mathrm{M},\mathrm{V},\mathrm{N}],\hfill \end{array}$$ (A.1)

where B(M, V) = (M ⊗ V′). Under stationarity, u = B(M, V)u. In fact, u does not depend on M. It is the unique left eigenvector of V corresponding to an eigenvalue of 1 (see Fu et al. 2003 for details).

Turning to stationary covariances, let Σ be the kSA dimensional stationary variance-covariance matrix of p. We define Δ=diag(Δ₁₁, …, Δ_kS) where

$${\Delta }_{\mathit{ij}}=\left[\mathit{Diag}\left({\mathrm{p}}_{\mathit{ij}}^{\ast \left(t\right)}\right)-{\mathrm{p}}_{\mathit{ij}}^{\ast \left(t\right)}{\left({\mathrm{p}}_{\mathit{ij}}^{\ast \left(t\right)}\right)}^{\prime }\right]∕2N_{\mathit{ij}},$$

with $\mathit{Diag}\left({\mathrm{p}}_{\mathit{ij}}^{\ast \left(t\right)}\right)=\mathit{Diag}\{p_{\mathit{ij}1}^{\ast \left(t\right)},\dots ,p_{\mathit{ijA}}^{\ast \left(t\right)}\}$. For convenience, we denote E(Δ) = diag(E(Δ₁₁), …, E(Δ_kS)). Then

$$\begin{array}{cc}\hfill {\Sigma }_{kSA\times kSA}& =\mathit{Var}({\mathrm{p}}^{(t+1)}\mid \mathrm{M},\mathrm{V},\mathrm{N})\hfill \\ \hfill & =\mathrm{B}\mathit{Var}({\mathrm{p}}^{\left(t\right)}\mid \mathrm{M},\mathrm{V},\mathrm{N}]){\mathrm{B}}^{\prime }+E(\Delta \mid \mathrm{M},\mathrm{V},\mathrm{N})\hfill \end{array}$$ (A.2)

since P*^(t) = Bp^(t) and ${\mathrm{p}}_{\mathit{ij}}^{\ast \left(t\right)}={\sum }_{l=1}^k{\sum }_{m=1}^S{\mathrm{B}}_{\mathit{ij},\mathit{lm}}{\mathrm{p}}_{\mathit{lm}}^{\left(t\right)}$ where B = B(M, V) and B_ij,lm denote the (ij, lm)^th A × A block matrix of B.

We calculate $E[\mathit{Diag}\left({\mathrm{p}}_{\mathit{ij}}^{\ast \left(t\right)}\right)\mid \mathrm{M},\mathrm{V},\mathrm{N}]$ and $E[{\mathrm{p}}_{\mathit{ij}}^{\ast \left(t\right)}{\left({\mathrm{p}}_{\mathit{ij}}^{\ast \left(t\right)}\right)}^{\prime }\mid \mathrm{M},\mathrm{V},\mathrm{N}]$ to obtain E(Δ_ij|M, V, N). First, we observe that

$$E({\Delta }_{\mathit{ij}}\mid \mathrm{M},\mathrm{V},\mathrm{N})=\mathit{Diag}\left(\sum _{l=1}^k\sum _{m=1}^S{\mathrm{B}}_{\mathit{ij},\mathit{lm}}E[{\mathrm{p}}_{\mathit{lm}}^{\left(t\right)}\mid \mathrm{M},\mathrm{V},\mathrm{N}]\right).$$

Next,

$$\begin{array}{cc}\hfill E[{\mathrm{p}}_{\mathit{ij}}^{\ast \left(t\right)}\left({\mathrm{p}}_{\mathit{ij}}^{\ast \left(t\right)}\right)\prime \mid \mathrm{M},\mathrm{V},\mathrm{N}]& =\mathit{Var}[{\mathrm{p}}_{\mathit{ij}}^{\ast \left(t\right)}\mid \mathrm{M},\mathrm{V},\mathrm{N}]\hfill \\ & +E[{\mathrm{p}}_{\mathit{ij}}^{\ast \left(t\right)}\mid \mathrm{M},\mathrm{V},\mathrm{N}]{\left\{E[{\mathrm{p}}_{\mathit{ij}}^{\ast \left(t\right)}\mid \mathrm{M},\mathrm{V},\mathrm{N}]\right\}}^{\prime }\\ & =\sum _{l=1}^k\sum _{m=1}^S\sum _{l^{\prime }=1}^k\sum _{m^{\prime }=1}^S{\mathrm{B}}_{\mathit{ij},\mathit{lm}}\mathit{Cov}[{\mathrm{p}}_{\mathit{lm}}^{\left(t\right)},{\mathrm{p}}_{l^{\prime }{m}^{\prime }}^{\left(t\right)}\mid \mathrm{M},\mathrm{V},\mathrm{N}]{{\mathrm{B}}^{\prime }}_{\mathit{ij},l^{\prime }{m}^{\prime }}\hfill \\ & +{\mathrm{B}}_{\mathit{ij},\mathit{lm}}E[{\mathrm{p}}_{\mathit{lm}}^{\left(t\right)}\mid \mathrm{M},\mathrm{V},\mathrm{N}]{\left\{E[{\mathrm{p}}_{l^{\prime }{m}^{\prime }}^{\left(t\right)}\mid \mathrm{M},\mathrm{V},\mathrm{N}]\right\}}^{\prime }{{\mathrm{B}}^{\prime }}_{\mathit{ij},l^{\prime }{m}^{\prime }}.\end{array}$$

Therefore,

$$\begin{array}{cc}\hfill E[{\Delta }_{\mathit{ij}}\mid & \mathrm{M},\mathrm{V},\mathrm{N}]=\frac{1}{2N_{\mathit{ij}}}\{\mathit{Diag}\left(\sum _{l=1}^k\sum _{m=1}^S{\mathrm{B}}_{\mathit{ij},\mathit{lm}}E({\mathrm{p}}_{\mathit{lm}}^{\left(t\right)}\mid \mathrm{M},\mathrm{V},\mathrm{N})\right)\hfill \\ \hfill & -{\mathrm{B}}_{\mathit{ij},\mathit{lm}}E[{\mathrm{p}}_{\mathit{lm}}^{\left(t\right)}\mid \mathrm{M},\mathrm{V},\mathrm{N}]{\left\{E[{\mathrm{p}}_{l^{\prime }{m}^{\prime }}^{\left(t\right)}\mid \mathrm{M},\mathrm{V},\mathrm{N}]\right\}}^{\prime }{{\mathrm{B}}^{\prime }}_{\mathit{ij},l^{\prime }{m}^{\prime }}\hfill \\ \hfill & -\sum _{l=1}^k\sum _{m=1}^S\sum _{l^{\prime }=1}^k\sum _{m^{\prime }=1}^S{\mathrm{B}}_{\mathit{ij},\mathit{lm}}\mathit{Cov}[{\mathrm{p}}_{\mathit{lm}}^{\left(t\right)},{\mathrm{p}}_{l^{\prime }{m}^{\prime }}^{\left(t\right)}\mid \mathrm{M},\mathrm{V},\mathrm{N}]{{\mathrm{B}}^{\prime }}_{\mathit{ij},l^{\prime }{m}^{\prime }}\}\hfill \end{array}$$ (A.3)

Under stationarity, E(Δ_ij|M, V, N) becomes

$$\frac{1}{2N_{\mathit{ij}}}[\mathit{Diag}\left({\mathrm{u}}_{\mathit{ij}}\right)-{\mathrm{u}}_{\mathit{ij}}{{\mathrm{u}}^{\prime }}_{\mathit{ij}}-{\left(\mathrm{B}\Sigma {\mathrm{B}}^{\prime }\right)}_{\mathit{ij},\mathit{ij}}],$$ (A.4)

since u = Bu. Thus, for i, i′ = 1, …, k and j, j′ = 1, …, S we have the A × A diagonal matrix of Σ,

$${\Sigma }_{\mathit{ij},\mathit{ij}}=\left(1-\frac{1}{2N_{\mathit{ij}}}\right){\left(\mathrm{B}\Sigma {\mathrm{B}}^{\prime }\right)}_{\mathit{ij},\mathit{ij}}+\frac{1}{2N_{\mathit{ij}}}[\mathit{Diag}\left({\mathrm{u}}_{\mathit{ij}}\right)-{\mathrm{u}}_{\mathit{ij}}{{\mathrm{u}}^{\prime }}_{\mathit{ij}}]$$ (A.5)

and the A × A diagonal matrix,

$${\Sigma }_{\mathit{ij},i^{\prime }{j}^{\prime }}={\left(\mathrm{B}\Sigma {\mathrm{B}}^{\prime }\right)}_{\mathit{ij},\mathit{ij}},$$

for i ≠ i′ or j ≠ j′.

APPENDIX B

Recalling that V is the mutation matrix, we let

$$\begin{array}{cc}\hfill \mathrm{B}{(\mathrm{M},\mathrm{V})}_{kSA\times kSA}& =\mathrm{M}\otimes {\mathrm{V}}^{\prime }\hfill \\ \hfill & =\left(\begin{array}{cccc}\hfill {\mathrm{M}}_1\otimes {\mathrm{V}}^{\prime }\hfill & \hfill {\mathrm{M}}_2\otimes {\mathrm{V}}^{\prime }\hfill & \hfill \dots \hfill & \hfill {\mathrm{M}}_2\otimes {\mathrm{V}}^{\prime }\hfill \\ \hfill {\mathrm{M}}_2\otimes {\mathrm{V}}^{\prime }\hfill & \hfill {\mathrm{M}}_1\otimes {\mathrm{V}}^{\prime }\hfill & \hfill \dots \hfill & \hfill {\mathrm{M}}_2\otimes {\mathrm{V}}^{\prime }\hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill {\mathrm{M}}_2\otimes {\mathrm{V}}^{\prime }\hfill & \hfill {\mathrm{M}}_2\otimes {\mathrm{V}}^{\prime }\hfill & \hfill \dots \hfill & \hfill {\mathrm{M}}_1\otimes {\mathrm{V}}^{\prime }\hfill \end{array}\right).\hfill \end{array}$$

Similarly,

$${\mathrm{B}}^{\prime }={(\mathrm{M}\otimes {\mathrm{V}}^{\prime })}^{\prime }=\mathrm{M}\otimes \mathrm{V},$$

since M is symmetric matrix. Thus ∑_kSA×kSA reduces to

$${\Sigma }_{kSA\times kSA}=\left(\begin{array}{cccc}\hfill {\Sigma }^{11}\hfill & \hfill {\Sigma }^{12}\hfill & \hfill \dots \hfill & \hfill {\Sigma }^{12}\hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill {\Sigma }^{12}\hfill & \hfill {\Sigma }^{11}\hfill & \hfill \dots \hfill & \hfill {\Sigma }^{12}\hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill ⋮\hfill & \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill {\Sigma }^{12}\hfill & \hfill {\Sigma }^{12}\hfill & \hfill \dots \hfill & \hfill {\Sigma }^{11}\hfill \end{array}\right)$$

For simplifying the equation (3), we need to get (B∑B′) which consists of the following matrices, (M _i ⊗ V′) ∑^{i′ j′} (M_j ⊗ V′) where i, i′, j, j′ = 1, 2:

(M₁ ⊗ V′)∑¹¹(M₁ ⊗ V′) consists of the following A × A submatrices: diagonal matrix is

$${\mathrm{V}}^{\prime }\left[(m_0^2+\frac{m_1^2}{S-1}){\Sigma }_1^{11}+\left(2m_0{m}_1+\frac{(S-2)m_1^2}{S-1}\right){\Sigma }_2^{11}\right]\mathrm{V}$$

and off-diagonal matrix is

$${\mathrm{V}}^{\prime }\left[\left(\frac{2m_0{m}_1}{S-1}+\frac{(S-2)m_1^2}{{(S-1)}^2}\right){\Sigma }_1^{11}+\left\{\frac{m_1^2}{S-1}+{\left(m_0+\frac{(S-2)m_1^2}{{(S-1)}^2}\right)}^2\right\}{\Sigma }_2^{11}\right]\mathrm{V}.$$

Further

$$\begin{array}{cc}\hfill ({\mathrm{M}}_1\otimes {\mathrm{V}}^{\prime }){\Sigma }^{11}({\mathrm{M}}_2\otimes {\mathrm{V}}^{\prime })& ={\mathrm{V}}^{\prime }\left[\frac{m_2(m_0+m_1)}{S(k-1)}{\Sigma }_1^{11}+\frac{(S-1)m_2(m_0+m_1)}{S(k-1)}{\Sigma }_2^{11}\right]\mathrm{V}\hfill \\ \hfill & =({\mathrm{M}}_2\otimes {\mathrm{V}}^{\prime }){\Sigma }^{11}({\mathrm{M}}_1\otimes {\mathrm{V}}^{\prime }),\hfill \\ \hfill ({\mathrm{M}}_2\otimes {\mathrm{V}}^{\prime }){\Sigma }^{11}({\mathrm{M}}_2\otimes {\mathrm{V}}^{\prime })& ={\mathrm{V}}^{\prime }\left[\frac{m_2^2}{S{(k-1)}^2}{\Sigma }_1^{11}+\frac{(S-1)m_2^2}{S{(k-1)}^2}{\Sigma }_2^{11}\right]\mathrm{V},\hfill \\ \hfill ({\mathrm{M}}_1\otimes {\mathrm{V}}^{\prime }){\Sigma }^{12}({\mathrm{M}}_1\otimes {\mathrm{V}}^{\prime })& ={\mathrm{V}}^{\prime }\left[{(m_0+m_1)}^2{\Sigma }_3^{12}\right]\mathrm{V},\hfill \\ \hfill ({\mathrm{M}}_1\otimes {\mathrm{V}}^{\prime }){\Sigma }^{12}({\mathrm{M}}_2\otimes {\mathrm{V}}^{\prime })& ={\mathrm{V}}^{\prime }\left[\frac{(m_0+m_1)m_2}{k-1}{\Sigma }_3^{12}\right]\mathrm{V}\hfill \\ \hfill & =({\mathrm{M}}_2\otimes {\mathrm{V}}^{\prime }){\Sigma }^{12}({\mathrm{M}}_1\otimes {\mathrm{V}}^{\prime })\hfill \end{array}$$

and

$$({\mathrm{M}}_2\otimes {\mathrm{V}}^{\prime }){\Sigma }^{12}({\mathrm{M}}_2\otimes {\mathrm{V}}^{\prime })=V^{\prime }\left[\frac{m_2^2}{{(k-1)}^2}{\Sigma }_3^{12}\right]\mathrm{V}.$$

After a straightforward but tedious calculation, it can be shown that

$$\begin{array}{cc}\hfill {\left(\mathrm{B}\Sigma {\mathrm{B}}^{\prime }\right)}_1^{11}& ={\mathrm{V}}^{\prime }\left[(1-r_{1,S}-r_{2,k}+r_{3,k,S}){\Sigma }_1^{11}+(r_{1,S}+r_{3,k,S}){\Sigma }_2^{11}+r_{2,k}{\Sigma }_3^{12}\right]\mathrm{V},\hfill \\ \hfill {\left(\mathrm{B}\Sigma {\mathrm{B}}^{\prime }\right)}_2^{11}& ={\mathrm{V}}^{\prime }\left[\frac{r_{1,S}-r_{3,k,S}}{S-1}{\Sigma }_1^{11}+\left(1-r_{2,k}-\frac{r_{1,S}-r_{3,k,S}}{S-1}\right){\Sigma }_2^{11}+r_{2,k}{\Sigma }_3^{12}\right]\mathrm{V}\hfill \end{array}$$

and

$${\left(\mathrm{B}\Sigma {\mathrm{B}}^{\prime }\right)}_3^{12}={\mathrm{V}}^{\prime }[\frac{r_{2,k}}{S(k-1)}{\Sigma }_1^{11}+\frac{S-1}{S(k-1)}{r}_{2,k}{\Sigma }_2^{11}+(1-\frac{r_{2,k}}{k-1}){\Sigma }_3^{12}]\mathrm{V}.$$

Finally, we obtain

$$\begin{array}{cc}\hfill {\Sigma }_1^{11}& =(1-\frac{1}{2N}){\mathrm{V}}^{\prime }\left[(1-r_{1,S}-r_{2,k}+r_{3,k,S}){\Sigma }_1^{11}+(r_{1,S}-r_{3,k,S}){\Sigma }_2^{11}+r_{2,k}{\Sigma }_3^{12}\right]\mathrm{V}+\frac{1}{2N}(\mathit{Diag}\left({\mathrm{u}}_{11}\right)-{\mathrm{u}}_{11}{{\mathrm{u}}_{11}}^{\prime }),\hfill \\ \hfill {\Sigma }_2^{11}& ={\mathrm{V}}^{\prime }\left[\frac{r_{1,S}-r_{3,k,S}}{S-1}{\Sigma }_1^{11}+\left(1-r_{2,k}-\frac{r_{1,S}-r_{3,k,S}}{S-1}\right){\Sigma }_2^{11}+r_{2,k}{\Sigma }_3^{12}\right]\mathrm{V}\hfill \end{array}$$

and

$${\Sigma }_3^{12}={\mathrm{V}}^{\prime }[\frac{r_{2,k}}{S(k-1)}{\Sigma }_1^{11}+\frac{S-1}{S(k-1)}{r}_{2,k}{\Sigma }_2^{11}+\left(1-\frac{r_{2,k}}{k-1}\right){\Sigma }_3^{12}]\mathrm{V}.$$