Control by cytochrome c oxidase of the cellular oxidative phosphorylation system depends on the mitochondrial energy state

Abstract

Recent measurements of the flux control exerted by cytochrome c oxidase on the respiratory activity in intact cells have led to a re-appraisal of its regulatory function. We have further extended this in vivo study in the framework of the Metabolic Control Analysis and evaluated the impact of the mitochondrial transmembrane electrochemical potential (Δμ_H⁺) on the control strength of the oxidase. The results indicate that, under conditions mimicking the mitochondrial State 4 of respiration, both the flux control coefficient and the threshold value of cytochrome oxidase are modified with respect to the uncoupled condition. The results obtained are consistent with a model based on changes in the assembly state of the oxidative phosphorylation enzyme complexes and possible implications in the understanding of exercise-intolerance of human neuromuscular degenerative diseases are discussed.

INTRODUCTION

Mitochondrial OXPHOS (oxidative phosphorylation) constitutes the major cellular ATP-producing mechanism under aerobic conditions. According to the chemiosmotic hypothesis, the flux of electrons through the complexes of the respiratory chain from the NADH- and FADH₂-linked substrates to O₂ is coupled with generation of Δμ_H⁺ (mitochondrial transmembrane electrochemical potential) across the mitochondrial inner membrane [1]. Δμ_H⁺, comprising an electrical and a chemical component [ΔΨ (transmembrane electrical potential) and ΔpH (transmembrane pH gradient) respectively], is then exploited to drive endoergonic reactions such as, first of all, the ATP synthesis by the F₁F_o-H⁺-ATP synthase. ATP generated in the mitochondrial matrix is then exported to the cytoplasm by the adenine nucleotide translocator, in exchange with ADP, to fulfil the cytoplasmic energy demand. If the availability of ADP in the mitochondrial matrix becomes limiting, the transmembrane electrochemical H⁺ gradient accumulates and, in turn, inhibits further unnecessary electron transfer along the respiratory complexes. This negative loop allows modulation of the rate of respiration to the cellular energy demand and constitutes the basis of mitochondrial respiratory control [2].

The multi-component structure of the OXPHOS network [3] poses the question as to which step(s) is (are) critical in controlling the efficiency of the overall process. An understanding of this specific point, besides its interest in basic research, is also important for elucidating the aetiopathogenesis of a number of human diseases characterized by impairment in OXPHOS efficiency [4]. MFCA (Metabolic Flux Control Analysis) constitutes a solid theoretical and experimental tool that has contributed to our understanding of the molecular mechanism that determines how metabolic pathway fluxes are controlled [5,6]. It has been extensively applied to the mitochondrial OXPHOS system to estimate the control strength exerted by specific enzymatic steps to the overall process (i.e. respiratory rate and/or ATP synthesis) [7–9]. The survey of the results produced by these studies would indicate that the control of the OXPHOS system is shared among different steps, with none of them showing a large control coefficient. As most of these studies have been carried out on isolated mitochondria and more recently on permeabilized cells [10,11], concern about the compliance of the conclusions to the in vivo situation has been raised [12–15]. Extension of MFCA to intact cells has revealed, indeed, that COX (cytochrome c oxidase) exhibits a much lower reserve capacity than in isolated mitochondria, thus promoting COX to a pivotal role in controlling respiration and OXPHOS.

It must be pointed out, however, that either ex vivo or in vivo MFCA of mitochondrial respiration has been almost exclusively studied under uncoupled conditions (achieved in the presence of an excess of ADP or upon treatment of the sample with uncouplers of respiration), which limits the survey to a situation that does not encompass the physiological impact of the membrane potential on the performance of mitochondrial OXPHOS. Therefore the aim of the present study was to explore if the depressing effect of the membrane potential on the overall mitochondrial respiration modifies the control strength exerted by a given isolated step (specifically COX) or simply superimposes a thermodynamic control without altering its kinetic reserve capacity.

MATERIALS AND METHODS

Cell culture

The human hepatoma cell line HepG2 was maintained in culture with DMEM (Dulbecco's modified Eagle's medium) and 10% (v/v) fetal bovine serum. Cells were allowed to grow to 70–80% confluence before harvesting. Cells were detached from 150-mm-diameter Petri dishes with 2 ml of trypsin (0.05%)/EDTA (0.02%) and washed in 20 ml of PBS, pH 7.4, with 5% (v/v) calf serum, centrifuged at 500 g, resuspended in 200 μl of PBS, counted and immediately used. Cell viability, as determined by Trypan Blue exclusion, was typically never below 98%.

Isolation of mitochondria, COX purification and liposome reconstitution

Mitochondria from bovine heart (‘heavy’ fraction) and rat liver were isolated by differential centrifugation as described in [16] and [17] respectively. COX was purified from bovine heart mitochondria, as described in [18], tested for structural and functional parameters as described in [19] and reconstituted in small unilamellar vesicles by the cholate-dialysis method [20]. The respiratory control ratio of COX vesicles was tested as described in [20] and was found to be routinely higher than 10.

Polarographic measurements

The rate of oxygen consumption was measured polarographically with a Clark-type oxygen electrode in a thermostatically controlled chamber equipped with a magnetic stirring device (the instrumental setting was computer-controlled) and a gas-tight stopper fitted with a narrow port for additions via a Hamilton microsyringe. The medium/buffer used for measurement was 50 mM KH₂PO₄, 10 mM Hepes, 1 mM EDTA, pH 7.4, air-equilibrated at 37 °C (volume 0.5 ml) and the concentration of viable HepG2 cells was typically 10×10⁶ cells/ml. Inhibition titration of the cellular respiratory activity was carried out by adding sequentially 0.5–1 μl of freshly prepared KCN solutions (0.01, 0.1 and 1 M). The respiratory activities were corrected for the instrumental and/or medium-linked oxygen-consumption drifts.

Laser-scanning-confocal-microscopical analysis

Cells were seeded at low density on to fibronectin-coated 35-mm-diameter glass-bottom dishes. After adhesion, living cells were directly incubated for 20 min at 37 °C with MitoCapture™ Apoptosis Detection Kit [at 1:1000 dilution, following the manufacturer's (Biovision, Mountain View, CA, U.S.A.) recommendations]. Thereafter cells were washed twice with PBS and examined with a Nikon TE 2000 microscope [images collected using a 60× objective (1.4 numerical aperture)] coupled to a Radiance 2100 dual laser (four lines, Ar/Kr; single line, helium/neon)-scanning-confocal-microscopy system (Bio-Rad). The fluorescence signal of the double-emitter probe was examined sequentially, exciting first with the Ar/Kr laser beam (λ_ex 488 nm) and then with the He/Ne laser beam (λ_ex 543 nm). Confocal planes of 0.2 μm thickness were examined along the z-axes, going from the top to the bottom of the cells. Acquisition, storage and analysis of data were made by using LaserSharp and LaserPix software from Bio-Rad. Quantification of the emitted fluorescence signal was achieved by producing a xz-intensity profile of the average value of the pixels within marked edges, including a single cell, as a function of each focal plane. Correction was made for minimal background by repeating the procedure in a cell-free field. The integrated value of the xz profile was taken as a measure of the fluorescence intensity of that individual cell.

MCA

For the estimation of the control coefficient, c₀, exerted by COX over the cell respiration, two procedures were adopted. In one the ratios of the initial slopes from the cyanide titration curves of1 the integrated flow and isolated step were calculated by least-square linear-regression analysis. In this case the flux control coefficient is operatively defined as:

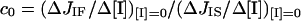where ΔJ_IF and ΔJ_IS are the changes in the respiratory rates of the integrated flow and isolated step respectively, taken at the same interval of the inhibitor concentration, tending to 0.

The alternative way of calculating c₀ was that developed in [21] for non-competitive inhibition. In this case the final equation given in [21] was simplified as follows:

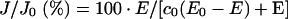with

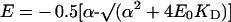and

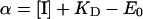where E and E₀ are the concentrations of the active enzyme at a given concentration of the inhibitor ([I]) and at [I]=0 respectively; K_D is the dissociation constant of the EI complex; J and J₀ are the respiratory rates measured at a given concentration of the inhibitor ([I]) and at [I]=0 respectively. With respect to the equation given in [21], an empirical exponent, n, was assumed to be 1 and because at a high concentration of the inhibitor (i.e. E=0) the residual measurable respiratory rate was negligible, J_i was assumed to be 0 (cf. with eqn 5 in [21]). Imposing E₀=100, the entire data set of the inhibitor titration curve for the integrated flow was fitted with the percentage of the uninhibited activity given as a function of the concentration of the inhibitor. The parameters c₀ and K_D were estimated by the program GraFit 4.0.13 (Erithacus Software Ltd., Horley, Surrey, U.K.). The accuracy of the fitting procedure was further tested by analysing the data of the inhibition titration curve for the isolated step. In this case a c₀ value of 1 was imposed and the estimated K_D was shown to be comparable with that obtained from the fit of the integrated flow.

Kinetic simulation

Modelling of a metabolic flow mimicking a multi-step electron-transfer system was carried out with the freeware software package Chemical Kinetics Simulator (available at http://www.almaden.ibm.com/st/computational_science/ck/msim/). This program does not integrate sets of coupled differential equations to predict the time course of a chemical system. Instead, it uses a general, rigorously accurate stochastic algorithm to propagate a reaction. The stochastic method is comparable in efficiency to integration for simple kinetic schemes, and significantly faster for stiff systems [22].

Materials

The HepG2 cell line was from the A.T.C.C., DMEM, PBS, trypsin (0.05%)/EDTA (0.02%), penicillin (10000 units/ml)/streptomycin (10000 μg/ml) and fetal bovine serum were from EuroClone (Milan, Italy); oligomycin, antimycin A, actractiloside, valinomycin, CCCP (carbonyl cyanide m-chlorophenylhydrazone) and cytochrome c were from Sigma; ascorbate was from Boehringer and TMPD (N,N,N′,N′-tetramethyl-p-phenylenediamine) was from Fluka. All other chemicals were of the highest purity available.

Statistical analysis

The two-tailed Student's t test was applied to evaluate the significance of differences measured throughout the data sets reported.

RESULTS

Measurement of endogenous respiration and COX activity in intact cells

HepG2 is a human hepatoma cell line the metabolism of which, in the late exponential growth phase, is mainly sustained by mitochondrial OXPHOS [23] and was therefore chosen for the present study.

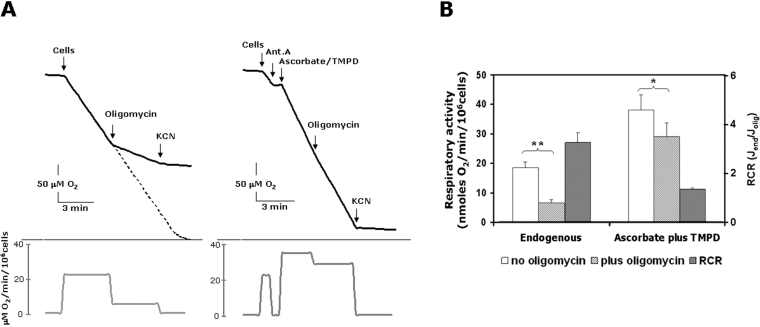
Figure 1(A) shows a typical output of respirometric measurements for oxygen consumption, carried out on intact HepG2 cells. The respiratory rate was sustained by endogenous substrates and relied almost completely on the mitochondrial contribution, as it was fully inhibited by KCN. The amount of the endogenous oxidizable substrates was apparently never limiting, since oxygen consumption was linear up to the instrumental detection limit (<5% oxygen saturation). Addition of the ATP synthase inhibitor oligomycin resulted in a marked depression of the oxygen consumption rate, documenting a feature of an active phosphorylating State III for the endogenous respiration. The respiratory control ratio (State III_endogenous/State IV_oligomycin) was 3.3±0.4 (n=10) (Figure 1B). Atractiloside, an inhibitor of the mitochondrial adenine nucleotide translocator, resulted in depression of the endogenous respiration to an extent comparable with that attained by oligomycin (results not shown). Uncouplers of the OXPHOS [DNP (2,4-dinitrophenol) or CCCP] stimulated the oligomycin (or actractiloside)-settled respiratory rate, but never exceeded that elicited in State III_endogenous (results not shown).

Figure 1. Measurement of O₂ consumption rates in HepG2 cells.

(A) Polarographic traces showing the endogenous respiration in intact cells (on the left) and the in situ activity of COX (on the right). In the latter case the endogenous respiration was inhibited by 1 μg/ml antimycin A (Ant. A) and the COX activity was rescued by addition 10 mM ascorbate plus 200 μM of the membrane-permeant compound TMPD. Where indicated, 2 μg/ml oligomycin and 2 mM KCN were added. The changes in the rates of O₂ consumption throughout the assays are given as first derivatives in the panels below the corresponding traces. (B) Statistical evaluation of the effect of oligomycin on the activities of the respiratory endogenous flow (means±S.E.M., n=10) and COX isolated step (means±S.E.M., n=6). The respiratory control ratios (RCRs) of the rates of O₂ consumption in the absence J_end and in the presence of oligomycin J_olig are also shown. Paired Student's t test analysis: *P<0.05; **P<0.001.

These results confirmed qualitatively, at the cellular level, the bioenergetic paradigms well established in classical experiments carried out on isolated mitochondria [2] and showed that transmembrane potential exerts, in vivo, a tight control on respiration.

Figure 1(A) shows also that antimycin A, a specific inhibitor of cytochrome c reductase, completely inhibited endogenous respiration and that successive addition of ascorbate plus the membrane-permeant redox-recycling compound TMPD by-passed the block, delivering electrons directly to COX via cytochrome c reduction. Unlike the situation observed with endogenous respiration, the ascorbate/TMPD-fuelled COX activity was only slightly repressed by oligomycin, resulting in a respiratory control ratio of 1.3±0.1 (n=6).

Measurement of mitochondrial membrane potential in intact cells

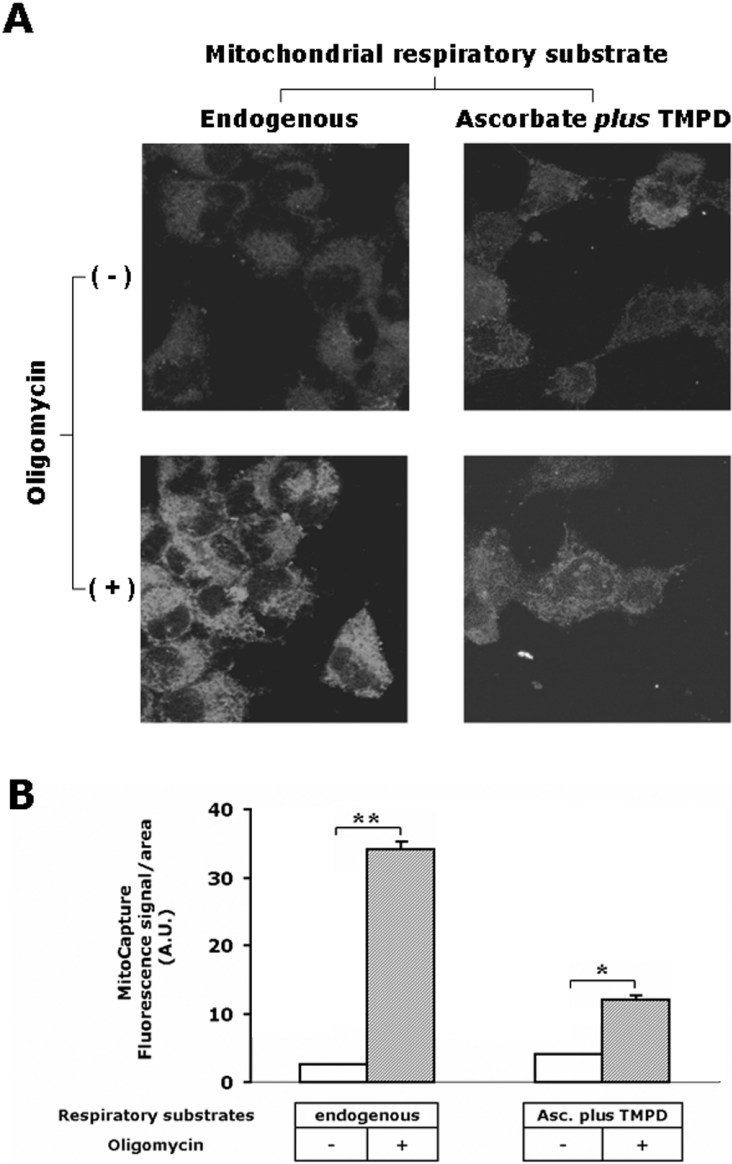
The involvement of the membrane potential in the control of mitochondrial respiration in intact cells was directly assessed by laser-scanning confocal microscopy using the probe MitoCapture™ (Figure 2). Depending on the extent of the transmembrane electrical potential, the dye accumulates as monomer (green emitter) or dimer (red emitter, in hyperpolarized mitochondria) resembling other dual-emitting ΔΨ probes [24]. Figure 2(A) shows that the fluorescence signal due to accumulation of the probe in response to membrane potential was barely detectable under conditions of endogenous respiration, but strongly increased (10-fold) when the cell samples were incubated with oligomycin. In line with the polarographic measurements, Figure 2 also shows that the membrane potential generated in the presence of oligomycin by COX was lower than that observed under endogenous respiration, but was, however, greater than that seen with the fully active ATP synthase. This is not surprising, since the protonmotive force generated by COX is only a fraction of that produced by the entire respiratory chain, which operates with the other two in-series proton-pumping respiratory complexes (NADH dehydrogenase and cytochrome c reductase) [3]. Moreover, it has been shown that the coupling efficiency of the COX redox-linked proton pump is negatively controlled by the extent of Δμ_H⁺ [25].

Figure 2. Confocal-microscopic analysis of respiration-driven mitochondrial membrane potential in HepG2 cells.

(A) Imaging of the fluorescence signal of the probe MitoCapture™ in live cells. The upper two panels show the analysis carried out under respiratory conditions sustained by endogenous substrates (on the left) and by activation of COX as an isolated step (on the right). The lower two panels show the effect of pre-incubation of the cells with 2 μg/ml oligomycin on the mitochondrial membrane potential generation under endogenous (on the left) and isolated step (on the right) respiratory activities. The images shown are superimpositions of confocal planes and are representative of four different experiments. (B) Single-cell analysis of the green fluorescence intensity of MitoCapture™ under the four conditions described in (A). The fluorescence intensities were quantified as described in the Materials and methods section and normalized to the surface of the selected area; 20–30 cells were analysed for each condition and the results shown are means±S.E.M. for the experiment shown in (A). Paired Student's t test analysis for the fluorescence intensity of oligomycin-untreated versus oligomycin-treated cells: *P<0.01; **P<0.001. Abbreviation used: A.U., arbitrary units (being pixel intensity normalized to the selected area).

MCA of COX in intact cells

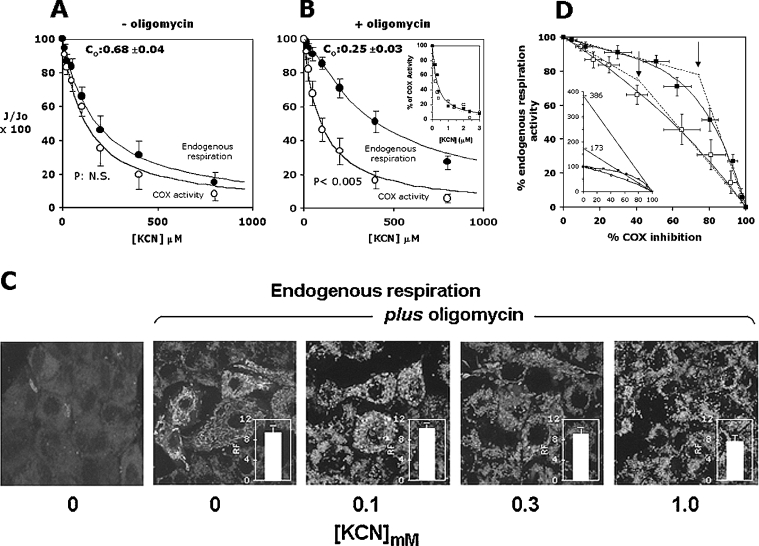
The control exerted by COX over cell respiration and the effect of the mitochondrial membrane energization state upon it were tested by applying MFCA to intact cells. Figure 3(A) shows the results of KCN titrations on the oxygen consumption rates sustained either by endogenous substrates or by ascorbate plus TMPD. One can see that inhibition of cell respiratory flux resulted in a normalized titration curve almost superimposable on that of the functionally isolated step. The flux control coefficient, c₀, measured either by the ratio of the slopes attained in the initial low inhibitor concentration ranges and by non-linear fitting of the entire experimental data set of the integrated flow, was 0.6–0.7. When the same analysis was carried out with oligomycin-pretreated cells, the KCN titration curve of the integrated flow revealed a much higher resistance to inhibition when compared with that of the isolated step and a more sigmoidal shape (Figure 3B). The calculated c₀ was about 0.25.

Figure 3. MCA of COX control over endogenous respiration in intact HepG2 cell line: effect of Δμ_H⁺.

Titration curves for KCN inhibition of the endogenous respiration (●) and of ascorbate/TMPD-dependent respiration (○) in the absence (A) and in the presence (B) of oligomycin. The residual activity is given as a percentage of the uninhibited respiratory rate. See the legend to Figure 1(A) and the Materials and methods section for experimental details. The data points shown are the means±S.E.M. for at least five different titrations for each condition. P represents the statistical significance provided by the Student's t test analysis when applied to the data points for the endogenous and COX activity in the [KCN] range 50–500 μM. The continuous lines are the best fit of the data points obtained applying the equation for non-linear regression analysis given in the Materials and methods section; parameter settings: K_D=130±7 μM and 90±7 μM for the endogenous fluxes without and with oligomycin respectively, with the relative computed c₀ values indicated in the panels. When the control coefficients were calculated from the ratios of the initial tangents of the integrated versus the isolated step, values of 0.65 and 0.22 were estimated. The inset to (B) shows KCN titration curves for purified ox heart COX reconstituted in liposomes; the concentration of COX vesicles was 50 nM, and the respiratory activity was measured polarographically (as in Figure 1A) in the presence of 10 mM ascorbate, 200 μM TMPD and 20 μM cytochrome c under coupled (□) and fully uncoupled (valinomycin+CCCP) (■) conditions (mean for two experiments). (C) Confocal-microscopic analysis using MitoCapture™ of the effect of KCN titration on the mitochondrial membrane potential in cells respiring with endogenous substrates in the presence of oligomycin. The experimental conditions are those illustrated for (B). KCN was added, at the indicated concentrations, directly to the dishes 5 min before the addition of MitoCapture™. For comparison, imaging of the ΔΨ probe in HepG2 cells respiring in the absence of oligomycin is shown under identical instrumental setting conditions. The bars quantify the relative fluorescence (RF) signal (green emission) in the oligomycin-treated cells normalized to that of the cells respiring in the absence of oligomycin (see the legend to Figure 2B for the quantification procedure). The images selected are superimposition of confocal planes and are representative for three independent experiments. See the Materials and methods section for further details. (D) Threshold plots for COX activity over the endogenous respiration in the absence (□) and in the presence (■) of oligomycin are from the inhibitor titration data presented in (A) and (B) respectively. The continuous lines derive from the combination of the equations fitting the titration curves in (A) and (B). The arrows indicate the threshold values for the two plots obtained from the intercepts of the lines tangent to the initial and final part of the curves. The calculated values for the threshold points are about 40 and 75% of COX inhibition for the plots obtained in the absence and in the presence of oligomycin respectively. The inset to (C) shows an expansion of the same plot along the ordinate axis, enabling one to pinpoint the maximum COX capacities as intercepts from the extrapolated lines fitting the points at the highest percentage of COX inhibition [12,13].

The inset in Figure 3(B) shows that the KCN inhibition titrations carried out on purified COX reconstituted in liposomes under coupled (respiratory control ratio ≥10) and uncoupled conditions resulted in superimposable curves with practically identical K_i50 (concentration giving half-maximal inhibition) for KCN. This control clearly ruled out the possibility of an effect of ΔΨ on the accessibility/affinity of CN⁻ to the COX active site [26].

Figure 3(C) shows that addition of KCN (up to 300 μM) to oligomycin-treated endogenously respiring HepG2 cells did not cause any appreciable change in the mitochondrial-ΔΨ-dependent accumulation of MitoCapture™. Some decrease of the fluorescent signal was recorded at 1 mM inhibitor. Thus, in spite of the inhibition of respiration, the mitochondrial ΔΨ was substantially maintained throughout the cyanide titration assay (see the Discussion).

When the experimental data were presented as a threshold plot, i.e. percentage of the endogenous respiratory activity as a function of the percentage of COX inhibition at the same KCN concentrations (Figure 3D), a difference emerged. Whereas in the absence of membrane potential COX exerted a strong control over the respiratory metabolic flux, such that any degree of inhibition of the isolated step resulted in an almost identical level of inhibition of the integrated respiratory flux, in the presence of oligomycin (i.e. with an established Δμ_H⁺) the control strength of COX over the respiratory flux was decreased so that a 50–60% inhibition of the isolated step resulted in only a 10% decrease of the integrated flux. The threshold plots are usually characterized by a more evident biphasic behaviour with a net break point that allows for estimation of the threshold value [27]. Instead, the results presented here fit with a continuous curve that is predicted by the metabolic control theory and which reveals the occurrence of compensatory changes of intermediates in the sequential array of enzymatic steps constituting the metabolic network [28] (see the Discussion). In the presence of oligomycin, a tentative threshold value might be set at around 75% inhibition of the isolated step. Further information deriving from the analysis of the threshold plot is the maximal reserve capacity of the isolated step, which can be estimated by extrapolation of the linear part of the threshold plot at the highest degrees of inhibition of the isolated step [13]. From the results shown in Figure 3(D), it was estimated that the maximal reserve capacity of COX exceeded the theoretical capacity to sustain the full activity of the respiratory flux by 73 and 286% in the absence and in the presence of oligomycin respectively.

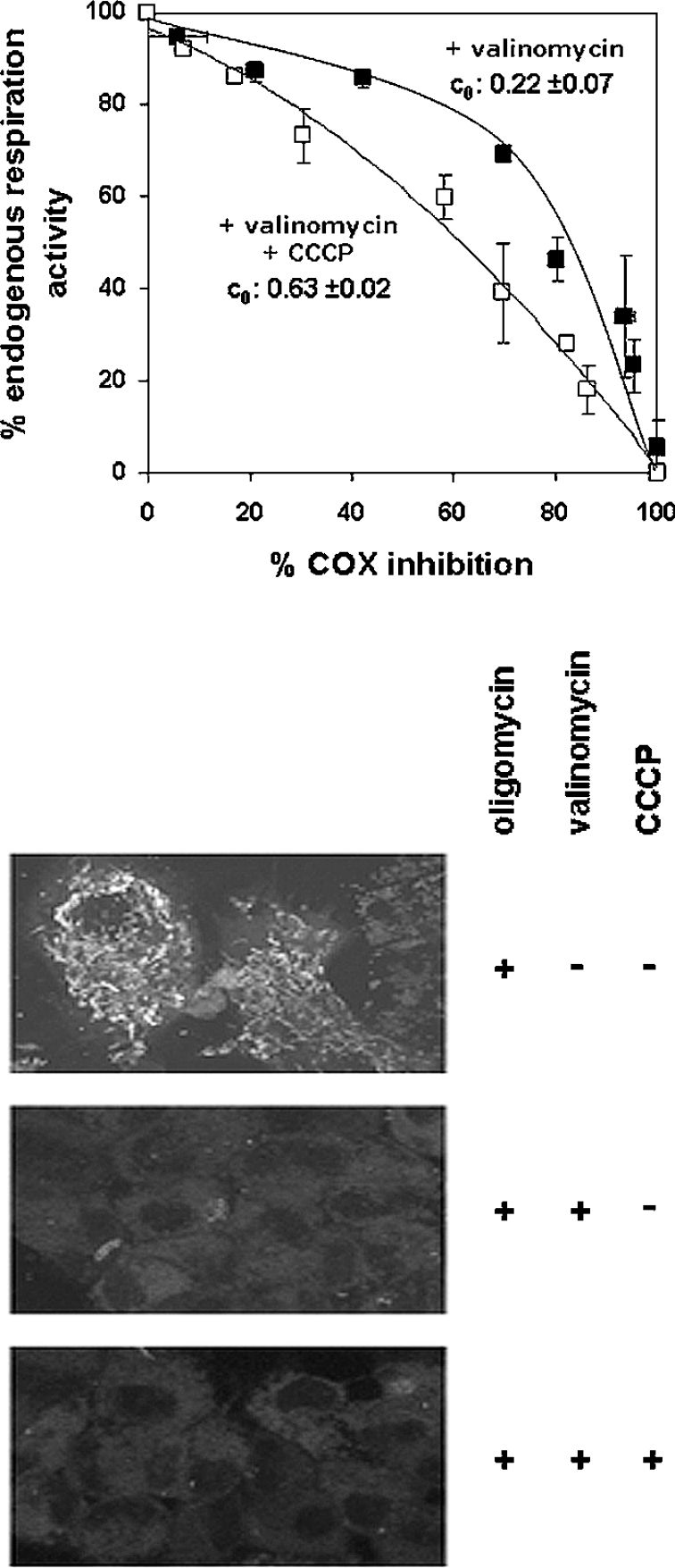
To exclude the possiblity that what was observed was not due to an undesired side effect of oligomycin on COX MFCA, an experiment was carried out on HepG2 cells preincubated with oligomycin, but in the presence of valinomycin plus CCCP. It can be seen that the fully uncoupling effect of the two ionophors resulted in a threshold curve that was undistinguishable from that obtained under endogenous respiration (Figure 4; cf. Figure 3D). Interestingly, when the MCA was performed in the presence of oligomycin supplemented with just valinomycin, the threshold plot did not change with respect to that observed in the presence of oligomycin alone. As an enhancement of the ΔpH component of the Δμ_H⁺ is expected to compensate for the K⁺/valinomycin-mediated dissipation of the mitochondrial ΔΨ [29], the result presented in Figure 4 would suggest that the relative decrease in COX control of the cell respiration in the presence of a mitochondrial transmembrane protonmotive force is independent of which of the two thermodynamical components is operative, with ΔΨ and ΔpH being equally effective.

Figure 4. Effect of ionophores on the threshold plots for COX activity over the endogenous respiration in oligomycin-treated HepG2 cells.

The experimental conditions for the inhibitor titrations are similar to those shown in Figure 1(B), but cells were preincubated with 4 μg/ml valinomycin alone (■) or in combination with 4 μM CCCP (□). The data points are the average for three independent experiments for each condition (± S.E.M.). The lower panels show imaging by confocal-microscopic analysis and illustrate the effect of valinomycin, without and with CCCP, on the mitochondrial ΔΨ in cells respiring with endogenous substrates in the presence of oligomycin. Ionophores were added directly to the dishes 5 min before the addition of the probe MitoCapture™ at the concentrations used for the KCN titration assays. For comparison, the imaging of cells untreated with ionophores is also shown.

MCA of COX in isolated mitochondria

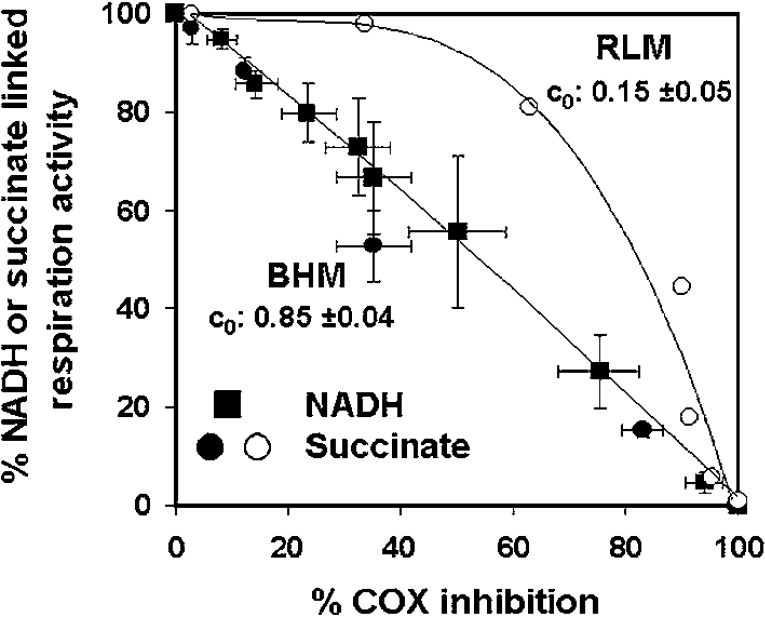
The results presented here on one hand confirm what has been reported for other cell types in culture [12,13], and, on the other hand, contrast with the results of MFCA carried out on isolated mitochondria [7–9], which, depending on the mammalian organ source, resulted in a flux control coefficient for COX of 0.15–0.25 on the respiratory flux fuelled with either NADH-linked substrates or succinate [9]. Therefore we extended (as intralaboratory control) the MFCA on mitochondria isolated from ox heart and rat liver. To rule out differences in the coupling efficiency that may arise from diverse protocols in the separation procedures, we performed the MFCA on fully uncoupled frozen–thawed mitochondria. Figure 5 illustrates the results obtained as a threshold plot. It is shown that, for the succinate-sustained respiratory flux, COX displayed a very low reserve capacity (about 30%) and a c₀ of 0.7–0.8. As the freezing–thawing treatment of isolated mitochondria enables the substrate-binding site of Complex I to be freely accessible, it was also possible to apply the MFCA to respiratory flow directly fuelled by NADH. Also, in this case, the threshold plot demonstrated, for heart mitochondria, a tight control of COX, with a maximal reserve capacity and control coefficient undistinguishable, on a statistical basis, from those measured for the succinate-sustained respiration. Addition of cytochrome c to compensate for its possible loss from the mitochondrial intermembrane space did not result in any significant difference (results not shown). Surprisingly, when the same analysis was carried out on mitochondria isolated from rat liver, the threshold curve for COX on the succinate-driven respiration was markedly different, with a much lower control strength (both in terms of larger excess capacity and lower control coefficient). Table 1 summarizes the metabolic-flux-control parameters calculated for COX under all the conditions reported throughout the present study.

Figure 5. MCA of COX control in isolated mitochondria.

A portion (1 mg of protein/ml) of frozen–thawed mitochondria isolated from ox (‘beef’) heart mitochondria (BHM; ■, ●) or rat liver mitochondria (RLM; ○) were fuelled with 200 μM NADH (■) or 5 mM succinate (●, ○) (in the presence of 1μg/ml rotenone) and the respiratory rates subjected to KCN inhibition titration. An identical KCN range was used to titrate the activity of COX as an isolated step sustained by 10 mM ascorbate plus 0.2 mM TMPD. The results of the inhibition titrations are directly shown as threshold plots of the COX activity on the NADH- and succinate-sustained respiration.

Table 1. MFCA of COX control of the respiratory activity of intact cells and isolated mitochondria.

This is a summary of the results presented throughout the paper. c₀ is the control coefficient calculated from the CN titration curves either by dividing the slopes attained in the initial low inhibitor concentration ranges and by non-linear fitting of the entire experimental data set of the integrated flow (see the Materials and methods section); the values reported are the means of results obtained by the two procedures differing by less than 10%. MRC is the maximal reserve capacity, calculated from the threshold plots by extrapolating, to 0% COX activity, the experimental points attained at the highest inhibitor concentration. Thresholds values refer to the intercepts of the straight lines of the experimental points attained at the lowest and highest inhibitor concentrations and interpolated on the % COX inhibition axis. For experimental details, see the legends to Figures 3–5.

		COX
Sample	Respiratory substrate(s) and/or conditions	c0	MRC	Threshold
Intact HepG2 cells	Endogenous respiration	0.68±0.04	173	48.5
	+Oligomycin	0.25±0.03	386	74.5
	+Oligomycin+valinomycin	0.22±0.07	315	77.9
	+Oligomycin+valinomycin	0.63±0.02	140	52.9
	+CCCP
Ox heart mitochondria	Succinate	0.90±0.03	107	48.3
	NADH	0.85±0.04	110	49.4
Rat liver mitochondria	Succinate	0.15±0.05	314	73.2

DISCUSSION

The results here reported on the MCA of COX control over cell respiration resumed and extended previous studies carried out on intact cells. Under uncoupled conditions, it was confirmed that COX exhibits a low reserve capacity and a large control coefficient over the endogenous cell respiration, but mimicking the State III respiration by blocking the H⁺-ATP synthase clearly showed that COX decreased its apparent control efficiency and that this effect can be attributable to the establishment of a steady-state Δμ_H⁺. To our knowledge this is the first case of a study carried out in intact cells, under close physiological conditions, where a comparison was made under two different bioenergetic states.

To avoid misinterpretations of the results we have carefully considered a number of points.

First, a criticism that could be raised to our experimental approach is that the membrane potential changed during the KCN inhibitory titration. We checked this specific point, and found that the addition of up to 300 μM cyanide (which caused 40% inhibition of the endogenous respiration in the presence of oligomycin) showed no effect on the in situ extent of mitochondrial ΔΨ. Some decrease in ΔΨ was detected at 1 mM cyanide, with a 70% inhibition of respiration. These results can be rationalized in terms of a non-ohmic flow force relationship explainable in terms of a progressive change of either the passive proton conductance of the membrane [30] and/or the intrinsic the proton pumping efficiency of the respiratory-chain complexes [31]. As the metabolic control coefficient, c₀, was estimated from the ratio of the initial slopes of the integrated flow and the isolated step, it was, therefore, not affected by a decrease of the membrane potential that took place at much greater inhibition of the respiratory rates.

It might be argued that, according to the summation principle, a variation in the number of steps contributing to the metabolic flux would be expected to result in a redistribution of the control coefficients, whose sum must remain 1.0 [32]. Application of a static-head Δμ_H⁺ on isolated mitochondria indeed introduces the H⁺ back-leak as a new factor controlling the rate of respiration. Nevertheless the experiment on valinomycin-treated cells presented in Figure 4 shows that substitution of the transmembrane electrical potential with a pH gradient resulted in no change in COX control. Given the large difference in membrane conductivity of protons with respect to other cations or anions (the membrane conductance for H⁺ is at least 10⁶ times higher than for K⁺ [33]), one would expect a tighter control of ΔpH in the metabolic network and, as a consequence, a compensatory decrease of the control coefficients of the other steps. But this was not the case for COX (cf. Figure 3D and 4).

Another possibility that one could imagine is that the membrane potential might change the catalytic features (i.e. K_m, K_cat) of COX [34]. Given that the other complexes of the mitochondrial respiratory chain (which contain electrogenic steps in their catalytic mechanisms) would not escape such a change, differentiated variations in the relative catalytic features of the enzymatic steps in the network might cause a redistribution of the control coefficients. Although this sounds plausible, it is not immediately clear how the conversion of an electrical potential in a pH gradient might mechanistically produce the same effect. This would be the case if a protogenic step in COX (as well as in the other respiratory complexes) coincided with an electrogenic step that was rate-limiting, a situation thought to be very unlikely [35,36].

The structural organization in the membrane of the many components of the mitochondrial OXPHOS system has been the object in the past of a dispute between a model representing the enzymatic complexes acting as isolated entities and one in which the occurrence of clustered structuring was considered [37,38]. The latter hypothesis has been recently reappraised on more solid experimental basis, indicating the presence, in mitochondria of different species, of assembled supercomplexes with defined stoichiometry [38,39].

The so called ‘respirasomes’ would gain a higher catalytic efficiency because of the channelling of mobile intermediates (like ubiquinol and cytochrome c) and of the contiguity between the ΔμH⁺ producers and utilizers. The alternative, random-collision-controlled model, however, should not be completely abandoned. Indeed one can imagine a situation where the two organizational modes, respirasome versus isolated complexes, coexist in a dynamic equilibrium, with the relative occupancy of the two structural subsets depending on the actual bioenergetic needs of the cell. The higher the membrane potential is, the lower is, in principle, the energy demand of the cell, because a lower rate of ATP utilization does not make ADP available for the ATP synthase, which, in turn, cannot dissipate the redoxlinked protonmotive force generated by the respiratory chain. Under this metabolic condition, the respirasome would dissociate its constituting complexes, and this would decrease the rate of oxygen consumption, because diffusional steps between redox intermediates and enzymatic complexes would be introduced. On the other hand, when the cell hydrolyses more ATP, because of a larger bioenergetic request, ADP no longer limits the activity of the ATP synthase, the transmembrane potential promptly collapses and the required higher rate of respiration is satisfied by the assembly of the respiratory enzymes in supercomplexes. Under these conditions, the channelling of the redox intermediates will speed up the rate of electron transfer.

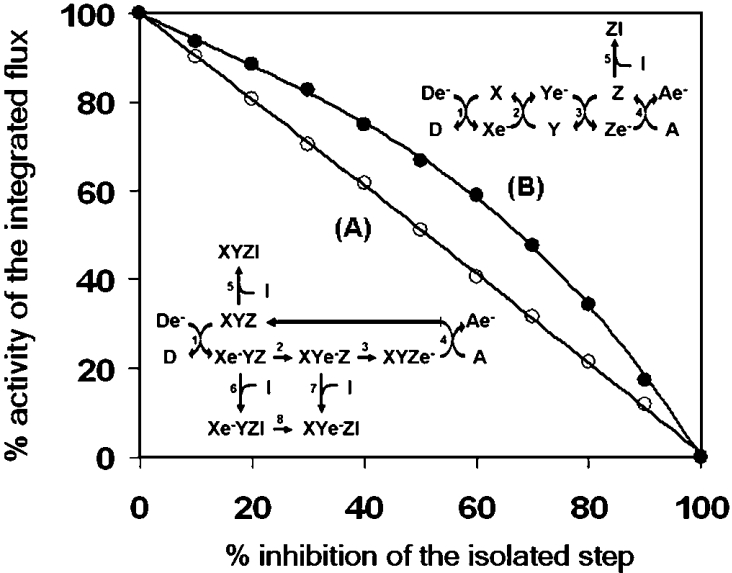
To test the hypothesis that a change in the control strength of an individual step might be featured in terms of equilibrium between different organizational structures of the enzymatic steps constituting the integrated flow, a mathematical simulation was performed. A simple electron-transfer process was designed with three putative redox catalysts (X, Y and Z) transferring in sequence an electron from an initial donor (De⁻) to a final acceptor (A). The three catalytic steps formed an assembled complex (XYZ) or, alternatively, were isolated from each other, and the transfer of the electron was controlled by a channelled or collisional diffusion mechanism respectively (see the schemes inset into Figure 6). The results of a modelled inhibitory titration of the catalyst Z are shown in Figure 6 as a threshold-like plot. One can see that, when Z is part of the XYZ complex, the overall rate of the flux correlates linearly with the amount of the controlling step, whereas when Z operates as an isolated step, a decrease in its amount results in a clear deviation from a linear impact on the flux. It must be pointed out that, under the two modelled conditions, the rate constants for each simulated catalytic step were identical. Therefore the change in the control exerted by the catalyst Z depends simply on the fact that, when the catalyst is not complexed, its partial inhibition results in an increase of the steady-state concentration of Ye⁻. This reacts, according to a second-order reaction, with the residual fraction of the uninhibited Z, and compensates, with a fractional increase in its actual transfer rate, for the expected inhibition of the overall electron flux. This does not occur when Z is part of a complex, because the intermediate XYe⁻Z_inhibited cannot transfer e⁻ to the uninhibited XYZ complexes. Consequently, that step will lose its controlling strength. In the framework metabolic control theory, an identical result would be predicted in the so-called ‘network attenuation’ [40], which, however, applies when each individual step of the network is working at a velocity substantially lower than maximal.

Figure 6. Kinetic simulation of the metabolic flow throughout aggregated or isolated steps: effect on the control of a single step.

A metabolic flow mimicking electron transfer throughout three enzymatic steps from an initial donor De⁻ to a final acceptor, A, was simulated. Two models were tested; in one the three steps were assumed to be physically assembled in a single complex with an internal e⁻ transfer (A); in the other the three steps were assumed to be isolated and the e⁻ transfer occurred by stochastic events controlled by random collision. In addition, one of the three putative enzymes, Z, was possibly blocked by an inhibitor, I. The rates of the overall simulated e⁻ transfer to the acceptor was estimated in the presence of increasing concentrations of the inhibitor, inducing a progressive 10% stepwise inhibition of the isolated step irrespective of its assembly state. The graph displays, as threshold plots, the results of the simulations for both models. The numerical values for the kinetic constants were: 1.0 for steps 1–4, 8 and 100 for steps 5–7, in simulation (A), and 1.0 for steps 1–4 and 100 for step 5, in simulation (B). See the Materials and methods section for details of the software used.

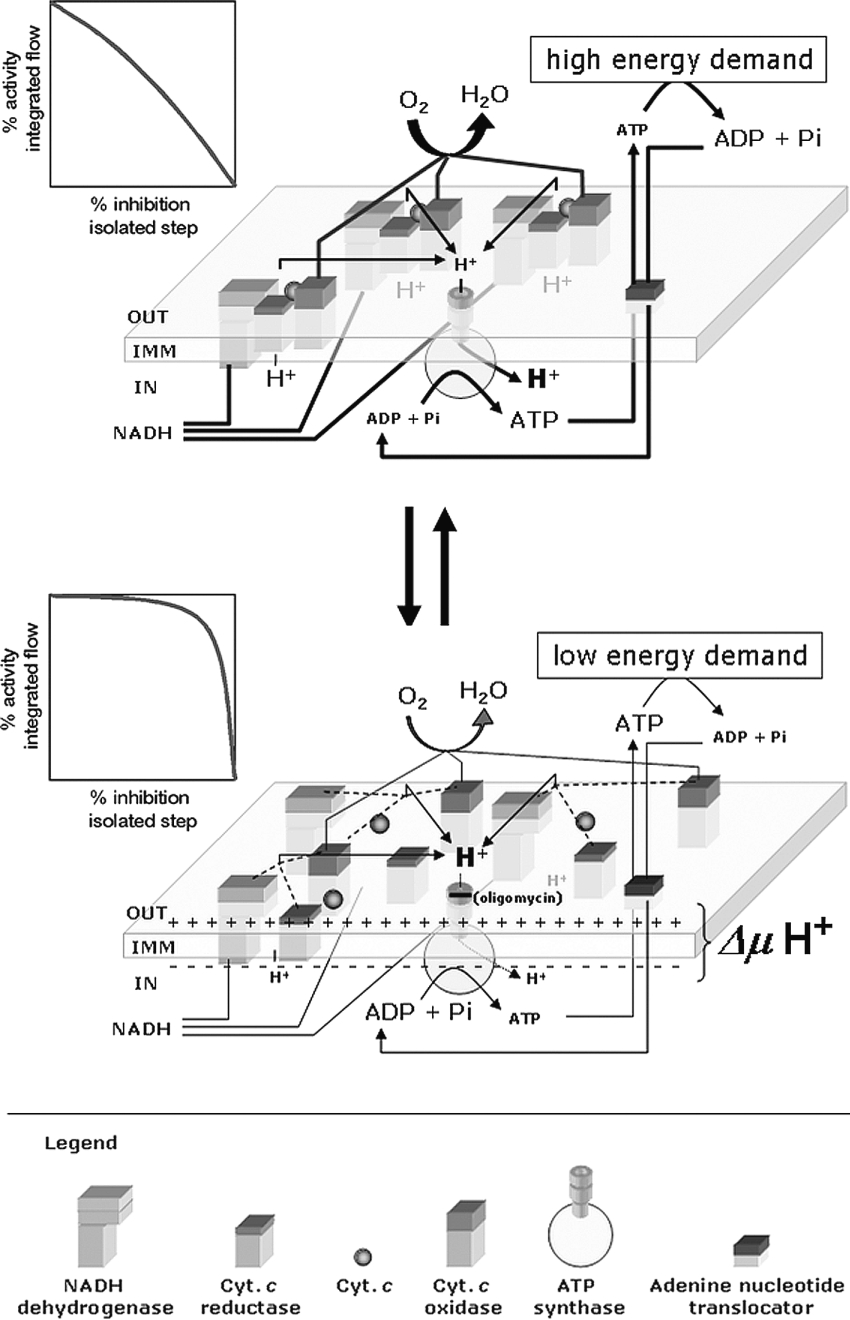
The above-depicted scenario implies that a change in the Δμ_H⁺ itself might be, at the same time, the physiological signal and the trigger causing the structural reorganization of the enzymatic complexes of the mitochondrial OXPHOS system (see the model hypothesis depicted in Scheme 1). Although the driving forces leading to the assembly/disassembly of the supercomplexes have been not yet defined, it is not unconceivable that, given the membrane-integrated nature of the single complexes, electrostatic as well as hydrophobic interactions must enter into play. Recently published observations [41] have indicated, for cardiolipin (di-phosphatidylglycerol), an essential role in promoting the formation of mitochondrial respiratory supercomplexes. Indeed, knocking out the gene coding for cardiolipin synthase in yeast resulted in the disappearance of the mitochondrial respirasomes without affecting the catalytic activities of the isolated complexes [42]. Cardiolipin is a four-acyl-tail anionic phospholipid with a large dipole potential, able to sense electrical gradient as well as pH (the pK_a2 of the phosphate headgroup is ≥8, [43]) and to alter the physical properties of the membrane [44]. Moreover, binding sites on the known crystallographic three-diemnsional structures of cytochrome c reductase and COX have been clearly localized [45,46]. Therefore cardiolipin (almost exclusively localized in the mitochondrial inner membranes) might well be the molecular sensor of the energy state of the mitochondrial membrane, enabling the complexes of the OXPHOS system to change their assembly in response to the Δμ_H⁺.

Scheme 1. Working model illustrating the effect of the mitochondrial membrane energy state on the supermolecular structure of the enzymatic components of the OXPHOS system.

The respiratory complexes are illustrated as boxes embedded in the inner mitochondrial membrane (IMM). The stoichiometry of the complexes in the respirasomes shown in the upper part of the Scheme are purely indicative (see [38] for experimentally defined stoichiometries). Moreover, the assembled supercomplexes might include the H⁺-ATP synthase and mitochondrial substrate carriers as well. The graphs on the left show the expected threshold plots of the major controlling isolated step on the basis of a combination of kinetic and thermodynamic features in the two assembly states (see the Discussion). Abbreviation: Cyt. c, cytochrome c.

Consistent with our proposal are the results obtained with isolated bovine heart mitochondria, confirming the tight control exerted by COX on uncoupled NADH- or FADH₂-linked respiration. Cardiolipin, as well as the OXPHOS enzymatic content, is known to vary in mitochondria from different organs, with the heart being the richest one [47]. Mitochondria isolated from tissue relatively poorer in cardiolipin (such as liver) or that are more vulnerable to modification during the isolation procedure (i.e. peroxidation) would tend to maintain the complexes isolated, even in the absence of a membrane potential, thus resulting in an apparent low flux control by COX.

The cardiolipin-mediated (controlled) change in the electrostatic/hydrophobic interaction of the mitochondrial OXPHOS complexes might provide, therefore, a ‘bioenergetic signal transduction system' that resembles the described function of plasma membrane rafts in stabilizing a local platform for integrating the many components of the signal-transduction network [48], though based on different membrane components.

Finally, the observations reported here provide a rationale with which to understand some aspects of the stress-related symptoms of patients suffering of neuromuscular diseases caused by defects of the mitochondrial COX [49] or, more generally, by impairments of the OXPHOS system [4,50]. Although the mitochondrial diseases encompass rare human inherited pathologies (1 case in 5000 newborns), an understanding of their aetiopathological mechanism may help in managing a larger number of more common pathologies where the involvement of defects in the mitochondrial respiratory chain has been defined [50]. The manifestation and severity of diseases linked to mutations in mtDNA (mitochondrial DNA) is often correlated with the level of heteroplasmy (the situation in which, within a single cell, there is a mixture of mitochondria, some containing mutant DNA and some containing normal DNA) [51]. In the same cell of a given tissue, mitochondria harbouring mutated and/or wild-type DNA can co-exist. When the amount of mutated mtDNA is such that the gene product provided by the wild-type mtDNA does not compensate for the defect of the mutated mtDNA, the bioenergetic competence of the cell is compromised. Thus a genetic threshold for the mutated mtDNA must be overcome to cause the disease to manifest itself, and a wide array of clinical symptoms with different degrees of severity may arise from the same mtDNA mutation, depending on its level of heteroplasmy [28,51]. A clinical feature shared among patients suffering directly or indirectly of impairments of the COX complex is their intolerance to muscular work overload [52,53]. An active state at the tissue level (in terms of bioenergetic balance) means a condition of increased ATP consumption to perform work, which, at the mitochondrial level, produces a compensatory enhancement of the ATP synthase activity, given the larger availability of ADP, and thus a decrease in steady-state Δμ_H⁺. Under this ‘stress’ condition a defective COX activity will cause, according to our findings, an almost proportional decrease of the overall aerobic flux, which, if it is not able to satisfy the enhanced bioenergetic demand, will result in an unbalanced anaerobic cell metabolism. In addition to this, it is conceivable that an accumulation of redox intermediates upstream of COX will favour formation of oxygen free radicals with further aggravation of the already debilitated patient condition [54]. At rest, the same level of COX deficit might not be relevant, because the redistribution of the flux control coefficients will attenuate its impact on the overall respiratory rate.