Potentiometric sensors for trace-level analysis

Abstract

This review summarizes recent progress in the development and application of potentiometric sensors with limits of detection (LODs) in the range 10⁻⁸–10⁻¹¹ M. These LODs relate to total sample concentrations and are defined according to a definition unique to potentiometric sensors. LODs calculated according to traditional protocols (three times the standard deviation of the noise) yield values that are two orders of magnitude lower. We are targeting this article at analytical chemists who are non-specialists in the development of such sensors so that this technology may be adopted by a growing number of research groups to solve real-world analytical problems.

We discuss the unique response features of potentiometric sensors and compare them to other analytical techniques, emphasizing that the choice of the method must depend on the problem of interest. We discuss recent directions in sensor design and development and present a list of 23 sensors with low LODs, with references. We give recent examples where potentiometric sensors have been used to solve trace-level analytical problems, including the speciation of lead and copper ions in drinking water, the measurement of free copper in sea water, and the uptake of cadmium ions by plant roots as a function of their speciation.

1. Introduction – What are potentiometric sensors good for?

In recent years, the well-established field of potentiometric sensors has undergone a quiet revolution that did not go unnoticed in the general analytical chemistry community. While it has been traditional wisdom that such sensors may reach only mediocre limits of detection (LODs) around the micromolar range, they have now been improved to make possible true trace-level analysis at sub-nanomolar (low parts per trillion) concentrations. Clearly, this improvement asks for new applications for which this technique has not been used traditionally.

This review is targeted at the general analytical chemist, not necessarily the specialist in ion-selective electrode (ISE) development, for whom a variety of reviews and specialized articles have already appeared in recent years [1–6]. Here, we introduce the basic response principles of potentiometric sensors and compare them to other analytical techniques used for trace-level analysis, discuss the vastly different definition of the LOD, and explain how interference effects can be relatively conveniently predicted. We discuss the state-of-the art of current development of ISEs based on polymeric, solid, or glass-membrane materials in view of reaching low LODs, as are early examples of trace-level analysis applications in the real world.

Ideally, potentiometric sensors detect the ion activity in the sample. This makes it a unique class of chemical sensors that may be very useful in bioavailability or speciation studies. The Nernst Equation is normally used to describe the ideal response of such a cell:

$$\text{EMF}=K+RT / zF\mathrm{\hspace{0.17em} }\text{ln\hspace{0.17em}}{a}_{\text{I}},$$ (1)

where EMF is the electromotive force (the observed potential at zero current), K is a constant potential contribution that often includes the liquid-junction potential at the reference electrode, a_I is the sample activity for the ion I with charge z, and R, T, and F are the gas constant, absolute temperature, and Faraday constant, respectively. Note that the ion activity effectively describes the so-called free, or uncomplexed, concentration of the analyte, which is often the relevant driving force in chemical or biochemical reactions. This quantity may be orders of magnitude smaller than the total analyte concentration if a complexing agent is present in the sample.

Fig. 1 illustrates the quantities that the three principal classes of trace analytical methods are able to detect. As explained, potentiometry gives information about the ion activity. By contrast, voltammetric techniques detect analytes that have a sufficiently high electrochemical turnover rate at the electrode. Complexes that are chemically inert, or analytes that are bound to suspended particles, for example, are normally not detectable. Voltammetric techniques, therefore, yield information on the concentration of chemically available (labile) analytes. However, atomic spectrometric methods atomize the entire sample and do not distinguish between the different forms of the analyte. They yield the total concentration of the analyte of interest. While some samples can be constructed or treated to give the same results with any of the three principal methods mentioned above, the analytical results are generally different. Note, therefore, that the preference of one method over another must be based on the question that must be answered by the analysis.

Figure 1.

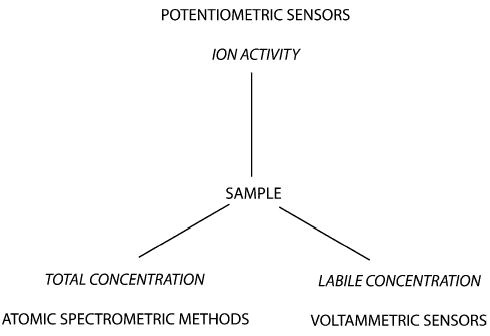
Schematic representation of the three principal classes of instrumental methods for trace-level analysis. The analytical information obtained from a given sample may be drastically different, especially if the analyte is complexed, chemically inert, or chemically adsorbed on particulate matter. Depending on the analytical information desired, the use of any of the three methods is attractive. Note that the analytical information obtained from each method may be varied to some extent by using sample pretreatment or analytical separation before the actual measuring step.

Clearly, the unique response principles of potentiometry should be understood and appreciated by a larger number of analytical chemists. Each technique, be it based on potentiometry, voltammetry, or atomic spectrometry, may indeed be very useful to understand the composition and behavior of the sample of interest.

2. What does LOD mean?

In general, the lower LOD is defined as the concentration of the analyte at which the signal is increased relative to the background level by three times the standard deviation of the noise [7]. According to IUPAC recommendations [8], the definition of the lower LOD in potentiometry is unique. This is somewhat unfortunate because a direct comparison with corresponding figures of other methods is not appropriate. This is especially confusing because of the recent improvement of potentiometric sensors that resulted in the performance of the main methods of trace analysis being comparable, as covered in this Special Issue.

The potentiometric response [1,2,9], the EMF, is a linear function of the logarithm of the activity of the free (uncomplexed) ions I^zI in solution (see Fig. 2). Its slope is described by the Nernst Equation (1) as 59.2/z_I mV/decade (at 25°C). Below the LOD, it has a constant value, which is ideally defined by the response of the sensor to another (interfering) ion J^zJ.

Figure 2.

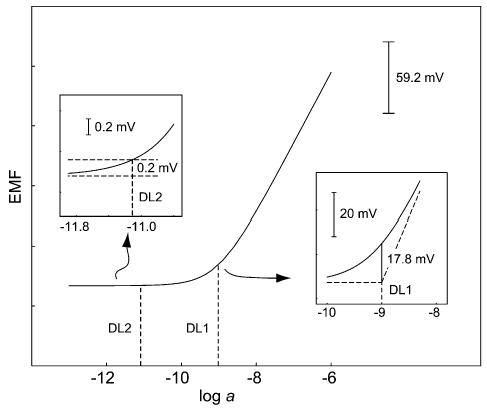
The traditional definition of the lower LOD of potentiometric sensors is defined as the cross-section of both extrapolated linear portions of the calibration curve (DL1) [8]. It is about two orders of magnitude higher than the LOD (DL2) calculated according to the procedure for all other analytical methods (i.e. three times the standard deviation of the background noise). Direct comparisons of different methods are valid only if the same definition of the lower LOD is used.

The potentiometric lower LOD is defined as the cross-section of the two linear parts of the response function (Fig. 2). Besides its ease of determination, it also has a mechanistic meaning. For ideally behaved polymeric membrane electrodes at the LOD, a well-defined part (50% for z_I = z_J) of the primary ions is replaced by interfering ions in the organic phase [10]. According to this definition, the deviation of the EMF from its final value is 17.8/z_I mV. However, typical noise during potentiometric measurements may be as low as 0.06–0.08 mV. The LOD according to the general definition used in analytical chemistry (three times the standard deviation of this noise) is therefore orders of magnitude lower than that given by the definition for potentiometry (see Fig. 2) [11].

At trace levels, ion fluxes from the membrane to the sample or vice versa may influence the response function [12,13]. However, its general shape remains similar and the above statements are also valid in such cases.

3. Potentiometric sensors at trace levels: the state of the art

Traditionally, ISEs are distinguished by the underlying membrane material. Polymeric membrane-based sensors are a group of very high chemical versatility and tunability because the selectivity is given by the extraction of ions into a polymer and complexation with a selective receptor that may be chemically designed [3]. Glass electrodes, including chalcogenide glasses, are an attractive material for a variety of ions, including H⁺, but the fine tuning of their electrochemical response is chemically more difficult. Solid-state membranes, such as precipitate-based systems (e.g., silver halides or metal sulfides) are well established for a number of cations and anions, but little research has been performed to lower their LOD, which is ideally a direct function of the solubility product of the materials [14] but often deteriorated by dissolution of impurities [9,15–18].

Here, we will first focus on the extensive efforts to the lower the LOD of polymeric membrane sensors, and follow with a review of progress with other membrane materials. Table 1 summarizes the current state of the art of potentiometric sensors with low LODs.

Table 1.

Potentiometric sensors for trace analysis realized to date

Analyte ion	LODDL1a, Mb	Membrane composition and comments	Reference
Na+	3 × 10−8	Filled monolithic column	[19]
K+	5 × 10−9	Polymeric; resin in inner solution	[20]
NH4+	2 × 10−8	Polymeric; resin in inner solution	[20]
Ca2+	ca. 10−10	Polymeric; microparticles in membrane	[21]
	3 × 10−9	Polymeric; EDTA in inner solution	[22]
	2 × 10−9	Polymeric; resin in inner solution	[20]
	ca. 10−11	Polymeric; EDTA in inner solution	[23]
	3 × 10−9	Filled monolithic column	[19]
Ag+	10−9	Polymeric; resin in inner solution	[13]
	2 × 10−9	Filled monolithic column	[19]
Pb2+	8 × 10−11	Polymeric; EDTA in inner solution	[22]
	10−9	Polymeric; NTA in inner solution; optimized for rugged response	[24,25]
	6 × 10−11	Polymeric; rotating electrode	[26]
	10−9	Polymeric; covalently attached ligand	[27]
	5 × 10−10	Polymeric (plasticizer-free); solid inner contact	[28]
	10−9	Polymeric; solid inner contact	[29]
Cd2+	10−10	Polymeric; NTA in inner solution	[30]
	10−10	Polymeric; Et4NNO3 in inner solution	[31]
Cu2+	10−9	Solid state; rotating electrode	[18]
	10−8	Polymeric	[32]
	2 × 10−9	Polymeric; hard membrane, Et4NNO3 in inner solution	[33]
Vitamin B1	10−8	Polymeric; very lipophilic ion exchanger	[34]
ClO4−	2 × 10−8	Polymeric; resin in inner solution	[35]
I−	2 × 10−9	Polymeric; resin in inner solution	[35]

^aLower LOD defined according to the convention for potentiometry [8], (DL1, see Fig. 2). For comparing with other methods, the numbers should be lowered by about 2 logarithmic units (DL2, see Fig. 2).

^bThe numbers refer to total sample concentrations.

3.1. Polymeric membrane potentiometric sensors with aqueous inner contacts

Here, a hydrophobic polymeric membrane is doped with active sensing ingredients, typically a lipophilic ion-exchanger and a highly selective ionophore [1–3,9]. Generally, the ion-exchanger is responsible for attracting a fixed concentration of counterions (the analyte) into the membrane phase, while the ionophore selectively binds this analyte ion. The selectivity [4] of the resulting potentiometric sensor is characterized by the lipophilicity of the analyte ion relative to an interfering ion, and the relative strength of the complexes formed in the membrane [2]. If the charges of the two ions being compared are different, or the complexes formed have different stoichiometries, the membrane composition may be tuned to optimize the selectivity [2]. Please consult appropriate reviews to learn more about the general principles of response [2,9,36].

In most cases, the polymeric membrane separates the aqueous sample from an aqueous inner solution (a reference electrode is immersed into each solution to complete the circuit). One has to realize that this system is not at equilibrium if the two aqueous solutions do not have identical compositions. The lower LOD may originate from two principal processes. In the first, ideal, scenario, the analyte ions are displaced from the membrane by interfering ions. This selectivity breakdown corresponds to the thermodynamic LOD. With membranes of high selectivity in contact with dilute solutions, it may be calculated to be in the femtomolar range or lower. Such low LODs have never been observed in unbuffered sample solutions, but they may be achieved by using samples that are buffered to a low ion activity with a much higher total analyte concentration [37,38]. However, in contact with unbuffered sample solutions, highly selective membranes have an LOD that is normally dictated by a different mechanism, which originates from the asymmetry of the two contacting aqueous solutions mentioned above. Fortunately, ions are normally prohibited from simply diffusing to the compartment of lower activity because such a process would generate a current across the cell, which is prohibited by the instrument in zero-current measurements. However, ions may diffuse under zero-current conditions by compensating for the charge imbalance by co-diffusing with a counterion (so-called co-diffusion process) or by letting an ion of the same charge sign diffuse in the opposite direction (so-called counterdiffusion process) [5,6]. If the sample solution is more dilute than the inner solution, ion diffusion at zero current may lead to an enrichment of analyte ions at the sample–membrane interface. If this local sample concentration is substantially larger than the concentration in the bulk sample, the observed potential no longer changes upon further dilution of the sample. Note that, in such cases, the displacement of analyte ions in the membrane is insignificant compared to the thermodynamic case discussed above. The LODs, according to this second, kinetic mechanism, are therefore higher [12,13].

Breakthroughs in lowering the LODs of polymeric membrane ISEs have involved understanding the reduction of analyte ion fluxes from the membrane in the direction of the sample phase (the kinetic mechanism explained above) [39,40]. Note that, with an aqueous inner solution, the system becomes asymmetric as soon as the sample solution is varied to some extent, as in real-world measurements. The resulting ion fluxes can therefore be minimized only and never completely eliminated. Assuming linear concentration gradients across the membrane phase and the aqueous Nernst diffusion layer at the sample side, and considering Fick’s first law of diffusion for a one-dimensional system, the problem may be illustrated with the following steady-state relationship [12]:

$$\frac{c_{\text{I},\text{aq}}(\text{pb})-c_{\text{I},\text{aq}}(\text{bulk})}{c_{\text{IL},\text{org}}(\text{inside})-c_{\text{IL},\text{org}(\text{pb})}}=q=\frac{D_{\text{org}}{\delta }_{\text{aq}}}{D_{\text{aq}}{\delta }_{\text{org}}},$$ (2)

where c_I,aq is the aqueous concentration of the analyte ion at the sample–membrane phase boundary (pb) and in the bulk sample (bulk), and c_IL,org is the membrane concentration of the complexed analyte at the inner membrane side (inner) and at the sample-membrane phase boundary (pb). The parameter q incorporates the ratio of the diffusion coefficients of the analyte ion in both phases (D_org and D_aq) and the diffusion-layer thicknesses of the membrane and aqueous phase (δ_org and δ_aq). At the LOD, c_I,aq(bulk) is negligible and c_I,aq(pb) is equal to the LOD, DL1. Equation (2) may therefore be rewritten as

$$DL1=\frac{D_{\text{org}}{\delta }_{\text{aq}}}{D_{\text{aq}}{\delta }_{\text{org}}}(c_{\text{IL},\text{org}}(\text{inside})-c_{\text{IL},\text{org}}(\text{pb})).$$ (3)

Clearly, six different parameters may influence the LOD under steady-state conditions. The concentration of the analyte at the inner membrane side is dictated by the composition of the contacting inner solution and must be chosen to give minimal concentration gradients across the membrane. Initially, large improvements in the LOD were observed by using a chelator, such as NTA or EDTA, for the analyte ion in the inner solution [22,39]. Later, ion-exchange resins were used for the same purpose [20]. Such resins are not extracted into the membrane phase and bind to a wide variety of ions for which no chelators are available, and the resulting LODs have been found to correlate quantitatively with theoretical predictions [13,41]. More recently, a lipophilic interfering ion in the inner solution was used together with a salt of the analyte ion [31,33]. The concentration of analyte at the membrane side facing the sample must be kept as constant as possible to minimize the concentration gradients across the membrane during sample changes. This may be achieved by using only membranes of high selectivity, where interfering ions are excluded as much as possible from the membrane phase. Besides these experimentally most challenging points, the LOD may also be improved by reducing the thickness of the aqueous Nernst diffusion layer. This has been achieved by sample stirring [42], or using a rotating electrode configuration [26] or a wall–jet system [43]. Fig. 3 shows the time traces for a Pb²⁺-selective membrane in a rotating electrode set-up, with the membrane placed off-center from the rotating axis [26]. The thickness of the diffusion layer of the membrane phase may be increased as well, and this has indeed shown promise [19,42]. Note that a higher membrane resistance and longer membrane-conditioning times are drawbacks of this technique.

Figure 3.

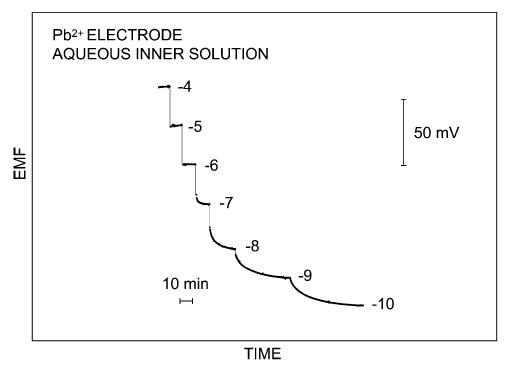
Experimental time traces, obtained by serial dilution of the sample, for a Pb²⁺-selective electrode based on a polymeric membrane containing an aqueous inner solution, in a rotating electrode set-up [26]. The numbers shown are logarithmic molar concentrations of the sample, and the LOD (DL1, see Fig. 2) was found as 6 × 10⁻¹¹ M. The membrane was placed off-center of the rotating axis for maximum reduction of the aqueous Nernst diffusion layer thickness.

The LOD has also been lowered by reducing the diffusion coefficients in the organic phase (e.g., by using a lower plasticizer content of the polymeric membrane [33,42], other membrane materials [28,44], or ionophores that are covalently attached, rather than freely dissolved in the membrane phase [27,45]). Note that lower diffusion coefficients normally lead to higher membrane resistances as well as longer conditioning times. Normally, the diffusion coefficients in the aqueous phase may not be increased. Recently, a lowering of the LOD that was independent of the composition of the inner solution was also achieved by partially blocking the sample side of the membrane by using inert lipophilic microparticles that were embedded during membrane construction [21].

A number of potentiometric sensors with aqueous inner solutions have now been optimized to lower their LODs. They are summarized in Table 1, and include sensors for Na⁺, K⁺, NH₄⁺, Ag⁺, Pb²⁺, Cd²⁺, Cu²⁺, Vitamin B1, I⁻¹, and ClO₄⁻. Note that the achievable LODs of sensors with an aqueous inner contact may be conveniently predicted if one assumes a steady-state concentration gradient across the membrane and if the selectivity and the composition of the membrane are known [13]. Moreover, the optimal inner solution composition may be predicted for well-behaved cases [13,41] and the level of optimization of the electrode may be assessed by performing stir experiments [41]. These advances are likely soon to lead to a unified approach to the development of such sensors with low LODs, and that may be easily adopted by researchers less familiar with the technology.

3.2. Polymeric membrane potentiometric sensors with solid inner contacts

The ultimate goal of improving the LODs of potentiometric sensors is the realization of the thermodynamic limit, where substantial displacement of the analyte ion from the membrane takes place in line with the principles of competitive extraction. One strategy towards this end is elimination of the inner solution by using a solid inner contact. Ideally, the problem would be simplified to a two-phase system where the undesired, kinetically controlled ion fluxes mentioned above may be reduced or even fully eliminated. In recent years, therefore, research has intensified to develop solid contact electrodes with low LODs. Note that corresponding optical sensors, which do not possess an inner solution, are promising platforms to lower the LODs to trace levels as well [38,46,47].

For this purpose, Michalska et al. [48,49] have explored electrochemically deposited conducting polymers, such as polypyrrole, as intermediate layers between an electron-conducting substrate and the sensing membrane. They have identified the spontaneous discharge of the conducting polymer as a possible drawback of their systems, because the discharge reaction is coupled to an analyte-ion flux in the direction of the sample, thereby increasing the LOD in a similar manner to traditional sensors with an aqueous inner contact [48]. The authors have proposed using a compensating applied current (such currents have also been utilized with aqueous inner contacts [50]), but, so far, LODs have remained at relatively high levels.

The group of Pretsch has identified a spontaneously formed water layer as a source of instability with membranes directly placed on top of a metal substrate [51]. This water layer acts as an electrolyte reservoir that is re-equilibrated on every change in sample composition, thereby leading to potential instabilities and high LODs.

Recently, it was found that membranes placed on electrochemically deposited conducting polymers, such as poly(octylthiophene), showed unimpressive LODs, perhaps because of such a water layer [28]. The LOD was found to improve to nanomolar levels when the conducting polymer was deposited by solvent casting [28].

Fig. 4 shows the time traces for a Pb²⁺-selective electrode prepared with this protocol [28]. This is currently the lowest LOD (5 × 10⁻¹⁰ M) found for a potentiometric sensor with a solid or polymeric inner contact, rather than an aqueous inner solution. This result was found with a methacrylic plasticizer-free polymer as membrane material.

Figure 4.

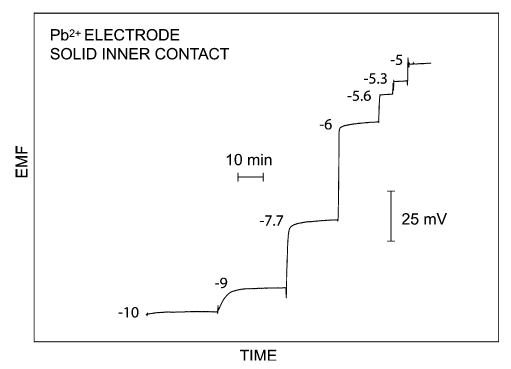
Experimental time traces, obtained by standard addition, for a Pb²⁺-selective electrode based on a plasticizer-free polymeric membrane with poly(octylthiophene) placed on gold as a solid inner contact at the rear of the membrane [28]. The numbers shown are logarithmic molar sample concentrations. The observed LOD was 5 × 10⁻¹⁰ M.

Very recently, similarly low LODs were found with the more traditional plasticized poly(vinyl chloride) when the conducting polymer polypyrrole was generated on top of a gold substrate [29].

Clearly, developments in solid contact potentiometric sensors exhibiting nanomolar LODs or lower are currently advancing at a rapid pace and form a highly promising platform for future work.

3.3. Solid-state and glass membranes with low LODs

In contrast to the polymeric membranes discussed above, less research has been published on improving the LOD of glass and solid-state membranes. Note that it was recognized a long time ago that membranes based on silver sulfide, for example, showed practical LODs that were much higher than those predicted thermodynamically. Buck argued that this is probably caused by impurities in the sensing material [16], but clear improvements in such systems still need to be made [18]. As with the polymeric membrane systems mentioned above, in the classical literature, impressively low LODs with such membrane materials were achieved using only ion-buffered systems, and not dilute solution of the analyte ion [52–54].

Recent achievements in lowering LODs were described for chalcogenide glass electrodes and jalpaite (coprecipitated CuS/Ag₂S) membranes [18]. Such membrane materials are responsive to metal ions, such as Cu²⁺, Fe³⁺, and Hg²⁺, with impressive selectivities [18,54,55]. De Marco critically evaluated the LOD of such systems and found that the use of a rotating electrode configuration decreased the LOD to impressively low levels. Indeed, a commercial copper(II) electrode based on a jalpaite membrane exhibited an improved LOD of about 10⁻⁹ M, simply by using a rotating electrode set-up that decreased the thickness of the diffusion layer in the contacting aqueous phase (see Table 1). An improvement was also achieved by adding excess Na₂S to a jalpaite membrane, seemingly to reduce the concentration of impurities that may leach out from the membrane and increase the sensor LOD [18].

4. Predictability of interference effects with potentiometric sensors

An important characteristic of potentiometry is that the response function may be predicted on the basis of fundamental relationships and measurable parameters. In the case of polymer membrane electrodes, the response function is related to thermodynamic constants and the composition of the membrane. The contribution of the individual ions to the EMF can be calculated with potentiometric selectivity coefficient K_IJ^pot, which is determined from measurements on simple solutions (pure solutions or mixtures of known composition) [4]. Such measurements also provide information about the validity of the underlying model, since the response to the individual (primary and interfering) ions must follow the Nernst equation (1) [4]. Equation (4) describes the response if only monovalent and divalent ions are present (a somewhat more complicated relationship is available for mono-, di-, and trivalent ions [36]).

$$\begin{array}{l}\text{EMF}=K+\frac{RT}{z_{\text{I}}F}\mathrm{\hspace{0.17em} }\text{ln\hspace{0.28em}}[\frac{1}{2}\sum _{\text{m}1}{K}_{\text{I},\text{m}1}^{\text{pot\hspace{0.17em}}1/z_{\text{I}}}{a}_{\text{m}1}\\ {+\sqrt{{\left(\frac{1}{2}\sum _{\text{m}1}{K}_{\text{I},\text{m}1}^{\text{pot\hspace{0.17em}}1/z_{\text{I}}}{a}_{\text{m}1}\right)}^2+\sum _{\text{m2}}{K}_{\text{I},\text{m2}}^{\text{pot\hspace{0.17em}}2/z_{\text{I}}}{a}_{\text{m2}}}]}^{z_{\text{I}}}.\end{array}$$ (4)

The summations in Equation (4) are each performed for all monovalent (m1) and divalent (m2) sample ions. The monovalent or divalent primary ion is included in this summation with $K_{\text{I},\text{I}}^{\text{pot}}=1.$

In the presence of only one kind of dominating interfering ion, its contribution can be easily estimated. It is negligible as long as $a_{\text{I}}>K_{\text{IJ}}^{\text{pot}}{a}_{\text{J}}^{z_{\text{I}}/z_{\text{J}}}.$

The selectivity coefficients are directly related to the complexing properties of lipophilic ligands (ionophores) incorporated into the polymeric membrane phase. These values may be extremely low (down to <10⁻¹⁵) [5,6], which is essential in trace analysis. Note that even in otherwise pure samples, hydrogen or hydroxide ions are present as potentially interfering ions.

At sub-micromolar sample–ion activities, the above relationships must be extended because of the effects of ion fluxes from the membrane of the sample, or vice versa [13]. As shown in Section 3 above, the influence of such fluxes is directly related to the diffusion coefficients in the membrane and the sample, and the thickness of the diffusion layer (see Section 3.1 and Fig. 3). Much of the recent improvement in potentiometric sensors for trace analysis had to do with the reduction in the relevant flux parameter q (see Equation (2)). Today, values of 10⁻⁴–10⁻⁶ are achievable and further improvements are likely.

The calculated response function in the presence of ion fluxes is rather complicated [13]. However, for polymeric membranes with an aqueous inner solution, it is straightforward to estimate the lower LOD c_I(DL) from the concentration of interfering ions c_J on the basis of the selectivity coefficients $K_{\text{IJ}}^{\text{pot}}$, the flux parameter q, and the concentration of the ion exchanger in the membrane R_T as [13]:

$$\text{log\hspace{0.17em}}{c}_{\text{I}}(DL)=\left(\frac{1}{2}+(z_{\text{J}}-z_{\text{I}})\frac{1}{6}\right)\mathrm{\hspace{0.17em} }\text{log\hspace{0.17em}}\left({\left(\frac{q{R}_{\text{T}}}{z_{\text{I}}}\right)}^{z_{\text{I}} / z_{\text{J}}}\sum K_{\text{IJ}}^{\text{pot}}{c}_{\text{J}}^{z_{\text{I}}/z_{\text{J}}}\right).$$ (5)

Here, the selectivity coefficient is still the decisive parameter, but the lower LOD is deteriorated because of ion fluxes. As indicated by Equation (5), the adverse effect of ion fluxes diminishes with decreasing flux.

5. Applications of ISEs with low LODs

The focused development of polymeric membrane electrodes for trace analysis started less than 10 years ago [39,40] although some early examples of trace-level measurements with a Cu²⁺-selective electrode are known [56,57]. More recently, different solid-state electrodes have been applied for trace-level measurements in seawater. The Cu²⁺-electrode based on an optimized jalpaite membrane in the rotating disk configuration was used to analyze San Diego Bay seawater samples [18]. The LODs were in the nanomolar range of total Cu²⁺ concentrations, which correspond to free Cu²⁺ activities down to 2.5 × 10⁻¹³ M in this matrix. Additionally, electrodes based on chalcogenide glasses as sensing materials have been used for the analysis of Fe³⁺ [54] and Hg²⁺ [55] in seawater. Activities down to 10⁻²⁵ M were assessed, but the total concentrations of 10⁻³–10⁻⁵ M were rather high. These applications show the important role of potentiometry in speciation analysis [58].

In trace analysis, the performance of polymer-membrane electrodes in terms of accessible ions, selectivities, response time, and ruggedness has been steadily improved during recent years [5,6]. Within the short time of their development, several reports have already documented their applicability for trace analysis in analytical practice.

In the first report on potentiometric trace analysis, a Pb²⁺-selective electrode was optimized in measurements in drinking water samples [24]. Its lower LOD was 0.7 ppb (3 nM) (i.e. 20-fold lower than the 15-ppb action limit for Pb imposed by the US). Environmental Protection Agency. This LOD was poorer than the best currently available (cf. Table 1), because the electrodes were optimized in terms of ruggedness and response time.

For samples between micromolar and nanomolar concentrations, the calibration procedure with five-fold standard addition required ca. 10 min. For unspiked and spiked environmental samples with concentrations ≥ 3 nM, no statistically significant deviation has been observed between potentiometric and ICP-MS measurements (see also [59]). It was demonstrated that the potentiometric sensors are also useful tools for the speciation analysis of lead in water. Depending on sample pH, lead ions are partly complexed by carbonate and the total lead concentration corresponds approximately to the free lead activity only at pH values lower than about 4 (see Fig. 5).

Figure 5.

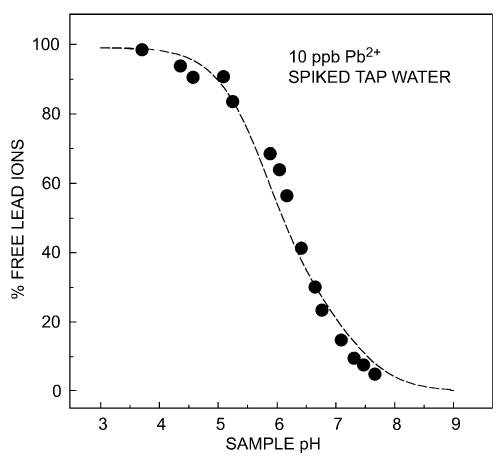
Speciation analysis of drinking water spiked with 10 ppb Pb²⁺ as a function of the sample pH, performed with a potentiometric sensor [24]. The dotted line represents the calculated behavior based on the stability of the lead-carbonate complexes in the sample. As shown in Fig. 1, such sensors are responsive to the activity (free concentration) of the analyte.

The same Pb²⁺-selective electrode was used to study the relationship between lead speciation in the presence of the Suwannee River fulvic acid (SRFA) and its bioavailability to the freshwater alga, Chlorella kessleri [60]. Perhaps surprisingly, the uptake of Pb²⁺ did not correlate with the free-ion activities or the total concentrations.

More recently, an ISE has been developed for the determination of Cu²⁺ in drinking water [33]. Its lower LOD was optimized for measurements with different electrolyte backgrounds. In various drinking water samples containing ≥ 5 × 10⁻⁷ M Cu²⁺ (i.e. ca. 50 times lower than the limit set by the official regulation), the deviations between the results obtained by potentiometry and ICP-MS were ≤30% of the measured values. Long-term measurements showed that during the first 7 days, the responses of both types of membranes changed only slightly, but, after 7 days, the lower LOD deteriorated by about 0.5 logarithmic units. However, in the long term, it remained at <10⁻⁸ M Cu²⁺ over 55 days [33].

In another recent application, the uptake of Cd²⁺ by yeast and Arabidopsis-cell cultures was monitored with a Cd²⁺-selective electrode [31]. Its lower LOD was 10⁻¹⁰ and 10⁻⁸ M Cd²⁺ in the presence of Ca(NO₃)₂ and 0.5× Murashige and Skoog basal medium for yeast and plants cells, respectively. Differences between wild-type yeast and a mutant with deleted glutathione-conjugate pumps [61] were found, and control experiments using AAS confirmed that the decrease in Cd²⁺ activities was caused by the uptake of the metal by the cells under investigation.

6. Future directions

The last few years have witnessed significant activity in understanding the principles that may dictate the low LODs of potentiometric sensors and in finding protocols and examples of successful improvements. Because of this, perhaps, a novice in the field may seem somewhat overwhelmed by the various choices. It will therefore be crucial to see a unified, simplified approach to producing potentiometric sensors with low LODs, rapid response time, sufficient chemical ruggedness and long lifetime, so that they become widely accepted in a range of applications. It is very likely that such a standard protocol will use conditions where the inner solution is no longer relevant to the sensor response, or will use a solid inner contact. Recent developments towards this goal have been very promising.

While potentiometric sensors with low LODs have already been developed for a variety of ions, the list needs to be increased. Important analytes for which low LODs have not yet been demonstrated are, for example, nickel, manganese, mercury and arsenate ions. An important bottleneck to the development of such sensors is, clearly, selective ionophore design. Hopefully, synthetic chemists will rise to the challenge and develop selective receptors that will achieve reach this goal.

Potentiometric sensors with low LODs need to be miniaturized. Potentiometric microelectrodes have been known for a long time, but, to date, low LODs have been demonstrated for macroelectrodes only. Microelectrodes will allow one to accurately map very low chemical concentrations as a function of distance (e.g., in chemical microscopy or the study of ion uptake by the roots of living plants [62]). Because, ideally, potentiometric sensors do not chemically perturb the sample, such microelectrodes will be suitable for measuring low concentrations in very small sample volumes. This will translate into extremely small detectable total quantities that may surpass the characteristics of any other electrochemical technique, and perhaps most other analytical methods.

Improvements will be made to enhance the sensitivity of such sensors (i.e. robust sensors with super-Nernstian response slopes will be developed [63]). This will alleviate the need for robust, accurate reference electrodes, although the response will then be based on kinetic, rather than thermodynamic, principles. Advances in this direction have recently been realized with instrumentally controlled membranes in double- or triple-pulse experiments, where defined current and potential pulses are imposed on the measuring cell for accurate control of otherwise highly transient transport and extraction processes [64].