Abstract
The structures of the unit cells of lipid phases that exhibit long-range crystalline order but short-range liquid-like disorder are of biological interests. In particular, the recently discovered rhombohedral phase has a unit cell containing either the structure of a membrane fusion intermediate state or that of a peptide-induced transmembrane pore, depending on the lipid composition and participating peptides. Diffraction from such systems generally presents a difficult phase problem. The existing methods of phase determination all have their limitations. Therefore it is of general interest to develop a new phasing method. The method of multi-wavelength anomalous dispersion is routinely used in protein crystallography, but the same method is difficult for lipid systems for the practical reason that the commonly used lipid samples for diffraction do not have a well-defined thickness. Here we describe a practical approach to use the multi-wavelength anomalous dispersion method for lipid structures. The procedure is demonstrated with the lamellar phase of a brominated lipid. The method is general to all phases as long as anomalous diffraction is applicable.
INTRODUCTION
The experimental method described here was developed during our research to resolve the structures of peptide-induced membrane fusion intermediate states (1,2) and membrane pores (3). These problems are related to the questions as to how the lipid components and peptides are distributed in a curved monolayer or bilayer. One way to study these problems is to make use of the nonlamellar phases of the peptide-lipid systems, and use x-ray diffraction to resolve the structures of the unit cells. These lipid phases exhibit long-range order (periodicity) but their unit cells usually contain disordered conformations. The existing methods of phase determination for lipid systems, such as swelling (4,5), pattern recognition (6,7), and methyl trough search (8,9) are limited in their applicability. In protein crystallography the most reliable phase-determining method is the method of multi-wavelength anomalous dispersion (MAD) (10–16). We found that the standard method of MAD analysis is difficult for lipid systems. Through trial and error we have arrived at a new procedure of MAD analysis that works well for lipid systems. We believe that the method is of general interest to lipid structure research. Here we use a simple lamellar system to illustrate the method.
In the standard MAD method, one uses an equation relating three quantities; i.e., the magnitude of the normal diffraction amplitude of the host molecules, the magnitude of the normal diffraction amplitude of the anomalous atoms, and the relative phase angle between the two amplitudes, with coefficients that are wavelength dependent. A set of diffraction measurements are then recorded at wavelengths below and above the absorption edge of the anomalous atom so as to vary these coefficients as much as possible to allow the three unknowns to be determined. We previously applied this standard method to a gramicidin-lipid bilayer system (17). This required the sample to have a well-defined thickness; hence the sample was sandwiched between two substrates, with one of them being a thin, polished beryllium plate for x-ray transmission. However, more commonly used and much more conveniently prepared lipid samples are deposited on one substrate only. Such samples can be subject to a rapid hydration change, which is important for synchrotron radiation experiment. One drawback of these open samples is that the thickness of the jellylike lipid deposition is known only approximately due to at least two reasons: 1), although the amount of lipid can be precise, the lipid is difficult to confine to a well-defined area; and 2), the thickness may vary with hydration. As a result the length of the beam path through the sample is known only approximately. Therefore the correction for the x-ray absorption can be significantly uncertain, particularly if the absorption coefficient is large and sensitive to wavelength.
To alleviate the difficulty of absorption correction, we choose our x-ray energies below the absorption edge, where the x-ray absorption coefficient is relatively small and almost independent of wavelength. We measured diffraction at eight different wavelengths so as to solve the unknowns by a straight-line fitting instead of solving nonlinear equations. Even assuming that the absorption correction is error free, the multiple solutions of the simultaneous nonlinear equations constructed from MAD measurement can be ambiguous. This is because the coefficients in the equations inevitably contain experimental errors. We can imagine that if the coefficients of the equations were precise, the correct solutions would be reproduced by overdeterminations (by using more than three different wavelengths). One could then single out the correct solutions from the non-physical ones. But this is in general not the case due to the imprecise coefficients. We found the method of straight-line fitting much more straightforward by comparison.
We will use the lamellar phase of distearoyl phosphatidylcholine with brominated chains to illustrate this procedure. Interestingly the commonly used swelling method (4,5) cannot resolve the phase problem of this lamellar system. We will demonstrate that the MAD method correctly determines the phases.
EXPERIMENTAL METHODS
Materials, sample preparation, and experimental setup
1,2-Distearoyl(9-10dibromo)-sn-glycero-3-phosphocholine (abbreviated as di18:0(9,10dibromo)PC) was purchased from Avanti Polar Lipids (Alabaster, AL). Silicon wafers (〈100〉 surface, P-doped), 300-μm thick, were purchased from Virginia Semiconductor (Fredericksburg, VA).
Preparation for oriented samples followed the method described in Ludtke et al (18). Di18:0(9,10dibromo)PC was first dissolved in a 1:1 trifluoroethanol (TFE)-chloroform solvent and then uniformly deposited onto a clean, flat silicon substrate. The organic solvent was evaporated in vacuum or open air for ∼1 h. The deposit was then hydrated with saturated water vapor and incubated in an oven at 35°C overnight. The result was 0.4 mg of lipid spread over an area of 10 × 10 mm2, thus with an approximately uniform thickness of 4 μm. For diffraction experiment, the sample was kept inside a humidity-temperature chamber (2). The substrate was attached to a temperature-controlled aluminum mount by heat-sink paste. Directly facing the sample surface was a water reservoir, where the water temperature was adjusted to vary the relative humidity (RH) inside the sample chamber. A temperature transducer (AD590, Analog Devices, Norwood, MA) and a relative humidity sensor (HC-600, Ohmic, Easton, MD) were mounted close to the sample to monitor the sample condition. The outputs from the sensing elements were fed to PID feedback control circuits, which in turn powered two sets of Peltier modules (Melcor, NJ), one for heating or cooling the sample and another for heating or cooling the water reservoir. The chamber was covered by a double-layered insulating wall with Kapton windows for the passage of x ray. Between the two layers, a resistive heating coil maintained the surface temperature of the chamber above that of the sample so as to avoid water condensation on the Kapton windows.
At room temperature the lipid formed hydrated bilayers parallel to the substrate. Diffraction from the lamellar phase was measured at 25°C and 90%RH. This unusual choice of humidity level requires an explanation. It is well known that for the majority of lipids, peak broadening and progressive weakening of the reflection orders occur when the humidity level exceeds ∼98%RH, due to the undulation fluctuations of the membranes in water (19). For this lipid, the diffraction pattern began to lose high orders and exhibit peak broadening above ∼92%RH. This was found repeatedly in experiments with freshly prepared samples, except that once or twice the disordering started around 96%RH.
X-ray experiment was performed at the beamline X21 of the National Synchrotron Light Source, Brookhaven National Laboratory (Upton, NY). The setup was similar to the one described in Yang and Huang (2). The x-ray beam was collimated by two sets of slits before the sample chamber, resulting in a beam size of 0.5 × 0.5 mm2 at the sample. Diffraction by the lamellar phase was recorded on a MarCCD detector (Mar USA, Evanston, IL). A niobium (Nb) attenuator was used to keep the first two orders from saturating the detector. The intensity of the incident beam was monitored by a Bicron scintillation detector (Saint-Gobain Crystals, Newbury, OH) that measured the elastic scattering from a 0.9-μm-thick polyethylene film inserted in the incident beam. The detector was positioned at 90° angle from the incident beam and perpendicular to the incident polarization.
Wavelength dependence of detectors
It is imperative to measure and correct for the wavelength dependence of the detectors and the attenuator. All the diffraction intensities were normalized to a fixed incident photon flux (photon number per area per time). We used an air-filled ion chamber (with 8-μm-thick Kapton windows) as the reference whose wavelength dependence is contained in the expression 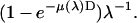 The first factor
The first factor 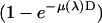 is the absorption ratio of the x ray passing through the ion chamber, where
is the absorption ratio of the x ray passing through the ion chamber, where 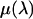 is the absorption coefficient for air and D the length of the ion chamber. The second factor
is the absorption coefficient for air and D the length of the ion chamber. The second factor 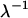 comes from the energy of photon, because an ion chamber is an energy detector. An empirical expression for
comes from the energy of photon, because an ion chamber is an energy detector. An empirical expression for 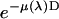 is given by the Center for X-Ray Optics of the Lawrence Berkeley Laboratory (20). For D = 8 cm at 1 atm and 25°C,
is given by the Center for X-Ray Optics of the Lawrence Berkeley Laboratory (20). For D = 8 cm at 1 atm and 25°C, 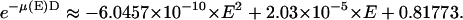 The wavelength dependence of the detectors and of the Nb attenuator is included in Table 1 for reference. Note that the insignificant wavelength dependence for the Bicron detector shown in Table 1 could be misleading; the detector has much stronger wavelength dependence outside of the range of wavelength shown. (Ion chambers were not used in the diffraction experiment due to space limitation.)
The wavelength dependence of the detectors and of the Nb attenuator is included in Table 1 for reference. Note that the insignificant wavelength dependence for the Bicron detector shown in Table 1 could be misleading; the detector has much stronger wavelength dependence outside of the range of wavelength shown. (Ion chambers were not used in the diffraction experiment due to space limitation.)
TABLE 1.
Br anomalous scattering factor and wavelength dependence of detectors and attenuator
| n | En (eV) | f′ | f″ | IC | BI | ATT | CCD |
|---|---|---|---|---|---|---|---|
| 1 | 13468.8 | −7.00 | 0.68 | 1.0000 | 1.0000 | 0.001591 | 1.0000 |
| 2 | 13465.5 | −6.50 | 0.59 | 1.0005 | 1.0001 | 0.001589 | 1.0059 |
| 3 | 13460.3 | −6.01 | 0.54 | 1.0012 | 1.0002 | 0.001580 | 1.0000 |
| 4 | 13451.5 | −5.50 | 0.51 | 1.0025 | 1.0004 | 0.001567 | 0.9765 |
| 5 | 13437.2 | −5.00 | 0.50 | 1.0045 | 1.0007 | 0.001546 | 0.9824 |
| 6 | 13413.7 | −4.50 | 0.51 | 1.0079 | 1.0010 | 0.001502 | 0.9706 |
| 7 | 13370.0 | −4.00 | 0.52 | 1.0142 | 1.0012 | 0.001417 | 0.9706 |
| 8 | 13297.4 | −3.50 | 0.51 | 1.0249 | 1.0006 | 0.001282 | 0.9941 |
En's are the energies chosen for MAD measurement (the K-edge of Br is 13.474 keV). 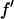 and
and 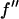 are the real and imaginary parts of the bromine atom's anomalous scattering factor (in the unit of electron). En's are chosen so that the incremental change of
are the real and imaginary parts of the bromine atom's anomalous scattering factor (in the unit of electron). En's are chosen so that the incremental change of 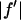 from one energy to the next is a constant 0.5. The wavelength dependence of ion chamber (IC) was calculated as explained in the text. The wavelength dependences of Bicron scintillation detector (BI), the niobium attenuator (ATT), and MarCCD detector are the deviations from that of the ion chamber (normalized at the first energy).
from one energy to the next is a constant 0.5. The wavelength dependence of ion chamber (IC) was calculated as explained in the text. The wavelength dependences of Bicron scintillation detector (BI), the niobium attenuator (ATT), and MarCCD detector are the deviations from that of the ion chamber (normalized at the first energy).
Anomalous scattering factor of bromine
It is well known that the absorption edge and the scattering factor near the edge are influenced by the chemical environment of the atom. Therefore one measures the anomalous scattering factor of the label atom in the actual sample. The absorption spectrum was measured in the fluorescence mode with the scintillation detector positioned at 90° angle from the incident beam and in the direction of the incident polarization. After the Br K-edge was identified at 13.474 keV, the absorption curve was measured over both sides of the edge. The absorption curve was then converted to the imaginary scattering factor 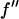 by using the theoretical values calculated by Cromer and Libermann (21). The real part
by using the theoretical values calculated by Cromer and Libermann (21). The real part 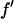 was calculated by the dispersion relation using the CHOOCH program by Evans and Pettifer (22). Below the absorption edge eight energies (wavelengths) were chosen with a step size
was calculated by the dispersion relation using the CHOOCH program by Evans and Pettifer (22). Below the absorption edge eight energies (wavelengths) were chosen with a step size 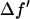 = 0.5 (in the unit of electron) for each successive energy as shown in Table 1 where the values of
= 0.5 (in the unit of electron) for each successive energy as shown in Table 1 where the values of 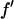 and
and 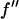 are listed.
are listed.
Multi-wavelength anomalous diffraction
Diffraction by the lamellar phase was measured by rotating the substrate 1°/s (2) from incident angle θ ∼ 0° to ∼ 10°, at eight x-ray wavelengths chosen above. Well-aligned lipid lamella diffract strongly (which we routinely measure on a sealed-tube x-ray diffractometer; see below), thus a moderate beam intensity was used by narrowing the slits. The beam was blocked between scans so the sample was exposed to radiation only during data collection. We first completed the scans for eight wavelengths at the same sample position. Then we displaced the substrate to a previously unexposed sample position and completed the eight scans in the reversed order of wavelengths. We found that the results were consistent with each other indicating no deterioration effect from radiation damage. After the experiment the sample was examined by thin layer chromatography as described in Yang et al. (23); the result did not show extra spots as compared with fresh lipid. All data were also reproduced by at least two freshly prepared samples.
We also applied the swelling method to the samples by normal diffraction collected on a sealed-tube x-ray generator and a Huber four-cycle goniometer, with a line-focused (1 × 10 mm) Cu Kα source (λ = 1.542 Å) operating at 40 kV and 15–30 mA. The characteristics of this experimental setup have been described in detail previously (24,25).
Reduction of the MAD data
The intensities of the diffraction peaks were integrated directly on the detector image in two ways. 1), The peaks were fit by two-dimensional Gaussian functions plus a background, and then integrated. 2), The peaks were first integrated in the direction parallel to the substrate surface over a width slightly wider than the apparent peak widths. The result was plotted along the substrate normal. On this one-dimensional profile, the background was obtained by using the intensities between the peaks and extrapolated into the peak regions. After the background removal, each peak was fit with a Gaussian and then integrated. The results of the two methods were consistent with each other.
The integrated intensities were corrected for the polarization factor, the Lorentz factor, diffraction volume, and x-ray absorption (2). These are the standard corrections for normal lamellar diffraction. For MAD, there is an additional wavelength-dependent correction of λ3 (26). All these corrections are straightforward, except for the x-ray absorption. In general, the jellylike lipid samples made by the deposit method do not have a well-defined thickness, therefore there is an uncertainty in the absorption correction. This uncertainty is greatly magnified if the multi-wavelength measurement includes energies above the K-edge where the absorption coefficient is large and sensitive to wavelength. Below the K-edge, the absorption coefficient is almost constant (Table 1). Thus the absorption correction does not affect the relative magnitudes of the intensities measured at different wavelengths. For this reason we limited our MAD measurement to energies below the K-edge. As will be seen below, even in the region below the absorption edge there are sufficient dispersion variations in diffraction intensity for MAD analysis.
The diffraction amplitude from a system containing atoms of an element with anomalous scattering factor 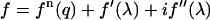 is written as
is written as
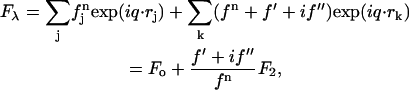 |
(1) |
where q is the x-ray scattering vector, 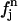 is the normal scattering factor of atom j at position
is the normal scattering factor of atom j at position 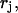 and
and 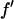 and
and 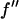 are the real and imaginary parts of the anomalous scattering factor; their values for Br are shown in Table 1. The index j includes all atoms except for the anomalous atoms. The index k includes all the anomalous atoms. Fo is the normal diffraction amplitude of the whole system. F2 is the normal diffraction amplitude of the anomalous atoms alone. We will assume that the unit cell of the lipid structure is centrosymmetric, so that both Fo and F2 are real (rather than complex) quantities and their phases are the signs of the amplitudes. The following analysis will test whether this assumption is valid. From Eq. 1, we have
are the real and imaginary parts of the anomalous scattering factor; their values for Br are shown in Table 1. The index j includes all atoms except for the anomalous atoms. The index k includes all the anomalous atoms. Fo is the normal diffraction amplitude of the whole system. F2 is the normal diffraction amplitude of the anomalous atoms alone. We will assume that the unit cell of the lipid structure is centrosymmetric, so that both Fo and F2 are real (rather than complex) quantities and their phases are the signs of the amplitudes. The following analysis will test whether this assumption is valid. From Eq. 1, we have
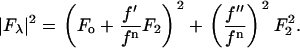 |
(2) |
However, the second term is ∼1% of the first term, because at energies below the absorption edge 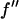 ∼ 0.5, which is ∼10% of
∼ 0.5, which is ∼10% of 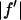 (Table 1). Therefore we have the approximate relation
(Table 1). Therefore we have the approximate relation
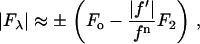 |
(3) |
where we have replaced 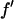 by
by 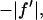 since
since 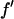 is negative below the absorption edge.
is negative below the absorption edge.
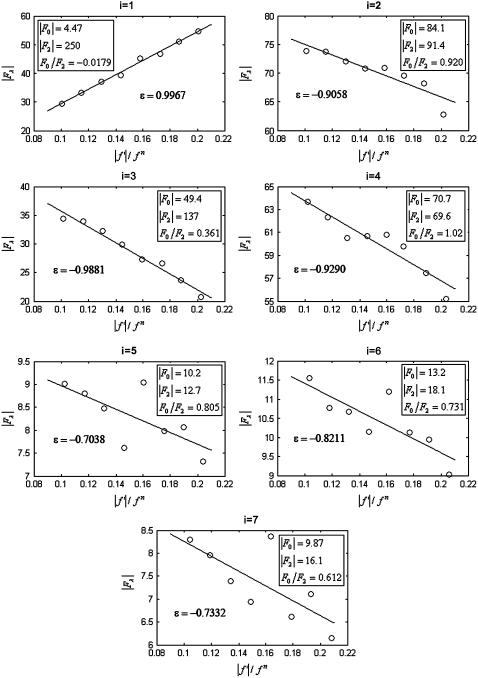
We plotted 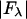 against
against 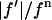 for each peak (Fig. 1). The data for every peak appear to satisfy a linear relation (i.e., approximately fit to a straight line). Because Eq. 3 is the combined result of a), both Fo and F2 are real quantities and b), the linear approximation from Eq. 2 to Eq. 3, we conclude that both the assumption of centrosymmetry and the assumption of linear approximation are valid. In each plot, we fitted the data with a straight line (Fig. 1). (The correlation coefficient of the fit is also given in the figure.) From Eq. 3, we see that the intercept of the fitted line gives
for each peak (Fig. 1). The data for every peak appear to satisfy a linear relation (i.e., approximately fit to a straight line). Because Eq. 3 is the combined result of a), both Fo and F2 are real quantities and b), the linear approximation from Eq. 2 to Eq. 3, we conclude that both the assumption of centrosymmetry and the assumption of linear approximation are valid. In each plot, we fitted the data with a straight line (Fig. 1). (The correlation coefficient of the fit is also given in the figure.) From Eq. 3, we see that the intercept of the fitted line gives 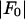 ; the magnitude of the slope gives
; the magnitude of the slope gives 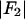 ; and the sign of the slope gives the sign of
; and the sign of the slope gives the sign of 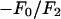 (Fig. 1, insets).
(Fig. 1, insets).
FIGURE 1.
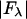 (ordinate) is plotted against
(ordinate) is plotted against 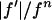 (abscissa) for the seven lamellar peaks, order i = 1–7. The data on each panel was fit by a straight line; ɛ is the correlation coefficient of the fit. From Eq. 3, the intercept of the line gives
(abscissa) for the seven lamellar peaks, order i = 1–7. The data on each panel was fit by a straight line; ɛ is the correlation coefficient of the fit. From Eq. 3, the intercept of the line gives 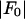 ; the magnitude of the slope gives
; the magnitude of the slope gives 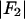 ; and the sign of the slope gives the sign of
; and the sign of the slope gives the sign of 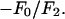
This is the most essential step of MAD analysis. It reduces the phase problem of the whole system to the phase problem of the label atoms alone. The latter problem is much simpler than the original phase problem. And once the phases of 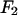 's are determined, so are those of
's are determined, so are those of 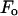 's.
's.
Distribution of the bromine label and electron density profile of the bilayer
We use the amplitudes 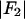 to build the Patterson function (26) for the Br distribution
to build the Patterson function (26) for the Br distribution
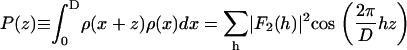 |
(4) |
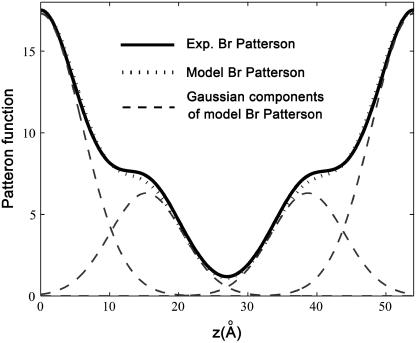
The result is displayed in Fig. 2. The Patterson function shows pairs of peaks at position z and D−z. The pair of  is from self-correlation. Another pair at
is from self-correlation. Another pair at  is from intercorrelation, indicating that there are two Br peaks in the bilayer separated by a distance
is from intercorrelation, indicating that there are two Br peaks in the bilayer separated by a distance 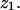 The data can be modeled by a density
The data can be modeled by a density
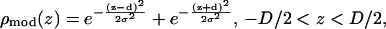 |
(5) |
where 2d (approximately equal to z1) is the distance between the two Br peaks and σ the Gaussian width for each peak. The density extends beyond the unit cell by the periodic condition. It is easy to show that the Patterson function of 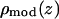 is
is
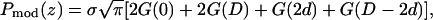 |
(6) |
where 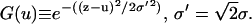 The Patterson function of a model distribution with parameters d = 7.5 Å and σ = 4 Å closely reproduces the experimental Patterson function as shown in Fig. 2. The points to note are: 1), the width of a Patterson peak is
The Patterson function of a model distribution with parameters d = 7.5 Å and σ = 4 Å closely reproduces the experimental Patterson function as shown in Fig. 2. The points to note are: 1), the width of a Patterson peak is 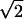 times that of the corresponding peak in real space, and 2), the amplitudes of the intercorrelation peaks (located at
times that of the corresponding peak in real space, and 2), the amplitudes of the intercorrelation peaks (located at 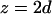 and
and 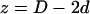 on the Patterson coordinate) are one-half of the self-correlation peaks at
on the Patterson coordinate) are one-half of the self-correlation peaks at 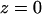 and
and 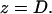
FIGURE 2.
Patterson function of the Br distribution plotted from z = 0 to D (solid line). A model Patterson function (Eqs. 5 and 6) with parameters d = 7.5 Å and σ = 4 Å (dotted line) is shown for comparison. Dashed line shows the Gaussian components of the model Patterson function. The experimental Patterson and the model Patterson are normalized to each other by the relation: 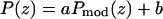 ; a and b were chosen to match the maximum and minimum points of the two functions.
; a and b were chosen to match the maximum and minimum points of the two functions.
From the model density 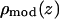 that closely reproduces the experimental Patterson, one calculates the model amplitudes
that closely reproduces the experimental Patterson, one calculates the model amplitudes
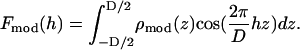 |
(7) |
The phases of 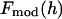 determine the phases of experimental F2 and, from the sign of Fo / F2 obtained from the MAD analysis, those of Fo.
determine the phases of experimental F2 and, from the sign of Fo / F2 obtained from the MAD analysis, those of Fo.
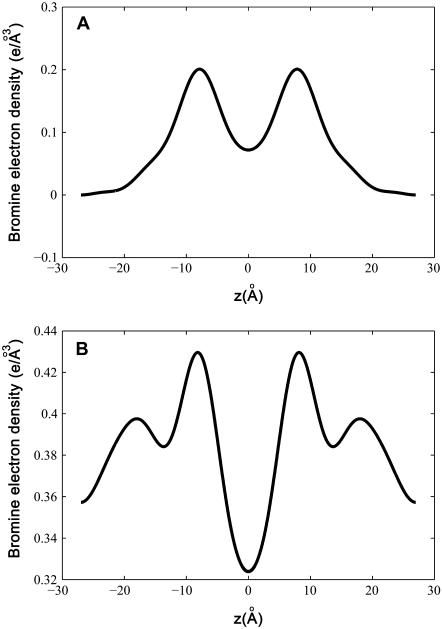
With their phases (signs) determined, F2 and Fo are used to construct the experimental electron density profiles for the Br distribution (Fig. 3 A) and for the whole lipid (Fig. 3 B), respectively. The experimental electron densities are normalized to the real densities by three parameters a, b, and 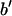 :
: 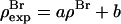 and
and 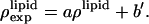 The three parameters are determined by the three conditions: 1), Br electron density vanishes in the water region, 2), the integration of
The three parameters are determined by the three conditions: 1), Br electron density vanishes in the water region, 2), the integration of 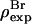 from −D/2 to D/2 equals to the total number of Br electrons in two lipids divided by the lipid cross section, 3), the integration of
from −D/2 to D/2 equals to the total number of Br electrons in two lipids divided by the lipid cross section, 3), the integration of 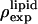 from −D/2 to D/2 equals to the total number of electrons in two lipids plus 20 water molecules divided by the lipid cross section. The lipid cross section was obtained by the use of the phosphate-to-phosphate distance in Fig. 3 B and the relevant lipid volume (27). (The number of water molecules used here is somewhat arbitrary. This number could be more precisely measured (27), but was not done, because it would not affect the discussion here.)
from −D/2 to D/2 equals to the total number of electrons in two lipids plus 20 water molecules divided by the lipid cross section. The lipid cross section was obtained by the use of the phosphate-to-phosphate distance in Fig. 3 B and the relevant lipid volume (27). (The number of water molecules used here is somewhat arbitrary. This number could be more precisely measured (27), but was not done, because it would not affect the discussion here.)
FIGURE 3.
Electron density profiles from z = −D/2 to D/2, measured by the MAD method. (A) The bromine distribution. (B) The whole lipid bilayer.
Swelling method
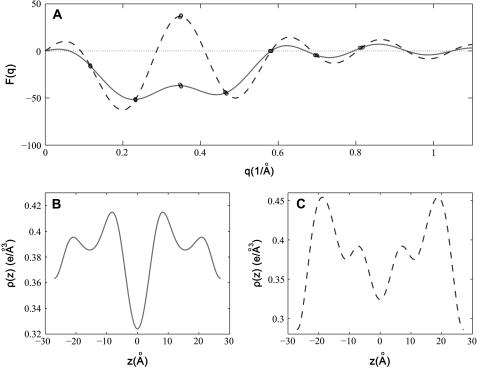
The phase problem for the lamellar phase is conventionally solved by the swelling method (4,5). For example, the bilayers of a series of 16:0-18:0(dibromo)PC were successfully phased by this method (28). To check the result of the MAD method, we also applied the swelling method to our brominated lipid using a laboratory diffractometer (24,25). As noted in “Sample preparation”, the quality of diffraction pattern from this lipid deteriorated when the humidity was above ∼92% (peak broadening and losing high orders). Thus the swelling experiment was performed from 89% to 91%RH. As one sees from Fig. 4 A, the sign of the third order cannot be clearly determined by the swelling method. In fact judging from the overall agreement between the Shannon constructions (24,25) and the data (particularly the second and the fourth orders), one might favor the choice 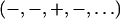 for the phases, instead of
for the phases, instead of 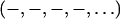 as determined by the MAD method. Also there is no obvious reason, based on a bilayer structure, to reject either one of the two electron density profiles built with either a positive or a negative third order (Fig. 4, B and C). (For example, in Fig. 4 C, the high central region relative to the water region could be explained as due to the contribution of bromines to the central region.)
as determined by the MAD method. Also there is no obvious reason, based on a bilayer structure, to reject either one of the two electron density profiles built with either a positive or a negative third order (Fig. 4, B and C). (For example, in Fig. 4 C, the high central region relative to the water region could be explained as due to the contribution of bromines to the central region.)
FIGURE 4.
The results of the swelling method on the lamellar phase of di18:0(9,10dibromo)PC, measured on a laboratory diffractometer using Cu Kα radiation. (A) The phasing diagram by the swelling method. The three data points (circles) measured at 89%, 90%, and 91%RH partially overlap. The solid and dashed lines are the Shannon constructions (4,5) for different choices of sign for the third order. (B) The electron density profile if the third order is negative. This profile is slightly different from Fig. 3 B. It could be due to a difference in the hydration level—the two hydrometers used in the two different experiments were not calibrated to each other. (C) The electron density profile if the third order is positive. (In panels B and C, we used the same electron density normalization constants that were obtained for Fig. 3.)
DISCUSSION
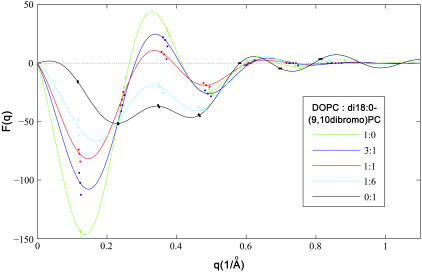
To see if the phases 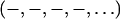 determined by the MAD method for the di18:0(9,10dibromo)PC bilayers are correct, we measured a series of lipid mixtures of di18:1PC (DOPC) and di18:0(9,10dibromo)PC. Starting with pure DOPC where the third order is positive (as determined by the swelling method), the magnitude of the third order first diminished with the increasing fraction of di18:0(9,10dibromo)PC and then increased (Fig. 5). This is consistent with the sign change of the third order as the fraction of di18:0(9,10dibromo)PC increases. That explains the phases
determined by the MAD method for the di18:0(9,10dibromo)PC bilayers are correct, we measured a series of lipid mixtures of di18:1PC (DOPC) and di18:0(9,10dibromo)PC. Starting with pure DOPC where the third order is positive (as determined by the swelling method), the magnitude of the third order first diminished with the increasing fraction of di18:0(9,10dibromo)PC and then increased (Fig. 5). This is consistent with the sign change of the third order as the fraction of di18:0(9,10dibromo)PC increases. That explains the phases 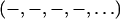 for pure di18:0(9,10dibromo)PC. The reason for the positive third order for most lipids is that the position of the headgroup is about D/3 from the center of the bilayer. However, the bromine peaks in the middle of the chain give a negative third order. Thus the sign of the third order depends on their relative contributions. Apparently the bromine peaks dominate the sign when there are two bromines per chain.
for pure di18:0(9,10dibromo)PC. The reason for the positive third order for most lipids is that the position of the headgroup is about D/3 from the center of the bilayer. However, the bromine peaks in the middle of the chain give a negative third order. Thus the sign of the third order depends on their relative contributions. Apparently the bromine peaks dominate the sign when there are two bromines per chain.
FIGURE 5.
Comparison of five DOPC/di18:0(9,10dibromo)PC mixtures (ratios shown in the inset). The solid lines are the Shannon constructions (4,5). The data suggest that the third order changes from positive to negative as the fraction of di18:0(9,10dibromo)PC increases.
At the beginning of this anomalous diffraction experiment, we had tried to use the standard method of MAD analysis (10–16) to solve the phase problem for the brominated lipids, since previously we used this method to solve the phase problem for a gramicidin-lipid bilayer system labeled with thallium ions bound to the gramicidin channels (17). As explained in “Introduction”, the sample preparations were different for the two systems. The gramicidin-lipid sample had a well-defined thickness between two substrates, whereas the brominated lipid sample was deposited on one surface that in general would not provide a well-defined thickness. On the other hand, one-substrate samples are easy to prepare and, more importantly, can be subject to a rapid hydration change (either for the purpose of changing phases or for sample calibration). The phasing method described here works well for one-substrate samples despite the fact that their thicknesses are known only approximately. Other advantages include: 1), straight-line fitting is simple and straightforward, compared with the procedure of solving nonlinear equations. 2), Experimental errors are inevitable, but in the straight-line fitting method, a small number of bad data (that do not fit the linear relation) can be excluded if the majority of the data fit a linear relation. Bad data are much less obvious in the method of solving nonlinear equations. 3), One problem of using x-ray energies above the absorption edge is a high fluorescence background due to the strong absorption. A large background would contribute to errors in integrated intensities. By limiting the x-ray energies below the absorption edge we have avoided this problem.
In protein crystallography, heavy atoms are attached to proteins isomorphously. The purpose of MAD is to solve the structures of the native proteins. For lipids, heavy atom labels are used in a different way, because such labels often alter the property of the original lipid. For example, the property of di18:0(9,10dibromo)PC is somewhat between that of di18:0PC and of di18:1PC. By osmotic pressure it undergoes a transition from the lamellar phase to a rhombohedral phase, similar to di18:1PC but at a different phase boundary (29), whereas di18:0PC does not exhibit such a phase transition. The mixture of cholesterol and di18:0(9,10dibromo)PC can be induced to a rhombohedral phase with or without peptides ((30); the authors' unpublished data). In such cases, the unit cell structure could be a fusion intermediate state, called a stalk (1,2) or a transmembrane pore (3). With the application of anomalous diffraction, the bromine labels serve the dual purposes of 1), phase determination thus resolving the electron density distribution within the unit cell; and 2), highlighting the lipid chains of the PC thus making it possible to distinguish the distributions of PC and cholesterol separately.
The MAD method supplements the existing methods of phase determination including swelling (4,5), pattern recognition (6,7), and methyl trough search (8,9). Although in one previous case a combination of swelling and pattern recognition solved the phase problem for a rhombohedral phase (1,2), we found that the swelling method is often not applicable to nonlamellar phases either because the range of swelling is insufficient or because swelling changes the unit cell structure (e.g., in the inverted hexagonal phase). The method of pattern recognition relies on the presumed invariance of density moments between different phases of the same lipid (6,7). This does not apply to the cases where the lipid components might redistribute depending on the degree of bending (31). The use of methyl trough search (8,9) is limited to the cases where the mathematical property of the monolayer surface is known. In comparison, the MAD method is founded on a firmer theoretical basis (10), as demonstrated by its general applicability in protein crystallography (10–16). We believe that its applications to lipid systems are yet to be explored.
Acknowledgments
This work was supported by National Institutes of Health grant GM55203 and the Robert A. Welch Foundation Grant C-0991. The experiment was carried out in part at the National Synchrotron Light Source, Brookhaven National Laboratory, which is supported by the U.S. Department of Energy, Division of Materials Sciences and Division of Chemical Sciences, under contract No. DE-AC02-98CH10886.
Wenhan Liu is on leave from Dept. of Physics, University of Sciences and Technology of China, Hefei, China.
References
- 1.Yang, L., and H. W. Huang. 2002. Observation of a membrane fusion intermediate structure. Science. 297:1877–1879. [DOI] [PubMed] [Google Scholar]
- 2.Yang, L., and H. W. Huang. 2003. A rhombohedral phase of lipid containing a membrane fusion intermediate structure. Biophys. J. 84:1808–1817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Yang, L., T. M. Weiss, and H. W. Huang. 2000. Crystallization of antimicrobial pores in membranes: magainin and protegrin. Biophys. J. 79:2002–2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Blaurock, A. E. 1971. Structure of the nerve myelin membrane: proof of the low-resolution profile. J. Mol. Biol. 56:35–52. [DOI] [PubMed] [Google Scholar]
- 5.Torbet, J., and M. H. Wilkins. 1976. X-ray diffraction studies of lecithin bilayers. J. Theor. Biol. 62:447–458. [DOI] [PubMed] [Google Scholar]
- 6.Luzzati, V., A. Tardieu, and D. Taupin. 1972. A pattern-recognition approach to the phase problem: application to the X-ray diffraction study of biological membranes and model systems. J. Mol. Biol. 64:269–286. [DOI] [PubMed] [Google Scholar]
- 7.Mariani, P., V. Luzzati, and H. Delacroix. 1988. Cubic phases of lipid-containing systems. Structure analysis and biological implications. J. Mol. Biol. 204:165–189. [DOI] [PubMed] [Google Scholar]
- 8.Harper, P. E., and S. M. Gruner. 2000. Electron density modeling and reconstruction of infinite periodic minimal surfaces (IPMS) based phases in lipid-water systems. I. Modeling IPMS-based phases. Eur. Phys. J. E. 2:217–228. [Google Scholar]
- 9.Harper, P. E., S. M. Gruner, R. N. Lewis, and R. N. McElhaney. 2000. Electron density modeling and reconstruction of infinite periodic minimal surfaces (IPMS) based phases in lipid-water systems. II. Reconstruction of D surface based phases. Eur. Phys. J. E. 2:229–245. [Google Scholar]
- 10.Karle, J. 1989. Macromolecular structure from anomalous dispersion. Phys. Today. 42:22–29. [Google Scholar]
- 11.Guss, J. M., E. A. Merritt, R. P. Phizackerley, B. Hedman, M. Murata, K. O. Hodgson, and H. C. Freeman. 1988. Phase determination by multiple-wavelength x-ray diffraction: crystal structure of a basic “blue” copper protein from cucumbers. Science. 241:806–811. [DOI] [PubMed] [Google Scholar]
- 12.Hendrickson, W. A., J. L. Smith, R. P. Phizackerley, and E. A. Merritt. 1988. Crystallographic structure analysis of lamprey hemoglobin from anomalous dispersion of synchrotron radiation. Proteins. 4:77–88. [DOI] [PubMed] [Google Scholar]
- 13.Hendrickson, W. A., J. R. Horton, H. M. Murthy, A. Pahler, and J. L. Smith. 1989. Multiwavelength anomalous diffraction as a direct phasing vehicle in macromolecular crystallography. Basic Life Sci. 51:317–324. [DOI] [PubMed] [Google Scholar]
- 14.Kahn, R., R. Fourme, R. Bosshard, M. Chiadmi, J. L. Risler, O. Dideberg, and J. P. Wery. 1985. Crystal structure study of Opsanus tau parvalbumin by multiwavelength anomalous diffraction. FEBS Lett. 179:133–137. [DOI] [PubMed] [Google Scholar]
- 15.Murthy, H. M., W. A. Hendrickson, W. H. Orme-Johnson, E. A. Merritt, and R. P. Phizackerley. 1988. Crystal structure of clostridium acidi-urici ferredoxin at 5-Å resolution based on measurements of anomalous X-ray scattering at multiple wavelengths. J. Biol. Chem. 263:18430–18436. [PubMed] [Google Scholar]
- 16.Hendrickson, W. A. 1991. Determination of macromolecular structures from anomalous diffraction of synchrotron radiation. Science. 254:51–58. [DOI] [PubMed] [Google Scholar]
- 17.Liu, W., T. Y. Teng, Y. Wu, and H. W. Huang. 1991. Phase determination for membrane diffraction by anomalous dispersion. Acta Crystallogr. A47:553–559. [Google Scholar]
- 18.Ludtke, S., K. He, and H. Huang. 1995. Membrane thinning caused by magainin 2. Biochemistry. 34:16764–16769. [DOI] [PubMed] [Google Scholar]
- 19.Chen, F. Y., W. C. Hung, and H. W. Huang. 1997. Critical swelling of phospholipid bilayers. Phys. Rev. Lett. 79:4026–4029. [Google Scholar]
- 20.Laboratory, Center for X-ray Optics of the Lawrence Berkeley. http://www-cxro.lbl.gov/optical_constants. [Online.].
- 21.Cromer, D. T., and D. Libermann. 1970. Relativistic calculation of anomalous scattering factors for X rays. J. Chem. Phys. 53:1891–1898. [Google Scholar]
- 22.Evans, G., and R. F. Pettifer. 2001. CHOOCH: a program for deriving anomalous-scattering factors from X-ray fluorescence spectra. J. Appl. Crystallogr. 34:82–86. [Google Scholar]
- 23.Yang, L., T. A. Harroun, T. M. Weiss, L. Ding, and H. W. Huang. 2001. Barrel-stave model or toroidal model? A case study on melittin pores. Biophys. J. 81:1475–1485. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Olah, G. A., H. W. Huang, W. H. Liu, and Y. L. Wu. 1991. Location of ion-binding sites in the gramicidin channel by X-ray diffraction. J. Mol. Biol. 218:847–858. [DOI] [PubMed] [Google Scholar]
- 25.Weiss, T. M., L. Yang, L. Ding, A. J. Waring, R. I. Lehrer, and H. W. Huang. 2002. Two states of cyclic antimicrobial peptide RTD-1 in lipid bilayers. Biochemistry. 41:10070–10076. [DOI] [PubMed] [Google Scholar]
- 26.Warren, B. E. 1969. X-Ray Diffraction. Section 4.1, 9.3. Dover Publications, New York.
- 27.Nagle, J. F., and S. Tristram-Nagle. 2000. Structure of lipid bilayers. Biochim. Biophys. Acta. 1469:159–195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.McIntosh, T. J., and P. W. Holloway. 1987. Determination of the depth of bromine atoms in bilayers formed from bromolipid probes. Biochemistry. 26:1783–1788. [DOI] [PubMed] [Google Scholar]
- 29.Yang, L., L. Ding, and H. W. Huang. 2003. New phases of phospholipids and implications to the membrane fusion problem. Biochemistry. 42:6631–6635. [DOI] [PubMed] [Google Scholar]
- 30.Pan, D., W. Wang, W. Liu, L. Yang, and H. W. Huang. 2006. Chain packing in the inverted hexagonal phase of phospholipids: a study by X-ray anomalous diffraction on bromine-labeled chains. J. Am. Chem. Soc. In press. [DOI] [PMC free article] [PubMed]
- 31.Ding, L., T. M. Weiss, G. Fragneto, W. Liu, L. Yang, and H. W. Huang. 2005. Distorted hexagonal phase studied by neutron diffraction: lipid components demixed in a bent monolayer. Langmuir. 21:203–210. [DOI] [PubMed] [Google Scholar]