Mechanism of Titin Unfolding by Force: Insight from Quasi-Equilibrium Molecular Dynamics Calculations

Abstract

We have studied the unfolding by force of one of the immunoglobulin domains of the muscle protein titin using molecular dynamics simulations at 300 K. Previous studies, done at constant pulling rates, showed that under the effect of the force two strands connected to each other by six backbone H-bonds are pulled apart. No details about the mechanism of H-bond breaking were provided. Our simulation protocol “pull and wait” was designed to correspond to very slow pulling, more similar to the rates used in experiments than are the protocols used in previous computational studies. Under these conditions interstrand backbone H-bonds are not “ripped apart” by the application of the force. Instead, small elongations produced by the force weaken specific backbone H-bonds with respect to water-backbone H-bonds. These weakened bonds allow a single water molecule to make H-bonds to the CO and the NH of the same backbone H-bond while they are still bound to each other. The backbone H-bond then breaks (distance >3.6 Å), but its donor and acceptor atoms remain bound to the same water molecule. Further separation of the chains takes place when a second water molecule makes an H-bond with either the protein backbone donor or acceptor atom. Thus, the force does not directly break the main chain H-bonds: it destabilizes them in such a way that they are replaced by H-bonds to water. With this mechanism, the force necessary to break all the H-bonds required to separate the two strands will be strongly dependent on the pulling speed. Further simulations carried out at low forces but long waiting times (≥ 500 ps, ≤ 10 ns) show that, given enough time, even a very small pulling force (<400 pN) is sufficient to destabilize the interstrand H-bonds and allow them to be replaced by H-bonds to two water molecules. As expected, increasing the temperature to 350 K allows the interstrand H-bonds to break at lower forces than those required at 300 K.

INTRODUCTION

Single molecule experiments in which proteins are stretched by mechanical forces have revealed a wealth of information about their mechanical properties (1–6). Atomic-level computer simulations (7–12) of the same process provided details about the mechanism of the proteins' response to tensile loading. TI I27, the 27th immunoglobulin (Ig) domain of the I-band of human muscle titin (Fig. 1) has been extensively studied by these experimental (1,6,7,11,12) and computational (8,10,11) methods. In experiments, the mean domain unfolding force usually exhibits a weakly logarithmic dependence on the pulling speed, the dependence generally expected when unfolding is driven by thermally activated barrier crossing (13). Simulations show that the initial events involve rupture of hydrogen bonds between terminal β-strands, resulting in an unfolding intermediate that, upon further pulling, unfolds in an all-or-none fashion (8). Studies on ubiquitin (14) and the lipoyl domain of pyruvate dehydrogenase (15) have recently yielded similar results, showing in addition that not only the number and nature of intrastrand hydrogen bonds but also the orientation of the strands relative to the pulling direction contribute to the resistance of a β-sheet to disruption by a force.

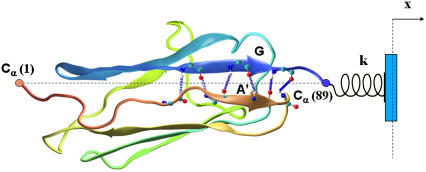
FIGURE 1.

Titin immunoglobulin domain I27 (TI27). I27 is a β-sandwich with four β-strands on each sheet. Hydrogen bonds between the N-terminal β-strand A′ and the C-terminal strand G are shown. The simulations are carried out by moving the restraint point (blue) to the right by fixed distances followed by MD calculations. Simulations are carried out for values of the spring constant k ranging from 0.5 to 5.0 kcal/mol Ų.

A direct comparison of single-molecule pulling experiments to MD simulations of force-driven unfolding has been difficult because of the disparity in timescales. At the much faster pulling rates typical of MD simulations proteins may unfold by mechanisms different from those operative in experimental studies (16).

Several approaches have been developed recently to extrapolate single-molecule data to slower pulling speeds. Jarzynski (17,18) and subsequently Hummer and Szabo (19) showed that the equilibrium free energy dependence can, in principle, be reconstructed from single molecule experiments or simulations even when those are performed far from equilibrium. This approach has been tested experimentally (20) and by simulations (21). Very recently, Collin et al., (22) estimated the difference in free energy of unfolding between a wild-type and a mutant small RNA hairpin from multiple nonequilibrium experimental unfolding and folding events using Crook's fluctuation theorem (23). Although a similar approach could be used in simulations, since it involves averaging over a large number of single-molecule trajectories, it is computationally expensive.

To overcome these difficulties, we investigated the unfolding by force of TI I27 with an alternative, speed-independent simulation protocol the “pull and wait” technique (PNW). As part of this study we performed a detailed analysis of the events leading to strand separation and explored the mechanism of hydrogen bond-breaking events and in particular the role of water molecules in this process.

METHODS

All simulations were carried out with the program CHARMM (24,25), using an integration time step of 1 fs, a uniform dielectric constant of 1, and a cutoff of Coulomb forces with a switching function starting at distance of 10 Å and reaching zero at 14 Å (10–12 Å for van der Waals terms). Simulations were performed at 300 K and 350 K. The starting model was one of the NMR structures of TI I27 (PDB accession code 1TIT; (26)). The structure of TI I27 was placed in a box (93.13 × 40.37 × 37.25 Å) containing 4680 preequilibrated TIP3P water molecules (27) and periodic boundary conditions were used. No counterions were included in the calculations.

All atoms, including hydrogens, were modeled explicitly, resulting in a system containing 13,926 atoms.

Pulling of TI I27 was accomplished by fixing the Cα of the N-terminal leucine (Leu-1) and applying an external force to the Cα of the C-terminal leucine (Leu-89). The force was applied by harmonically restraining the pulled end to a fixed restraint point positioned along the line joining the N- and C-terminal Cα atoms, 4 Å further away from the last position (Fig. 1). The system was allowed to relax for 30–50 ps. After each equilibration the simulation was followed for times ranging from 30 to 150 ps (short simulations). Average forces and extensions were calculated without including the relaxation period. At the completion of each run, the restraint point was moved in one step an additional 4 Å along the same line and the simulations were repeated using the same protocol. This PNW process was repeated until a final extension of 16.8 Å was reached. Some of the simulations were extended to 500 ps and two sets (set A and set B) were extended to 10 ns. Sets A and B include points that occurred one step (set A) and two steps (set B) before strand separation in the “short simulations”. The box used is big enough to accommodate the molecule at the maximum extension used in this study without crossing the box boundary.

For simulations at 300 K, at each extension the simulation was repeated with five different spring constants (values between 0.5–5 kcal/mol Ų). Similar simulations were carried out at 350 K, using a single spring constant of 2 kcal/mol Ų.

RESULTS

Force extension profile

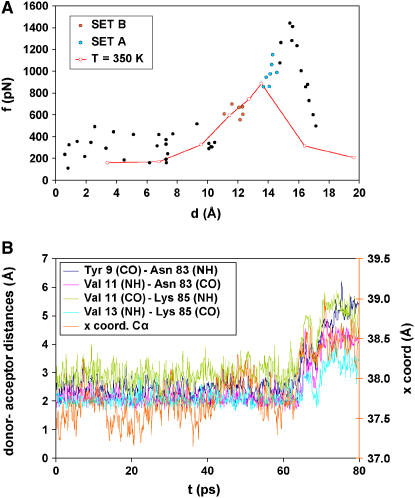
The force versus extension curve calculated at 300 K (Fig. 2 A) shows the average equilibrium extensions of simulations carried out with different spring constants ranging from 0.5 to 5.0 kcal/mol Ų. The results of the simulations show a peak of ∼1440 pN at an extension of 15.5 Å. This peak corresponds to the main energy barrier separating the folded and the unfolded states of the domain that occurs at the highest point of the experimental force versus extension curves. After the barrier is overcome, the force decreases rapidly to average values of ∼300 pN.

FIGURE 2.

(A) Force extension profile of the I27 domain observed in the simulations. The forces and extensions shown in this figure are average values calculated after the system was allowed to relax after the displacement of the restraint point (see Methods). The solid black, red, and green circles correspond to the results of the “short simulations”. Simulations for the green (set A) and the red (set B) points were further extended to 10 ns. Sets A and B include points that occurred one step (set A) and two steps (set B) before strand separation in the “short simulations”. The results of the “long simulations” are not shown in this figure. The red line and red open circles represent the force versus extension curve for 350 K with a elastic constant of 2 kcal/mol Ų. (B) Time course of the distances between donors and acceptors of the H-bonds between β-strands A′ and G of I27. The x-position of the Leu-89 Cα during the first 80 ps of equilibration is also shown.

Backbone hydrogen-bond breaking

A full analysis of the H-bond behavior during the short simulations shows that before the force peak the H-bonds remain mainly formed during the process, although they break and re-form frequently. Of the six H-bonds between strands A′ and G, the middle four bonds are highly stable, but the two at the ends are more fragile.

The trajectory of the MD simulation corresponding to the extension of maximal force reveals that four hydrogen bonds between β-strands A′ and G break concurrently, as described previously (12,28). The CO-NH distances of the backbone H-bonds between β-strands A′ and G during this event are shown in Fig. 2 B. (Two H-bonds between β-strands A′ and G and the H-bonds between β-strands A and B break at an early step in the same trajectory; not shown.)

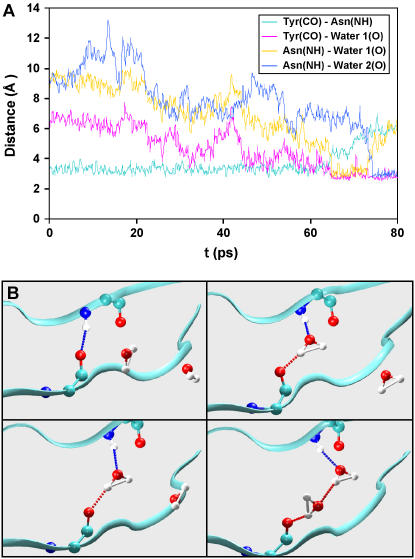
Fig. 3, A and B, show a breaking event at a force of 1400 pN for the H-bond between the main chains of Tyr-9 (CO) and Asn-83 (NH). Until 65 ps into the equilibration run, this backbone H-bond is still formed; the closest water molecule is at least 3 Å away from either of the H-bond partners (Fig. 3 B, upper left). At 65 ps, a water molecule approaches and in a short time (∼0.3 ps) forms one donor and one acceptor H-bond with Tyr-9 (CO) and Asn-83 (NH) (Fig. 3 B, upper right). Immediately after this (∼0.1 ps), the backbone H-bond between Tyr-9 (CO) and Asn-83 (NH) is broken (donor-acceptor distance >3.5 Å). Although this bond remains broken, the CO-NH distance remains below 4 Å, allowing both groups to make H-bonds to the same water molecule (Fig. 3 B, lower left). At 75 ps, a second water molecule approaches and forms an H-bond with Asn-83 (NH) (Fig. 3 B, lower right). Several picoseconds later the bond of the first water molecule to the Asn-8 NH is broken and the backbone CO-NH distance increases beyond 5 Å. Similar behavior is observed in the remaining H-bonds: two water molecules are involved in permanently breaking each main-chain main-chain H-bond.

FIGURE 3.

(A) Distances between the carbonyl oxygen of Tyr-9, the backbone amide nitrogen Asn-83, and the oxygen atoms of two molecules of water during the first 80 ps of a simulation at 300 K. (B) Snapshots of the behavior of the H-bond between Tyr-98 (CO) and Asn-83 (NH). Two water molecules are involved in the H-bond breaking event. (These figures were created with VMD (32)).

Behavior in long time simulations

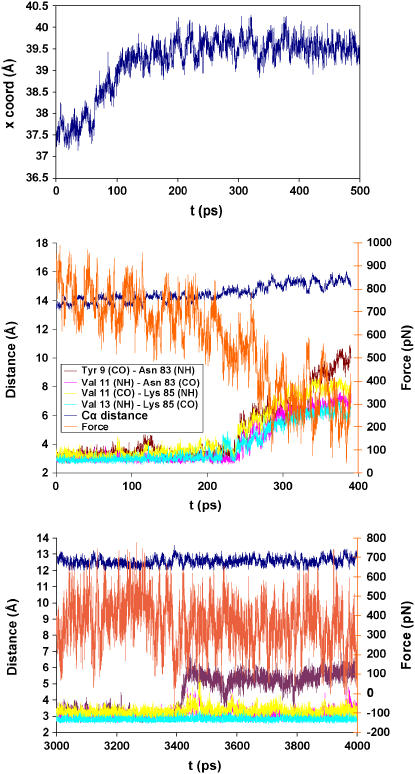
At the step where the peak force was reached, the simulation time was extended to 500 ps (Fig. 4, top panel). After the initial ∼100 ps it shows a characteristic “equilibrium behavior” of the coordinate x of the pulled atom (Leu-89 Cα) as a function of time (i.e., the x-values reach a stable average). Simulations for other points along force versus extension curve were extended in a similar manner and the same behavior was observed in all cases (results not shown).

FIGURE 4.

(Top panel) Behavior of the x-coordinate of the Cα of the C-terminal leucine (Leu-89) during a 500-ps simulation. (Middle panel) Distances between H-bond donors and acceptors of β-strands A′ and G of I27 during the extended simulations of Set A. Additionally the elastic force and the distance between the starting and final position of the pulled Cα are shown. (Bottom panel) Behavior of the H-bond between Tyr-9 (CO) and Asn-83 (HN) in a run of set B during the last nanosecond of simulation. Additionally, the elastic force and distance between the starting and final position of the pulled Cα are shown.

To evaluate the effect of the simulation time on the force required for H-bond breaking, simulations for two of the runs were extended to 10 ns. The set of points chosen for this test correspond to the two extensions preceding the point of maximal force (set A and set B in Fig. 2 A). During the 150 ps of simulation, no H-bond breaking occurred as a result of the extension. When the simulation was extended for set A, H-bond breaking events were registered with forces between 340 and 500 pN (Fig. 4, middle panel) at 400–800 ps of simulation. During this process, some H-bonds break for short periods of time but they remain broken only when water molecules make H-bonds to the donor and acceptor groups of the protein. In the 10-ns simulation carried out for set B, just a single H-bond (Tyr-9 (CO)-Asn-83 (HN)) breaks with forces ranging between 300 and 600 pN. The rest of the H-bonds remain formed (Fig. 4, bottom panel). On this step the longest distance reached was 12.5 Å. To rule out the possibility that even in the absence of a force some interstrand H-bonds may break in 10 ns, the initial unextended structure was subjected to a 10-ns simulation with the two ends fixed at their original positions. In this run, although interstrand H-bond break and reform, none remains broken for an extended period of time.

Force extension profile at high temperature

A force versus extension curve at 350 K with a single elastic constant of 2 kcal/mol Ų (Fig. 2 A) shows a peak of 880 pN at an extension of 13.5 Å. The H-bond breaking events occur at an earlier step in the pulling process but the overall behavior is highly similar.

DISCUSSION

AFM and optical tweezers have been used successfully to monitor pulling of single protein molecules but understanding of the molecular mechanism of unfolding by application of force remains elusive. Molecular dynamics simulations that are consistent with the experiments have provided details about the mechanism of this process. They showed, for example, that breakage of the main chain H-bonds between β-strands A and B occurs early in the extension, but the highest barrier opposing protein extension corresponds to the separation of strands A′ and G (28). However, because of the short simulation times imposed by limitations of computer resources, steered molecular dynamics (SMD) (29) simulations “pull” Titin Ig domains at speeds six to eight orders of magnitude faster than those used in AFM and optical tweezers experiments, and they yield force peaks that are one order of magnitude larger than the experimental values. This is because SMD simulations operate in a regime where forces are large enough to pull the system above energy barriers at high pulling speeds, whereas AFM experiments operate in a regime in which forces are low but there is enough time to allow the system to thermally equilibrate (at least partially) (18), lowering the barriers and promoting crossing on the millisecond experimental time scale (8,30). By using the PNW protocol, short extensions followed by long equilibrations, we carried out simulations that correspond more closely to the conditions of the experimental work. This protocol is similar to the constant velocity SMD stretching but with one main difference. Instead of moving the restraint point at constant speed, the point is moved in leaps that stretch the spring. The protein is allowed to equilibrate to the new situation and, after stabilization of the force, the simulation is continued for varied amounts of time to collect information about the force, the extension and the details of the events that take place. PNW has two advantages with respect to SMD that may be important in some situations. First, in SMD the protein is continuously trying to “catch up” with the extension, such that the dynamical consequences of the change in position of the moving point are always lagging the actual extension. In PNW, each MD simulation is carried out in an unchanging situation, giving the system, in principle, the possibility to equilibrate. Second, PNW allows the possibility of spending long equilibration times in steps in which important mechanistic events are taking place. This protocol, for example, allowed us to explore the events that take place close to separation of the A′ and G strands using long simulation times at selected points along the extension.

The rates of extension of SMD simulations (28,31) varied between 0.1 and 1.0 Å/ps. Although the PNW protocol does not involve a constant speed movement of the restraint point, an “equivalent rate” can be obtained by dividing the total extension of any given set of MD runs by the sum of all the simulation times in the same set. Based on this type of estimate the rates of extension of our PNW short runs varied between 0.016 and 0.081 Å/ps. In the long runs, the equivalent rates were even slower.

Our simulations show features of the unfolding process and force profiles similar to those reported by others (28), but with significant differences in the force peak value and in the timing of the events. Monitoring individual participating hydrogen bonds reveals that resistance of TI I27 to unfolding under external forces can be attributed to inter-β-strand backbone hydrogen bond breaking, with water molecules playing a key role. During the equilibration (Fig. 2 B), backbone H-bonds fluctuate between formed and broken states due to attacks by water molecules but remain intact for most of the time. Under pulling forces, the backbone H-bonds are on average slightly longer and therefore become less stable, although they do not break. Obviously, H-bonds involving water molecules are not affected by the force. Under these conditions, backbone H-bonds with water molecules gain a slight energetic advantage with respect to H-bonds between backbone atoms.

At low forces water molecules constantly make and break H-bonds to H-bonded main chain atoms. Sometimes, the same water molecule makes H-bonds with both the NH and the CO of a main chain H-bond pair. These are temporary events that do not affect the overall structure. As the force increases and approaches the simulation's peak force, once the same water molecule makes H-bonds to the donor and the acceptor of a main chain bond, the bond may break and the distance between the NH and the CO can extend beyond 3.5 Å, but remains below 4.0 Å, maintaining both H-bonds to the single water molecule.

Full separation of the strands does not occur until a second water molecule makes an H-bond to either the CO or the NH, and the first water molecule can then release one of the groups. Therefore, with long equilibration times water molecules do not replace backbone H-bonds after they break; rather they form hydrogen bonds to the backbone groups before the backbone H-bonds can break. The mechanism observed, in which first a single water molecule makes two H-bonds, one to the NH and one to the CO, and then a second water molecule replaces one of the two H-bonds, allows the replacement of two backbone H-bonds by bonds to two different water molecules without any of the groups being left without an H-bond partner and without requiring a multi-body event. The involvement of water molecules in the force unfolding of TI27 was discussed before as part of an SMD study (28,31), but these reports describe only major intermediates that include bound water molecules without reference to their direct participation in the actual process of H-bond breaking.

To analyze the relation between kinetic and thermodynamic effects, the simulation time for five points before the observed break was extended to 500 ps (Fig. 4, top panel). The maxima of the force obtained with this “quasi-equilibrium” protocol were reached at different times depending on the length of the simulation but in general the force associated with each extended equilibration was always lower than that in the equivalent shorter run. In other words, by extending the simulation time for each step the final force at each pulling length is significantly smaller. These results are a clear indication that the force necessary to disrupt the structure in these simulations (and in the experiments as well) is determined not only by the intrinsic stability of the structure, but also by the time that one waits at any given extension. Support for this notion is provided by the simulations showing that if the temperature is increased to 350 K, the H-bond breaking mechanism remains the same as the mechanism at 300 K, though the force required to break the bonds is decreased and breaking occurs at shorter extensions.

For simulations in which the equilibration time was extended to 10 ns (set A and set B), the maximal force needed to break the H-bond cluster shows an even greater diminution, close to values measured in AFM experiments. These long time simulations show that, given enough time, even a very small pulling force (<400 pN) is sufficient to destabilize interstrand H-bonds and allow them to be replaced by H-bonds to two water molecules. The four critical hydrogen bonds between the A′ and G strands only break in each set of simulations when the total extension is at least 15 Å from the initial position (set A; Fig. 4, middle panel). At shorter extensions (set B) only a single H-bond (the one closest to the fixed Cα) breaks at different times, at total extensions between 12.0 and 12.5 Å and pulling forces between 300 and 600 pN (Fig. 4, bottom panel). When the simulations are carried out with zero extension, no interstrand H-bonds are broken, indicating that in the absence of a force the simulations do not result in broken H-bonds even at long times.

In summary, the simulations presented here provide details about the events leading to the unfolding of the TI27 Ig domain of titin using force. Disruption of the structure requires breakage of the six H-bonds connecting the N-terminal and C-terminal β-strands. Given adequate time, these H-bonds are not broken directly by the applied force. Instead, the force destabilizes these bonds with respect to the H-bonds the backbone groups can make to water molecules and allows the formation of stable H-bonds between single water molecules and the donor and acceptor groups of the interstrand H-bonds. Formation of these bonds allows the backbone groups to separate up to 4 Å. Further separation requires that a second water molecule bind to the donor or the acceptor groups of each pair. This mechanism, in which first one water molecule binds to both donor and acceptor of the backbone H-bond weakening and lengthening the bond, and then one of the bonds is replaced by an H-bond to another water molecule, ensures that no H-bond is broken before it is replaced. Furthermore, by virtue of taking place in two distinct steps, the mechanism does not require simultaneous three-molecule collisions. Another consequence of this mechanism is that the barrier for the separation of the two strands is in part kinetically determined and becomes larger as the speed of application of the force increases in agreement with experimental observations.