Gradual Change or Phase Transition: Characterizing Fluid Lipid-Cholesterol Membranes on the Basis of Thermal Volume Changes

Abstract

Cholesterol has been reported to govern biomembrane permeability, elasticity, and the formation of lipid rafts. There has been a controversy whether binary lipid-cholesterol membranes should better be described in terms of a phase separation (liquid-ordered and liquid-disordered phases) or of gradual changes in largely homogeneous membranes. We present a new approach for detecting and characterizing phase equilibria in colloidal dispersions using pressure perturbation calorimetry (PPC). We apply this to the study of the thermal expansivity of mixtures of 1-palmitoyl-2-oleoyl sn-glycero-3-phosphatidylcholine (POPC) and cholesterol as a function of composition and temperature. We show that cholesterol can condense lipids not only laterally (with respect to interfacial area) but also in volume. A quantitative comparison with expansivity curves simulated assuming either phase separation or random mixing within one phase reveals that the real system shows an intermediate behavior due to submicroscopic demixing effects. However, both models yield consistent system parameters and are thus found to be useful for describing the systems to a similar approximation. Accordingly, one cholesterol may condense 3 ± 1 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphatidylcholine molecules by ∼−(1.4 ± 0.5) vol % at 2°C; both absolute values decrease with increasing temperature.

INTRODUCTION

Cholesterol plays a key role in biological membrane function including the regulation of membrane elasticity and permeability and has been considered essential for the formation of lipid rafts. These phenomena are of utmost biological, medical, and pharmaceutical interest. However, details of the interactions of cholesterol with lipid membranes are still a matter of controversy, despite enormous efforts dedicated to the issue over several decades (to specify only a few reviews (1–4)).

It is widely accepted that cholesterol can induce a liquid ordered (ℓ_o) state in lipid membranes, which has intermediate properties between a gel phase (ordered acyl chains) and a liquid-disordered (ℓ_d), fluid phase (high lateral mobility, no crystalline arrangement) (5,6). A macroscopic separation of two liquid (ℓ_o and ℓ_d) phases has been observed for ternary mixtures of, e.g., 1,2-di-oleoyl-sn-glycero-3-phosphocholine (DOPC), dipalmitoylphosphatidylcholine (DPPC), and cholesterol, whereas binary lipid-cholesterol mixtures were found to exhibit, at the most, submicroscopic domain formation (7–9). There is, however, an ongoing debate whether also binary mixtures are best described assuming ℓ_o − ℓ_d coexistence in a certain composition and temperature range (see, e.g., (3,4,10)), and the literature is particularly controversial for the 1-palmitoyl-2-oleoyl sn-glycero-3-phosphatidylcholine (POPC)-cholesterol system. Phase diagrams including a liquid-liquid (ℓ_o and ℓ_d) coexistence have been established for DPPC and sphingomyelin mixed with cholesterol (11,12) and ergosterol (13) and also for unsaturated lipids such as PPetPC (6) and POPC (14,15). However, NMR studies on POPC cholesterol did not provide unequivocal evidence for an ℓ_o and ℓ_d two-phase range (7,10,16) and were interpreted in terms of a single ℓ_d phase at all cholesterol contents up to 40°C and temperatures >25°C (7). The mechanical properties of POPC-cholesterol membranes studied by micropipette aspiration and vesicle fluctuation analysis revealed no indication of a phase separation as well (10). Results of molecular dynamics simulations of cholesterol-induced ordering and lateral area compression of DPPC could also be well discussed in terms of a continuous change in membrane properties (17).

When it comes to discuss whether lipid mixtures are best described by a phase coexistence, one should recall that thermodynamic phases in the strict sense are macroscopically separate, so that micro- or nanoscopic domains in membranes can only approximately be treated as phases. Nanoscopic domains show additional phenomena such as an entropy of mixing with other domains, an edge energy related to the line tension between the domains, a limited lifetime, and an exchange of molecules between domains. Hence, the question whether a microheterogeneous system qualifies approximately as a phase coexistence or not cannot be answered on the basis of the existence and size of domains alone. Therefore, we pursued the strategy to characterize whether the macroscopic system as a whole behaves like a two-phase or a one-phase system. We selected POPC-cholesterol since this is particularly ambiguous. We show that the thermal volume expansion provides an excellent criterion for that purpose. We discuss the data in terms of one- and two-phase models in parallel, thus allowing for a direct comparison.

It should be noted that the results provide important new insight also apart from the phase issue. So far, very little has been known about cholesterol-induced changes in the (temperature-dependent) partial volume of phospholipids. What has long been clear is that cholesterol may increase the order of saturated acyl chains of neighboring lipids, which results in their effective stretching, an increase in membrane thickness, and a lateral condensation of membrane area (1,2). The volume of the lipid has usually been assumed to be virtually conserved upon this change in chain order and membrane geometry since no excess volume of these mixtures arising from cholesterol-induced lipid volume condensation could be measured. This may be surprising taking into account the variety of precise methods to measure densities or partial volumes of lipids (18–20). The problem is, however, to distinguish between the intrinsic volume of cholesterol and the excess volume that is due to cholesterol-induced lipid ordering, since there is no pure cholesterol membrane that could serve as a reference state. Melchior et al. (18) interpreted their finding that the density of fluid DPPC membranes increases nonlinearly with increasing mol fraction of cholesterol qualitatively in terms of a cholesterol-induced membrane condensation but did not attempt to quantify the excess volume. A current, high-precision study by Nagle and co-workers (21) reveals a constant partial volume of cholesterol in mixtures with POPC, which is slightly smaller than that in DOPC but shows no sudden changes (e.g., at X = 0.2) as in DPPC. This result would be consistent with a gradual condensation of POPC by cholesterol since the intrinsic volume of cholesterol (which is not straightforward to be defined) should not depend on the phospholipid, whereas the partial volume includes additionally cholesterol-induced volume changes of the PC.

Another approach is to determine the volume change accompanying lipid melting, which is reduced by cholesterol from 2% for pure POPC to 1.7% (cholesterol mol fraction X = 0.05), 1.5% (0.1), and 1.0% (0.2), suggesting a more densely packed fluid phase and/or less dense gel phase in the presence of cholesterol (22). However, cholesterol effects on the gel and the fluid phase cannot be distinguished this way. Tauc et al. (14) showed that the “effective” phase boundaries in the cholesterol-POPC system are substantially shifted in favor of the ℓ_o phase by high pressure, which implies that the partial volume of the molecules in the ℓ_o state is significantly lower. For example at 25°C, the coexistence range was shifted from cholesterol mol fractions X from ∼0.10–0.40 at 1 bar to ∼0.03–0.24 at 600 bar. This X-shift of the boundaries corresponds to a shift in the transition temperature of the order of 12 K/kbar, which is comparable to the pressure dependence of gel phase melting of unsaturated lipids (23). A direct quantification of the volume change of the order-disorder transition at ambient pressure is, however, not straightforward and was not attempted by these authors.

We use a novel method, pressure perturbation calorimetry (PPC) (24), which measures not the volume per se but the heat response of a sample to a small pressure perturbation. This is directly related to the thermal volume expansion at constant pressure. The advantage of measuring not a parameter representing packing (area, order, volume) but its derivative is that the latter exhibits a sudden jump at a phase boundary, where the integral parameters show only a change in slope. The results are compared with model curves derived for a two-phase system and for cholesterol-induced condensation of POPC in a randomly mixed, one-phase membrane. The approach presented here helps resolving the apparent inconsistencies between the models used in the literature and may be important for deriving a more precise, more complex model explicitly considering the microheterogeneity of the membranes.

EXPERIMENTAL

Materials

1-Palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) was purchased from Avanti Polar Lipids (Alabaster, AL) and cholesterol was from Fluka (Buchs, Switzerland). Mixtures of POPC and cholesterol were prepared by dissolution of appropriate amounts of the dry substances in chloroform/methanol. Multilamellar vesicles were prepared by a standard method involving drying of the mixed lipids and resuspension in pure water as described elsewhere (25). Cholesterol concentrations >50 mol % were avoided; they would require another preparation technique (26). PPC experiments were performed at a constant POPC concentration of 15 mM including various amounts of cholesterol as specified.

Pressure perturbation calorimetry

PPC measurements were carried out in a VP DSC calorimeter from MicroCal (Northampton, MA), equipped with a PPC accessory from the same manufacturer. The sample cell (0.5 mL) was filled with the lipid suspension and the reference cell with water. The technique is explained elsewhere (24,27). Briefly, the sample and reference cell are subject to small pressure jumps of Δp ∼ 5 bar and the system measures the heat required to compensate that induced by the pressure jump (thus keeping the temperature, T, constant). Blank measurements with both cells filled with water are conducted to correct for technical imperfections. The procedure is repeated automatically at many temperatures. Hence, the technique measures the heat response of the lipid to a very small pressure change at constant temperature, approximately corresponding to the differential ∂Q/∂p|_T. This differential heat is related to the isobaric, thermal volume expansion, ∂V/∂T|_p, which can be seen by inserting the equation for the heat of a reversible process, dS = dQ/T, into the Maxwell relation for the isothermal entropy change with pressure, ∂S/∂p|_T:

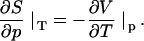(1)

The results can be expressed as the coefficient of thermal expansion, α = ∂V/(V∂T)|_p, or as the change in partial molar volume with temperature, V′ = ∂V/∂T|_p, at constant pressure. A good estimate for the partial molar volume of the mixed membrane, V, as a function of the mol fraction of cholesterol, X, is obtained using 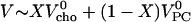using partial volumes of 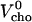∼ 325 mL/mol (17) and 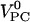∼ 760 mL/mol (19). The small excess volume can be neglected.

THEORY

Composition-dependent expansivity in general

For curve fitting, it is advantageous to use molar expansivities, V′ = ∂V/∂T (given in mL/(mol K)) since contributions to V′ from different components or moieties are additive. For obtaining an expression for V′ as a function the mol fraction of cholesterol, X, we may write the partial molar volume of the membrane, V, as a combination of the partial molar volumes of disordered PC and cholesterol (V_PCd and V_cho, respectively, which are assumed to mix ideally) and a contribution from cholesterol-induced condensation of PC, which is quantified by the volume change, ΔV = V_PCo − V_PCd, and the degree of ordering of PC, ξ_PC = [PC_o]/[PC]:

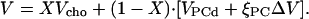(2)

Like the degree of a reaction, ξ_PC changes from 0 for a fully disordered to 1 for a fully ordered membrane. This model assumes implicitly that the excess volume of cholesterol-induced ordering is largely a property of the PC whereas cholesterol requires a similar intrinsic volume in an ordered or disordered environment. Differentiation yields the model equation for V′:

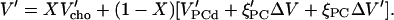(3)

The different models of the mixed membrane to be compared here provide different expressions for ξ_PC and ξ_PC′ = dξ_PC/dT as outlined in the following.

Phase model

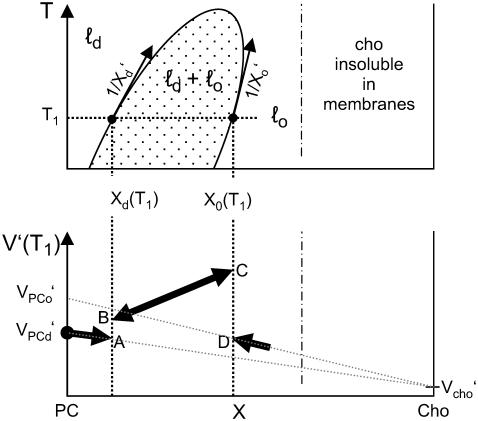
The phase model describes the system in terms of three phase ranges with phase boundaries at X_d and X_o as illustrated by Fig. 1 (top). These are the liquid-disordered (ℓ_d) range at X < X_d, the ℓ_d + ℓ_o coexistence range (X_d < X < X_o, dotted area in Fig. 1), and the liquid-ordered (ℓ_o) range (X_o < X).

FIGURE 1.

Schematic illustration of the phase model. (Top) Phase diagram with liquid-disordered (ℓ_d), liquid-ordered (ℓ_o), and ℓ_d + ℓ_o coexistence (dotted area) ranges in the space defined by temperature T and the mol fraction of cholesterol in the membrane, X. The solubility limit of cholesterol in membranes is about X ≤ 0.66 (26) (temperature dependence unknown). (Bottom) The resulting schematic behavior of the expansivity, V′, as a function of X. See text for details.

In the ℓ_d range, no PC is ordered (ξ_PC = 0) and no PC becomes ordered (ξ_PC′ = 0) so that Eq. 3 becomes:

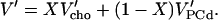(4)

In the ℓ_o range, ξ_PC = 1 and ξ′_PC = 0 so that we obtain with V′_PCo = V′_PCd + ΔV′:

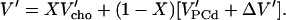(5)

Note that both Eqs. 4 and 5 are linear in X as illustrated by the bold solid lines in Fig. 1 (bottom). Note that the expansivity of cholesterol is assumed to be largely independent of the phase state, V_cho = V_cho,d = V_cho,o. The value of V_cho cannot directly be measured since cholesterol alone forms no membranes; the limit for cholesterol mixing with the membrane is X = 0.66 (26) (we are not aware of information regarding the temperature dependence of this limit). The fact that Fig. 1 is based on V′_PCd < V′_PCo corresponds to ΔV′ > 0 so that the more dense phase, ℓ_o, expands “faster” with increasing T than ℓ_d and its partial molar volume “catches up” with that of ℓ_d. At a critical point, the differences between the phases vanish and V_PCo = V_PCd.

In the ℓ_d + ℓ_o coexistence range, we obtain (see Appendix):

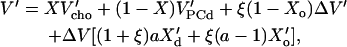(6)

with the constant a:

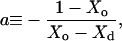(7)

and the derivatives X′_d = dX_d/dT and X′_o = dX_o/dT, which are just the inverse slopes of the phase boundaries (see Fig. 1 and Appendix for derivation). The first three terms in Eq. 6 correspond to a straight line from point A to D in Fig. 1 (bottom), i.e., a weighted sum of the expansivities of the ℓ_d and ℓ_o phases. Additionally, there is the term in the rectangular bracket times ΔV, which appears suddenly at the phase boundaries and corresponds to the temperature-driven conversion of ℓ_o into the ℓ_d phase. At the onset of the coexistence range, at X_d, the degree of ordered molecules is ξ = 0 and the step in V′ arising from the phase conversion term becomes V′(B) − V′(A) = ΔVaX′_d. If ΔV > 0 (disordering causes expansion) and X′_d > 0 (the slope of the X_d boundary is positive), this step is positive (upward) as shown in Fig. 1 (bottom). Note that an increasing phase boundary X_d (i.e., 1/X′_d > 0, X′_d > 0, as shown in Fig. 1) means that increasing T shifts the system in the vicinity of the boundary toward the ℓ_d state, i.e., ℓ_o “melts” to ℓ_d. Within the coexistence range, ξ increases linearly with X (lever rule; see Appendix, Eq. 10, so that the phase conversion term follows a straight line. Approaching the X_o boundary, ξ → 1 and the phase conversion term becomes V′(C) − V′(D) = ΔV[2aX′_d + (a − 1)X′_o], which is positive for ΔV > 0, a > 1, and both phase boundaries increasing, X′_d > 0 and X′_o > 0.

With increasing temperature, the thermal phase conversion per se may become stronger (if the slopes of the boundaries decrease) but ΔV becomes weaker, finally vanishing at the critical point. If, however, the phase boundaries become very steep (i.e., X′_d → 0, X′_o → 0), the phase conversion term (and, thus, the steps in V′ at the boundaries) vanish also if the system remains in the coexistence range (ΔV > 0). That means, vanishing steps in V′ at the phase boundaries does not necessarily imply the proximity of the critical temperature.

Random-neighbor model

This model is based on the idea that the molecules mix randomly in the membrane and each cholesterol molecule can order up to n PC molecules in its neighborhood. A second cholesterol that interacts with a previously ordered PC has no further effect. That means the fraction of condensed PC increases linearly with X at low X and shows a saturation when the cholesterol molecules start to interfere with each other. Edholm and Nagle (17) have derived an elegant expression for the cholesterol-dependent area of such a membrane, which is analogous to Eq. 2 with a probability of a PC to be ordered, ξ_PC:

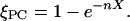(8)

If the temperature changes at a given composition X, the amount of ordered lipid changes as:

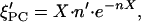(9)

if n is temperature dependent so that n′ = dn/dT does not vanish. The effect on V′ is obtained by inserting Eqs. 8 and 9 into Eq. 3.

RESULTS

Fig. 2 A shows the “PPC curves”, i.e., the temperature dependencies of the coefficient of thermal volume expansion, α(T), for mixtures of POPC with different amounts of cholesterol. All values are of the order of one per mille per degree, or in other words, increasing the temperature by 10 K expands the volume by ∼1%. The curve for pure POPC is in good agreement with α = 0.8 × 10⁻³K⁻¹ measured for POPC with the neutral buoyancy method (20). However, there are significant systematic differences between cholesterol-containing and pure PC membranes. Two characteristic patterns are found (Fig. 2, A and B) depending on the cholesterol content, X. Moderate addition of cholesterol (Fig. 2 A) leads to an enhanced expansion at low temperature, which can be explained in terms of a cholesterol-condensed state that is relaxed upon increasing temperature. At higher temperatures, the curves approach that of pure PC. At intermediate X (Fig. 2 B), the strong initial decrease of α(T) vanishes and the maximum of α shifts to higher temperatures, suggesting that the condensed state is stabilized by higher cholesterol contents and requires higher temperature to be relaxed. At X ≥ 0.4, there is virtually no structural transition observed to proceed upon varying temperature.

FIGURE 2.

The coefficient of thermal expansion, α, as a function of temperature, T, of POPC-cholesterol vesicles with cholesterol mol fractions, X, as specified in the plots. Up to X ∼ 0.2, α(2°C) increases with X (A) but at higher cholesterol contents, it decreases again (B).

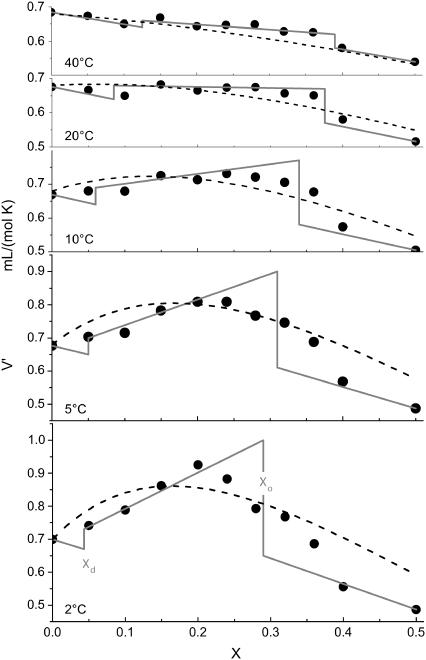
The range of anomalously enhanced α is illustrated by Fig. 3. An enhanced thermal expansion at X ∼ 0.2–0.3 can also be deduced for fluid DPPC/cholesterol from the distance between the lines in Fig. 3 of Melchior et al. (18). The axes of the plot shown here are those of a phase diagram and the range of enhanced α resembles, to some extent, the shape and position of the coexistence range in published phase diagrams. We should, however, emphasize that the range of enhanced α is not necessarily identical with a phase range (see section on phase model in Theory). To elucidate this issue, we have plotted V′(X) for a series of selected temperatures (Fig. 4) and compared it with the phase model, Eqs. 4–6.

FIGURE 3.

The relative deviation of thermal expansion coefficients, α, of mixed membranes at given cholesterol content, X, and temperature, T, from the values in the absence of cholesterol.

FIGURE 4.

The thermal volume expansion, V′, as a function of the cholesterol mol fraction in the membrane, X, at selected temperatures as indicated in the plot. The curves correspond to the phase model (solid lines; perpendicular at phase boundaries) and the random-neighbor model (dashed lines). The corresponding parameters are discussed in the text.

The solid lines in Fig. 4 were obtained from the phase model by a global, visual optimization of X_d, X_o, ΔV, and V′_cho at all selected temperatures (see Fig. 1 for an illustration of the effect of the parameters). V′_PCd is identified with the experimental value of V′ for pure PC (i.e., X = 0). The derivatives X′_d, X′_o, and ΔV′ are obtained from the change in the input parameters from one panel (i.e., temperature) to another. The values for X_d and X_o are visible as steps in Fig. 4. The position of the phase boundaries at, e.g., 20°C (X_d; X_o = 0.085; 0.375) agrees very well with the results of Tauc et al. (14) (0.09; 0.34), which is between the ranges discussed by Henriksen et al. (10) (0.05; 0.3) and measured by de Almeida et al. (15) (0.11; 0.45). It should be noted that different methods may, for example, differ in the minimum size or lifetime of a domain to become detectable. Therefore, they are likely to yield different “effective” phase boundaries in a system that shows no true phase separation but only an approximate two-phase behavior.

The absolute values of ΔV decrease from −10 mL/mol (∼−1.3 vol %) at 2°C to −9 mL/mol at 10°C and −5 mL/mol (0.7 vol %) at 40°C, estimated errors are ±3 mL/mol. The extrapolated expansivity of hypothetic cholesterol membranes, V′_cho, increases with T from ∼0.1 mL/(mol K) at 2°C to ∼0.4 mL/(mol K) at 40°C.

The random-neighbor model yields the dashed curves in Fig. 4 by choosing values for n, ΔV, and V_cho′ for each panel. Again, the curves in the panels depend on each other and have to be optimized globally since n′ and ΔV′ are obtained from the variation of n and ΔV between the panels. The parameters for the presented curves are, for example, n = 3 at 2°C, 2 at 10°C, and 1 at 40°C, ΔV = −12 mL/mol at 2°C, −9 mL/mol at 10°C, and −6 mL/mol at 40°C; V′_cho ranged from 0 at 2°C to 0.3 mL/(mol K) at 40°C.

DISCUSSION

Phase coexistence or gradual transition?

Inspection of Fig. 4 reveals that the behavior of the experimental data is intermediate between the curves obtained by the phase and the random-neighbor model. At very low cholesterol concentration, the condensing effect is weaker than suggested by the random-neighbor model. This implies that the cholesterol molecules do not act fully independently and a concerted action of more than one cholesterol molecule can give rise to a stronger effect. Substantial deviations from the phase model are observed in particular at high X where a gradual decrease of V′ is found instead of the sudden drop predicted for a phase boundary. On the other hand, the decrease of V′ is still steeper than what can be understood in terms of the random-neighbor model. It must be emphasized that, although the model assumptions and fits are different, the parameters of the two models are consistent with each other (see below). That means our direct, quantitative comparison of the two competing models does not imply one model to be correct and the other to be wrong. Both models are similarly good (or bad) approximations for the real behavior, which is intermediate between the extreme cases represented by the models.

The intermediate behavior found here is in accord with the existence of nanoscopic domains or composition fluctuations that have some properties of a phase but show additional effects that do not apply to true phases. Such nanoscopic domains could be kinetically stabilized by energy barriers between closely apposed ordered domains. These were predicted to arise from the lipid splay and tilt required to avoid the exposure of hydrophobic surface at the domain boundaries (28). Other parameters affecting the merger of small domains are the entropy of mixing, the line tension of the boundaries, and the spontaneous curvature (28). Alternatively, the nanoscopic domains could be density fluctuations that appear in the vicinity of a critical point (4). This would also account for enhanced thermal expansion and its deviations from the behavior predicted for random mixing.

We emphasize that the significant deviation between the experimental data (V′(X,T)) and the behavior expected for a true two-phase as well as a true one-phase system is not a weakness but an advantage of this approach. Although it is theoretically obvious that these models are not perfect, many other observables have been discussed in the literature in terms of one of these models without noticing an inconsistency (see Introduction). These parameters are not applicable to quantify the accuracy of the models. The PPC approach can, in contrast, aid the development of a refined model taking into account the microheterogeneity of the system. For POPC, this refined model is, as expected, not that of condensed, stoichiometric complexes that were reported for other lipids but not for POPC (29,30). Modeling the data on the basis of V′ of complex formation (not shown) did, in spite of one additional adjustable parameter, not yield a considerably improved fit.

Cholesterol-induced volume changes

So far, it has usually been assumed that the well-known chain ordering and stretching effect of cholesterol on PC is fully compensated by an area condensation so that the partial volume of PC remains virtually unchanged, i.e., there would be no excess volume in PC-cholesterol mixtures. Melchior et al. (18) obtained evidence for a negative excess volume but did not quantify it. Despite the limitations of the models discussed above, both yield similar volume changes of cholesterol-induced ordering of PC. At 2°C, both models are in line with a volume change of ΔV = −(11 ± 4) mL/mol of at maximum n = 2.7 ± 0.3 POPC molecules. Using a molar volume of POPC of 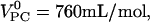this corresponds to a relative change of the volume of POPC upon condensation by ∼−1.4%. This value decreases to ∼−1% at 20°C and to ∼0.6% at 40°C. We can convert these results into a change in the partial volume of cholesterol (which refers to the overall volume change of the membrane upon addition of cholesterol without assigning this change to a certain molecule). Accordingly, the partial volume of cholesterol condensing n POPC molecules is reduced by ∼−9% at 2°C, −4% at 20°C, and −1% at 40°C. This result is in line with the finding that the partial volume of cholesterol at 30°C in mixtures with POPC is by ∼2% smaller than that with DOPC (21), since DOPC is expected to show no or very little volume condensation.

The extent of cholesterol-induced condensation of POPC, up to ∼−1.4 vol %, is much less than the corresponding area and membrane thickness changes (e.g., of the order of 20% (17)) so that it is indeed a reasonable approximation to ignore ΔV upon calculating lipid area changes from changes in order parameter profiles (NMR) or bilayer repeat distances or thickness changes from area data (Langmuir trough). However, the value of −1.4 vol % is large when the volume or packing density changes per se are concerned, since it is close to -2.0 vol % accompanying the freezing of pure POPC into a gel phase (22,31). The latter value can be considered the maximum volume change that is conceivable upon lipid packing changes.

It should be noted that the fact that the orientation of the headgroup is only slightly changed by addition of cholesterol (32) does not mean that it would not contribute to ΔV. Changes in hydration (33) have a strong influence on the partial volume of the membrane constituents; water molecules bound to polar groups are known to exhibit a larger density than bulk water since the latter establishes a space-consuming network of hydrogen bonds (24,34).

The number of condensed lipid molecules per cholesterol

The phase model suggests a phase boundary to the ℓ_o state proceeding from X_o ∼ 0.3 at 2°C to 0.35 between 10°C and 20°C and 0.4 at ∼40°C (Fig. 3). Because the position of the phase boundary corresponds to the minimum cholesterol content of the ℓ_o phase, we may conclude that one cholesterol molecule may order ∼2 POPC molecules at 2°C and 1.5 at 40°C. The fits of the random-neighbor model shown in Fig. 3 suggest that a cholesterol can condense n = 3 ± 1 POPC molecules at 2°C, ∼2 at 10°C, and ∼1 at 40°C. Hence, the parameters of the random-neighbor model agree within error with those of the phase model, suggesting only a somewhat steeper temperature dependence of n. Larger values of n ∼ 4–7.5 were published for DPPC using phase and random-neighbor models (17,21), which is in line with many reports indicating that the effect of cholesterol on saturated lipids is stronger than that on unsaturated lipids.

For ΔV/V_PCd = −1.4% and n = 3 PC molecules per cholesterol, one obtains a lipid volume change of about −4.2 vol % per cholesterol (in the low X range where the lipid is in excess). This value applying specifically to liquid (ℓ_d or ℓ_o) membranes is close to −4.9 vol % per cholesterol derived from the slope of the volume change of the gel-to-liquid transition of POPC with increasing cholesterol content (22). This implies that the effect of cholesterol on the lipid volume in the gel phase is much smaller than that in the fluid phase.

CONCLUSIONS

1. Cholesterol-induced ordering of fluid, unsaturated phospholipid is accompanied by a volume condensation and its thermal relaxation is revealed by anomalously enhanced thermal volume expansivity.

2. A quantitative consideration of the expansivity behavior allows for a direct comparison with the predictions for phase separation and random mixing. The real system shows intermediate properties as suggested for nanoscopic demixing or domain formation but the two models yield consistent interaction parameters. That means both models are similarly good approximations.

3. The relative volume change of fluid unsaturated lipid (POPC) induced by cholesterol at 2°C amounts to ∼−(1.4 ± 0.5)%, close to the condensation upon freezing to a gel phase (−2.0%). Each cholesterol molecule can condense n = 3 ± 1 POPC molecules. Both |ΔV| and n decrease with increasing temperature but the effect remains detectable up to ∼70°C.

APPENDIX: DERIVATION OF EQ. 6

Let us assume that the lipid volume is smaller in the more densely packed ℓ_o state than in the ℓ_d state. Then, a positive contribution to the thermal expansion will arise if increasing temperature leads to a “melting” of ℓ_o domains to ℓ_d.

We have derived a quantitative model for the thermally induced conversion from ℓ_o into ℓ_d and the subsequent, composition-dependent expansivity, V′(X), at a given T in a system showing phase separation. In the one-phase ranges, there is no phase conversion.

In the coexistence range (X_d < X < X_o), the internal composition of the two phases is constant with cholesterol mol fractions of X_o and X_d in the ℓ_o and ℓ_d phase, respectively. What changes as a function of the total cholesterol fraction, X, is only the proportion between the two phases. The fraction of all molecules that is in the ℓ_o phase, ξ (note difference to ξ_PCd), is given by the lever rule (4,35):

(10)

Because the local fraction of PC in the ℓ_o phase is 1 − X_o, we obtain for the fraction of PC in the ordered phase referred to the whole membrane:

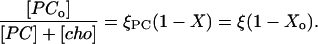(11)

Equation 3 relates V′ to ξ_PC and ξ′_PC. Differentiating Eq. 11 with respect to T (and determining ξ′ from Eq. 10) at a given sample composition (X = const., X′ = 0), one obtains:

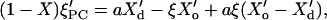(12)

with the constant a:

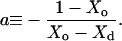(13)

Insertion into Eq. 3 yields Eq. 6.