Abstract
Existing methods of domain identification in proteins usually provide no information about the degree of domain independence and stability. However, this information is vital for many areas of protein research. The recently developed hierarchical clustering of correlation patterns (HCCP) technique provides machine-based domain identification in a computationally simple and physically consistent way. Here we present the modification of this technique, which not only allows determination of the most plausible number of dynamic domains but also makes it possible to estimate the degree of their independence (the extent of correlated motion) and stability (the range of environmental conditions, where domains remain intact). With this technique we provided domain assignments and calculated intra- and interdomain correlations and interdomain energies for >2500 test proteins. It is shown that mean intradomain correlation of motions can serve as a quantitative criterion of domain independence, and the HCCP stability gap is a measure of their stability. Our data show that the motions of domains with high stability are usually independent. In contrast, the domains with moderate stability usually exhibit a substantial degree of correlated motions. It is shown that in multidomain proteins the domains are most stable if they are of similar size, and this correlates with the observed abundance of such proteins.
INTRODUCTION
Domains can be loosely defined as quasi-independent parts of protein molecules serving as the structural blocks and functional units (1,2). The concept of protein domains is very productive in analyzing the mechanisms of protein folding (3) and their stability and structural transformations in various conditions (2,4–6). The functional (catalytic and ligand-binding) sites of protein molecules are frequently located at interdomain interfaces (2). There are also examples of separation of catalytic and effector functions between two or several domains, as this is particularly observed in different ATPases (7,8). Domains tend to move as rigid bodies in response to interactions with substrates and products of enzyme reaction (9,10). Often, domains retain their structural integrity and function when isolated as fragments (11), and this property is actively used in biotechnology to generate single-chain antibody fragments (12). Genetic recombinant techniques allow reorganization of domains in an amino acid sequence (such as circular permutations) (13) and fusion of domains belonging to different proteins (14,15), which in turn allows generation of new protein functions.
Primarily, the term domain means the distinct structural block of a protein, but quite different criteria are presently used to identify this block. Identification can be based on observation of independent folding (2), sequence motifs (16), presence of a distinct hydrophobic core (17), functional activity (17,18), contact classification (19), topology (20), structural homology (21), independent mobility (22–25), and other properties. Since domain-domain interactions can occur in a broad range, varying from almost complete structural and dynamic independence to their complete integrity, the application of these criteria may lead to quite different results. Different definitions of domains and methods of identifying them can be grouped around three key concepts.
A domain is a recognizable (often visually) substructure within a protein as a compact, folded part of the molecule connected to other domains by very few structural elements (or even only one) such as a loop or a helix. Because of that, the number of bonds involved in interdomain interactions and their strength are much smaller than those of bonds that stabilize the intradomain structure. Various algorithms for finding such structural domains have been suggested (20,23–30). Based on these algorithms, several domain databases were constructed (31–33). The knowledge of high-resolution three-dimensional structure of the protein is necessary for implementation of this concept. Some limitations regarding the analyzed proteins should also exist. Particularly, this concept is not expected to work very well when the contact area between domains is large and their interactions are strong (such as in elastase) or when domains wrap “arms” around each other (as in papain) (34).
A domain is part of a protein molecule that behaves in a quasi-independent manner with respect to the action of different factors inducing structural transitions in protein. Thus, domains can exhibit thermal unfolding in the narrow interval of temperatures independent of the rest of the protein (6,35–38). Domains are often considered as cooperative units in protein folding (39,40). This concept is extensively explored in experimental protein biophysics in relation to protein conformational transitions studied by optical methods and scanning calorimetry. If domains are independent and different then the number of transition points may indicate the number of domains. Moreover, isolated protein fragments that incorporate these domains may exhibit the same transitions (36,41,42). This concept can also be applied to proteins for which the three-dimensional structure is not known—for instance, to fibrinogen (41)—but it fails when the domain-domain interactions are strong (3,43). Moreover, since different factors may influence domain-domain interactions, one may reveal a different number of domains depending on experimental conditions (44).
A domain is a relatively compact part of a protein that is characterized by its own pattern of intramolecular collective dynamics, which can be distinguished from those of other domains (22–25). It can be seen that this concept provides the most physically justified definition of domain, which allows employment of objective computational procedures for identification of domains. Several attempts to develop such procedures were made. The best known are normal-mode calculations with simplified potentials (24,25,45) and the analysis of the shape of slowest Gaussian network model (GNM) normal mode (30).
These three concepts capture essential features of domains as the structural blocks of proteins, but they offer different procedures for domain identification. One essential feature that cannot always be treated properly must be noted. The bonds inside the domains are on average stronger than the bonds between the domains. The strength of the latter bonds can be influenced by a number of factors. These bonds can appear or disappear and the domains merge or come apart depending on the medium conditions, such as temperature and pressure, pH, and ion concentration. They may change upon incorporation of protein into a larger unit or integration into the biomembrane. In the fluctuating environment, only the bonds with energy larger than several kBT can be considered “strong”. Changes of temperature and other environmental factors can destabilize large structural blocks and cause their breakage into several smaller parts or, alternatively, can stabilize their connections and fuse them to larger units. In reality, the protein can possess only a single dynamic domain at cryogenic temperatures, two or three at higher temperatures closer to physiological temperature, and no distinct domains at all above the denaturation point. The question arises, which number of domains is intrinsic for the given protein in given conditions? It is logical to assume that the domains, which determine the functioning of the protein, should be stable in a wide range of external factors that determine “native” conditions. For example, the domains of many ligand-binding proteins should perform hinge-bending motions to facilitate capture and release of the ligand. If these domains are disrupted or, alternatively, merged into a rigid unit, the protein loses its function. Thus, domain composition cannot be considered as strictly defined and may depend upon many conditions, so the factors of domain stability and domain-domain interactions have to be taken into account.
The general solution of the problem of domain recognition will become possible within the concept of dynamic domains if ways are found to analyze properly the strengths of intradomain and interdomain interactions. Domains can be treated as independent units if interdomain interactions are weaker than interactions inside the domains. In this case, domains will maintain their integrity and move more or less like independent units. The degree of this independence can be described as correlation of domain motions. If domains are completely independent, the correlation of their motion should be essentially zero. In contrast, if domains are dependent on each other they will exhibit significant correlation of motion. This idea is exploited in different ways in several methods of domain identification (24,25,30,45). An attractive possibility is to relate the correlations of domain motions to the energies of intra- and interdomain interactions in a quantitative manner. Finding simple algorithms based on this concept, which allow us to scan protein databases and obtain objective domain identification for every protein, is the first goal of this research.
The other goal is to formalize and incorporate into an analysis the concept of domain stability. As stated above, the character of motions in the protein depends strongly on many environmental factors, such as temperature, pH, salt concentration, etc. Each domain remains a stable and independently moving unit only in a certain range of conditions. The estimated width of this range can be used to evaluate the stability of a particular domain and to determine if it is “native” for the protein in physiological conditions.
Based on these concepts, we make an attempt to develop a practical criterion that will allow us to determine the most plausible number of domains as the elements of structure stable under extensive variation of environmental conditions. A supplementary quantitative measure should estimate the degree of domain independence. In this work, we develop these criteria using the coarse-grained residue-level description of the proteins.
We used the Gaussian network model (46,47) and the hierarchical clustering of correlation patterns (HCCP) method (48) to identify the domains in a large set of Protein Data Bank (PDB) structures and calculate the correlations of their motion. Two sets of protein structures were used. The first set contains 522 proteins with manually assigned domains. The second set contains 2022 proteins, which represent all major protein folds, with no domain assignment data available (see Supplementary Material for the list of proteins). We used the residue-level knowledge-based DFIRE potentials (statistical potentials based on a distance-scaled finite ideal-gas reference energy) (49,50) to compute the energies of interdomain interactions and the interactions inside the domains for each structure, and compared these energies with motion correlations revealed by HCCP. It is shown that the mean correlations of residue motion inside the domains can serve as a reliable quantitative measure of domain independence. The domains cannot be considered independent if this quantity is below a certain well-defined critical value. We developed the procedure, which allows us to determine the most plausible number of domains in the proteins using HCCP and to estimate the reliability of domain assignment. This procedure is based on the concept of the stability gap, which is described in detail in Theory and Methods.
Finally, after collecting the results on domain identification and interaction and stability for a significant number of proteins we made an attempt to provide statistical analysis of their properties. We found that the maximum size of the domain is limited by the strength of the intradomain interactions. It was revealed that the domains of the same protein are usually of similar size, which increases their stability. Finally the statistics of interdomain linkages and their role on domain stability are analyzed.
THEORY AND METHODS
The Gaussian network model
One of the most popular methods of protein dynamics studies is the normal-mode analysis (NMA) (24,51). This method makes possible an investigation of the whole spectrum of motions under the assumption of small harmonic deviations from the local energy minimum. Although limited by this assumption, NMA nevertheless provides important information about slow motions, which are not currently accessible by other computational techniques like molecular dynamics simulations. However, conventional NMA is extremely intensive computationally because of the enormous number of degrees of freedom in the atomistic model of the protein. This number may not be needed, since it has been shown (52) that the normal modes of the proteins are relatively insensitive to the small-scale details of the modeled protein structure and used empirical force fields. Thus, all-atom NMA appears to be too slow, expensive, and excessively detailed for those applications, where fine atomic-scale details are not required. That is why several simplified protein models were suggested for NMA (24,29). Recently the greatly simplified Gaussian network model (46,47,53–55) became a popular method of choice in determining the character of large-scale motions in the folded proteins. A detailed description of GNM can be found elsewhere (46,47). Here we present only the aspects essential for further analysis.
The GNM can be viewed as an extremely simplified version of NMA, where realistic potentials of the atom-atom interactions are substituted by residue-level harmonic potentials (47). The GNM describes the protein as a network of identical harmonic springs that connect the Cα atoms of the residues located in close spatial proximity (within cut-off distance rc) regardless of their positions in the sequence. Equilibrium lengths of the springs are assumed to be equal to the distances between Cα atoms in the x-ray structure, and deviations from these distances are considered to be purely harmonic. Normal modes of such a network of elastic interacting particles can be computed easily. It has been shown that GNM describes harmonic motions of folded proteins surprisingly well and produces results that are often indistinguishable from those of full-scale NMA (47,52).
Using the computed normal modes, the cross-correlations between the motions of any residue i with the other j, (cij), can be easily calculated in the GNM. This procedure is described in detail in original GNM articles (46,47) and in our previous work (48). Here cij is a square matrix of size N, where N is the number of residues in the protein. This matrix is also used for domain identification in our HCCP method.
The hierarchical clustering of correlation patterns
Existing methods of domain identification can be classified into two major classes, those that compare two different conformations of the same proteins (21,22), and those that analyze a single structure by various techniques (20,23–30). The methods of the latter group are the most general and are applicable to any protein with known structure. However, these methods can produce different domain assignments for different conformations of the same protein, which means that domain assignment cannot be considered reliable. To our knowledge, no special attention has been paid to this fact, and no efforts have been made to improve the reliability of domain assignment by testing domain identification methods on different conformations of the same protein. Therefore, the HCCP method was designed as a technique that could allow reliable identification of domains regardless of their spatial position and orientation in the complex proteins (48). It has been shown that HCCP produces essentially identical domain assignments for different native conformations of the same multidomain protein. HCCP makes it possible to obtain a quantitative description of correlations of motions inside the domains and cross-correlation of motions of different domains, a feature that makes this method especially attractive for the study of domain stability and interdependence. Detailed description of the original HCCP method can be found in our previous article (48). Here we give a brief description of HCCP and discuss important improvements introduced to the original method.
HCCP utilizes the correlation matrix cij, obtained from GNM calculations or from other sources (full-scale NMA, molecular dynamics, essential dynamics analysis, etc.). This cij contains all information about the correlation of motions that can be extracted from the normal-mode vibrations of individual residues. However, it has one serious limitation. The cij matrix contains only pairwise correlations. Thus, only the motions of two selected residues can be compared to each other, regardless of the motion of the rest of the protein. Therefore, even small changes in protein structure can lead to changes in the GNM eigenvectors, which results in a different cij matrix. The overall structure of the matrix remains essentially the same, but individual values can change significantly. As a result, according to this changed value of the pairwise correlation, the same residue can be assigned to different domains. In other words, domain assignment based on the cij matrix is sensitive to small variations in the input data.
To eliminate this problem, instead of pairwise correlations we considered the correlation patterns, the essence of which is that a single kth column (or row) of the cij matrix contains correlations of the given residue k with all other residues in the system (including self-correlation, which is always 1). We will call such a column vector the correlation pattern of the residue k. The new matrix, the correlation matrix of correlation patterns pij, can be defined as:
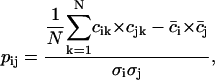 |
where 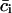 is the mean of the ith column of the matrix c, and
is the mean of the ith column of the matrix c, and 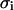 is the root mean square deviation of the ith column of the matrix c. The pij matrix is of dimension
is the root mean square deviation of the ith column of the matrix c. The pij matrix is of dimension 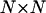 and its elements show to what extent the correlation patterns of elements i and j are similar in terms of linear correlation. The matrix pij provides a much more robust way of comparing the motions of residues than does the conventional correlation matrix cij. Comparing the correlation patterns, one compares the whole set of correlations of two given residues with the rest of the protein, not only the pairwise correlations between them. Small variations in protein structure may change only a few pairwise correlations without changing the correlations between whole columns of the cij matrix significantly. Therefore, the results of subsequent domain assignment will not be sensitive to small changes in protein structure or in the correlation matrix itself.
and its elements show to what extent the correlation patterns of elements i and j are similar in terms of linear correlation. The matrix pij provides a much more robust way of comparing the motions of residues than does the conventional correlation matrix cij. Comparing the correlation patterns, one compares the whole set of correlations of two given residues with the rest of the protein, not only the pairwise correlations between them. Small variations in protein structure may change only a few pairwise correlations without changing the correlations between whole columns of the cij matrix significantly. Therefore, the results of subsequent domain assignment will not be sensitive to small changes in protein structure or in the correlation matrix itself.
At the next step, the residues with similar correlation patterns can be combined into larger clusters that share the same character of motion. Several such clusters can be further combined as having weaker motion similarities and so on. This idea is utilized in the hierarchical clustering procedure we use to identify the domains. For this purpose, we developed the modified agglomerative clustering scheme with average linkage. In this scheme, the most similar clusters are merged (agglomerated) at each step to produce larger clusters. Pairwise similarity criteria are applied to all intercluster pairs and then averaged to calculate the similarity between the clusters. The details of the clustering algorithm are as follows:
Each amino acid residue of the protein is assigned to be the simplest cluster of size 1.
Minimal vmin and maximal vmax elements of pij are found. The interval (vmin/vmax) is divided into M bins vmax > v1 > v2 > … > vM−1 > vmin (M = 1000 in this study). The index of the current bin is set to k = 1.
The pair of residues whose correlation is pij > vk is found. If no such pairs exist, then the index of the current bin k is increased by 1 and step 3 is repeated.
- Residues from the matching pair of residues are merged into a single cluster. The matrix pij is recalculated by the following rule:
where mi and mj are the numbers of elements in clusters i and j; Mi and Mj are the vectors of sizes mi and mj, respectively, which contain the indexes of the residues in these clusters. In other words, the average correlation of all intercluster pairs is calculated. (In this study, we will use only p values as a measure of correlation between two residues or clusters of residues. Thus, for the sake of simplicity we will use the term “correlation of two clusters” instead of “correlation of the correlation patterns of two clusters” henceforth.)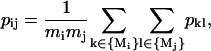
(1)
Step 3 is continued until all residues are merged and the whole protein becomes a single cluster.
Because the values of the correlation pattern matrix p are used in the clustering procedure, we call this procedure hierarchical clustering of correlations patterns.
The HCCP algorithm used in this study contains several improvements on the original one (48):
A more accurate diagonalization algorithm is used for the eigenvector search.
It was implied that if several pairs meet the criteria at step 3 of the algorithm, the pair with the largest values of pij is merged first (the pair that is first in the sequence was used in the previous version).
The intercalating segments elimination procedure (ISE), which is described below, was introduced.
Intercalating segments elimination
In the course of this work, when the large number of proteins was analyzed by HCCP, the following problem was detected. If one of the domains in a particular protein contains loops or other segments that protrude to the interdomain interface, these loops are sometimes assigned to another domain. We call such incorrectly assigned regions “intercalating segments”. The appearance of intercalating segments is not surprising if the GNM is used to produce the correlation matrices. The GNM is not based on information on protein sequence; the residues are considered to be connected if they are sufficiently close sterically to each other. As a result, the residues in the protruding loop appear to be connected with both domains by an approximately equal number of harmonic springs. This leads to approximately equal correlations with both clusters and ambiguous assignment. In our view, this problem is specific to the GNM and it will not exist if correlation matrices of different origin (molecular dynamics simulation or all-atom NMA) are used. Although the number of proteins for which this problem is essential is rather small (a few dozen out of >2500 studied proteins), some corrective procedure for avoiding it should be applied on the level of the GNM correlation matrixes. We call this procedure intercalating segments elimination.
Let us give a strict definition of the intercalating segment first. The clusters found by the HCCP algorithm on any hierarchical level can be coded by the vector 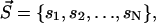 where N is the number of residues and si is the index of the cluster, which includes residue i. For example, the clusters of the first hierarchical level are coded by
where N is the number of residues and si is the index of the cluster, which includes residue i. For example, the clusters of the first hierarchical level are coded by 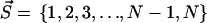 and two clusters of the last hierarchical level can be coded by
and two clusters of the last hierarchical level can be coded by 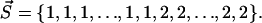 The cluster with index i consists of mi segments, which are continuous in sequence (
The cluster with index i consists of mi segments, which are continuous in sequence (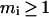 ). The segment is called an intercalating segment if
). The segment is called an intercalating segment if
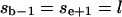 (the given segment is surrounded in sequence by two segments of the other cluster j);
(the given segment is surrounded in sequence by two segments of the other cluster j);mi > 1 (the given segment is not the only segment in the cluster i);
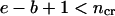 (the given segment is smaller than some critical size).
(the given segment is smaller than some critical size).
Here, b and e are the first and last residues in the segment and ncr is a critical number of residues in the segment. If the segment is larger than this number, it is excluded from consideration. This allows us to distinguish between small ambiguously assigned segments and whole domains surrounded by other domains in sequence. In this work, we used 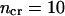 ; however, the procedure is almost insensitive to this value in the range from 5 to 50 (data not shown). We will call cluster l the enclosing cluster for the intercalating segment. For example, the coding vector
; however, the procedure is almost insensitive to this value in the range from 5 to 50 (data not shown). We will call cluster l the enclosing cluster for the intercalating segment. For example, the coding vector 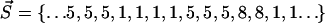 contains the intercalating segment in cluster 1. The enclosing cluster is cluster 5.
contains the intercalating segment in cluster 1. The enclosing cluster is cluster 5.
Intercalating segments can appear and disappear in the course of hierarchical clustering, but only some of them should be treated as incorrectly assigned. We propose the following natural criterion: an intercalating cluster is assigned incorrectly if its motion is correlated more closely with the motion of the enclosing cluster than with the motion of its own cluster. To formalize this criterion, we introduce three vectors: 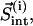 which contains all residues of the intercalating segment from cluster i;
which contains all residues of the intercalating segment from cluster i; 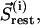 which contains all the remaining residues from cluster I; and
which contains all the remaining residues from cluster I; and 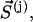 which contains all the residues from the enclosing cluster j. Correlations are computed by analogy with Eq. 1:
which contains all the residues from the enclosing cluster j. Correlations are computed by analogy with Eq. 1:
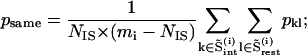 |
(2) |
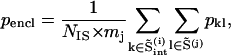 |
(3) |
where psame is the correlation of an intercalating segment with its own cluster and pencl is its correlation with the enclosing cluster; 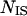 is the number of residues in the intercalating segment;
is the number of residues in the intercalating segment; 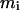 is the number of residues in cluster i that contain an intercalating segment; mj is the number of residues in the enclosing cluster; and p is the matrix of correlation patterns on the hierarchical level in question. The intercalating cluster is assigned incorrectly if
is the number of residues in cluster i that contain an intercalating segment; mj is the number of residues in the enclosing cluster; and p is the matrix of correlation patterns on the hierarchical level in question. The intercalating cluster is assigned incorrectly if 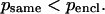
Implementation of ISE into the HCCP algorithm is straightforward. Simply, the ISE procedure is applied at every step of hierarchical clustering. If an incorrectly assigned intercalating segment is found, then it is cut out from its cluster and merged with the enclosing cluster. After that, the p matrix is updated to accommodate the changes. This procedure is applied until all incorrectly assigned intercalating segments are reassigned. The time taken by the ISE procedure is only a small percentage of the total computation time.
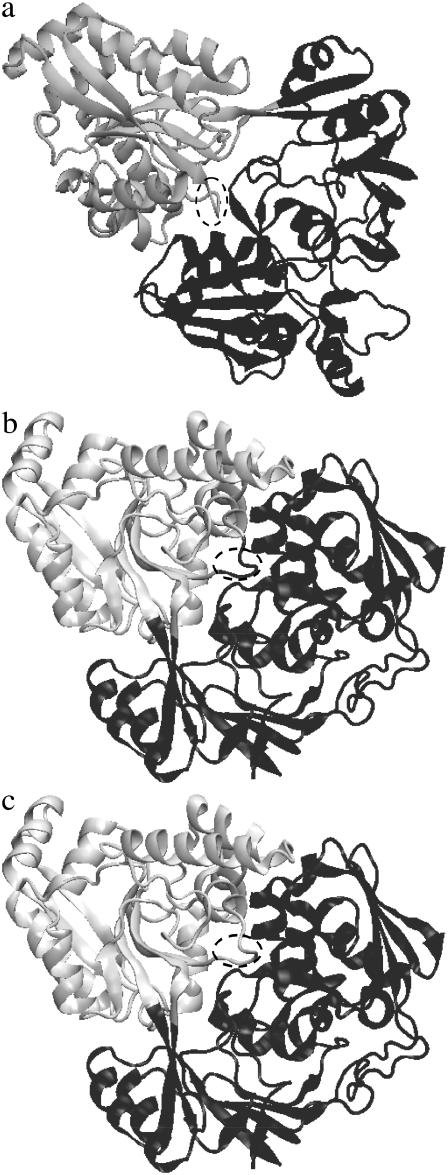
The advantages of ISE are illustrated by the domain identification of the dipeptide-binding protein (dipeptide permease) from Escherichia coli. This classical hinge-bending protein is crystallized in both closed (PDB code 1DPP) and open (1DPE) conformations. In the open conformation, two well-defined domains are situated quite far from each other. As a result, HCCP identifies them correctly without any artifacts (Fig. 1 a). In contrast, in the closed conformation, HCCP produces an incorrectly assigned loop. This loop includes residues 408–411 and protrudes into the cleft between domains (Fig. 1 b). It is assigned to the first domain (black), whereas in fact it belongs to the second domain (gray) that is assigned in the open conformation. As seen in Fig. 1 c, implementation of the ISE procedure resolves this problem.
FIGURE 1.
Domains identified by the HCCP method in the dipeptide-binding protein from E. coli (PDB codes 1DPP for the closed form and 1DPE for the open form). The loop containing residues 408–411 is marked by the dashed oval. (a) Open form. (b) Closed form without ISE (the loop belongs to the “dark” domain). (c) Closed form with ISE (the loop belongs to the “light” domain).
It is necessary to emphasize the difference between the ISE procedure and the “refinement” or “post-processing” schemes used in other domain identification algorithms (25–27,30). ISE is based on the same principles as the HCCP algorithm itself: it compares the correlations between the “suspicious” segment and two clusters, which can contain it. No additional principles are implemented. Thus it is different from common refinement schemes that utilize various empirical criteria that are different from the domain identification criteria and are usually hard to justify.
Comparison of HCCP with other techniques
Dynamic data (correlation matrices) are used in the HCCP method to identify the domains, which is why it is not practical to compare it with techniques that are based on static structural information (17,19,20,26) or comparison of the primary sequences (21). We will focus on the techniques that are the most similar to our approach.
Several techniques that utilize GNM normal modes or the graph theory approach were developed recently for domain identification. The method of automatic domain decomposition developed by Kundu and co-workers (30) is based on the analysis of a single eigenvector that corresponds to the lowest nonzero eigenvalue of the GNM. The shape of this eigenvector allows us to detect the structural regions that move in opposite directions along the slowest normal mode and assign them to different clusters. These clusters are postprocessed (“filtered”) to find the domains. Being very simple and intuitive, Kundu's method has several serious limitations.
It is limited to the GNM or other methods of normal-mode calculations.
Only one normal mode is considered, which leads to considerable loss of information.
The analysis is qualitative: only direction, and not the amplitude of motion, is used for domain detection; thus, the degree of internal correlation of motions in the cluster cannot be estimated.
No hierarchical features, such as rigid subdomains, can be found.
The filters applied to initial clusters contain many adjustable parameters that are hard to justify.
The other very similar method of Sista at al. (56) utilizes the approach based on graph theory. It is based on the construction of a Laplacian matrix, which can be built using Cα atoms (in this case, it is identical to the GNM Kirchhoff matrix) or the side chains of the protein. This matrix is then diagonalized and the first lowest eigenvector with nonzero eigenvalue is used for domain identification. Although adjustable cut-off is used for matrix construction and the shape of the eigenvector is analyzed using a somewhat different procedure, this method possesses essentially the same limitations as the previous approach. Since these methods rely on the shape of the single eigenvector they are likely to be very sensitive to small variations in the initial connectivity matrix and thus can show large discrepancies in domain boundaries for different conformations.
The approach most similar to ours is that used by Keskin et al. to study the functional motions of tubulin (57). In this work, the cluster analysis of correlation matrix cij was implemented to identify the regions that share the same motion pattern. This technique is almost identical (except for the details of the clustering procedure) to the hierarchical clustering of correlations method used in our previous work (48) as a reference point for the validation of HCCP. The main problem of domain assignment based on the cij matrix is the sensitivity to those variations of the structure that leave the domains intact but change their position and orientation (48). In addition, the changes of the individual pairwise correlations can change the position of the domain boundary, as discussed above. Introduction of pij matrices in HCCP allows us to overcome these difficulties.
It is probably due to these limitations that none of the mentioned methods was tested on different native conformations of the same protein (and to our knowledge, the same is true for all other proposed techniques). That is why HCCP is currently the only method of dynamic domain identification, which was designed and tested to allow reliable identification of intact domains regardless of their spatial position and orientation.
The major advantages of HCCP are as follows.
It is based on the pair-correlation matrices of any origin.
Introduction of the correlations of correlation patterns allows one to eliminate the sensitivity to small variations in the initial correlation matrix.
All normal modes are accounted for if the GNM is used to form the pair-correlation matrices.
The analysis is quantitative: not only the sign, but also the value of correlation, is used for clustering.
Hierarchical clustering allows us to detect substructures of different levels and estimate their rigidity in terms of internal correlations.
No postprocessing steps and adjustable parameters are needed.
Domain stability criterion and determination of the most plausible number of domains
In the course of HCCP clustering, the system goes through stages with different numbers of clusters, from N to 1. At what stage can the clusters be identified as domains? In our previous work (48), we considered well-defined two-domain proteins only, and this problem did not appear. In this work, we developed and applied an automatic criterion that determines the most plausible number of domains in the system. In the course of clustering, the value of correlation gradually reduces from 1 to −1 in a series of small discrete intervals (bins). Pairs of clusters with correlation smaller than this current value of correlation are combined until such pairs are exhausted. Thus, each bin corresponds to a particular number of clusters in the system, which is stable on the current level of correlation (none of the existing clusters can be combined before moving to the next bin). Let us assume, for example, that the state with M clusters appears on bin number K1 by fusion of smaller clusters. Some of these M clusters can merge only if the correlation threshold becomes smaller than their cross-correlation. This happens on bin number K2 (K2 > K1). In the region between K1 and K2, the number of clusters in the system remains stable. We call the length of this region the stability gap, defined as 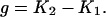
The stability gap can be interpreted from the physical point of view. The real protein structure is always perturbed by thermal fluctuations and other external factors. As a result, all noncovalent bonds in the protein associate and dissociate stochastically. The probability of finding a particular bond in its associated state can be estimated roughly using the Kramers reaction rate theory:
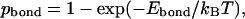 |
where Ebond is the energy of the bond (the difference between the energies in the associated and dissociated states), kB is the Boltzmann constant, and T is the absolute temperature. This probability can change from ∼1 for very strong bonds ( 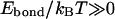 ) to nearly zero for very weak ones (
) to nearly zero for very weak ones ( 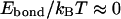 ). Some critical value of pcr can be adopted to distinguish between the “bonded” (
). Some critical value of pcr can be adopted to distinguish between the “bonded” ( 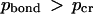 ) and “dissociated” (
) and “dissociated” ( 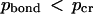 ) states of each bond for each given temperature (pbond = 0.5 is the most logical choice). Once such a critical value is assigned, one can say that the bond breaks (or forms) at a certain critical temperature determined from
) states of each bond for each given temperature (pbond = 0.5 is the most logical choice). Once such a critical value is assigned, one can say that the bond breaks (or forms) at a certain critical temperature determined from 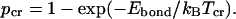 These considerations can be applied to define the domains. At “physiological” temperature, external factors cannot break relatively strong bonds between the residues inside the domains, but are likely to destroy weaker bonds between them. As a result, domains will move as a whole in a diffusional manner, being relatively independent from each other.
These considerations can be applied to define the domains. At “physiological” temperature, external factors cannot break relatively strong bonds between the residues inside the domains, but are likely to destroy weaker bonds between them. As a result, domains will move as a whole in a diffusional manner, being relatively independent from each other.
Let us consider the events occurring in the protein on slow lowering of the temperature. At some critical temperature the thermal fluctuations become too weak to break the interdomain bonds, and the domains that have the strongest interdomain interactions “freeze” and begin to move as a single entity. As a result, the effective number of domains in the protein becomes smaller. One can also heat the system gradually to increase the level of fluctuations and observe the opposite picture: larger domains would break into smaller parts (the domain would “unfreeze”). It is evident that the critical temperatures where the number of domains in the protein will change are abstract points, where the probabilities of certain interdomain bonds become equal to pcr. Critical temperatures subdivide the gradual change of dynamic properties of the protein into several discrete regimes (characterized by the number of dynamic domains) according to objective criteria. There is no abrupt change of the protein dynamics pattern in these points.
In the course of clustering in HCCP, smaller clusters are combined into larger aggregates as the value of correlation decreases. Thus, lowering the temperature is in some sense analogous to lowering the correlation threshold in HCCP. The interval of temperatures at which the effective number of domains does not change is analogous to the range of domain stability (the stability gap). However, this analogy is not absolute. In the GNM, the temperature is a free parameter: it only influences the amplitude of harmonic motions along the eigenvectors, whereas the correlation patterns are independent from temperature. As a result, the mapping between temperature and correlations is somewhat arbitrary. However, this does not change the qualitative picture: the larger the stability gap, the larger the changes of temperature that can be tolerated by the protein without changing the effective number of independently moving domains. Other factors, like pH, salt concentration, applied pressure, etc., can be considered to produce similar effects. Thus, the stability gap indicates the extent to which the corresponding effective number of clusters is resistant to environmental changes.
In this respect, it is important to distinguish between environmental changes, which only change the effective number of dynamic domains, leaving the whole protein in its folded state, and those that lead to unfolding. We assume here that the clustering procedure models only the range of conditions in which the protein remains folded. It is necessary to emphasize that the changes in number of dynamic domains (“domain unfreezing”) are different from domain melting observed experimentally. In these experiments, independent melting of individual domains of the multidomain protein was observed at certain temperatures (36,39,41,42). Melting of domains has the character of phase transition and leads to partial unfolding of the protein, whereas the events of domain “unfreezing” presume that the domains remain in their folded state.
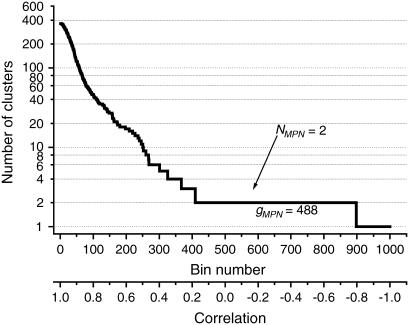
We define the most plausible number of domains (NMPN) as the number of clusters observed in the region of the largest stability gap. The NMPN is the intrinsic characteristics of the protein, which shows the number of domains that can characterize it under normal conditions. We can select a different number of domains, but they would be less stable against temperature perturbations and other changing conditions, and thus less likely to be observed. The concept of MPN is illustrated in Fig. 2. The number of clusters decreases with the decrease of correlation strength. This function has a number of horizontal regions (“steps”) that correspond to a particular number of clusters in the system that are stable in a particular range of correlations. This range (the length of the “step”) is, by definition, a stability gap for the corresponding number of clusters.
FIGURE 2.
Number of clusters as a function of the bin number for the UDP-n-acetylglucosamine 2-epimerase from Thermus thermophilus (PDB code 1V4V). The arrow indicates a horizontal region that corresponds to the most plausible number of domains.
DFIRE potentials
To calculate the energy of domain interaction and the energy of domains itself we used residue-level knowledge-based DFIRE potentials that proved to be quite accurate in determining the native states of various proteins among decoys (55,56). Their accuracy is comparable to those of empirical all-atom potentials used in molecular dynamics simulations. DFIRE potentials describe the pair interaction energy between two residues at a given distance. Residues are modeled as point objects, “force centroids”. There are several modifications of DFIRE potentials that use different force centroids. We used the most accurate DFIRE-SCM potential, with the force centroid at the geometrical center of the heavy side-chain atoms of the residue. In the case of glycine, which lacks the side chain, the Cα atom is used.
Calculation details
All PDB structures were preprocessed to extract the single chains. Manual domain assignment data from the web site http://www.bmm.icnet.uk/∼domains/ were converted to machine-readable form. Prepared structures were analyzed by our HCCP program (available at http://www.geocities.com/yesint3/hccp.html). The cut-off of 7 Å was adopted. The force constant in GNM is assumed to be 1 (this value only scales eigenvectors and does not influence the normalized correlation matrices). All eigenvectors with nonzero eigenvalues were used for computing the correlation matrices. The following steps were performed after the hierarchical clustering procedure.
The NMPN and gMPN were determined as described above.
- The mean intradomain correlation was computed as
where Nk is the number of residues in the kth domain and Dk is a vector that contains the indexes of the residues from the kth domain.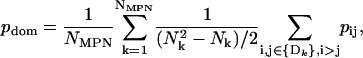
(4) - The interdomain correlation was computed as
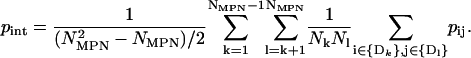
(5) - Mean intradomain energy per residue was calculated as
where Nk is the number of residues in the kth domain; EDFIRE is the DFIRE-SCM energy between the residues of types si and sj, situated at a distance rij between their force centroids.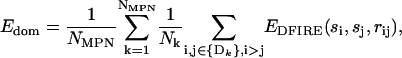
(6) - Mean interdomain energy per residue was calculated as
where N is the total number of residues in the protein.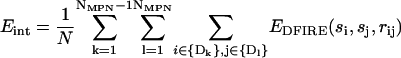
(7) The mismatch between the manual domain assignment and HCCP assignment was calculated for the first set of the test proteins. The mismatch was computed as a number of residues that are assigned to different domains by these two methods expressed as a percent of the total protein size.
All these energies were computed per residue to eliminate the effect of the variable size of the protein.
It is important to emphasize that the obtained results are not sensitive to the protein motions as a whole (these motions are described by the eigenvectors with zero eigenvalues, which are excluded from consideration). Consequently, the sum of all pair correlations in the protein is always zero. It is easy to see that the sum of pdom and pint is equal to the sum of all pair correlations if all domains have the same size. In this case, pdom = −pint. It is possible to show that the deviations from this equality caused by different domain sizes remain quite small in most cases. Thus, one can expect that 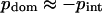 for almost all proteins except those with rare unusual structures.
for almost all proteins except those with rare unusual structures.
All calculations were performed using the modified HCCP program written in FORTRAN 95. Total computation time for ∼2500 proteins is ∼6.5 h on a 1.5-GHz PC.
Test proteins
We used two sets of protein structures. The first set, collected from the protein domain server (http://www.bmm.icnet.uk/∼domains/), was used for comparing the HCCP assignments with the manual ones. Manual assignments in this collection were either made previously in original publications, or deduced by the authors of this database based on sequence homology with known proteins. The authors of the corresponding original articles most frequently used a visual inspection of the structure (the references for each particular protein are available at the protein domain server). The criteria used for visual domain identifications were often not specified. Only the single-chain structures that were marked as two-domain proteins were selected. The following database entries were excluded from consideration: 1), invalid entries (missed numbers, domains that contain only one residue, etc.); 2), structures obtained by NMR, because the GNM has not proved to work well with NMR structures; 3), entries that were replaced by other structures in later releases of the PDB. This was done because manual assignments of older data are inconsistent with new entries in the PDB; 4), the number of residues is different, residue indexes do not match, etc. For every protein crystallized as a multimer, only one of identical subunits was used. Those proteins for which only Cα atoms or only backbone atoms are resolved were excluded from energy calculations but still used for domain assignment. The total number of selected protein structures in this set is 522. There is a significant number of highly homologous structures among them.
All proteins from this set are presumed to have two domains. To make the comparison with the manual-assignment data possible, we made our program consider all proteins on the double-domain level, even if the most plausible number of domains NMPN was different.
The second set of test proteins was used to perform systematic HCCP calculations on the representative nonhomologous structures from all major protein families. We used a subset of all PDB structures that share <20% homology and are determined by x-ray diffraction with resolution >2 Å obtained from the protein-sequence-culling server http://dunbrack.fccc.edu/PISCES.php (58). All entries contain a single chain (this chain can be a part of larger complex). No information about domain assignment is available for these proteins. This set of proteins is the most representative collection of all major protein folds described in the available databases; it contains no homologous proteins. Thus, this database is not biased by any manual selection procedure and is able to reveal fundamental relations between the correlations, energies, and number of domains in the studied proteins. The total number of proteins in this set is 2022.
The list of PDB codes of the proteins from both test sets is provided as Supplementary Material. The databases and the HCCP program itself are available upon e-mail request addressed to the authors, or from the web site http://www.geocities.com/yesint3/hccp.html.
RESULTS
Test set 1 (522 manually assigned two-domain proteins)
Correlation and mismatch between HCCP and manual assignment
HCCP was developed as an objective automatic method of domain identification based on the concept of dynamic domains (48). In contrast, the commonly used manual domain assignment is based on visual inspection of the static structural features of the protein, topology, similarity to known homologous domain structures, and stability or activity of isolated domains as fragments. Among these methods, visual inspection of the topology of a polypeptide chain is the most popular. Because of this difference in concepts we did not expect exact one-to-one correspondence of the domains found by these two methods. Meanwhile, analysis of the obtained data shows that the results on HCCP domain assignment are quite close to those of manual assignment. The mean mismatch of all 522 proteins of the first test set is 16.9%. This correspondence is comparable with the performance of other automatic domain identification techniques (26). This signifies that the number of HCCP assignments that coincide with manual assignments is roughly the same in comparison with other methods. The observed mismatch is quite significant, but it must be emphasized that the domain identification technique, which may exhibit a smaller mismatch with manual assignment, is not necessarily better. A very small mismatch would show that the method “mimics” the peculiarities of human perception during visual assignment and is likely to reproduce human error as well. In addition, the two approaches are really very different conceptually, and clarifying the origin of these differences may permit a deeper understanding of protein properties.
Therefore, the cases for which the results of domain analysis by HCCP and manual assignment are different were most carefully analyzed. Although all proteins from the first test set are manually assigned as having two domains, the HCCP procedure identified 116 out of 522 proteins as being single-domain proteins. We attempted to evaluate the properties of those proteins at a two-domain level and got the result that intradomain correlation for all these single-domain proteins is <0.6. This is in contrast to the data obtained for many double-domain proteins that have very high intradomain correlations of 0.8 or more. In other words, if the protein that is identified by HCCP as a single-domain structure is artificially forced to have two domains, these domains appear to be unresolved. This shows that determination of the most plausible number of domains in HCCP works quite well, producing self-consistent results.
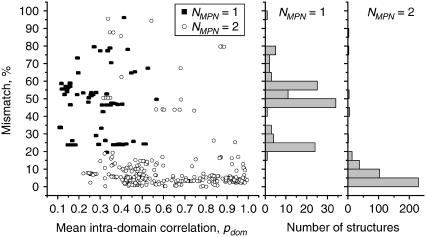
Further analysis revealed an interesting relationship between mismatch within the first test protein set and the mean intradomain correlation pdom. Fig. 3 shows this mismatch as a function of pdom. It is clearly seen that the mismatch for the majority of structures is <20%. Meanwhile, several “anomalous” structures have very large mismatches of 40% or more. The histograms linked to Fig. 3 show that double-domain proteins have an almost exponential distribution of mismatch values. The most frequently observed are very small mismatches and only a few proteins have mismatch >20%. In contrast, the proteins recognized as single-domain structures have a much broader mismatch distribution, with the most pronounced peaks near 20%, 45%, and 60%. Analysis of the proteins (both single- and double-domain) with large mismatch values shows that they can be roughly classified into two well-defined classes.
FIGURE 3.
The mismatch as a function of pdom for 522 proteins from test set 1. The distributions of the single- and double-domain structures are shown as stacked histograms.
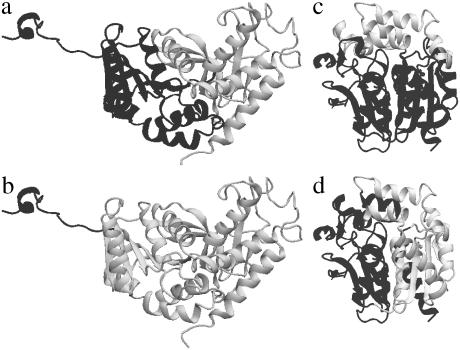
The first class contains proteins that possess long, flexible unfolded loops or a large content of segments that lack secondary structure. We call this class proteins with unfolded segments. These proteins are not unique and their segment flexibility is often functionally important (59,60). A representative example of this class is apolactate dehydrogenase from Mus musculus (PDB code 2LDX) (51) (Fig. 4). The reason for very large mismatch in this class of proteins is easy to understand. Manual structural assignment treats the compact part of the protein as two closely packed domains and the flexible loop as a part of the first domain (Fig. 4 a). In contrast, HCCP accounts for dynamical properties of the flexible loop. Since the motion of the loop is not correlated with the motion of the compact globule, the loop is recognized as a separate domain, whereas the globule constitutes another domain (Fig. 4 b). Proteins with unfolded segments are scattered over a wide range of correlation and mismatch values. This reflects the fact that this group is very heterogeneous.
FIGURE 4.
(a and b) Domain assignment for apolactate dehydrogenase, from Mus musculus (PDB code 2LDX): (a) manual assignment; (b) HCCP assignment. (c and d) Domain assignment for haloalcane dehalogenase from Xanthobacter autotrophicus (PDB code 2DHC): (c) manual assignment; (d) HCCP assignment.
The second class of “anomalous” proteins consists of very compact, almost “spherical” proteins that lack visually detectable features like weakly bound lobes or well-recognizable domains. A representative example of this class is haloalcane dehalogenase from Xanthobacter autotrophicus (PDB code 2DHC) (61) (Fig. 4, c and d). The most remarkable feature of the proteins in this class is a very small value of pdom, which is often <0.2. This means that in these proteins the domains are very “fuzzy” and internally highly flexible. This is a consequence of compact fusion of two domains in the protein, in which intra- and interdomain interactions are of similar strength. Due to the lack of visually detectable features that can be used for manual assignment, such assignment of structural domains for these proteins is error-prone and often absolutely different from HCCP assignment.
Thus, based on these mismatch cases, we demonstrate that our domain assignment is more productive, not only because it is strongly physically motivated, but because it offers the possibility of revealing the mechanistic relation between submolecular structure and function.
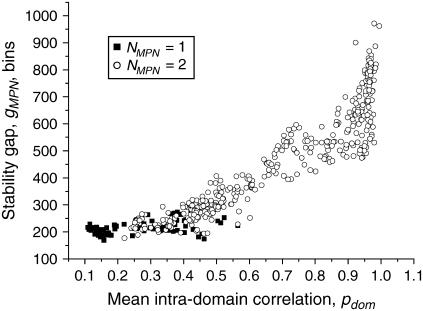
Intradomain correlation and stability gap
As stated in “Methods”, the stability gap is a certain extended range of correlations of motions for which the given set of clusters is stable. The maximal stability gap gMPN corresponds to the most plausible number of domains in the protein NMPN under normal conditions. It is obvious that the stability gap depends on internal stability of the domains and on their interaction; thus, it is important to compare the mean intradomain correlation pdom and the stability gap gMPN values (Fig. 5). We observe that there is a strong positive correlation between pdom and gMPN. This reflects the fact that “tight” domains with stronger intradomain correlations exhibit broader stability gaps. Since the stability gap can be interpreted as a range of external factors in which domains maintain their structure, it is possible to conclude that domains with large intradomain correlations maintain stability in a wider range of external conditions.
FIGURE 5.
Stability gap gMPN as a function of the mean intradomain correlation pdom for the single-domain (NMPN = 1) and double-domain (NMPN = 2) proteins from test set 1.
These data provide further justification of the approach we used for the determination of the most plausible number of domains as the stable structures existing in a broad range of external conditions.
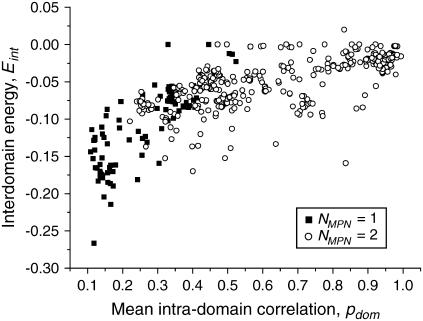
Intradomain correlation and interdomain energy
We analyzed the connection between intradomain correlations and different energy contributions to protein stability. To do so, we calculated the mean intradomain interaction energies, interdomain energies, and total energies. To account for the variation in protein size, the energies per one residue were obtained. We observed that the scatter of the mean intradomain energies and total energies is rather chaotic. These quantities do not correlate with any other computed parameter, such as inter- and intradomain correlations or interdomain energy (data not shown). This reflects the expected result that the energy of an average residue located in the compact and relatively independent dynamic domain is independent of other properties of this domain and its surroundings. In contrast, the interdomain energy shows a significant correlation with the mean intradomain correlation (Fig. 6). This statement does not sound logical, but one should bear in mind that 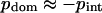 (see Methods for details). Thus, for the majority of proteins, the values of intradomain correlation are equal to the interdomain correlations with the opposite sign.
(see Methods for details). Thus, for the majority of proteins, the values of intradomain correlation are equal to the interdomain correlations with the opposite sign.
FIGURE 6.
Mean interdomain energy Eint as a function of the mean intradomain correlation pdom for single-domain (NMPN = 1) and double-domain (NMPN = 2) proteins from test set 1.
It is clear that the stronger is the intradomain correlation, the smaller is the average interdomain energy. Thus, if the domains are very compact and independent from each other, then their interaction is weak and vice versa: if the domains are “fuzzy” and interdependent, then their interaction is strong. Single-domain proteins on average have lower energies than double-domain proteins. This is explained by the fact that if we artificially divide a single-domain protein into two domains, these domains remain in fact parts of a single domain with a strong interaction between them.
Test set 2 (2022 nonhomological structures with unknown domain assignment)
Number of domains
The second test set was used to perform extended HCCP calculations on proteins from all the major protein families and reveal the features that are universal for all of them. The second test set contains 2022 nonhomologous protein chains. Using HCCP, 1080 of them were identified as having one domain, 870 as having two domains, 31 as having three domains, and 39 as having more than three domains. Two remaining proteins were identified as having two and three domains, respectively, but one of their domains is the size of one residue. Closer inspection of our data shows that these two chains, and also those chains identified as possessing more than three domains, are surprisingly very short—of typically >40 residues. Such small proteins lack real intradomain structures, and therefore the assignment to them of three or more domains represented by short-chain segments would be superficial. Therefore, we conclude that the method we used to find the most plausible number of domains is not applicable to these very short proteins (<50 residues).
Treatment of single-domain proteins
Those proteins identified by HCCP in test set 2 as single-domain structures need special attention. Single-domain proteins have zero intradomain correlation, because in this case the domain is the entire protein. The program does not detect its move as a whole (corresponding GNM eigenvectors with zero eigenvalues are excluded from consideration). Because only one domain is present, the interdomain energies are also equal to zero. This means that the useful properties computed for multidomain proteins cannot be described for single-domain proteins and comparison of single- and multi-domain proteins becomes meaningless.
To avoid this complication, we forced our program to calculate all correlations and energies for single-domain proteins at the level of two domains. The single-domain protein was artificially split into two parts that are less stable than the single “native” domain. Such treatment allows us to describe both single- and double-domain proteins using the same parameters, such as intradomain correlations and interdomain energies. This allows an effective comparison of these two sets of proteins and determination of whether the proposed method of finding the most plausible number of domains is justified.
The same procedure was used as for test set 1. In this case, it additionally allows us to compare HCCP domain assignments with the manual assignments available for this set.
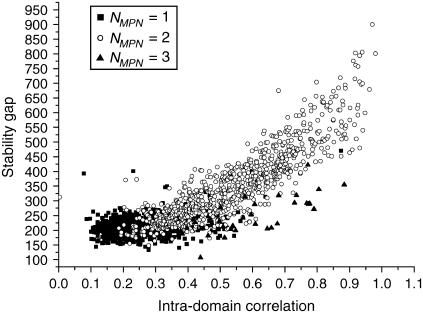
Intradomain correlation and stability gap
Fig. 7 shows the stability gap as a function of intradomain correlation for the proteins from test set 2. The proteins with one domain, which are artificially split into two parts, form a tight group with stability gaps <300 (the stability gap is measured as the number of bins; see Methods for details) and intradomain correlations scattered around 0.25–0.3. In contrast, the proteins with two and three domains are scattered along a well-defined line and exhibit very strong correlations between pdom and gMPN . The three-domain proteins have systematically lower stability gaps in comparison with the double-domain proteins with the same pdom.
FIGURE 7.
Stability gap gMPN as a function of the mean intradomain correlation pdom for the proteins from test set 2.
It is remarkable that there are no multidomain proteins observed with an intradomain correlation <0.2.
The same critical value is found in the analysis of proteins from the first test set. In contrast, a significant amount of the artificially “split” single-domain proteins have intradomain correlation <0.2. This shows that “artificial” domains in the single-domain proteins are different from “natural” domains: they are less compact and less stable. We can thus conclude that our procedure for finding the most plausible number of domains allows us to distinguish between real domains and subdomains, which are less stable and exhibit much weaker intradomain correlations.
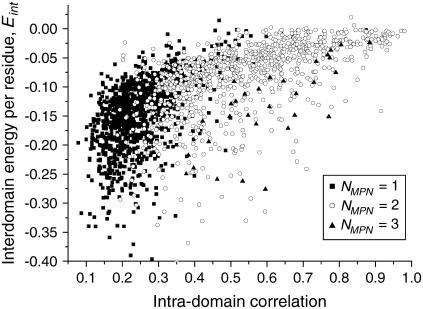
Intradomain correlation and interdomain energy
The interdomain energies as a function of intradomain correlations are shown in Fig. 8. The scatter of the interdomain energies per residue is quite large for all the values of intradomain correlations. However, there is a general trend showing that the energy of interaction between domains, Eint, is lower for smaller values of intradomain correlation, pdom. The same trend is observed for test set 1. Proteins with three domains have systematically lower Eint than double-domain proteins with the same value of pdom. This feature is easy to explain by the fact that proteins with three domains have two or three domain-domain interfaces, with more interactions possible, whereas double-domain proteins have only one interface. Single-domain proteins split into two artificial domains have, in general, lower interdomain energy than “natural” double-domain proteins. This shows that the domains produced by artificial splitting of protein structure are strongly bound, which shows that they are in fact the parts of a single domain.
FIGURE 8.
Mean interdomain energy Eint as a function of the mean intradomain correlation pdom for proteins from test set 2.
Statistics of domain sizes and number of interdomain linkages
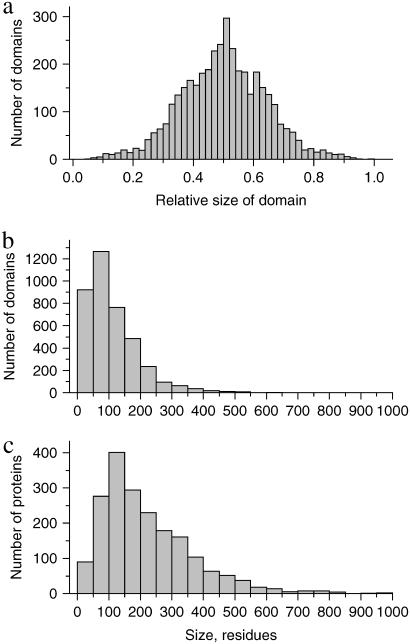
The large size of test set 2 and the fact that it contains representative proteins from all major classes makes it possible to collect the statistics of various domain properties. Since only 80 proteins of test set 2 have more than two domains, we limit our analysis to 1950 proteins that have one or two domains. Single-domain proteins were artificially split into two subdomains, as described above. For each protein, the following properties were computed: relative sizes of domains in the protein 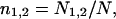 where n1,2 is the relative size of domains 1 and 2, respectively, N1,2 is the number of residues in domains 1 and 2, respectively, and N is the number of residues in the whole protein. The relative domain size is the absolute number of residues in the domain divided by N.
where n1,2 is the relative size of domains 1 and 2, respectively, N1,2 is the number of residues in domains 1 and 2, respectively, and N is the number of residues in the whole protein. The relative domain size is the absolute number of residues in the domain divided by N.
Fig. 9 shows the distribution of the relative sizes of domains. It is clearly seen that this distribution has a sharp peak at the value of 0.5. This means that in a two-domain protein the great majority of domains constitute approximately one-half of the whole protein. Very large (n1,2 > 0.8) and very small (n1,2 < 0.2) domains are extremely rare. We need to find an explanation for this intriguing fact. Let us consider an idealized protein with two domains of sizes N1 and N2. Let us assume that all pair correlations inside the domains are equal to p0 and all interdomain pair correlations are equal to p12 (p0 > 0; p12 < 0). As stated above, the sum of all pair correlations in the protein is zero, so
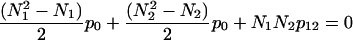 |
or
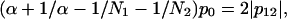 |
where 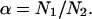
FIGURE 9.
Distributions of the relative domain sizes (a), absolute domain sizes (b), and protein sizes (c) for the single- and double-domain proteins from test set 2.
If both domains are large enough, this equality can be further simplified by neglecting the terms 1/N1,2:
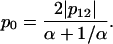 |
Let us then assume that p12 is fixed and allow variation of the ratios of domain sizes α and the intradomain correlations p0. It is easy to see that maximal value of p0 is achieved for α = 1. For any other α, the value of p0 will be smaller. The small values of p0 mean that the domains are very “fuzzy” and unstable. This leads us to an important conclusion: the domains of similar size ( 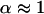 ) possess maximal stability, whereas domains of very different size (α is far from 1) are very unstable. Thus, if the evolutionary pressure selects the most stable domains, then the majority of proteins should have domains of similar size. This conclusion is in perfect agreement with the data shown in Fig. 9 a. The domains of similar size (relative size ∼0.5) are the most abundant.
) possess maximal stability, whereas domains of very different size (α is far from 1) are very unstable. Thus, if the evolutionary pressure selects the most stable domains, then the majority of proteins should have domains of similar size. This conclusion is in perfect agreement with the data shown in Fig. 9 a. The domains of similar size (relative size ∼0.5) are the most abundant.
Fig. 9 b shows the distribution of absolute domain sizes and Fig. 9 c the distribution of protein sizes. The most common protein size, which corresponds to the maxim of distribution, is 150 residues. Since the majority of domains constitute one-half of the whole protein, the maximum distribution of the absolute domain sizes corresponds to 75 residues. Domains of >400 residues are extremely rare, whereas there are a significant number of proteins larger than 400 residues, because very large proteins typically contain two domains. This shows that the size of an independent dynamic domain cannot be >400–500 residues. A possible explanation for this is the limited strength of the residue-residue interactions, which are unable to maintain their integrity in very large domains. In contrast, the number of very small domains (<50 residues) is significant. This is because a single element of secondary structure, like short α-helix or small β-hairpin, can constitute a domain.
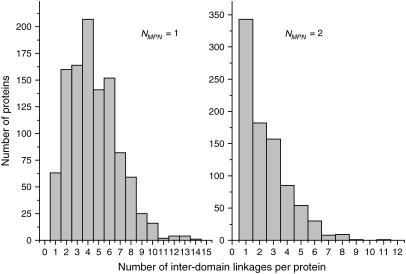
Fig. 10 shows the distribution of the number of interdomain linkages for single- and double-domain proteins from test set 2. The linkages are defined as the places where the chain crosses the boundary between two domains. If the protein exhibits a pronounced hinge-bending motion, these places are likely to behave like mechanical hinges. The domains that are combined by a large number of linkages are likely to be tightly bound, whereas those with only one or two linkages can move more or less freely around them. It is clearly seen, that the single-domain proteins, which were artificially split into two subdomains, have on average a much larger number of linkages than the double-domain proteins. The maximum of the distribution is 4 for single-domain proteins and only 1 for double-domain proteins. This means that because of the numerous interdomain linkages the motions of subdomains in the single-domain proteins are interdependent. This observation correlates perfectly with the fact that the interaction between the subdomains of single-domain proteins is much stronger than that between the domains of double-domain proteins (Fig. 8).
FIGURE 10.
Distribution of the number of hinges for the single- and double-domain proteins from test set 2.
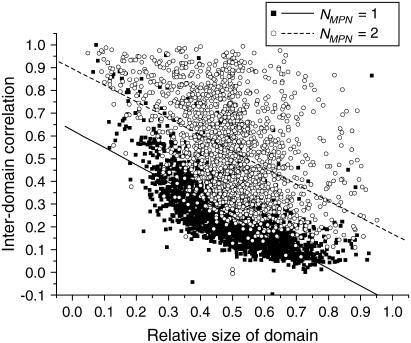
We also studied the dependence of intradomain correlation on the relative size of domain (Fig. 11). One should expect that very small domains, which contain only several residues, are quite compact and thus possess large intradomain correlation. In contrast, very large “fuzzy” domains are likely to have smaller intradomain correlation values. Such trends, visualized by the linear fits, are easily seen in Fig. 11 for both single- and double-domain proteins. The negative correlation between the intradomain correlation (pdom) and the relative size of domain (n) for the single-domain proteins is very strong (−0.73). This means that the compactness of artificial subdomains of the single-domain proteins depends strongly on their size. Large subdomains possess many strong interdomain contacts, which decreases their internal motion correlation. In contrast, the correlation between pdom and n for the double-domain proteins is weak (−0.47). This reflects the fact that the domains of double-domain proteins are relatively independent and interact with each other weakly. It is also remarkable that pdom for double domain-proteins is on average higher than pdom for single-domain-proteins, by 0.2–0.3 for all domain sizes (the linear fit for double-domain proteins goes under the corresponding line for single-domain proteins). This is a clear visual indication of the fact that the artificial subdomains of the single-domain proteins are not real dynamic domains because of their small intradomain correlations.
FIGURE 11.
Dependence of the intradomain correlation on the relative size of domain for single- and double-domain proteins from test set 2.
DISCUSSION AND SUMMARY
The problem of identifying dynamic domains is addressed in a number of studies. However, no universally accepted algorithm of domain identification exists to date. Existing techniques (22–25) usually contain a large number of parameters and postprocessing procedures (“filters”), which often lack clear physical meaning and make the internal logic of the proposed algorithms quite complex and hard to understand. Therefore, the results of domain identification in these techniques depend on the choice of empirical parameters, which are derived by comparison with some other domain assignment available for a limited set of test proteins. This can make the choice of applied parameters biased and prone to human error. Various postprocessing filters often utilize principles that are absolutely different from those used in basic domain identification techniques. They are purely empirical “tricks” that serve to correct the mistakes of the basic algorithm. Another problem of existing techniques is the reliability of results. To our knowledge, no special studies have been made to show that domain identification made by a particular automated technique remains the same if some other conformation of the same protein is used as input. To solve these problems, the HCCP algorithm was developed. It was shown (48) that HCCP is a very robust technique that produces essentially the same domain assignments for different conformations of the same protein. As an important step toward further development of this approach, in the current article we introduce the ICE procedure. This eliminates ambiguity in assignment for those residues that are close to the hinge regions or interdomain interfaces. The ISE procedure is fundamentally different from various postprocessing techniques in other methods. It uses the same physical principle as the HCCP algorithm itself to assign the problematic residues and requires only one empirical parameter, which is easy to interpret.
As discussed in the introduction, dynamic domains can be defined as units that possess strong intradomain interactions and weak interdomain interactions. This criterion can be formulated in terms of correlations of motion. The correlations inside the domain should be much stronger than the correlations between the domains. It is obvious, therefore, that the dynamic domain is not a strictly defined concept to satisfy all possible cases of intradomain and interdomain interactions. To distinguish between separate domains and parts of the same domain, the cut-off value of correlation has to be chosen. This value is different for different proteins and cannot be easily determined. However, in the course of hierarchical clustering, all correlation values and the domains that correspond to these values are scanned. Thus, determining the most plausible number of domains in the proteins is equivalent to finding the cut-off value of correlation mentioned above.
The number of dynamic domains in a particular protein depends on external factors like temperature and pH, which influence the character of motions in the protein. Domains that determine the functioning of a protein are likely to be stable in a wide range of external conditions (40). Therefore, it is logical to assume that the principle of broad-range stability operates on a larger scale, and it can be used in the identification of dynamic domains. This simple assumption, introduced in this article for the first time that we know of, demonstrates its applicability. It is shown that the number of dynamic domains found by our technique coincides with the number of domains found by manual assignment in proteins that are suitable for visual domain determination (from our test set 1). These domains can be considered as “intrinsic” for the given protein. The number of intrinsic domains is the most plausible number of domains that can be observed in the protein in a relatively broad range of conditions. Therefore, to find the most plausible number of domains, one should inspect the correlation of motions, especially slow collective motions, of a given protein in a wide range of conditions. It is obvious that this task cannot be performed by modern computational techniques (like molecular dynamics simulations) even for the smallest proteins. We overcome this problem by using the HCCP hierarchical clustering technique, in which variation of the level of correlations is to some extent equivalent to variation of the external conditions.
The suggested HCCP approach (48) makes it possible to obtain clusters that can be considered as independently moving structural blocks at any given level of correlation between them. As stated in Theory and Methods, the level of correlation in HCCP can be related to the level of energy of thermal fluctuations for real proteins. Thus, the hierarchical clustering is in some sense analogous (but not identical) to lowering the temperature. The stability gap (the range of correlations where the number of clusters does not change) is thus equivalent to the range of temperatures where a given set of clusters is stable. Therefore, the largest stability gap can be chosen for finding the most plausible number of domains in the system.
We tested our criterion of the most plausible number of domains by calculating the interdomain correlations and the energies of interdomain interactions over two large sets of test proteins. The first test set with manual domain assignment available revealed that our criterion identifies the majority of double-domain proteins in exact correspondence with this assignment. The mismatch between manual and HCCP assignments is quite tolerable. However, some of the proteins that have two domains according to manual assignment are identified by HCCP as single-domain proteins. To verify our result, we treated these proteins as two-domain structures. The correlations between two “artificial” domains appear to be very high and the interdomain interactions are very strong in comparison with the majority of native double-domain proteins. This indicates that the “problematic” proteins are indeed single-domain structures and our algorithm works correctly. This makes possible an important conclusion: the dynamic domains coincide with the static domains identified by other techniques in many, but not all, cases.
Our data reveal important trends between the intradomain correlation, stability gap, and interdomain energy. These trends are essentially the same for both sets of test proteins. The stability gap is broader for the higher values of intradomain correlation. This is a direct consequence of the fact that the domains with strong internal bonds are more stable and maintain their integrity in a broader range of external conditions. In contrast, interdomain energy decreases with increase of intradomain correlation. This indicates that domains with strong internal bonds interact with each other weakly and vice versa.
This interpretation is proved by analysis in which the single-domain proteins were considered at the double-domain level, which is not native for them. At this level, two domains show low internal stability and a very strong interaction with each other, justifying their assignment to a single dynamic unit. Additionally, proof of this view comes from statistical analysis of the number of interdomain linkages in the proteins from test set 2. Single-domain proteins that are artificially split into two domains have a large number of interdomain linkages, which impose many constraints on domain motion. In contrast, real double-domain proteins are typically linked at only one or two sites, which allows the domains to move relatively freely around them. In this case, the interdomain linkages can be viewed as mechanical hinges.
It is shown that the interdomain correlations of individual domains depend on the relative size of domain (the number of residues in the domain divided by the number of residues in the whole protein). “Artificial” domains of the single-domain proteins possess lower interdomain correlations than real domains of the double-domain proteins for all domain sizes. This reflects their lower stability and higher interdependence.
Our approach allows us to simplify computational work at the cost of atomic detail. This made it possible for the first time that we know of to apply the concept of dynamic domains for domain identification to a significant number (2548) of proteins and to find several interesting correlations. Statistical analysis of our data revealed that the majority of double-domain proteins possess domains of very similar size (the domain boundary splits the protein into two almost equal parts). Based on our analysis we found a simple explanation for this fact, namely that domains of similar size are the most stable, whereas domains of very different size become very “fuzzy” and unstable. We can conclude from the abundance of proteins with domains of similar size that the evolutionary pressure tends to select domains with the highest compactness and stability.
We also revealed that very large domains (>400–500 residues) are extremely rare. This indicates that the interdomain interactions cannot support the integrity of very large aggregates. Another possible explanation comes from the fact that the domains are also folding units. It is plausible that very large domains cannot fold effectively and thus are eliminated by evolutionary pressure.
Introduction of the intradomain correlation function makes possible a quantitative measure of interdependence of domain motions. According to our data, no proteins that possess more than one domain have an intradomain correlation <0.2. In contrast, if single-domain proteins are considered at the two-domain level, the intradomain correlation is often (but not always) <0.2, but always <0.6. From these data, we can formulate the following simple rule: if the mean internal correlation inside the given structural blocks, pdom, is <0.2, these blocks cannot be considered as independent dynamic domains. If pdom > 0.6, these blocks are the domains with almost completely independent mobility. Finally, if 0.2 < pdom < 0.6, the blocks are likely to be domains that are only partially independent.
The results on calculations of domain assignments for all proteins from both test sets can be used by the research community for studies of structure, dynamics, and function of individual proteins and, particularly, for extracting from protein databases the structures with desired domain composition and interactions. We believe that with the aid of these data the results of limited proteolysis of proteins, which is used for obtaining protein fragments containing intact and active domains, will become more predictable. Our approach will also help in manipulating protein domains on a genetic level. To make all the data presented here available, we compiled two databases that represent two sets of test proteins. Each database entry contains information about the most plausible number of domains, stability gap, intra- and interdomain correlations and DFIRE energies, and the boundaries of domains in a format that is readable by both humans and machines.
Analysis of our data produces the following conclusions:
Improved HCCP technique, which includes the ISE algorithm, identifies the most plausible number of domains and their boundaries with high accuracy.
The most plausible number of domains in a given protein can be determined using the principle of the largest stability gap. The domain, found by using this concept are likely to maintain their integrity in the widest range of physical conditions and thus are most likely to be observed in a real protein at native conditions.
The mean intradomain correlation pdom can be used as a quantitative criterion of domain independence and stability. According to this criterion, proteins can be separated into two groups: those possessing “fuzzy” domains with weak intradomain bonds (0.2 < pdom < 0.6) and those with almost independent (very well separated) domains with very strong intradomain and very weak interdomain interactions (pdom > 0.6). No multidomain proteins with pdom < 0.2 were identified. If such small values are observed for domains assigned by other methods, this assignment might represent not dynamic domains but a single-domain structure.
SUPPLEMENTARY MATERIAL
An online supplement to this article can be found by visiting BJ Online at http://www.biophysj.org.
References
- 1.Janin, J., and S. J. Wodak. 2002. Protein modules and protein-protein interaction. Introduction. Adv. Protein Chem. 61:1–8. [DOI] [PubMed] [Google Scholar]
- 2.Janin, J., and S. J. Wodak. 1983. Structural domains in proteins and their role in the dynamics of protein function. Prog. Biophys. Mol. Biol. 42:21–78. [DOI] [PubMed] [Google Scholar]
- 3.Cunningham, E. L., and D. A. Agard. 2003. Interdependent folding of the N- and C-terminal domains defines the cooperative folding of α-lytic protease. Biochemistry. 42:13212–13219. [DOI] [PubMed] [Google Scholar]
- 4.Tayyab, S., N. Sharma, and M. Mushahid Khan. 2000. Use of domain specific ligands to study urea-induced unfolding of bovine serum albumin. Biochem. Biophys. Res. Commun. 277:83–88. [DOI] [PubMed] [Google Scholar]
- 5.Ahmad, B., M. Z. Kamal, and R. H. Khan. 2004. Alkali-induced conformational transition in different domains of bovine serum albumin. Protein Pept. Lett. 11:307–315. [DOI] [PubMed] [Google Scholar]
- 6.Fessas, D., S. Iametti, A. Schiraldi, and F. Bonomi. 2001. Thermal unfolding of monomeric and dimeric β-lactoglobulins. Eur. J. Biochem. 268:5439–5448. [DOI] [PubMed] [Google Scholar]
- 7.Ito, K., T. Q. Uyeda, Y. Suzuki, K. Sutoh, and K. Yamamoto. 2003. Requirement of domain-domain interaction for conformational change and functional ATP hydrolysis in myosin. J. Biol. Chem. 278:31049–31057. [DOI] [PubMed] [Google Scholar]
- 8.Popp, S., L. Packschies, N. Radzwill, K. P. Vogel, H. J. Steinhoff, and J. Reinstein. 2005. Structural dynamics of the DnaK-peptide complex. J. Mol. Biol. 347:1039–1052. [DOI] [PubMed] [Google Scholar]
- 9.Zhang, X. J., J. A. Wozniak, and B. W. Matthews. 1995. Protein flexibility and adaptability seen in 25 crystal forms of T4 lysozyme. J. Mol. Biol. 250:527–552. [DOI] [PubMed] [Google Scholar]
- 10.Gerstein, M., B. F. Anderson, G. E. Norris, E. N. Baker, A. M. Lesk, and C. Chothia. 1993. Domain closure in lactoferrin. Two hinges produce a see-saw motion between alternative close-packed interfaces. J. Mol. Biol. 234:357–372. [DOI] [PubMed] [Google Scholar]
- 11.Beckstead, J. A., B. L. Block, J. K. Bielicki, C. M. Kay, M. N. Oda, and R. O. Ryan. 2005. Combined N- and C-terminal truncation of human apolipoprotein A-I yields a folded, functional central domain. Biochemistry. 44:4591–4599. [DOI] [PubMed] [Google Scholar]
- 12.Dumoulin, M., K. Conrath, A. Van Meirhaeghe, F. Meersman, K. Heremans, L. G. Frenken, S. Muyldermans, L. Wyns, and A. Matagne. 2002. Single-domain antibody fragments with high conformational stability. Protein Sci. 11:500–515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Chen, J., J. Wang, and W. Wang. 2004. Transition states for folding of circular-permuted proteins. Proteins. 57:153–171. [DOI] [PubMed] [Google Scholar]
- 14.Chenal, A., P. Nizard, V. Forge, M. Pugniere, M. O. Roy, J. C. Mani, F. Guillain, and D. Gillet. 2002. Does fusion of domains from unrelated proteins affect their folding pathways and the structural changes involved in their function? A case study with the diphtheria toxin T domain. Protein Eng. 15:383–391. [DOI] [PubMed] [Google Scholar]
- 15.Ostermeier, M. 2005. Engineering allosteric protein switches by domain insertion. Protein Eng. Des. Sel. 18:359–364. [DOI] [PubMed] [Google Scholar]
- 16.Falquet, L., M. Pagni, P. Bucher, N. Hulo, C. J. Sigrist, K. Hofmann, and A. Bairoch. 2002. The PROSITE database, its status in 2002. Nucleic Acids Res. 30:235–238. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Nagar, B., W. G. Bornmann, P. Pellicena, T. Schindler, D. R. Veach, W. T. Miller, B. Clarkson, and J. Kuriyan. 2002. Crystal structures of the kinase domain of c-Abl in complex with the small molecule inhibitors PD173955 and imatinib (STI-571). Cancer Res. 62:4236–4243. [PubMed] [Google Scholar]
- 18.Schmitt, L., and R. Tampe. 2002. Structure and mechanism of ABC transporters. Curr. Opin. Struct. Biol. 12:754–760. [DOI] [PubMed] [Google Scholar]
- 19.Fischer, K. F., and S. Marqusee. 2000. A rapid test for identification of autonomous folding units in proteins. J. Mol. Biol. 302:701–712. [DOI] [PubMed] [Google Scholar]
- 20.Anselmi, C., G. Bocchinfuso, A. Scipioni, and P. De Santis. 2001. Identification of protein domains on topological basis. Biopolymers. 58:218–229. [DOI] [PubMed] [Google Scholar]
- 21.Nichols, W. L., G. D. Rose, L. F. Ten Eyck, and B. H. Zimm. 1995. Rigid domains in proteins: an algorithmic approach to their identification. Proteins. 23:38–48. [DOI] [PubMed] [Google Scholar]
- 22.Wriggers, W., and K. Schulten. 1997. Protein domain movements: detection of rigid domains and visualization of hinges in comparisons of atomic coordinates. Proteins. 29:1–14. [PubMed] [Google Scholar]
- 23.Hayward, S., and H. J. Berendsen. 1998. Systematic analysis of domain motions in proteins from conformational change: new results on citrate synthase and T4 lysozyme. Proteins. 30:144–154. [PubMed] [Google Scholar]
- 24.Hinsen, K. 1998. Analysis of domain motions by approximate normal mode calculations. Proteins. 33:417–429. [DOI] [PubMed] [Google Scholar]
- 25.Hinsen, K., A. Thomas, and M. J. Field. 1999. Analysis of domain motions in large proteins. Proteins. 34:369–382. [PubMed] [Google Scholar]
- 26.Alexandrov, N., and I. Shindyalov. 2003. PDP: protein domain parser. Bioinformatics. 19:429–430. [DOI] [PubMed] [Google Scholar]
- 27.Holm, L., and C. Sander. 1994. Parser for protein folding units. Proteins. 19:256–268. [DOI] [PubMed] [Google Scholar]
- 28.Hayward, S., and N. Go. 1995. Collective variable description of native protein dynamics. Annu. Rev. Phys. Chem. 46:223–250. [DOI] [PubMed] [Google Scholar]
- 29.Schuyler, A. D., and G. S. Chirikjian. 2005. Efficient determination of low-frequency normal modes of large protein structures by cluster-NMA. J. Mol. Graph. Model. 24:46–58. [DOI] [PubMed] [Google Scholar]
- 30.Kundu, S., D. C. Sorensen, and G. N. Phillips, Jr. 2004. Automatic domain decomposition of proteins by a Gaussian Network Model. Proteins. 57:725–733. [DOI] [PubMed] [Google Scholar]
- 31.Orengo, C. A., A. D. Michie, S. Jones, D. T. Jones, M. B. Swindells, and J. M. Thornton. 1997. CATH–a hierarchic classification of protein domain structures. Structure. 5:1093–1108. [DOI] [PubMed] [Google Scholar]
- 32.Stein, A., R. B. Russell, and P. Aloy. 2005. 3did: interacting protein domains of known three-dimensional structure. Nucleic Acids Res. 33(Database issue):D413–D417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Gong, S., G. Yoon, I. Jang, D. Bolser, P. Dafas, M. Schroeder, H. Choi, Y. Cho, K. Han, S. Lee, M. Lappe, L. Holm, S. Kim, D. Oh, and J. Bhak. 2005. PSIbase: a database of Protein Structural Interactome map (PSIMAP). Bioinformatics. 21:2541–2543. [DOI] [PubMed] [Google Scholar]
- 34.Richardson, J. S. 1981. The anatomy and taxonomy of protein structure. Adv. Protein Chem. 34:167–339. [DOI] [PubMed] [Google Scholar]
- 35.Medved, L. V., S. V. Litvinovich, and P. L. Privalov. 1986. Domain organization of the terminal parts in the fibrinogen molecule. FEBS Lett. 202:298–302. [DOI] [PubMed] [Google Scholar]
- 36.Novokhatny, V. V., S. A. Kudinov, and P. L. Privalov. 1984. Domains in human plasminogen. J. Mol. Biol. 179:215–232. [DOI] [PubMed] [Google Scholar]
- 37.Hendrix, T. M., Y. Griko, and P. Privalov. 1996. Energetics of structural domains in alpha-lactalbumin. Protein Sci. 5:923–931. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Manfrinato, M. C., T. Bellini, M. Masserini, M. Tomasi, and F. Dallocchio. 2001. Thermal stability of the hemagglutinin-neuraminidase from Sendai virus evidences two folding domains. FEBS Lett. 495:48–51. [DOI] [PubMed] [Google Scholar]
- 39.Sato, S., B. Kuhlman, W. J. Wu, and D. P. Raleigh. 1999. Folding of the multidomain ribosomal protein L9: the two domains fold independently with remarkably different rates. Biochemistry. 38:5643–5650. [DOI] [PubMed] [Google Scholar]
- 40.Jaenicke, R. 1999. Stability and folding of domain proteins. Prog. Biophys. Mol. Biol. 71:155–241. [DOI] [PubMed] [Google Scholar]
- 41.Privalov, P. L., and L. V. Medved. 1982. Domains in the fibrinogen molecule. J. Mol. Biol. 159:665–683. [DOI] [PubMed] [Google Scholar]
- 42.Tatunashvili, L. V., V. V. Filimonov, P. L. Privalov, M. L. Metsis, V. E. Koteliansky, K. C. Ingham, and L. V. Medved. 1990. Co-operative domains in fibronectin. J. Mol. Biol. 211:161–169. [DOI] [PubMed] [Google Scholar]
- 43.Jager, M., and A. Pluckthun. 1999. Domain interactions in antibody Fv and scFv fragments: effects on unfolding kinetics and equilibria. FEBS Lett. 462:307–312. [DOI] [PubMed] [Google Scholar]
- 44.Kumar, D. P., A. Tiwari, and R. Bhat. 2004. Effect of pH on the stability and structure of yeast hexokinase A. Acidic amino acid residues in the cleft region are critical for the opening and the closing of the structure. J. Biol. Chem. 279:32093–32099. [DOI] [PubMed] [Google Scholar]
- 45.Tama, F., F. X. Gadea, O. Marques, and Y. H. Sanejouand. 2000. Building-block approach for determining low-frequency normal modes of macromolecules. Proteins. 41:1–7. [DOI] [PubMed] [Google Scholar]
- 46.Atilgan, A. R., S. R. Durell, R. L. Jernigan, M. C. Demirel, O. Keskin, and I. Bahar. 2001. Anisotropy of fluctuation dynamics of proteins with an elastic network model. Biophys. J. 80:505–515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Bahar, I., A. R. Atilgan, and B. Erman. 1997. Direct evaluation of thermal fluctuations in proteins using a single-parameter harmonic potential. Fold. Des. 2:173–181. [DOI] [PubMed] [Google Scholar]
- 48.Yesylevskyy, S. O., V. N. Kharkyanen, and A. P. Demchenko. 2006. Hierarchical clustering of the correlation patterns: new method of domain identification in proteins. Biophys. Chem. 119:84–93. [DOI] [PubMed] [Google Scholar]
- 49.Zhang, C., S. Liu, H. Zhou, and Y. Zhou. 2004. An accurate, residue-level, pair potential of mean force for folding and binding based on the distance-scaled, ideal-gas reference state. Protein Sci. 13:400–411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Zhou, H., and Y. Zhou. 2002. Distance-scaled, finite ideal-gas reference state improves structure-derived potentials of mean force for structure selection and stability prediction. Protein Sci. 11:2714–2726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Levitt, M., C. Sander, and P. S. Stern. 1985. Protein normal-mode dynamics: trypsin inhibitor, crambin, ribonuclease and lysozyme. J. Mol. Biol. 181:423–447. [DOI] [PubMed] [Google Scholar]
- 52.Bahar, I., and A. Rader. 2005. Coarse-grained normal mode analysis in structural biology. Curr. Opin. Struct. Biol. 15:586–592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Yildirim, Y., and P. Doruker. 2004. Collective motions of RNA polymerases. Analysis of core enzyme, elongation complex and holoenzyme. J. Biomol. Struct. Dyn. 22:267–280. [DOI] [PubMed] [Google Scholar]
- 54.Keskin, O. 2002. Comparison of full-atomic and coarse-grained models to examine the molecular fluctuations of c-AMP dependent protein kinase. J. Biomol. Struct. Dyn. 20:333–345. [DOI] [PubMed] [Google Scholar]
- 55.Doruker, P., A. R. Atilgan, and I. Bahar. 2000. Dynamics of proteins predicted by molecular dynamics simulations and analytical approaches: Application to a-amylase inhibitor. Proteins. 40:512–524. [PubMed] [Google Scholar]
- 56.Sista, R., K. V. Brinda, and S. Vishveshwara. 2005. Identification of domains and domain interface residues in multidomain proteins from graph spectral method. Proteins. 59:616–626. [DOI] [PubMed] [Google Scholar]
- 57.Keskin, O., S. R. Durell, I. Bahar, R. L. Jernigan, and D. G. Covell. 2002. Relating molecular flexibility to function: a case study of tubulin. Biophys. J. 83:663–680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Wang, G., and R. L. Dunbrack, Jr. 2003. PISCES: a protein sequence culling server. Bioinformatics. 19:1589–1591. [DOI] [PubMed] [Google Scholar]
- 59.Demchenko, A. P. 2001. Recognition between flexible protein molecules: induced and assisted folding. J. Mol. Recognit. 14:42–61. [DOI] [PubMed] [Google Scholar]
- 60.Tompa, P. 2002. Intrinsically unstructured proteins. Trends Biochem. Sci. 27:527–533. [DOI] [PubMed] [Google Scholar]
- 61.Musick, W. D., and M. G. Rossmann. 1979. The structure of mouse testicular lactate dehydrogenase isoenzyme C4 at 2.9 A resolution. J. Biol. Chem. 254:7611–7620. [DOI] [PubMed] [Google Scholar]