Abstract
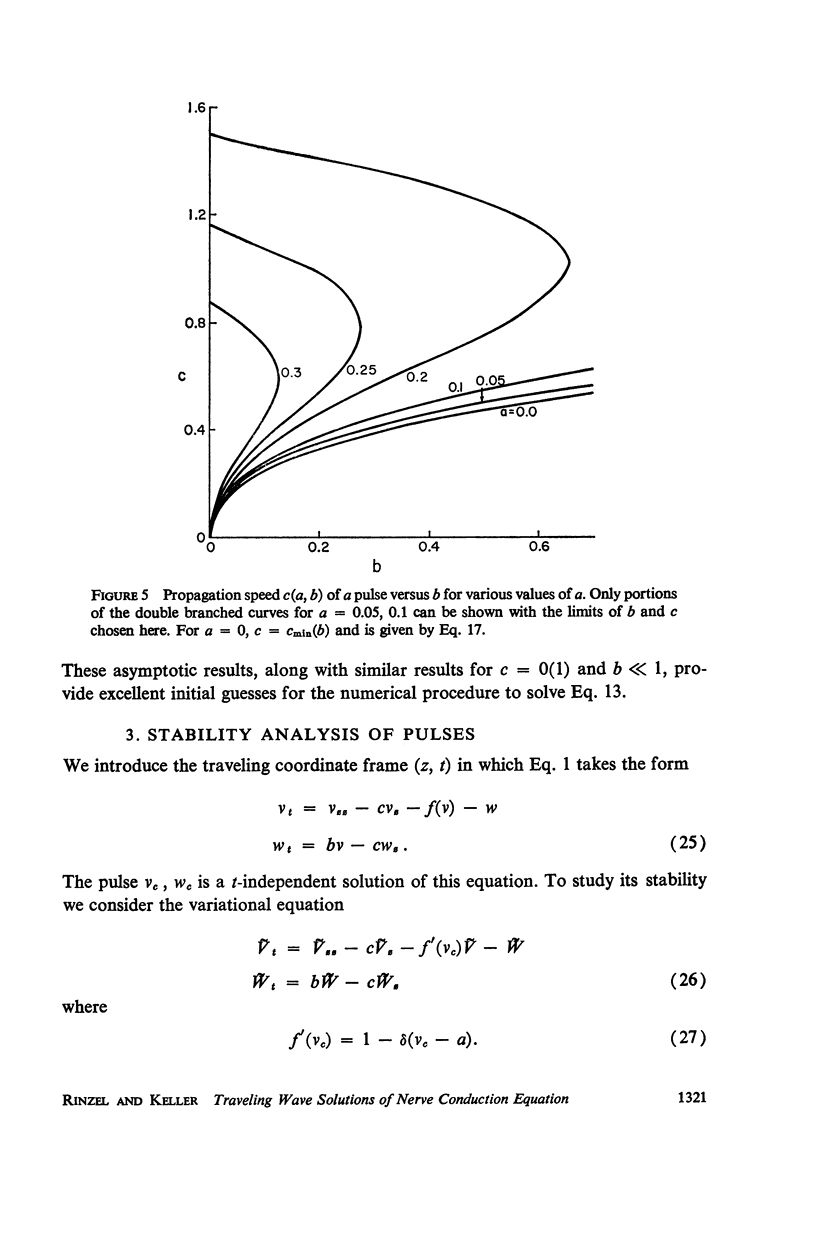
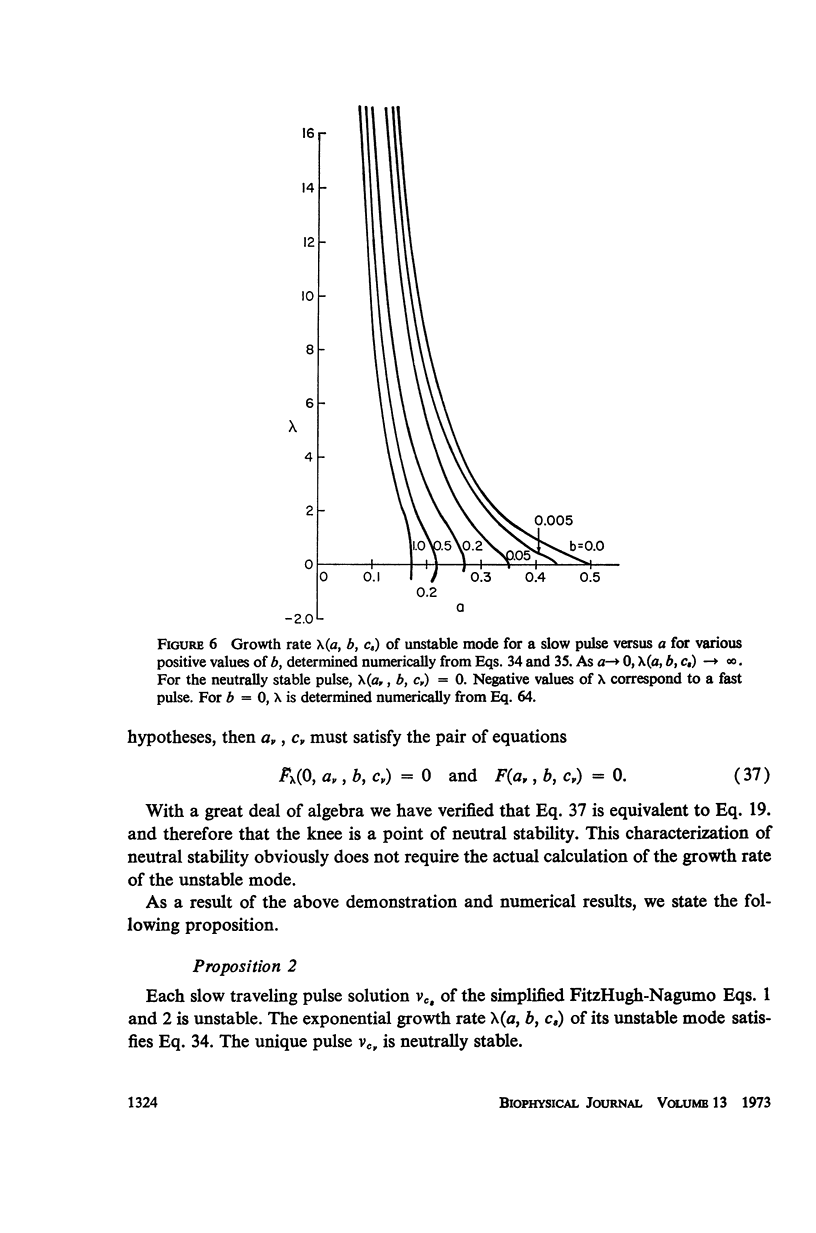
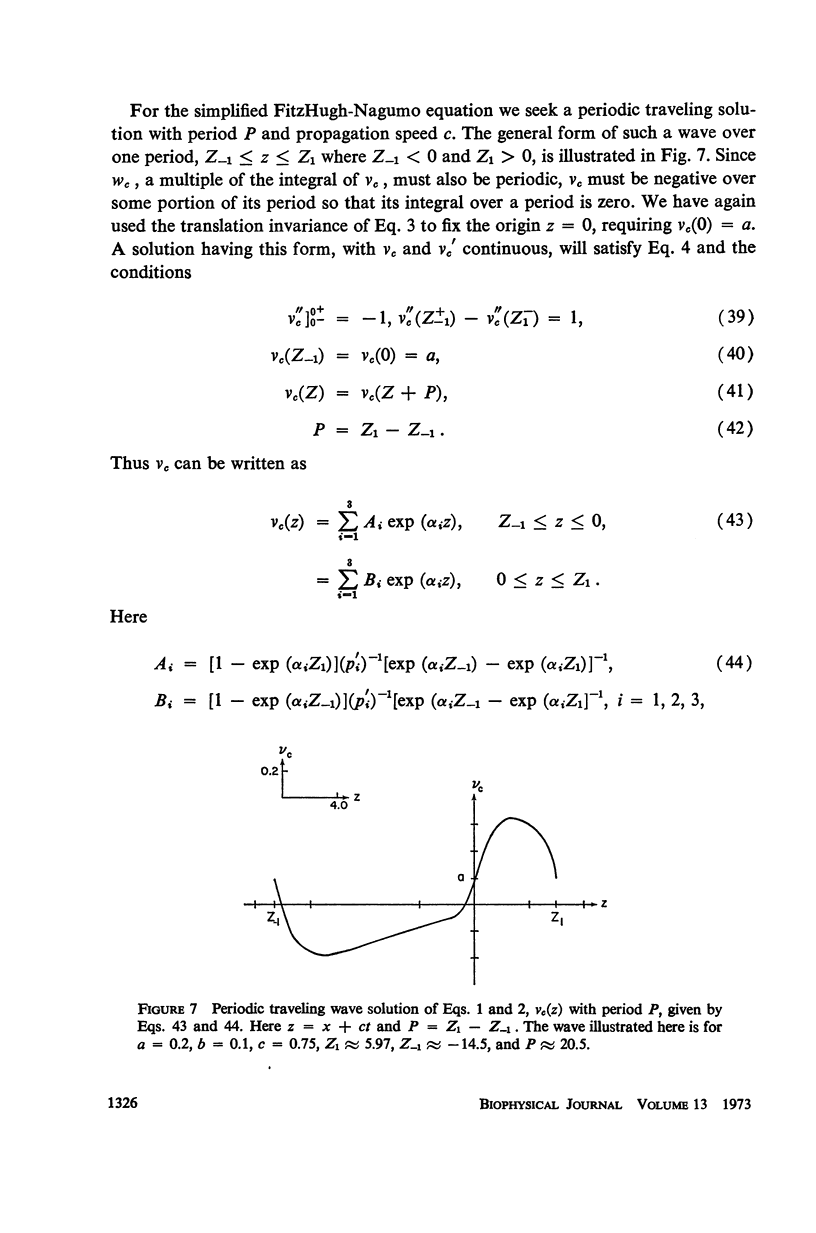
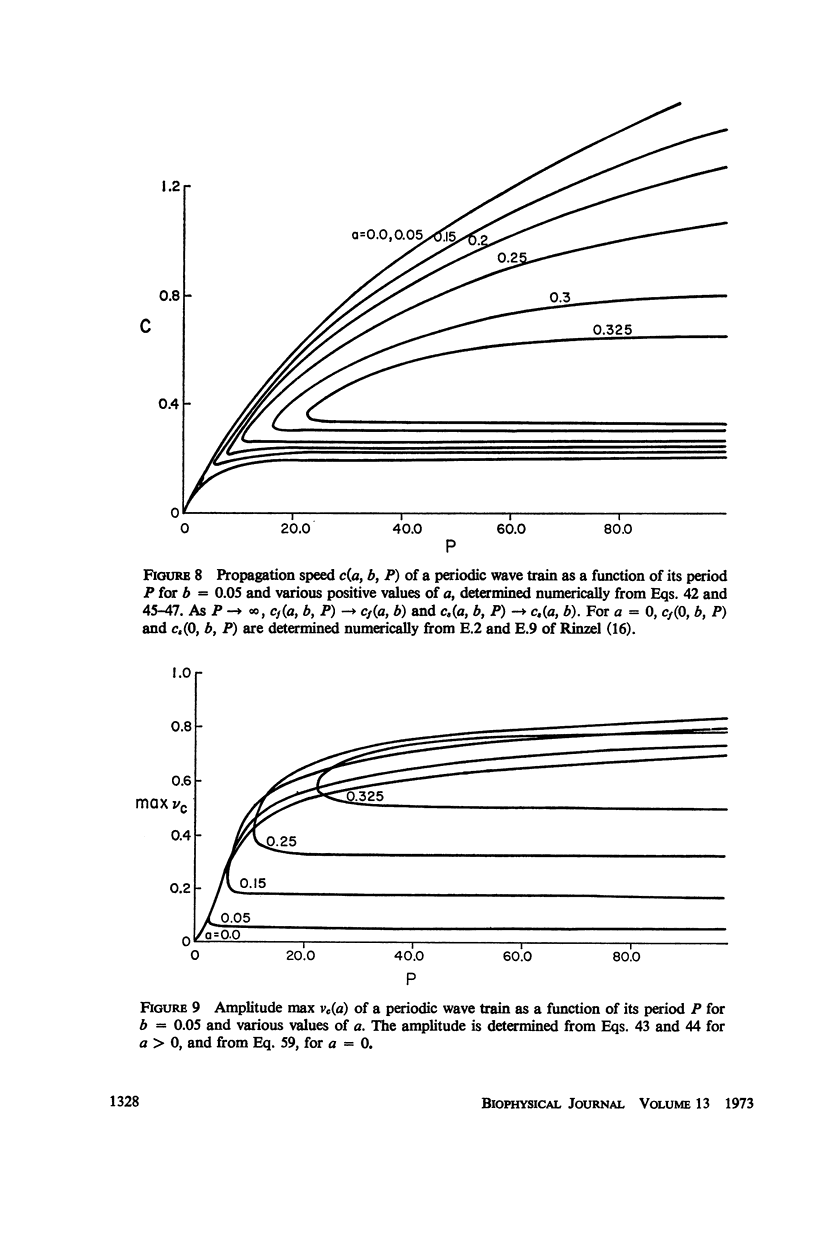
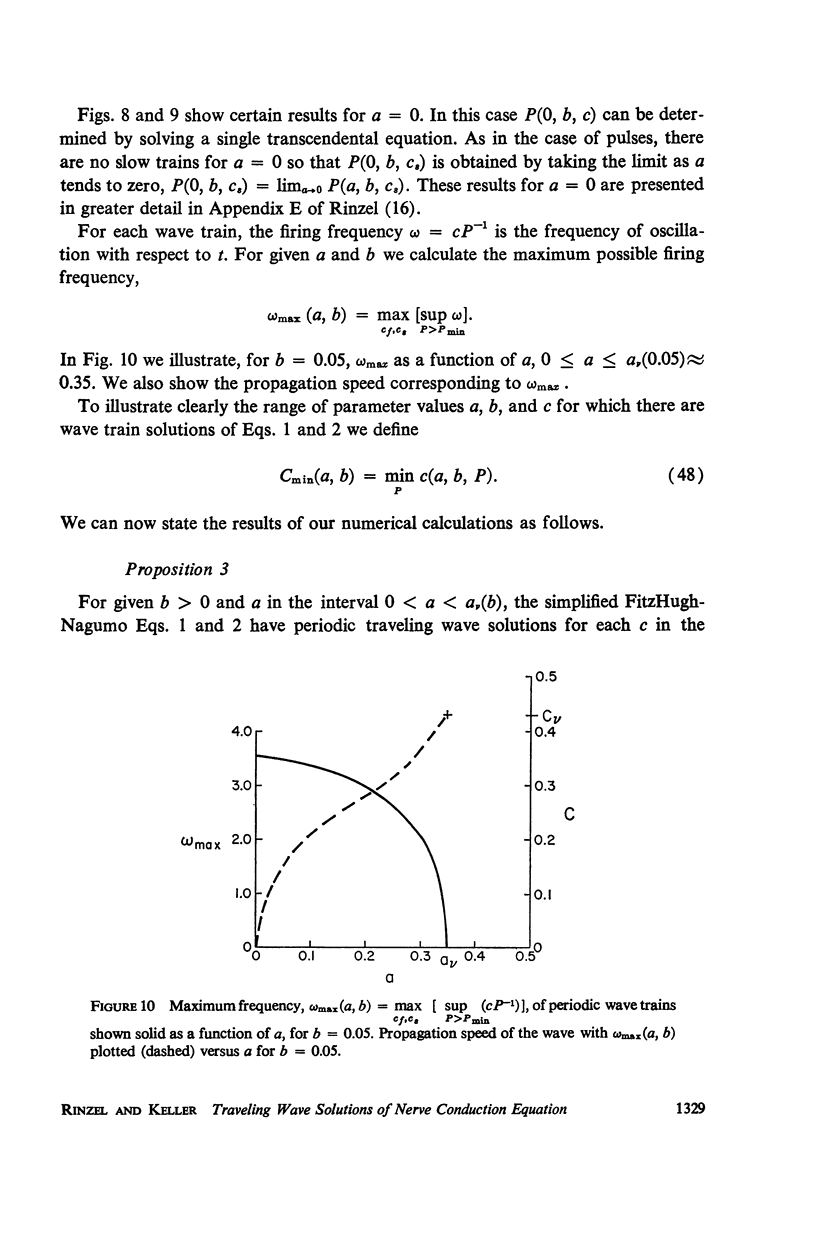
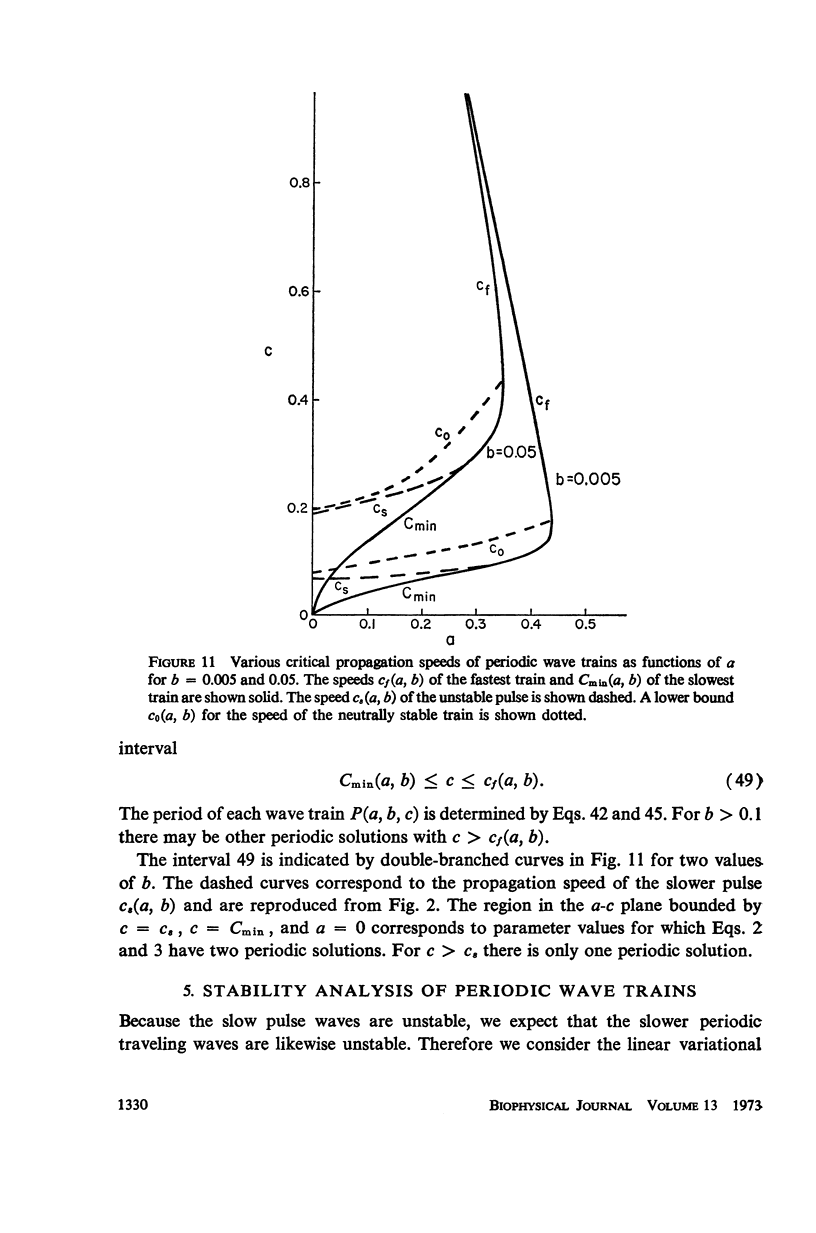
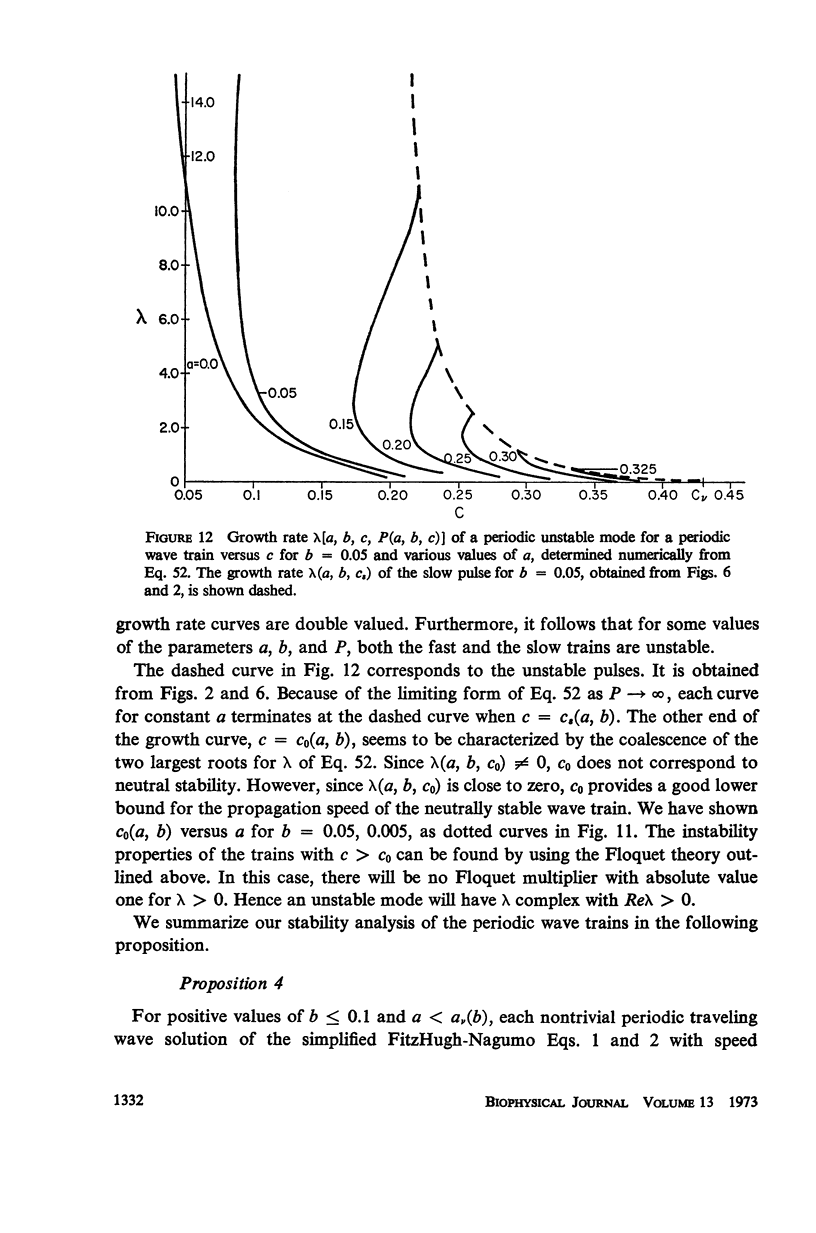
We consider a pair of differential equations whose solutions exhibit the qualitative properties of nerve conduction, yet which are simple enough to be solved exactly and explicitly. The equations are of the FitzHugh-Nagumo type, with a piecewise linear nonlinearity, and they contain two parameters. All the pulse and periodic solutions, and their propagation speeds, are found for these equations, and the stability of the solutions is analyzed. For certain parameter values, there are two different pulse-shaped waves with different propagation speeds. The slower pulse is shown to be unstable and the faster one to be stable, confirming conjectures which have been made before for other nerve conduction equations. Two periodic waves, representing trains of propagated impulses, are also found for each period greater than some minimum which depends on the parameters. The slower train is unstable and the faster one is usually stable, although in some cases both are unstable.
Full text
PDF

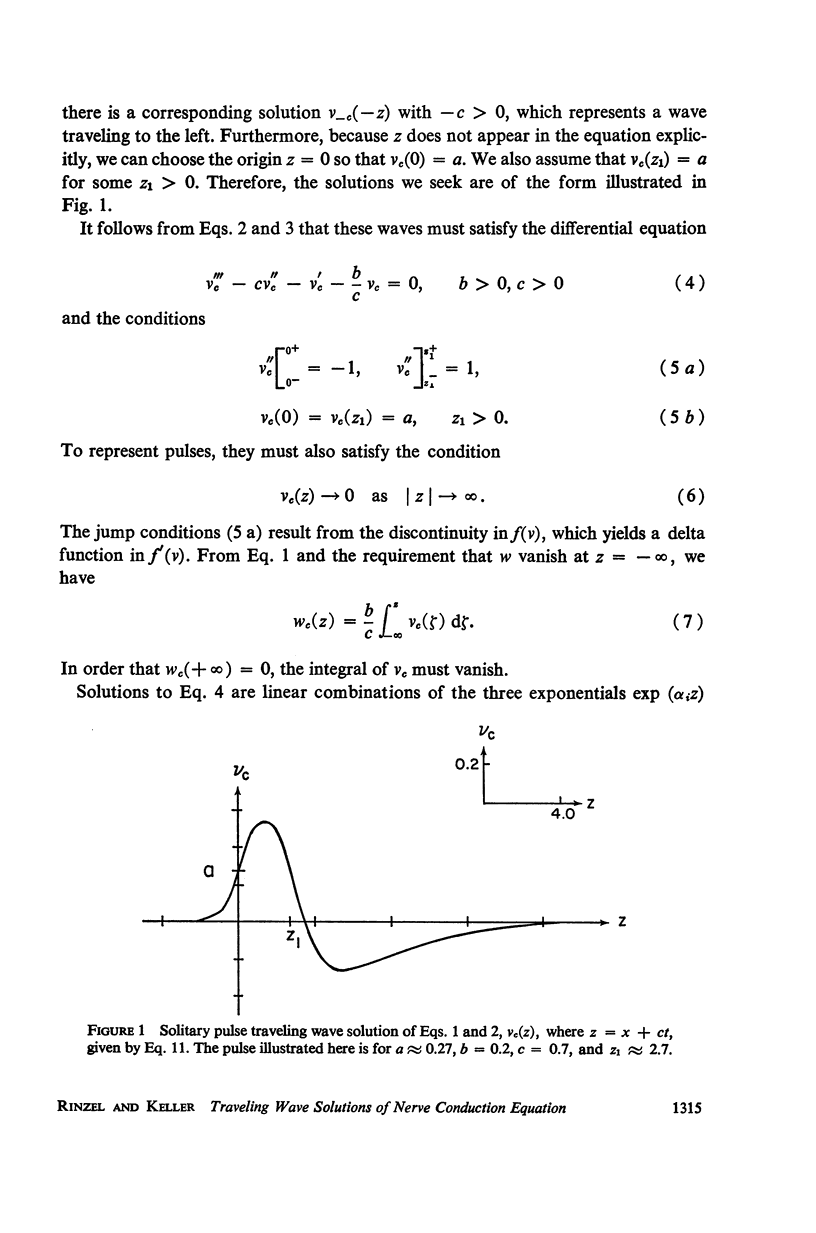


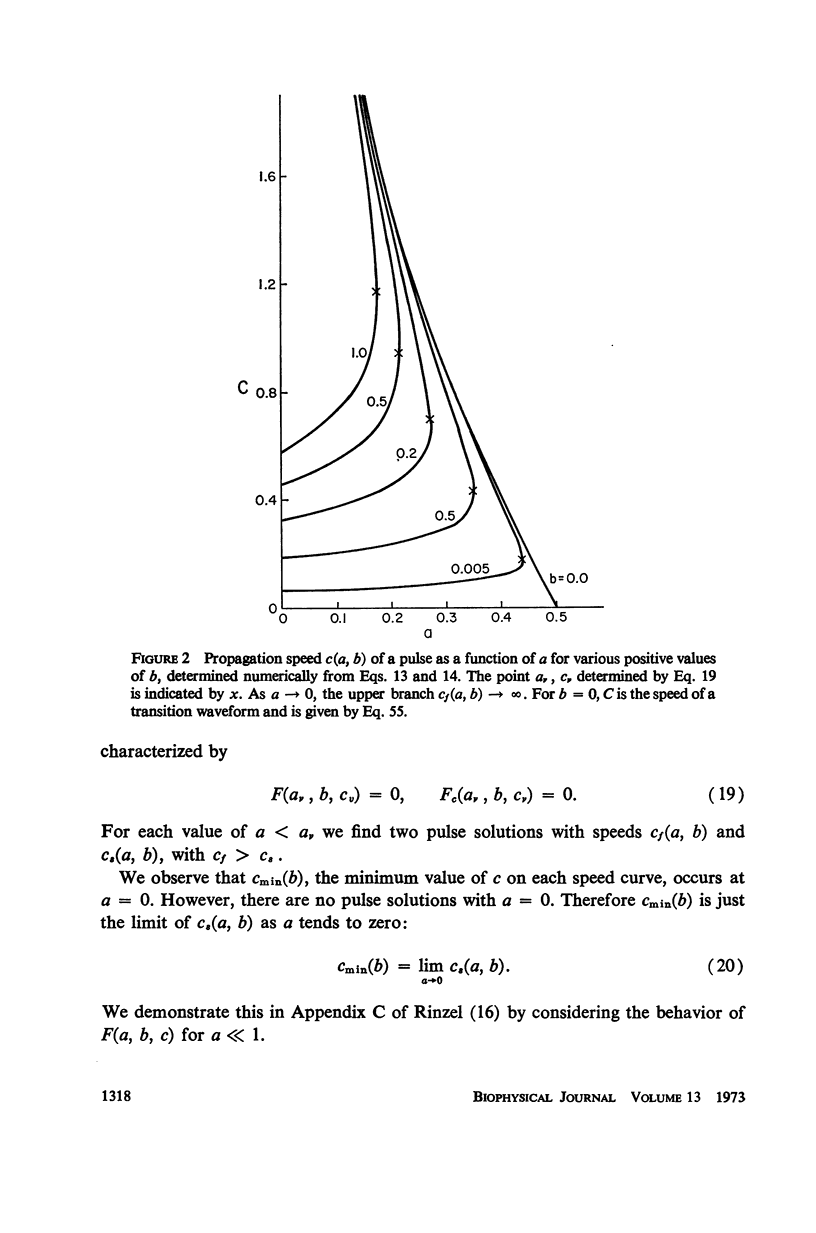
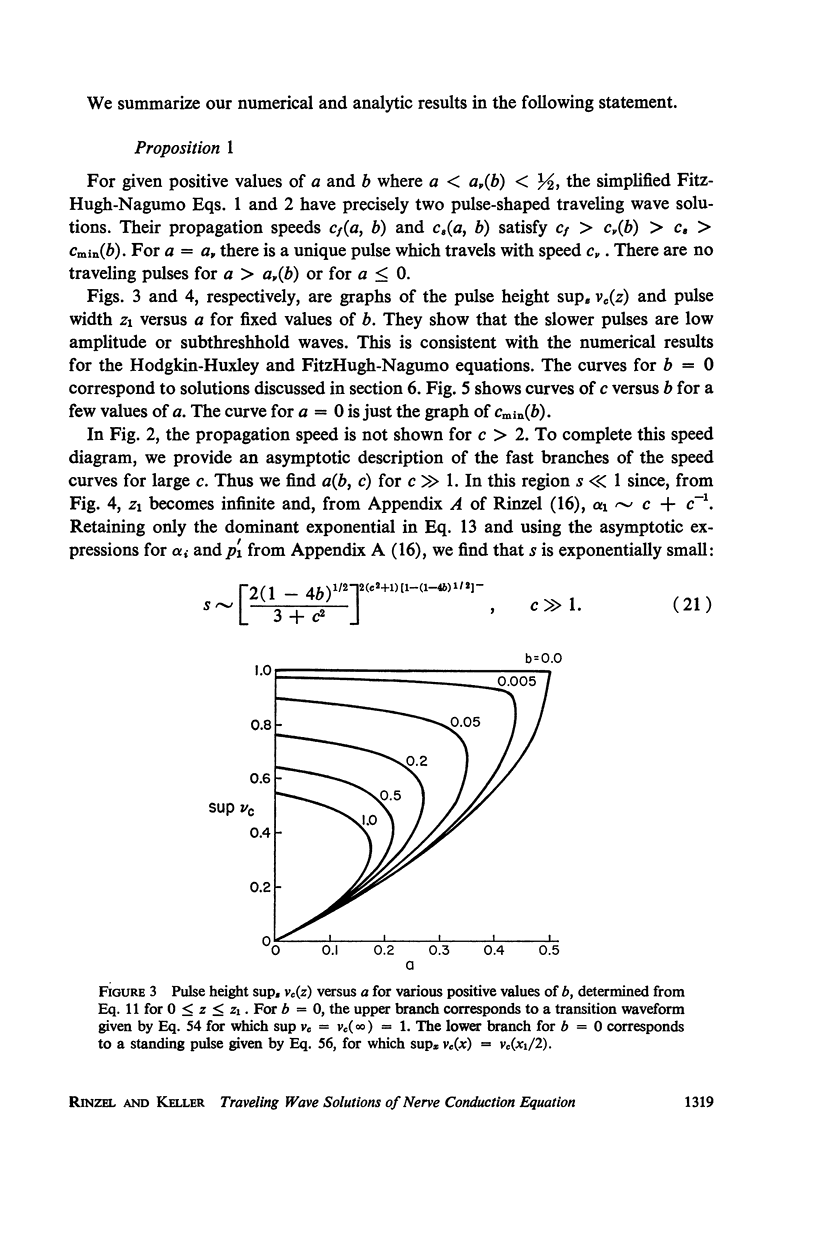
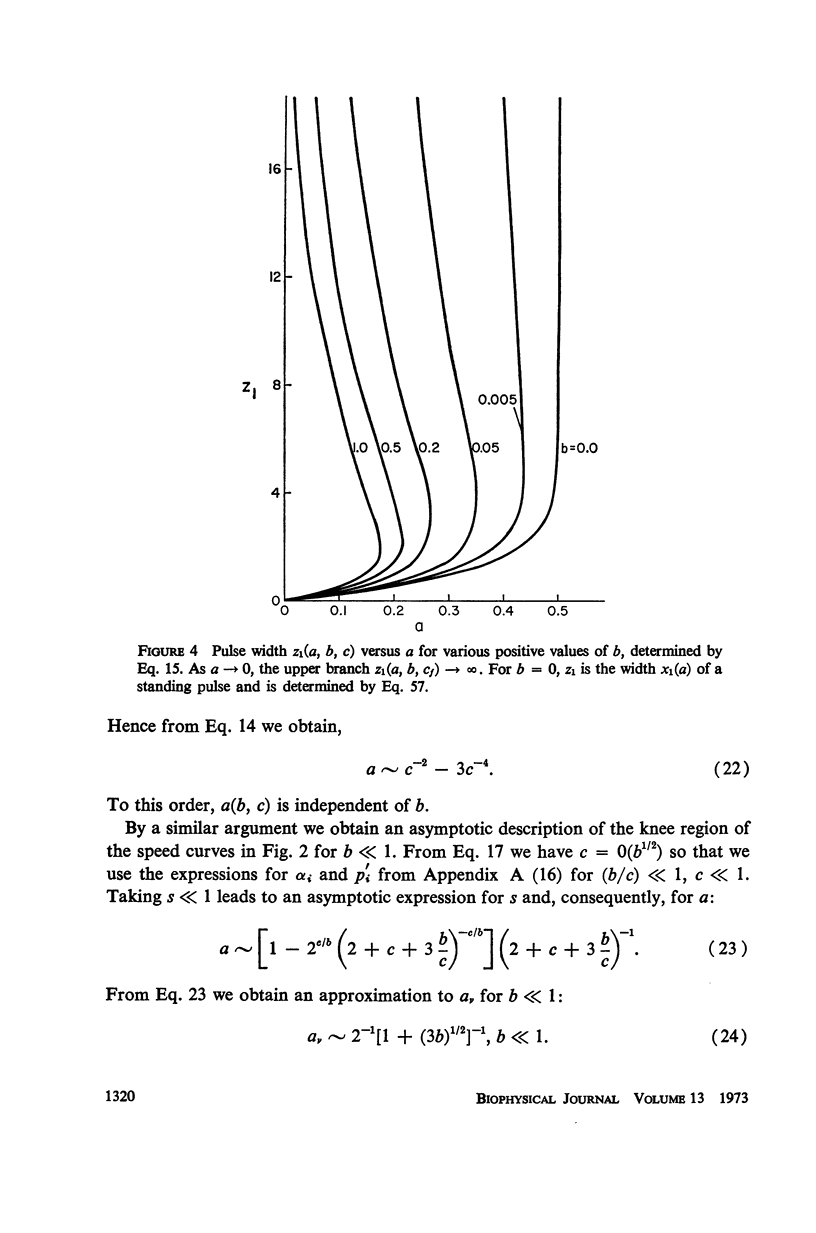










Selected References
These references are in PubMed. This may not be the complete list of references from this article.
- Cooley J. W., Dodge F. A., Jr Digital computer solutions for excitation and propagation of the nerve impulse. Biophys J. 1966 Sep;6(5):583–599. doi: 10.1016/S0006-3495(66)86679-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fitzhugh R. Impulses and Physiological States in Theoretical Models of Nerve Membrane. Biophys J. 1961 Jul;1(6):445–466. doi: 10.1016/s0006-3495(61)86902-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- HODGKIN A. L., HUXLEY A. F. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol. 1952 Aug;117(4):500–544. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]


