Ubiquitous selective constraints in the Drosophila genome revealed by a genome-wide interspecies comparison

Abstract

Non-coding DNA comprises ∼80% of the euchromatic portion of the Drosophila melanogaster genome. Non-coding sequences are known to contain functionally important elements controlling gene expression, but the proportion of sites that are selectively constrained is still largely unknown. We have compared the complete D. melanogaster and Drosophila simulans genome sequences to estimate mean selective constraint (the fraction of mutations that are eliminated by selection) in coding and non-coding DNA by standardizing to substitution rates in putatively unconstrained sequences. We show that constraint is positively correlated with intronic and intergenic sequence length and is generally remarkably strong in non-coding DNA, implying that more than half of all point mutations in the Drosophila genome are deleterious. This fraction is also likely to be an underestimate if many substitutions in non-coding DNA are adaptively driven to fixation. We also show that substitutions in long introns and intergenic sequences are clustered, such that there is an excess of substitutions <8 bp apart and a deficit farther apart. These results suggest that there are blocks of constrained nucleotides, presumably involved in gene expression control, that are concentrated in long non-coding sequences. Furthermore, we infer that there is more than three times as much functional non-coding DNA as protein-coding DNA in the Drosophila genome. Most deleterious mutations therefore occur in non-coding DNA, and these may make an important contribution to a wide variety of evolutionary processes.

Non-protein-coding DNA (here referred to as non-coding DNA) forms the majority of the genomes of many multicellular eukaryotes and is known to be functionally important in many respects. For example, non-coding sequences are involved in the regulation of gene expression, DNA replication, chromosome packaging, and mRNA secondary structure. Although the number of genes varies surprisingly little between organisms as diverse as Caenorhabditis elegans (∼19,000), Drosophila (∼14,000), Arabidopsis (∼25,000), and humans (∼25,000), the amount of non-coding DNA and corresponding genome size varies by more than an order of magnitude between these species (e.g., ∼180 Mb in Drosophila compared to ∼3400 Mb in hominids). Establishing what fraction of this non-coding DNA is functionally important in different species will help to shed light on the apparent lack of relationship between genome size and organismal complexity—the “C-value paradox” (Thomas 1971). Estimating this fraction is also important for our understanding of many aspects of evolution including the evolution and maintenance of sexual reproduction (Charlesworth and Charlesworth 1998). However, surprisingly little is known about the functional importance of non-coding DNA, even in a model species such as Drosophila.

Until recently, the genome-wide analysis of divergence and selective constraints in Drosophila non-coding DNA has been limited by a lack of data from closely related species. This has led to apparent discrepancies between inferences from different studies. Bergman and Kreitman (2001) estimated that 22%–26% of intronic sequences are highly constrained (i.e., located within blocks of >70% identity) between Drosophila melanogaster and Drosophila virilis. However, a study by Halligan et al. (2004) found no support for this conclusion, finding instead that intronic sites (excluding sites involved in splicing) evolve ∼17% faster than fourfold degenerate synonymous sites, on average. It is likely that the discrepancy is due to biases in the data sets with respect to the lengths of introns studied (Haddrill et al. 2005). Drosophila introns have a very skewed length distribution such that there is a sharp peak close to the minimum intron length (∼59–62 bp) and a very long tail of longer introns (Hawkins 1988; Comeron and Kreitman 2000). This has led to the classification of Drosophila introns into two size categories: short (within the peak, <80–90 bp) and long (within the tail) (Mount et al. 1992). The Halligan et al. (2004) data set consisted mostly of introns within the short class, whereas the Bergman and Kreitman (2001) data set consisted only of long introns. A subsequent analysis suggested that substitution rates differ significantly between these two classes of introns (Parsch 2003), and, more recently, two studies demonstrated a negative correlation between divergence and intron length (Haddrill et al. 2005; Marais et al. 2005).

In intergenic sequences, most studies have found evidence for a substantial fraction of conserved sites, although estimates vary between 22% and 60%. A single gene study of divergence around even-skipped (eve) between D. melanogaster and D. simulans showed that mean divergence in the 5′ flanking region (0.024) was ∼35% lower than that of an intron of the gene (Ludwig and Kreitman 1995), suggesting that there could be many selectively constrained sites in the flanking non-coding DNA. Bergman and Kreitman (2001) also found evidence for strong constraints in intergenic DNA by inferring that there are similar numbers of conserved bases in intergenic sequences as in introns (22%–26%). Halligan et al. (2004) showed that this fraction may be as high as ∼44% in an analysis of 119 intergenic DNA fragments flanking known genes. This is supported by two more recent studies. First, in a comparison of D. melanogaster, Drosophila yakuba, and Drosophila pseudoobscura, Siepel et al. (2005) found that 37%–53% of the Drosophila genome corresponded to “conserved elements”; and second, in a study of 51 intergenic sequence fragments on the X chromosome, Andolfatto (2005) inferred that constraints in intergenic DNA could be higher still; his analysis suggested that 50% of (non-UTR) intergenic sites and as many as 60% of sites within UTRs are selectively constrained. Since Andolfatto’s study included some intergenic sequences that are distant from known genes, this suggests that constraint may be high, even at considerable distances from coding regions.

Two other, more indirect, lines of evidence support the conclusion that there may be substantial selective constraints in Drosophila non-coding DNA. First, there is evidence for a strong deletion bias in Drosophila. Phylogenetic analysis of “dead-on-arrival” Helena elements has revealed that they lose DNA at a surprisingly high rate (Petrov et al. 1996; Petrov and Hartl 1998; Blumenstiel et al. 2002), a result that is consistent with similar observations for Drosophila pseudogenes (Petrov and Hartl 2000), although the generality and strength of this deletion bias have been debated (Gregory 2004). If a genome-wide deletion bias exists, then this would be expected to lead to a compact genome containing little unconstrained DNA; indeed, Drosophila has few bona fide pseudogenes and transposable elements (Harrison et al. 2003; Quesneville et al. 2005). Furthermore, a recent study has shown that genes with complex functions in Drosophila are flanked by significantly more non-coding DNA than genes with simple functions, suggesting that long intergenic regions contain more regulatory sequences (Nelson et al. 2004), a result that would be expected in a highly compact genome. Second, recent evidence indicates that transcription outside of coding sequences is extensive, suggesting that currently annotated expressed sequences may form only a small part of the constrained DNA in the genome (Johnson et al. 2005).

The purpose of our study is to investigate patterns of selective constraints in Drosophila non-coding DNA using a whole-genome approach that avoids the biases arising from the sampling of regions that has affected previous studies. D. simulans is sufficiently closely related to D. melanogaster (divergence at synonymous sites is ∼10%) such that long tracts of non-coding sequence can be reliably aligned using the appropriate alignment tools (Keightley and Johnson 2004; Pollard et al. 2004). Furthermore, since divergence is low, there are likely to be fewer genes that have diverged in function or lost/gained function in comparison to more divergent species.

Results

Divergence and intron size

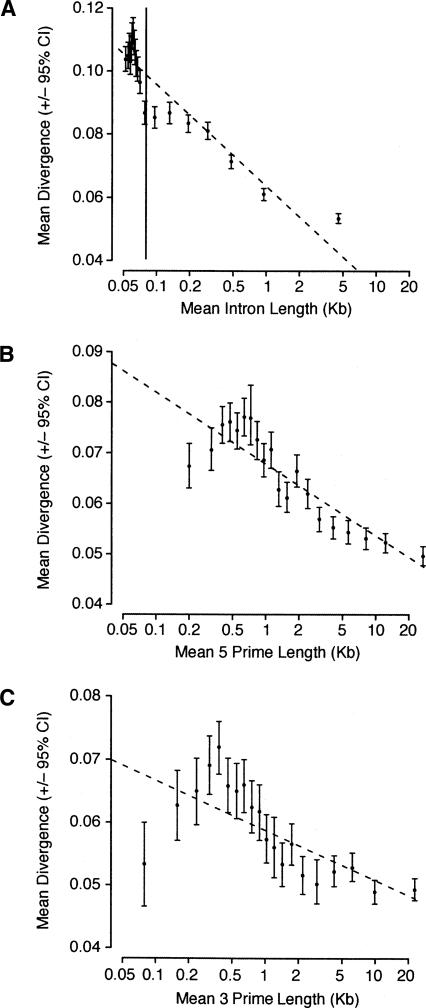
We analyzed pairwise alignments of all annotated homologous introns from the D. melanogaster and D. simulans genomes to investigate patterns of divergence in introns with respect to intron size. Consistent with previous observations (Parsch 2003; Haddrill et al. 2005; Marais et al. 2005), we found a negative correlation between intron length and divergence (Spearman correlation, r = −0.279 [se = 0.00758] for complete introns, and −0.305 [0.00744] for a data set in which the first 6 bp and last 16 bp are removed from each intron). To investigate how divergence changes as a function of intron length, we divided the data into 20 categories, based on length, with equal numbers of observations in each category, and plotted mean divergence against mean length in each category (Fig. 1A). It is evident that divergence decreases substantially at the division between the two previously defined categories of intron size (80 bp), indicating the presence of constrained blocks within the long intron class, evidence for which has also been found previously (Bergman and Kreitman 2001). It is also apparent that, even within the long intron class, divergence continues to decrease with intron length. For example, divergence in the longest intron category (mean length = 4543 bp) is significantly lower (P < 0.0001) than in the second longest category (mean length = 949 bp). This implies that the frequency of constrained blocks may increase with intron length.

Figure 1.

Mean divergence (±95% confidence interval) versus mean length for different length categories of (A) introns, (B) 5′ intergenic sequences, and (C) 3′ intergenic sequences. Within each class of site, we divided the data into 20 categories, based on length, such that there were equal numbers of observations in each category. Divergence estimates were corrected for multiple hits using the method of Kimura (1980), and confidence intervals were obtained by bootstrapping 1000 times by observation. The dashed line for each class of site shows the linear regression of divergence on log length. The solid vertical line in A is drawn at the division between the long and short intron class (80 bp).

Marais et al. (2005) found that the negative correlation between divergence and intron length was present in both first and non-first introns (although the correlation was nonsignificant for non-first introns). This correlation was subsequently found to be significant for both classes in a larger data set (Haddrill et al. 2005). In the still larger data set presented here, both correlations are highly significant, and, interestingly, the correlation is marginally stronger for non-first introns (Spearman r = −0.279 [0.00894], compared to −0.258 [0.0132] in first introns).

Divergence and intergenic size

We also analyzed pairwise alignments of homologous intergenic DNA adjacent to the exons of annotated genes. The intergenic DNA between the coding sequence of the gene of interest and that of neighboring genes was divided in half, and the segments were assigned to the adjacent gene, such that the intergenic DNA associated with neighboring genes was non-overlapping. Paralleling the results for introns, we find significant negative correlations between intergenic sequence length and divergence for both 5′ and 3′ sequences (Spearman r = −0.259 [0.0124] and −0.0943 [0.0132] for 5′ and 3′ sequences, respectively). We then investigated how divergence varies with intergenic sequence length by dividing the 5′ and 3′ intergenic sequence data sets into 20 equally sized length categories and plotting mean divergence against mean length for each category (Fig. 1B,C). Divergence peaks at a length of ∼500 bp for both 5′ and 3′ intergenic sequences. The pattern for intergenic sequences greater than ∼500 bp in length is similar to the pattern observed in long introns, suggesting that similar evolutionary processes may be operating in intergenic and intronic DNA above this length, consistent with the results of Bergman and Kreitman (2001). However, divergence also decreases for sequences shorter than ∼500 bp. One possible explanation for this observation is the presence of UTRs within the intergenic DNA, since UTRs constitute a greater proportion of the total intergenic length in short sequences (data not shown), and they are more highly constrained than surrounding non-UTR intergenic DNA (see below). The correlation between sequence length and divergence is also substantially stronger for 5′ than for 3′ sequences. This can also be explained by the presence of UTRs since 3′-UTRs in Drosophila are longer than 5′-UTRs on average (mean length = 280 bp and 148 bp for 3′- and 5′-UTRs, respectively). When non-UTR intergenic DNA sequences are analyzed (using only those genes that have annotated UTRs in D. melanogaster), the correlations between sequence length and divergence are found to be much stronger (Spearman r = −0.375 [0.0277] and −0.325 [0.0295] for 5′ and 3′ sequences, respectively).

Fastest evolving sites

Selective constraint is defined here as the fraction of mutations removed by selection. We estimated this by comparing the number of substitutions observed in a sequence of interest to the number expected if the mutation rate were the same as putatively unconstrained sequences from the same ∼100-kb section of the genome (see Methods). We estimated constraint using an unconstrained standard from the same section of the genome in order to account for large-scale variation in the mutation rate. We identified two classes of putatively unconstrained sequence (the fastest evolving intronic [FEI] sites and the fastest evolving fourfold degenerate [FEF] sites) by searching for the fastest evolving (FE) sites in the genome. Our calculation of constraint assumes that there is no positive or negative selection within the FE sites. If there is negative selection acting on FE sites, then constraint will be underestimated, whereas positive selection will lead to overestimates of constraint. Differences in the base composition of the FE sites and the test sequence are accounted for by using four pairwise substitution rates within the FE sites to predict the number of pairwise substitutions of each type within the test sequence, given its base composition (see Methods).

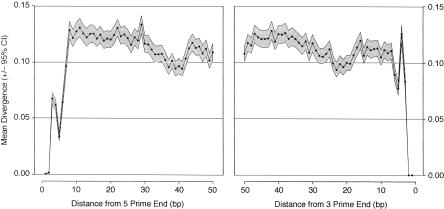
The negative correlation between divergence and intron length suggests that the fastest evolving intron sites reside within short introns (≤80 bp). However, it is known that introns contain sites that are necessary for splicing (Green 1986). In Drosophila, these include the branchpoint, the polypyrimidine tract, and the 5′- and 3′-splice sites. In order to infer the location of any putatively unconstrained sites within short introns, and to exclude those sites involved in splicing, we plotted mean divergence against position within an intron (Fig. 2). As expected, there is substantially lower divergence in short introns within the 5′- and 3′-splice site sequences, and a decrease in divergence for sites corresponding to the location of the branchpoint (∼40 bp downstream from the 5′-end and ∼25 bp upstream from the 3′-end) (Mount et al. 1992). There is also noticeably lower divergence close to the 3′-end, in the region that corresponds to the location of a polypyrimidine tract (Kennedy and Berget 1997). In total, ∼7 bp at the 5′-end and up to ∼30 bp at the 3′-end appear to be significantly conserved, giving a total of 37 bp, which is only marginally shorter than the length of the smallest intron in our data set (40 bp). However, positions 8–30 from the 5′-end have the highest divergence on average, and are therefore candidates for unconstrained sequence. For introns ≤65 bp in length, divergence within this subsection is consistently high (Supplemental Fig. S1). We therefore designated base pairs 8–30 in introns ≤65 bp in length as one class of putatively unconstrained sequence (FEI sites).

Figure 2.

Mean divergence (±95% confidence interval as a gray box) in short introns plotted as a function of distance from the 5′- and 3′-ends of the intron. Divergence estimates for each position were corrected for multiple hits using the method of Kimura (1980). The 95% confidence interval of the mean for each position was obtained by bootstrapping 1000 times by intron.

It is also thought that fourfold degenerate sites are subject to little selective constraint in Drosophila (Akashi 1995). However, there is preferential use of certain codons within Drosophila genes that may be due to selection for translational efficiency (Shields et al. 1988; Akashi 1995, 1996) although this selection appears to have become relaxed in the D. melanogaster lineage (McVean and Vieira 2001). Furthermore, codon-usage bias has been found to be stronger at the edge of exons than in the center, and this is thought to be due to an increase in the effectiveness of selection at the edges (Comeron and Guthrie 2005). For our second class of putatively unconstrained sequence (FEF sites), we therefore use only fourfold degenerate sites from genes with little or no codon usage bias, and exclude sites at the edges of exons (see Methods for more details).

The mean divergence for the FEI sites (0.128 [95% CI = 0.125–0.130]) is nonsignificantly (P = 0.078) different from the mean divergence for the FEF sites (0.122 [0.116–0.129]). Furthermore, the mean GC content of the FEI sites (0.357 [0.352–0.362]) is very close to the predicted equilibrium GC content for highly recombining regions in Drosophila (0.35), based on substitution rates among paralogous copies of transposable elements (Singh et al. 2005). The mean GC content of the FEF sites (0.489 [0.479–0.499]) was found to be significantly higher than 0.35, but is closer than the mean GC content of all fourfold sites (0.666 [0.663–0.669]). Furthermore, divergence within a data set of 151 orthologous D. melanogaster and D. simulans dead-on-arrival DNAREP1_DM elements is only marginally higher than that observed in both classes of FE sites (0.137 [0.133–0.142]), lending support to the hypothesis that FE sites are subject to little selective constraint (J. Wang, D.L. Halligan, and P.D. Keightley, unpubl.).

Constraints in introns

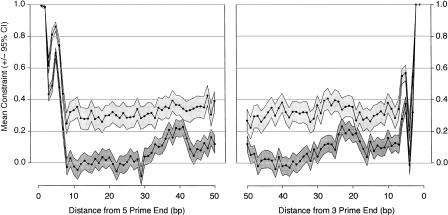
We estimated mean constraint in introns for the two defined classes of intron size as a function of position in the intron (Fig. 3). Consistent with the results for divergence in short introns (Fig. 2), there are significant positive constraints at sites involved in splicing (splice site sequences and the branchpoint) for both classes of introns. Interestingly, however, there is a significant difference in mean constraint between short and long introns, even with the 5′- and 3′-splice sequences. There are also strong and significantly positive constraints in long introns at all sites tested outside the splice sequences. This implies that the positive correlation we observe between intron length and constraint (Spearman r = 0.227 [0.00804]) is not solely due to high constraints in regions distant from known genes, but is a result of an even distribution of constraints, on average, across long introns.

Figure 3.

Mean constraint (±95% confidence interval as a gray box) for short (dark gray) and long (light gray) introns, plotted as a function of distance from the 5′- and 3′-ends of the intron. Confidence intervals were obtained by bootstrapping 1000 times by genomic section.

Constraints in intergenic sequences

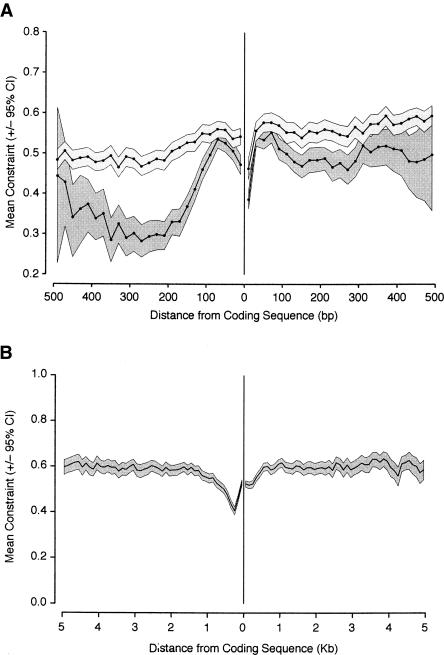
In order to investigate patterns of constraints in the intergenic sequences immediately flanking the coding sequence of genes, we estimated mean constraint in 20-bp non-overlapping blocks of intergenic sequence up to 500 bp upstream and downstream from the coding sequence boundary (see Fig. 4A). This was done for two classes of intergenic sequence length (short and long, split arbitrarily at 500 bp), in order to reveal any patterns associated with differences in intergenic sequence length (constraint is positively correlated with length, Spearman r = 0.187 [0.0134] and 0.0414 [0.0136] for 5′ and 3′ intergenic sequences, respectively). We observed high and significant mean constraint in 5′ and 3′ sequences at all sites tested in both length categories. We also found significantly lower mean constraint in short compared to long intergenic sequences, even within 500 bp of the coding sequence boundary (P < 0.001 for both 5′ and 3′ sequences). Furthermore, we observed significantly higher mean constraint in 3′ (0.539 [0.526–0.552]) than in 5′ (0.475 [0.462–0.488]) sequences (P < 0.001) within this region, and the difference is larger for the short intergenic sequence class. This observation may be explained by constraints within UTRs. The mean constraint within the 5′-UTRs (0.588 [0.562–0.611]) and 3′-UTRs (0.608 [0.584–0.629]) is significantly higher than that observed in the 500 bp of non-UTR intergenic sequence flanking the UTRs (C = 0.437 and 0.442 for the 5′ and 3′ flanks, respectively). The differences in mean constraint between the 5′ and 3′ flanks of UTRs and between the 5′- and 3′-UTRs were both nonsignificant (P < 0.39 and P < 0.111, respectively).

Figure 4.

Mean constraint (±95% confidence interval as a gray box) in intergenic sequences flanking coding sequences, plotted as a function of distance from the coding sequence boundary. Constraint in 5′ sequences is shown on the left, and constraint in 3′ sequences is shown on the right. (A) Mean constraint in the first 500 bp flanking a coding sequence plotted for two arbitrary size classes of intergenic DNA; short (≤500 bp; dark gray) and long (>500 bp; light gray). (B) Mean constraint for 5 kb of flanking sequence in all lengths of intergenic sequence. Mean constraint was calculated for 20-bp nonoverlapping blocks, and the confidence interval for each block was obtained by bootstrapping 1000 times by genomic section.

In order to investigate how constraint varies with distance from coding sequences on a larger scale, we estimated mean constraint in 20-bp blocks up to 5 kb from the coding sequence boundary (Fig. 4B). There is a slight decrease in mean constraint close to the coding sequence boundary, which can be explained by the contribution of short intergenic sequences to estimates of mean constraint in this region. However, at greater distances, we observed very little decrease in mean constraint with distance. This contrasts sharply with mammals, where mean constraint estimates drop to low levels within 3 kb of the coding sequence boundary in murids (Keightley and Gaffney 2003), and within 1 kb of the coding sequence boundary in hominids (Keightley et al. 2005). This observation suggests that the constrained elements within intergenic DNA are relatively evenly dispersed, on average, with respect to distance from the coding sequence boundary, and are not clustered close to, or far from, coding sequences.

Genome-wide estimates of constraint

We calculated estimates of mean constraint per base pair for different classes of sites in the Drosophila genome using both the FEI and the FEF sites as unconstrained standards (Tables 1 and 2). It is apparent that constraint estimates are very similar when calculated with either unconstrained standard, but are less noisy when calculated using FEI sites. Using the FEI sites as the unconstrained standard, mean constraint is ∼0.9 for nondegenerate sites in coding sequences, confirming previous findings that most amino-acid-changing mutations are removed by selection (Kimura 1983), and is low but still significantly positive for fourfold degenerate sites, consistent with the result of McVean and Vieira (1999). However, mean constraint is surprisingly high within all three categories of non-coding sequence, suggesting that >50% of newly arising mutations are removed by selection in long introns and intergenic sequences. This high estimate of mean constraint per base pair in intronic and intergenic DNA can be attributed to the fact that most non-coding sites reside in long non-coding sequences, and constraint is positively correlated with non-coding sequence length. Since intergenic and intronic sites comprise ∼3.8 times as much DNA as coding sequences and mean constraint is only marginally higher in coding (0.664 [0.657–0.672]) than in non-coding sequences (0.551 [0.545–0.558]), we infer that most functional sequence in the Drosophila genome is non-coding.

Table 1.

Estimates of constraint per base pair, calculated using FEI sites, for different classes of site

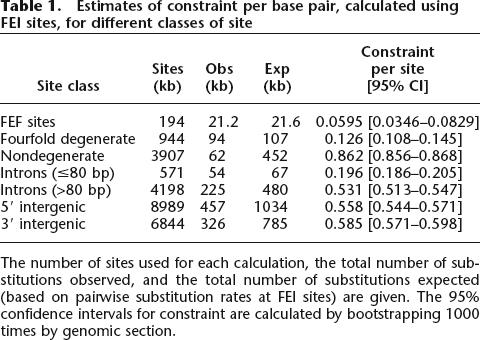
The number of sites used for each calculation, the total number of substitutions observed, and the total number of substitutions expected (based on pairwise substitution rates at FEI sites) are given. The 95% confidence intervals for constraint are calculated by bootstrapping 1000 times by genomic section.

Table 2.

Estimates of constraint per base pair, calculated using FEF sites, for different classes of site

The number of sites used for each calculation, the total number of substitutions observed, and the total number of substitutions expected (based on pairwise substitution rates at FEF sites) are given. The 95% confidence intervals for constraint are calculated by bootstrapping 1000 times by genomic section.

We investigated whether the high estimates of constraint observed in non-coding sequences could be explained by the presence of annotated alternatively spliced exons, annotated RNA genes, or interspersed repeats. We masked transposable elements using RepeatMasker (A.F.A. Smit, R. Hubley and P. Green, unpubl., http://www.repeatmasker.org) and alternatively spliced exons and RNA genes using the D. melanogaster annotation, in all non-coding alignments. Estimates of mean constraint in non-coding sequences remain virtually unchanged after masking (Supplemental Table S1). We also tested whether high estimates of constraint could be caused by variation in the mutation rate within the defined genomic sections. In order to test this, the constraint for each test sequence was recalculated using FE sites from the same gene rather than the same genomic section. Again, resulting estimates of mean constraint remained virtually unchanged (data not shown). This observation suggests that variation in mutation rate within genomic sections cannot explain the high estimates of mean constraint observed in non-coding DNA. However, we cannot rule out the possibility that the high constraint observed in non-coding DNA is due to extreme mutation rate variation over very short distances of the genome.

Clustering of substitutions

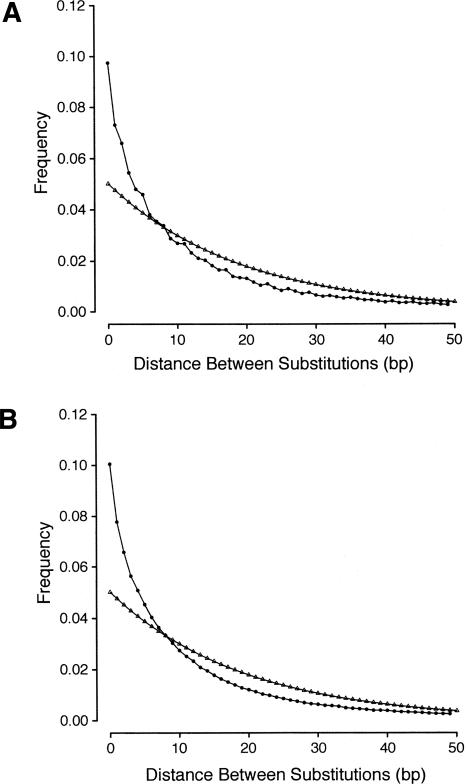
If the locations of substitutions are uncorrelated, then distances between substitutions along a sequence are expected to follow a geometric distribution. The distribution of distances between mismatches at sites in an alignment (excluding any indels) will also be geometrically distributed, providing that the alignment is sufficiently long that there are many substitutions and that there is no correlation between point and indel mutation. However, a correlation between substitution and indel rates has been observed in vertebrates (Hardison et al. 2003). To examine whether a correlation exists in putatively unconstrained sequences in Drosophila, we analyzed a data set of orthologous D. melanogaster and D. simulans transposable element remnants (J. Wang, D.L. Halligan, and P.D. Keightley, unpubl.). This analysis shows that indel substitutions per site and point substitutions per site are nonsignificantly correlated in such sequences (r = 0.127 [0.0812]), supporting the assumption of our model. We therefore compared the distribution of distances between substitutions at aligned sites (after removing any sites opposite a gap) in intergenic and intronic sequences >1 kb in length to the geometric distribution in order to test whether substitutions are under- or overdispersed. In intronic and non-UTR intergenic sequence, the distribution of distances between substitutions is much more leptokurtic than a geometric distribution, suggesting that substitutions are underdispersed (Fig. 5). This is manifest as a substantial excess of substitutions <8 bp apart, and a deficit of substitutions farther apart. The difference between the observed and expected distributions is also much more pronounced than the difference observed for a 1.5-Mb region of the human/baboon genome, the majority of which is believed to be unconstrained (Fig. 3A; Silva and Kondrashov 2002). This observed clustering of substitutions implies that constraint varies between sites within these sequences, and could therefore be explained by the presence of constrained and unconstrained blocks within long introns and intergenic sequences. This result is consistent with a previous study that found marginally significant clustering of polymorphic (within D. melanogaster) and divergent (between D. melanogaster and D. simulans/Drosophila sechellia) sites within the regulatory regions of four Drosophila genes (Dermitzakis et al. 2003). Furthermore, it is consistent with the observation that highly conserved non-coding sequences are non-randomly distributed in both Drosophila (Bergman et al. 2002) and Caenorhabditis (Webb et al. 2002).

Figure 5.

Observed (circles) and predicted (triangles) frequency distributions of distances between substitutions for (A) introns and (B) intergenic sequences longer than 1000 bp. The predicted frequency distribution assumes that the distances between substitutions are geometrically distributed and that the mean distance between substitutions is equal to that observed in the real data.

Discussion

The genome-wide analysis presented here indicates that functional constraints in non-coding Drosophila DNA are of similar magnitudes within intronic and intergenic sequences, consistent with the results of Bergman and Kreitman (2001), and are generally surprisingly high. We estimate that >50% of point mutations in both types of sequence are removed by negative selection. This level of constraint is somewhat unexpected since it has long been thought that most non-coding DNA in multicellular eukaryotic genomes is unconstrained. The high estimates of mean constraint observed in non-coding DNA are not inflated by constraints within any currently annotated features (i.e., alternatively spliced exons or RNA genes). In addition, we show that the observed estimates are unlikely to be explained by large-scale variation in the mutation rate, since constraint is calibrated using putatively unconstrained sites from the same ∼100-kb region of the genome. Furthermore, similar estimates are obtained when constraint for each non-coding sequence is calibrated using only FEI sites from the associated gene.

Our estimates of constraints in non-coding DNA are broadly consistent with previous studies (Bergman and Kreitman 2001; Halligan et al. 2004), after intron length biases in the data sets are accounted for (Haddrill et al. 2005). They are also in broad agreement with a recent small-scale study of 51 sections of non-coding DNA on the X chromosome, where constraint was estimated to be ∼40% in introns and ∼50% in intergenic DNA (Andolfatto 2005). We also demonstrate that, consistent with previous observations (Haddrill et al. 2005; Marais et al. 2005), constraint (and divergence) is significantly correlated with intronic sequence length, such that long introns have a greater proportion of constrained sites, and furthermore, we show that this applies to intergenic sequences as well. We demonstrate that substitutions in long non-coding sequences are clustered, implying the presence of blocks of constrained and unconstrained sequence. However, mean constraint in long non-coding sequences is high even very close to exon boundaries, suggesting that, on average, these constrained blocks do not tend to be concentrated in the center, or at the edges, of long non-coding sequences.

It is important to note that our estimates of constraint may well be underestimates. Despite efforts to remove classes of sites under negative selection from the two unconstrained standard sequences, there may be sites in both that are evolving under weak purifying selection (both classes are transcribed and may therefore be under selection, e.g., for pre-mRNA secondary structure). Furthermore, our estimates of constraint will underestimate the fraction of sites that are functional if many of the observed substitutions in non-coding DNA were driven to fixation by positive selection. This may well be the case, since it has been estimated that ∼15% of substitutions in (non-UTR) intergenic sequences and ∼20% of substitutions in intronic sequences on the X chromosome are adaptive when low-frequency polymorphisms are excluded (Andolfatto 2005). If we assume that the fraction of positively selected substitutions (α) for these classes of sites is the same for autosomes as for the X chromosome, we can use the approach of Andolfatto (2005) to infer the fraction of functionally relevant nucleotides (FRN) in intergenic DNA from our estimates of mean constraint (C), FRN ≈ C + (1 − C)α. However, since estimates of constraint in intergenic sequences are high (>0.5) and the corresponding estimate of α is ∼0.2, the estimates of FRN are <10% larger than estimates of C (FRN = 0.626 and 0.648 for 5′ and 3′ intergenic sequences, respectively). However, as noted by Andolfatto (2005), constraint may substantially underestimate the fraction of relevant nucleotides in UTRs if adaptive evolution within these sites is commonplace, as the results of his study imply.

Conversely, our estimates of constraint per site in the Drosophila genome could also be overestimates, since we have assumed that constraint within aligned sites (where constraint can be measured) is the same on average as in sites that are opposite a gap in either species (where constraint cannot be estimated). However, if we make the conservative assumption that constraint in unalignable sites is completely absent, then estimated constraint per site for the various classes of site tested is only marginally reduced (C = 0.493 [0.478–0.506], 0.513 [0.499–0.527], 0.485 [0.468–0.501], and 0.189 [0.179–0.198] for 5′ intergenic, 3′ intergenic, long introns, and short introns, respectively).

The observed pattern of constraint in non-coding DNA is markedly different from that observed in murids, where constraint was found to decrease to low levels within ∼3 kb of the coding sequence in intergenic DNA and appeared to be absent in all but the first ∼3 kb of first introns (Keightley and Gaffney 2003). It is in even sharper contrast to hominids, where mean constraint surrounding coding sequences was found to be even lower (Keightley et al. 2005). The striking differences between Drosophila and mammals could be due to differences in genome size, which differ by more than an order of magnitude between these taxa. There is now increasing evidence that the Drosophila genome may be highly compact and contain very little nonfunctional DNA. Firstly, there is evidence for a strong mutational deletion bias in Drosophila, which could result in a compact genome by removing nonfunctional DNA. This evidence comes from a study of dead-on-arrival Helena elements in both D. virilis and D. melanogaster, where a deletion bias of ∼8:1 was observed (Petrov et al. 1996; Petrov and Hartl 1998; Blumenstiel et al. 2002). It has been suggested that this deletion bias is unlikely to be a result of direct selection on deletions, but rather a reflection of the underlying mutational spectrum (Petrov and Hartl 2000). Secondly, there is a general lack of bona fide pseudogenes, and this may be the result of rampant deletion of nonfunctional DNA in the Drosophila genome. For example, a recent survey found only ∼100 pseudogenes in the D. melanogaster genome (Harrison et al. 2003).

If the Drosophila genome is highly compact, then how can we explain the observed lack of constraint outside of splice sites in short introns? The sharp peak in the distribution of intron lengths, close to the minimum length, suggests that these introns are under strong stabilizing selection to be as close to the minimum size possible. It is known that very small introns do not splice well, and the modal intron size is close to that required for proper splicing (Upholt and Sandell 1986; Tsurushita and Korn 1987; Mount et al. 1992). Furthermore, there is indirect evidence for very small introns being deleterious, since they are often associated with low recombination-rate regions in Drosophila (Carvalho and Clark 1999). It might therefore be expected that short introns would have very few, if any, unconstrained sites. However, we hypothesize that short introns may contain DNA that, although not constrained at the sequence level, is nonetheless necessary for efficient splicing. One possibility is that this DNA functions as a “spacer” that is necessary for the correct formation of stem–loop structures within the mRNA.

A highly compact Drosophila genome also implies that sequence in long introns and long intergenic sequences must be maintained by selection. It has been suggested that this could be due to indirect selection on intron length to reduce the deleterious consequences of linkage (Comeron and Kreitman 2000). However, our results show that there is considerable negative selection at the sequence level, and this may be sufficient to explain the long-term maintenance of these sequences. This is also supported by observed differences in polymorphic deletion biases, which is much lower in long introns and intergenic sequences than in dead-on-arrival Helena elements (Comeron and Kreitman 2000; Ptak and Petrov 2002; Ometto et al. 2005), and it has been suggested that this could be due to differences in sequence constraints (Ptak and Petrov 2002; Kawahara et al. 2004; Ometto et al. 2005).

Although it is clear that some of the observed constraints in intergenic DNA are due to the presence of UTRs, alternative explanations need to be sought for the high constraints observed at large distances from coding sequences. This may be due to the presence of large numbers of cis-regulatory elements; indeed, some recent studies have shown that known cis-regulatory modules correspond to regions that are conserved between D. melanogaster and D. pseudoobscura (Bergman et al. 2002; Emberly et al. 2003). It has also been shown in some cases that identified conserved nongenic sequences correspond to regulatory elements (Sironi et al. 2005). The conclusion that long non-coding sequences are highly constrained because of the presence of gene-control elements is supported by two other observations. First, a recent study has shown that genes with complex expression patterns in Drosophila tend to be associated with long intergenic sequences (Nelson et al. 2004). Second, there is evidence from mammals that regulatory elements are more frequent in first introns than non-first introns (Majewski and Ott 2002; Keightley and Gaffney 2003). If this were also true for Drosophila, then first introns would be expected to be longer, on average, than non-first introns, and this has been shown to be the case (Duret 2001; Marais et al. 2005).

A second, although not mutually exclusive explanation for the high level of constraint in long introns and long intergenic sequences could be the presence of unannotated transcribed sequences, such as RNA or protein-coding genes. There is evidence to suggest that non-coding DNA contains many unannotated transcribed sequences (Johnson et al. 2005). For example, a Drosophila microarray tiling experiment, using 36mer probes, found that 41% of probes associated with RNA expression correspond to intronic and intergenic regions (Stolc et al. 2004), and that probes associated with transcription showed an increase in sequence identity between D. melanogaster and D. pseudoobscura. Furthermore, although it is thought that the majority of protein-coding genes have been annotated, several recent studies have suggested that non-coding RNA genes may be far more abundant than current annotations of the Drosophila genome indicate (Storz 2002).

Finally, we have calculated the number of mutations that are removed by natural selection, per genome, per generation in Drosophila, by combining our estimate of constraint with an estimate of the genome-wide point and insertion–deletion mutation rate, obtained by scanning the genomes of Drosophila mutation accumulation (MA) lines for mutations (M. Dorris, C. Liautard-Haag, X. Maside, S. Macaskill, B. Charlesworth, and P.D. Keightley, unpubl.). This gives an estimate of the deleterious mutation rate, per site, per generation of ∼4 × 10⁻⁹. Assuming that there are 120 Mb of euchromatic DNA in the haploid Drosophila genome, we estimate that the genomic deleterious mutation rate per diploid is U ≈ 1. However, many such mutations are likely to have very small effects. Nonetheless, this high rate arises principally because the majority of sites in Drosophila euchromatic non-coding DNA appear to be functional, and much organismal complexity, associated with gene regulation, is encoded outside of coding regions. The function of this vast amount of constrained non-coding DNA sequences implied by this study remains to be elucidated.

Methods

Compilation of sequence data

A data set of coding and adjacent non-coding DNA sequences from orthologous D. melanogaster and D. simulans loci was compiled by first obtaining a list of all currently annotated D. melanogaster genes from NCBI’s Entrez Gene (using release 4.1 of the D. melanogaster genome; http://flybase.org). This retrieved a total of 14,183 annotations. From this list, RNA genes and poorly annotated genes were excluded (this was achieved by examining the FlyBase synopsis report for each gene, and excluding genes that were based on BLASTX data or gene prediction data only). GenBank format files were then downloaded for the remaining genes (including all 5′ and 3′ intergenic sequence and all annotated splice forms) to give a data set of GenBank files for 11,267 genes. All annotated introns, exons, and 5′ and 3′ intergenic sequence were then extracted for a randomly chosen splice form from each gene. The intergenic sequences (defined as the sites between the start/stop codons of two adjacent genes) were divided in half when analyzing 5′ and 3′ sequences, so that the intergenic sequence associated with neighboring genes was non-overlapping. A reciprocal best-hits BLAST approach was used to identify and extract homologous exons from the April 2005 consensus assembly of the D. simulans genome sequence from the Genome Sequencing Center WUSTL School of Medicine. The start and end positions of the exons within the D. simulans genome were then used to extract the adjacent D. simulans intronic and 5′ and 3′ intergenic sequences. Short exons (<40 bp) were joined where possible to an adjacent section of non-coding DNA prior to BLASTing, to increase the chance of a reciprocal best hit.

Sequence alignment

Homologous sections of non-coding DNA were initially aligned using MAVID (Bray and Pachter 2004), and were then realigned at a finer scale using MCALIGN2 (J. Wang, P.D. Keightley and T. Johnson, unpubl.) by splitting the MAVID alignments into sections of ∼500 bp at regions of high homology (defined as a >10-bp run of ungapped matches). MCALIGN2 is an improved version of MCALIGN (Keightley and Johnson 2004) that uses a procedure that attempts to find the most probable alignment according to a specific model of insertion–deletion evolution; a model suitable for Drosophila non-coding DNA was chosen (Keightley and Johnson 2004). Coding DNA sequences (formed by concatenating the retrieved exons) were aligned using the amino acid alignment obtained from CLUSTALW (Thompson et al. 1994).

Alignment processing

All alignments (intergenic, intronic, or coding) with <10 valid bases (A, T, G, or C), or <20 valid/invalid bases (A, T, G, C, or N) in either species were discarded. Any clear nonhomologous sections were masked from all alignments (defined as regions where divergence was above 0.25 within a 40–60-bp sliding window). Genes were removed from the data set if the coding sequence was invalid in either species. A coding sequence was considered to be valid if it started with the start codon, ended with a stop codon, was a multiple of 3 bp in length, and contained no internal stop codons. Similarly, genes were removed if any introns did not start and end with a 2-bp consensus sequence (AT, GT, or GC at the 5′-end and AG at the 3′-end).

Estimating divergence and constraint

Divergence estimates were corrected for multiple hits (Kimura 1980), and mean divergence for sites within coding sequences, intergenic sequences, or introns was calculated per site (i.e., the average was weighted by the number of sites per sequence). Confidence intervals for mean divergence were calculated by bootstrapping the results by coding sequence, intergenic sequence, or intron. Constraint (C) is the estimated fraction of mutations removed by selection, and was calculated using a modified version of a method described previously (Keightley and Gaffney 2003). We used substitution rates within a putatively unconstrained standard sequence (FEI or FEF sites) from the same section of the genome to predict expected numbers (E) of substitutions in adjacent non-coding test sequences. Genomic sections were defined by splitting each chromosome into ∼100-kb chunks. For each section, all FEI sites and FEF sites were concatenated together to create two independent, unconstrained standards that were used to calculate constraint for sequences within that section. The method used accounts for differences in the base composition of the putatively unconstrained and test sequences by using estimates of four pairwise substitution rates to predict the expected number of substitutions in the test sequence given its base composition (A↔T, C↔G, A↔C/T↔G, A↔G/T↔C). This method assumes that point mutation rates of each possible kind are equal for the unconstrained standard sequences and the test sequence (Keightley and Gaffney 2003). Confidence intervals for statistics derived from constraint estimates were obtained by bootstrapping the results by genomic section.

Selecting FEI sites

Base pairs 8–30 (inclusively, from the 5′-end of the intron) within short introns are a good candidate for unconstrained sequence, since they have uniformly high divergence, on average (Fig. 2). A previous study has also shown that short introns (excluding splice-control regions) evolve faster than fourfold degenerate sites in D. melanogaster (Halligan et al. 2004), and there is evidence that fourfold sites in this species are subject to little selective constraint (Akashi 1995). However, even within these sites, divergence is correlated with intron length (Spearman r = −0.0575 [0.0102]). We plotted mean divergence for this subsection of introns against intron length to establish the intron lengths for which divergence within these sites was highest (Supplemental Fig. S1). For introns ≤65 bp in length, divergence is consistently high and thus we designated base pairs 8–30 from these introns only, as a class of putatively unconstrained sequence.

Selecting FEF sites

Negative selection for translational efficiency is thought to have shaped codon usage in Drosophila, resulting in codon-usage bias (Akashi 1995). This bias is known to vary between genes but also varies within the exons of a gene, such that it is stronger at the edges of exons than in the center (Comeron and Guthrie 2005), suggesting that selection is stronger at the edges of exons. This is thought to be caused by interference selection among fourfold sites in the center of exons, which results from their tight linkage (Comeron and Kreitman 2002). In order to select unconstrained fourfold degenerate sites, we attempted to remove the effects of selection for translational efficiency. In order to do this, we plotted mean divergence in fourfold sites as a function of distance from the edges of exons within non-overlapping blocks. When this is done, it is clear that divergence is lower at the edges of exons than in the center (Supplemental Fig. S2). However, divergence appears to be consistently high outside of the first and last 150 bp of each exon. Therefore, only fourfold sites from the centers of exons (excluding the first and last 150 bp), in genes with little or no codon-usage bias (where the “frequency of optimal codons” was <0.4), were used for the FEF unconstrained standard.