The Vacuole System Is a Significant Intracellular Pathway for Longitudinal Solute Transport in Basidiomycete Fungi

Abstract

Mycelial fungi have a growth form which is unique among multicellular organisms. The data presented here suggest that they have developed a unique solution to internal solute translocation involving a complex, extended vacuole. In all filamentous fungi examined, this extended vacuole forms an interconnected network, dynamically linked by tubules, which has been hypothesized to act as an internal distribution system. We have tested this hypothesis directly by quantifying solute movement within the organelle by photobleaching a fluorescent vacuolar marker. Predictive simulation models were then used to determine the transport characteristics over extended length scales. This modeling showed that the vacuolar organelle forms a functionally important, bidirectional diffusive transport pathway over distances of millimeters to centimeters. Flux through the pathway is regulated by the dynamic tubular connections involving homotypic fusion and fission. There is also a strongly predicted interaction among vacuolar organization, predicted diffusion transport distances, and the architecture of the branching colony margin.

Mycelial fungi have a growth form which is unique among multicellular organisms and which maintains a highly polarized internal cellular organization to support tip extension. Saprotrophic fungi are particularly adept at foraging for resources, often over inert substrates. This demands a bidirectional internal transport system to provide the tip with sufficient nutrients to maintain growth and to return newly discovered resources to the parent colony. However, despite the central importance of nutrient translocation to fungal growth, the mechanism(s) that drives transport and the identity of the transport pathway(s) are not known (5).

It is well established that the vacuole serves as a storage compartment for (poly)phosphate (1, 2) and nitrogen (N), particularly as N-rich amino acids (19), and as these compounds are also extensively translocated in both mycorrhizal and saprotrophic fungi (3, 5), it has been proposed that the vacuole system may be directly involved in their longitudinal movement (1, 3). Vacuolar organization is unique in the filamentous fungi, with all species so far examined possessing a highly dynamic pleiomorphic tubular vacuolar system (1, 2, 6, 16, 25, 28, 32, 33, 36). While superficially similar reticulate vacuolar networks appear during normal vacuole ontogeny in yeasts (39) and plants (e.g., see reference 20) or in specialized cells such as pollen tubes (14), only in the filamentous fungi does the vacuole form a constitutive, physically contiguous, extended organelle spanning several cell (septal) compartments over a considerable physical distance. If this vacuole supported transport, it would provide an internal compartment, separate from the cytoplasm, with high concentrations of solutes and would contribute to bidirectional solute movement (2). However, despite the unique nature and considerable potential importance of such an intracellular transport system to filamentous fungi, to date there has been no direct experimental test of either the mechanism or the rate of transport that such a vacuole system could support.

Fluorescence recovery after photobleaching (FRAP) of an internalized fluorescent marker is a commonly used approach to determine the connectivity of membranous compartments in vivo (23, 37). We have adapted such methods to quantify transport in fungal vacuoles of Phanerochaete velutina as a model of a fast-growing saprotrophic fungus. We first describe longitudinal vacuole development and dynamics, since the organization of the vacuole system changes markedly with the distance from the tip. Second, we quantify intra- and intervacuolar solute movements using FRAP for the different levels of vacuolar organization found in the system. Third, we construct a predictive simulation model from these data to determine the transport characteristics of the system over an extended length scale. Finally, to assess the importance of such transport in vivo, we predict the distance over which such a transport system could usefully operate.

This approach reveals that the vacuole system has a major impact on solute transport, on a scale of millimeters to centimeters, and may be particularly important in bidirectional solute transport against the direction of mass flow. Furthermore, it highlights the hypothesis that tubule formation and homotypic fusion events could act to regulate flux through the system. There is also a strongly predicted interaction among vacuolar organization, available nutrient levels, the predicted diffusion transport distances, and the architecture of the branching colony margin.

MATERIALS AND METHODS

Fungal material.

Cultures of Phanerochaete velutina were originally provided by L. Boddy, University of Cardiff, Cardiff, United Kingdom, and maintained in the Department of Plant Sciences, Oxford, United Kingdom, for the last 5 years. The fungus was grown on 2% malt agar (2% Oxoid no. 3 agar, 2% Oxoid malt extract) at 22 ± 1°C in darkness in a temperature-controlled incubator (Gallenkamp, England).

Fluorochrome loading and confocal microscopy.

A stock solution of carboxydifluorofluorescein diacetate (cDFFDA) (Oregon green 488 carboxylic acid diacetate; Molecular Probes, OR) was made at 10 mg ml⁻¹ in acetone and stored at −20°C. Fresh solutions were prepared daily by diluting the stock with deionized water to a final concentration of 5 μM. A 1- to 2-mm layer of agar containing the growing tips of the fungus was cut submarginally from 2- to 3-day-old cultures of P. velutina and floated on a solution containing 5 μM cDFFDA for 10 min. The sample was then washed for 10 min in deionized water, rinsed, and mounted in a chamber cut from layers of electrical insulation tape (Instant Tapes Ltd., Worthing, United Kingdom) to match the thickness of the agar slab. The chamber was sealed with a no. 1.5 thickness coverslip (Dow Corning, Barry, United Kingdom) and secured at the edges with high-vacuum grease (BDH, Poole, United Kingdom).

Fungal vacuoles labeled with cDFFDA were imaged using a Zeiss LSM 510 confocal microscope (Carl Zeiss, Jena, Germany) with a 1.2-numerical-aperture C-Apochromat 40× water immersion lens (Carl Zeiss, Jena, Germany). Carboxydifluorofluorescein (cDFF), released by intracellular esterases, was excited with a 488-nm line from a 30-mW Ar ion laser operating with a tube current of 6.1 A attenuated to <1 to 2% of full power. The intensity at the objective was 3 to 6 μW, measured with a Newport 1815-C power meter (Newport Corporation, Irvine, California). Fluorescence emission was detected using a 505- to 550-nm band-pass filter. Three-dimensional (3D) (x,y,z) or (x,y,t) and 4D (x,y,z,t) images were collected over a variable rectangular area aligned with the long axis of the hyphae, typically with (x,y) pixel spacing of 0.23 μm, or occasionally 0.45 μm, and z-section intervals of 1 μm, unless indicated otherwise in the figure legends. No temporal averaging was used to increase the framing rate. Time intervals between images are given in the figure legends. Typically, the confocal pinhole was set at ca. 2 to 4 Airy units as a compromise between the optical-section thickness (around 1.7 to 4.0 μm) and the signal intensity.

Image presentation.

For presentation, (x,y) images were normalized for each time point to account for normal levels of photobleaching during acquisition and the median values were taken from three to five consecutive time points on a pixel-by-pixel basis to reduce noise with MatLab 7.01 software (The MathWorks, Inc., Natick, MA). The intensity in (x,t) images was not adjusted.

Estimating the diffusion coefficient of cDFF in fungal vacuoles.

The diffusion coefficient of cDFF was measured in individual 20- to 40-μm-long vacuoles in vivo by FRAP. As dye movement is rapid over this length, images were collected over a small area and at a framing rate of around 40 ms. The dye in half of each vacuole was bleached using 40- to 100-ms scans, with 100% power for both the 458-nm and 488-nm laser lines. The average signal for the two halves of the vacuole was measured and normalized to the average intensity prior to the bleachingand after subtraction of the local background value. Data were corrected for the loss in fluorescence during normal scanning.

The vacuole was approximated as a uniform cylinder with flat ends, allowing diffusive transport to be collapsed to a one-dimensional spatial system. Half of the vacuole (of length L) was photobleached at a rate, B, for the time period T_b, giving the continuity equation for diffusion and reaction in the vacuole as the following:

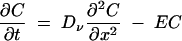(1)

where E = B when x is ≤0.5L and t is ≤T_b, and E = 0 when x is >0.5L or t is >T_b.

Neumann zero-flux boundary conditions were imposed at x = 0 and x = L. C is the concentration (intensity) of cDFF in the vacuole. B was estimated from the loss of fluorescence after photobleaching. The raw model output of concentration versus distance was integrated over the lengths of the bleached and unbleached regions to give paired values for each time point to compare against the experimental data, allowing the estimation of the vacuolar diffusion coefficient, D_ν.

Estimating the tube diameter connecting discrete vacuoles in a single hypha.

Rates of dye transfer were estimated on a vacuole-by-vacuole basis across a range of vacuole types following FRAP of single entire vacuoles. Framing rates were around 1 to 2 s for 150 to 300 s, with (x,y) pixel spacing at 0.23 μm. The overall bleaching duration depended on the size and number of vacuoles bleached and ranged from 2 to 20 s, with up to four regions bleached in separate hyphae per experiment. The depth of the bleaching under these conditions ranged from 40 to 90%. Data were visualized as animated (x,y) sequences or maximum projections along the hyphal width over time to give (x,t) images. For quantitative analysis, the average fluorescence intensity was measured for the bleached vacuole, all adjacent vacuoles, and the local background. The average background fluorescence was subtracted, and the data were corrected for the loss in signal during normal scanning, measured from vacuoles in adjacent hyphae that were not bleached. Correction values varied depending on the precise laser intensity and scan zoom but averaged 0.11% ± 0.6% s⁻¹. The volumes of the vacuoles were estimated from length and width (diameter) measurements, assuming a spherical, ovoid, or cylindrical geometry as appropriate.

For modeling purposes, as the longitudinal flux within the vacuoles was much faster than that between vacuoles connected by thin tubes, vacuoles were treated as blunt-ended cylinders of the same lengths and overall volumes. The physical system to be simulated consisted of a pair of vacuoles (lengths of left-hand vacuole [L_l] and right-hand vacuole [L_r]) connected by a relatively thin tube of length L_t. Equation 2 gives the diffusion of tracer within a cylindrical vacuole or within a connecting tube but is here subject to different constraints, i.e.,

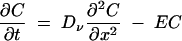(2)

where E = B when x is ≤L_t and t is ≤T_b, and E = 0 when x equals L_t or t is >T_b, with Neumann boundary conditions at x = 0 and x = L_l + L_t + L_r. C is the concentration of tracer expressed as the mass of tracer per area of the larger vacuole. The interface between the left-hand vacuole (C_l) and the connecting tube (C_t) is given by:

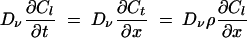(3)

at x = L_l, where ρC_l = C_t.

At equilibrium, the concentrations of tracer in the vacuole and in the connecting tube will be equal, so in terms of tracer mass distribution,

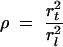(4)

where r_l² and r_t² are the radii of the left-hand vacuole and connecting tube, respectively. A similar interfacial condition applies at x = L_l + L_t.

The raw model output was the distribution of tracer in the system over time, but this output was integrated to give the average concentrations in the left-hand and right-hand vacuoles over time for comparison with experimental data. The unknown tube diameter was optimized against experimental data.

Estimating the connectivity in tubular vacuoles in a single hypha.

In tip regions with highly complex reticulate vacuolar systems, the aggregate rate of cDFF movement was estimated by FRAP of whole segments of hyphae spanning 9 to 21 μm using similar bleaching protocols for the individual vacuoles. For quantitative analysis, the average fluorescence intensities were measured in the bleached area during recovery.

The one-dimensional (1D) physical model has bilateral symmetry and approximates a semi-infinite cylinder with a bleached zone extending from zero to half the length of the bleached zone (length, L_b). The continuity equation is similar to equation 4 except that the value of the diffusion coefficient, D_ν, is replaced by a composite constant, D_TV, through a tubular vacuole (TV), where D_TV = D_ν · β and where β has a range of 0 to 1 and represents the combined effects of reduced cross-sectional area and increased path length (tortuosity):

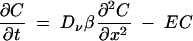(5)

where E = B when x is ≤0.5L_b and t is ≤T_b, and E = 0 when x is >0.5L_b or t is >T_b, with Neumann boundary conditions at x = 0. T_b is the duration of bleaching, as defined above. Note that the value of B depends to some extent on D_TV, because significant quantities of tracer can diffuse into the bleached zone during the bleaching period and subsequently become bleached. B and β were adjusted to obtain the best least-sum-of-squares fit between the experimental and the predicted data. The predicted concentrations in the bleached zones were integrated and averaged to compare with the experimental data. All the equations were solved numerically using finite difference methods (24).

Parameterization of N demand and vacuolar N content.

The N demand at the hyphal tip is the product of the rate of new biomass formation and the tip's N content, where the former is measured here as 132 μm h⁻¹, equivalent to production of 3.7 × 10⁻⁶ cm³ of new fungal biomass per cm⁻² cross-sectional area of hyphal tips per second. The research literature provides values for N content that have been determined from a wide range of experimental systems, including colonies growing under natural conditions. A minimum figure of 0.1 to 0.2% N (dry weight) has been reported for fungi with various life strategies on media with high C-to-N ratios (22). This would require a flux of approximately 3.7 × 10⁻⁷ mg N cm⁻² s⁻¹ to support maximum tip growth. The N content on media with low C-to-N ratios ranges from 1.3 to 5.0% (22). Others have reported a range of 1 to 8% N for different fungi in culture (13) or 2 to 4% N for woodland saprophytes (38).

Vacuolar amino acids, particularly arginine (4N), citrulline (3N), ornithine (2N), and glutamine (2N), are reported to reach concentrations of around 250 to 300 mM in mycelium grown on standard medium (∼0.5 to 1 M N), increasing to 1 M (∼2 to 3 M N) with an additional amino acid supply (7, 13, 18, 29). Taking into account the variable N content of different amino acids, a vacuolar concentration of 1 M N (14 mg N cm⁻³) seems a reasonable value derived from these data.

RESULTS

Vacuoles form a basipetal developmental sequence from the hyphal tip.

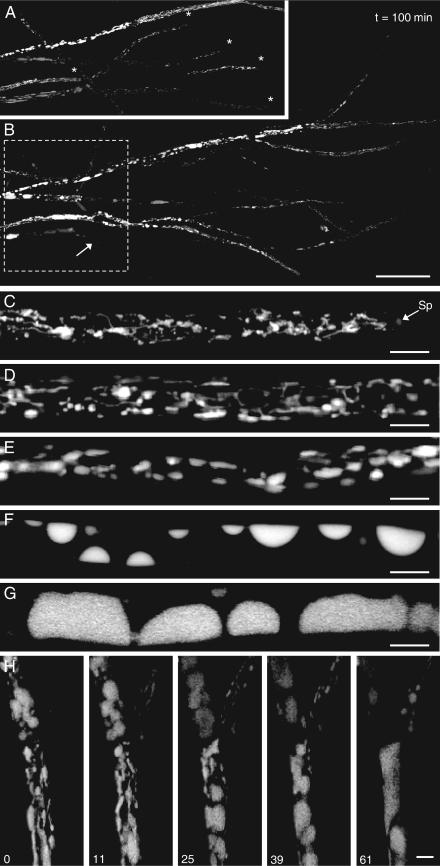
We optimized dye loading and confocal imaging conditions for P. velutina to give good signal-to-noise with minimal perturbation of hyphal growth rate. Rapid (5- to 10-min) pulse-chase labeling of hyphae with low concentrations (5 μM) of cDFFDA and low laser power (3 to 6 μW at the specimen) did not perturb tip growth (unloaded growth rate, 124.2 ± 5.4 μm h⁻¹; loaded growth rate, 122.2 ± 4.8 μm h⁻¹; loaded and imaged growth rate, 132.1 ± 4.1 μm h⁻¹) or branching (Fig. 1A and B).

FIG. 1.

Confocal imaging of vacuole morphology and ontogeny in growing hyphae of Phanerochaete velutina. (A and B) Tiled montages of maximum projections from 3D (x,y,z) images at the colony margin at times (t) of 0 (A) and 100 (B) min. In the intervening period, a sequence of 12 time-lapse 4D (x,y,z,t) images were collected from the region enclosed by the box (dashed outline). Loading and imaging did not affect the average growth rate. Thus, the growth rate of the tips marked with an asterisk in panel A was 127 ± 34 μm h⁻¹, comparable to that of unlabeled controls. Bar = 100 μm. (C to G) Maximum projections of 3D images moving basipetally (i.e., from the tip) to illustrate the developmental changes in vacuole organization. Sp, Spitzenkörper. Bars = 10 μm. (H) Maximum projections of the short hyphae (such as those indicated by the arrow in panel B), showing that the vacuolar system reverted to a tubular form during branch emergence. Bar = 10 μm. Time periods are given in min.

There was a predominantly longitudinal reticulate tubular system at the hyphal tip interspersed with various numbers of small (1- to 2-μm) vesicles (Fig. 1C), similar to the vacuole systems reported for other more slowly growing species (2). Occasionally, faint labeling of the Spitzenkörper was observed (Fig. 1C). The number of vesicles increased toward the base of the apical compartment, but the system was still dominated by the tubular component (Fig. 1D). This tubular network was distinct from the endoplasmic reticulum and elongate mitochondria (data not shown). More distal from the tip, the vesicles increased in size, and the frequency of tubes decreased (Fig. 1E). As the vacuoles reached ∼5 μm in diameter, they appeared to be appressed to the plasma membrane and shifted from a spherical or ovoid profile to a lens shape (Fig. 1F). With increasing distance from the tip, vacuoles enlarged further, and some filled the hyphal lumen (Fig. 1G). We subdivided the developmental continuum into four categories termed TV, located predominantly at the tip (Fig. 1C and D); mixed tubular and vesicular (MV), located in the subapical compartment (Fig. 1E); small vacuolar (SV), with vacuoles around half the hyphal diameter (Fig.1F); and large vacuolar (LV) (Fig. 1G). The extent of each zone was quite variable: sometimes the entire ontogenic sequence was complete within the first four septal compartments, or there could be an extended SV zone for several compartments before the development of the LV system. Prior to and during subapical branch emergence, the vacuolar system reverted to a tubular form, and the ontogenic sequence was reiterated during branch outgrowth (Fig. 1H). At a distance of more than 2,000 μm from the tip, the mycelium became too branched and entangled to clearly delineate vacuolar types and hyphal ancestry. Thus, rather than attempt a quantitative analysis, we simply note that much of the vacuole system throughout the peripheral growth zone conformed to the SV and LV patterns.

The vacuolar system is highly dynamic.

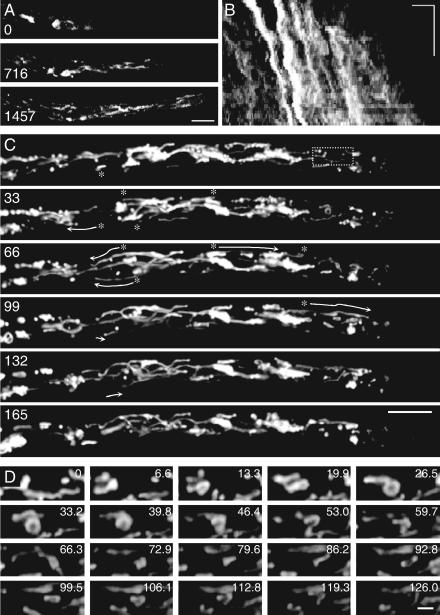
Highly dynamic tubular connections between vacuoles were observed throughout the vacuole system. At the very tip, part of the TV system maintained its organization with respect to the apex, roughly keeping pace with the rate of hyphal extension (Fig. 2A), observed as approximately parallel angled traces in distance-time (x,t) images (Fig. 2B). In addition, many rapid but intermittent short-range (10- to 50-μm) excursions of isolated tubes or tubular extensions from larger vesicles that subsequently either fused with other vacuoles or retracted were observed. Movement was bidirectional but was not organized in a coherent streaming pattern (Fig. 2C; see Video S2C in the supplemental material). In addition to net translocation, transiently isolated tubules also rearranged to form branched, Y-shaped structures or loops or collapsed back to form vesicles (Fig. 2D; see Video S2D in the supplemental material).

FIG. 2.

Tubuledynamics in the tips of growing hyphae of P. velutina. Vacuole dynamics were followed using time-lapse 3D (x,y,t) and 4D (x,y,z,t) confocal imaging. (A) Three images of a hyphal tip at the times indicated in seconds from a sequence lasting 1,440 s. (B) The corresponding maximum distance-time projection (x,t) is also shown. The growth rate (∼80 μm h⁻¹) was estimated from the gradient of the tip trace in the (x,t) image. Vesicles within the vacuolar system that keep pace with the tip leave angled tracks, approximately parallel to the tip. Horizontal bar = 10 μm; vertical bar = 600 s. (C) More-rapid and -complex tubule dynamics in maximum projections at the times (s) indicated . Images were cropped from a 4D image collected with (x,y) pixel spacing of 0.23 μm, with three optical sections at 3.7 μm in z and a sampling interval of 3.31 s (see Video S2C in the supplemental material). Tracks for selected tubules near the periphery are indicated (asterisks and arrows) and show rapid, bidirectional longitudinal movement. Bar = 10 μm; section spacing, 3.7 μm in z. Tubules were also observed to form loops and branched structures. (D) Enlargement of a sequence of every second image over a 2-min period from the boxed area in panel C showing a loop forming and resolving (see Video S2D in the supplemental material). Bar = 2 μm.

Once the vacuoles had enlarged and become immobilized in the MV and SV zones, they remained interconnected by an active network of fine tubes (Fig. 3A; see Video S3A in the supplemental material). Often, multiple tubes simultaneously connected adjacent vacuoles or even more-distant vacuoles. Occasionally, large vacuoles would become detached and move acropetally (Fig. 3B); this was observed in less than 10% of all experiments. The septal pores were closed immediately following mounting of the specimen, but they appeared to open within a few minutes of observation, because tubular connections and occasional vacuoles progressed between septal compartments. At a minimum, such an interconnected system must support diffusion, so we set out to quantify the extent and importance of diffusion to the longitudinal solute transport.

FIG. 3.

Vacuoledynamics and interconnection in hyphae of P. velutina using time-lapse 4D confocal imaging. (A) Maximum projections cropped from every 12th image of a 4D (984 by 143 by 8 by 67 pixels) sequence at the times (s) indicated. A series of large vacuoles are appressed to the plasma membrane but remain connected by a highly dynamic set of longitudinal tubules, often with more than one tube (arrows) connecting each vacuole (see Video S3A in the supplemental material). Bar = 10 μm. (B) Movement of a detached large vacuole (arrows), visualized as maximum projections cropped from a 4D (512 by 512 by 11 by 12 pixels) sequence lasting 60 min at the times (s) indicated. Bar = 10 μm.

Movement of cDFF within fungal vacuoles in vivo is consistent with a diffusion model.

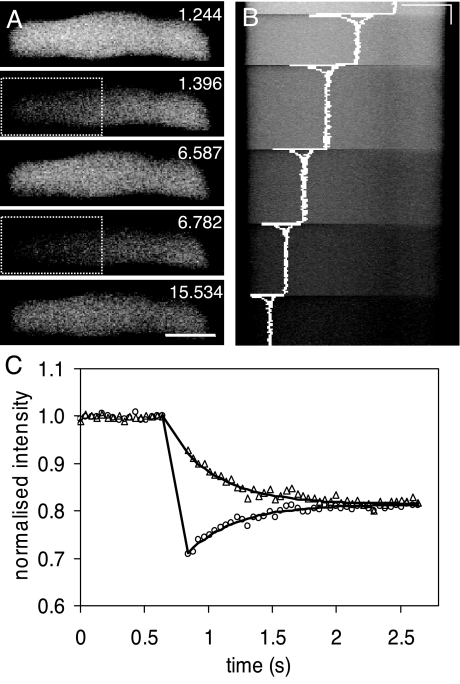
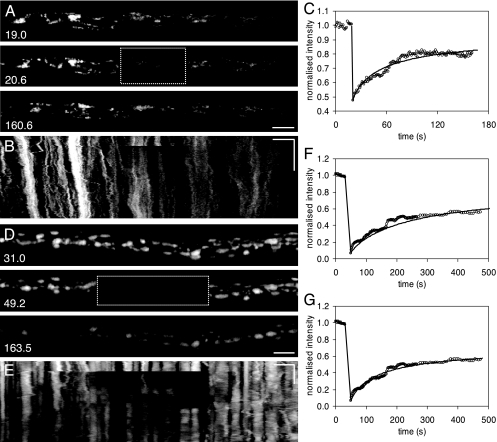
The diffusion coefficient of cDFF was measured by FRAP in extended, large vacuoles (25 to 35 μm long) that remained isolated from their neighbors. Approximately half of the vacuole was bleached (Fig. 4A), followed by a rapid recovery in the bleached area and a concomitant loss in the unbleached half (Fig. 4A and B). A one-dimensional diffusion model (equation 1) was optimized against the average intensity from each half of the vacuole, including changes taking place during the bleaching period itself (4). A typical FRAP data set is shown in Fig. 4C, together with the best-fit curve from the diffusion model, which accounted for 94% of the variance in the data. Five vacuoles were analyzed, with multiple FRAP experiments performed with each vacuole (Fig. 4B). The mean self-diffusion coefficient (D_ν) was (0.34 ± 0.046) × 10⁻⁵ cm² s⁻¹ at 20°C, with a median value of (0.31 ± 0.046) × 10⁻⁵ cm² s⁻¹. The agreement between the data and the model strongly supports diffusion as the only transport mechanism within vacuoles. The results also show that equilibration within a vacuole was rapid, reaching a steady state within a few seconds, even for the longest vacuoles examined.

FIG.4.

Measurement of the vacuolar diffusion coefficient for cDFF in vivo using FRAP. (A) Approximately half of a large vacuole, indicated by a box, was repeatedly photobleached at intervals, and 3D (x,y,t) images (216 by 64 by 834) were collected at a 43-ms framing rate. The prebleaching, immediate postbleaching, and recovery images are shown for the first two bleaching cycles at the times (s) indicated. Bar = 10 μm. (B) The (x,t) image for the full sequence, with the average intensity trace for the bleached and unbleached sides of the vacuole superimposed (white line). The intensity trace is plotted with relative intensity on the x axis and shows the total reduction in fluorophore signal caused by repeated photobleaching together with the very rapid equilibration after bleaching between the two halves of the vacuole. (C) The normalized trace for the first bleaching , with the bleached and unbleached regions shown as circles and triangles, respectively, together with the output of a 1D diffusion model fit to the data (solid lines) with a diffusion coefficient (D_ν) of 0.31 × 10⁻⁵ cm² s⁻¹.

The solute movement between vacuoles is consistent with diffusion through narrow interconnecting tubes.

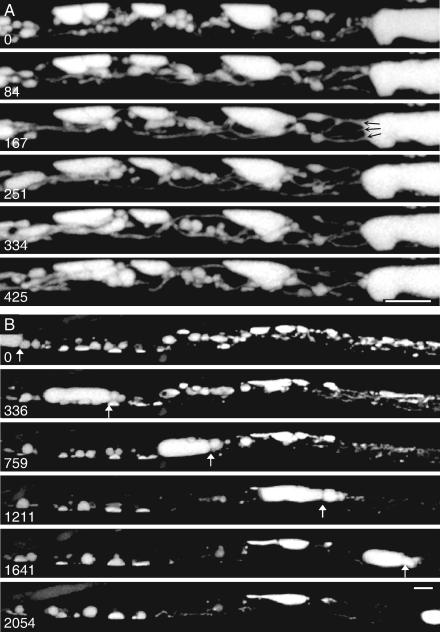
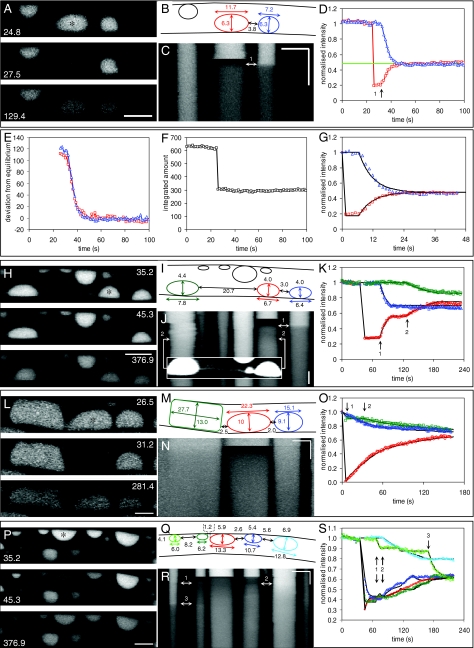
To explore whether a similar diffusive process could account for solute movement between vacuoles connected by narrow tubes, FRAP was used on entire individual vacuoles. Figure 5A illustrates the simplest case involving only two vacuoles. Immediately postbleaching, a decrease in intensity was visible throughout the bleached vacuole, with no indication of any internal diffusion gradient, as predicted from D_ν and the vacuole dimensions (Fig. 5B). In this experiment, there was no tubular connection during or immediately after the bleaching. However, after about 7 s, a connection that allowed the exchange of cDFF, visible as the equilibration of the internal concentrations in the (x, t) images, appeared (Fig. 5C). The final concentrations converged to the level predicted from the vacuole geometry and the starting concentrations (Fig. 5D). Furthermore, all the material appearing in the recovering vacuole was matched by a corresponding symmetrical loss from its neighbor (Fig. 5E), maintaining mass conservation (Fig. 5F). The exchange between the two vacuoles was well described by a diffusion model (equation 2) fit to the data using D_ν, the measured vacuole dimensions and separations (Fig. 5B), in which the only unknown was the functional diameter of the connecting tube (T_d) (Fig. 5G). In this example, T_d was 0.6 μm, giving rise to equilibration within 20 s following FRAP. Table 1 shows summary statistics for 11 cases that were clearly identified as isolated pairs of vacuoles which were suitable for estimating T_d. The average T_d was just under half a micrometer (mean, 0.48 ± 0.31 μm; median, 0.44 μm), although the range was quite wide. This finding compares with tube diameters of 0.24 to 0.48 μm measured using cryoelectron microscopy (28) or diameters of <0.5 μm measured with confocal laser scanning microscopy (36). The agreement between data and model and the consistency in tube dimensions measured using different approaches strongly support the hypothesis that longitudinal transport between vacuoles connected by tubes can be fully accounted for by a diffusive process.

FIG. 5.

Measurement of longitudinal transport through discrete vacuoles interconnected by fine tubes by FRAP. Movement of cDFF was measured by FRAP of entire individual vacuoles, marked with asterisks. Panel A shows the prebleaching, immediate postbleaching, and recovery images at the times (s) indicated, with the corresponding (x,t) image in panel C and the intensity trace for the bleached vacuole (red squares) and its neighbor (blue triangles) in panel D. The final position converged to the predicted equilibrium (green line in panel D). All the material appearing in the recovering vacuole was matched by a corresponding symmetrical loss from its neighbor (E), maintaining mass conservation (F). Exchange between the two vacuoles was well described by a diffusion model (G, solid lines) fit to the data using D_ν and the measured vacuole dimensions and separation, shown diagrammatically in panel B, with a functional tube diameter of 0.6 μm. Panels H to K show a sequence involving two sequential tubular connections, initially to the right-hand vacuole (transition 1) and subsequently the distant left-hand vacuole (transition 2). The connecting tube formed at transition 2 is shown as an inset in panel J. The diffusion model (K, solid lines) is fit with tube diameters of 0.19 μm and 0.3 μm, respectively. Panels L to O show a sequence with simultaneous connections present initially between the adjacent vacuoles, followed by transient disconnection (transition 1) and reconnection (transition 2). The data were fit to a discontinuous partial differential equation model (solid lines in O) with tube diameters of 0.3 μm and 0.4 μm. Panels P to S show a complex sequence involving five vacuoles requiring 12 tube connections or disconnections to reproduce the data (see Video S5P in the supplemental material). All horizontal bars = 10 μm; all vertical bars = 60 s.

TABLE 1.

Estimation of functional tube diameter in vivo

Vacuole type	Dimensions (length × ht) of vacuole pairs (μm)		Connecting tube
	Left	Right	Length (μm)	Diama (μm)
Small	8.6 × 9.0	8.0 × 9.0	3.7	0.55
	11.7 × 6.5	7.2 × 6.3	3.8	0.6
Large	24.1 × 6.6	18.5 × 7.4	6.0	0.6
	21.7 × 6.8	16.1 × 6.8	2.6	0.525
	20.1 × 7.2	19.5 × 7.5	15.6	1.5
	27.7 × 13.0	22.3 × 10.0	1.8	0.4, 0.32
	22.3 × 10.0	15.5 × 9.2	1.8	0.3, 0.18
	6.0 × 4.1	6.2 × 3.6	8.2	0.25, 0.5
	6.2 × 3.6	13.3 × 5.9	1.2	0.35
	13.3 × 5.9	10.7 × 5.4	2.6	0.6, 0.48
	10.7 × 5.4	12.8 × 6.9	5.6	0.28, 0.17

^aThe functional tube diameter connecting pairs of vacuoles was estimated by fitting a 1D diffusion model to recovery curves following photobleaching of the fluorescence in one vacuole of the pair. In some cases where disconnection and then reconnection occured, the functional tube diameter was estimated for both tubes independently.

Transport through multiple interconnected vacuole systems follows a diffusive process.

In many cases, the recovery process was more complex than the simple exchange between two vacuoles. Multiple connections (and disconnections) were visible in the time-series images. In some cases (Fig. 5H to K), separate connection events were seen as sequential steps in the recovery profile. By use of the earlier criteria of mass balance and flux symmetry, vacuoles involved in the exchange were identified even if they were nonadjacent (Fig. 5H). For example, as shown in Fig. 5H, 39 after a vacuole had been bleached, a tubular connection formed to the right-hand vacuole, 3 μm away (Fig. 5J and K, transition 1). This connection was severed about 20 s later. A second connection was then made to a vacuole lying 21 μm away to its left, 91 s postbleaching (Fig. 5J and K, transition 2). The very faint signal from the connecting tube is visible if the intensity is increased to saturate the signal from the adjoining vacuoles (Fig. 5J). The vacuoles on the opposite face of the hypha did not contribute to the recovery, even though they were physically much closer (Fig. 5I and J). In other cases, tubular connections were present initially between one or more vacuoles but became transiently or permanently disconnected. For example, as shown in Fig. 5L, one bleached vacuole was initially connected to both the left and right adjacent vacuoles. While the vacuole on the right remained connected throughout the recovery period, the tubular connection on the left broke after 9.5 s (Fig. 5O, transition 1) and then reformed after 33 s (Fig. 5O, transition 2).

To accommodate transient connections and disconnections of tubes, the original two-vacuole model was extended by decomposition into two separate partial differential equation models with Neumann boundary conditions during tube breakage and subsequent resynthesis after the tube connections reformed by using the internal boundary conditions (equation 2). The model was further extended to encompass multiple vacuoles connected in a series by such dynamic tubes. The output for this discontinuous diffusion model is shown for Fig. 5H to J and Fig. 5L to N in Fig. 5K and O, respectively. In all cases, good fits were achieved by varying the timing and diameter of the tubular connections from within the range of T_d. Thus, the model fit shown in Fig. 5K used tube diameters of 0.19 μm and 0.3 μm, respectively, for left and right connections, and the model shown in Fig. 5O used tubes of 0.4 μm and 0.3 μm diameter, respectively.

Even in cases with multiple interacting vacuoles and complex kinetics, combinations of T_d and connection timing were sufficient to well describe the patterns of individual vacuole responses. For example, in Fig. 5P, connections already existed between the bleached vacuole and the two smaller neighbors, leading to a considerable loss of signal in all three vacuoles during the bleaching phase and fairly rapid equilibration postbleaching. A complex series of 12 connections/disconnections were then observed. The most significant one started at 32 s with a small (0.25-μm-diameter) tube transiently connecting for ∼8 s to the next vacuole on the left (Fig. 5R and S, transition 1). Shortly afterward, a 0.28-μm-diameter tube connected to the larger vacuole on the right (Fig. 5R and S, transition 2) that gave a slow recovery within all three connected vacuoles. At around 140 s postbleaching, this connection was lost, before the vacuoles reached equilibrium. Conversely, the small vacuole on the left again connected (Fig. 5R and S, transition 3), and this time the tube was maintained for a sufficiently long time to effect complete equilibration with the initial triplet of vacuoles (see Video S5P in the supplemental material). This example serves to illustrate that even extremely complex bleaching recovery patterns were consistent within a discontinuous diffusion model.

The transport dynamics in different hyphal compartments can be simulated by extension of the geometrical diffusion model.

While FRAP experiments on individual vacuoles and small vacuole strings provided strong evidence for the diffusive movement of solutes on a local scale, they cannot be used to assess transport on a larger scale. For this, we used an extension of the simulation framework to link results from separate regions. We measured the width, length, and separation of vacuoles for each compartment type (Fig. 6A to C) and then resampled these distributions with replacements to build representative strings of connected vacuoles in silico. The strings of vacuoles were connected by tubes, with T_d set at the median value (0.44 μm), and run with Dirichlet boundary conditions of C = 0 and C = 1 at the two ends of the string until a steady state was reached. Figure 6D shows a single-time snapshot of the simulation after 500 s for a model system with evenly sized and spaced vacuoles for simplicity. Four scenarios were examined. The simplest was single tubes continuously connected (Fig. 6D, row i), which revealed that longitudinal transport was primarily controlled by the tube connections, with vacuoles filling up in a step-wise manner (Fig. 6E). The last tube filled in the sequence had the greatest impact on the net flux because of the low concentration gradient across it. The effect of intermittent connection, averaging 70% of the total time, was then examined (Fig. 6D, row ii). This reduced the rate of equilibration roughly in proportion to the decrease in average connection time (Fig. 6F). Finally, from the imaging data, on average, half of all vacuoles were connected by two or even three tubes (Fig. 3; Table 2). Thus, the effect of randomly assigning one to three tubes between each vacuole pair in the string was simulated with continuous (Fig. 6D, row iii) or discontinuous (Fig. 6D, row iv) connections. This resulted in a higher rate of equilibration for both continuously (Fig. 6G) and intermittently (Fig. 6H) connected strings.

FIG. 6.

Construction of a geometric diffusion model for longitudinal transport through discrete vacuoles. The frequency distributions for vacuole length (A), width (B), and separation (C) were measured from confocal images of hyphae with mixed tubular and vesicular vacuole organization (hatched bars, MV [n = 49]; open bars, SV [n = 52]; solid bars, LV [n = 110]). (D) Simulation of solute diffusion in regular 205-μm-long vacuole strings consisting of 13- by 6.5-μm vacuoles connected by 0.44-μm tubes for 500 s with Dirichlet boundaries of C = 1 (red) and C = 0 (blue) at the left- and right-hand ends, respectively. Vacuole pairs were connected by either one tube continuously (row i), one tube connected intermittently (row ii), one to three randomly assigned tubes present continuously (row iii), or one to three tubes randomly assigned and connected intermittently (row iv). Intermittent connections constituted 70% of the connections, on average, over time. (E to H) Distribution of solute for four cases described in panel D after 7.5, 62, 124, 248, and 500 s. (I) Representative strings of vacuoles assembled by random selection with replacement from the distributions shown in panels A to C and simulated under the same initial and boundary conditions as shown in panel D for LV (rows i and ii), SV (rows iii and iv), and MV (rows v and vi) systems. The first string in each pair is connected continuously, while the second is randomly disconnected/connected such that vacuoles remain connected 70% of the time (see Video S6I in the supplemental material). (J to L) Monte Carlo simulations of 400-μm strings like those shown in panel I were used to generate the diffusional efficiencies (α [see text]) for LV (J), SV (K), and MV (L) systems.

TABLE 2.

Frequency of tubular connections for different vacuole types

Vacuole type	n	No. (%) of vacuoles with fluorescence recovery			No. (%) with multiple tubes
		Immediate	Delayed	Total
Tubular	12	12 (100)	0	12 (100)	NAa
Mixed	24	21 (87.5)	1 (4.2)	22 (92)	12 (50)
Small	20	12 (60)	5 (25)	17 (85)	8 (40)
Large	21	13 (62)	4 (19)	17 (81)	12 (57)

^aNA, not applicable.

Diffusion through less regular strings representative of the different vacuole types with one to three randomly assigned tubes was then examined with both continuous and discontinuous connections. A single snapshot at 248 s is shown for LV (Fig. 6I, rows i and ii), SV (Fig. 6I, rows iii and iv), and MV (Fig. 6I, rows v and vi; and see Video S6I in the supplemental material). This shows that MV, SV, and LV strings equilibrate at different rates, as do differently sized vacuoles within a string. The effect of disconnection was more pronounced for vacuoles of different sizes than for uniformly sized vacuoles.

The effective diffusion coefficient for individual vacuole strings can be calculated.

At steady state with Dirichlet boundaries, the mass flux, J, through the composite vacuole string will be the same everywhere. This allowed the calculation of an effective diffusion coefficient for the whole string with Fick's first law, i.e., J = αD_ν(Δc/Δx). The α coefficient has a range from 0 to 1 and measures the reduction in the vacuolar diffusion coefficient, D_ν, caused by the inclusion of many smaller vacuoles and tubes in the string relative to a vacuole with a uniform diameter of the same length. The average length of each septal compartment (400 μm) was used as the length of the string. These results were then used to confirm that an adaptation of an analytical solution for laminates given by Crank (8) was sufficiently accurate for estimation at steady state:

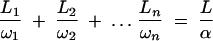(6)

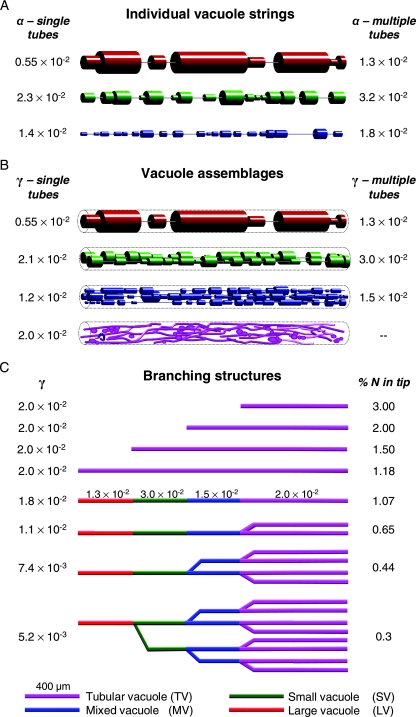
where L₁, L₂ … L_n is the sequence of vacuoles and tube lengths and ω₁, ω₂ … ω_n is the sequence of vacuoles and tube cross-sectional areas. Monte Carlo simulations of composite LV, SV, and MV vacuolar strings with intermittent connections gave mean values for α of 5.5 × 10⁻³, 2.3 × 10⁻², and 1.4 × 10⁻², respectively, for single tubes but with right-skewed distributions (Fig. 6J to L) or 1.3 × 10⁻², 3.2 × 10⁻², and 1.8 × 10⁻², respectively, for one to three randomly assigned tubes (see Fig. 8A). These α values relate to vacuolar strings with mean maximum diameters of 11.6 μm, 7.9 μm, and 5.3 μm for LV, SV, and MV regions, respectively.

FIG. 8.

Effect of vacuole organization and hyphal branching architecture on diffusive efficiency. (A) One thousand Monte Carlo simulations gave mean values of α (equation 1) for 400-μm lengths of vacuole strings either continuously connected by one tube (single tubes) or connected by a random number of tubes in the range of one to three vacuoles (multiple tubes). (B) γ values (equation 2) for 400-μm lengths of hyphae containing one (LV), two (SV), or four (MV) independent vacuolar strings (mean values from 1,000 Monte Carlo simulations). The β value for the tubular vacuolar region is shown for comparison (see text). (C) Values for γ of different branching structures are shown (ν) as well as the values indicating the maximum tip nitrogen content that can be supported by diffusion in the structure to tips growing at their maximum rate (% N in tip).

The solute movement through the tubular vacuole system can also be described by a diffusion model.

While the geometrical diffusion model worked well for the discrete vacuolar systems, it was impossible to define the geometric organization of the TV system. We therefore analyzed the TV system as a system of interconnected longitudinal tubes occupying a fraction of the hyphal cross section, through which diffusion could take place. Over a scale of reasonable length, such a system approximates a quasi-homogeneous porous body in which Fickian laws of diffusion operate but with a greatly reduced apparent diffusion coefficient because of the reduced cross-sectional area for diffusion and the tortuous nature (increased path length) of the small tubes.

Extended areas spanning the full hyphal width were bleached to quantify transport. For example, FRAP in a 29-μm-long region near the tip (Fig. 7A) showed recovery in some small fixed vesicles (vertical traces) and dynamic incursions of structures into the bleached areas in the (x,t) image (Fig. 7B), both of which would contribute to the net rate of recovery. A diffusion model was fitted to the recovery profile (Fig. 7C) to obtain an apparent diffusion coefficient for the TV region(D_νβ, equation 5). However, in most cases, particularly near MV regions, a single-compartment model did not describe the TV recovery profiles well, with evidence of underfitting early and overfitting later. In these experiments, tubular connections and disconnections were evident from the rapid filling of a number of fixed vesicular structures in a series of steps (Fig. 7D to F; see Video S7D in the supplemental material). While many of these vesicles were connected during the recovery phase, we inferred that a number remained functionally isolated. The model was therefore modified to include an immobile phase which stored a proportion (P) of the tracer but did not exchange it within the diffusional timescale. This gave a better fit to the data (Fig. 7G, P = 20%). The results for 10 data sets analyzed for the TV region are shown in Table 3. The mean value for β was (2.0 ± 0.5) × 10⁻², while the mean value for P was 21% ± 4%.

FIG. 7.

Measurement by FRAP and modeling of longitudinal transport through the tubular vacuole system at the hyphal tip. (A) Images are shown prebleaching, immediately postbleaching, and after recovery from photobleaching in the boxed region at the times (s) indicated . (B) In the corresponding (x,t) projection, the slight angle of the traces for prominent vesicles matches the rate of tip growth as in Fig. 1B. The average intensity for the bleached region is shown in panel C, together with the model output for a β of 0.015. Panels D and E show equivalent figures for a second hypha with an MV system, which showed evidence of systematic bias in the fit with underfitting early and overfitting late to the data (F) (β = 0.002) (see Video S7D in the supplemental material). The model was modified to allow for a proportion, P, of tracer occurring in an immobile form (see text), and panel G shows the fit with this two-parameter model (β = 0.005; P = 20%). Horizontal bars = 10 μm; vertical bars = 60 s.

TABLE 3.

Summary statistics for the tubular vacuole system

Location	βa	Pb
Tip	0.005	0.2
	0.0065	0.32
	0.015	0
	0.025	0
	0.04	0.35
Subtip	0.005	0.2
	0.025	0.35
	0.025	0.2
	0.05	0.325
Mixed	0.005	0.2

^aCoefficient β measures the reduction in the diffusion coefficient (D_ν) caused by diffusion that is restricted to tubules and small vacuoles which occupy only a small fraction of the hyphal lumen.

^bP, proportion, represents the fraction of the fluorescence tracer that was immobile and did not contribute to diffusion over the time period measured.

Scaling up to in silico hyphae.

To represent diffusion along the whole hyphal lumen, it was necessary to include the total cross-sectional area (θ) of the lumen occupied by the vacuole strings. Both the TV and LV systems effectively filled the hypha, while single strings of MVs and SVs occupied maximum proportions of 0.21 and 0.46 of the lumen, respectively. Visual inspection of the hyphae suggested that MV compartments typically had a vacuole system assembled from four parallel strings, while SV had two strings (Fig. 8B). Using these vacuole assemblages, the diffusion coefficients on a hyphal basis (γD_ν, where γ = nθα) gave γ coefficients of 1.2 × 10⁻², 2.1 × 10⁻², and 0.55 × 10⁻² for MV, SV, and LV, respectively, with single tube connections. These values increased to 1.5 × 10⁻², 3.0 × 10⁻², and 1.3 × 10⁻², respectively, for systems with up to three randomly assigned tube connections. These latter values were used for the simulations described below, together with the value for the TV hyphae of 2.0 × 10⁻².

With experimentally derived estimates of γD_ν in each of the four classes of vacuolar compartments, it was possible to build larger-scale simulation models of composite hyphal structures with different compartment compositions and branching architectures (Fig. 8C). The composite (c) diffusion parameter (D_c) for these branched systems was calculated for TV, MV, SV, and LV hyphal compartments using either a modification of the numerical methods used to simulate the α values or an extension of equation 6. For example, equation 7 below gives D_c for a fully branched hypha (eight tips) with a total length of 2.0 mm, representing 400-μm LV, SV, and MV septal compartments growing from the stub of an open-vessel hypha and 8- by 800-μm TV compartments at the tip (L_TV) just before septation:

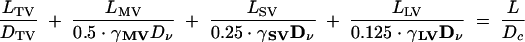(7)

The D_c for this fully branched structure was 1.6 × 10⁻⁸ cm² s⁻¹. This diffusion rate is about 4-fold lower than that of the equivalent unbranched system and about 60-fold lower than that calculated if the entire lumen of the same branched structure was available for diffusion (9.7 × 10⁻⁷ cm² s⁻¹). Branching progressively reduces the D_c over a 2-mm length (Fig. 8C). For comparison, a 2-mm unbranched hypha with the entire lumen available for transport would have a D_c value about 200-fold higher (3.1 × 10⁻⁶ cm² s⁻¹).

The diffusive transport is physiologically relevant over a scale of millimeters.

We have demonstrated that longitudinal transport through a vacuolar pathway is fully compatible with a diffusive process and have quantified the process. Intermittent tubular connections enabled solute movement between otherwise discrete vacuole compartments, but the overall rate was considerably lower than if the whole hyphal lumen were available for transport. However, to determine whether this pathway is of any physiological significance to solute transport, we need to consider the quantitative transport requirements of the hyphae. A suitable context for this would be the supply of N from an N-rich colony center to the tips growing across an N-poor substrate. While we do not imply that this is the main transport route for nitrogen in this situation, we can assess whether it could be by calculating N flux through the vacuolar pathway from Fick's first law:

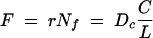(8)

where F is the N flux required to allow maximum tip growth, r is the maximum tip growth rate, N_f is the fractional volumetric tip N content, D_c is the composite diffusion coefficient for the hyphal structure (D_ν for amino acids is assumed to be similar to cDFF on a molecular weight [MW] basis), C is the constant concentration of vacuolar N being maintained at the distal end of the LV compartment, and L is the distance between this region and the tip. In the limiting case, we assume that the vacuolar N content at the tip is zero, as all the nitrogen is withdrawn for growth. We parameterized this equation from literature sources (see Materials and Methods) and solved it for a variety of hyphal structures and values of N_f. For example, an unbranched hypha composed entirely of TV vacuoles with a 0.1% N demand at the tip could be supplied via diffusion over a 24-mm length. A fully branched, 2-mm hyphal structure with TV vacuoles could have 0.37% N at the tip and still support unlimited tip growth by diffusion. Other scenarios are shown in Fig. 8C.

DISCUSSION

The dynamic, pleiomorphic vacuolar system in P. velutina is similar to that in other basidiomycetes.

The organization and dynamics of the vacuolar system in P. velutina visualized in vivo closely matched descriptions for a wide range of fungi, including slower-growing mycorrhizal species such as Pisolithus tinctorius (1, 2). We therefore believe that the results presented here will be applicable to all basidiomycetes. The relatively rapid growth of P. velutina allowed the observation of developmental sequences, such as the reversion to a TV system during branch emergence, that were previously not possible to observe. We have not addressed the mechanism underlying tubule motility in this study. By reference to other filamentous fungi, it is likely to involve microtubules rather than microfilaments (15, 34). A subtle role for actin in homotypic fusion is possible (11) but has not yet been examined for filamentous fungi.

The environment in the vacuole is predominantly aqueous.

We estimate the diffusion coefficient for cDFF in water to be 0.4 × 10⁻⁵ cm² s⁻¹ by interpolation between the reported values for fluorescein (MW, 332) of 0.48 × 10⁻⁵ cm² s⁻¹ and for rhodamine green (MW, 508) of 0.27 × 10⁻⁵ cm² s⁻¹ (9, 10). Thus, the D_ν measured in vacuoles in vivo was ∼75% of that in pure water, with the difference probably due to molecular crowding by high concentrations of other solutes (12). This study is the first report of a vacuolar diffusion coefficient and confirms that the environment of the vacuole is predominantly aqueous. For comparison, the diffusion coefficient of both low- and high-MW molecules in cytoplasm is about fourfold lower than in pure water (17, 31).

The intervacuolar solute movement can be described by a diffusion model.

Transport through the interconnected vacuolar system was fully accounted for by diffusion. This intravacuolar transport pathway would operate in parallel with any mass flow in the cytoplasm or apoplast. Indeed, the observations that the vacuoles are anchored to the plasma membrane (6) and appear to be buffeted by a mass-flow stream may suggest that one function of the vacuole network is to allow transport against the acropetal mass flow needed to support tip extension. Although occasional apical movement of detached large vacuoles was observed, the low frequency and number of vacuoles (<10% of all hyphae observed) do not suggest that this mechanism contributes substantially to longitudinal transport. Likewise, small vesicle movements, “crawling” of large vacuoles, or even peristalsis-like contractions of tubular vacuoles have been observed in other species and could contribute to net solute movement (1, 2, 6) but were not explicitly required to explain the movement of cDFF in P. velutina reported here.

The diffusive efficiencies remain similar despite major changes in vacuolar organization with distance from the tip.

Although the vacuole system undergoes major changes in organization with development, the effects of various tube numbers and connectivities result in comparable diffusive efficiencies in all septal compartments. If we assume that all the reduction in diffusive flux is due to a reduction in cross-sectional area rather than tortuosity, then the effective cross-sectional area of the TV system is 2% or equivalent to 10 tubes continuously connected throughout the length of the network. As the vacuoles become larger, the local flux through them is greatly increased in comparison to the flux in the TV system, but overall flux is significantly reduced by the narrow, intermittent tubular connections. Thus, in the LV region, a single connecting tube reduces the flux to 27% of the equivalent length of the TV system. However, as most of the bleaching data suggest, vacuoles in the SV and LV regions have at least two to three tubes, bringing the total predicted flux up to comparable levels across the entire system. It is also significant that the distribution of predicted efficiencies in simulated hyphae is skewed toward larger values (Fig. 6J to L), with some hyphae having two or even three times the mean predicted rate of transport. If this simulation translates into differential transport in a real colony, it would suggest that a subset of hyphae would benefit from more rapid nutrient transport, presumably growing faster and perhaps emerging as leading hyphae.

The vacuolar transport pathway could be locally regulated.

In the LV region, it is clear that the thin tubes connect vacuoles only periodically and that this has a major impact on the total flux. This raises the possibility that the regulation of tube connection/disconnection frequency and the number of connecting tubes would allow the hyphae to modify the rate of solute transport according to local conditions. There has been extensive characterization of the molecular events underlying homotypic vacuole fusion and its control in Saccharomyces cerevisiae which has identified a complement of proteins associated with vesicle docking and fusion, interaction with the actin cytoskeleton, and regulation by kinases and dynamin GTPases (21, 27, 30, 39). At this stage, virtually nothing is known about the molecular processes underlying tubule extension, vesicle motility, and control of vacuole fusion in filamentous fungi. Where comparisons have been made, the putative role of homologous genes is matched by their mutant phenotypes. Thus, in Aspergillus nidulans, mutation of the vpsA homologue of VPS1 (35) or the avaA homologue of VAM/YPT7 both give a fragmented vacuole phenotype similar to that observed for comparable mutants in S. cerevisiae (26). Thus, one of the next major goals will be to apply the knowledge gained from genetically tractable systems such as S. cerevisiae to systems such as P. velutina, in which homotypic vacuolar fusion appears to have a profound impact on the physiology and survival of the entire organism.

Vacuoles provide an important and independent transport pathway.

The elaboration of an internal longitudinal transport compartment provides a unique solution to the problem of nutrient translocation. Diffusive movement through this system permits bidirectional transport along source-sink gradients and may be particularly important for solute movement against mass flow needed for turgor-driven tip extension. The organization of the system into discrete vacuoles connected by dynamic tubes has the potential for sophisticated control of flux, through the regulation of both tube elongation and homotypic vacuole fusion. Tubular connections spanning the septal pore maintain continuity over an extended length scale (28, 32), but it is also clear that the pore can temporarily close following shock to the system. Furthermore, as diffusion is concentration dependent, dynamic manipulation of the vacuolar volume at different locations within the hyphae could also locally shift the direction of solute flux.

This study provides the first quantitative assessment of the role for the vacuole in longitudinal transport for a filamentous fungus. The widespread occurrence of such vacuole systems among the basidiomycete fungi and the generic nature of the model suggest that the approach and results presented here have predictive value across a significant number of organisms in a diverse range of habitats.