Collective Bacterial Dynamics Revealed Using a Three-Dimensional Population-Scale Defocused Particle Tracking Technique

Abstract

An ability to monitor bacterial locomotion and collective dynamics is crucial to our understanding of a number of well-characterized phenotypes including biofilm formation, chemotaxis, and virulence. Here, we report the tracking of multiple swimming Escherichia coli cells in three spatial dimensions and at single-cell resolution using a novel three-dimensional (3D) defocused particle tracking (DPT) method. The 3D trajectories were generated for wild-type Escherichia coli strain RP437 as well as for isogenic derivatives that display smooth swimming due to a cheA deletion (strain RP9535) or incessant tumbling behavior due to a cheZ deletion (strain RP1616). The 3D DPT method successfully differentiated these three modes of locomotion and allowed direct calculation of the diffusion coefficient for each strain. As expected, we found that the smooth swimmer diffused more readily than the wild type, and both the smooth swimmer and the wild-type cells exhibited diffusion coefficients that were at least two orders of magnitude larger than that of the tumbler. Finally, we found that the diffusion coefficient increased with increasing cell density, a phenomenon that can be attributed to the hydrodynamic disturbances caused by neighboring bacteria.

Diffusion of passive small particles (micron and submicron size) surrounded by a fluid medium is a classical problem in fluid mechanics, where the diffusion process results from the random thermal forces acting on the small particles (34). The relationship between the macroscopic parameter, the diffusion coefficient, and the microscopic behavior, the thermal fluctuation, was derived by Einstein about 50 years ago and is now known as the Stokes-Einstein equation. Recently, it has been shown that a diffusive process can arise in suspensions of small active particles, a phenomenon commonly associated with peritrichously flagellated bacteria. Particular focus has been given to understanding the biochemical and biophysical cues governing the movement of individual Escherichia coli cells (6, 11, 23, 26) and how the response to these cues is coordinated throughout a population of cells (4, 20, 31, 32, 39, 42).

In a uniform environment, E. coli cells exhibit swimming behavior that has been characterized as a three-dimensional (3D) random walk (5, 8, 11). This behavior arises from a collection of extracellular helical thread-like filaments known as flagella. Each of these filaments is equipped with a bidirectional, ion-driven rotary motor at its base (8, 10). Counterclockwise motor rotation causes the flagella to form a polar-localized bundle that propels the cell forward in a “run” mode. These smooth runs are terminated by short episodes of erratic motion without net translation that are known as the “tumble” (40). Tumbling is caused by clockwise motor rotation that, in turn, disrupts the flagellar bundle. Following each tumble the bacterium moves in a new, seemingly random direction. Thus, in an isotropic medium lacking gradients of chemoattractants, an individual cell performs a random walk where the distribution of run times is exponential and has a mean of ∼1 s (11).

These modes of locomotive behavior of swimming E. coli can be monitored using a variety of experimental techniques. For instance, single-cell tracking can be accomplished using cinematography (21, 28), computer tracking (36), fluctuation spectroscopy (3, 38), laser intensity correlation spectroscopy (29), stroboscopic photography (27), and videotape analysis (18). It should be noted, however, that all of these approaches are limited to two-dimensional analysis where swimming behavior is likely to be modified due to confinement (17) and where accurate measurements of the turn angle are difficult to make since a single cell rarely stays in the same plane of focus for subsequent runs. To overcome these limitations, Berg successfully tracked single swimming E. coli cells in three dimensions using a tracking microscope (6, 9). In Berg's studies, the position (x, y, and z axes) of the microscope stage was controlled electronically such that one swimming E. coli cell was always in focus. The electronic signal controlling the microscope stage was used to infer the 3D trajectory of the swimming bacterium. Using this approach, Berg and coworkers elucidated many important features of bacterial locomotion as well as its relation to the cell's chemical sensory system (11). In addition, the diffusion coefficient of a bacterial suspension could be inferred from single bacterial cell tracks in conjunction with a theoretical model (25). A limitation of the tracking microscope is that it is restricted to the analysis of a single cell and cannot access population-scale behavior. The capillary assay (1, 35) is the most commonly used population-scale motility and chemotaxis assay, especially for quantitative analysis (24). Other commonly used population-scale assays include the swarm plate (2) and temporal gradient assays, performed by imposing an abrupt change in concentration using a temporal gradient apparatus (27) or a stopped-flow diffusion chamber (15, 16). All of these assays allow for direct quantification of macroscopic transport parameters; however, they are incapable of directly probing individual cell dynamics.

When cells swim through a fluid medium, the flagella exert a force driving the cell motion, while the body of the bacteria experiences an equal and opposite drag force. These forces can be expected to produce fluid motion, and this motion can be monitored experimentally by tracking the motion of passive particles (e.g., polystyrene beads) embedded in bacterial suspensions (19, 22, 39, 42). Using this approach, Wu and Libchaber tracked micrometer-sized particles seeded in an E. coli bath confined in a two-dimensional soap film (42). They found that seeded micron-scale particles diffused more readily when they were surrounded by swimming bacteria, compared to the situation where the passive particles were surrounded by a fluid medium only (42). The mean-square displacement of the particles increased linearly with time (normal diffusion) when time t was larger than a correlation time yet increased faster than linearly with time (corresponding to “superdiffusion”) when time t was less than the correlation time. The relatively large correlation time and tracer particle diffusion coefficients observed in these experiments suggest that the fluid flows are associated with a collective motion of groups of bacteria rather than simply a sum of random, uncorrelated fluid velocity disturbances due to individual cells. More recently, the diffusion coefficient of passive tracer particles was measured by flowing two streams of fluids adjacent to each other in a microfluidic channel where one stream contained a mixture of microspheres and bacterial cells and the other stream contained blank buffer (22). The gradient diffusion coefficients of the microspheres were found to increase by two orders of magnitude compared to the situation where no bacteria were present.

In this study, we explored the diffusion process of an active particle suspension composed of E. coli cells by using a novel 3D particle tracking procedure that relies on defocused imaging. Using this approach, we have effectively extended 3D tracking of single bacterial cells (6) to allow multicellular tracking at single-cell resolution. The ability to track multiple cells simultaneously allows us to probe the characteristics of an individual bacterium (e.g., motor power and motility) and, at the same time, its collective behavior (e.g., diffusion coefficient, collective dynamics, and quorum sensing). In particular, we investigated the roles that microscopic behavior of bacteria, bacterial locomotion, and cell-cell interactions have on each cell's ability to disperse in space. We found that the diffusion coefficient of smooth-swimmer E. coli cells is one order of magnitude greater than that of wild-type cells, and both wild-type and smooth swimmers had diffusion coefficients that were at least one order of magnitude larger than tumble-only cells. We also measured diffusion coefficients of the bacterial suspension as a function of cell density and observed an increase in the diffusion coefficient as cell density was increased. This counterintuitive behavior is reminiscent of the larger-scale cooperative motions that have been observed previously for swimming bacteria (19, 22, 39, 42). To our knowledge, this is the first study to investigate bacterial diffusion at cell concentrations high enough for cell-cell hydrodynamic interactions to be important, where the suspension was not confined to a film whose thickness is comparable with the persistence distance of the bacteria. The ability to make these observations is enabled by the unique combination of 3D cell tracking and fluorescent-nonfluorescent cell mixing.

MATERIALS AND METHODS

Strains, plasmids, and growth conditions.

The E. coli strains used in this study were kindly provided by Sandy Parkinson and included the following: RP437, wild type for chemotaxis (33); RP9535 [Δ(cheA)1643 (eda⁺) lacY1] (37); and RP1616 [Δ(cheZ)m67-25]. In order to confer fluorescence to bacteria, we transformed cells with the plasmid pTG which expresses the gfpmut2 gene (12), a variant of the green fluorescent protein that fluoresces more intensely, under control of the arabinose-inducible pBAD promoter (13).

Preparation of bacteria was similar to that described previously (14). Briefly, bacterial cultures were grown overnight at 30°C in 10 ml of Luria-Bertani medium supplemented with 20 μg/ml chloramphenicol (Sigma) in a 125-ml shaker flask. Overnight cells were diluted 1:100 into fresh medium and grown at 30°C until the attenuance at 600 nm (D₆₀₀) reached 0.2, at which time 0.2% arabinose (Sigma) was introduced into the culture to induce green fluorescent protein expression. When the D₆₀₀ reached 1.0, cells were harvested by centrifugation at 2,200 × g at room temperature for 10 min and then resuspended in minimal M9 medium just prior to microscopy analysis. Microscopy work was typically performed immediately following cell harvesting.

Bacterial suspensions of different cell density, but with an identical number of fluorescent cells, were achieved by mixing nonfluorescent cells (either cells lacking the pTG plasmid or cells carrying the pTG plasmid but no chemical induction) with the fluorescent cells. For optimal tracking results, the fluorescent cell concentration was fixed at 1 × 10⁷ cells/ml. Cell concentration was determined from D₆₀₀ measurements, where a D₆₀₀ value of 1 corresponds to a cell concentration of 10⁹ cells/ml. The cell chamber was made by sandwiching a rubber O-ring (height, 1.5 mm; diameter, 8 mm) between two glass microscope slides (25.4 mm by 76.4 mm by 1 mm). A total of 100 μl of a bacterial suspension was loaded inside the O-ring before the chamber was sealed. Finally, a thin layer of Vaseline was applied around the O-ring to ensure that it was watertight.

Microscope and camera.

An Olympus epifluorescent microscope (BX51) with a 20× Olympus objective lens (UPlan; numerical aperture, 0.5), a fluorescein filter cube (excitation wavelength, 480 nm; emission wavelength, 535 nm; Chroma Technology Inc.), and a 100 W mercury lamp were used for all the data shown below. The microscope has a manual 3D (x, y, and z directions) microtranslation stage. Along the z direction, the distance is controlled by both a coarse and fine adjustment knob. The fine adjustment knob has a z distance reading with a resolution of 1 μm. We used a cooled charge-coupled-device camera (CoolSNAP HQ, Photometrics, California). The charge-coupled-device array contains 1,392 by 1,040 pixels, and each pixel has a physical dimension of 6.45 μm by 6.45 μm. The viewing volume is 449 μm by 335 μm by 75 μm using the combination of this lens and camera. The images were processed using a Matlab (Mathworks Inc., Massachusetts) routine to obtain the x, y, and z coordinates of each bacterial cell. To address the reproducibility of the technique, replicate movies tracking the same cells were generated, and the resulting estimates of the macroscopic transport parameters (e.g., diffusion coefficient, D) exhibited an error of ≤10% error.

RESULTS

Three-dimensional tracking of individual bacterial cells using defocused light.

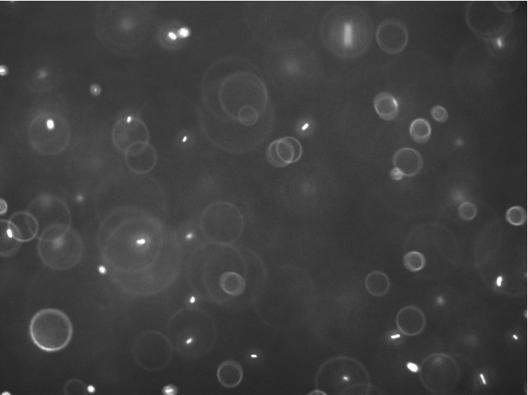
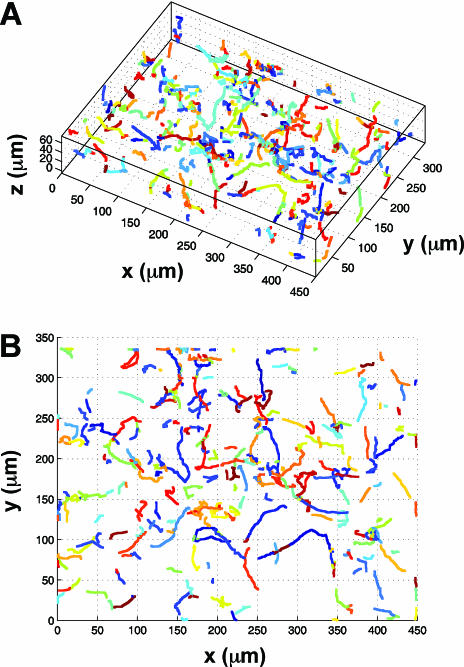
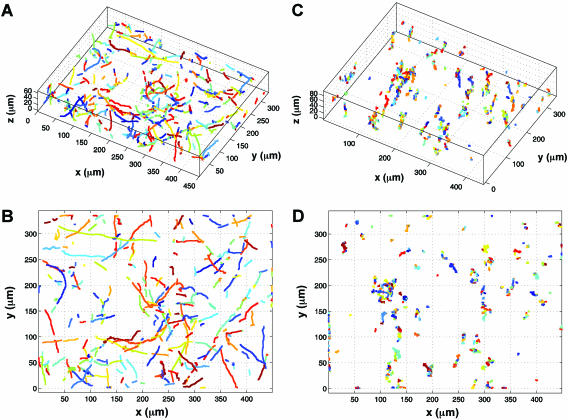
We first investigated the locomotion of bacterial cells using the wild-type E. coli strain RP437 (wild type for chemotaxis) and two of its derivatives, namely RP9535 (smooth swimmer) and RP1616 (tumbler), in conjunction with a novel 3D defocused particle tracking (3D DPT) technique. To ensure that the observed swimming behavior was not influenced by the chamber surfaces, we adjusted the microscope stage in such a way that the focal plane was ∼500 μm under the bottom surface of the top glass slide. This was achieved by first focusing on the cells attached to the top glass slide and then adjusting the microscope stage upwards by ∼500 μm using the manual micrometer attached to the microscope stage. Once the stage was properly positioned, we captured a sequence of images using ImagePro Plus (Media Cybernetics Inc.) image processing software. The typical time between consecutive images was 150 ms, and each time sequence consisted of 300 images. A movie of the swimming bacteria coming into and out of the plane of focus can be viewed online at http://www.mae.cornell.edu/mingming/RecentResearch/Ecoli/Ecoli.htm. It should be noted that rings will appear only when the bacteria move away from the focal plane and toward the imaging plane. When the bacteria move in the opposite direction, their images become fuzzy dots and disappear. Details can be found in Wu et al. (41). Shown in Fig. 1 is an original image of the swimming bacteria. The bright dots are images of individual cells that are in focus, while the rings are images of bacterial cells that swim between the focal plane and the imaging plane. The most important feature of the 3D DPT technique relies on capturing the third dimension via the quantitative use of the information contained in the defocused ring image. Here, the ring diameter is directly related to the distance between the objective lens and the object producing the ring (e.g., an individual cell). Prior to each experiment, a calibration procedure was carried out as described previously (41), where images of a 1-μm fluorescent bead at various z locations were taken. The relation of the defocused ring radius as a function of the third dimension z was then obtained. Using an in-house software package, we identified the center as well as the ring size of each bacterium depicted in Fig. 1. This information was then translated into the coordinates (x, y, and z) for each bacterial cell in the image, and the process was repeated for all the images in a time series. The final step involved forming the trajectories of each bacterial cell using the nearest-neighbor method (30). A 3D rendition of 630 trajectories for swimming RP437 cells is shown in Fig. 2A, while the projection of the 3D trajectory to a 2D plane (the x-y plane) is shown in Fig. 2B. The characteristic run and tumble behavior for this strain is clearly seen in the plot. Additional experiments were performed using isogenic strains derived from RP437, namely RP9535 and RP1616, which are known to exhibit smooth swimming and tumble-only behavior, respectively (37). The trajectories of the RP9535 cells (Fig. 3A and B) clearly show that the cells swim smoothly, as evidenced by the lack of abrupt turns seen above for RP437 (compare Fig. 2B and 3B). This swim-only behavior was expected as the Δ(cheA)1643 mutation carried by RP9535 causes the flagellar bundle to rotate only in the counterclockwise direction, thereby preventing cells from tumbling. In the case of RP1616, the cells tumbled in a fixed spatial location (Fig. 3C and D). This tumble-only behavior was due to the fact that RP1616 carries a Δ(cheZ)m67-25 mutation that causes its flagella to only rotate in the clockwise direction such that cells tumble all the time.

FIG. 1.

Microscope image of swimming E. coli strain RP437 (wild type for motility and chemotaxis). The image size is 449 μm by 335 μm. The bright oblong spots depict cells that are in the plane of focus. The rings depict cells that are out of the plane of focus. The ring size is directly proportional to the distance of the cell to the focal plane and is used to obtain the z dimension.

FIG. 2.

Swimming trajectories of wild-type RP437 derived from a sequence of images using ImagePro Plus (Media Cybernetics, Inc.) image processing software. The typical time between consecutive images was 150 ms, and each time sequence consisted of 300 images. Using an in-house software package, we determined the locations and the ring size for each bacterium shown in Fig. 1. This information was then translated into the coordinates (x, y, and z) for each bacterial cell in the image, and the process was repeated for all the images in a time series. The 3D trajectories of each bacterial cell generated using the nearest-neighbor method (A) and the projection of the 3D trajectory to the x-y plane (B). Different colors represent different trajectories.

FIG. 3.

Swimming trajectories of smooth swimmers (RP9535) and tumblers (RP1616). 3D trajectories (A) and 2D projection (B) for strain RP9535. 3D trajectories (C) and 2D projection (D) for strain RP1616. Different colors represent different trajectories.

Determination of the macroscopic transport coefficients.

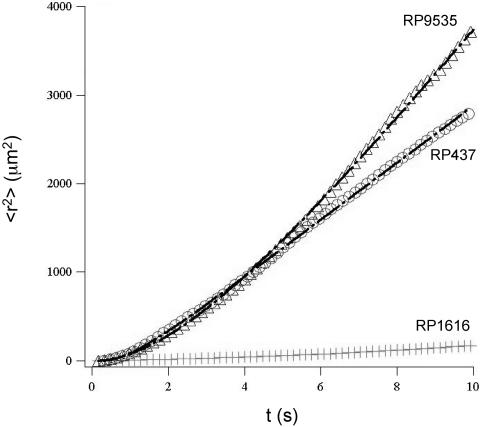
To quantify the macroscopic transport properties, we plotted the square of the distance traveled, <r²>, versus time for all three strains using the trajectory data shown in Fig. 2 and 3. Note that the symbol < > represents the ensemble average over different trajectories and that the total number of trajectories used for averaging ranged from 200 to 1,000. As shown in Fig. 4, the smooth-swimmer cells diffused more efficiently than wild-type RP437 cells, and both the smooth-swimmer and wild-type cells diffused much more rapidly than the tumblers. It is noteworthy that all three strains were grown under the same conditions for these experiments, thus providing a consistent basis for comparison of diffusive behavior.

FIG. 4.

The population average of the square distance to the origin as a function of time (t) for the wild-type RP437 strain (circle) and its isogenic derivatives RP9535 (triangle) and RP1616 (diamond) at a cell concentration of 10⁷ cells/ml. The solid lines for RP9535 and RP437 are fits to equation 1 (see text). The solid line for RP1616 is a fit to a linear function. The diffusion coefficients D and the characteristic times τ were extracted from the fits. For RP437, D = 53.2 μm²/s and τ = 1.8 s; for RP9535, D = 458.0 μm²/s and τ = 6.6 s; for RP1616, D = 2.0 μm²/s.

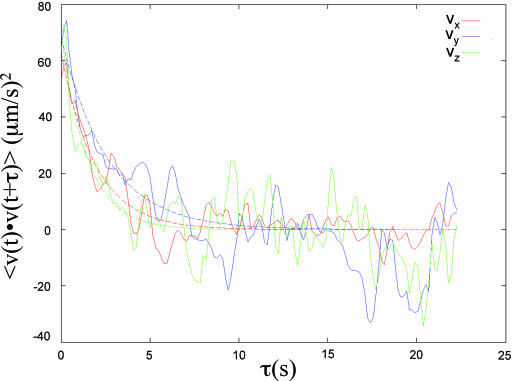
The two-time velocity auto-correlation function is an important measure of the stochastic temporal motion of particles or molecules such as the molecules in a gas (34). Shown in Fig. 5 is the velocity auto-correlation function plot of swimming bacteria for the velocity component along the x, y, and z directions (v_x, v_y, and v_z, respectively). We found that the 3D velocity auto-correlation could be fit by an exponential decay function, 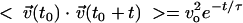, where  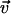is the velocity vector of the bacteria and v_o is the root-mean-square of the bacterial velocity. This is similar to the 2D velocity auto-correlation observed for passive particles embedded in a confined bacterial suspension (42). To extract the diffusion coefficient and characteristic time scale of bacterial locomotion, we derived a relationship between < r² > and t based on the exponential velocity auto-correlation, as follows:

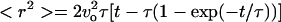(1)

Here, we assume that diffusion is the same in all three dimensions, which is supported by Fig. 5. The above equation shows that for t ≪ τ, < r² > = v_o²t² represents a superdiffusion region; and for t ≫ τ, the population average of the square of the displacement represents a region of normal Fickian diffusion and follows Einstein's relation, < r² > = (2v_o²τ)t = 6Dt, where D is the macroscopic random motility coefficient (7). Shown in Fig. 4 are data taken using cells of different strains at cell concentration of 10⁷ cells/ml. A fit of the < r² > versus t data (Fig. 4) to the above equation yields both the characteristic time τ and the diffusion coefficient D. The diffusion coefficients for the wild-type RP437 cells and the smooth-swimmer RP9535 cells were found to be 53.2 and 458.0 μm²/s, respectively. The characteristic time for the wild-type cells was 1.8 s, whereas a τ value of 6.6 s was observed for the smooth-swimmer cells. Finally, the diffusion coefficient for the tumbler cells was estimated from the slope of < r² > versus t (Fig. 4) and found to be 2.0 μm²/s.

FIG. 5.

Velocity auto-correlation of wild-type E. coli strain RP437 for velocity components along the x, y, and z directions (red, v_x; blue, v_y; green, v_z). The solid lines depict fits to an exponential decay function.

Quantifying the effect of cell-cell interactions on bacterial diffusion.

To investigate the influence that cell-cell interactions have on the motion of bacterial cells, we measured the diffusion coefficient of swimming bacteria as a function of cell concentration. In order to prevent imaging biases caused by an increase in the number of fluorescent cells (the 3D DPT method performs optimally for a fluorescent cell concentration of less than ∼10⁸ cells/ml based on our unpublished observations), we mixed fluorescent cells of a fixed volume fraction (1 × 10⁷ cells/ml) with nonfluorescent cells and adjusted the number of nonfluorescent cells to achieve the desired cell concentration. The fluorescent cells are those carrying the pTG plasmid that are induced by 0.2% (wt/vol) arabinose. The nonfluorescent cells are those that either do not carry pTG or carry pTG but do not receive a bolus of the inducer arabinose. It should be noted that the results described below were nearly identical regardless of the type of nonfluorescent cell used in the mixing procedure. Importantly, we observed that the diffusion coefficients for wild-type and smooth-swimmer cells both increased with increasing cell concentrations, reaching peak values of 100.0 and 1148.0 μm²/s, respectively, at a cell concentration of 1 × 10⁸ cells/ml before decreasing at very high cell concentrations. Shown in Table 1 are values for the diffusion coefficient and characteristic time for different concentrations of RP437 and RP9535 cells. There are several factors that may influence the concentration dependence of cell diffusion. First, cells might interact through chemical or hydrodynamic signals in a pairwise fashion when they swim within about 10 μm of one another. In wild-type cells such a signal might induce tumbling, thereby decreasing the diffusion coefficient. In smooth swimmers, the fluid flow caused by a neighbor could induce a slight change in the orientation of a cell, thereby again decreasing its correlation time. These effects seem to be absent or negligible in our experiments since the first effect of increasing cell concentration is an increase in correlation time and diffusion coefficient. Second, fluid flow structures that persist over distances that are large compared with the individual cells may enhance the diffusion coefficient. Such flows could occur if the hydrodynamic interactions among the cells lead them to adopt a common alignment, and this alignment may be expected to persist over distances comparable with the persistence length l_p = v_oτ for the motion and orientation of individual cells. This enhancement would be expected to arise when nl_p³ is >1 (where n is the number of cells in one milliliter) so that there are multiple cells within this persistence length. Consistent with this hypothesis, we observe a large increase in the diffusivity when nl_p³ is comparable with 1 and when the cell-cell separation distance is still much smaller than the size of the cell and its flagella. We also observe that the diffusivity of the smooth-swimming cells, whose motion is more persistent, increases by a larger factor than the diffusivity of the wild-type cells, whose orientation changes more frequently due to tumbling. Previous experimental measurements have shown that the diffusivity of passive tracer particles in bacteria suspensions also grows with increasing cell concentration (22, 39, 42), and numerical simulations have found an increase in the diffusivity of both active and passive particles in suspensions of hydrodynamically interacting swimming particles (19). A third manner in which cells may interact is by hindering one another's motion by direct collisions. This may be expected to occur when nL³ becomes comparable with 1, where L = 12 μm is the length of the cell plus its flagella. In our experiments, nL³ approaches a value of 1 at the highest cell concentrations, and we observe a dramatic decrease in the diffusivities of both wild-type and smooth-swimming cells at these concentrations. Further experiments are now under way to monitor simultaneously the motion of active and passive particles to confirm the role of long-range flow disturbances in enhancing the diffusion coefficients of bacteria at moderately high cell concentrations.

TABLE 1.

The effect of cell concentration on the macroscopic transport parameters

Strain	Density (cells/ml)	D (μm2/s)	τ (s)
RP437 (wild type)	1 × 107	53.2	1.8
	5 × 107	66.0	3.6
	1 × 108	100.0	2.9
	5 × 108	36.3	0.4
	1 × 109	41.4	0.7
RP9535 (smooth swimmer)	1 × 107	458.0	6.6
	5 × 107	446.0	10.3
	1 × 108	1,148.0	20.5
	5 × 108	18.4	2.2

DISCUSSION

In this paper, we demonstrated a 3D DPT method for the study of bacterial dynamics. The novelty of this approach is its ability to follow the dynamics of multiple bacterial cells in 3D at single-cell resolution. The unique combination of the 3D DPT technique and the mixing of fluorescent and nonfluorescent cells together allows us to probe the diffusion process in bacterial suspensions at various cell densities.

An advantage conferred by our 3D DPT strategy is that macroscopic transport parameters can be obtained using a multitude of individual cell tracks (we generated 630) gathered from a single experiment in a relatively short period of time (∼1 min). In contrast, experimental determination of the diffusion coefficient using the 3D tracking microscope requires a large number of individual tracking experiments; Lewus and Ford performed 66 separate bacterial tracks (24). Another advantage of 3D DPT is that, by allowing multicellular tracking at single-cell resolution, it enables investigators to explore the collective dynamics of bacterial cells including phenomena such as hydrodynamic coupling, long-range pattern formation of chemotactic cells, and chemical signal-mediated behavior coordination (e.g., quorum sensing). An example of this type of interbacterial coordination was demonstrated above where the diffusion coefficient was observed to increase with increasing cell density.