Use of Probabilistic Modeling within a Physiologically Based Pharmacokinetic Model To Predict Sulfamethazine Residue Withdrawal Times in Edible Tissues in Swine

Abstract

The presence of antimicrobial agents in edible tissues of food-producing animals remains a major public health concern. Probabilistic modeling techniques incorporated into a physiologically based pharmacokinetic (PBPK) model were used to predict the amounts of sulfamethazine residues in edible tissues in swine. A PBPK model for sulfamethazine in swine was adapted to include an oral dosing route. The distributions for sensitive parameters were determined and were used in a Monte Carlo analysis to predict tissue residue times. Validation of the distributions was done by comparison of the results of a Monte Carlo analysis to those obtained with an external data set from the literature and an in vivo pilot study. The model was used to predict the upper limit of the 95% confidence interval of the 99th percentile of the population, as recommended by the U.S. Food and Drug Administration (FDA). The external data set was used to calculate the withdrawal time by using the tolerance limit algorithm designed by FDA. The withdrawal times obtained by both methods were compared to the labeled withdrawal time for the same dose. The Monte Carlo method predicted a withdrawal time of 21 days, based on the amounts of residues in the kidneys. The tolerance limit method applied to the time-limited data set predicted a withdrawal time of 12 days. The existing FDA label withdrawal time is 15 days. PBPK models can incorporate probabilistic modeling techniques that make them useful for prediction of tissue residue times. These models can be used to calculate the parameters required by FDA and explore those conditions where the established withdrawal time may not be sufficient.

Sulfamethazine is a sulfonamide antibiotic used in the swine industry as a feed or water additive. It is labeled for the treatment of bacterial pneumonia, cervical abscesses, and bacterial swine enteritis, as well as for the prevention of these diseases during times of stress, maintenance of weight gains in the presence of atrophic rhinitis, growth promotion, and increased feed efficiency (14). Research has shown that high concentrations of this drug may cause thyroid tumors in specific strains of rats (35). Also, a wide range of human allergic reactions are related to sulfonamide drugs in general (37, 43). Thus, there is a large public health concern relating to the possible adverse health effects of consuming sulfamethazine residues found in the edible tissues of swine, warranting the development of predictive pharmacokinetic models.

Meat withdrawal periods are required by the U.S. Food and Drug Administration (FDA) to ensure the safety of the meat supply and to address this public health concern. A meat withdrawal period is the time between when a chemotherapeutic is administered to a food animal and the time when that animal is sent to slaughter. These periods are designed to guarantee that the amounts of drug residues in edible tissues will be below tolerance levels before animals are sent to slaughter. Currently, withdrawal times are determined by the tolerance limit method. This method predicts a withdrawal time by calculating a regression line for the linear portion of the depletion curve. Data for individual animals are then used to calculate the perceived population variance of the line and, thus, to predict the upper limit of the 95% confidence interval for the 99th percentile of the population for the rate of elimination. The withdrawal time is calculated by using the newly calculated regression line (1). The current tolerance level for sulfamethazine in swine was established in 1968 at 0.1 ppm (μg/ml for plasma and μg/mg for tissues) for all edible tissues. According to the 2003 Food Safety Inspection Service Red Book, sulfamethazine was the only sulfonamide found in violation of tolerance levels in swine (2), again stressing the public health significance of this compound.

Physiologically based pharmacokinetic (PBPK) models are predictive models that use mass balance equations to link tissue compartments via a plasma compartment. Unlike other pharmacokinetic modeling techniques, they are based on physiologic mechanisms and can be used over a large range of doses and routes of administration (36). Briefly, PBPK models consist of a number of tissue blocks linked together via blood flow through a communal plasma block. Each tissue block is mathematically modeled with mass balance equations and such parameters as tissue volume (rather than the traditional volume of distribution), blood:tissue partition coefficients, and percent tissue blood flow (17). Bioavailability is incorporated into PBPK models by mechanistically describing oral absorption rates and the first-pass metabolism inherent within the portal circulation. For the purposes of this report, the term “parameter” refers to the physiologic aspects incorporated into the mathematical model. PBPK models have been used in toxicology to predict internal dose metrics which are applied to human health risk assessment (4, 12, 16). The U.S. Environmental Protection Agency has recently published draft guidance, available for public review, on the incorporation of PBPK models in risk assessment (3). In human medicine, PBPK models are used to calculate individual dosing regimens in situations in which drugs with low therapeutic indices are needed, such as chemotherapeutics, or when there are severe alterations in patient physiology, such as infancy or pregnancy (5, 23, 41). PBPK models are also used in drug development studies (6). Currently, only a handful of PBPK models have been published for veterinary medicine (7, 8, 10, 11). Our previous work predicted meat withdrawal times after the extralabel use of sulfamethazine intravenously (i.v.) in swine for the mean of the population (8). However, sulfamethazine is rarely used as an i.v. preparation. Also, while the model is useful for the prediction of a meat withdrawal time for extralabel drug use under the guidelines of the Animal Medicinal Drug Use Clarification Act (42), it does not take into account population variability. Therefore, it cannot be used in industry to satisfy the stringent FDA regulatory requirements.

The Monte Carlo technique is a probabilistic modeling technique that uses distributions rather than single points to define parameters. Random values from the set distributions are generated and then incorporated into the model for each simulation run. The number of simulations is defined by the user and can range from a single simulation to thousands of simulations. This allows an output for multiple simulations whose scope represents the possible differences within a target population. Several studies in the literature show how this type of distribution sampling can be incorporated into PBPK modeling and have been applied to human health risk assessment (9, 21, 38, 40). It has also been postulated that the use of Monte Carlo techniques would be advantageous in the estimation of meat withdrawal times (13). In veterinary medicine, the use of Monte Carlo techniques is mostly found in epidemiology, in which it is used to determine the risk factors for disease, model prevalence within a population, and investigate different strategies in disease prevention and control (18, 20, 22). To our knowledge, no published studies have applied Monte Carlo techniques to issues of meat safety.

The purpose of this study was to incorporate Monte Carlo techniques into a PBPK model and use that model to compute a meat withdrawal time according to the current FDA standards. Sulfamethazine was used as the representative drug in the representative species of swine.

MATERIALS AND METHODS

Model development.

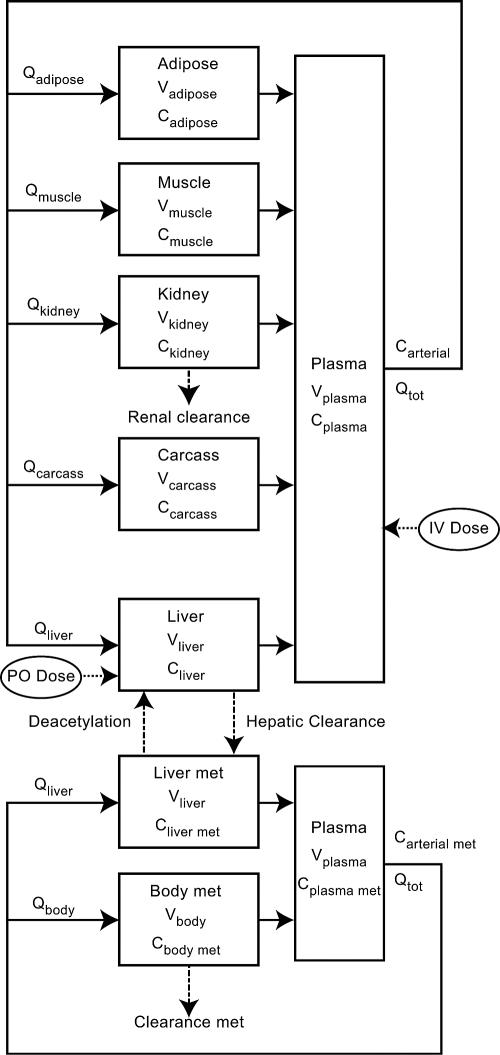
The PBPK model (Fig. 1) used in this research was adapted from a previously published model of sulfamethazine in swine (8). Briefly, the model contains five tissue blocks (adipose, kidney, liver, muscle, and carcass) as well as a plasma compartment for sulfamethazine. It is linked through the liver to a two-tissue compartment (liver and body) model for the N₄-acetyl metabolite. Elimination was modeled through renal clearance as well as hepatic clearance for both the parent compound and its metabolite and was assumed to be first order. The original model also included an intravenous route of administration. Tissue concentrations were defined as a homogenate of drug found within the tissue as well as drug found within the tissue blood. Concentrations represent those of total drug. Concentrations were modeled by using standard flow-limited mass balance equations. We refer the reader to the work of Buur et al. for detailed information regarding the basic model (8). An oral dosing module consisting of a two-tissue-compartment model that included the stomach and intestine (Fig. 2) has now been incorporated into the model. It was assumed that all of the drug was immediately available in the stomach. Distribution into the intestine was controlled by the rate of gastric emptying (K_st). Once in the intestine, drug absorption was governed by the rate of absorption (K_a) by using the following equation:

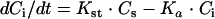where C_s (g/liter) and C_i (g/liter) are the concentrations of the drug in the stomach and intestine, respectively; K_st is the rate of gastric emptying; K_a is the rate of absorption; and t is time. Drug absorption was assumed to go directly into the liver from the portal circulation. Both the rate of gastric emptying and the rate of absorption were assumed to be linear processes.

FIG. 1.

Schematic diagram of the PBPK model for sulfamethazine in pigs. V, tissue volume; C, tissue concentration; Q, tissue blood flow; Q_tot, cardiac output.

FIG. 2.

Schematic diagram of the oral dosing route of administration.

Parameter distributions.

All parameters were subjected to sensitivity analysis to determine which had the largest effect on drug distribution (data not shown) after oral dosing. Sensitive parameters were defined to be those parameters that had a significant effect on sulfamethazine plasma pharmacokinetics relative to the effects of the other parameters. Insensitive parameters were defined by point estimates and were not subjected to Monte Carlo analysis. The insensitive parameters and their values are presented in Table 1. Readers are referred to the work of Buur et al. for details regarding how these parameters were established (8). Only parameters judged to be sensitive were subject to Monte Carlo analysis. Sensitive parameters included K_a, K_st, hepatic clearance of sulfamethazine, plasma protein binding of sulfamethazine, and plasma protein binding of the N₄-acetyl metabolite (Table 2). The distributions for these sensitive parameters were taken from the literature (19, 24-26, 29-31, 34, 39, 44). Boundaries for the distributions were determined by taking the largest reported standard deviation and then adding that to the maximum value reported in the literature or subtracting that from the minimum value reported in the literature. Distributions were assumed to be lognormal. Means and standard deviations for the resulting distributions were determined by using an online freeware applet (www.stat.vt.edu/∼sundar/java/applets/). Briefly, the probability density function was adjusted to visually represent the published means and ranges. The applet then reported the mean and standard deviation for a lognormal distribution having that shape. Final distributions as well as nontransformed ranges are presented in Table 2.

TABLE 1.

Final values for insensitive parameters used in model simulations

Parameter	Valuea
Partition coefficient (plasma:tissue)
Adipose	0.336
Kidney	1.68
Liver	0.378
Muscle	0.08
Acetyl metabolite liver	0.079
Acetyl metabolite body	1.297
Blood flow (% of total cardiac output)
Liver blood flow	0.38
Kidney blood flow	0.1188
Muscle blood flow	0.25
Adipose blood flow	0.08
Metabolism of N4-acetyl metabolite
Rate of deacetylation (1/h)	3.66
Acetyl metabolite clearance (ml/min kg)	2.558

^aSpecifics on how these values were obtained can be found in the work of Buur et al. (8).

TABLE 2.

Final distributions for sensitive parameters used in the Monte Carlo analysis

Parameter (units)a	Mean	Mean (transformed)	Variance	Lower boundd	Upper boundd	References
Ka (1/h)	0.1	−1	0.88	0.0682	3.01	24, 34, 39
Kst (1/h)	0.1	−1	0.4	0.0183	1.05	19, 24
CL hepaticb (ml/min/kg)	0.39	−0.4	0.32	0.05	1.5	29, 30, 39, 44
P binding SMZc (%)	0.42	−0.38	0.1	0.37	0.99	25, 26, 29, 30, 31
P binding metc (%)	0.35	−0.45	0.11	0.34	0.92	25, 26, 29, 30, 31

^aThe distribution was lognormal for all parameters.

^bCL hepatic, hepatic clearance.

^cP binding is protein binding of either sulfamethazine (SMZ) or the N₄-acetyl metabolite (met).

^dBoundaries reflect the range of nontransformed values seen throughout the lognormal distribution.

In vivo study.

All procedures were approved by the North Carolina State University Institutional Animal Care and Use Committee. Five female Yorkshire cross pigs weighing between 82 and 105 kg were purchased from North Carolina State University Research Unit 2 and underwent jugular catheterization 3 days prior to the study. A single i.v. dose of 35 mg/kg of body weight sodium sulfamethazine was administered in the auricular vein; and plasma samples were taken at 0, 0.5, 1, 2, 6, 8, 12, 24, 31, 48, 54, 72, and 96 h. Due to catheter malfunctions, not all plasma samples were available for every animal. Animals were euthanized at 4, 28, 51, 76, and 99 h; and muscle, adipose, liver, and kidney tissues were harvested for analysis. Blood samples were centrifuged and plasma was harvested within 1 h of sample collection. All tissue and plasma samples were frozen at −80C until they were analyzed. Analysis occurred within 1 week of sampling. Tissues and plasma samples were analyzed by the high-pressure liquid chromatography (HPLC) methods described below.

HPLC methods. (i) Sample preparation.

Sample preparation for each tissue was based upon the method published by Furusawa (15). Briefly, for muscle, liver, adipose, and kidney tissues, 1 g of tissue was accurately weighed and added to 2 ml of 10% perchloric acid. Each sample was homogenized with a Brinkman Polytron homogenizer (Razdale, Ontario, Canada) for 45 s and was then centrifuged at 1,200 rpm for 10 min at 24°C. Adipose tissue was centrifuged at 15°C. The supernatant from the muscle tissue was filtered through a 45-μm-pore-size disk filter and injected into the HPLC system. The supernatants from liver and kidney tissues as well as the aqueous phase from adipose tissue were processed further by solid-phase extraction. An Oasis MCX 3cc 60-mg sorbent weight (Waters, Milford, MA) cartridge was conditioned with 1 ml of methanol and 1 ml of water. The sample was added and the cartridge was then washed with 1 ml 0.1 N HCl and 1 ml methanol. The cartridges were dried under vacuum for 30 s. Samples were eluted with 1 ml ammonium hydroxide-acetonitrile (5:95; vol/vol) and the cartridges were again dried under vacuum. Elution volumes were evaporated to dryness in a Turbo Vap LV evaporator (Zymark; Hopkington, MA) for 15 min at 50°C and 15 mm Hg lb/in² reagent-grade nitrogen gas. Residue was reconstituted in 0.5 ml ammonium acetate buffer (pH 4.5, 0.1 M), vortexed, and then injected in the HPLC system. One milliliter of plasma was acidified by addition of 20 μl o-phosphoric acid and then subjected to the solid-phase extraction process detailed above.

For all methods, the coefficients of variation for both interday and intraday validations were below 15% and recoveries were between 90 and 105%. Standard curves were linear from 0.1 to 2.5 μg/ml. Any samples above the limits of the standard curve were diluted until the results fell within the curve limits. Quality control samples were run on the day of analysis, and recoveries were greater than 90%.

(ii) HPLC system.

The HPLC system consisted of a Waters 600 controller with a Waters 717 Plus autosampler and a Waters 996 photodiode array detector. A Zorbax SB-C8 column (4.6 by 150 mm, 5 μm; Agilent, Wilmington, DE) was used. All injection volumes were 10 μl, and flow rates were 1 ml/min. Autosampler and column temperatures were maintained at 25°C and 30°C, respectively. The optimum detector wavelength was 267 nm. Mobile-phase conditions for tissue samples and plasma samples were acetonitrile-ammonium acetate buffer (pH 4.5, 0.1 M) (19:81; vol/vol) and acetonitrile-ammonium acetate buffer (pH 4.5, 0.1 M) (17:83; vol/vol), respectively. All reagents used were HPLC grade.

Monte Carlo analysis.

Monte Carlo analysis was performed by using the Monte Carlo wizard included in the ACSLxtreme 2.01 software (Aegis Technology Group, Huntsville, AL). Each Monte Carlo run included 100 simulations for validation and 1,000 simulations for meat withdrawal time prediction. Every Monte Carlo analysis, no matter the number of simulations, was performed identically in a stepwise manner. For each simulation, a number was randomly generated for each sensitive parameter according to the distributions defined in Table 2. Those numbers were incorporated into the mathematical model and used to generate both tissue and plasma concentration-time curves. This was repeated for the specified number of simulations. For validation of the distributions, the distributions from a single Monte Carlo analysis of 100 simulations were compared to the distributions obtained with an external data set created from the literature and from an in vivo pilot study. Data from published in vivo pharmacokinetic studies were excluded from the data set based on the physiologic status of the swine as well as the assay methodology. The results from colorimetric analysis of drug concentrations, general anesthesia, and experimentally infected pigs were all excluded from the data set. The external data set for the i.v. route included data from four published in vivo study data and the in vivo pilot study data. Five published data sets for single oral dosing and four published in vivo data sets for multiple oral dosing were included in the external data set for the oral route. All concentration datum points were normalized by dose or the ratio of the accumulation factors, as needed, and were weighted equally. Each datum point from the published studies represents the mean value (UN-SCAN-IT, version 6.0; Silk Scientific Inc., Orem, UT) for the sulfamethazine concentration reported in the literature. The datum points were also converted to μg/liter or μg/g for comparison of plasma and tissue concentrations, respectively. The mean number of animals ranged from 2 to 23 pigs. Overall, there were a total of nine studies, four of which included tissue data, and the in vivo pilot study described above (27-30, 32-34, 39, 44). Doses ranged from 2.36 mg/kg to 50 mg/kg. Because the carcass block represents all portions of the pig not included in the other tissue blocks and thus cannot be quantitated, it was not included in the validation and application procedures. The validation run for the i.v. route was simulated at 1 mg/kg. For the oral route, the dose was 10 mg/kg once daily for 7 days. The parameter distributions were considered acceptable if, upon comparison with the external data set, most of the datum points were within the scope of the simulations.

Prediction of withdrawal time. (i) Monte Carlo method.

For each edible tissue, a series of 100 Monte Carlo runs (of 1,000 simulations each) were made by using the FDA labeled dose of 237.6 mg/kg orally on day 1, followed by 118.8 mg/kg orally on days 2, 3, and 4. For each run, a withdrawal time was calculated for the 99th percentile of the population. The withdrawal time for the 99th percentile of the population for each run was calculated to be the time when 99% of all simulations had concentrations below the tolerance level. A 95th percent confidence interval was then calculated for each set of 100 withdrawal times. The longest withdrawal time calculated by using the upper limit of the 95th percent confidence interval was taken to be the estimated withdrawal time.

(ii) Tolerance limit method.

In addition, the data set compiled for use in the validation was used to calculate the withdrawal time based on the tolerance limit algorithm recommended by FDA. Readers are referred to FDA Guidance 3 for specific information regarding the exact method (1). Briefly, this method calculates an equation for the linear portion of the depletion curve for each tissue for the 99th percentile of the population by using the datum points gathered during an in vivo study. The variance is calculated and assumed to be equal along all points of the elimination curve and is used to calculate the 95% confidence interval. The tissue with the longest withdrawal time is selected to be the basis for the withdrawal time. Both withdrawal times calculated (Monte Carlo method and tolerance limit method) were compared to the existing FDA label withdrawal time of 15 days for sulfamethazine.

RESULTS

In vivo study.

The data from the in vivo study closely resembled the means reported in the literature. Tables 3 and 4 present the specific plasma and tissue concentrations, respectively, found from this pilot study. The plasma data showed slight variations at 1 and 24 h that deviated from the expected continual decline from an i.v. dose.

TABLE 3.

Plasma concentrations after i.v. injection of 35 mg/kg sulfamethazine

Time (h)	Mean (μg/ml)	SD (μg/ml)	No. of animals
0.5	181.3	14.9	4
1	121.5	31.9	4
2	149.2	9.4	4
6	125.1	24.4	5
8	100.4	20.2	4
12	64.1	20.6	3
24	74.1	8.6	4
31	56.1	21.4	3
48	29.6	2.7	3
54	18.3	8.8	2
72	9.1	7.3	2
96	7.1	NAa	1

^aNA, not applicable.

TABLE 4.

Tissue concentrations from i.v. injection of 35 mg/kg sulfamethazine

Time (h)	Tissue concn (μg/mg) (n = 1)
	Kidney	Liver	Adipose	Muscle
4.2	35.5	34.0	14.9	27.6
27.6	17.4	17.7	4.1	13.2
50.8	5.8	6.6	2.1	4.0
75.7	1.5	2.0	0.6	1.6
98.3	1.0	1.9	0.3	0.7

Monte Carlo analysis.

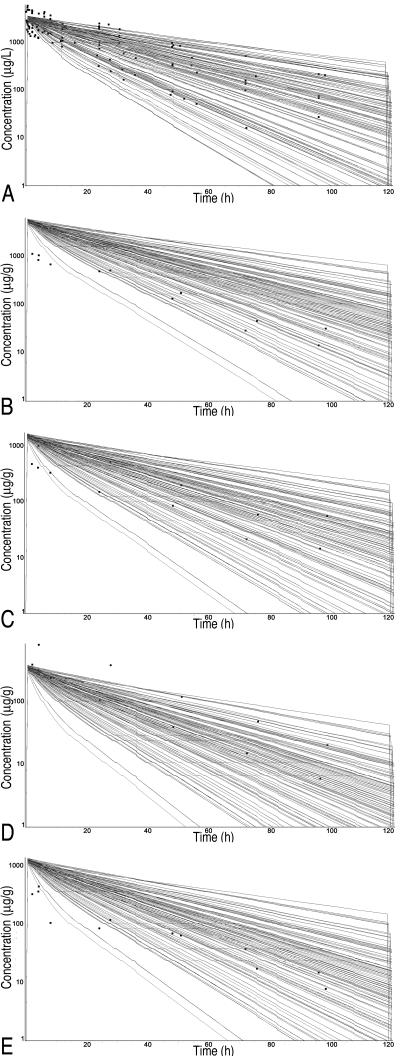
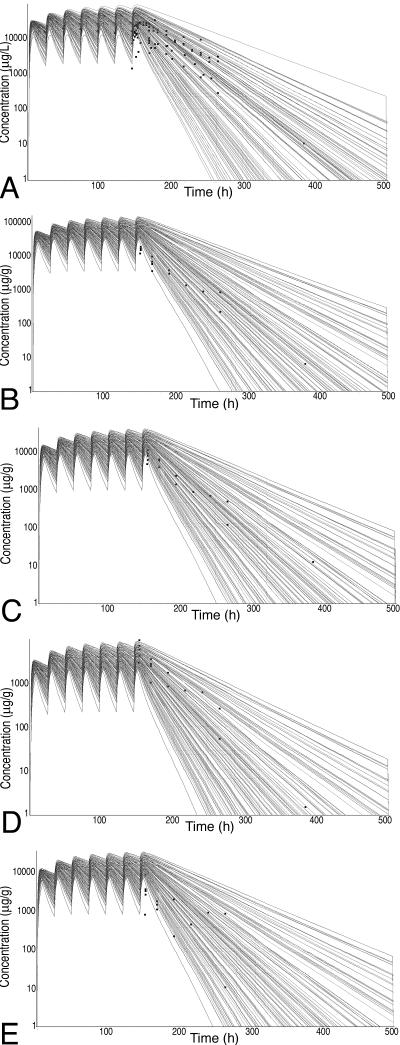
Representative Monte Carlo runs for each tissue are presented in Fig. 3 (i.v. route) and Fig. 4 (oral route). Note that the results of the simulations are reported in μg/liter or μg/g for plasma and tissue concentrations, respectively. As evidenced by the large number of datum points covered by the simulations, excellent coverage was achieved for all tissues for the i.v. route of administration. The model tended to overpredict concentrations at early time points for all tissues but muscle but covered all points during the elimination phase. Some early time points were underpredicted for muscle. For the oral route of administration, the only points not covered by the spread were the early time points that occurred during the absorption phase. Again, the terminal time points had excellent coverage by the simulation spread. The terminal points are the most relevant to withdrawal time determination.

FIG. 3.

Monte Carlo simulations for sulfamethazine concentrations in edible tissues after intravenous administration. Squares, datum points from the external data set (means from published studies and data for individual pigs from in vivo pilot study) normalized to a dose of 1 mg/kg. (A) Plasma; (B) kidney; (C) liver; (D) muscle; (E) fat.

FIG. 4.

Monte Carlo simulations for sulfamethazine concentration in edible tissues after oral administration. Doses were normalized to a standard dose of 10 mg/kg once daily for 7 days. Squares, datum points from the external data set (means from published studies). (A) Plasma; (B) kidney; (C) liver; (D) muscle; (E) fat.

Prediction of withdrawal time. (i) Monte Carlo method.

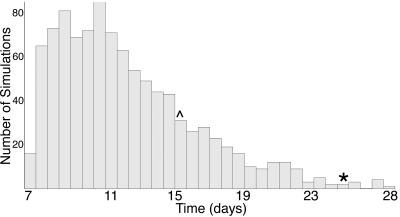
A representative distribution of withdrawal times from a Monte Carlo run for the label dose in kidney tissue is presented in Fig. 5. Similar distributions were seen for all other tissues. Table 5 shows the results of the multiple Monte Carlo runs for each tissue and their corresponding confidence intervals. It can be seen that kidney tissue had the longest withdrawal time. We predict a withdrawal time of 21 days based on this analysis. This is 6 days longer than the current label withdrawal time of 15 days.

FIG. 5.

Representative distribution of the time that it takes for sulfamethazine concentrations to fall below the tolerance of 0.1 ppm in kidney tissue from a Monte Carlo run of 1,000 simulations. *, 99th percentile of the distribution; ^, current withdrawal time of 15 days.

TABLE 5.

Withdrawal time predictions and 95% confidence intervals for the 99th percentile of the population for each edible tissue after 100 Monte Carlo runs of 1,000 simulations

Tissue	Mean (days)	95% confidence interval (days)
		Lower bound	Upper bound
Plasma	19.76	19.64	19.88
Kidney	20.84	20.72	20.97
Liver	17.97	17.86	18.07
Adipose	17.49	17.39	17.60
Muscle	14.69	14.60	14.79

(ii) Tolerance limit method.

The tolerance limit method predicts a withdrawal time of 12 days. This is 3 days less than the label withdrawal time of 15 days.

DISCUSSION

We have successfully incorporated probabilistic modeling into a PBPK model and applied it to the prediction of meat withdrawal times. We were able to predict the upper limit of a 95% confidence interval for the 99th percentile of the population. Thus, the method applied allows simulations that meet the recommendations for establishment of meat withdrawal times established by FDA to be conducted.

The validity of this model is directly dependent upon the distributions used to define key parameters. It was noted during the creation of these distributions that several probability density functions that would describe the same mean and range that were found in the published literature could be used. The different distributions did produce different population spreads (data not shown). Ranges of values for the parameter distributions were taken to be the broadest in terms of both variability in the population and uncertainty in the distributions reported. This would increase the overall spread of the Monte Carlo output and allow a more conservative estimate of the withdrawal time. The distributions could also overestimate population variance since we were unable to correct for the variance inherent within the literature studies. The wider distributions contribute to a more conservative estimate for a meat withdrawal time and should be considered when the model is applied to practical situations. However, from a public health standpoint, it is better to err by creating a more conservative meat withdrawal time than risk the consequences of the possible presence of residues in tissue. Furthermore, the model can easily be updated as more data on the true distributions of the parameters are generated.

Lognormal distributions were assumed for the parameters on the basis of their acceptance within regulatory agencies such as FDA and the U.S. Environmental Protection Agency with regards to population estimation. Again, further research into the exact distributions for both parameters and populations would continue to increase the accuracy of this model. It should be noted that a strength of this type of probabilistic modeling is the transparency with which the assumptions and results are reported. The 99th percentile of the population was established without assuming any specific distribution.

The accuracy of the model was determined by its ability to predict concentrations similar to those found in the external data set. Each point of the external data set represented a mean concentration from the pigs (the number of which ranged from three to six) used in the published studies. In order to get a more robust estimate of individual pig variations, a small in vivo pilot study was performed. While this study produced only a single datum point for each tissue at each slaughter time, the results of the pilot study coincided well with previously published results for all tissues and allowed us to accept the means with a greater degree of confidence. In fact, although the data from the pilot study had minor idiosyncrasies, the data were graphically indistinguishable from data from other studies when they were plotted together (Fig. 3). This again helped to establish robustness within the external data set. The external data set also incorporated a wide range of dosing regimens. Dose independence, due to the mechanistic nature of PBPK models, is a strength of PBPK models. This allows validation against a wide range of doses and application to a dose not found within the external data set. The model tended to overpredict the concentrations at early time points. This may reflect a difference between absorption in vivo and how absorption was calculated in the model. However, the time points in the elimination portion of the curves were well covered by the Monte Carlo analysis. Since we are applying the model to the prediction of meat withdrawal times, the accuracy of prediction for later time points is more important. Further refining of the model could be made to increase the accuracy of the predictions for early time points.

Another source of variability within the population could be due to breed differences in metabolism and protein binding. To our knowledge, there are no reports of this for sulfamethazine or for any other drug in swine. Breed differences are most likely incorporated into the parameter distributions that were taken from the literature since these studies were carried out with various breeds and cross-breeds of swine. Variability within pigs can also be increased if the drug was given in feed to a pen of animals. Differences in social hierarchy and interpig personalities will mean a difference in overall drug intake and, thus, in the dose administered. For all studies used for validation that used oral dosing, dosing was done in such a manner (i.e., gavage) as to be able to accurately determine the true dose given to each pig. Variability in the pharmacokinetics of the N₄-acetyl metabolite could also affect the population pharmacokinetics of sulfamethazine. The metabolite was included in the model due to the unique deaceytlation pathway that increases the concentration of the parent compound at later time points. In fact, the plasma protein binding of this metabolite was determined to be a sensitive parameter and was included in the Monte Carlo analysis. Ultimately, there are an infinite number of sources of variability between pigs in terms of drug disposition. Sensitivity analyses help to narrow the scope by identifying those parameters which affect pharmacokinetic predictions. Therefore, the Monte Carlo analysis did not include parameter distributions where parameters were determined to be insensitive.

The oral withdrawal time predicted by the Monte Carlo method is 6 days longer than the labeled withdrawal time. Sulfamethazine had an original withdrawal time of 5 days, which was established in 1968. In 1980, the current withdrawal time of 15 days was established by using an algorithm based on the sensitivity of the analytical tests available at that time. While this was the standard practice at that time, the sensitivities and specificities of analytical techniques have substantially increased over the last 25 years. Thus, the labeled withdrawal time may not cover the population according to the current rigorous standards now required by FDA. Our model shows that the withdrawal time for approximately 20% of the population is often greater than the 15 days currently used. This could account for the significant amount of tissue residue violations found with this drug (2). Beyond the differences between the methods used, other reasons for the differences in withdrawal times could be related to the distributions used. As was discussed above, multiple distributions can provide curves with the same shapes and ranges. Also, we are comparing the means of several studies rather than data for individuals. One would expect an even greater spread between datum points if more individuals were included. Data for individual pigs could contribute to an even longer withdrawal time if even larger variability was shown. The addition of data from the in vivo study for i.v. route did create a more robust external data set and allowed us to evaluate the model in terms of individual variability. Thus, the model provided excellent coverage of individuals as well as means.

The tolerance limit method predicted a withdrawal time 3 days less than the label withdrawal time. This is most likely because the data set did not include points beyond 5 days posttreatment, a limitation not present in a PBPK model. A major assumption in this method is that there are enough time points on the depletion portion of the concentration-time curve to accurately assess the terminal slope. Given the kinetics of sulfamethazine in swine, the data set most likely does not have enough data to accurately determine that terminal slope. Thus, the tolerance limit method is descriptive in nature and dependent upon the sample used. The PBPK model, on the other hand, is not dependent upon the data set for the exact determination of terminal slopes. Thus, its predictive nature, rather than the descriptive nature of the tolerance limit method, provides a strength for the prediction of withdrawal times.

In conclusion, we were able to incorporate probabilistic modeling into a PBPK model using Monte Carlo sampling and then successfully use the model to predict the tissue kinetics of sulfamethazine in swine. As a result of this, we believe that the current withdrawal time of 15 days may be inadequate to cover the upper limit of the 95% confidence interval for the 99th percentile of the swine population and should be reevaluated in light of public health concerns over the presence of sulfamethazine residue.