Formation of the Arabidopsis Pentatricopeptide Repeat Family^,

Abstract

In Arabidopsis (Arabidopsis thaliana) the 466 pentatricopeptide repeat (PPR) proteins are putative RNA-binding proteins with essential roles in organelles. Roughly half of the PPR proteins form the plant combinatorial and modular protein (PCMP) subfamily, which is land-plant specific. PCMPs exhibit a large and variable tandem repeat of a standard pattern of three PPR variant motifs. The association or not of this repeat with three non-PPR motifs at their C terminus defines four distinct classes of PCMPs. The highly structured arrangement of these motifs and the similar repartition of these arrangements in the four classes suggest precise relationships between motif organization and substrate specificity. This study is an attempt to reconstruct an evolutionary scenario of the PCMP family. We developed an innovative approach based on comparisons of the proteins at two levels: namely the succession of motifs along the protein and the amino acid sequence of the motifs. It enabled us to infer evolutionary relationships between proteins as well as between the inter- and intraprotein repeats. First, we observed a polarized elongation of the repeat from the C terminus toward the N-terminal region, suggesting local recombinations of motifs. Second, the most N-terminal PPR triple motif proved to evolve under different constraints than the remaining repeat. Altogether, the evidence indicates different evolution for the PPR region and the C-terminal one in PCMPs, which points to distinct functions for these regions. Moreover, local sequence homogeneity observed across PCMP classes may be due to interclass shuffling of motifs, or to deletions/insertions of non-PPR motifs at the C terminus.

The pentatricopeptide repeat (PPR) gene family of 466 genes is one of the largest gene families discovered in the complete sequence of the Arabidopsis (Arabidopsis thaliana) genome (Aubourg et al., 2000; Small and Peeters, 2000). The PPR genes code for PPR proteins (PPRPs) that are putative RNA-binding proteins (Lurin et al., 2004). PPRPs are characterized by the presence, in their amino-terminal region, of repeats of a motif named P. The P motif is a pentatricopeptide motif, i.e. a degenerated polypeptide of 35 amino acids, highly specific to PPRPs. The PPRP family has been divided, on the basis of their motif content and organization, into two subfamilies containing about the same number of members: the PPRP-P and the plant combinatorial and modular proteins (PCMPs; synonym for PLS proteins).

At the time of its discovery in 2000, the PPR family was completely orphan of function, but a number of members of this gene family recently received an increasing interest from different laboratories. Some PPRPs are involved in plant development (Cushing et al., 2005; Prasad et al., 2005), others are restorers of cytoplasmic male sterilities (Bentolila et al., 2002; Brown et al., 2003; Desloire et al., 2003; Koizuka et al., 2003; Akagi et al., 2004; Oguchi et al., 2004; Klein et al., 2005; Schmitz-Linneweber et al., 2005), and many have essential roles in mitochondria and chloroplasts (Meierhoff et al., 2003; Nakamura et al., 2003; Williams and Barkan, 2003; Lurin et al., 2004; Yamazaki et al., 2004; Gothandam et al., 2005; Schmitz-Linneweber et al., 2005). Recently, one PPRP has been shown to be involved in RNA editing in chloroplasts (Kotera et al., 2005).

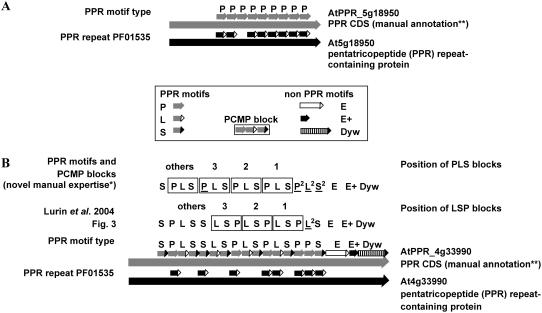
The description of the unusually complex motif organization of PPRPs is progressively improving. The different motif organizations of Arabidopsis PPRPs are summarized in Table I. Figure 1 gives a brief history of the structural annotation of this complex family and shows gene models and different representations of the motif organizations provided by different approaches for one PPRP-P and one PCMP. In the PPRP-P subfamily, the P motifs are usually adjacent to each other, i.e. in tandem repeats. The modular organization in PCMPs is more complex than in PPRP-Ps, but it nonetheless follows a small number of systematic rules (Aubourg et al., 2000; Lurin et al., 2004). First, in the amino-terminal region, the P motifs are not adjacent as in PPRP-Ps, but they are usually separated by two different motifs named L and S. The L and S motifs are related to the P motif both in size and in sequence. Thus below, P, L, and S will be collectively designed as PPR motifs. In PCMPs, PPR motifs are often present in an ordered association of the three motifs, P, L, and S, constituting the standard PCMP block. Furthermore, the PCMP block is usually present in tandem repeats containing up to seven copies. Derived from the standard PCMP block, there are different variants due to internal tandem repeats of S. In brief, in the Arabidopsis genome, there are 198 PCMPs containing almost 600 PCMP blocks of triple motifs and 2,700 PPR individual motifs. Second, in PCMPs, the amino-terminal region containing the tandem repeat of PCMP blocks is usually associated to a carboxy-terminal region characterized by one to three non-PPR motifs named E, E⁺, and Dyw. Thus, the carboxy terminus of PCMPs is either a PPR motif, an E motif, an EE⁺, or an EE⁺Dyw sequence of motifs.

Table I.

A synthetic representation of the PPRP family in Arabidopsis

The PPRP-P subfamily is characterized by tandem repeats of the P motif, i.e. a degenerated polypeptide of 35 amino acids. The PCMP subfamily is characterized by tandem repeats of the PLS block, i.e. an ordered association of the motifs P, L, and S. The PCMP subfamily is subdivided into four classes containing three groups each. Hyphens separate the different parts of the PCMP: (1) the amino terminus often made of an incomplete PLS block, (2) the PLS block repeat region, (3) the P²L²S² block, and (4) the three conserved non-PPR motifs E, E⁺, and Dyw. Classes are defined by the nature of the non-PPR motifs at the carboxy terminus. Each class is divided in three groups based on the motif present at the amino terminus of the protein. Groups are shown only for class H, but are present in all classes. Variable numbers of repeats are indicated by the letters l, m, n, and k; l is between 2 and at least 26 (Lurin et al., 2004), m between 1 and 5, k between 1 and 10, and n between 1 and 7.

Subfamily	Sequence of Motifs				Class	Group
		1	2	3			4
PCMP	L(S)k-	[PL(S)m]n-	P2L2S2-	EE+Dyw	H	a
	(S)k-	[PL(S)m]n-	P2L2S2-	EE+Dyw	H	b
		[PL(S)m]n-	P2L2S2-	EE+Dyw	H	c
		[PL(S)m]n-	P2L2S2-	EE+	F
		[PL(S)m]n-	P2L2S2-	E	E
		[PL(S)m]n-	P2L2S2-		A
PPRP-P		(P)l

Figure 1.

Protein motifs and motif block organization in PPRPs. The gene models and protein structures, redrawn from FLAGdb++ (http://urgv.evry.inra.fr/FLAGdb), are shown for a representative of each subfamily, a PPRP in A and a PCMP in B. The black arrows at the bottom of the two figures represent the TIGR (http://www.tigr.org/) gene model and it is associated with the PPR repeat tagged by the PFAM motif PF01535 (Bateman et al., 2004). The manual annotations of PPR CDS and the associated organization of the PPR motifs come from the Small's Laboratory (URGV, Evry, France). In B, the organization of the PPR motifs from novel manual expertise has been obtained in the course of this work and the motif organization of the 198 PCMPs of Arabidopsis is given in Supplemental Table VII. Differences between annotations are underlined. Note that P motifs are more similar to the PF01535 motif than L and S. Two kinds of tandem repeats are shown: (1) the PPR motif repeat, i.e. a tandem repeat of P motifs in PPRPs, and (2) the PCMP block repeat highlighted by black borders in B, top line. PCMP blocks are either PLS, LSP, SPL, or PL²S (=P²L²S²) blocks.

The characterization of the proteins of a given family often relies on the detection of regions of their sequences shared by all family members. Computing the consensus of such regions provides a motif that is used to recognize new members of the family (Servant et al., 2002). Among the various representations of motifs, hidden Markov models (HMMs) prove to be the most sensitive. The construction of HMMs for several PPR motifs is at the basis of the discovery of the PCMP's modular organization (Aubourg et al., 2000).

A peculiarity of PCMPs is that they may also be considered as a specific sequence of a variable number of PPR motifs, P, L, or S, and of PCMP blocks, either PLS, LSP, or SPL, associated or not with three different kinds of non-PPR motifs. The motif sequence of a given PCMP, at the level of the organization of both the PPR motifs and the PCMP blocks, has been shaped during evolution by a succession of duplication and functionalization events. Selection pressure was clearly critical on the motif sequence as evidenced by the unusually high constraint on the motif pattern in spite of the important increase in both the number of genes and the number of motifs. Furthermore, despite the high number of PCMP block repeats into the whole genome, the PCMP blocks are absolutely specific to the PCMP family.

It is evident that the interest for the function of PPRPs has only started. The complex and highly structured arrangement of PCMP motifs suggests precise relationships between the organization of motifs and protein substrate specificity. This prompted us to undertake an exhaustive study of the organization of PCMP blocks over the whole PCMP family and to investigate how this family has developed. The number of different PCMPs (198) and PCMP blocks (about 600) is both a challenge and a chance. One difficulty is to carry out an expert, and thus time-consuming annotation of the whole PCMP family including the characterization of all the motifs. This annotation involved many manual steps and was based on the structural annotation of PCMP genes available at GeneFarm (Aubourg et al., 2005). Traditional approaches to uncover the evolution of a protein family involve a multiple alignment of the amino acid sequences, followed by the reconstruction of a gene tree from the alignment. Large families are generally difficult to analyze in this way but alternatives exist. For instance, using comparisons of the entire sequence and a whole-protein-based hierarchical clustering approach it has been possible to cluster 1,100 protein kinases from both yeast (Saccharomyces cerevisiae) and Arabidopsis (Wang et al., 2003). Unfortunately, PCMP protein sequences are not amenable to alignment by nature (Thompson et al., 1999) and thus to homology-based phylograms, because of the level of sequence divergence and the wide range of protein sizes due to the numerous tandem repeats described above. Even BLAST comparisons of two PPRPs of the same size give multiple hits between each of the different occurrences of the motif repeats and E-values are drastically lowered. However, the set of motifs is large enough to allow the study of PCMP relationships by comparing the proteins at two levels: the amino acid sequence of the PCMP blocks and the motif sequence. We designed two different methods for these purposes and asked three different questions concerning the mechanisms involved in the formation of the PCMP family. First, we built up evolutionary trees for the PCMP family to evaluate the monophylety of the different PCMP classes. Second, we searched for the elementary PCMP block that might have been duplicated to extend the proteins. Third, we examined the possibility that the elongation of the proteins proceeded either in a preferred direction or by block shuffling. From the results, we infer an evolutionary scenario for the formation of this large, plant specific, and essential gene family.

No doubt that evidence for PCMP functions will be soon provided by experimental data on PCMP targets. In this context, we believe that our study will greatly help the functional investigation of PCMPs. Indeed, there are indications both in chloroplasts (Miyamoto et al., 2004) and in mitochondria (Choury et al., 2004) of a set of proteins involved in the editing of specific recognition sites that adopt distinct spatial configurations. A possible CRP1, a PPRP-P recognition motif, has been identified by a RNA immunoprecipitation and microarray analysis (Schmitz-Linneweber et al., 2005). Indeed, the elucidation of the recognition mechanism needs comparative approaches on sequences of both the target RNAs and the corresponding trans-acting proteins.

RESULTS

Overview of the PCMP Blocks in PCMPs

Up to recently, two different terminologies have been used to describe the modular organization of PPRPs depending on the fusion of PPRP-Ps and PCMPs into one (Small and Peeters, 2000) or two distinct families (Aubourg et al., 2000). A first convergence has been done recently (Lurin et al., 2004). We now propose a unified terminology for PCMPs (Fig. 1). This novel terminology takes into consideration results discussed in this report and thus a better definition of homologous relationships between the different PPR motifs. In their amino-terminal end, PCMPs exhibit a tandem repeat of a block of motifs, with the more represented block being PLS (or LSP, or SPL, which is equivalent in a tandem repeat). This repeat is denoted [PL(S)_m]_n-P²L²S² in Table I. This points out that the S motif happens to be itself repeated in tandem inside some blocks (hence a block may contain more than three motifs) and that the last block, P²L²S², while being homologous to the PLS block, differs in sequence. Indeed, the L² motif has previously been discriminated from other L motifs using a HMM (Lurin et al., 2004). Likewise, we show below that the P² motif is a distinct variant of the P motif. Although we did not test whether the S² motif is a divergent and paralogous copy of the S motif, our data suggest it is, and we propose to name the most carboxy-terminal PCMP block P²L²S² to point out this divergence. PCMP proteins may further be separated into four classes, A, E, F, and H, on the basis of the nature of their carboxy-terminal region (Table I). This region is either a P²L²S² block in class A, a P²L²S²E motif sequence in class E, a P²L²S²EE⁺ in class F, or a P²L²S²EE⁺Dyw sequence of motifs in class H. The number of proteins containing a Dyw motif is similar in Arabidopsis and Oryza sativa: 88 and 87, respectively. In Arabidopsis, there is one protein with a Dyw motif but without PLS block. Even if the block pattern is easy to recognize in any PCMP, it is often disturbed by local repeats of the S motif and by incomplete blocks at the amino terminus. In 78 PCMP proteins at least one block is altered by tandem repeats of the S motif. Furthermore, tandem repeats containing two to 10 copies of the S motif are observed at the amino terminus of 23 PCMPs. Conversely, tandem repeats of P or of L do not occur in PCMPs, while P repeats are the major component of PPRP-Ps.

On average, PCMPs have 3.8 PCMP blocks made of L, S, and P motifs and slightly more than half of the PCMPs have either three or four PLS blocks, not accounting for the P²L²S² block present in each protein. Supplemental Table I gives the repartition of the number of tandem repetitions of PLS blocks in both the all-PCMP (198 proteins) and the nonredundant (nr)-PCMP (109 proteins) sequence databases of PCMPs. In the aggregate, the two sequence databases are similar and the repartition of the number of block repeats (maximum at 3–4) is the same in the different classes. Thus, globally, the diversification of the PCMP family in four classes is not correlated to a clustering of different protein structures between the four classes. Nevertheless, there is one intriguing exception in class H with one protein structure made of three PCMP blocks that is observed in 11 proteins.

Evolutionary Trees for the PCMP Family

Trees from Block Sequences

To recover an evolutionary scenario for the PCMP family, we designed an innovative approach that considers the proteins at the level where most important events are detectable: i.e. not at the amino acid level, but at the level of the sequence of motifs and blocks. The data is the nr set of proteins encoded as motif sequences; these sequences were obtained from the reannotation of the PCMP family (Aubourg et al., 2005). Our strategy involves two steps. The first step is the pairwise comparison of all block sequences with an alignment procedure devised for tandem repeats, MS_Align (Bérard and Rivals, 2003). MS_Align was adapted to account for both S motif and triplet amplifications/contractions (i.e. events S <-> SS and LSP <-> LSPLSP). As it already considers single-letter insertions or deletions, all motif-related events are taken into account in the alignment. The search for the optimal alignment depends on the cost parameters attributed to each type of event. The all-against-all sequence comparison yields a distance matrix in which an entry gives the distance between any two PCMPs. The second step is an evolutionary tree reconstruction with a distance-based method derived from the Neighbor-Joining algorithm (Desper and Gascuel, 2002). To evaluate the quality of the resulting tree, we computed treeness indicators of the original alignment distances, as well as confidence values of internal branches (Guénoche and Garreta, 2000) and repeated the whole protocol for 126 sets of alignment parameter values. This allows us to explore the parameter space of the approach, to evaluate its robustness, and to choose the best evolutionary tree with respect to mathematical criteria.

Supplemental Table II gives the values of five treeness criteria (Guénoche and Garreta, 2000) of the trees obtained with 126 combinations of alignment parameters. The first four criteria behave quite similarly so we look solely at the variance accounted for (VAF) and at the fifth criteria, the rate of well designed elementary quadruples (Re). The Re for an internal edge is the percentage of quadruples that support that edge; thus, it is a confidence value for that edge. The tree Re is its average over all internal edges. Among the trees having the best VAF value (0.99) and the highest Re, we choose the best ones according to the other criteria. The two best trees are for parameters Am = 1, Ip = 8, Ab = 3, and In = 50, and Am = 1, Ip = 10, Ab = 3, and In = 50, and have a VAF of 0.99 (VAF is a value in [0,1]) and a Re value of 0.64 (with the maximum observed being 0.65). A VAF of 0.99 is typical of trees recovered from good classical phylogenetic data (with noise distortion below 5%), and which do not suffer from the long branch attraction problem (Guénoche and Garreta, 2000).

An Optimal Tree and the Relationships between PCMP Classes

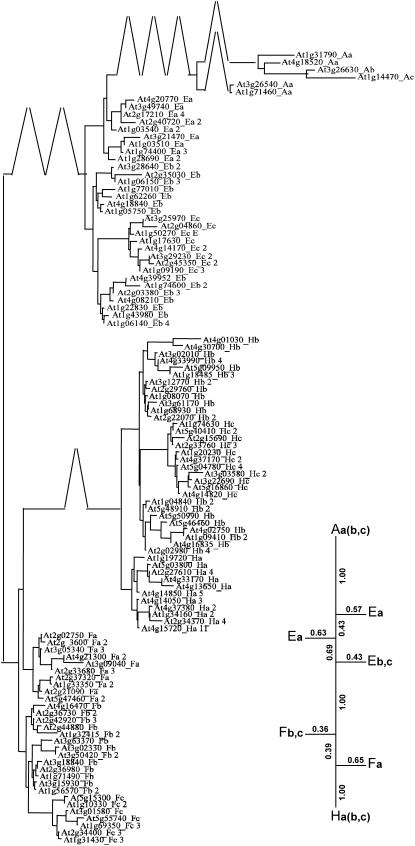
The most reliable tree (parameters Am = 1, Ip = 8, Ab = 3, and In = 50) is shown in Figure 2. First, classes A and H are monophyletic, i.e. the lowest common ancestor of all proteins in such a class is not an ancestor of any protein not in that class. A contrario, classes E and F are not monophyletic. Indeed, classes E and F are split in three and two subtrees respectively, and class F branches out between two E subtrees, while class H branches out between two F subtrees. The proteins from different classes are not mixed together in the tree. However, the support Re varies among the internal edges leading to the classes: A|EFH, AEF|H, as well as AE|FH have a confidence value equal to 1 (i.e. maximal), showing that the monophyleties of A and of H are well supported. For both classes E and F, the edge leading to one of their subgroups is less supported by the data: Fa (0.65), Fbc (0.36), Ea (0.69), and Ebc (0.43). Indeed, the edges that split F in two are short and not well supported while the edge leading to H is perfectly supported. Another feature is that the subtree of each class is further split according to the N-terminal block of the proteins. This block may be incomplete, and if one reads LSP blocks in the motif sequence the first block is (LS)_k in group a, (S)_k in group b, and (PLS)_k in group c (Table I), with k larger than or equal to 1. In the subtree of each class, c is monophyletic and branches out between two group b subtrees. In classes H and F, group a is monophyletic. Moreover, group a is in general the nearest group to the neighbor class, suggesting that its proteins may more likely change their class by losing some non-PPR motifs at their C terminus. This structure may be explained by the relatively high frequency of two events that alter preferentially the N-terminal block: motif loss and S motif tandem duplication.

Figure 2.

An evolutionary tree of the PCMP family based on the nr-PCMP set of proteins (branches scale: 20 units per cm). It is the best tree inferred from the matrix of distances between block sequences of the proteins according to the treeness criteria defined by (Guénoche and Garreta, 2000). The treeness criteria VAF equals 0.99 for the whole tree (see Supplemental Fig. 1 for comparison with trees obtained from different alignment parameters). The schematic representation appearing in the lower part of the Figure displays only the innermost branches that separate the PCMP classes A, E, F, and H, as well as the confidence values of those branches. Clearly, classes A and H are monophyletic (Re value of 1), while classes F and E are split in two and three subtrees. Indeed, the subtree of class H branches out between the two subtrees of class F, and class A subtree separates two subtrees of class E (group a). The split AE|FH is also supported by a maximal confidence value (Re of 1). In the complete tree, some branches are compressed to fit in the page. One observes that the subtrees corresponding to each class are organized similarly: they distinguish the groups as defined in Table I. The AGI-ID is followed, first by a capital letter indicating the PCMP-class, then by a lowercase letter for the PCMP group, and then by a figure giving the number of PCMP genes coding for proteins with the same block sequence.

Several trees computed with different parameter values have VAF and Re values similar to that of the optimal trees. To see whether the PCMP evolution looks different in a suboptimal tree we compare the optimal tree with the tree computed for parameters Am = 1, Ip = 6, Ab = 3, and In = 50, whose VAF and Re values equal 0.99 and 0.63, respectively (Supplemental Fig. 1). The differences between the two trees are at the lower level of the trees. The group subtrees are modified as well as the repartition of the proteins between the two group b subtrees of each PCMP class. The picture of the evolution of PCMP classes and the relative positions of the groups inside these PCMP classes remain exactly the same.

Similarity between Amino Acid Sequences in the Set of PCMP Blocks

In a relatively large range of evolutionary distances between organisms, the level of similarity of amino acid sequences between orthologs is generally higher than between paralogs. This observation is exploited, for instance, in the database of clusters of orthologous genes (Tatusov et al., 2003). Evolution of the PCMP family involved both duplications of genes and internal tandem duplications of blocks. These events affect differently the distribution of the distances between amino acid sequences of blocks and their relationships. We thus face a complex situation for which we need to define a block relationship. We may proceed by analogy with definitions for duplicated genes. Under the assumption of a functional role associated to block positions, blocks at the same position in duplicated genes may be called orthologs. Therefore, after gene duplication blocks at the same position in the resulting genes should be more similar than two blocks in one gene. On the other hand, internal block duplications create paralogous blocks. However, the consequence on the sequence similarity between two blocks depends on the mechanism of block addition. These mechanisms might be of two kinds. First, internal tandem duplications create adjacent blocks that are more similar than more distant blocks. Second, shuffling of blocks between independent genes disturbs paralogous and orthologous relationships between blocks. Both mechanisms of block addition might have operated during evolution. Nevertheless, the unusually high level of conservation of the structural organization of PCMPs (Table I) suggests that the very intense amplification and diversification of the family should have involved only a small number of mechanisms under the control of high functional constraints. We thus expected that current proteins might exhibit some related footprints left by these mechanisms.

By looking at the similarity of the amino acid sequences of blocks, we attempt to determine: (1) at which positions in the tandem array, blocks show paralogous or orthologous relationships as defined above, (2) if the array was extended in a preferential direction, i.e. toward the N or the C terminus and, (3) if extension depended on a preferential phase for block addition (PLS or LSP). For this sake, we searched in the whole set of blocks for homogeneous groups according to sequence similarity, i.e. for groups of blocks that are more similar to each other than to blocks not in the group. We performed this analysis starting either with blocks from the same class of proteins or with blocks located at the same position in the tandem array of proteins from different classes. As previously explained, classical techniques for amino acid sequence comparison are not adapted to PCMPs; we thus develop an approach based on HMMs and on a graphical display of their results (for details see “Materials and Methods”).

Amino Acid Distances and Alternate Forms of the PCMP Block

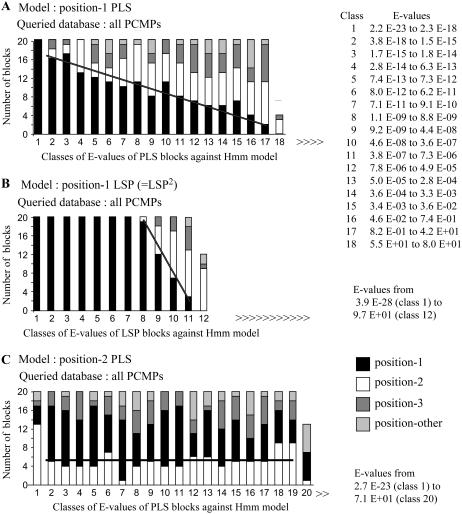
Depending on the reading phase, the most frequent PCMP block may be read either PLS, LSP, or SPL. We first asked the question of which one of these PCMP blocks has been duplicated during the formation of the PCMPs. Thus, a HMM has been built up with 20 sequences of PLS or LSP blocks located at the most carboxy side of the PCMP block repeat region (region two in Table I) of 20 proteins, i.e. at position 1 (Fig. 1B). At this step we based our determination of the positions of the blocks in the proteins on the fact that the most carboxy-terminal PCMP block (PL²S, line “Lurin et al. 2004 Fig. 3” in Fig. 1B) contains a variant of the L motif, L², that differs in sequence and occurs only once in each protein (Lurin et al., 2004). We distinguished the PCMP blocks containing L² from the standard PLS blocks and excluded them from the experiments corresponding to Figure 3 and 4. The HMMs obtained were, respectively, named the position-1 PLS and the position-1 LSP models. The position-1 PLS model has then been used to search the all-PCMP sequence database (see “Material and Methods”) and 344 PLS blocks (17 columns of 20 blocks + 1 column with 4) out of the 557 possible PLS blocks (62%) were found to be similar to the HMM (Fig. 3A). The result of a search using the position-1 LSP model is different since, in this case, similarity was only found with 232 LSP blocks (11 columns of 20 blocks + 1 column with 12) out of the 560 possible LSP blocks (41%; Fig. 3B). The latter difference can only be explained by the nature of the HMMs that were built from the same LS motifs but from a different P motif. Indeed, the P of the position-1 LSP block is the one of the PL²S blocks, while the P of the position-1 PLS is the P motif of a standard PLS block. The difference of similarity between the HMM model and PCMP blocks is due to the contribution of the P motif of the position-1 LSP block. Thus, this peculiar P motif should be considered as a variant of the P motif and will be called P² from now on. Similarly, to better mark the difference of the position-1 PCMP block we renamed it P²L²S² (line “PPR motifs and PCMP blocks-novel manual expertise” in Fig. 1), even if we do not have an argument for S² as a variant of S. The all-PCMP sequence database searched with the HMMs contains 198 LSP² blocks among which 181 are found to be similar to the LSP² model and 159 sequence block comparisons have E-values lower than 7.7E-11. It is only when the E-value increases above this level that we also observe similarity with only 51 standard LSP blocks.

Figure 3.

Sequence similarity between PLS or LSP² in the sequence database containing all the PCMPs. HMMs have been built up with 20 amino acid block sequences from either position-1 PLS (A), position-1 LSP (= LSP²; B), or position-2 PLS (C). The PLS block at position 1 is the first PLS block on the N-terminal side of the P²L²S² (or PL²S) block in the proteins (Table I; Fig. 1). The PLS block at position 2 is the next one toward the N terminus of the protein and so on for position 3 and others. Hmmsearch output, sorted by increasing E-value, has been organized in classes of 20 PCMP blocks as shown for A in the insert at the top right corner. E-value classes, illustrated by a bar, are ordered along the abscissa by increasing E-values. The E-value class of rank 1 (E-value class 1), contains the 20 PCMP blocks showing the highest similarity with the HMM and the similarity decreases with increased E-value class ranks. For other sequence comparisons, in B and C, only the highest and lowest E-values are given. Different patterns in bars indicate the numbers of PCMP blocks that are located at different protein positions: black for blocks at position 1, white for blocks at position 2, dark gray for blocks at position 3, and light gray for those at other positions. The number of blocks at the bottom of each bar (or E-value classes) is always for the blocks belonging to the same category as the 20 blocks used to build up the HMM. A regression line has been calculated for the number of these blocks. The line has been forced to horizontal when the slope was not significant. The stronger the slope the higher is the similarity of blocks belonging to the same category as the 20 blocks used for building the HMM (A) or the distance with blocks of other categories (B).

Figure 4.

Sequence similarity between position-1 PLS blocks from the three different classes of PCMP: H, F, and E. HMMs have been built up with amino acid sequences of 20 blocks from position 1 in one of the three different classes of PCMPs and used to search for similarity in the sequence database containing all the PCMPs. The protocol is as in Figure 3 but the HMMs were built up with sequences of PCMP blocks either from PCMP class H (A), class F (B), or class E (C). For more details on the representation of the results, see the legend of Figure 3.

Hence, the LSP² model has a high similarity with most of the LSP² blocks and a comparatively low similarity with most of the LSP blocks. These results confirm that the P²L²S² block and the PLS block have a common ancestor that has been duplicated, and provided two blocks that diverged significantly to generate P²L²S² and PLS. As all PCMPs have only one P²L²S² and at least one PLS block, this very first duplication probably took place before the advent of the family, i.e. in an ancestral protein common to all PCMPs. Since many PCMPs have more than one PLS, the homology between P²L²S² and PLS suggests an extension of the protein from its carboxy end toward its amino-terminal region. The protein extended first by a duplication of an ancestral PCMP block followed by successive additions of PLS blocks either by recruitment from ectopic loci or by tandem duplication. We further try to discriminate between these two nonexclusive hypotheses by looking at the similarity between blocks at the same position in different proteins or adjacent in the same protein.

For each analysis we retrieved two different information: first, the total number of PCMP blocks that was found similar to a given HMM and, second, the slope of the regression line for the number of blocks belonging to the same category. An instance of category is the set of blocks occupying the same position into different proteins, than the 20 blocks used to build up the HMM. The combination of these two results gives an indication of the similarity between the blocks in the category of the HMM and the blocks from other categories. There is a negative correlation between the numbers of position-1 PLS blocks similar to the position-1 PLS model per group of 20 blocks (columns in Fig. 3A) and the E-values of the sequence comparison (Fig. 3A, inset in the top right corner). For instance, in column 2 of Figure 3A, the E-value goes from 3.8 E-18 to 1.5 E-15 and 16 out of 20 PLS blocks are at position 1 into proteins, while in column 17, the E-value is from 8.2 E-01 to 4.2 E+01 and only two PLS blocks are at position 1 in their respective proteins. The equation of the regression line is −0.82x +17.1 (R² = 0.90), with a significance lower than 10⁻³ for both the slope and the origin. We repeated the above experiment three times, with each time a position-1 PLS model built up with 20 different blocks sampled independently from the all-PCMP sequence database. The three experiments gave similar equations and confidence levels: 0.90x + 17.9 (R² = 0.85); 0.97x + 18.7 (R² = 0.82); and 1.05x +18.7 (R² = 0.83). Therefore, a HMM model built up with a sample of 20 PLS blocks can be representative of the whole set of 557 PLS blocks. To estimate the sequence similarity between position-1 PLS blocks and PLS blocks at a position other than position 1 in proteins, we accumulated the data from the four repetitions to work on higher numbers in each E-value class (results in Supplemental Table III). There is a positive correlation between the relative numbers of PLS blocks located at positions 2, 3, or others in the proteins and the E-values. The slopes are equal to 1.42, 1.57, and 0.70 for position 2, 3, and others, respectively, with a significance better than 10⁻³ for the first two and better than 10⁻² for the last one. For comparison, in this cumulative experiment, the slope for position-1 PLS blocks is −3.70. Thus, the PLS model built up with a representative set of position-1 PLS blocks has an affinity for PLS blocks that decreases from position 1, in the carboxy terminus of the proteins, to position 3 and above, toward the amino terminus.

The result obtained with the complete set of PCMPs cannot be explained by a bias introduced by the redundancy of block sequences. Indeed, a similar result was obtained when the experiment was carried out with the nr-PCMP sequence database and a position-1 PLS matrix (result in Supplemental Table IV) even if the numbers of proteins and blocks are twice less. The equation of the regression line is −1.65x + 18.6 (R² = 0.80) and the significances are better than 10⁻² for the slope and than 10⁻³ for the origin. This latter experimental verification is well in accordance with the direct characterization of redundancy in the four PCMP classes (Supplemental Table I). Indeed, the pattern of redundancy is quite similar in PCMP classes E, F, and H.

Results shown in Figure 3C using a HMM model built up with 20 sequences of PLS position-2 blocks are clearly different from those shown in Figure 3A using a model built up with 20 sequences of PLS position-1 blocks. In Figure 3C there is neither a significant negative correlation between the number of position-2 PLSs and the E-values nor between PLSs at other positions. Moreover, the total number of PLS blocks similar to the PLS position-2 model, 395 (Fig. 3C, 19 columns with 20 blocks + column 20 with 15 blocks), is remarkably higher than with the position-1 model 344 (Fig. 3A). As before, we repeated the experiments three times and all gave results similar to those in Fig. 3C. In the experiment shown in Fig. 3C, there are only 18 position-2 blocks in the two first columns (E-values from 2.7 E-23–7.9 E-15). For 11 of the 18 proteins that contain these position-2 PLS blocks, the position-1 block is in the first five columns while the expected value of the repartition was by chance only 0.967, i.e. more than 10 times less. Thus, PLS blocks at position 2 may be more similar to the blocks surrounding them in a given protein (paralogous blocks in one protein) than to blocks at the same position in other proteins (orthologous blocks in duplicated genes).

Collectively these results suggest three major trends in the formation of the PCMP family. First, the PCMP blocks that have been duplicated from an ancestral block are of the PLS kind rather than LSP. Second, a significant part of the block duplication events might have involved tandem duplication more often than block recruitment from different chromosome loci. Third, a substantial part of the tandem duplications have added PLS blocks at the amino-terminal region of proteins.

PLS Amino Acid Distances and PCMP Classes

Gene duplications have been very frequent during the formation of the family and we observe four classes of proteins defined by the presence of non-PPR motifs at the carboxy terminus of the proteins (Table I). The results described in the previous paragraph suggest that the evolution of the carboxy- and the amino-terminal regions may have been independent. This is in favor of more than one generation of ancestral proteins for the four classes during the formation of the family, rather than an early formation of the classes from four different ancestors. This is a testable hypothesis using the three protein classes containing a large number of members, the class E, F, and H. In the case of an early formation of the PCMP classes from one or a small number of ancestors, a HMM built up with sequences of 20 PLS blocks from one class of PCMP should be more similar to sequences of PLS blocks from this PCMP class than to sequences of PLS blocks from the two other PCMP classes. We expect an opposite result in the case of a continuous generation of the PCMP classes by independent events of deletion/insertion of non-PPR motifs.

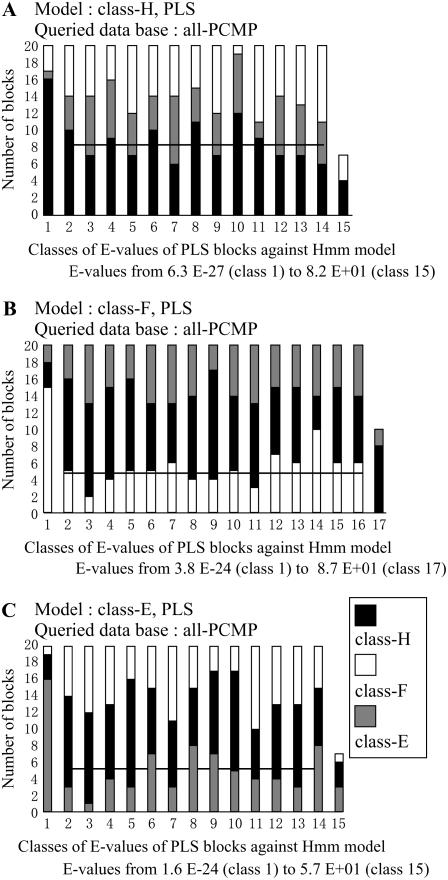
The number of PLS blocks belonging to different PCMP classes (E, F, and H) and found similar to a class-specific HMM is not changing with the E-value class, i.e. whatever the E-value we observed an equivalent number of PLS blocks belonging to each PCMP (Fig. 4, A–C). The best horizontal line that may be computed through the E-value classes is at a number of blocks roughly proportional to the number of blocks in each PCMP class (54 E, 51 F, and 87 H). Our data show that the distribution of pair distances between amino acid sequences of PLS blocks in one PCMP class or between the three PCMP classes is similar. In other words, the PLS blocks of one PCMP class are not more similar in sequence to PLS blocks belonging to proteins in the same class than to PLS blocks from proteins belonging to the two other classes of PCMPs. It is interesting to highlight that the HMM obtained with a sample of 20 sequences of PLS blocks from class-F proteins (Fig. 3B) recovers a higher number of blocks than both the HMMs built up with 20 PLS blocks belonging to PCMP class H or E. This result is best explained by an oriented flux of gene transformation either from genes coding for proteins of class H toward proteins of class-E through class-F proteins, or the opposite. It suggests also that the evolution of the PLS tandem region and of the carboxy region containing the non-PPR motifs has been, to a large extent, independent. Indeed, non-PPR blocks have been either inserted or deleted independently of the events of gene duplication and of elongation by tandem duplication of PLS blocks of the amino-terminal region.

P²L²S² Amino Acid Distances and PCMP Classes

The next question concerns the direction of the gene flux observed between the three PCMP classes. Similar to the non-PPR motifs, the P²L²S² blocks have undergone a different evolutionary history from the other PCMP blocks. Indeed, even if the homology with the PLS block is clear, the P²L²S² blocks do not appear in tandem in these proteins. Hence, P²L²S² blocks are good candidates to investigate the direction of gene duplication between PCMP-H, -F, and -E, and to ask the question about the relative importance of intraclass duplications during the formation of the extant PCMP family. The sequences of the P²L²S² block are less divergent than the PLS block ones and present in only one copy at a conserved position adjacent to the non-PPR motifs thought to form the active site of the protein. All these data are consistent with a higher functional pressure on P²L²S² than PLS blocks. The sequence similarity between two P²L²S² blocks might thus be a better indicator of the divergence time since the ancestral gene duplication than the distances between PLS blocks.

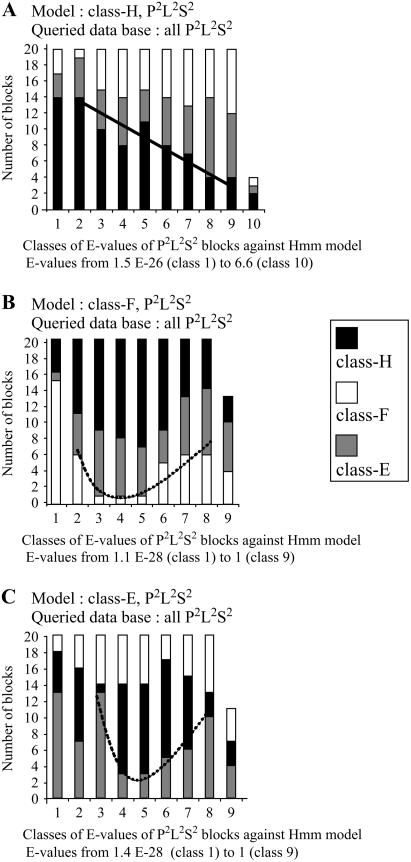
Thus, we analyzed the similarity between the amino acid sequences of P²L²S² blocks using HMMs built up with 20 sequences from either class-H, -F, or -E proteins (Fig. 5). The three class-specific HMMs output 184, 173, and 171 P²L²S² blocks out of 198, for classes -H, -F, and -E, respectively. The results obtained with P²L²S² HMMs differ completely from those obtained with PLS position-1 HMMs (Fig. 4). With the P²L²S² model from class H, the number of P²L²S² blocks belonging to class H in a E-value class is correlated negatively with the E-value (Fig. 5A). Thus, the P²L²S² blocks exhibit a large range of decreasing similarity with the HMM, and contrary to PLS blocks at position 1 (Fig. 4A), P²L²S² blocks from class-H proteins are globally more similar between them than to P²L²S² from classes E and F (Fig. 5A).

Figure 5.

Sequence similarity between P²L²S² blocks of PCMPs. HMMs have been built up with 20 sequences of P²L²S² blocks from either PCMP class H (A), class F (B), or class E and used to search for similarity in the sequence database containing only the P²L²S² blocks from all the PCMPs. For more details on the representation of the results, see the legend of Figure 3.

The results obtained with the two other HMMs built up with P²L²S² sequences either from PCMP-F (Fig. 5B) or -E (Fig. 5C) proteins are different from those described above with PLS from the same PCMP class (Fig. 4, B and C) and also different from those with PCMP-H HMMs for P²L²S² (Fig. 5A). Both with PCMP-F (Fig. 5B) and -E HMMs (Fig. 5C) we observed a minimum of blocks similar to the class model at intermediate E-values, i.e. at intermediate similarity between P²L²S² blocks and the model. Thus, opposite to what we observed with the PCMP-H model (Fig. 5A), the distributions of pairwise distances between P²L²S² sequences are not homogeneously organized in PCMP-E and -F. Rather they are clustered by the HMMs in three distinct groups. A HMM built up from 20 sequences has first a high similarity with a limited group of sequences: the sequences used to build up the model and some other sequences probably generated by intraclass gene duplications. This is what we observed in the first two or three columns in PCMP-F (Fig. 5B) and -E (Fig. 5C), respectively. Second, at intermediate E-values, a PCMP class-specific HMM is similar to a second group of P²L²S² blocks that mainly belongs to proteins of other PCMP classes and particularly to PCMP-H. Third, at higher E-values, i.e. lower similarity, a PCMP class-specific HMM is similar to an increasing number of P²L²S² blocks from the PCMP class used to build up the HMM. The second and third groups contain P²L²S² blocks that may not share a direct common ancestor with the sequences used for the HMM. Rather, they might derive from proteins that changed in PCMP class after gene duplication. Two PCMP-F or -E genes may be generated by a duplication of a PCMP-Hs followed by non-PPR motif deletions. The number of events necessary to pass from class H to class E should in mean be higher, deletions of two non-PPR motifs, than to pass from class H to class F, only a deletion of the Dyw motif. Thus, the mean time since duplication of the PCMP-H ancestor and, as a consequence, the sequence similarity, should be lower between P²L²S² blocks inside of PCMP-F and PCMP-E than between them and P²L²S² blocks of some PCMP-H. At the opposite in genes generated by intraclass duplications, P²L²S² should be more similar between them than they should be to P²L²S² in proteins either of the same class (-F or -E), but generated by a duplication of a PCMP-H gene followed by non-PPR motif deletions or to P²L²S² from PCMP-H. Consistent with this hypothesis, the minimum of sequences for proteins of the same group as the protein used to build up the HMM is displaced more toward the high E-values for PCMP-E (Fig. 5B) than for PCMP-H (Fig. 5C). Thus, collectively these results may be explained by a preeminent and oriented flux of gene duplications from the PCMP-H proteins toward the PCMP-E through the PCMP-F and a somehow less important contribution of intraclass duplications.

DISCUSSION

Methodological Improvements

Numerous proteins, often members of large families, contain tandem repeats. In such protein families, the number of copies of the motif usually varies among members of the family and makes these proteins difficult to align (Thompson et al., 1999; Bahr et al., 2001), as in the case of PCMPs. Therefore, classical phylogenetic reconstruction methods that require a multiple alignment yield poorly supported trees on such data. With such approaches, the solution usually employed is to restrict the alignment to the nonrepeated part of the sequences. Since the tandem repeat often represents a long region of the protein, the size of the aligned parts may then limit the amount of evolutionary signal available for tree reconstruction, and using this solution, one disregards the evolution of the repeated part of the proteins. Here, we propose an innovative approach based on comparisons of the proteins at two levels: the succession of motifs along the protein, which we term the motif sequence, and at the amino acid sequence of the different motifs. The level of the amino acid sequences is used twice: first, to infer the motifs, and thus to determine the motif sequence of each protein, this was already mostly completed for PCMPs (Lurin et al., 2004), and second, to infer evolutionary relationships between the repeated motifs. A phylogenetic analysis with mucin and VWD tandem repeats of the zonadhesin family (Hunt et al., 2005) indicated relationships between tandem repeat domains at identical positions in homologous proteins from fish to humans. In our study, at the motif sequence level, all parts of the proteins are taken into account, both through the motifs themselves and through their succession, and all events of duplications are detectable. An alignment procedure of motif sequences accounting for duplications (Bérard and Rivals, 2003) yields pairwise distances between proteins. These distances serve then as data to reconstruct an evolutionary tree for the family. For PCMPs, this approach enabled us to recover trees that are well supported by the data and prove to be robust to the variation of alignment parameters. Moreover, it allowed gathering evidence on the elongation of the tandem repeat, suggesting a scenario for the formation of the family and the nature of the ancestral protein.

Evolution of the Family

The tree obtained from the motif sequences (Fig. 2) supports the clustering of PCMPs in four classes. Indeed, it provides evidence for the monophylety of classes A and H and is in favor of separated origins of classes E and F. The search results of the HMM built with P²L²S² motifs, the only part of the sequence that is common to all PCMPs, showed that the interclass divergence is higher than the intraclass divergence and agrees with the tree results. For PCMP-E and -F, the results suggest that these two classes do not originate from a single ancestor gene, but rather from a few ones.

Concerning the PLS tandem repeat (excepting P²L²S²), our results suggest that the block that preferentially underwent duplication is PLS rather than LSP. Searches performed with the most N-terminal blocks (data not shown) and with the PLS blocks in position 1 also gave weight to a preferred direction, from the most C-terminal block toward the most N-terminal block, in the elongation of the tandem repeat. The distinct behavior of the HMMs built from any PLS block or from P²L²S² blocks reveals that the PPR motifs that composed them are homologous but different. We can thus infer that a common ancestor of PCMPs contained at least a PLS block and a P²L²S² block, and that these blocks probably resulted from the duplication of an ancestral PLS block. Moreover, the results from HMMs built with PLS blocks from different classes gives a blurred view of the class relationships, as if the PLS repeat was a region that underwent interclass homogenization. Homogenization of sequences may be the effect either of an interclass shuffling of blocks or of deletions/insertions into the carboxy-terminal region resulting in a change of class for a given protein. The second hypothesis is better supported by the results shown in Figure 4 as well as by the interclass similarity in both the redundancy of block structures and the repartition of the number of blocks (Supplemental Table I).

Evolution and Function

The PCMP family in Arabidopsis and in O. sativa accounts for 198 and 229 members. Although the advent of the family predated the separation between mono- and dicotyledon plants, the conservation of the number of proteins is surprising. On one hand, the amino acid sequences of PLS blocks are highly divergent. But on the other hand, the three largest PCMP classes (E, F, and H) exhibit a similar redundancy, as well as an overall homogeneity in the composition of their PLS repeat, indicating an evolutionary constraint. Altogether, the results suggest that the PLS repeat existed before the separation between mono- and dicotyledons and has evolved since then under a functional selection pressure. This mode of evolution seems to differ from the one of the C-terminal region, which we think begins with the P²L²S² block (included). This partition in two regions having a distinct evolution, and the diversity of PLS repeats observed throughout the family lead to the belief that the PLS repeat could serve as a RNA-binding domain in which the succession of motifs encodes the information needed for specific recognition of a given binding partner (Lurin et al., 2004). In the C-terminal region, the conservation of the relationships between the PCMP classes is in favor of a catalytic function for this region. The proteins of class A lack non-PPR motifs but might nonetheless be functional. The protein EE⁺Dyw (gene At1g47560) or the three genes without complete PLS blocks upstream to the P²L²S² one (At2g25520, At2g34370, and At4g32450) might be recruited for the catalytic function, and thus complement functionally proteins lacking all or part of this carboxy-terminal region.

Scenario and Mechanisms

The gene family coding for PPRPs expanded vastly during the evolution of the land plants. A recent estimation using FLAGdb++ (Samson et al., 2004) indicates that there are 268 and 260 PPRP-Ps and 198 and 229 PCMPs, respectively, in the Arabidopsis (The Institute for Genomic Research [TIGR] R5.0) and O. sativa (TIGR R3.0) genomes. While PPRP-Ps are present in both animal and fungi proteomes PCMPs are found only in land plants (Aubourg et al., 2000), including the basal moss Physcomitrella patens (Hattori et al., 2004). Thus, the formation of the PCMP subfamily postdated the apparition of PPRP-Ps, but predated the separation of mono- and dicotyledon plants. We propose the following scenario for the formation of the PCMP family (see Fig. 6). The probable ancestor of the PPR family has been formed by a duplication of P motifs. In one gene, three successive P motifs accumulate mutations to generate the ancestor of the PLS and P²L²S² blocks, this ancestral block is then duplicated in tandem and the offspring blocks evolve into a PLS block and a P²L²S² block. Further block duplications create a PLS repeat. Before the advent of land plants, a fusion with an ancestor of the EE⁺Dyw protein yields the ancestor of the PCMP family, which is the first member of class H. The ancestral genes of other PCMP classes are created by duplications and some independent events of loss of motif at the C terminus. Thus, a gene of class H gives rise to a gene of class F, a gene of class F to a gene of class E, and so on. In each class, further gene duplications as well as block and S motif tandem duplications occur under functional constraints to produce the observed classes and the diversity in PLS repeat. Our proposition to place the H class at the root of the evolution is supported both by the existence of a gene that codes only for the EE⁺Dyw motifs and by the results presented in Figure 5.

Figure 6.

A scenario for the advent of the PCMP family. An ancestral protein containing both a PLS and a P²L²S² block (eventually belonging to class A) is fused with another protein containing the EE⁺Dyw block of non-PPR motifs. Then, the other classes appear each by subsequent losses of a C-terminal motif. In class H (ending with a Dyw motif), F (ending with a E⁺ motif), and E (ending with a E motif) the number of proteins increases by gene duplication, and the tandem array of PLS blocks in each protein varies in length through events of tandem amplification or contraction.

CONCLUSION

Several features of the PCMPs help to figure out the mechanisms involved in the evolution of the family. The paucity of introns in PCMPs as compared to the mean number of introns in Arabidopsis genes suggests that this family expanded mainly by reverse transcription events promoting duplicate dispersal through the genome (Lecharny et al., 2003). In the genome of Arabidopsis, despite their large number, PCMP genes are rarely clustered in tandems and therefore, recombination events between recently (not too divergent) duplicate motifs, either in the same gene or in recently reverse transcribed genes, have been probably lessened. One of the most attractive hypotheses for PCMP block duplication is the involvement of local microrecombinations as previously suggested for the formation of a gene coding for a maize (Zea mays) membrane protein, TM20, made of 20 hydrophobic domains that can be grouped in five homologous classes of four domains (Stiefel et al., 1999). For PCMPs as for membrane polypeptides, physicochemical properties or secondary structures are the direct object of selection rather than the amino acid sequence stricto sensu and, even in the exceptionally favorable case of TM20, the sequence divergence between different repeats largely obscured the evolutionary relationships between them. Moreover, the high level of sequence divergence between PCMP blocks seems to rule out frequent conversion between blocks.

Our approach may be relevant for other families of proteins with repeated motifs (Patthy, 2003). The Arabidopsis genome contains 1,316 proteins including the 446 PPRPs, annotated with repeat in their keywords on gene function. For instance, there are 111 proteins containing repeats of the Kelch motif often associated to a F-box domain, 202 WD repeat-containing proteins, and 315 proteins with Leu-rich repeats frequently associated to a protein kinase domain. Others cases are armadillo (61) and ankyrin (75) containing proteins. In some of these families, the region containing the repeats is a large part of the proteins. Interestingly as for PPRs, most of the genes with repeated domains are less frequently interrupted by introns than other genes. This suggests the existence of general constraints acting on the formation of the protein repeat region. One may envisage two alternative hypothetical mechanisms: either one involving reverse transcription of mRNAs as previously suggested for PCMPs (Lecharny et al., 2003) or one based on negative selection on insertion of introns. Thus, the approach experimented here could help to shed light on the formation of families of repeat-containing proteins, and more widely on the principles that govern the evolution of these families.

MATERIALS AND METHODS

Data Sets, Motif Sequence, and Classes

In this study, we used the whole Arabidopsis (Arabidopsis thaliana) family as annotated in GeneFarm (Aubourg et al., 2000, 2005): 198 PCMPs. We named this set the all-PCMP sequence database. Several PPR- (P, L, S, and L²) and non-PPR motifs (E, E⁺, and Dyw) have been defined based on the sequence similarity between regions of the PCMP amino acid sequences. These motifs were located twice independently in the proteins using different tools: MEME (Grundy et al., 1997) and HMMER (Eddy, 1998). We systematically solved inconsistancies in the motif annotation by a manual expertise. The motif occurrences are adjacent in the amino acid sequences; thus, we define the motif sequence of a protein as the succession of motifs read from the N toward the C terminus. For example, to protein At3g61170 corresponds the motif sequence SSSSPLSSPLSPLSPL²SEE⁺Dyw.

In all PCMPs, the C-terminal region is a succession of non-PPR motifs. Depending on this region, PCMPs were divided into four classes: H, F, E, and A (see “Results” section “Overview of PCMP Blocks” for details; Supplemental Table I). The repartition of PCMPs is: 87 in class H, 51 in class F, 54 in class E, and six in class A. In GeneFarm classes F and E are fused in a unique class F. The correspondence between GeneFarm and Arabidopsis Genome Initiative identifications (AGI-IDs) is shown in Supplemental Table IV.

Some PCMPs share the same motif sequence. As we used these sequences to compare the proteins, we excluded this redundancy and built up a nr set, the nr-PCMP sequence database, which contains 109 proteins. A protein or motif sequence identifier in the nr-PCMP set is made of the protein AGI-ID concatenated with a label indicating its class followed by its group (i.e. At4g16470_Fb for a class-F protein of group b). Supplemental Table V gives the list of nr-PCMP proteins, the motif sequences, and the associated proteins that share the same motif sequence but are not in nr-PCMP.

Block Sequences

The N-terminal part of all PCMP proteins is a tandem repeat of a block of PPR motifs. The most represented block is the triple LSP, and all other internal blocks are of the form L(S)_nP with n > 1. Note that in a tandem repeat, which has a cyclic structure, LSP, SPL, or PLS are equivalent. The most N-terminal block is a suffix of a L(S)_nP block. To code the block sequence, we consider arbitrarily a block to start with a L motif (or with the protein N terminus), and to end with the beginning of the next L or L² motif. We encoded each different block observed in the all-PCMP set, as well as each non-PPR motif, by a single letter (block letter code in Supplemental Table VI). We then recoded the motif sequence of each protein as a sequence of block letters. This defines the block sequence. As the block code is univoque, the block sequence of a protein is strictly equivalent to its motif sequence. We used the block sequences to perform adequate protein comparisons as described below.

Evolutionary Model and PCMP Comparisons Based on Block Sequence

We computed a mutation cost between any pairs of blocks. Any block can be transformed into any other block by insertion or loss of one or two PPR motifs (e.g. LSP <-> SP) and by tandem duplication of the S motif (e.g. LSP <-> LSSP). For example, the block LSP can be transformed in LSSSSP by three S motif duplications, while LSP can be obtained from the N-terminal block SSP by a S motif contraction and the insertion of a motif L. We denote by Am (for amplification of motif) the cost of an S motif amplification/contraction (the word amplification is used as a synonym for duplication), and by Ip the cost of a PPR motif insertion/deletion. The mutation costs were calculated for different values of the ratio Am/Ip; with Am = 1 and Ip = 10, 12, 15, 20, or 30. The rationale is that an insertion of a motif is less probable than a duplication/contraction. For fixed costs (e.g. Am = 1 and Ip = 12), the mutation costs are stored in a matrix (all matrices are given in Supplemental Table VI) as amino acid substitution costs are recorded in a PAM matrix for classical alignment.

We compare pairwise the block sequences of the 109 nr-PCMPs using an alignment method, MS_Align (Bérard and Rivals, 2003), originally conceived for aligning minisatellite alleles in the evolution of which amplification and contraction events play a major role. Here, MS_Align takes into account block mutations, but also block amplifications (cost denoted Ab, e.g. LSP<-> LSPLSP) as well as non-PPR motif insertion/deletion (cost denoted In; e.g. LSPL²S <-> LSPL²SE). MS_Align is a method that computes an alignment of optimal cost. The result of a complete comparison is a quadratic matrix, D, containing the distance between any two proteins. Performing the comparisons this way, first preprocessing the block mutation costs and then using MS_Align to compare the block sequences, enables us to account in a single distance measure for all important mutational events at the motif sequence level: single PPR motif duplication, insertion or loss, block duplication/contraction, as well as non-PPR motif insertion/loss.

Comparisons were performed using several parameter sets, all combinations of the following parameters: Am = 1; Ip = 10, 12, 15, 20, or 30; Ab = 3, 4, 5, or 6; and In= 12, 15, 20, 30, 40, or 50. Our evolutionary model is symmetrical: The costs of dual events are identical; for instance, a deletion cost equals an insertion cost. The choice of parameter values reflects several facts about the motifs that form PCMPs. First, amplifications/contractions of the S motif and of PCMP blocks have been frequent events, since their numbers vary greatly among the PCMPs. Thus, we give lower costs to these events (Am = 1; Ab = 3, 4, 5, or 6) as compared to insertion/deletion costs. Second, as non-PPR motifs are not homologous to any other motifs, we forbid such motif mutations by giving them an infinite cost. The parameter values of different experiments depart from each other notably in the ratio Am/Ip and in the difference (In − Ip), which was kept positive. Also, a PPR motif insertion (Ip) costs less than a non-PPR motif insertion (In), since it seems plausible that the former could be obtained by amplification of any other PPR motif and subsequent mutations in the amino acid sequence, while the latter could only be acquired by insertion.

Evolutionary Tree Reconstruction and Reliability

An important issue concerns the reliability of the approach. Is it sound to measure the evolution with the alignment procedure used in our approach? Or in other words, can those distances be reliably represented by a tree? In a valuated tree, the distance between any two nodes is a tree distance, i.e. it satisfies the four points condition (Buneman, 1974). The tree reconstruction program computes the tree distance from the alignment distance such that it fits a tree structure, but the resulting tree distance may differ from the alignment distance. If the difference is too large, a tree is not an appropriate model for the original distance. The criteria used below evaluate the difference between these distances.

Precisely, we use the alignment distance matrix D to feed a distance-based phylogenetic reconstruction program, FastMe, which implements an improved neighbor-joining algorithm (Desper and Gascuel, 2002). To infer an evolutionary tree for the proteins, FastMe computes implicitly for each protein pair (i,j) a tree distance, T(i,j). The goal is to optimize T(i,j) such that it is as near as possible to D(i,j) for all (i,j), and satisfies the constraint of a tree distance, i.e. the so-called four points condition (Buneman, 1974). In the resulting tree, T(i,j) equals the sum of the branches' lengths on the path from leaf i to leaf j. As there is no known way to compute bootstrap values for the nodes of our trees, we compute two quality criteria (Guénoche and Garreta, 2000) to evaluate the trees. These criteria were defined and tested in Guénoche and Garreta (2000), where it is shown that they reliably measure the adequacy of representating a distance D by a tree. The first, called the VAF, measures how close T(i,j) is from D(i,j). Let Dm be the average of the D(i,j); the VAF is defined by:

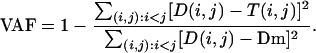It assesses if a tree is a good model to represent D(i,j).The second is a topological criterion called the Re. Consider a subset of four proteins, {i,j,k,l}, and an internal edge of the tree that separates {i,j} from {k,l}. In the tree, the distances between {i,j,k,l} must satisfy the four points condition (Buneman, 1974) given by:

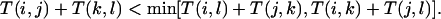The edge e is correct if this condition is also satisfied by the distance D. In this case, one says the quartet {i,j,k,l} supports the edge e. The support value for edge e, denoted R(e), is defined as the average number of quartets that support e. The Re is simply the average value of R(e) over all internal edges. The Re for an internal edge is a confidence value for that edge.

Supplemental Table II gives the values of five treeness criteria (Guénoche and Garreta, 2000) for 126 combinations of alignment parameters. The two best trees are for parameters Am = 1, Ip = 8, Ab = 3, In = 50, and Am = 1, Ip = 10, Ab = 3, In = 50, and have a VAF of 0.99 (VAF is a value in [0,1]) and a Re value of 0.64 (with the maximum observed being 0.65). A VAF of 0.99 is typical of trees recovered from good classical phylogenetic data (with noise distortion below 5%), and which do not suffer from the long branch attraction problem (Guénoche and Garreta, 2000).

On the other hand, a Re value of 0.64 corresponds to trees that do have long external branches and to data that incorporates between 15% and 20% of noise. The Re is a very stringent criteria: with real data, it is usually lower than the VAF (although, its theoretical maximum also is 1), and it seems more dependent to noise and to the presence of long edges. Nevertheless, up to 20% of noise, the inferred tree remains reliable (Guénoche and Garreta, 2000). Both criteria suggest the tree model is adequate for our distance data with many parameter combinations. It is thus reasonable to compare PCMP proteins at the level of their block sequence and to derive an evolutionary tree from the resulting distances. Besides, the smooth variation of the criteria for a wide range of parameter combinations argues in favor of the robustness of our approach. Another evidence in this direction is the fact that the two best trees are identical although their Ip parameter values differ. With this comparison, we can select the combinations of parameters that yields the best tree. Two trends can be seen when the parameters (Ip, Ab, and In) vary. First, the best trees are obtained with middle values of Ip, that is a middle ratio Ip/Am (since Am = 1 always). The average VAF criteria over all parameter combinations with the same Ip value decreases with Ip (as the first four criteria). Second, with fixed values of Ip and Ab, the VAF always increases with In. In fact, it seems that the higher the ratio of In/Ip, the higher the VAF value and the better the tree. So, the parameters combinations Am = 1, Ip = 8, Ab = 3, In = 50, and Am = 1, Ip = 10, Ab = 3, In = 50, which give an optimal VAF value and a nearly optimal Re of 0.64, are in agreement with these two trends.

Classification Based on the Amino Acid Sequence of the PCMP Blocks

A PCMP block is an ordered association of the three PPR motifs, P, L, and S. Depending on the phasing, three different PCMP blocks are encountered, either PLS, LSP, or SPL. Other possible arrangements, as PSL for instance, are not present in PCMPs. Trees derived from multiple alignments of the amino acid sequences of PCMP blocks exhibit low bootstrap values at their nodes (data not shown). As already mentioned, in the data, a large number of short and divergent sequences is inadequate for this type of analysis. To classify the PCMP blocks we designed an alternative approach based on the HMMer package (Eddy, 1998). The class A was excluded from this study because of its small number of genes. We first built HMM models using Hmmbuild, from a multiple sequence alignment of 20 block sequences taken at random. In the sample of 20 blocks, the numbers of blocks from each class, E, F, and H, are proportional to the percentage of genes from that class in the family (5 E, 5 F, and 10 H). The 20 blocks are aligned using ClustalW (Chenna et al., 2003) and the alignment is cured manually. The most conserved region of each of the three motifs P, L, and S, 54 amino acids all together, are then used to build up a HMM model. The HMM profile is used with Hmmsearch to search for significantly similar sequence matches in different PCMP databases. Sequence databases are either the all-PCMP set, the nr-PCMP set, or a subset of the all-PCMP set. The output consists of a ranked list of the best scoring blocks with a HMM E-value between 0 and 100. As we search only PCMPs, it is possible to use a relatively high threshold value. The E-value gives an indication on how a PCMP block into the searched database fits the HMM model derived from our training set of 20 blocks. The result from a given Hmmsearch is organized by increasing E-value, i.e. decreasing similarity, and the list is split in groups of 20 blocks. In figures, groups are ordered from 1 to n along the abscissa, each bar representing a group of 20 blocks. The first group, rank 1, contains the 20 PCMP blocks with the lowest E-values and the last group, the 20 blocks with the highest E-values. Each PCMP block is associated to three pieces of information, the AGI-ID (i.e. At3g50420), the GeneFarm-ID containing the PCMP class of the protein (i.e. F51), and its position into the protein indicated by a cardinal after a hyphen following the GeneFarm-ID (i.e. F51-1). PCMP block positions into the protein are numbered from the most carboxy-terminal PLS block (immediately upstream of the PL²S block) toward the amino terminus. All blocks at a position higher than 3 are considered together in a position called others. Thus, in Figures 3 to 5, for each group of 20 PCMP blocks (illustrated by a full column) in the output of HMMsearch it is possible to know the number of PCMP blocks belonging either to a given PCMP class (E, F, or H) or to a given position in the protein (illustrated by different color pattern). Thus, this data representation delivers two different pieces of information: (1) the total number of PCMP blocks found similar to a given model by Hmmsearch, and (2) the number of PCMP blocks with different levels of similarity to the model and present at different positions in proteins from a given sequence database.

Note that when searching for PLS triple motifs, we can potentially recover all the PLS, even those that are part of a PL(S)_n block, while when seeking for LSP triple motifs, we cannot fetch the L(S)_nP variants. Nevertheless, the total numbers of PL(S)_n and LSP are similar: 553 and 538, respectively. The advantage is to avoid a possible bias due to a higher similarity between S motifs in tandem repeats than between dispersed S. In Figures 3 to 5, regressions were computed with the function lm of R after excluding the first group of PCMP blocks (abscissa 1) that, often, mainly contains the training PCMP blocks, and the last group that does not necessarily contain 20 blocks.