Modeling of Transfer Kinetics at the Serum-Cerebrospinal Fluid Barrier in Rabbits with Experimental Meningitis: Application to Grepafloxacin

Abstract

The goals of the present study were to model the population kinetics of in vivo influx and efflux processes of grepafloxacin at the serum-cerebrospinal fluid (CSF) barrier and to propose a simulation-based approach to optimize the design of dose-finding trials in the meningitis rabbit model. Twenty-nine rabbits with pneumococcal meningitis receiving grepafloxacin at 15 mg/kg of body weight (intravenous administration at 0 h), 30 mg/kg (at 0 h), or 50 mg/kg twice (at 0 and 4 h) were studied. A three-compartment population pharmacokinetic model was fit to the data with the program NONMEM (Nonlinear Mixed Effects Modeling). Passive diffusion clearance (CL_diff) and active efflux clearance (CL_active) are transfer kinetic modeling parameters. Influx clearance is assumed to be equal to CL_diff, and efflux clearance is the sum of CL_diff, CL_active, and bulk flow clearance (CL_bulk). The average influx clearance for the population was 0.0055 ml/min (interindividual variability, 17%). Passive diffusion clearance was greater in rabbits receiving grepafloxacin at 15 mg/kg than in those treated with higher doses (0.0088 versus 0.0034 ml/min). Assuming a CL_bulk of 0.01 ml/min, CL_active was estimated to be 0.017 ml/min (11%), and clearance by total efflux was estimated to be 0.032 ml/min. The population kinetic model allows not only to quantify in vivo efflux and influx mechanisms at the serum-CSF barrier but also to analyze the effects of different dose regimens on transfer kinetic parameters in the rabbit meningitis model. The modeling-based approach also provides a tool for the simulation and prediction of various outcomes in which researchers might be interested, which is of great potential in designing dose-finding trials.

New quinolones have been shown to have enhanced activities against gram-positive bacteria, especially penicillin-resistant pneumococcal strains (3, 7, 19, 20). Grepafloxacin [1-cyclopropyl-6-fluoro-1,4-dihydro-5-methyl-7-(3-methyl-1-piperazinyl)-4-oxo-3-quinoline carboxylic acid hydrochloride], one of these potent broad-spectrum quinolones, has been shown to have high levels of bactericidal activity in the treatment of pneumococcal meningitis (14).

The extent to which a drug is distributed into the cerebrospinal fluid (CSF) depends on the relationship between rates of transport into and out of the CSF (i.e., the influx and efflux clearances) relative to the concentrations driving those rates (15, 20). Furthermore, the transport of drug at the serum-CSF barrier is influenced by the capacity of active influx and/or efflux mechanisms. A full description of these transport mechanisms at the serum-CSF barrier requires a parametric (usually compartmental) model (15).

The animal model most widely used to study serum-CSF pharmacokinetics in experimental meningitis is the rabbit meningitis model (11, 18, 25), since it allows sequential in vivo sampling of serum and CSF for measurement of drug concentrations at the same time. The goals of this study are threefold: first, to develop a multicompartment model to describe in vivo transport mechanisms at the serum-CSF barrier in rabbits with experimental meningitis; second, to analyze the effects of different dose regimens on transfer kinetic parameters such as passive diffusion clearance and active efflux clearance; and third, to propose a simulation-based approach to optimize the design of dose-finding trials (27) in experimental meningitis models.

MATERIALS AND METHODS

Rabbit model.

This paper presents a new analysis of data for 29 young New Zealand rabbits (weight, 2 to 2.5 kg) reported by Gerber et al. (14). An inoculum containing 10⁵ CFU of a penicillin-resistant pneumococcus of serotype 6 was injected into the cisterna magna. Antibiotic therapy was started 14 h after inoculation in the following dose regimens: (i) 15 mg/kg of body weight at 0 h, (ii) 30 mg/kg at 0 h, and (iii) 50 mg/kg at 0 and 4 h. Grepafloxacin was administered as a bolus through an ear vein.

Measurements of grepafloxacin concentrations.

A catheter was placed in the femoral artery for periodic withdrawal of plasma samples, and a spinal needle was inserted into the cisterna magna for collection of CSF samples. Plasma samples for measurement of grepafloxacin concentrations were collected at 0, 0.25, 0.5, 1, 1.5, 2, 4, 6, and 8 h for single-dose therapy. If the antibiotic was administered twice, additional plasma samples were drawn at 4.25, 4.5, and 5 h. In parallel, CSF samples for measurement of grepafloxacin concentrations were collected at 0, 0.75, 2.5, 4, 6, and 8 h. At 8 h all animals were killed by intravenous injection of an overdose of pentobarbital.

Analytical procedures.

Grepafloxacin concentrations in CSF were measured by an agar diffusion bioassay with antibiotic medium 11 (Difco Laboratories, Detroit, Mich.). Bacillus subtilis ATCC 6633 was used as the test strain for all measurements (28). Standard curves were generated in saline with 5% rabbit plasma for measurement of the antibiotic concentrations in CSF, in order to mimic the CSF protein concentration in meningitis.

Population kinetic model.

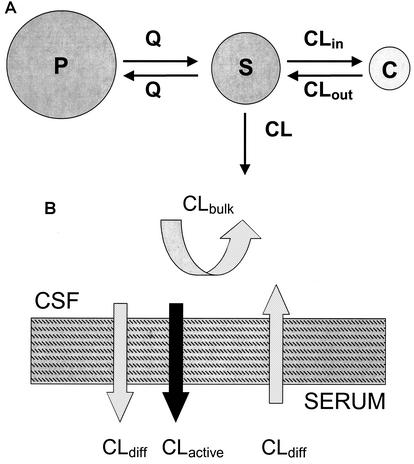
A zero-order input (bolus injection), first-order elimination, three-compartment model was used to describe the time course of serum and CSF drug concentrations. Both the second (peripheral) and the third (CSF) compartments were linked to the central (serum) compartment (Fig. 1A). The relevant differential equations defining the population kinetic model are given in the Appendix. CSF influx and efflux transport processes such as passive transcellular clearance and active efflux clearance were modeled (Fig. 1B; also see the Appendix). Influx clearance was assumed to be equal to passive diffusion clearance; and efflux clearance is the sum of diffusion clearance, active efflux clearance, and bulk flow clearance. Clearance from CSF by drug metabolism is assumed to be negligible (20).

FIG. 1.

(A) Population kinetic three-compartment model. S, central compartment (serum); P, peripheral compartment; C, CSF compartment; Q, intercompartmental clearance between the central and peripheral compartments; CL, total clearance; CL_in, total CSF influx clearance; CL_out, total CSF efflux clearance. (B) Transfer kinetic processes at the serum-CSF barrier. CL_diff, clearance by passive transcellular diffusion; CL_active, clearance by active efflux; CL_bulk, clearance by CSF bulk flow.

Fitting of population kinetic model.

The population kinetic model was fit to all serum and CSF grepafloxacin concentrations measured for all 29 rabbits with the computer program NONMEM (Nonlinear Mixed Effects Modeling; NONMEM Project Group, University of California, San Francisco) (4, 5). The output of NONMEM when it is used to fit a population model consists, among other things, of the value of the objective function at convergence (approximately minus twice the maximized log likelihood of the data). This can be used to test the merit of a more complex model (a larger model with more parameters) over a less complex submodel (6). Descriptive statistical analyses were performed with the software package Splus 5 for UNIX (MathSoft, Inc., Seattle, Wash.). The t test was applied as appropriate. Details of the population kinetic model and the hierarchical statistical model are given in the Appendix.

Simulation for dose-concentration relationship.

The CSF grepafloxacin concentration-versus-time profile at given doses was simulated as follows: for each dose, 400 rabbits were simulated from the model, with fixed effect parameters drawn from their approximate posterior distribution given the data. Two hundred replications of such simulations were performed to obtain a 90% certainty interval around the concentration-versus-time curve at a given dose.

Simulation for dose-AUC_CSF/MIC relationship.

It has been shown that achievement of a certain level of the area under the concentration-time curve (AUC) for grepafloxacin in CSF (AUC_CSF) versus the MIC is a key to therapeutic success. To show how the model can be used to simulate the ratio, we did the following: for each dose, 400 rabbits were simulated from the model, with fixed effect parameters drawn from their approximate posterior distribution given the data. The ratios of the AUC_CSF for grepafloxacin versus the MIC were obtained. Two hundred replications of such simulations were performed to obtain a 90% certainty interval around the ratio-versus-dose curve.

RESULTS

Kinetic parameter estimates.

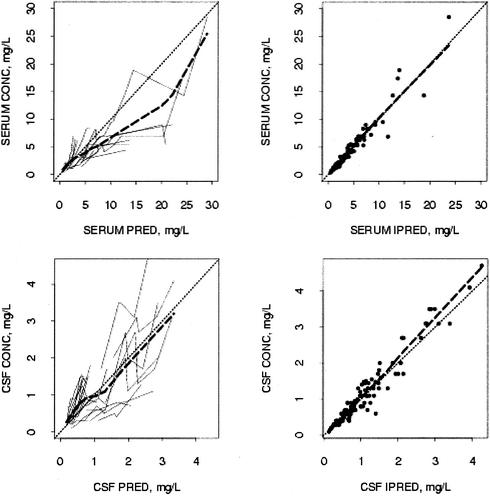
The three-compartment population kinetic model fit the data well. Figure 2 shows the goodness of fit of the model to the data for grepafloxacin. Table 1 presents the estimates of the population parameters. The estimated standard deviations of the residual unexplained errors were 17% for grepafloxacin measurements in serum and 23% for grepafloxacin measurements in CSF.

FIG. 2.

Goodness-of-fit plots of the three-compartment pharmacokinetic model for grepafloxacin. (Upper panels) Measured concentrations in serum versus predictions for the population (PRED) and predictions for individuals (IPRED). (Lower panels) Measured concentrations in CSF versus predictions for the population and predictions for individuals. Each fine solid line in the left panels represents one animal. Fine dashed lines, lines of identity; heavy dashed lines, smoothed curves for the measured concentrations versus the predictions for the population and predictions for individuals, as illustrated in the corresponding plot.

TABLE 1.

Population kinetic parameters for grepafloxacin in serum and CSF

Parameter	Mean	% CVa
Kinetic parameters
Central volume of distribution (ml)	230	21
Peripheral volume of distribution (ml)	3,900	4.7
Intercompartmental clearance between central and peripheral compartments (ml/min)	31.7
Total clearance (ml/min)	22.4	11
CSF-serum barrier transfer parameters
Influx clearance (ml/min)	0.0055	17
Active efflux clearance (ml/min)	0.017	11
Clearance by bulk flow (ml/min)	0.01b
Efflux clearance (ml/min)	0.032
CSF/serum partition coefficient (%)c	16.9

^aCV, coefficient of variation (interindividual variability).

^bClearance by bulk flow, set to a physiological value (16).

^cPC, calculated as the ratio of influx clearance/efflux clearance, where influx clearance is equal to passive diffusion clearance.

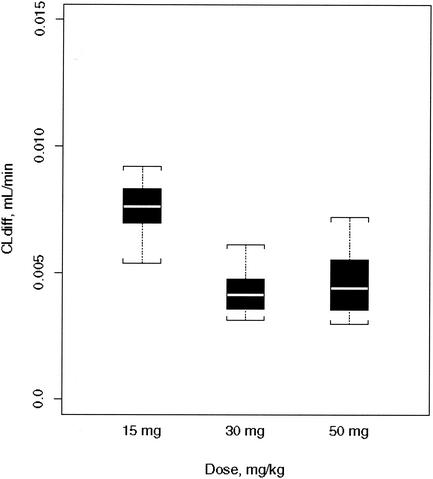
The average influx clearance is larger in rabbits given 15 mg of grepafloxacin per kg than in those given higher doses (0.0088 versus 0.0034 ml/min; P < 0.01) (Fig. 3). Allowing the inclusion of a group effect on the influx clearance (see the Appendix for details) improved the model (change in the value of the objective function [Δobj], −19). Efflux clearance (in excess of influx clearance, i.e., the sum of active efflux clearance and bulk flow clearance) was not different between rabbits treated with 15 mg of grepafloxacin per kg and those treated with higher doses. Inclusion of a group effect on efflux clearance (in excess of influx clearance) did not improve the model.

FIG. 3.

Passive transcellular diffusion clearance (CL_diff) for different intravenous grepafloxacin dose regimens (15 mg/kg once, 30 mg/kg once, and 50 mg/kg twice). Boxes delimit the interquartile range R (third quartile to first quartile); whiskers indicate 1.5R.

Dose-concentration relationship (based on simulations).

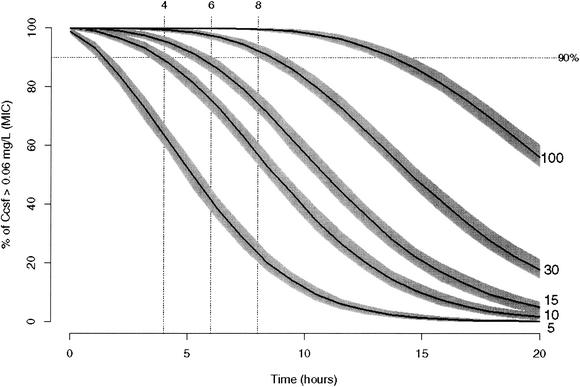
Figure 4 shows the fraction of simulated rabbits with a CSF grepafloxacin concentration greater than 0.06 mg/liter for different dose-versus-time profiles. If a concentration in the CSF of 90% of rabbits at, e.g., 4 or 8 h of >0.06 mg/liter (the MIC in CSF) is the dosing goal, it can be achieved by giving a dose of ≥10 or 30 mg/kg, respectively. The shaded areas in Fig. 4 reflect 90% certainty intervals for estimates of the relationship depicted by the curves. The lower (upper) border of the polygon is determined pointwise as the 5th (95th) percentile of 200 simulations of the fraction of concentrations in CSF that exceed the MIC for 400 simulated rabbits.

FIG. 4.

Percentage of fraction of CSF grepafloxacin concentrations greater than 0.06 mg/liter versus time as a function of dose for 400 simulated rabbits. Solid lines, profiles when the indicated dose is given; shaded areas around solid lines, 90% certainty intervals for the curves (see text); dotted line, 90% probability of having a CSF grepafloxacin concentration greater than the MIC.

Dose-AUC_CSF/MIC ratio relationship (based on simulations).

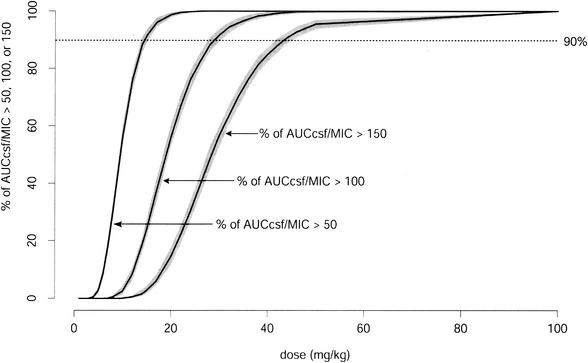
Figure 5 shows the fraction of simulated rabbits for which the AUC_CSF/MIC ratio is higher than 50, 100, or 150 at different doses. If a ratio above 100 for 90% of rabbits is the dosing goal, a single dose of 40 mg/kg is sufficient. The shaded areas in Fig. 5 reflect 90% certainty intervals for estimates of the relationship depicted by the curve. The lower (upper) border of the polygon is determined pointwise as the 5th (95th) percentile of 200 simulations of the fraction of AUC_CSF/MIC ratios that exceeds 50, 100, and 150 for 400 simulated rabbits, as illustrated in Fig. 5.

FIG. 5.

Percentage of AUC_CSF/MIC ratios higher than 50, 100, or 150 at different doses for 400 simulated rabbits. Solid lines, profiles when the indicated dose is given; shaded areas around solid lines, 90% certainty intervals for the curves (see text); dotted line, 90% probability of having the ratio greater than 50, 100, or 150.

DISCUSSION

This study presents a new multicompartment model describing in vivo influx and efflux processes at the serum-CSF barrier in rabbits with pneumococcal meningitis. The model differs from previous population kinetic models in that not only the partition coefficient but also passive diffusion and active transport mechanisms at the serum-CSF barrier for different dose regimens are estimated (1, 32). Given the fitted model, simulations are used to estimate features of the dose-CSF concentration relationship (see below).

We found a high volume of distribution in the peripheral (tissue) compartment. This is consistent with previous studies (8, 13, 31) and predictions based on the high lipophilicity of the drug. The average partition coefficient is close to the value obtained by descriptive analysis (16.9 versus 16.0%) (14). In a previous study, Karol et al. (16) applied the diffusion and flow model with unidirectional efflux (17) to analyze the concentration in CSF-versus-time profiles of ofloxacin in rabbits. The blood-CSF diffusion clearance and the efflux clearance of ofloxacin were estimated to be 0.0058 and 0.0337 ml/min, respectively, which are close to the values for grepafloxacin obtained with the population kinetic model (0.0055 and 0.032 ml/min, respectively; Table 1).

The estimate of efflux clearance in excess of influx clearance explains the relatively low concentrations of the drug in CSF compared to the high concentrations in other peripheral compartments (20). The estimated difference between population average efflux and influx clearances is larger than the previously described clearance by CSF bulk flow (0.027 versus 0.01 ml/min) (17, 22, 30). This can be explained by the existence of an active efflux mechanism at the serum-CSF barrier. It has been shown that an active transport system for quinolones (located in the choroid plexus) transports fluoroquinolones from the CSF to the circulation (21). One may argue that the bulk flow clearance may be increased in rabbits with meningitis. However, the CSF production rate is reduced by meningitis (24), as inflammation can diminish the efficiency of the choroid plexus pump. Thus, bulk flow clearance in rabbits with experimental meningitis is less rather than more than that in healthy animals. Furthermore, the relatively low partition coefficient of grepafloxacin compared to those of other new quinolones (i.e., BMS 284756; partition coefficient, 44% [10]) indicates active efflux.

Interestingly, the average influx clearance was higher in rabbits given grepafloxacin at 15 mg/kg than in those given higher doses (0.0088 versus 0.0034 ml/min; P < 0.01), and inclusion of a group effect on the influx clearance improved the model. We cannot explain this finding at present. If active efflux is saturated at higher doses, influx clearance should increase, not decrease. Similarly, saturable protein binding at higher doses should increase and not decrease influx clearance. However, perhaps those rabbits given the lowest grepafloxacin dose developed a more pronounced inflammation of the serum-CSF barrier than those given higher doses, which might have resulted in an increased passive diffusion clearance at the serum-CSF barrier (12, 29). If increased inflammation at the lower dose increases average influx clearance, one could expect a decreased efflux clearance (in excess of the influx clearance), as inflammation can reduce bulk flow clearance (see above). In our analysis, however, we did not find a difference in efflux clearance (in excess of influx clearance) in rabbits treated with grepafloxacin at 15 mg/kg compared to the efflux clearance in those treated with higher doses.

A mechanistic modeling-based approach allows not only to study the effects of different dose regimens on transport mechanisms at the serum-CSF barrier but also to analyze of the effect of P glycoprotein at the serum-CSF barrier (9, 26) or the effects of drugs (e.g., methylprednisolone [21]) on transfer kinetic parameters. It permits the prediction of transfer kinetics at the serum-CSF barrier in humans from rabbit data, given appropriate scaling. As demonstrated in Fig. 4, simulations based on a mechanistic model allow to describe dose-concentration in CSF relationships for any dose regimen. As an example, if the desired target concentration in CSF for a study is 0.06 mg/liter (MIC) at 6 h in 90% of the study subjects, a grepafloxacin dose of 15 mg/kg is required (Fig. 4). This may be helpful in the design of pharmacokinetic studies in rabbits with experimental meningitis. One could also create nomograms for doses required to achieve a desired drug exposure after a given dose regimen by using the same model. Other investigators (2, 23) have shown that the AUC_CSF/MIC ratio at 24 h is a predictor of bacterial killing in vivo. If the same criterion is to be used in rabbits with experimental meningitis, the model can predict the dose required to achieve a given pharmacodynamic breakpoint (i.e., an AUC_CSF/MIC ratio of 100 at 24 h) (Fig. 5). Indeed, the model-based approach is a useful, cost-effective tool providing insight into various outcomes, in lieu of resource-intensive in vivo experiments.

Appendix

Pharmacokinetic three-compartment model.

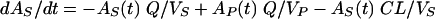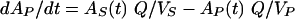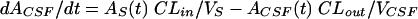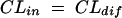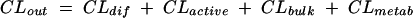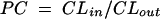where A_S(t) is the amount of drug in the central compartment (serum) at any time t, A_CSF(t) is the amount of drug in the CSF compartment at any time t, V_S is the volume of distribution in the central compartment (in liters), V_P is the volume of distribution in the peripheral compartment (in liters), V_CSF is the volume of distribution in CSF (in liters), CL is the body clearance (in milliliters per hour), Q is the intercompartmental clearance between the central and peripheral compartments (in liters per hour), CL_in is the total clearance from the central compartment to the CSF compartment (in milliliters per minute), CL_diff is the passive transcellular diffusion clearance (i.e., active clearance influx is absent), CL_out is the total clearance from the CSF to the central compartment (in milliliters per minute); CL_active is the efflux clearance from the CSF to the central compartment via active transport systems; CL_bulk is the clearance by CSF bulk flow and is set to a physiological value of 0.01 ml/min (17), CL_metab is the clearance by drug metabolism in the CSF and is assumed to be negligible (20), and PC is the CSF/serum partition coefficient. The initial condition at time for A_S is the initial dose (bolus injection, 15 mg/kg).

Hierarchical statistical model.

The hierarchical statistical model expressed generically is

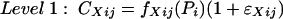where C_Xij is the concentration of grepafloxacin in compartment X (serum or CSF) observed at the jth scheduled time point during the study in the ith individual; f_Xij is a model for the expectation of C_Xij, conditional on P_i, a vector of kinetic parameters for grepafloxacin for the ith individual; and ɛ_Xij is an identically and independently normally distributed random error with mean zero and standard deviation σ_X.

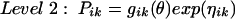where P_ik is the kth element of P_i, g_ik is a model for its (log) expectation, and η_ik is a normally distributed mean zero random effect. The vector θ consists of population parameters such as the volume of distribution in the central compartment, body clearance, passive transcellular diffusion clearance, and efflux clearance from the CSF to the central compartment via active transport systems.

Group effect on passive transcellular diffusion clearance.

A group effect (GE) on passive transcellular diffusion clearance is modeled as

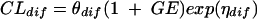if the dose is less than or equal to 15 mg/kg or as

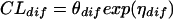if the dose is higher than 15 mg/kg, where θ_diff is the population passive transcellular diffusion clearance, and η_diff is the interindividual variance of passive transcellular diffusion clearance.